Abstract
The 4d transition metal ruthenium pyrochlore Dy2Ru2O7(s) was synthesized by solid state reaction route. High temperature studies on the ternary oxide Dy2Ru2O7(s) an important ferroelectric and magnetic material, has been carried out using solid-state electrochemical cell, with calcia stabilized zirconia electrolyte and the reversible electromotive force were measured. The Gibbs energy of formation of Dy2Ru2O7(s) from elements in their standard state, is:
The standard molar heat capacity C˚p,m(T) of Dy2Ru2O7(s), measured using a differential scanning calorimeter run in the heat flux mode as a function of temperature. The values fitted to a polynomial expression can be represented by:
Stability of Dy2Ru2O7(s) and high temperature thermodynamic functions of this transition metal pyrochlore were determined for the first time, an important fundamental study.
Similar content being viewed by others
1 Introduction
Pyrochlores with the general structural formula A2B2O7, wherein A is a trivalent rare earth ion and B is 3d, 4d or 5d transition metal ion, have evoked a lot of interest amongst researchers for their varied applications such as in “rad-waste matrices” [1], as catalysts [2], in oxygen evolution reactions [3] and thermal barrier coatings [4]. Pyrochlores also show interesting electronic and magnetic properties [5, 6]. Pyrochlores are good refractory materials, possess chemical durability and have structural flexibility and are able to incorporate trivalent lanthanides and tetravalent actinides, hence the acronym rad-waste matices [1, 7]. Catalytic properties of A2Ru2O7 were explored by Ashcroft and co-workers and used for the selective oxidation of methane to synthesis gas [2]. Pyrochlore electrocatalysts have been proposed by Parrondo et al. [8] for efficient alkaline water electrolysis. Recently the high performance pyrochlore type Y2Ru2O7(s) was proposed as an electrocatalysts for oxygen evolution reaction in acidic medium by Kim et al. [3]. La2Zr2O7(s) pyrochlore was proposed for thermal barrier coatings and its thermal stability was studied by annealing and thermal cycling by Cao et al. [4].
The electronic properties of the pyrochlore oxides wherein the transition metal is ruthenium(IV), range from Pauli paramagnets to semiconductors [5, 9]. Xu et al. [10] observed ferroelectricity in the double pyrochlore Dy2Ru2O7. Soderholm and Greedan investigated the magnetic properties of Ln2V2O7(s) (Ln = rare earth) pyrochlores and concluded that they were ferromagnetic semiconductors [11]. Nature of spin freezing transition of geometrically frustrated pyrochlore systems Ln2Ru2O7 (Ln = rare earth element) were first investigated by Ito et al. [12]. Taira et al. [6] carried out magnetic susceptibility measurements on the heavy rare earth ruthenate pyrochlores Ln2Ru2O7 (Ln = Gd–Yb). They observed a lambda type anomaly in the specific heat versus temperature plot at 103 K for Dy2Ru2O7 and a ferromagnetic transition below 1.8 K. Yao and co-workers synthesized Ln2Ru2O7 pyrochlore compounds by a hydrothermal method and measured magnetic susceptibility at low temperature [13]. Magnetic measurements on the Ho2Ru2O7 and Dy2Ru2O7 pyrochlores were carried out by Bansal et al. [14] to investigate the possibility of spin ice type magnetism in these systems and concluded from their investigations that these pyrochlore systems have a magnetic behavior similar to other spin ice systems.
Several properties of pyrochlores has been studied by researchers, however, high temperature studies on these systems are lacking. As part of systematic studies, to determine thermodynamic properties on the ternary oxides in the Ln–Ru–O systems in our laboratory, thermodynamic studies on the oxide Dy2Ru2O7(s) were carried out. A study of thermodynamic properties gives information on the thermodynamic stability domain of these compounds. From the thermodynamic properties of Dy2Ru2O7(s) process conditions can be devised to extract the valuable ruthenium from scrap and electronic waste. Further from the thermodynamic data of ternary oxides, phase diagrams of quaternary systems containing these elements can be readily computed. Hence based on phase relations, the Gibbs energy of formation of Dy2Ru2O7(s) was determined by an in house fabricated electrochemical cell using calcia stabilized zirconia (CSZ) as the solid electrolyte. The heat capacity of Dy2Ru2O7(s) was measured in the temperature range from 174 to 305 K using a differential scanning calorimeter (DSC-131). Other thermodynamic parameters at elevated temperatures were evaluated from these experimental data.
2 Materials and methods
2.1 Materials
The starting material Dy2O3(s) (0.9985 mass fraction, Leico Industries Inc. U.S.A.) was preheated to remove all traces of moisture. Dy2Ru2O7(s) was synthesized from stoichiometric proportions of preheated Dy2O3(s) and RuO2(s) (0.998 mass fraction, Prabhat Chemicals, India). The oxides were ground and the mixture was then pelletized using a die of tungsten carbide, sealed in an evacuated quartz ampoule and heated to T = 1400 K for 24 h. The possibility of interaction of the sample material with quartz ampoule was prevented by stacking pellets in the ampoule and using the pellet in contact with the quartz as the sacrificial pellet as described earlier [15]. The values of the interplanar d spacing obtained for Dy2Ru2O7(s) using STOE diffractometer with Cu-Kα radiation (λ = 1.5406 Ǻ) is in good agreement with those reported in JCPDS file number #82-2039 [16].
The oxide Dy2Ru2O7(s) lies on the tie line between Dy2O3(s) and RuO2(s) in the Dy–Ru–O system. Phase relations were explored of different phase mixtures of oxide phases and metal, by equilibration at 1200 K and phase analysis of quenched samples. The phase composition of {Dy2O3(s) + Dy2Ru2O7(s) + Ru(s)} remained the same by equilibration. A phase mixture of {Dy2O3(s) + Dy2Ru2O7(s) + Ru(s)} was pelletized into a pellet with the following dimension: 10 mm diameter and 2.5 mm in thickness in the molar ratio of 1:1:2 using tungsten carbide die at a pressure of 100 MPa. The pellet was sintered in high purity argon gas atmosphere at T = 1000 K for several hours and thereafter used for e.m.f. measurements.
2.2 The oxide cell assembly
A double compartment cell assembly with 0.15 mol fraction CSZ solid electrolyte tube with one end closed and flat was used to separate the gaseous environments of the two electrodes for electrochemical measurements and was in-house fabricated. Schematic diagram of the experimental set-up used and its description is shown in an earlier publication [17]. The cover gas of the cell was argon, flowing at a rate of 1 dm3 h−1, purified by passing through towers containing the reduced form of BASF catalyst, molecular sieves and magnesium perchlorate. The sample electrode compartment was initially evacuated and flushed with argon gas. This procedure was repeated several times while simultaneously heating the cell to around 573 K to dispel all moisture and other atmospheric gases present in the electrode compartment. The argon gas was bubbled out at a steady rate through an oil bubbler without disturbing the equilibrium at the working electrode. The argon cover gas was directed via an alumina guide tube to the working electrode. A Faraday cage was placed between the cell assembly and the furnace, the cage was grounded to minimize induced electro-motive force (e.m.f.) on the cell leads. Platinum leads sheathed in alumina were used to measure the e.m.f. Synthetic dry air was used as the reference electrode that ensured moisture free air. Temperature of the cell was measured by using a calibrated chromel–alumel thermocouple placed near the pellet. The e.m.f. of the cell was measured when its value was steady for 2–3 h using a high impedance Keithley 614 electrometer. Measurements at low temperatures were made after equilibrating the cell for more than 12 h. Voltages were reproducible in subsequent heating cycles. E.m.f. was measured after initially equilibrating the galvanic cells at 1000 K for at least 24 h. The following cell configuration was employed in the present study:
-
Cell I: (−)Pt/{Dy2O3(s) + Dy2Ru2O7(s) + Ru(s)}//CSZ//O2(p(O2) = 21.21 kPa)/Pt(+).
The reversibility of the solid-state electrochemical cell was checked by micro-coulometric titration in both directions. A small quantity of current was passed through the cell in either direction. Removal of the applied current returned the cell e.m.f. to its original value. The e.m.f. of the cell was also found to be independent of flow rate of the inert gas passing over the electrodes. The range of permissible oxygen partial pressures for purely ionic conduction for CSZ electrolytes is about 10−20 Pa at 1000 K and 10−13 Pa at 1273 K [18]. The oxygen partial pressure of the above designed cell falls within this range.
2.3 Measurement of low temperature heat capacity of Dy2Ru2O7(s)
Heat capacity measurements were carried out using a heat flux type differential scanning calorimeter (Model: DSC-131, Setaram Instrumentation, France). The transducer of DSC-131 has been designed using the technology of the plate shaped DSC rods made of chromel–costantan. It is arranged in a small furnace with a metal resistor of low-thermal inertia so as to produce high heating and cooling rates, thereby providing for high speed experiments. The transducer possesses very good sensitivity also over the entire temperature range (100–950 K). The temperature calibration of the calorimeter was carried out by: “the phase transition temperature of National Institute of Standards and Technology (NIST) reference materials (mercury: Tfus = 234.316 K; gallium: Tfus = 302.914 K; indium: Tfus = 429.748 K; tin Tfus = 505.078 K) and AR grade samples (n-pentane: Tfus = 140.490; cyclohexane: Tfus = 280.1 K, Ttrs = 190.0 K; deionised water: Tfus = 273.160 K”. Heat calibration of the calorimeter was carried out from the enthalpies of transition of the reference materials as given in an earlier publication [19]. For the determination of heat capacity, NIST synthetic sapphire (SRM 720) in the powder form was used as the reference material [20]. Heat capacity of the oxide was determined in the temperature range from 174 to 305 K.
The classical three-step method in the continuous heating mode was followed in this study to measure the specific heat in the first temperature range from 126 to 284 K. Liquid nitrogen was used in the low temperature range and was fed to the DSC instrument via a cryogenic device (jar). Heat flow as a function of temperature was measured at a heating rate of 5 K min−1 with high purity helium as a carrier gas with a flow rate of 2 dm3 h−1 as illustrated in the literature [21]. Three sets of experiments were carried out, performed under identical experimental conditions viz. heating rate, carrier gas flow rate, and delay time and temperature range. Two empty, aluminum crucibles with lids of identical masses were selected for the sample and reference cells. In the first experiment both the sample and reference cells were empty. The heat flow versus temperature was measured at a heating rate of 5 K min−1. In the second set of experiments weighed synthetic sapphire (SRM-720) was loaded in the sample cell the reference side was empty and the heat flow versus temperature was measured. In the third set of experiments, sample was weighed and loaded in the sample cell, reference cell being empty and the heat flow as a function of temperature was measured. About 300–350 mg of the sample was used for the heat capacity measurements.
The heat capacity of the sample under investigation was calculated by a simple comparison of the heat flow rates in three runs. If Ti, represents the initial temperature, the temperature interval step is chosen between Tj and Tj+1, we define: Tj = Ti + ΔT and Tj+1 = Ti + (j + i) ΔT. For the calculation of heat capacity of the sample the expression used was:
where HFblank, HFRef and HFsample represent heat flow during first, second and third runs respectively. Cp(Tj)sample and Cp(Tj)Ref represent the heat capacities of sample and reference material in J K−1 g−1 and Msample and MRef represent the mass of sample and reference, respectively. The heat capacity thus obtained was then converted to J K−1 mol−1. The accuracy of measurements was checked by measuring heat capacity of Fe2O3(s) (Alfa Aesar, mass fraction 0.998) and the values obtained were found to be within ± 3% in this temperature range as compared with the literature values [22].
3 Results and discussion
3.1 Solid-state electrochemical measurements using oxide cell
E.m.f. of the electrochemical cell using an oxide electrolyte is related to the partial pressure of oxygen at the two electrodes and can be given by the relation:
where “E, is the measured e.m.f. of the cell in volts, R = 8.3144 J· K−1· mol−1 is the universal gas constant, n is the number of electrons participating in the electrode reaction, F = 96,485.3 C mol−1 is the Faraday constant, T is the absolute temperature, t(O2−) is the effective transference number of O2− ion for the solid electrolyte and p″(O2) and p′(O2) are the equilibrium oxygen partial pressures at the positive and negative electrodes respectively”. The transport number of oxygen ion is nearly unity (t(O2−) > 0.99) at the oxygen pressures and temperatures covered in this study. Hence, the e.m.f. is directly proportional to logarithm of the ratio of partial pressures of oxygen at the electrodes:
Thus,
where “RT ln p″(O2) is the oxygen chemical potential over the positive electrode and RT ln p′(O2) is the oxygen chemical potential over the negative electrode”.
In the Dy–Ru–O system, along the Ru–O binary, only one oxide RuO2(s) exists, and has a tetragonal structure. Along the Dy–O binary the only oxide is Dy2O3(s) and has a cubic structure. Dy2Ru2O7(s) with pyrochlore structure lies on the tie line of these two stable oxides. The following two, three phase regions were explored:
-
(a)
Dy(s) + RuO2(s) + Dy2Ru2O7(s)
-
(b)
Dy2O3(s) + Ru(s) + Dy2Ru2O7(s).
In the three phase mixture (a) one of the components is metallic Dy(s). However this metal needs to be handled inside a glove box as it oxidizes easily to the very stable Dy2O3(s). Hence the phases involving Ru, Dy2O3(s) and Dy2Ru2O7(s) were equilibrated and used as the working electrode. However the electrochemical cell had platinum lead wires and as there is considerable solid solubility of Ru(s) in metallic Pt(s) the e.m.f. of the cell was found to continuously drift. Hence prior to the experiments involving Cell (I) the following symmetric cell was setup:
In the above cell a thin gold foil was placed between the platinum lead wires and the binary phase mixture on either side and cycled for several days at 1150 K. This not only enabled the gold foil saturated with ruthenium to bind with the platinum lead wire on either side but also gave a null e.m.f. Now the Cell(I) was setup with a phase mixture of Dy2O3(s):Dy2Ru2O7(s):Ru(s) in the molar ratio of 1:1:2 and used as the working electrode and air as the reference electrode.
The half-cell reaction at the cathode and the anode for the cell I in the oxide conducting domain of the electrolyte at elevated temperature can be given by:
and,
The net virtual cell reaction for the passage of eight Faradays of electricity obtained by combining the two half cell reactions is:
Within experimental uncertainty, the least square regression analysis of the e.m.f. gives:
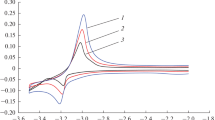
The uncertainties quoted are the standard deviation in e.m.f. The variation of e.m.f. as a function of temperature is presented in Fig. 1. The ΔrG˚(T) for the reaction given in Eq. (7) involves the transfer of eight electrons and hence from Nernst equation we get:
From Eqs. (7), (8) and (9) and literature value of ΔfG˚{Dy2O3(s)} [23], ΔfG˚ of Dy2Ru2O7 (s) has been obtained.
The error includes the standard deviation in e.m.f. and the uncertainty in the data taken from the literature. Gibbs energy of formation is a linear function of temperature within the experimental temperature range under consideration. The intercept and the slope of this equation correspond, respectively, to the average values of the standard molar enthalpy and entropy of formation of Dy2Ru2O7(s) in the temperature range under study. There is no thermodynamic data on Dy2Ru2O7(s) in the literature for comparing the results obtained in this study.
3.2 Standard molar heat capacity of Dy2Ru2O7(s)
The heat capacities of Dy2Ru2O7(s), were measured in the temperature range from 174 ≤ T (K) ≤ 305, were taken at ambient pressure, 101.3 kPa, using a differential scanning calorimeter and are given in Fig. 2. The values of heat capacities were best fitted in the following polynomial expression by the least squares method.
At 298.15 K, the standard molar heat capacity of Dy2Ru2O7(s) was calculated to be 235.2 J K−1 mol−1. Neumann–Kopp’s rule estimates the heat capacity and gives the heat capacity at 298.15 K of Dy2Ru2O7(s) as 222.3 J K−1 mol−1 [24]. This data for Dy2Ru2O7(s) has been reported for the first time. Based on the estimated entropy value of Dy2Ru2O7(s) and the measured heat capacity, the thermodynamic functions for Dy2Ru2O7(s) were calculated and are given in Table 1. The Gibbs energy data obtained in this study was used to calculate the decomposition temperature of Dy2Ru2O7(s) and is 1769 K in air. The decomposition temperature of RuO2(s) was calculated from the Gibbs free energy data of and is 1647 K. The decomposition temperature of Dy2Ru2O7(s) is higher than that of RuO2(s) as determined by Cordfunke [25], indicating higher stability for Dy2Ru2O7(s).
4 Conclusions
In summary, the ternary oxide Dy2Ru2O7(s), in the Dy–Ru–O system was prepared by the solid-state synthesis route. The Gibbs energies of formation of the ternary compound was obtained by using electrochemical oxide cell at high temperature. The Gibbs energy of formation of Dy2Ru2O7(s) from elements in their standard state is given by: {ΔfG˚(Dy2Ru2O7, s)/(kJ mol−1) ± 4.4} = − 2505 + 0.627· (T/K). Heat capacity is one of the essential thermophysical characterizations that determine thermal behavior of the material. The heat capacity was measured using a differential scanning calorimeter and the heat capacity of Dy2Ru2O7(s) at 298.15 K was determined to be 235.2 J K−1 mol−1. The decomposition temperature of Dy2Ru2O7(s) is higher than that of RuO2(s), indicating stability of the former. The determination of thermodynamic parameters for Dy2Ru2O7(s) will pave the way for a study on the systematic trends in stability of Ln2Ru2O7(s) as a function of ionic radii down the lanthanide series.
References
Pace S, Cannillo V, Wu J, Boccaccini DN, Seglem S, Boccaccini AR (2005) Processing glass–pyrochlore composites for nuclear waste encapsulation. J Nucl Mater 341:12–18
Ashcroft AT, Cheetham AK, Ford JS, Green MLH, Grey CP, Murrell AJ, Vernon PDF (1990) Selective oxidation of methane to synthesis gas using transition metal catalysts. Nature 344:319–321
Kim J, Shih PC, Tsao KC, Pan YT, Yin X, Sun CJ, Yang H (2017) High-performance pyrochlore-type yttrium ruthenate electrocatalyst for oxygen evolution reaction in acidic media. J Am Chem Soc 139:12076–12083
Cao XQ, Vassen R, Jungen W, Schwartz S, Tietz F, Stover D (2001) Thermal stability of lanthanum zirconate plasma-sprayed coating. J Am Ceram Soc 84:2086–2090
Bouchard RJ, Gillson JL (1971) A new family of bismuth - precious metal pyrochlores. Mater Res Bull 6:669–679
Taira N, Wakeshima M, Hinatsu Y (2002) Magnetic susceptibility and specific heat studies on heavy rare earth ruthenate pyrochlores R2Ru2O7 (R = Gd–Yb). J Mater Chem 12:1475–1479
Wang SX, Begg BD, Wang LM, Ewing RC, Weber WJ, Govindan Kutty KV (1999) Radiation stability of gadolinium zirconate: A waste form for plutonium disposition. J Mater Res 14(12):4470–4473
Parrondo J, George M, Capuano C, Ayers KE, Ramani V (2015) Pyrochlore electrocatalysts for efficient alkaline water electrolysis. J Mater Chem A 3:10819–10828
Cox PA, Egdell RG, Goodenough JB, Hamnett A, Naish CC (1983) The metal-to-semiconductor transition in ternary ruthenium (IV) oxides: a study by electron spectroscopy. J Phys C Solid State Phys 16:32
Xu ZC, Liu MF, Lin L, Liu H, Yan ZB, Liu JM (2014) Experimental observations of ferroelectricity in double pyrochlore Dy2Ru2O7. Front Phys 9(1):82–89
Sodderholm L, Stager CV, Greedan JE (1982) Crystal field effects on the magnetic behavior of Yb2V2O7 and Tm2V2O7. J Solid State Chem 43:175–180
Ito M, Yasui Y, Kanada Harashina Yoshii HS, Murata K, Sato M, Okumura H, Kakurai K (2001) Nature of spin freezing transition of geometrically frustrated pyrochlore system R2Ru2O7 (R = rare earth elements and Y). J Phys Chem Solids 62:337–341
Yao LR, Wang D, Peng W, Hu WW, Yuan HM, Feng SH (2011) Hydrothermal synthesis and characterization of rare-earth ruthenate pyrochlore compounds R2Ru2O7 (R = Pr3+, Sm3+–Ho3+). Sci China Chem 54(6):941–946
Bansal C, Kawanaka H, Bando H, Nishihara Y (2003) Magnetic properties of Ho2Ru2O7 and Dy2Ru2O7 pyrochlores. Physica B 329(2):1034–1035
Banerjee A (2013) System Er–Ru–O: high temperature study of the heavy rare earth pyrochlore Er2Ru2O7 (s) by electrochemical cell and differential scanning calorimeter. Solid State Ion 253:70–75
Yamamoto Y, Kanno R, Takeda Y, Yamamoto O, Kawamoto Y, Takano MJ (1994) Crystal structure and metal-semiconductor transition of the Bi2-xLnxRu2O7 pyrochlores. (Ln= Pr-Lu). Solid State Chem 109:372–383
Banerjee A, Singh Z, Venugopal V (2009) Heat capacity and Gibbs energy of formation of the ternary oxide CdRh2O4 (s. Solid State Ionics 180:1337–1341
Pratt JN (1990) Applications of solid electrolytes in thermodynamic studies of materials: A review. Metall Trans A 21:1223–1235
Rakshit SK, Parida SC, Dash S, Singh Z, Venugopal V (2006) Thermodynamics of BaNd2Fe2O7 (s) and BaNdFeO4 (s) in the system BaNdFeO. Thermochim Acta 443:98–104
Sabbah R, Xu-wu A, Chickos JS, Planas Leitao ML, Roux MV, Torres LA (1999) Reference materials for calorimetry and differential thermal analysis. Thermochim Acta 331:93
Hohne GWH, Hemminger WF, Flammershein HJ (2003) Differential scanning calorimetry, 2nd edn. Springer, Berlin
Chase MW Jr (1982) JANAF thermochemical tables, fourth ed. J Phys Chem 11(3):695–940 (monograph no. 91995)
FactSage, version 5.3.1 (1976–2004) Thermo-chemical database software, Thermfact. GTT Technologies, Herzogenrath
Kubachewski O, Alcock CB, Spencer PJ (1993) Materials thermochemistry, 6th edn. Pergamon, Oxford
Cordfunke EHP, Konings RJM (1988) The enthalpy of formation of RuO2. Thermochim Acta 129:63–69
Acknowledgements
The author is thankful to Dr. S Kannan, Head Fuel Chemistry Division and Dr. P. K. Pujari, Director R C & I Group, for their constant support and encouragement.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The author declares that there are no conflicts of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Banerjee, A. The ruthenium pyrochlore Dy2Ru2O7(s): Stability and calorimetry. SN Appl. Sci. 2, 1153 (2020). https://doi.org/10.1007/s42452-020-2948-0
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s42452-020-2948-0