Abstract
The aim of this study is to investigate the efficiency of using green ultra-high-performance concrete (GUHPC) with corrosion resistant alloy steel (MMFX) Bars in overcoming concrete cracking and steel corrosion, which will help in reducing inspection, maintenance, and repair works. To do so, a nonlinear finite element (FE) analysis was carried-out to model full-scale concrete beams which are often subjected to cracks during its service life time. The obtained results were compared with experimental data and the comparison was most satisfactory. In addition, a comparison was made between the proposed materials and traditional reinforced concrete in terms of crack widths, the intensity of cracks and service life period. The obtained results showed that using GUHPC and MMFX as a construction material in concrete structures provides high stiffness, high strength, enhanced service life and crack control beside its cost efficiency.
Similar content being viewed by others
1 Introduction
Due to the consequences of steel corrosion, it becomes very important, it is very to provide an innovative solution for extending the service life of reinforced concrete (RC) structures. Poursaee [1] mentioned that there is a few research in the field of studying the extension of the service life of RC subject to carbonation and chloride-laden environments such as the use of ultra-high-performance concrete and noncorrosive reinforcement.
1.1 Ultra-high performance concrete
Ultra-high performance concrete (UHPC) is characterized by high ductility, durability, and mechanical properties [2]. UHPC mix design is usually composed of silica fume (SF), high cement content, quartz sand (QS), quartz powder (QP), and steel fibers [3]. UHPC is recognized for its high compressive strength and resistance to corrosion [4]. The use of steel fibers improves the ductility and flexural capacity of UHPC. Its modulus of rupture may reach 15 MPa, compressive strength of more than 150 MPa, and elastic modulus of about 45 GPa, with minimum long-term creep [5]. Besides, UHPC has high resistance to carbonation, chloride penetration and freeze–thaw cycles with no visible damage [6]. Also it provides excellent protection for embedded steel reinforcement [7]. The main disadvantage of UHPC is its high expense compared to conventional concrete. One of the effective ways to overcome this problem is the utilization of green UHPC as used in this work.
Recycling post-consumption glass was done many times in different countries without changing its chemical and physical properties significantly. High risk of breaking, high recycling costs, or color mixing is considered barriers that stand against recycling large quantities of glass. As glass is less environmentally friendly and is not biodegradable, it is undesirable to use waste glass into landfill sites [8]. Recently, many trials have been done to use waste glass as an ultra-fine filler in concrete or as a cementitious material. Grounded glass (finer than 38 μm in its size) can increase concrete strength and durability through its pozzolanic behaviour [9, 10]. Besides it can replace cement partially in certain concrete types [11,12,13,14].
Based on the above discussion, GUHPC which was introduced by Soliman and Tagnit-Hamou [15] was used in this study. They developed it as an innovative sustainable, green UHPC with low-cost, by using the ground glass powder (GP). Soliman and Tagnit-Hamou [15] used GP as a replacement of quartz powder (QP) and cement, and keep Silica fume (SF) and Quartz sand (QS) quantities the same in all mixtures. Increasing flexural ductility and load-carrying capacity of UHPC can be obtained by adding of steel fibers (2% of the UHPC by volume). Furthermore, the addition of steel fibers can delay the occurrence of crack and change the crack patterns [16]. As discussed before using GP as an alternative to cement and QP can reduce the carbon footprint and decrease UHPC cost significantly. Due to its local availability GP can reduce the cost of transporting materials.
1.2 Noncorrosive reinforcement
Structural deterioration is mainly caused by steel corrosion. which is considered the most harmful damage that occurred in RC structures and is considered as a major reason that can cause concrete cracking.
Carbonation and chloride corrosion are considered the main causes of steel corrosion. Carbonation occurs in relatively dry environments where carbon oxide can spread through the concrete cover. However, in environments that contain chloride, the chloride can spread faster than the carbonation, and it can cause deterioration by reducing the structure’s resistance leading to service life termination of a structure [17]. The United States spent millions of dollars in rehabilitation programs and inspections of marine structures and railway over the last years [18]. Therefore, using non-corrosive steel will surely save our resources. Epoxy-coated bars, galvanized bars, stainless steel, fiber reinforced polymers (FRP) and MMFX steel bars are the most widely used bars as corrosive-resistance bars [19].
MMFX has many advantages: higher strength, higher resistance to corrosion, relatively low cost, and higher ductility compared to conventional steel reinforcement [20]. Nadh and Vasugi [21] compared the corrosion rate and the service life of structures when using a different type of reinforcement: carbon steel, stainless steel, and MMFX. It was observed that MMFX has less corrosion compared to stainless steel “ER 308L” and the carbon steel came last. A structure made of MMFX can have a service life of more than 100 years, and a service life between 90 and 100 years when using stainless steel bars and only between 40 and 50 years when using carbon steel bars.
1.3 Service-life
It is very important to predict the service life of a structure due to reinforcement corrosion. This is because it will be very difficult and too late to do any protection measures. Several mathematical and imperial models are available in the literature to predict the service life of corroded RC structures, Bazant [22], Morinaga [23], Wang [24], IRC [25], and El Maaddawy and Soudki [26] models are examples. The model prepared by El Maaddawy and Soudki [26] considered to be the best model to predict service life of RC structures when subjected to corrosion. This is because it considers the relationship between internal radial pressure caused by corrosion and the loss in steel mass and also considers, the mechanical properties of concrete. This is, also, agreed with the conclusion obtained by of Kumar et al. [27]. Corrosion usually happens as a result of diffusion of corrosion products in the air/capillary voids in cement paste which in turn moved to the porous zone around steel reinforcement that is caused by the transition from cement paste to steel [26].
1.4 Research significance
A new combination of the two promising materials (GUHPC and/or MMFX) was examined in this study with the structural performance of full-scale concrete beams made with the two mentioned materials was numerically analyzed utilizing the finite element method. The behaviour of the considered beams is evaluated in terms of load–deflection characteristics and the intensity and width of generated cracks under service and ultimate loads. The structural performance will reflect the need/need not for maintenance during the service life of RC structures. Also, the useful service life was computed for each studied beam to show the role of GUHPC and MMFX in extending the service life of RC structures when exposed to aggressive attack.
2 Finite element modeling
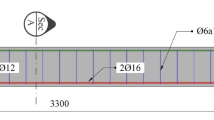
ABAQUS [28] finite element (FE) program was used to numerically analyse the considered 3D full scale RC beams That simulate typical field behaviour of RC beams application. Two 13 mm longitudinal bars (reinforcement ratio (ρ) is constant = 0.26% for all beams (under reinforced section)) were used as the bottom reinforcement, Eltahawy [20] recommended that the usage of lightly ρ of 0.26% to fully utilize the high-strength potential of the MMFX steel bars and produces a more ductile flexural failure. Two ϕ 10 mm (dia. (ϕ)) longitudinal bars were used for compression reinforcement for all beams. A mild steel mesh 8 mm (dia. (ϕ)) was used for top flange reinforcement. To prevent undesired shear failure in the beams. Adequate shear reinforcement closed stirrups of 10 mm (dia. (ϕ)) spaced at 100 mm center to center (Fig. 1). A minimum value of concrete cover or 20 mm was considered, when examining the structural efficiency of GUHPC and MMFX to extend the service life of RC beams. The detailed dimension and reinforcement for the considered beams are shown in Fig. 2 and Table 1.
2.1 Constitutive models
2.1.1 Concrete model
Concrete behaviour was modeled by using concrete damaged plasticity model. Two types of concrete were considered in the FE analysis; normal strength concrete (NSC) which represent the case of existing concrete structures and green ultra-high-performance concrete (GUHPC) which was developed by Soliman and Tagnit-Hamou [15]. The concrete mix is shown in Table 2. The stress–strain curve for concrete is shown in Fig. 3. It is based on the experimental results obtained by Soliman and Tagnit-Hamou [15].
Experimental stress–strain curves of the used concretes in FE models [15]
2.1.2 Reinforcement model
The considered stress–strain curve of the three types of the used steel reinforcement is an elastic–plastic model, Fig. 4.
Experimental stress–strain curves of the used steel reinforcement in FE models [20]
2.2 Elements and meshing
Concrete was modeled as an 8-noded three-dimensional first order reduced integration-brick element (C3D8R). Reinforcing bars are modeled by using a 2-nodes three-dimensional first order truss element (T3D2) where the main purpose of steel reinforcement is to transfer normal loads. All elements in the model have the same mesh size of 30 mm with a max aspect ratio of 2. To model the interface between steel bars and concrete, Embedded & host constrain was used, where steel bars were Embedded inside concrete.
3 Output results and discussion
3.1 Structural behaviour
3.1.1 Verification of FE model
The experimental results of Eltahawy [20] was used in FE model Verification. Two beams were considered. The first beam with NSC with conventional deformed bars (RB) but the other with MMFX steel bars (B1). The load–deflection curve and the ultimate capacities predicted by the FE model were compared with the corresponding experimental results of Eltahawy [20]. Figures 5 and 6 show that there is a good agreement between the load–deflection curve predicted by FE and that obtained from the experimental results. The ratio between load capacities obtained from the experimental results and that predicted by the FE model was 0.96 and 0.92 for beams RB and B1 respectively. The ratio between max. deflection obtained from the experimental results and that predicted by the FE model was 0.98 and 0.93 for beams RB and B1 respectively as indicated in Table 3. It can be concluded that there is a good agreement between the FE model and the experimental results. This gives confidence when using the proposed FE model in parametric studies.
3.1.2 Influence of using MMFX Rebars
Table 3 indicates that beam B1 (with MMFX steel bars) attained an increase in its ultimate flexural capacity and stiffness (computed based on model of Zeng et al. [29]). Those were 106% and 65%, respectively, over the control beam (RB). These results agree with Eltahawy [20]. Regarding the service loading stage, beam B1 also overtook on RB, as shown in Table 4, evidenced by an increase of service load by 117% where the service load of beam RB is 69.13 KN and of beam B1 is 150 KN. Crack widths of both beams are almost the same. Both RB and B1 satisfy the recommendation of ACI 224 [30] for normal environmental conditions (Max. allowable crack width are less than 0.3 mm). On the other hand, B1 did not meet with the requirement of ACI 318 [31] for service deflection control (max. allowable deflection limit = 5.9 mm). Excessive deflection of beam B1, due to low strength of used concrete leading to low stiffness.
3.1.3 Influence of use GUHPC
GUHPC as in beam B2 has achieved amazing results. This include an increase in ultimate capacity (Fig. 7), stiffness, first cracking load (load at the end of the initial linear zone in the load–deflection curve), and service load by about 480%, 1498%, 730%, and 481%, respectively, compared with control beam (RB) as shown in Tables 3 and 4. Under service loading, very minor cracks were initiated and propagated into GUHPC beam (B2) which cannot be seen and determined only from the FE method (width = 0.006 mm). A reduction of about 97% in crack width of GUHPC beam (B2) compared to the conventional beam (RB) under the same loading condition was observed, the reduction was calculated as follows: [(crack width in normal concrete − crack width in GUHPC)/(crack width in normal concrete)] × 100. Beam B2 satisfies the recommendation of ACI 224 [30] for aggressive environmental conditions unlike Beam RB (max. allowable crack width are less than 0.18 mm). Superior mechanical properties of GUHPC reflect its capability to control the service deflection of beam B2. The high stiffness of GUHPC beam (B2) reduces the value of service deflection (5 mm). Beam B2 considerably satisfies the requirement of ACI 318 [31] for deflection control.
3.1.4 Influence of combining GUHPC and MMFX reinforcement
To invest the advantages of combining GUHPC and MMFX steel bars, beam B12 was considered, and it gives a considerable increase in ultimate capacity (Fig. 8). The beam stiffness, first cracking load, and service load (Tables 3, 4) were increased by 515%, 1441%, 840%, and 516%, respectively, compared with the control beam (RB). Under service loading, cracks are almost null in beam B12 (width = 0.0019 mm); that is a 99% reduction in its crack width compared to the conventional one (RB). Beam B12 satisfies the recommendation of ACI 224 [30] for very aggressive environmental and water-retaining structures unlike RB (max. allowable crack width is less than 0.10 mm). Also, beam B12 meets the requirement of ACI 318 [31] for deflection control.
3.1.5 Failure mode and crack patterns
The failure of beam RB was due to the yielding of the steel reinforcement (followed by concrete crushing, which is a ductile mode of failure (or tension failure) which is the key for under reinforced section, as shown in Fig. 9. The failure of beam B1 (NSC with MMFX bars) occurred due to rupture of tensile reinforcement (Fig. 10), this failure match with that obtained by Malhas [32]. In which more severe failure occurs in MMFX beams that has smaller amount of reinforcement. No occurrence of bond failure between MMFX steel bars and surrounding concrete. Rather a strong bond is observed between them. This conclusion was supported as a result of the disappearance of any horizontal cracks at the level of the reinforcement. Figures 9 and 10 show the comparison between the experimental failure mode and that obtained by FE method for beams RB and B1. There is a good agreement observed between FE and experimental results.
MMFX-NSC beam (B1) with smaller amount of reinforcement experienced more severe failure mode, unlike MMFX-GUHPC beam (B12). The MMFX steel performed well and is more efficient with GUHPC without premature failure.
The crack behaviour of beams B2 (Conventional deformed steel (CDS)-GUHPC) and B12 (MMFX-GUHPC) was almost the same. Failure occurred mainly due to the bond loss between GUHPC and steel fibers, besides yielding of reinforcement. The failure mode of both beams (B2 and B12) was nearly the same as shown in Figs. 11 and 12 respectively. Obviously, tension yielding of MMFX bars under the load position was the main failure mode, followed by cracks occurrence in the tension zone at load location. This failure mode was caused as a result of bond loss between the steel fiber and GUHPC where the load carried by the fiber exceed the bond between GUHPC and the steel fiber leading to pulling-out of the fiber from concrete, which will, in turn, increase the load on the other fiber that still in contact with GUHPC concrete leading to the occurrence of more cracks.
The fibers beneath the applied load began to pull-out at the peak load. The crack width at this location increased significantly than any other crack in the beam as shown in Table 4. As the bond between fibers and GUHPC vanishes, the beam failure was accelerated besides yielding of rebars under the load position which is verified by visual inspection of the crack patterns of the verified and reliable FE models under service loading stage. Table 4 shows that the beam RB has a larger number of cracks. These cracks gradually reduced clearly with the use of MMFX steel reinforcement in beam (B1), GUHPC in beam (B2), and combination of them in beam (B12).
Control beam has a larger number of cracks. These cracks gradually reduced clearly with the use of MMFX steel reinforcement in beam (B1), GUHPC in beam (B2), and/or combination of them in beam (B12). Beam B12 considerably satisfies the requirement of ACI 224 [30] concerning control of crack width in very aggressive environmental and also the requirement of ACI 318 [31] for deflection control.
Regarding the load–deflection curves of all beams (control beam, GUHPC beam, MMFX beam and GUHPC + MMFX beam) showed similar behaviour. The deflection was linearly proportioned to the load until the initiation of cracking and then, the relation becomes nonlinear until failure.
3.2 Service life prediction
As mentioned before in the literature that the model prepared by El Maaddawy and Soudki [26] considered to be the best model to predict service life of RC structures when subjected to corrosion. Mathematical model of El Maaddawy and Soudki [26] is based on the modification of Tuutti [33], in which the propagation period (time from the beginning of corrosion to the start of corrosion cracking) Tcr, is divided into two different periods. The first period is the free expansion period, which is the time required for corrosion products to fill the porous region surrounding the corroded steel reinforcement. The second period includes the time in which these corrosion products, produce large pressure on the concrete surrounding the reinforcement. The model assumes that the produced pressure is directly proportioned with the volume of corrosion products and assumes a linear relation in between. The concrete cracking occurs when the tensile pressure produced in the porous zone exceeds the tensile strength of concrete. This model can be applied until the crack start after this non-uniform pressure distribution occurs. The occurrence of previously mention cracking (usually at the concrete cover) shows the end of the service life of the corroded structure and shows that the structure needs maintenance and rehabilitation.
Consequently, mathematical model of El Maaddawy, Soudki [26] as follows in Eq. 1:
where Tcr = Time (in days) from corrosion initiation to corrosion cracking, days, D = Diameter of steel reinforcing bar, mm, δ0 = Porous zone thickness which is generally in the range of 10–20 μm [34], υ = Poisson's ratio of concrete (0.18), C = Clear concrete cover, mm, Ψ = Factor depends on D′, C and δ0 and can be computed as follows
where D′ = D + 2 δ0, i = Current density, μA/cm2, Table 5 represent a guide for various corrosion current density cases.
Eef = Effective elastic modulus of concrete = Ec/(1 + ϕcr). Ec = Elastic modulus of concrete, MPa. ϕcr = Concrete creep coefficient (2.35 as per the CSA A23.3–94 [35]). fct = Tensile strength of concrete, MPa, [36]
Jolley et al. [37] reported that the average 280 days-corrosion rate (R) at severe corrosion condition (very high corrosion) of MMFX steel bars and conventional deformed steel (CDS) equal to 3.19 and 12.08 μm/year, respectively. The corrosion current density (μA/cm2) can be determined by the following equation (Eq. 2) [37]:
At severe corrosion conditions, current density of MMFX steel and CDS bars equal to 0.27 and 1.04 μA/cm2 respectively. Also, to account for the moderate case of corrosion, the current density can be taken as 0.50 μA/cm2 for CDS bars which equivalent to 0.13 μA/cm2 for MMFX bars. It should be noted that, Corrosion current density depend on reinforcement type only while service life depend on both reinforcement and concrete type.
The service life of a RC structure is the period for which a structure is to be used for its intended purpose with acceptable levels of structural safety, and also should meet with minimum levels of serviceability without major repair. Most public governmental structures, underground structures, and marine structures are always in continuous service and may be exposed to aggressive environments, from this point the design approach for durability described in this paper will ensure a satisfactory service life which can be used in different structures. To achieve this target, the promising low-cost durable material GUHPC and corrosive-resistance steel bars (MMFX) are used. Consequently, to examine the efficiency of using GUHPC and MMFX bars in RC structures, service life periods are predicted under severe aggressive environment and moderate conditions. Service life prediction was calculated using the model proposed by El Maaddawy and Soudki [26] for beams RB, B1, B2, and B12 under moderate and aggressive environmental conditions. The results are indicated in Table 6. The results are discussed in the next subsections.
3.2.1 Influence of GUHPC
Service life period of beam B2 (GUHPC + CDS) under both moderate and severe corrosions were 113 and 54 years respectively. On the other side service life period of control beam RB (NSC + CDS) were 55 and 27 years, respectively. Table 6. GUHPC increased the service life of the beam B2 by 105% and 100%, respectively for the two cases of exposures compared to the control beam. This noticeable increase was expected due to the superior mechanical properties and durability of GUHPC, which also provides a good protection to embedded steel reinforcement bars [15].
3.2.2 Influence of MMFX steel reinforcement
The results presented in Table 6 indicate that MMFX reinforcing bars largely extended the service life periods of beam B1(NSC + MMFX) by 287% and 463% under both moderate and severe corrosion conditions, respectively, compared to the control beam RB (NSC + CDS). Eltahawy [20] and Nadh and Vasugi [21] concluded that MMFX steel bars have superior corrosion resistance and longer service life. This is consistent with present paper results. Where the corrosion-resistant MMFX bars have a different composition than that of the conventional steel bars which could reduce the rate of corrosion and/or the volume expansion of the corrosion products.
3.2.3 Influence of combining GUHPC and MMFX steel reinforcement
Combining the high-performance materials (GUHPC and MMFX) gives good results. This became clear in this study upon combining GUHPC and MMFX bars as beam B12 (GUHPC + MMFX). It recorded highest values of service life periods and an unprecedented, whether exposed to moderate and severe corrosion conditions. The service life of beam B12 was about 330 and 209 years (increased by about 500% and 674% compared to the service life of control beam) under both exposure cases, respectively.
3.3 Analysis of different beams’ cost
Table 7 gives a details on the cost of mix component for NSC and GUHPC and the total price/cubic meter of the mix, the prices in the table are given in Egyptian pound (LE), the market price for reinforcing steel is LE 11,000/ton and for MMFX steel bars is LE 21,300/ton. After calculating the concrete’s quantitates and the weight of steel used in each beam (RB, B1, B2 and B12), the cost of each beam can be estimated as follows: LE 691 for RB, LE 1057 for B1, LE 1853 for B2, and LE 2219 for B12. It can be found that the cost of B12 is nearly 3 times the cost of RB. However, the strength of B12 is about 10 times RB’s strength. The cost for each MPa in the control beam RB is equal to LE 34.55/MPa while for Beam B12 is LE 10.09/MPa. Besides, B12’s service life is more than 6 times that of RB, which will save the cost of maintenance in the life time.
4 Case study
As an example, the studied case was the Vachon bridge which is RC bridge barrier wall in Laval, Canada [38]. It is required to make a comparison between two service-life periods. The first one was based on using the existing materials of the barrier. Whereas, the second one was based on using GUHPC beams reinforced with MMFX bars. Input parameters and results are shown in Tables 8 and 9 respectively.
It should be noted that the calculated service life period in Table 9 is based on the model proposed by El Maaddawy and Soudki [26]. From Table 9, it can be seen that the predicted service life of existing barrier wall when exposed to moderate rate of corrosion is equal to 150 years, which is close to the average value (160 years) which was computed previously by the mathematical models of Bazant [22] and Wang [24] as presented in the research work of Ranjith et al. [39].
Using GUHPC beams reinforced with MMFX bars for the barrier will lead to an increase in the service life of the Vachon bridge barrier wall, by about 240% over the existing case. It should be noted that the equation proposed by El Maaddawy, Soudki [26] which was used for predicting the service life is not designed and verified for GUHPC concrete and, therefore, more research is needed. This reflects the importance and effectiveness of using GUHPC beams reinforced with MMFX bars in RC structures, especially that is exposed to an aggressive environmental conditions in order to increase its service life time.
5 Conclusions
This paper introduced a new economic strategy; to reduce the government spending by saving the cost of maintenance by innovating the relatively low-cost and high-performance construction materials, which are able to extend the service life of RC structures regarding minimizing the need for inspection, repair works, and maintenance. This was achieved by combining GUHPC and MMFX reinforcement in RC structures. To examine the efficiency of MMFX steel reinforcement and GUHPC in RC applications, the structural behaviour and service-life prediction of full-scale T-section RC beams made with the two mentioned materials were studied. The considered beam were modeled using the FE method. For reliability and accuracy of results, FE models were calibrated firstly with a previous experimental work. The obtained conclusions in this study can be summarized as follows:
-
The proposed FE models attained a high accuracy compared to experimental ones. FE model is able to represent the behavior of control beam and others which made with MMFX and GUHPC.
-
Using MMFX steel bars can provide an increase in the load capacity, and stiffness by 117%, and 65% respectively, without significant effect in crack width. Service life periods can be increased by 287% and 463% under both moderate and severe corrosion conditions, respectively.
-
Using GUHPC can provide an increase in the load capacity, stiffness, first cracking load by 480%, 1498%, and 730%, respectively, with a reduction of 97% in crack width compared to NSC. An increase in service life of 105% and 100% can be achieved under both moderate and severe corrosion conditions, respectively.
-
Using both GUHPC and MMFX gives considerably increase of load capacity, stiffness, and first cracking load by 515%, 1441% and 840%, respectively, compared with control beam. A reduction of 99% in crack width was obtained. An increase of 500% and 674% in service live was achieved under moderate and severe corrosion conditions, respectively.
-
The case study presented on a RC bridge barrier wall (Vachon bridge, Laval, Canada) showed the technical and economic efficiency of using GUHPC beams reinforced with MMFX bars which leads to increase the service life of considered bridge by 240% over the existing case. Consequently, instead of spending on repair and maintenance works, money will be saved.
-
It can be concluded that the combining GUHPC with MMFX steel bars may be the best solution for obtaining ultimate structural performance, longer service life, and meets the all requirements of serviceability (deflection-control and crack width control under very aggressive environment).
For future research work more Experimental tests and numerical models are needed to assess structural safety and accurately define the actual service life. Studying the behavior of the considered beams under different loading cases such as static, dynamic, and aggressive environmental exposures is also needed. Additionally, the behaviour of full scale RC building having GUHPC and MMFX reinforcing bars is a must.
References
Poursaee A (2016) Corrosion of steel in concrete structures. Woodhead Publishing, USA
Richard P, Cheyrezy M (1995) Composition of reactive powder concretes. Cem Concr Res 25(7):1501–1511. https://doi.org/10.1016/0008-8846(95)00144-2
Richard P, Cheyrezy M (1994) Reactive powder concretes with high ductility and 200–800 MPa compressive strength. ACI SP 144, USA
Bahedh MA, Jaafar MS (2018) Ultra high-performance concrete utilizing fly ash as cement replacement under autoclaving technique. Case Stud Constr Mater 9:e00202. https://doi.org/10.1016/j.cscm.2018.e00202
Dugat J, Roux N, Bernier G (1996) Mechanical properties of reactive powder concretes. Mater Struct 29(4):233–240. https://doi.org/10.1007/bf02485945
Gu C, Sun W, Guo L, Wang Q, Liu J, Yang Y, Shi T (2018) Investigation of microstructural damage in ultrahigh-performance concrete under freezing-thawing action. Adv Mater Sci Eng 2018:9. https://doi.org/10.1155/2018/3701682
Roux N, Andrade C, Sanjuan MA (1996) Experimental study of durability of reactive powder concretes. J Mater Civ Eng 8(1):1–6. https://doi.org/10.1061/(ASCE)0899-1561(1996)8:1(1)
Shayan A, Xu A (2004) Value-added utilisation of waste glass in concrete. Cem Concr Res 34(1):81–89. https://doi.org/10.1016/S0008-8846(03)00251-5
Zidol A, Tognonvi MT, Tagnit-Hamou A (2017) Effect of glass powder on concrete sustainability. New J Glass Ceram 7:34–47. https://doi.org/10.4236/njgc.2017.72004
Terro M (2006) Properties of concrete made with recycled crushed glass at elevated temperatures. Build Environ. https://doi.org/10.1016/j.buildenv.2005.02.018
Shao Y, Lefort T, Moras S, Rodriguez D (2000) Studies on concrete containing ground waste glass. Cem Concr Res 30(1):91–100. https://doi.org/10.1016/S0008-8846(99)00213-6
Khmiri A, Samet B, Chaabouni M (2012) A cross mixture design to optimise the formulation of a ground waste glass blended cement. Constr Build Mater 28(1):680–686. https://doi.org/10.1016/j.conbuildmat.2011.10.032
Vaitkevičius V, Šerelis E, Hilbig H (2014) The effect of glass powder on the microstructure of ultra high performance concrete. Constr Build Mater 68:102–109. https://doi.org/10.1016/j.conbuildmat.2014.05.101
Soliman N, Aϊtcin P, Tagnit-Hamou A (2014) New generation of ultra-high performance glass concrete. Advanced concrete technology. In. RILEM and CEB-fib, pp 12–16
Soliman NA, Tagnit-Hamou A (2016) Development of ultra-high-performance concrete using glass powder – Towards ecofriendly concrete. Constr Build Mater 125:600–612. https://doi.org/10.1016/j.conbuildmat.2016.08.073
Shehab K, El-Din H, Husain M, Khater M (2013) Effect of steel fibers on flexural behavior of ultra high performance R.C. BEAMS. 16(1):10
Mehta PK, Odd E (1996) Symposium on concrete for marine structures. New Brunswick
Stewart MG, Rosowsky DV (1998) Time-dependent reliability of deteriorating reinforced concrete bridge decks. Struct Saf 20(1):91–109. https://doi.org/10.1016/S0167-4730(97)00021-0
Tikalsky PJ, Beh DE (2008) Synthesis Guide to Best Practices for Corrosion Resistant Concrete, Report No. UT-08.27. University of Utah Department of Civil and Environmental Engineering, USA
Eltahawy R (2008) Flexural behavior of concrete beams reinforced with high strength and corrosive resistant steel. Ain Shams University, El-Abaseya
Nadh VS, Vasugi K (2014) Corrosion resistance for different types of steels under, alkaline solution. Int Adv Res J Sci Eng Technol 1(1):23–25
Bazant ZP (1979) Physical model for steel corrosion in concrete sea structures–theory. ASCE J Struct Div 105(6):1137–1153
Morinaga S (1988) Prediction of Service Life of Reinforced Concrete Buildings Based on Rate of Corrosion of Reinforcing Steel. Report No. 23. Shimizu Corp, Japan
Wang XM, Zhao HY (1993) The residual service life prediction of RC structures. In: Nagataki S (ed) Durability of building materials and components. E & FN Spon, Washington
IRC (2002) IRC SP 060: An appraoch document for assessment of remaining life of concrete bridges. The Indian Roads Congress, Abhinav Prints New Delhi, New Delhi
El Maaddawy T, Soudki K (2007) A model for prediction of time from corrosion initiation to corrosion cracking. Cement Concr Compos 29(3):168–175. https://doi.org/10.1016/j.cemconcomp.2006.11.004
Kumar V, Singh R, Quraishi MA (2013) A study on corrosion of reinforcement in concrete and effect of inhibitor on service life of RCC. J Mater Environ Sci 4(5):726–731
ABAQUS (2016) ABAQUS standard user’s manual. Version 6:16
Zeng J-M, Duan L, Wang F-M, Chen W-F (1992) Flexural rigidity of reinforced concrete columns. Struct J. https://doi.org/10.14359/2926
ACI 224 (2001) Control of cracking in concrete structures, ACI 224R–01. American Concrete Institute, Detroit
ACI 318 (2014) Building code requirements for structural concrete and commentary, ACI 318–14. American Concrete Institute, Detroit
Malhas AF (2002) Preliminary experimental investigation of the flexural behavior of the flexural behavior of reinforced concrete beams using MMFX steel. MMFX Steel Corporation: Techinal Resources, Schaumburg
Tuutti K (1980) Service life of structures with regard to corrosion of embedded steel, Performance of concrete in marine environment, vol 1. ACI SP-65. American Concrete Institute, Detroit
Thoft-Christensen P (2000) Stochastic modeling of the crack initiation time for reinforced concrete structures. Advanced Technology in Structural Engineering. ASCE Structures Congress, Philadelphia, pp 1–8
CSA A23.3-94 (1994) Design of concrete structures. Canadian Standards Association, Rexadle, ON
Hollinshead K (1998) Corrosion of reinforcement in concrete: electrochemical monitoring. BREPress, Berkshire
Jolley M, Associates R, Fanous F, Phares B, Wipf TJ (2006) Evaluation of corrosion resistance of different steel reinforcement types. Center for Transportation Research and Education Iowa State University, Final Report
Cusson D, Lounis Z, Daigle L (2011) Durability monitoring for improved service life predictions of concrete bridge decks in corrosive environments. Comput-Aided Civil Infrastr Eng 26(7):524–541. https://doi.org/10.1111/j.1467-8667.2010.00710.x
Ranjith A, Balaji Rao K, Manjunath K (2016) Evaluating the effect of corrosion on service life prediction of RC structures—a parametric study. Int J Sustain Built Environ 5(2):587–603. https://doi.org/10.1016/j.ijsbe.2016.07.001
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix 1 (Solved example)
Appendix 1 (Solved example)
It is required to design a RC beams with span of 8 m and is loaded by two point loads equal to 6 ton (factored load). Each load is located at 1/3 of the beam span; it is required also to calculate the service life of that beam.
-
Solution-1 using GUHPC and the steel bars are MMFX (under reinforcement):
-
Concrete Fcu = 2200 kg/cm2
-
Steel Fy = 14,000 kg/cm2
-
Span = 8 m
-
2 point load = 6 ton
-
Moment = 16 m.t.
Sec
Ult. Moment
Breadth
Comp.fl
Depth
C1
J
Asmin
Used
Rft
Mu (m.t)
b (cm)
B (cm)
d (cm)
(cm2)
As
1
16
25
50
45
11.799
0.826
1.69
3.07
3
ϕ
12
-
D (mm) = 12
-
δ0 (mm) = 0.02
-
υ = 0.18
-
C (mm) = 45
-
Ψ =
-
Ψ = D′2/2C(C + D′)
-
Ψ = 0.028237806
-
D′ = 12.04
-
i (μA/cm2) = 0.13
-
Eef (MPa) = 16,417.91045
-
Ec (MPa) = 55,000
-
ϕcr = 2.35
-
fct (MPa) = 25
-
Tcr (days) = 11,285.9
-
Solution-2 using NSC and Conventional steel (under reinforcement):
-
Concrete Fcu = 250 kg/cm2
-
Steel Fy = 3600 kg/cm2
-
Span = 8 m
-
2 point load = 6 ton
-
Moment = 16 m.t
Sec | Ult. Moment | Breadth | Comp.fl | Depth | C1 | J | Asmin | Used | Rft. | ||
|---|---|---|---|---|---|---|---|---|---|---|---|
Mu (m.t) | b (cm) | B (cm) | d (cm) | (cm2) | As | ||||||
1 | 16 | 25 | 50 | 45 | 3.799 | 0.803 | 3.44 | 12.3 | 3 | ϕ | 25 |
-
D (mm) = 25
-
δ0 (mm) = 0.02
-
υ = 0.18
-
C (mm) = 45
-
Ψ =
-
Ψ = D′2/2C(C + D′)
-
Ψ = 0.099467225
-
D′ = 25.04
-
i (μA/cm2) = 0.5
-
Eef (MPa) = 6567.164179
-
Ec (MPa) = 22,000
-
ϕcr = 2.35
-
fct (MPa) = 2.5
-
Tcr (days) = 1194.4
Rights and permissions
About this article
Cite this article
Metwally, I.M., Ghannam, M. Behaviour of green ultra-high-performance concrete beams with corrosion resistant alloy steel (MMFX) bars. SN Appl. Sci. 2, 869 (2020). https://doi.org/10.1007/s42452-020-2632-4
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s42452-020-2632-4