1 Introduction

Scouring is a term used to describe the severe localised wear of bed material around the pier of a bridge that occurs when the corrosive strength of the water exceeds the capacity of the bed material [1, 2]. Scouring at the pier of a bridge considered to be the main reason for bridge failure and, as such, may lead to huge losses of life and economic impacts [3]. General scouring, contraction scouring and local scouring are among the main types of scouring patterns identified at bridge sites [4]. Across the world, researchers have studied the scouring problem under various conditions, determining that the main cause of concern about the stability of bridge foundations is indeed scouring around the bridge piers [5]. Deformation of the river bed is thus a major concern among hydraulic and infrastructure engineers [6, 7], as the presence of various hydraulic structures such as bridges that block flow tend to cause contractions of flow and scouring at the abutments and piers [8, 9].

It is important to anticipate the depth of local scouring around bridge piers for both safety and economic reasons, as over-prediction or under-prediction of the depth of scouring may lead to extra expense during the construction of the bridge or to failure in use [10]. There is, however, a significant amount disagreement and uncertainty relating to the prediction of scour depth in the field, and most bridge failures arise from failures in oversight with regard to the scour problem [11].

In recent years, thanks to the ongoing development of computer science and numerical modelling of hydraulic structures, computational fluid dynamics (CFD) has been used widely n the field of engineering to simulate the behaviours of fluid flow and the resulting depth of scouring at the piers of bridges [12]. A number of recent studies have used Flow-3D as a numerical modelling technique to simulate the depth of scouring around bridge piers [13,14,15], as local scouring around the pier of a bridge may be precisely simulated using the correct Flow-3D model. This Flow-3D model offers a powerful capacity to examine the manner in which gases and liquids move, allowing the solution of transient problems, free surface modelling, and the assessment of sediment transport [16]. The main aim in using a numerical model such as Flow-3D is that, instead of having to design a huge model and expensive appurtenances to allow measurement of specific factors, the behaviours of fundamental fluid movement, incorporating distribution velocity, bed shear, turbulent kinetic energy, and pressures, can be acquired through the application of Flow-3D [17].

Various field conditions effect on the depth of scouring at the piers of a bridge, including pier shape, intensity of flow, flow depth, width of pier, and angle of alignment. Field condition variations make determining the mechanisms of scouring at the pier of a bridge highly complex, making it hard to create a universal equation for predicting local depth of scouring at a given bridge pier. Several different methods have nevertheless been developed to predict the depth of scouring that may occur at a specific site under the described conditions. These methods were developed by specifying certain conditions and using techniques to dictate the depth of the scouring that must then take place. Within the previous literature, several predictive equations have thus been proposed to estimate the local depth of scouring at bridge piers using conventional regression-based mechanisms with both field and experimental data [18]. Recently, [19] indicated that Colorado State University work in [20] and [21] provided reasonable estimates, while [22] also predicted the depth of excessive scouring around a pier successfully, based on a comparison of several bridge pier scouring formulas utilising laboratory and field data. Equations to calculate depth of scouring were developed by these researchers by applying dimensional analysis followed by nonlinear regression analysis; however, this mechanism is low-precision, and its calculations are tedious. Advances in mathematical computation have since been achieved by applying artificial intelligence (AI) techniques, allowing modelling to be done easily, accurately and with little effort [23, 24]. The AI-based inductive modelling techniques revealed in the more recent literature are now widely applied to create complex response functions, including analysis of the scouring mechanisms that occur at bridge piers; these offer robust and nonlinear modelling structures and thus have the ability to define cause and effect relationships for such complicated operations. The relevant AI technologies include artificial neural networks (ANN), adaptive neural fuzzy inference system (ANFIS), genetic programming (GP), genetic algorithms (GA), and gene expression programming (GEP) [18, 25], as well as alternative synthesis processors that incorporate artificial neural networks with an adaptive neurotransmitter system [26]. The latter was recently adopted because it gives effective estimations of local scouring depth, while ANNs have been used frequently due to their reasonable solutions to various problems of hydraulic engineering that arise due to the extremely complicated non-linear relationships between input and output parameters for the corresponding data [27, 28]. Another key tool is the GEP Soft Computing Technologies tool, which has recently replaced several other tools due to its ease of coding, rapid calculations, and simple modelling. Several researchers in different fields of engineering have thus illustrated that the use of AI techniques is more exact and functional than the application of other, older, technologies [29, 30].

A review of existing studies suggested, however, that the application of GEP for the prediction of scour depth around bridge piers had not been implemented on a large scale, creating an immediate need for action in this regard. In the current study, therefore, the main objective is to develop a new scour depth formula based on the use of parameters such as flow depth, flow intensity, pier Froud number, pier width, and pier shape by using GEP with data from numerical simulation, to allow GEP performance to be compared with that of NLR models.

GEP and NLR models were thus used for formulaic prediction of the local depth of scouring at the pier of a bridge based on data obtained from numerical simulations in Flow-3D, which were divided into a training and a validation data set. The dimensionless parameters of flow intensity, pier width ratio, flow depth ratio, pier shape and pier Froude number were selected as the effective parameters for predicting local depth of scour, and these dimensionless parameters were utilised as output and input variables in both GEP and NLR models. The best technique for predicting local scouring depth around a bridge pier was assessed using three statistical parameters: RMSE, R2, and MAE. After the best technique was identified, sensitivity analysis was also conducted to identify the most sensitive parameter for the prediction of scour depth, for the purposes of focusing future studies.

2 Dimensional analysis of local scouring around a bridge pier

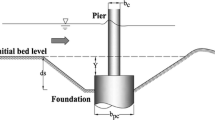
The first step towards determining the functional relationships affecting scour depth was the selection of the parameters controlling the depth of scouring, that is, the characteristics of bed heights upstream and downstream of the pier. The parameters that impact on the depth of scouring around a bridge pier under clear water conditions are illustrated in Fig. 1. In the current study, the important parameters affecting local scour depth were defined as the velocity of approaching flow (V), the critical velocity of approaching mean flow (Vc), flow depth (y), gravitational acceleration (g), fluid density (ρ), median sediment size (\(d_{50} )\), channel width (B), pier width (b), the pier shape factor (\(K_{s}\)), the correlation factor of flow alignment (\(K{\uptheta }),\) and flow time (t). Nine shapes of pier were used in this study: circular, square, rectangular, elliptic, oblong, ogival, lenticular, hexagonal, and octagonal. All pier models were aligned to the flow at a zero angle of alignment, causing the t correlation factor of flow alignment, \(K{\uptheta },{\text{ to be }}\) equal to one in all cases. The time of flow was similarly set as equal to 30 min. for all cases in this study. Studying the remaining effective factors influencing the depth of local scouring (ds) and its mechanisms thus allowed the functional relationships of general dimension analysis to be written as [17]

$$ds = f_{1} \left( {V,y,g,d_{50} ,V_{c} ,B,b,K_{s} ,K\theta ,\rho , t } \right)$$
(1)
Fig. 1
figure 1

Flow and local scouring and flow features around a circular pier of the bridge [32]

Full size image

The main reason for the use of dimensional analysis is to formulate a problem in way that describes the relationship between the various quantities based on the selection of their dimensions. By using Buckingham π-theorem and selecting ρ, V, and b as the repeated variables while considering ρ,\({ }d_{50}\), \(K{\uptheta }\), t as constant parameters so that their effects may be ignored, the final dimensionless function that describes the influence of the variables on local depth of scouring around the pier of a bridge was extracted as illustrated in Eq. (2).

$$\frac{{d_{s} }}{b} = f_{2} \left( { \frac{V}{{V_{c} }} , K_{s} , \frac{B}{b} , \frac{y}{b},\frac{V}{{\sqrt {gb} }}} \right)$$
(2)

where \(\frac{{{\text{d}}_{{\text{s}}} }}{{\text{b}}}\) represents the maximum scour depth ratio, \(\frac{V}{{V_{c} }}\) is the intensity of flow, \(\frac{B}{b}\) is the ratio of pier width, \(\frac{{\text{y}}}{{\text{b}}}{ }\) is the ratio of flow depth, and \(\frac{V}{{\sqrt {gb} }}\) represents the pier Froude number (\(Fr_{p} )\). These dimensionless parameters were then used to develop new scour depth formulae utilising GEP and NLR models.

3 Numerical simulation data sets

Localised scouring problems in bridge piers with different shapes of piers and various conditions of flow have been studied numerically by applying Flow-3D model previously. In particular, flow-3D models have been used to state the maximum depth of scouring occurring at a bridge pier to define the critical parameters in bridge design. To validate the efficacy of the Flow-3D model in terms of simulating the local scour depth at a bridge pier, the results from the Melville [8] laboratory model were compared with the results obtained from the relevant Flow-3D numerical simulation model. The error rate obtained from this comparison of results was equal to 10%, indicating good validation between the numerical simulation model and the Melville [8] laboratory model, and suggesting that Flow-3D is an effective method for simulating the depth of local scouring at the pier of a bridge. The total number of data sets obtained from numerical simulation was 243, each of which represented the maximum depth of local scouring occurring at the pier of a bridge with certain parameter values, based on variations in intensity of flow, flow depth ratio, pier shape factor, pier width ratio, and pier Froude number. The range of these parameters is summarised in Table 1. These data were then divided into an 80% training group and a 20% validation group before being modelled in GEP, ANN, and NLR to develop the required scour depth equations. Scour depth ratio (ds/b) was taken as the dependent parameter in the prediction formulae, while the other parameters were deemed to be independent. Three statistical parameters, R2, RMSE, and MAE, were then used to identify the best techniques for predicting the maximum scour depth ratio (ds/b) at a given bridge pier.

Table 1 The limitations of the variables used in the training and validating of the GEP and NLR models
Full size table

4 Gene Expression Programming (GEP)

GEP is a modern technology based on evolutionary artificial intelligence (AI) that may be considered an extension of genetic programming (GP). GEP combines the advantages of both GP and genetic algorithms (GA) in terms of providing both modest and fixed length linear chromosomes in the form of genomes and different shapes and sizes of branched structures known as expression trees (ETs) in the form of phenotypes, similar to those used in GP analysis trees [31, 32]. The goal of using the GEP method is to create a simple arithmetical model, and such arithmetical functions can be prepared by providing a data set to the GEP model. The mathematical equation implemented in the GEP model during the current study was a symbolic regression on most GA genotypes. The procedure of creating such a mathematical model begins with the generation of a random chromosome within a specific primary population; each chromosome from the primary population was thus evaluated using the fitness function against a group of fitness conditions. The selection of chromosomes relies on these fitness values, as chromosomes with higher fitness values have more chances to be selected for the next generation. After the selection of chromosomes, genetic operations may be introduced to make modifications to the selected chromosomes; these genetic operations include inversion, mutation, transposition of gene, root insertion sequence transposition (RIS), insertion sequence transposition (IS), recombination of the gene, and single or double crossover/recombination, as described in more detail in Ferreira [31]. Mutation is the most common genetic operation used to modify chromosomes. The process is then repeated until acceptable results have been obtained or a certain number of generations has passed [33].

These processes as used to create a mathematical model are represented in Fig. 2. GEP of this type has recently been applied in several different fields, including the transportation of sediment in sewer pipes [34], the syntax of sentence ordering functions [35], the development of rain runoff models [36], the prediction of hydraulic data [37], the modelling of time series [38], image compression, and multi-objective mining for classification base [39].

Fig. 2
figure 2

Gene expression algorithm flow diagram [34]

Full size image

The powerful software package GeneXproTools 5.0 was used in the current study to promote the development of GEP-based models for predicting the ultimate depth of scouring that may occur at the pier of a bridge. GEP provides an arithmetical function of a scouring model to solve the problem using symbolic regression (function finding). The resulting function can then be used to find a term that demonstrates the dependence satisfactorily.

5 Modelling the depth of local scouring around a bridge pier

5.1 GEP Model

To develop the GEP model to predict local scouring occurring around a bridge pier, 243 data sets were collected and simulated numerically using Flow-3D software. These data were then fed to the GEP in the form of a dependent output variable (ds/b) and independent input variables (\(\frac{V}{{V_{c} }},{ }\frac{{\text{B}}}{{\text{b}}},\frac{{\text{y}}}{{\text{b}}},{\text{K}}_{{\text{s}}} ,{\text{ Fr}}_{{\text{p}}} { }\)), with the output variable ds/b then developed using the GEP. The data were divided randomly by the GEP into validation and testing data (20%) and training data (80%) sets, with the training data used to build the GEP model. The parameters and processes within the GEP were then defined in six steps to facilitate the generation of the mathematical function required to predict local scouring around a bridge pier.

The first step was to generate an initial population group. Any size of population may be used at this stage, but the study done by Ferreira [33] suggested that a population of 30 to 100 offers optimal results. Several trials were thus done to select the optimum number, and the population used in the study was finally set to 50 chromosomes as this size of population offered the best results. The next stage was to measure the fitness function of each individual chromosome as calculated by RMSE. The third step was determining groups of both functions and terminals for each chromosome gene. The terminal set consisted of the independent parameters and a random numerical constant (RNC), so that T = {\(\frac{V}{{V_{c} }},{ }\frac{{\text{B}}}{{\text{b}}},{ }\frac{{\text{y}}}{{\text{b}}},{\text{ K}}_{{\text{s}}} { },{\text{Fr}}_{{\text{p}}} ,{\text{ X }}\)}, with X representing the RNC, while basic arithmetical operations and some mathematical functions were used for the function set, in the form F = {+ , −, *, /, power}.

The fourth stage managed the architecture of the chromosomes based on the selection of head length and gene number, as incrementing gene number from one to three in the chromosome helps with increasing the rate of success according to Ferreira [33]. The adopted length of chromosome head (h) in this study was thus set to eight, while the selected number of genes per chromosome was set to three. Five random floating types (Dc) in the range {−10,10} were then used to represent the random numerical constants. In stage five, a connect function between the sub expression trees (sub-ETs) was selected; as there were three genes per chromosome, the final equation of these sub-ETs was linked by addition ( +), and a selection of genetic operators to make allow variations in both type and rate of expression. A mix of all genetic operators was used in this study, including transposition (gene transposition, IS, and RIS), mutation, (gene recombination, both one-point and two-point), inversion, and Dc-specific genetic operations. The rates of these genetic operations are illustrated in Table 2.

Table 2 GEP model parameters for the local scouring problem
Full size table

After determining all genetic parameters, the model was simulated using GeneXproTools 5.0 for a number of generations in excess of 65,000. The resulting scour depth (ds/b) formula is represented in expression tree (ET) form in Fig. 3, while the corresponding equation is offered in Eq. 3.

Fig. 3
figure 3

GEP Expression Trees (ET) to formulate the scour depth formula

Full size image

The depth of scour (ds/b) equation was thus

$$\frac{ds}{b} = 7.24*\frac{V }{{V_{C} }}*\frac{b }{{B }} - \left( {\frac{V }{{V_{C} }}} \right)^{2} *\frac{b }{{B }} - \frac{V }{{V_{C} }}*\left( {\frac{b }{{B }}} \right)^{2} + \frac{\frac{b}{B}}{{\frac{b}{B}*\frac{V }{{V_{C} }} - \frac{y }{{b }} - \frac{b }{{B }}}} + \left[ {\left( {\frac{y }{{b }}*\frac{b }{B}*Fr_{P} + \left( {\frac{b }{{B }}} \right)^{2} *Fr_{P} } \right)*Ks^{2} *\frac{V }{{V_{C} }}} \right]$$
(3)

with the definition of parameters as used in Eq. 3 and the relevant ET represented in Table 3.

Table 3 Definition of parameters in ETs
Full size table

5.2 NLR Predicting model

For the non-linear regression (NLR) model, the data required were divided in a similar manner to that used in the development of the GEP model (training and validation data sets). The first step in building this predicting model was to try a linear model, which offered an R2 = 0.67, suggesting that this failed to represent an accurate prediction of scour depth. It was also found that all appropriate prediction models were nonlinear. Equation (4) thus displays the relationship between the relative scour depth (ds/b) and other independent parameters.

$$\frac{ds}{b} = 0.496 - 9.7 \frac{V}{{V_{C} }} + 0.01 \frac{y}{b} - 3.29 \frac{b}{B} - 0.388 K_{S} + 9.12 Fr_{p} - 0.282 \left( \frac{y}{b} \right)^{2}$$
(4)

6 Discussion

The main aim of this study was to evaluate GEP model efficiency in predicting local depth of scouring at the pier of a bridge by comparing the model’s performance with that of the NLR model. A total data set of 243 cases were obtained using Flow-3D numerical simulation software, and these data were then used to develop new scour depth around a bridge pier formula using GEP and NLR models. The predicted scour depth was computed using both GEP and NLR models and plotted against the measured scour depth, as represented in the scatterplots in Figs. 4, 5 for the training and testing data sets, respectively. The reason for using scatterplots was to investigate the degree of similarity between the measured ​​and the predicted values more intuitively. The statistical measures R2, MAE, and RMSE were also calculated for all models, as illustrated in Table 4. The statistical results shown in Table 4 identify the equation that offers the fewest errors in prediction, suggesting that GEP performs better than NLR. The GEP model produced a higher value of R2 (0.901) and smaller values for RMSE (0.141) and MAE (0.111), with less scatter around the line of agreement than the NLR. The unique properties of the GEP model also provide a clear, easy-to-use experimental expression of the bridge pier depth of scour model, as represented in Eq. 3. Although the NLR model offered worse performance than the GEP model, it still gave reasonably good results; GEP’s main contribution is thus this compressed and explicit arithmetic expression, which is likely to be useful for future designers.

Fig. 4
figure 4

Comparison between GEP and NLR modes for training data

Full size image
Fig. 5
figure 5

Comparison between GEP and NLR modes for testing data

Full size image
Table 4 The statistical results for GEP and NLR models
Full size table

7 Sensitivity test

In order to determine the influence of each of independent parameter on the predicted scour depth, to ensure the correct factors receive extensive attention in future studies, sensitivity testing was adopted to determine the most sensitive parameters. Many factors affect the value of local scouring depth around a bridge pier, including the flow intensity, width of pier, shape of pier, and depth of flow. Various different input combinations were studied, as illustrated in Table 4, with GEP models compared with each independent parameter by eliminating one input parameter in each case and determining the effect on the expected scour depth in terms of the root mean square error (RMSE) and coefficient of determination (R2), the same statistical parameters used for evaluating the main performance criteria. The results in Table 5 and Fig. 6 indicate that the depth of the flow approach has the most significant influence on the predicted depth of scouring after eliminating any remaining input parameters with no significant effect on the predicted depth of scouring.

Table 5 Sensitivity test for input parameters for the testing data
Full size table

8 Conclusion

The local scouring that occurs around a bridge pier is a complex phenomenon that can be difficult to measure; however, there is an urgent need to predict the depth of such scouring accurately to ensure safety. Numerical simulations were used to obtain 243 data sets that were then used to generate mathematical models that allowed a comparison of the use of GEP and NLR [5]. The results suggested that the performance of the local scour depth formula derived from the GEP model was better than that derived from the conventional NLR model, as shown in Table 4. The GEP produced smaller values of RMSE (0.141) and MAE (0.111) and a greater value of R2 (0.901). The GEP model was also characterised by a clear and brief equation suitable for easy use by bridge engineers. This feature makes the GEP option more effective as compared to the NLR model. The GEP model thus offers an effective modelling tool for predicting local scour depth as well as providing a simple empirical expression for the modelled response function. Sensitivity analysis then showed that the flow depth parameter has impact on scour depth prediction among the input parameters examined.

Equation 3, obtained from the GEP model, can thus help bridge pier designers to identify the maximum depth of scour that may occur at a bridge pier under conditions such as those covered in this study. The parameter limitations for Eq. 3 thus include intensity of flow (0.55 to 1), ratio of flow depth (0.2 to 2.95), ratio of pier width (0.11 to 0.2), pier shape factor (0.71 to 1.26) and for pier Froude number (0.12 to 0.47). In terms of future studies, the further development of Eq. (3) to include the influence of sediment size, alignment angle, and channel width, by using different ranges of these parameters to study their effects on local depth of scour, is recommended.