1 Introduction

Nowadays, micro-scale structures including beams and plates are widely used in industry and in the micro-electro-mechanical-systems (MEMS) due to their superior mechanical, chemical, and electronic properties [1,2,3]. Micro plates have a wide variety of applications as actuators or sensors in switches, pressure sensors, micro-pumps, and moving valves [3]. Therefore, there is a crucial need to study the behavior of these structures with sufficient accuracy. In the literature, it is shown that the behavior of micro-scale structures cannot be predicted correctly based on the classical continuum theories and higher order ones are needed. To consider the size effects and overcome the deficiency of the classical continuum models, some non-classical theories have been presented such as micropolar theory [4], non-local elasticity theory [5], strain gradient theory [6], surface elasticity theory [7], classical couple stress theory [8,9,10] and the modified couple stress theory (MCST) [11]. Based on the non-classical theories, a wide range of recent studies is devoted to investigate the mechanical behavior of size-dependent structures. To mention some more recent ones, some researchers used the strain gradient theory to study the behavior of micro/nano beams [12] and plates [13, 14], while some others used the non-local elasticity theory to analyze the size dependent beams [15, 16] and plates [17,18,19]. Among different non-classical continuum theories, the modified couple stress theory [11] incorporates only one length scale parameter and is preferred over the others due to its simplicity and has been intensively used to study the size dependent structures [20, 21]. Here, the studies on isotropic and homogenous micro plates including bending, buckling, and vibration behaviors using the MCST are reviewed.

Tsiatas [22] studied the bending behavior of a Kirchhoff micro plate with various boundary conditions using a meshless method. Roque et al. [23] carried out the bending analysis of an isotropic Mindlin micro plate using both the Navier method and a meshless method and presented the results for clamped and simply supported plates. Akbaş [24] studied the bending behavior of a Kirchhoff–Love rectangular nano plate using the differential quadrature method. They reported the results for simply supported nano plates. Shaat et al. [25] presented a bending analysis of simply supported Kirchhoff nano plates employing the Navier method. They used surface elasticity theory of Gurtin and Murdoch in conjunction with the MCST in order to include surface effects of nano plates. Based on the Kirchhoff plate theory, Tahani et al. [26] analyzed the free vibration of electrostatically pre-deformed rectangular micro plates using the finite element method. Based on the Kirchhoff plate theory, Yin et al. [27] carried out a vibration analysis of rectangular micro plates employing the Levy method. Jomezadeh et al. [28] performed a vibration analysis of rectangular Kirchhoff micro plates using a Levy-type solution method. Askari and Tahani [29] employed the extended Kantorovich method to analyze the vibration behavior of a Kirchhoff micro plate. They presented the results for a fully clamped micro plate. Asghari and Taati [30] proposed a general model for Kirchhoff micro plates with arbitrary shapes considering the MCST. Ke et al. [31] determined natural frequencies of a Mindlin rectangular micro plate adopting the P-version Ritz method to examine all the possible types of boundary conditions. Ma et al. [32] carried out the bending and free vibration analyses of a simply-supported Mindlin micro plate using the Navier method. Gao et al. [33] presented the Navier solution for bending and vibration analyses of isotropic simply supported micro plates based on the third-order shear deformation theory. Darijani and Shahdadi [34] employed a refined plate theory to analyze the bending and vibration of a rectangular micro plate with simply supported edges, using the Navier method. Lou et al. [35] performed the buckling and post-buckling analyses of piezoelectric hybrid micro plates subjected to thermo-electro-mechanical loads based on the Mindlin plate theory using the Navier method. Based on the MCST and strain gradient theory, Mohammadi and Fooladi Mahani [36] determined the buckling loads of Kirchhoff micro plates using the Levy method. They compared the results obtained within the two mentioned theories and studied the effects of length scale parameters on buckling loads. Mirsalehi et al. [37] used spline finite strip method to study the stability of a Kirchhoff micro plate. Akgöz and Civalek [38] investigated the bending, buckling and vibration of a size dependent Kirchhoff plate embedded in a Winkler’s elastic medium using the Navier method. Zhang et al. [39] used finite element method to study the bending, buckling, and free vibration of Mindlin micro plates based on the MCST. It is to be emphasized that boundary supports have significant influence on the mechanical behavior of plates and many attempts have been reported to study this effect via the Galerkin [14], Meshless [22], finite element [26, 39], Levy [27, 28], and spline finite strip [37] methods.

The classical plate theory (CPT) based on the Kirchhoff assumptions provides reliable results for thin plates since the transverse shear effect is neglected in this theory. To overcome shortcomings of the CPT, many shear deformation plate theories are introduced. Mindlin [40] and Reissner [41] proposed displacement-based and stress-based first-order shear deformation theories (FSDT), respectively, which result in constant transverse shear stresses and need shear correction factor. Reissner [42] was the first who uncoupled the six-order equations governing the mechanical behavior of isotropic homogenous plates within FSDT into edge-zone and interior equations. Recently, Nosier and Fallah [43, 44] and Fallah et al. [45] carried out such an uncoupling for tenth-order equations within FSDT, governing linear [43] and nonlinear [44] bending behavior of FG plates as well as stability of sandwich shells [45]. Here, since the deflection, the first three natural frequencies, and buckling load of thin and moderately thick homogenous isotropic plates are reported, the FSDT (Mindlin theory) is accurate enough, however, in order to accurately model FG, composite, and sandwich beams, plates, and shells and overcome the drawbacks of the FSDT, many higher-order shear deformation theories were proposed. More recently, there are attempts to reduce the number of unknowns and remove the need to shear correction factor in shear deformation theories [46]. Matouk et al. [15] and Bousahla et al. [47] used the integral Timoshenko beam theory with three unknowns which needs a shear correction factor to study the dynamic behavior of nano-beams, while Adda Bedia et al. [12] developed a hyperbolic three-unknown beam theory, which could capture shear deformation effects accurately and does not need any shear correction factor. Boutaleb et al. [19], Joshan et al. [48], and Tounsi et al. [49] employed the idea of considering an unknown integral term in the displacement field (as in [15, 47]) in conjunction with cubic, inverse hyperbolic, and trigonometric shear strain shape functions to have four-variable plate theories which consider transverse shear effects accurately. Sinusoidal and inverse hyperbolic shear strain shape functions as the plate models are used in [13, 50], respectively, which capture shear effects without any need to shear correction factor. The idea of considering the transverse deflection as a sum of two unknown functions representing the bending and shear effects as in [12] in conjunction with cubic and sinusoidal shape functions of transverse shear deformation were employed in [14, 51], respectively, resulting in four unknowns in displacement field while taking into account transverse shear effects.

Due to application of micro and nano plates as actuators and sensors, it is crucial to model them with enough accuracy. While the effects of transverse shear and effects of boundary supports on the mechanical responses of plates are significant, it appears from the literature review that there is no analytical solution for micro plates having different boundary conditions and being modeled within shear deformation plate theories in conjugation with MCST. Even though a Levy-type solution [27, 28, 36], or the extended Kantorovich method [29] has been implemented to analyze Kirchhoff micro plates, the governing equations within the first order or higher order micro plate theories are solved using just the Navier method [32,33,34,35] or numerical methods [23, 31, 39]. That is, to the best of authors’ knowledge, analytical solutions within shear deformation micro plate theories are available for just simply-supported ones. Since, not only the thickness of micro plate but also the boundary supports have significant effects on accuracy and validity of the Kirchhoff model, there is a gap in the literature for analytical solutions to mechanical behavior of Mindlin micro plates with different boundary conditions within MCST. In this paper, an attempt is made to develop analytical solution for bending, buckling and vibration problems of Mindlin micro plates with different boundary conditions within MCST for the first time. To this end, Hamilton's principle is used to derive the equations governing the bending, buckling and free vibration behavior of a micro plate with arbitrary boundary conditions based on the first-order shear deformation and modified couple stress theories. A Levy-type solution in conjunction with the state-space method is adopted to solve the governing equations for micro plates with two simple supports at opposite edges and arbitrary supports at the other ones. It is to be noted that the adoption of the state-space method in this problem was not straightforward, needed some mathematical operations, and is applicable within other shear deformation theories. Maybe this is the reason that the problem of Mindlin micro plate is not solved via the Levy method until now. The effect of different parameters on center deflections, buckling loads and natural frequencies of the micro plate is studied in detail. The analytical results presented here can be used as a benchmark for future studies.

2 Theoretical formulation

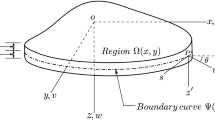
Here, an isotropic rectangular micro plate of length \(a\), width \(b\), and uniform thickness \(h\) under transverse (\(P\left( {x,y} \right)\)) and in-plane loadings (\(\hat{N}_{xx}\) and \(\hat{N}_{yy}\)) is considered. The geometry of the plate, the Cartesian coordinate system and the loadings are shown in Fig. 1.

Fig. 1
figure 1

Geometry of the rectangular plate, the coordinate system, and the loadings

Full size image

2.1 Equations of motion and boundary conditions

Based on the Hamilton's principle, the equations of motion of a rectangular micro plate are obtained. This principle can be expressed as [52]:

$$\mathop \int \limits_{0}^{t} \left( {\delta U + \delta V - \delta K} \right){\text{d}}t = 0$$
(1)

where \(U\) is the strain energy, \(K\) is the kinetic energy, and \(V\) is the potential of work done by the external forces which are defined as follows [11]:

$$K = \mathop \int \limits_{{\overline{V}}}\, \frac{1}{2}\rho \left( {\dot{u}_{i} \dot{u}_{i} } \right){\text{d}}\overline{V}, U = \mathop \int \limits_{{\overline{V} }} \frac{1}{2}\left( {\sigma_{ij} \varepsilon_{ij} + m_{ij} \chi_{ij} } \right){\text{d}}\overline{V},\quad i, j = x, y,z$$
(2a)
$$V = - \mathop \int \limits_{A} \left( {Pu_{z} - \frac{1}{2}\hat{N}_{xx} \left( {\frac{{\partial u_{z} }}{\partial x}} \right)^{2} - \frac{1}{2}\hat{N}_{yy} \left( {\frac{{\partial u_{z} }}{\partial y}} \right)^{2} } \right){\text{d}}A$$
(2b)

In Eq. (2), \(u_{i}\) are the components of the displacement vector, \(\sigma_{ij}\) and \(m_{ij}\) are components of the Cauchy stress tensor and the deviatoric symmetric couple stress tensor, respectively, \(\overline{V}\) is the volume of the plate, \(A\) denotes the surface of the mid-plane, and a dot over the variable (.) indicates differentiation with respect to time. In addition, in Eq. (2b), the first term in the right hand side of the relation is the potential of work done by the transverse pressure \(P\) (considered in bending analysis), while the second and third terms are the work done by the in-plane forces \(\hat{N}_{xx}\) and \(\hat{N}_{yy}\) in buckling analysis, in which any stretching of the middle plane is ignored and the in-plane forces are assumed to be constant during buckling [53]. Furthermore, the components of strain tensor \(\varepsilon_{ij}\), rotation vector \(\theta_{i}\), and symmetric curvature tensor \(\chi_{ij}\) are defined as follows [52]:

$$\varepsilon_{ij} = \frac{1}{2}\left[ {u_{i,j} + u_{j,i} } \right], \theta_{i} = \frac{1}{2}e_{ijk} u_{k,j} , \chi_{ij} = \frac{1}{2}\left[ {\theta_{i,j} + \theta_{j,i} } \right],\quad i, j, k = x, y, z$$
(3)

where a comma followed by a coordinate variable denotes partial derivative with respect to that variable and \(e_{ijk}\) is the permutation symbol.

The displacement field of the first-order shear deformation (Mindlin) plate theory is as follows:

$$\begin{aligned} u_{x} \left( {x,y,z,t} \right) & = u\left( {x,y,t} \right) - z\psi \left( {x,y,t} \right) \\ u_{y} \left( {x,y,z,t} \right) & = v\left( {x,y,t} \right) - z\phi \left( {x,y,t} \right) \\ u_{z} \left( {x,y,z,t} \right) & = w\left( {x,y,t} \right) \\ \end{aligned}$$
(4)

where \(u\), \(v\), and \(w\) denote the displacements of a point on the mid-plane of the plate along \(x\), \(y\), and \(z\) directions, respectively, and \(\psi\) and \(\phi\) represent the small rotations of a transverse normal about the \(y\) and \(x\) axis, respectively.

Upon substitution of Eqs. (4) into (3), the components of strain and curvature fields are obtained as follows:

$$\varepsilon_{x} = \varepsilon_{x}^{0} + zk_{x} , \varepsilon_{y} = \varepsilon_{y}^{0} + zk_{y} , \varepsilon_{z} = 0, \varepsilon_{xy} = \varepsilon_{xy}^{0} + zk_{xy} , \varepsilon_{xz} = k_{xz} , \varepsilon_{yz} = k_{yz}$$
(5a)

where

$$\begin{aligned} \varepsilon_{x}^{0} & = \frac{\partial u}{{\partial x}}, \quad \varepsilon_{y}^{0} = \frac{\partial v}{{\partial y}}, \quad \varepsilon_{xy}^{0} = \frac{1}{2}\left( {\frac{\partial u}{{\partial y}} + \frac{\partial v}{{\partial x}}} \right) \\ k_{x} & = - \frac{\partial \psi }{{\partial x}}, \quad k_{y} = - \frac{\partial \phi }{{\partial y}}, \quad k_{xy} = - \frac{1}{2}\left( {\frac{\partial \psi }{{\partial y}} + \frac{\partial \phi }{{\partial x}}} \right) \\ k_{xz} & = \frac{1}{2}\left( {\frac{\partial w}{{\partial x}} - \psi } \right), \quad k_{yz} = \frac{1}{2}\left( {\frac{\partial w}{{\partial y}} - \phi } \right) \\ \end{aligned}$$
(5b)

and

$$\chi_{x = } \chi_{x}^{0} , \chi_{y = } \chi_{y}^{0} , \chi_{z = } \chi_{z}^{0} , \chi_{xy = } \chi_{xy}^{0} , \chi_{xz = } \chi_{xz}^{0} + z\chi_{xz}^{1} , \chi_{yz = } \chi_{yz}^{0} + z\chi_{yz}^{1}$$
(5c)

where

$$\begin{aligned} \chi_{x}^{0} & = \frac{1}{2}\left( {\frac{{\partial^{2} w}}{\partial x\partial y} + \frac{\partial \phi }{{\partial x}}} \right), \quad \chi_{y}^{0} = - \frac{1}{2}\left( {\frac{{\partial^{2} w}}{\partial x\partial y} + \frac{\partial \psi }{{\partial y}}} \right), \quad \chi_{z}^{0} = - \frac{1}{2}\left( {\frac{\partial \phi }{{\partial x}} - \frac{\partial \psi }{{\partial y}}} \right) \\ \chi_{xy}^{0} & = \frac{1}{4}\left( {\frac{{\partial^{2} w}}{{\partial y^{2} }} + \frac{\partial \phi }{{\partial y}} - \frac{{\partial^{2} w}}{{\partial x^{2} }} - \frac{\partial \psi }{{\partial x}}} \right), \quad \chi_{xz}^{0} = \frac{1}{4}\left( {\frac{{\partial^{2} v}}{{\partial x^{2} }} - \frac{{\partial^{2} u}}{\partial x\partial y}} \right), \quad \chi_{yz}^{0} = \frac{1}{4}\left( {\frac{{\partial^{2} v}}{\partial x\partial y} - \frac{{\partial^{2} u}}{{\partial y^{2} }}} \right) \\ \chi_{xz}^{1} & = - \frac{1}{4}\left( {\frac{{\partial^{2} \phi }}{{\partial x^{2} }} - \frac{{\partial^{2} \psi }}{\partial x\partial y}} \right), \quad \chi_{yz}^{1} = - \frac{1}{4}\left( {\frac{{\partial^{2} \phi }}{\partial x\partial y} - \frac{{\partial^{2} \psi }}{{\partial y^{2} }}} \right) \\ \end{aligned}$$
(5d)

By substitution of Eq. (5) into Eqs. (1) and (2) and using the fundamental lemma of calculus of variation, the equations of motion of a micro plate subjected to transverse and in-plane loadings are obtained as follows:

$$\begin{aligned} & \delta u : \frac{{\partial N_{x} }}{\partial x} + \frac{{\partial N_{xy} }}{\partial y} + \frac{1}{2}\frac{{\partial^{2} H_{xz} }}{\partial x\partial y} + \frac{1}{2}\frac{{\partial^{2} H_{yz} }}{{\partial y^{2} }} = I_{0} \frac{{\partial^{2} u}}{{\partial t^{2} }} \\ & \delta v : \frac{{\partial N_{y} }}{\partial y} + \frac{{\partial N_{xy} }}{\partial x} - \frac{1}{2}\frac{{\partial^{2} H_{xz} }}{{\partial x^{2} }} - \frac{1}{2}\frac{{\partial^{2} H_{yz} }}{\partial x\partial y} = I_{0} \frac{{\partial^{2} v}}{{\partial t^{2} }} \\ & \delta \psi : \frac{{\partial M_{x} }}{\partial x} + \frac{{\partial M_{xy} }}{\partial y} - Q_{x} + \frac{1}{2}\frac{{\partial H_{y} }}{\partial y} - \frac{1}{2}\frac{{\partial H_{z} }}{\partial y} + \frac{1}{2}\frac{{\partial H_{xy} }}{\partial x} + \frac{1}{2}\frac{{\partial^{2} G_{xz} }}{\partial x\partial y} + \frac{1}{2}\frac{{\partial^{2} G_{yz} }}{{\partial y^{2} }} = I_{2} \frac{{\partial^{2} \psi }}{{\partial t^{2} }} \\ & \delta \phi : \frac{{\partial M_{y} }}{\partial y} + \frac{{\partial M_{xy} }}{\partial x} - Q_{y} - \frac{1}{2}\frac{{\partial H_{x} }}{\partial x} + \frac{1}{2}\frac{{\partial H_{z} }}{\partial x} - \frac{1}{2}\frac{{\partial H_{xy} }}{\partial y} - \frac{1}{2}\frac{{\partial^{2} G_{xz} }}{{\partial x^{2} }} - \frac{1}{2}\frac{{\partial^{2} G_{yz} }}{\partial x\partial y} = I_{2} \frac{{\partial^{2} \phi }}{{\partial t^{2} }} \\ & \delta w : \frac{{\partial Q_{x} }}{\partial x} + \frac{{\partial Q_{y} }}{\partial y} - \frac{1}{2}\frac{{\partial^{2} H_{x} }}{\partial x\partial y} + \frac{1}{2}\frac{{\partial^{2} H_{y} }}{\partial x\partial y} - \frac{1}{2}\frac{{\partial^{2} H_{xy} }}{{\partial y^{2} }} + \frac{1}{2}\frac{{\partial^{2} H_{xy} }}{{\partial x^{2} }} + P = I_{0} \frac{{\partial^{2} w}}{{\partial t^{2} }} - \hat{N}_{xx} \frac{{\partial^{2} w}}{{\partial x^{2} }} - \hat{N}_{yy} \frac{{\partial^{2} w}}{{\partial y^{2} }} \\ \end{aligned}$$
(6)

where the stress and moment resultants and the mass inertias, \(I_{0}\) and \(I_{2}\) in Eq. (6) are defined as follows:

$$\begin{aligned} & \left( {N_{x} , N_{y} ,N_{xy} } \right) = \mathop \int \limits_{{ - \frac{h}{2}}}^{\frac{h}{2}} \left( {\sigma_{xx} ,\sigma_{yy} ,\sigma_{xy} } \right){\text{d}}z, \left( {Q_{x} ,Q_{y} } \right) = k^{2} \mathop \int \limits_{{ - \frac{h}{2}}}^{\frac{h}{2}} \left( {\sigma_{xz} ,\sigma_{yz} } \right){\text{d}}z \\ & \left( {M_{x} ,M_{y} ,M_{xy} } \right) = \mathop \int \limits_{{ - \frac{h}{2}}}^{\frac{h}{2}} \left( {\sigma_{xx} ,\sigma_{yy} ,\sigma_{xy} } \right)z{\text{d}}z \\ & \left( {H_{x} ,H_{y} ,H_{xz} ,H_{yz} ,H_{xy} ,H_{z} } \right) = \mathop \int \limits_{{ - \frac{h}{2}}}^{\frac{h}{2}} \left( {m_{xx} ,m_{yy} ,m_{xz} ,m_{yz} ,m_{xy} ,m_{zz} } \right){\text{d}}z \\ & \left( {G_{xz} ,G_{yz} } \right) = \mathop \int \limits_{{ - \frac{h}{2}}}^{\frac{h}{2}} \left( {m_{xz} ,m_{yz} } \right)z{\text{d}}z \\ & I_{0} = \rho h, \quad I_{2} = \frac{1}{12}\rho h^{3} \\ \end{aligned}$$
(7)

where \(k^{2}\) is a shear correction factor. The boundary conditions corresponding to Eq. (6) require the specification of the followings:

$$\begin{aligned} & \delta u\;{\text{or}}\;(N_{x} + \frac{1}{2}\frac{{\partial H_{xz} }}{\partial y})n_{x} + \left( {N_{xy} + \frac{1}{2}\frac{{\partial H_{xz} }}{\partial x} + \frac{1}{2}\frac{{\partial H_{yz} }}{\partial y}} \right)n_{y} \\ & \delta \frac{\partial u}{{\partial y}}\;{\text{or}}\;H_{yz} n_{y} \\ & \delta v\;{\text{or}}\; \left( {N_{xy} - \frac{1}{2}\frac{{\partial H_{xz} }}{\partial x} - \frac{1}{2}\frac{{\partial H_{yz} }}{\partial y}} \right)n_{x} + \left( {N_{y} - \frac{1}{2}\frac{{\partial H_{yz} }}{\partial x}} \right)n_{y} \\ & \delta \frac{\partial v}{{\partial x}}\;{\text{or}}\;H_{xz} n_{x} \\ & \delta \psi \;{\text{or}}\;\left( {M_{x} + \frac{1}{2}H_{xy} + \frac{1}{2}\frac{{\partial G_{xz} }}{\partial y}} \right)n_{x} + \left( {M_{xy} + \frac{1}{2}H_{y} - \frac{1}{2}H_{z} + \frac{1}{2}\frac{{\partial G_{xz} }}{\partial x} + \frac{1}{2}\frac{{\partial G_{yz} }}{\partial y}} \right)n_{y} \\ & \delta \frac{\partial \psi }{{\partial y}}\;{\text{or}}\;G_{yz} n_{y} \\ & \delta \phi \;{\text{or}}\;\left( {M_{xy} - \frac{1}{2}H_{x} + \frac{1}{2}H_{z} - \frac{1}{2}\frac{{\partial G_{xz} }}{\partial x} - \frac{1}{2}\frac{{\partial G_{yz} }}{\partial y}} \right)n_{x} + \left( {M_{y} - \frac{1}{2}H_{xy} - \frac{1}{2}\frac{{\partial G_{yz} }}{\partial x}} \right)n_{y} \\ & \delta \frac{\partial \phi }{{\partial x}}\;{\text{or}}\;G_{xz} n_{x} \\ & \delta w\;{\text{or}}\;\left( {Q_{x} - \frac{1}{2}\frac{{\partial H_{x} }}{\partial y} + \frac{1}{2}\frac{{\partial H_{y} }}{\partial y} + \frac{1}{2}\frac{{\partial H_{xy} }}{\partial x}} \right)n_{x} + \left( {Q_{y} - \frac{1}{2}\frac{{\partial H_{x} }}{\partial x} + \frac{1}{2}\frac{{\partial H_{y} }}{\partial x} - \frac{1}{2}\frac{{\partial H_{xy} }}{\partial y}} \right)n_{y} \\ & \delta \frac{\partial w}{{\partial x}}\;{\text{or}}\;H_{xy} n_{x} \\ & \delta \frac{\partial w}{{\partial y}}\;{\text{or}}\;H_{xy} n_{y} \\ \end{aligned}$$
(8)

where \(n_{x}\) and \(n_{y}\) are the components of an outward unit normal vector to the boundary of the mid-plane.

2.2 Governing equations

The constitutive equations relate the symmetric part of the stress tensor and the deviatoric part of the couple stress tensor to the kinematic parameters as follows [11]:

$$\sigma_{ij} = \lambda \delta_{ij} {\text{tr}}(\varepsilon_{ij} ) + 2\mu \varepsilon_{ij} , m_{ij} = 2l^{2} \mu \chi_{ij}$$
(9)

where \(l\) is a material length scale parameter and \(\lambda\) and \(\mu\) are the Lamé’s constants:

$${\uplambda } = \frac{E\nu }{{\left( {1 + \nu } \right)\left( {1 - 2\nu } \right)}}, \mu = \frac{E}{{2\left( {1 + \nu } \right)}}$$
(10)

where \(E\) and \(\nu\) are the Young’s modulus and the Poisson’s ratio, respectively. Upon substitution of Eqs. (5) and (9) into (7) and the subsequent results into the equations of motion (6), the governing equations of motion of a rectangular micro plate are obtained as follows:

$$\delta u : A_{1} \frac{{\partial^{4} u}}{{\partial y^{4} }} + A_{1} \frac{{\partial^{4} u}}{{\partial x^{2} \partial y^{2} }} + A_{2} \frac{{\partial^{2} u}}{{\partial x^{2} }} + A_{3} \frac{{\partial^{2} u}}{{\partial y^{2} }} - A_{1} \frac{{\partial^{4} v}}{{\partial x^{3} \partial y}} - A_{1} \frac{{\partial^{4} v}}{{\partial x\partial y^{3} }} + A_{4} \frac{{\partial^{2} v}}{\partial x\partial y} = I_{0} \frac{{\partial^{2} u}}{{\partial t^{2} }}$$
(11a)
$$\delta v : - A_{1} \frac{{\partial^{4} u}}{{\partial x^{3} \partial y}} - A_{1} \frac{{\partial^{4} u}}{{\partial x\partial y^{3} }} + A_{4} \frac{{\partial^{2} u}}{\partial x\partial y} + A_{1} \frac{{\partial^{4} v}}{{\partial x^{4} }} + A_{1} \frac{{\partial^{4} v}}{{\partial x^{2} \partial y^{2} }} + A_{3} \frac{{\partial^{2} v}}{{\partial x^{2} }} + A_{2} \frac{{\partial^{2} v}}{{\partial y^{2} }} = I_{0} \frac{{\partial^{2} v}}{{\partial t^{2} }}$$
(11b)
$$\delta \psi : A_{5} \frac{{\partial^{4} \psi }}{{\partial y^{4} }} + A_{5} \frac{{\partial^{4} \psi }}{{\partial x^{2} \partial y^{2} }} + A_{6} \frac{{\partial^{2} \psi }}{{\partial x^{2} }} + A_{7} \frac{{\partial^{2} \psi }}{{\partial y^{2} }} + A_{3} \psi - A_{5} \frac{{\partial^{4} \phi }}{{\partial x^{3} \partial y}} - A_{5} \frac{{\partial^{4} \phi }}{{\partial x\partial y^{3} }} + A_{8} \frac{{\partial^{2} \phi }}{\partial x\partial y} + A_{1} \frac{{\partial^{3} w}}{{\partial x^{3} }} + A_{1} \frac{{\partial^{3} w}}{{\partial x\partial y^{2} }} - A_{3} \frac{\partial w}{{\partial x}} = I_{2} \frac{{\partial^{2} \psi }}{{\partial t^{2} }}$$
(11c)
$$\delta \phi : - A_{5} \frac{{\partial^{4} \psi }}{{\partial x^{3} \partial y}} - A_{5} \frac{{\partial^{4} \psi }}{{\partial x\partial y^{3} }} + A_{8} \frac{{\partial^{2} \psi }}{\partial x\partial y} + A_{5} \frac{{\partial^{4} \phi }}{{\partial x^{4} }} + A_{5} \frac{{\partial^{4} \phi }}{{\partial x^{2} \partial y^{2} }} + A_{7} \frac{{\partial^{2} \phi }}{{\partial x^{2} }} + A_{6} \frac{{\partial^{2} \phi }}{{\partial y^{2} }} + A_{3} \phi + A_{1} \frac{{\partial^{3} w}}{{\partial y^{3} }} + A_{1} \frac{{\partial^{3} w}}{{\partial x^{2} \partial y}} - A_{3} \frac{\partial w}{{\partial y}} = I_{2} \frac{{\partial^{2} \phi }}{{\partial t^{2} }}$$
(11d)
$$\delta w : A_{1} \frac{{\partial^{3} \psi }}{{\partial x^{3} }} + A_{1} \frac{{\partial^{3} \psi }}{{\partial x\partial y^{2} }} - A_{3} \frac{\partial \psi }{{\partial x}} + A_{1} \frac{{\partial^{3} \phi }}{{\partial y^{3} }} + A_{1} \frac{{\partial^{3} \phi }}{{\partial x^{2} \partial y}} - A_{3} \frac{\partial \phi }{{\partial y}} + A_{1} \frac{{\partial^{4} w}}{{\partial x^{4} }} + A_{1} \frac{{\partial^{4} w}}{{\partial y^{4} }} + 2A_{1} \frac{{\partial^{4} w}}{{\partial x^{2} \partial y^{2} }} + A_{3} \frac{{\partial^{2} w}}{{\partial x^{2} }} + A_{3} \frac{{\partial^{2} w}}{{\partial y^{2} }} + P = I_{0} \frac{{\partial^{2} w}}{{\partial t^{2} }} + \hat{N}_{xx} \frac{{\partial^{2} w}}{{\partial x^{2} }} + \hat{N}_{yy} \frac{{\partial^{2} w}}{{\partial y^{2} }}$$
(11e)

where the coefficients \(A_{i}\) \(\left( {i = 1, 2, \ldots , 10} \right)\) are presented in “Appendix 1”.

3 The solution

The linear partial differential equations in (11) are solved by the Levy method for a micro plate with simple supports at two opposite edges and arbitrary supports at the other ones. Here, it is assumed that edges at \(y = 0\) and \(y = b\) are simply supported. It is worth mentioning that \(u\) and \(v\) appear just in Eqs. (11a, b), i.e. extension and bending are decoupled in isotropic plates which results in \(u = v = 0\) in bending analysis of a rectangular plate with homogenous boundary conditions. On the other hand, in buckling analysis, the mid-plane stretching is ignored and in vibration analysis, only the bending vibration is taken into account. Therefore, in the remaining, only Eqs. (11c, d, e) are considered.

According to Eqs. (8), the boundary conditions associated with Eqs. (11c, d, e) for simply-supported edges at \(y = 0\) and \(y = b\), are reduced to what follows:

$$w = H_{xy} = \psi = G_{yz} = M_{y} - \frac{1}{2}H_{xy} - \frac{1}{2}\frac{{\partial G_{yz} }}{\partial x} = 0$$
(12)

The boundary conditions along the other two edges at \(x = 0\) and \(x = a\) (associated with Eqs. (11c, d, e)) can be simply supported (S), clamped (C), or free (F) which their relations according to Eqs. (8) are:

$$\begin{aligned} & S : w = H_{xy} = M_{x} + \frac{1}{2}H_{xy} + \frac{1}{2}\frac{{\partial G_{xz} }}{\partial y} = \phi = G_{xz} = 0 \\ & C : w = \frac{\partial w}{{\partial x}} = \psi = \phi = \frac{\partial \phi }{{\partial x}} = 0 \\ & F : Q_{x} - \frac{1}{2}\left( {\frac{{\partial H_{x} }}{\partial y} - \frac{{\partial H_{y} }}{\partial y} - \frac{{\partial H_{xy} }}{\partial x}} \right) = H_{xy} = M_{x} + \frac{1}{2}H_{xy} + \frac{1}{2}\frac{{\partial G_{xz} }}{\partial y} = \\ & M_{xy} - \frac{1}{2}\left( {H_{x} - H_{z} + \frac{{\partial G_{xz} }}{\partial x} + \frac{{\partial G_{yz} }}{\partial y}} \right) = G_{xz} = 0 \\ & T_{xz} = 0 \\ \end{aligned}$$
(13)

Using the Levy’s methoto satisfy Eqs. (12) and based on a harmonic motion assumption, the displacement field variables \(\psi\), \(\phi\), and \(w\). are assumed as follows [52]:

$$\begin{aligned} \psi \left( {x,y,t} \right) & = \mathop \sum \limits_{m = 1}^{\infty } \psi_{m} \left( x \right)\sin \left( {\frac{m\pi y}{b}} \right)e^{{i\omega_{m} t}} , \phi \left( {x,y,t} \right) = \mathop \sum \limits_{m = 1}^{\infty } \phi_{m} \left( x \right)\cos \left( {\frac{m\pi y}{b}} \right)e^{{i\omega_{m} t}} \\ w\left( {x,y,t} \right) & = \mathop \sum \limits_{m = 1}^{\infty } w_{m} \left( x \right)\sin \left( {\frac{m\pi y}{b}} \right)e^{{i\omega_{m} t}} \\ \end{aligned}$$
(14)

where \(i\) is the imaginary unit (\(i^{2} = - 1)\), \(w_{m}\),\(\psi_{m}\), and \(\phi_{m}\) are unknown functions of \(x\) and \(\omega_{m}\) is the natural frequency which is set to zero in bending and buckling analyses. In addition, the transverse load P(x, y) in bending analysis is expanded as follows [52]:

$$P(x,y) = \sum\limits_{m = 1}^{\infty } {P_{m} (x)\sin \left( {\frac{m\pi y}{b}} \right)}$$
(15)

where \(P_{m} \left( x \right) = \left( {2/b} \right)\mathop \int \limits_{0}^{b} P\left( {x,y} \right)\sin \left( {\frac{m\pi y}{b}} \right){\text{d}}y\). Substituting Eqs. (14) and (15) into Eqs. (11) yields three ordinary differential equations with total order of ten as follows:

$$\delta \psi : B_{1} \psi_{m}^{{\prime\prime}} + B_{2} \psi_{m} + B_{3} \phi_{m}^{{\prime\prime\prime}} + B_{4} \phi_{m}^{{\prime}} + B_{5} w_{m}^{{\prime\prime\prime}} + B_{6} w_{m}^{{\prime}} = - I_{2} \omega_{m}^{2} \psi_{m}$$
(16a)
$$\delta \phi : - B_{3} \psi_{m}^{{\prime\prime\prime}} - B_{4} \psi_{m}^{{\prime}} + B_{7} \phi_{m}^{{\prime\prime\prime\prime}} + B_{8} \phi_{m}^{{\prime\prime}} + B_{9} \phi_{m} + B_{10} w_{m}^{{\prime\prime}} + B_{11} w_{m} = - I_{2} \omega_{m}^{2} \phi_{m}$$
(16b)
$$\begin{gathered} \delta w : B_{5} \psi_{m}^{{\prime\prime\prime}} + B_{12} \psi_{m}^{{\prime}} - B_{10} \phi_{m}^{{\prime\prime}} - B_{11} \phi_{m} + B_{5} w_{m}^{{\prime\prime\prime\prime}} + B_{13} w_{m}^{{\prime\prime}} + B_{14} w_{m} = - P_{m} \hfill \\ \quad - I_{0} \omega_{m}^{2} w_{m} + \hat{N}_{xx} w_{m}^{{\prime\prime}} - \left( {\frac{m\pi }{b}} \right)^{2} \hat{N}_{yy} w_{m} \hfill \\ \end{gathered}$$
(16c)

where the coefficients \(B_{i} , \left( {i = 1 \ldots 12} \right)\) are defined in “Appendix 2”. There is a problem for solving Eqs. (16) via a state-space method [54]. That is, the highest derivative of \(\psi_{m}\) (which is a third-order derivative) is appearing in Eqs. (16b, c). To overcome this problem, Eq. (16a) is differentiated and the subsequent result is used to eliminate \(\psi_{m}^{{\prime\prime\prime}}\) from Eqs. (16b, c) as follows:

$$\delta \phi : \left( {\frac{{B_{3} B_{2} }}{{B_{1} }} - B_{4} } \right)\psi_{m}^{{\prime}} + \left( {\frac{{B_{3}^{2} }}{{B_{1} }} + B_{7} } \right)\phi_{m}^{{\prime\prime\prime\prime}} + \left( {\frac{{B_{3} B_{4} }}{{B_{1} }} + B_{8} } \right)\phi_{m}^{{\prime\prime}} + B_{9} \phi_{m} + \frac{{B_{3} B_{5} }}{{B_{1} }}w_{m}^{{\prime\prime\prime\prime}}$$
(17a)
$$\begin{gathered} + \left( {\frac{{B_{3} B_{6} }}{{B_{1} }} + B_{10} } \right)w_{m}^{{\prime\prime}} + B_{11} w_{m} = - I_{2} \frac{{B_{3} }}{{B_{1} }}\omega_{m}^{2} \psi_{m}^{{\prime}} - I_{2} \omega_{m}^{2} \phi_{m} \hfill \\ \delta w : \left( { - \frac{{B_{5} B_{2} }}{{B_{1} }} + B_{12} } \right)\psi_{m}^{{\prime}} - \frac{{B_{5} B_{3} }}{{B_{1} }}\phi_{m}^{{\prime\prime\prime\prime}} - \left( {\frac{{B_{5} B_{4} }}{{B_{1} }} + B_{10} } \right)\phi_{m}^{{\prime\prime}} - B_{11} \phi_{m} - \left( {\frac{{B_{5}^{2} }}{{B_{1} }} - B_{5} } \right)w_{m}^{{\prime\prime\prime\prime}} \hfill \\ - \left( {\frac{{B_{5} B_{6} }}{{B_{1} }} - B_{13} } \right)w_{m}^{{\prime\prime}} + B_{14} w_{m} = - P_{m} + \frac{{B_{5} }}{{B_{1} }}I_{2} \omega_{m}^{2} \psi_{m}^{{\prime}} + \hat{N}_{xx} w_{m}^{{\prime\prime}} - \left( {I_{0} \omega_{m}^{2} + \left( {\frac{m\pi }{b}} \right)^{2} \hat{N}_{yy} } \right)w_{m} \hfill \\ \end{gathered}$$
(17b)

Now, Eq. (16a), (17a, b) can be reduced to a system of first-order equations with total order of ten as presented in Eq. (18), because the highest order derivatives of \(\psi_{m}\), \(\phi_{m}\), and \(w_{m}\) (which are, respectively, second-order, fourth-order and fourth-order derivatives) appear in the associated equations, i.e. in Eqs. (16a), (17a, b), respectively.

$$\left\{ {Z^{\prime}} \right\} = \left[ A \right]\left\{ Z \right\} + \left\{ q \right\}$$
(18)

where

$$\left\{ Z \right\}^{T} = \left[ {\psi_{m} , \frac{{{\text{d}}\psi_{m} }}{{{\text{d}}x}}, \phi_{m} , \frac{{{\text{d}}\phi_{m} }}{{{\text{d}}x}}, \frac{{{\text{d}}^{2} \phi_{m} }}{{{\text{d}}^{2} x}}, \frac{{{\text{d}}^{3} \phi_{m} }}{{{\text{d}}^{3} x}}, w_{m} , \frac{{{\text{d}}w_{m} }}{{{\text{d}}x}}, \frac{{{\text{d}}^{2} w_{m} }}{{{\text{d}}x^{2} }}, \frac{{{\text{d}}^{3} w_{m} }}{{{\text{d}}x^{3} }} } \right]$$
(19)

and the matrix \(\left[ A \right]\) and the load vector \(\left\{ q \right\}\) are presented in “Appendix 3”. It is worth mentioning that the buckling loads, \(\hat{N}_{xx}\), \(\hat{N}_{yy}\) and the natural frequency, \(\omega_{m}\) appear in matrix \(\left[ A \right]\) as some unknowns in buckling and vibration analyses. The general solution of Eq. (18) is as follows [54]:

$$\left\{ Z \right.\} = \left[ U \right]\left[ D \right]\left\{ C \right\} + \left[ U \right]\left[ D \right]\mathop \int \limits_{{}}^{x} \left[ D \right]^{ - 1} \left[ U \right]^{ - 1} \left\{ q \right\}$$
(20)

where \(\left[ U \right]\) is the matrix of eigenvectors of \(\left[ A \right]_{10 \times 10}\), \(\left\{ C \right\}_{10 \times 1}\) is the vector of integration constants and \(\left[ D \right]_{10 \times 10}\) is the diagonal matrix defined as follows:

$$\left[ D \right] = {\text{diag}}\left( {e^{{\lambda_{1} x}} ,e^{{\lambda_{2} x}} , \ldots , e^{{\lambda_{10} x}} } \right)$$
(21)

where \(\lambda_{i}\) \(\left( {i = 1 \ldots 10} \right)\) are eigenvalues of \(\left[ A \right]\).

3.1 Bending analysis

In bending analysis, the in-plane forces \(\hat{N}_{xx}\), \(\hat{N}_{yy}\) and all the time derivatives and consequently \(\omega_{m}\) are set to zero. Therefore, there isn’t any unknown in matrix \(\left[ A \right]\) (see Eqs. (26) and (29) in “Appendix 3”). To find the integration constants, any arbitrary combination of boundary conditions at edges \(x = 0, a\) presented in Eq. (13) is imposed which yields inhomogeneous algebraic equations in terms of integration constants.

3.2 Buckling analysis

In buckling analysis, the transverse load \(P_{m}\) and all the time derivatives and consequently \(\omega_{m}\) are set to zero, while the buckling load is still unknown in matrix \(\left[ A \right]\) (see Eqs. (26) and (29) in “Appendix 3”). Imposing the appropriate boundary conditions at edges \(x = 0, a\) leads to a linear homogeneous system of algebraic equations in terms of integration constants in which the buckling load is still an unknown in the matrix of coefficients. If the determinant of coefficient matrix is set to zero for a nontrivial solution, the bucking load is determined.

3.3 Free vibration

In vibration analysis, all external forces including \(P\), \(\hat{N}_{xx}\) and \(\hat{N}_{yy}\) are set to zero, while the natural frequency is still an unknown in matrix \(\left[ A \right]\) (see Eqs. (26) and (29) in “Appendix 3”). By setting the determinant of the coefficient matrix of the linear homogenous system of algebraic equations (obtained by imposing the appropriate boundary conditions) to zero, the natural frequency is determined.

4 Numerical results

For the purpose of numerical illustration, unless mentioned otherwise, the material properties of the plate and its geometry are assumed to be \(E = 1.44 \times 10^{9} Pa, \nu = 0.38, \rho = 1.22 \times 10^{3} \frac{{{\text{Kg}}}}{{{\text{m}}^{3} }}, \,and\, l = 17.6 \times 10^{ - 6} {\text{m}}\) (which is determined experimentally) [55] and \(a = b = 20h\). Also, the shear correction factor is considered to be \(k^{2} = 0.8\) [23, 32].

4.1 Verification studies

Here, to verify the results of the present study, three examples including bending, buckling, and free vibration of a simply-supported micro plate are provided.

4.1.1 Bending

The dimensionless central deflections (\(w\left( {a/2,b/2} \right)/h\)) of a fully simply-supported micro plate subjected to sinusoidal (\(P\left( {x,y} \right) = 0.1\sin \left( {\frac{n\pi x}{a}} \right)\sin \left( {\frac{m\pi y}{b}} \right) {\text{N}}/{\text{m}})\) and uniform \(\left( {P = 0.1 {\text{N}}/{\text{m}}} \right)\) loadings for different ratios of length scale parameter to thickness are presented in Table 1 and compared with those reported by Roque et al. [23]. Excellent agreement is seen to exist between the results. It is recalled that in reference [23] the bending analysis of an isotropic Mindlin micro plate is carried out using the Navier method.

Table 1 Dimensionless center deflection of a simply supported square micro plate (SSSS) subjected to uniform and sinusoidal loads
Full size table

4.1.2 Buckling

In Table 2, the dimensionless buckling loads (\(N_{cr} (a^{2} /Eh^{3}\))) of a fully simply supported Mindlin micro plate under uniaxial \(\left( {\hat{N}_{xx} = N_{cr} , \hat{N}_{yy} = 0} \right)\) and biaxial \(\left( {\hat{N}_{xx} = \hat{N}_{yy} = N_{cr} } \right)\) in-plane compressive forces are presented and compared with those reported in Ref. [56]. It is again seen that the Levy solution presented here for the buckling analysis is in excellent agreement with the Navier solution in [56].

Table 2 Dimensionless buckling load parameter of a simply supported square micro plate (SSSS) \(\left( {a = b = 10h, k^{2} = 5/6, E = 14.4 \times 10^{9} {\text{Pa}}, \rho = 12.2 \times 10^{3} {\text{Kg}}/{\text{m}}^{3} } \right)\)
Full size table

4.1.3 Free vibration

In Table 3, the first two dimensionless natural frequencies \(\left( {\omega_{m} \left( {\frac{{a^{2} }}{h}\sqrt {\frac{\rho }{E}} } \right)} \right)\) of a fully simply supported Mindlin micro plate in the plane-stress state are given and compared to those presented in Ref. [56] in which the Navier method is employed. It is seen that the results are in excellent agreement [56].

Table 3 First two dimensionless natural frequencies of a simply supported square micro plate (SSSS), \(\left( {a = b = 10h, k^{2} = 5/6, E = 14.4 \times 10^{9} {\text{Pa}}, \rho = 12.2 \times 10^{3} {\text{Kg}}/{\text{m}}^{3} } \right)\)
Full size table

4.2 Parametric studies

Here, the bending, buckling and free vibration of micro plates with different boundary conditions subjected to two types of loadings; sinusoidal \(P = P_{0} \sin \left( {\frac{n\pi x}{a}} \right)\sin \left( {\frac{m\pi y}{b}} \right)\) and uniform \(P = P_{0}\) loadings are considered. Recall that the two edges at \(y = 0\) and \(y = b\) are simply supported and the others can have simple support (S), clamped support (C), or free edge (F). For convenience, the following dimensionless parameters are introduced:

$$\overline{w} = \frac{{100Eh^{3} }}{{P_{0} a^{4} }}w\left( {a/2,b/2} \right), \overline{\omega }_{m} = \omega_{m} \frac{{a^{2} }}{h}\sqrt {\frac{\rho }{E}} , \overline{N}_{cr} = \left( {N_{cr} \frac{{a^{2} }}{{Eh^{3} }}} \right)$$
(22)

4.2.1 Bending

The dimensionless center deflection, \(\overline{w}\) of micro plates with six possible types of boundary conditions subjected to both sinusoidal and uniform loadings are obtained and presented in Tables 4 and 5. In Table 4, various ratios of material length scale parameter to thickness \(\left( {l/h = 0, 0.2, 0.4, 0.6, 0.8, 1} \right)\) are considered and in Table 5 the effect of side-to-thickness ratio \(\left( {a/h = 5, 10, 15} \right)\) is studied. The variations of dimensionless center deflection of micro plates with three types of boundary conditions (SSSS, SSCC and SSFF) and two ratios of \(a/h = 10, 20\) versus \(l/h\) ratio are depicted in Fig. 2 and compared with the results of Kirchhoff micro plate (\(K^{2} \to \infty )\). In Table 4 and Fig. 2, it is observed that the classical continuum theory (\(l = 0\)) overestimates the deflection and by increasing the length scale parameter (\(l/h\)), the deflections of micro plates with all types of boundary supports become smaller, i.e. the micro plate becomes stiffer. In Table 5 and Fig. 2, it is seen that as the ratio of (a/h) increases, i.e. the micro plate becomes thinner; the dimensionless deflection decreases because it is nondimensionalized as in (22), however, the deflection per se increases, as expected. In addition, it is seen in Fig. 2 that the difference between the Kirchhoff micro plate (KP) and the Mindlin micro plate (MP) exists even for a thin plate (MP) especially for SSCC micro plate and this difference for all types of boundary supports increases as the micro plate becomes thicker or as l/h ratio reduces.

Table 4 Dimensionless center deflection of a square micro plate subjected to uniform and sinusoidal loads
Full size table
Table 5 Dimensionless center deflection of a square micro plate subjected to uniform and sinusoidal loadings (\(l/h = 1)\)
Full size table
Fig. 2
figure 2

Variations of dimensionless center deflection of a SSSS, b SSCC, c SSFF square micro plate under sinusoidal loading versus \(l/h\) ratio and its comparison with the results of Kirchhoff micro plate

Full size image

In Table 6, the effect of aspect ratio \(\left( {a/b} \right)\) on dimensionless center deflection, \(\overline{w}\) of micro plates with various types of boundary conditions subjected to both sinusoidal and uniform loadings are studied. It is observed that by increasing the aspect ratio \(\left( {a/b} \right)\), the dimensionless deflection (see Eq. (22)) reduces while the deflection per se increases, as expected.

Table 6 Dimensionless center deflection of a rectangular micro plate subjected to uniform and sinusoidal loads (\(l/h = 1, b = 20h\))
Full size table

Variations of dimensionless deflection of a square micro plate under sinusoidal load along \({ }x\) axis for all six possible boundary conditions are shown in Fig. 3. In Fig. 3 and Tables 4, 5, and 6, it is expectedly seen that as the boundaries become more rigid, the deflections decrease, e.g. among three types of boundary conditions SSFF, SSCF and SSSF, plates with SSFF supports have the largest deflections and plates with SSFC supports have the smallest ones.

Fig. 3
figure 3

Dimensionless deflection of a square micro plate under sinusoidal load along x axis for various boundary conditions (\(l/h = 1\))

Full size image

4.2.2 Buckling

Dimensionless buckling load, \(\overline{N}_{cr}\), of a micro plate with six possible types of boundary conditions subjected to uniaxial \(\left( {\hat{N}_{xx} = N_{cr} , \hat{N}_{yy} = 0} \right)\) and biaxial in-plane compressive forces \((\hat{N}_{xx} = \hat{N}_{yy} = N_{cr}\)) for different ratios of length scale parameter to thickness \(\left( {l/h = 0,0.2, 0.4, 0.6, 0.8, 1} \right)\) and side-to-thickness ratio \(\left( {a/h = 5, 10, 15} \right)\) are obtained and presented in Tables 7 and 8, respectively. The variations of buckling load of a plate under uniaxial loading versus \(l/h\) ratio for three types of boundary conditions (SSSS, SSCC and SSFF) and two ratios of \(a/h = 10 and 20\) are presented in Fig. 4 and compared with those of Kirchhoff micro plate (\(K^{2} \to \infty )\). In Table 7 and Fig. 4, it is observed that the classical continuum theory (\(l = 0\)) underestimates the buckling load and increasing the length scale parameter (\(l/h)\) or using more rigid boundaries leads to a stiffer micro plate and larger buckling loads. In Table 8 and Fig. 4, it is seen that as the ratio of \(\left( {a/h} \right)\) increases, i.e. the micro plate becomes thinner; the dimensionless buckling load increases because it is nondimensionalized as in (22), while the buckling load per se decreases. In addition, it is seen in Fig. 4 that the difference between the Kirchhoff micro plate (KP) and the Mindlin micro plate (MP) is more pronounced in SSCC micro plates and this difference for all types of boundary supports increases as the micro plate becomes thicker or as \(l/h\) ratio increases. The differences in buckling loads predicted by the Kirchhoff and the Mindlin plate models for \(a/h = 20\) (which is considered to be a thin plate and results of the Kirchhoff model is valid for) and \(l/h = 1\) are 8.5%, 3.7%, and 2.1% for, respectively, SSCC, SSSS, and SSFF boundary conditions.

Table 7 Dimensionless buckling load parameter of a square micro plate
Full size table
Table 8 Dimensionless buckling load parameter of a square micro plate (l/h = 1)
Full size table
Fig. 4
figure 4

Variations of dimensionless buckling load of a SSSS, b SSCC, c SSFF square micro plate under uniaxial loading versus \(l/h\) ratio and its comparison with the results of Kirchhoff micro plate

Full size image

4.2.3 Vibration

Two first dimensionless frequencies, \(\overline{\omega }_{m}\), of square micro plates with six possible types of boundary conditions for different ratios of length scale parameter to thickness \(\left( {l/h = 0,0.2, 0.4, 0.6, 0.8, 1} \right)\) and side-to-thickness ratio \(\left( {a/h = 5, 10, 15} \right)\) are presented in Tables 9 and 10, respectively. In addition, the variations of fundamental dimensionless frequency in terms of \(l/h\) for three types of boundary conditions (SSSS, SSCC and SSFF) and two ratios of \(a/h = 10, 20\) are presented in Fig. 5 and compared with those of Kirchhoff micro plate (\(K^{2} \to \infty )\). In Table 9 and Fig. 5, it is observed that the classical continuum theory (\(l = 0\)) underestimates the natural frequencies and increasing the length scale parameter (1/h) or using more rigid boundaries leads to a stiffer micro plate and larger natural frequencies. In Table 10 and Fig. 5, it is seen that as the ratio of \(\left( {a/h} \right)\) increases, the dimensionless frequencies (see Eq. (22)) increases, while the natural frequencies per se decrease. In addition, it is seen in Fig. 4 that the difference between natural frequencies within the Kirchhoff micro plate (KP) and the Mindlin micro plate (MP) is more pronounced in SSCC plates. This difference for all types of boundary supports increases as the micro plate becomes thicker (as expected) or as \(l/h\) ratio increases. For \(a/h = 20\) and \(l/h = 1\), the differences between fundamental frequencies within the Kirchhoff and the Mindlin plate models are 5.1%, 2.1%, and 2.8% for, respectively, SSCC, SSSS, and SSFF boundary supports.

Fig. 5
figure 5

Variations of dimensionless fundamental frequencies of a SSSS, b SSCC, c SSFF square micro plate versus \(l/h\) ratio and its comparison with the results of Kirchhoff micro plate

Full size image
Table 9 Dimensionless two first frequencies (\(m = 1\)) of a square micro plate
Full size table
Table 10 Dimensionless first- and second-mode frequencies of a square micro plate, (\(l/h = 1, m = 1\))
Full size table

5 Conclusion

In this study, bending, buckling, and free vibration behavior of a rectangular micro plate is studied considering the modified couple stress theory and first-order shear deformation plate theory. The equations of motion are derived using the Hamilton's principle and solved by the Levy’s method and the state-space method. However, some mathematical operations are necessary to render the state-space method feasible. The results are verified with the ones available for fully simply supported micro plates in the literature. The Levy’s solution available in the literature for micro-plates is limited to the Kirchhoff micro-plates. Consequently, the results presented here for the Mindlin micro-plates with different boundary conditions using an analytical approach can serve as a benchmark and are more accurate than the results within the Kirchhoff theory for thicker plates (even for a micro-plate with \(a/h = 20)\). The difference in results obtained by the Kirchhoff and the Mindin plate models depends not only on the plate thickness but also on the length scale parameter to thickness ratio (\(l/h)\) as well as on the boundary supports. This difference is more pronounced in SSCC boundary supports and for higher ratios of \(l/h\), the difference in results of natural frequencies and buckling loads between the Kirchhoff and the Mindlin plate theories increases. In addition, the numerical results show that the fundamental frequencies and buckling loads increase (and transverse deflection decreases) with increasing the \(l/h\) ratio and decreasing the side-to-thickness ratio (a/h). Furthermore, more rigid boundary conditions increase frequencies and buckling loads and reduce the transverse deflection, as expected. It is to be noted that the micro plates considered in this study are limited to the ones with the two opposite edges simply supported and arbitrary conditions of support on the remaining edges. Presenting semi-analytical solutions for micro plates with completely arbitrary boundary conditions should be addressed in future studies.