1 Introduction

1.1 Introduction of natural convection

No one can deny that studying of the natural convection is very important especially in the porous media because it has a lot of application in industrial, engineering and agricultural such as building insulation, grain storage, groundwater decontamination, solar collector, thermal drying process, casting solidification and petroleum reserve, etc. All these applications and other are widely reviewed in [1,2,3,4,5,6] As a result of this large numbers of applications of this phenomenon, it has become an important research topic in the recent centuries. In general, the researchers focus on investigating of the numerical solution of convection for triangular, square or rectangular enclosures because of it is easy to solve. Varol et al. [7]. At first, they used finite difference method then they applied successive under relaxation method. Temperature diffusion and flow field were discussion at different aspect ratio and Rayleigh numbers. They noted that the location of heater has effect such as when located it at the bottom wall a lot of whirlpool were formed and the highest heat transfer obtained conferring to the of other cases. Mansour and Ahmed [8] studied the free convection heat transfer in a slanted triangular cavity contained nanofluid (Cu-water) in porous media under the effect generation of heat. They found that the average Nusselt number became better when increase the nanoparticle volume fraction also, increasing parameter of heat generation causes to low in the value of the average Nusselt number. A numerical studied of unstable magneto hydrodynamic natural convection in a slanted cavity contain a porous medium with heat generation inside has been performed by Mansour et al. [9]. They studied two cases, the first case considered all wall of enclosure at zero degree of temperature and the second case the vertical walls are kept adiabatic and they presented results of the average Nusselt number for some variables conditions. In 2011, Mansour et al. [10] discussed the problem of double-expanded convection in slanted triangular cavity containing a porous medium with different sinusoidal of the boundary conditions in the being of sink heat source, numerically. They found that the fluid motion is accelerated in case of the being of heat sink and the fluid motion is decayed in the presence of heat source.

1.2 Brief introduction on fractional calculus

The fractional calculus attracted a lot of researches in the last and present centuries. The theory of fractional calculus improved as theoretical branch for mathematicians. Recently many papers have been presented in the fractional derivatives rules which aiming to generalize rules of ordinary derivatives. Also, there are a lot of applications of this direction in mechanics, control theory, chemistry and physics, so on [11, 12]. It was begun in 1695, when L’Hopital asked if the expression \(\frac{{d^{0.5} }}{{dx^{0.5} }}\) has any meaning. Since then, many researches started to try to replace the concept of the usual derivative to fractional derivatives. The most famous of them, Riemann–Liouville which relied on repeating the integral operator \(n\) time and used the famous Cauchy formula, at the end changed n! to the Gamma function and then the definition of the fractional integral of non-integer order for \(\alpha \in \left[ {n - 1,n} \right]\) can be written in form:

$$D_{a}^{ \propto } \left( f \right)\left( t \right) = \frac{1}{{\Gamma \left( {n - \alpha } \right)}}\frac{{d^{n} }}{{dt^{n} }}\mathop \int \limits_{a}^{t} \frac{f\left( x \right)}{{\left( {t - x} \right)^{\alpha - n + 1} }}dx .$$
(1)

Then, Caputo used the integrals to define fractional derivatives for \(\alpha \in [n - 1,n)\) in the form

$$D_{a}^{ \propto } \left( f \right)\left( t \right) = \frac{1}{{\Gamma \left( {n - \alpha } \right)}}\mathop \int \limits_{a}^{t} \frac{{f^{\left( n \right)} \left( x \right)}}{{\left( {t - x} \right)^{\alpha - n + 1} }}dx .$$
(2)

In another direction, Grunwald–Letnikov depended on repeated the time derivative \(\alpha\) and then analyzing by using the Gamma function in the binomial coefficients [13,14,15,16,17]. But all the previous fractional derivatives were complicated, and they lost a lot of the main properties of ordinary derivatives like chain rule and product rule. Recently, it is appeared a new fractional derivative definition “the conformable fractional derivative” and that definition is perpendicular on the fundamentals definitions of the derivative for \(0 < \alpha \le 1\) and \(t > 0\):

$$D^{\alpha } f\left( t \right) = \mathop {\lim }\limits_{\varepsilon \to 0} \frac{{f\left( {t + \varepsilon t^{1 - \alpha } } \right) - f\left( t \right)}}{\varepsilon },$$
(3)

and at zero the fractional derivative is knowing as \(f^{\alpha } \left( 0 \right) = \lim_{{t \to 0^{ + } }} f^{\alpha } \left( t \right)\) [18, 19]. When \(\alpha = 1\), this fractional derivative reduces to the ordinary derivative. The conformable fractional derivative has the following properties:

$$\begin{aligned} D^{\alpha } \,t^{p} &= p\,t^{p - \alpha } ,\quad p \in z,\quad D^{\alpha } c = 0,\quad \forall \,f(t) = c, \\ & D^{\alpha } (a\,f + b\,g) = a\,D^{\alpha } f + b\,D^{\alpha } g,\quad \forall \,a,b \in {\mathbb{R}}, \\ & D^{\alpha } (f\,g) = f\,D^{\alpha } g\, + f\,D^{\alpha } g,\, \\ D^{\alpha } \,f(g) & = \frac{df}{dg}\,D^{\alpha } g,\quad D^{\alpha } \,f(t) = t^{1 - \alpha } \frac{df}{dg}, \\ \end{aligned}$$

where \(f,\,\,g\) are two \(\,\alpha -\) differentiable functions and \(c\) is an arbitrary constant. The last equations are proved by Khalil et al. in [18]. The conformable fractional derivative of some functions

$$\begin{aligned} & D^{\alpha } e^{c\,t} = c\,t^{1 - \alpha } e^{c\,t} ,\quad D^{\alpha } \sin (ct) = c\,t^{1 - \alpha } \cos (ct),\quad D^{\alpha } \cos (ct) = - c\,t^{1 - \alpha } \sin (ct), \\ & D^{\alpha } e^{{c\,t^{\alpha } }} = c\,\alpha e^{{c\,t^{\alpha } }} ,\quad D^{\alpha } \sin (ct^{\alpha } ) = c\,\alpha \cos (ct^{\alpha } ),\quad D^{\alpha } \cos (ct^{\alpha } ) = - c\alpha \sin (ct^{\alpha } ). \\ \end{aligned}$$

Karayer et al. [20] introduced the conformable fractional Nikiforov–Uvarov (NU) method for some prospect in quantum mechanics which gives accurate Eigen case solutions of Schrodinger equation (SE). Zhao et al. [21] discuss a new connotation of the delta conformable fractional derivative which has the identity factor on time scales. In, Ünal et al. [22] evidenced the power series solutions about given point in case of conformable fractional differential equations of linear sequential homogeneous of order 2α and introduced the Hermite conformable fractional polynomials as well as the basic properties of these polynomials. Abu Hammad and Khalil [23] introduced the conformable fractional Fourier series. Cenesiz and Ali [24] establish the solution of conformable fractional heat equations for time and space by conformable Fourier transform. Jena and Chakraverty in [25] solved Navier–Stokes equations of fractional order by using a hybrid technique called homotopy perturbation Elzaki transform method. They merge Elzaki transform and homotopy perturbation method. This method was verified by using it on 3 different problems. It was shown that this proposed method is reliable, effective and easy to carry out various problems relating of science and engineering. Jena et al. [26] introduced the solution of a damped beam equation whose damping characteristics are well defined by the fractional derivative. They applied the homotopy analysis method for calculating the dynamic response and they compared the obtained results with the solutions achieved by Adomian decomposition method (ADM) to show the accuracy and efficiency of this method. Jena and Chakraverty [27] presented a new technique namely residual power series method to find the analytical solution of the Fractional Black–Scholes equation with an initial condition for European option pricing problem. Caputo sense is used to define the fractional derivative. This technique is based on expansion of the fractional power series. The method proved its effectiveness through the obtained solutions which compared with exact solutions solved by other techniques. Jena and Chakraverty [28] solved the time-fractional model of vibration equation of large membranes by using an iterative technique namely residual power series method (RPSM) and they used Caputo sense to define the fractional derivative. This method proved its efficacy and the results obtained are verified graphically.

In this leaf, the fractional derivative is applied to discuss the unsteady free convection flow for a slanted cavity contained a porous medium and checked the effects of the fractional parameter on properties of the heat transfer and fluid motion for various values of the inclination angle, Rayleigh numbers and the aspect ratio. Also, one of the aims of this research is to achieve the heat and fluid flow in irregular enclosures not only in case of ordinary derivatives but also in case of fractional derivatives. It is difficult to work with a slanted cavity so, by using the nonlinear axis transformations, the computational field is charted into an orthogonal shape as proposed in [29]. The finite difference method is used to find the numerical solution of the governing equations; this method is presented in [30, 31] with some modifications.

2 Problem description and mathematical analysis

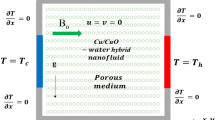
The considered physical model is an enclosure containing porous medium fluid. Figure 1 shows that the wall length is L and the tendency angle of the cavity walls is \(\Phi\). \(T_{h}\) refer to inclined left wall and \(T_{c}\) refer to right walls, while the horizontal walls are thermally insulated. It assumed that Darcy’s law is contract, the fluid is normal and the inertial effects and Bossiness fluid are ignored within the porous medium. Considering all these suppositions, the conservation equations in the fractional form are expressed as:

Fig. 1
figure 1

a Physical model and b transformed computational domain

Full size image
$$D_{x}^{\alpha \alpha } \psi + D_{y}^{\alpha \alpha } \psi = - \frac{gK\beta }{\nu }D_{x}^{\alpha } {\text{T }}$$
(4)
$$\sigma D_{t}^{\beta } T + uD_{x}^{\alpha } T + \nu D_{y}^{\alpha } T = \alpha (D_{x}^{\alpha \alpha } T + D_{y}^{\alpha \alpha } T) \,$$
(5)

Equations (4) and (5) are a generalization of the following equations, see Nield and Bejan [1]:

$$D_{y} u - D_{x} v = - \frac{gK\beta }{\nu }D_{x} {\text{T}} . { }$$
(6)
$$\sigma D_{t} T + uD_{x} T + \nu D_{y} T = \alpha (D_{xx} T + D_{yy} T) \, .$$
(7)

where \(u = \frac{\partial \psi }{\partial y}, \, \nu = - \frac{\partial \psi }{\partial x}\) are the velocity components and \(D^{\alpha }\) is the fractional differential operator.

Introducing the following grid transformations:

$$X = x - y\tan \Phi , Y = y$$
(8)
$$D_{x} \, = \, D_{X} , \, D_{y} \, = \, D_{Y} \, - \tan \Phi D_{X} \,$$
(9)

Substituting Eqs. (8) and (9) into Eqs. (4) and (5), the following system is obtained:

$$D_{X}^{\alpha \alpha } \psi - 2\sin \Phi \cos \Phi D_{X}^{\alpha } (D_{Y}^{\alpha } \psi ) + \cos^{2} \Phi D_{Y}^{\alpha \alpha } \psi = - \frac{gK\beta }{\nu }D_{X}^{\alpha } T\cos^{2} \Phi .$$
(10)
$$\sigma D_{t}^{\beta } + D_{y}^{\alpha } \psi D_{x}^{\alpha } T - D_{x}^{\alpha } \psi D_{y}^{\alpha } T = \frac{\alpha }{{\cos^{2} \Phi }}\left[ {D_{x}^{\alpha \alpha } T - 2\sin \Phi \cos \Phi D_{x}^{\alpha } (D_{y}^{\alpha } T) + \cos^{2} \Phi D_{y}^{\alpha \alpha } T} \right].$$
(11)

Using the following dimensionless parameter:

$$\begin{aligned} & \eta \, = {\text{Y}}/({\text{L}}\cos \Phi ),\quad \tau = t(\bar{\alpha }/\sigma aL\cos \Phi ),\quad \zeta = X/a, \\ & \varPsi = \psi /\bar{\alpha },\quad \theta = ({\text{T}} - {\text{T}}_{r} )/\Delta T \\ \end{aligned}$$
(12)

where \(T_{r} = (T_{h} + T_{c} )/2\;{\text{and}}\;\Delta {\text{T = T}}_{h} - T_{c} \, \;{\text{with }}\;{\text{T}}_{h} > T_{c}\).

Substituting Eq. (12) into Eqs. (10), (11), the following system is obtained:

$$D_{\zeta }^{\alpha \alpha } \varPsi - 2\frac{\sin \Phi }{A}D_{\zeta }^{\alpha } (D_{\eta }^{\alpha } \varPsi ) + \frac{1}{{A^{2} }}D_{\eta }^{\alpha \alpha } \varPsi = - Ra\cos^{2} \Phi \, D_{\zeta }^{\alpha } \theta .$$
(13)
$$\frac{A}{\cos \Phi }(D_{\zeta }^{\alpha \alpha } \theta - \frac{2\sin \Phi }{A}D_{\zeta }^{\alpha } (D_{\eta }^{\alpha } \theta ) + \frac{1}{{A^{2} }}D_{\eta }^{\alpha \alpha } \theta ){ = }D_{\eta }^{\alpha } \varPsi D_{\zeta }^{\alpha } \theta + D_{\tau }^{\beta } \theta - D_{\zeta }^{\alpha } \varPsi D_{\eta }^{\alpha } \theta .$$
(14)

where A is the aspect ratio of the cavity and \(Ra\) is the Rayleigh number:

$$\, A = a/L,\quad {\text{Ra}} = \frac{{a\Delta T\overline{\beta } gk}}{{\nu \overline{\alpha } }}$$
(15)

The subjected boundary conditions are given by:

$$\begin{aligned} & \varPsi = 0,\quad \theta = \frac{1}{2},\quad {\text{on}}\;\zeta = 0 \\ & \varPsi = 0,\quad \theta = - \frac{1}{2}\quad {\text{on}}\;\zeta = 1 \\ & \varPsi = 0,\quad \frac{\partial \theta }{\partial \eta } - A\sin \Phi \frac{\partial \theta }{\partial \zeta } = 0\quad {\text{on}}\;\eta = 0,1 \\ \end{aligned}$$
(16)

The local Nusselt number takes the form:

$$Nu(\zeta ,\eta ) = \frac{{a \, q_{w} }}{\Delta Tk},$$
(17)

Since, \(q_{w}\) is the heat transfer rate, it can be evaluated at the slanted walls as:

$$q_{w} = - kn.\nabla T,$$
(18)

In Eq. (18), \(k\) is the porous medium thermal conductivity and \(n\) is the unit vector normal to the slanted walls.

$$n = \{ - \cos \Phi \, i,\sin \Phi j\} .$$
(19)

Substituting Eqs. (16) and (17) in Eq. (15), the local Nusselt number being in the form:

$$Nu(\zeta ,\eta ) = \frac{ - 1}{\cos \Phi }(\frac{\sin \Phi }{A}\frac{\partial \theta }{\partial \eta } - \frac{\partial \theta }{\partial \zeta })_{\zeta = 0,1}$$
(20)

Also, the average Nusselt number is given by:

$$\overline{Nu} (\zeta ) = \int_{0}^{1} {Nu(\zeta ,\eta )} {\text{ d}}\eta$$
(21)

3 Numerical method and validation

In this part, the finite differences method is applied to find numerically the solution of the fractional partial differential Eqs. (12) and (13) subjected to the boundary conditions (15). The fractional derivatives are approximated using the definition in Eq. (3), then the second differences approaches are used to implement the first and second derivatives. The resulting algebraic system is solved using SUR method with successive parameter \(\varepsilon = 0.7\). The grid \(101 \times 101\) is chosen for all computations after conducting a grid dependency study. The convergence criteria of \(10^{ - 6}\) are applied to terminate the loops and many validation tests are reported.

3.1 The finite difference method in the fractional derivative

Since Guranwald letnikov derivatives with order α > 0 defined as follow:

$$D_{a,t }^{\alpha } f\left( t \right) = \mathop {\lim }\limits_{h \to 0,Nh \to t - a} h^{ - \alpha } \mathop \sum \limits_{j = 0}^{N} \left( { - 1} \right)^{j} \left( {\begin{array}{*{20}c} \alpha \\ j \\ \end{array} } \right)f\left( {t - jh} \right)$$
(22)

The Riemann–Liouville derivatives for α > 0 in the form

$${\text{D}}_{\text{a}}^{\upalpha} {\text{f}}\left( {\text{t}} \right) = \frac{1}{{{\Gamma}\left( {n - \alpha } \right)}}\frac{{d^{n} }}{{dt^{n} }}\mathop \int \limits_{a}^{t} \left( {t - s} \right)^{n - \propto - 1} f\left( s \right)ds$$
(23)

where \(n\) is an integer number and \(n - 1 \le \alpha < n\).

The caputo definition for α > 0

$${\text{cD}}_{\text{a}}^{\upalpha} {\text{f}}\left( {\text{t}} \right) = \frac{1}{{{\Gamma}\left( {n - \alpha } \right)}}\mathop \int \limits_{a}^{t} \left( {t - s} \right)^{n - \propto - 1} f^{\left( n \right)} \left( s \right)ds$$
(24)

The relation between Riemann and Caputo given in the following

$${\text{D}}_{{{\text{a}},{\text{t}}}}^{\upalpha} {\text{f}}\left( {\text{t}} \right) = {\text{cD}}_{{{\text{a}},{\text{t}}}}^{\upalpha} {\text{f}}\left( {\text{t}} \right) + \mathop \sum \limits_{k = 0}^{n - 1} \frac{{f^{\left( k \right)} \left( a \right)\left( {t - a} \right)^{k - a} }}{{{\Gamma}\left( {1 - \alpha } \right)}}$$
(25)

In Eq. (22) let \(\omega_{j}^{\alpha } = \left( { - 1} \right)^{j} \left( {\begin{array}{*{20}c} \alpha \\ j \\ \end{array} } \right)\).

Then

$$D_{{t_{0} ,t }}^{\alpha } u\left( t \right) = \mathop {\lim }\limits_{h \to 0,Nh \to t - t0} \Delta T^{ - \alpha } \mathop \sum \limits_{j = 0}^{N} \omega_{j}^{\alpha } u\left( {t_{k - j} } \right)$$
(26)

where \(u \left( t \right)\) is defined on [\(t_{0} ,t]\), \(\Delta t = \frac{{\left( {t_{0} - t} \right)}}{{n_{t} }}\) (uniform time step), \(n_{t}\) is a positive integer \(t_{k}\) is the temporal grid points,\(t_{k} = t_{0} + k\Delta t\), k = 0, …, \(n_{t}\).

Then the Riemann–Liouville derivative can be approximated

$$D_{{t_{0} ,t }}^{\alpha } u\left( {t_{k} } \right) \approx D_{{t_{0} ,t }}^{\alpha } {\check{u}}\left( {t_{k} } \right) = \Delta t^{ - \alpha } \mathop \sum \limits_{j = 0}^{k} \omega_{j}^{\alpha } u\left( {t_{k - j} } \right)$$
(27)

Equation (27) is called slandered formula, for \(1 < \alpha < 2\) the formula is more stable

$$D_{{t_{0} ,t }}^{\alpha } u\left( {t_{k} } \right) \approx D_{{t_{0} ,t }}^{{\check{\alpha}}} u\left( {t_{k} } \right) = \Delta t^{ - \alpha } \mathop \sum \limits_{j = 0}^{k} \omega_{j}^{\alpha } u\left( {t_{k - j + 1} } \right)$$
(28)

The relation (28) has one order convergence which the numerical scheme is more stable \(\{ \omega_{j}^{\alpha } \}_{j = 0}^{k}\) is the first \(k + 1\) coefficient of the Taylor series.

The active way to approximate the Riemann–Liouville derivative of order \(\alpha (0 < \alpha < 1)\) by using the Eq. (25):

$${\text{D}}_{{{\text{a}},{\text{t}}}}^{{\upalpha}} {\text{f}}\left( {\text{t}} \right) = {\text{cD}}_{{{\text{a}},{\text{t}}}}^{{\upalpha}} {\text{f}}\left( {\text{t}} \right) + \mathop \sum \limits_{k = 0}^{n - 1} \frac{{f^{\left( k \right)} \left( a \right)\left( {t - a} \right)^{k - a} }}{{{\Gamma}\left( {1 - \alpha } \right)}}$$
(29)

The \(L_{1}\) scheme obtained in form:

$$D_{{t_{0} ,t }}^{\alpha } u\left( {t_{k + 1} } \right) = \frac{{u\left( {t_{0} } \right)\left( {t_{k + 1} - t_{0} } \right)}}{{{\Gamma}\left( {1 - \alpha } \right)}} + \frac{1}{{{\Gamma}\left( {1 - \alpha } \right)}}\mathop \sum \limits_{j = 0}^{k} \mathop \int \limits_{{t_{j} }}^{{t_{j + 1} }} \left( {t_{k + 1} - s} \right)^{ - \alpha } u^{\prime}\left( s \right)ds$$
(30)

where \(\mathop \int \limits_{{t_{j} }}^{{t_{j + 1} }} \left( {t_{k + 1} - s} \right)^{ - \alpha } u^{\prime}\left( s \right)ds\) is approximated by \(\mathop \int \limits_{{t_{j} }}^{{t_{j + 1} }} \frac{{u\left( {t_{j + 1} } \right) - \left( {t_{j} } \right)}}{\Delta t}\left( {t_{k + 1} - s} \right)^{ - \alpha } ds\), then \(L_{1}\) scheme is:

$$D_{{t_{0} ,t }}^{\alpha } {\check{u}}\left( {t_{k + 1} } \right) = \frac{{u\left( {t_{0} } \right)\left( {t_{k + 1} - t_{0} } \right)}}{{\Gamma \left( {1 - \alpha } \right)}} + \frac{{\Delta t^{ - \alpha } }}{{\Gamma \left( {2 - \alpha } \right)}}\mathop \sum \limits_{j = 0}^{k} b_{j,k} \left[ {u\left( {t_{j + 1} } \right) - u(t_{j } )} \right]$$
(31)

where \(b_{{j,k = \left( {k - j + 1} \right)^{1 - \alpha } - \left( {k - j} \right)^{1 - \alpha } }}\) \(j = 0, \ldots , k\).

In the similar manner the \(L_{2}\) scheme in case of \(\alpha (1 < \alpha < 2)\) is given by:

$$D_{{t_{0} ,t }}^{\alpha } u\left( {t_{k + 1} } \right) = \frac{{u\left( {t_{0} } \right)\left( {t_{k + 1} - t_{0} } \right)^{ - \alpha } }}{{{\Gamma}\left( {1 - \alpha } \right)}} + \frac{{u^{\prime}\left( {t_{0} } \right)\left( {t_{k + 1} - t_{0} } \right)^{1 - \alpha } }}{{{\Gamma}\left( {2 - \alpha } \right)}} + \frac{1}{{{\Gamma}\left( {2 - \alpha } \right)}}\mathop \sum \limits_{j = 0}^{k} \mathop \int \limits_{{t_{j} }}^{{t_{j + 1} }} s^{1 - \alpha } u^{\prime\prime}\left( {t_{k + 1} - s} \right)ds$$
(32)
$$u^{\prime\prime}\left( {t_{k + 1} - s} \right) \approx \frac{{u\left( {t_{k - j - 1} } \right) - 2u\left( {t_{k - j} } \right) + u(t_{k + 1 - j)} }}{{\Delta t^{2} }}$$
(33)

By using (32) in (33)

$$\begin{aligned} D_{{t_{0} ,t }}^{\alpha } {\check{u}}\left( {t_{k + 1} } \right) & = \frac{{u\left( {t_{0} } \right)\left( {t_{k + 1} - t_{0} } \right)^{ - \alpha } }}{{\Gamma \left( {1 - \alpha } \right)}} + \frac{{u^{\prime}\left( {t_{0} } \right)\left( {t_{k + 1} - t_{0} } \right)^{1 - \alpha } }}{{\Gamma \left( {2 - \alpha } \right)}} + \frac{{\Delta t^{ - \alpha } }}{{\Gamma \left( {3 - \alpha } \right)}}\mathop \sum \limits_{j = 0}^{k} b_{j} \left[ {u\left( {t_{k - j - 1} } \right) - 2u\left( {t_{k - j} } \right) + u\left( {t_{k + 1 - j} } \right)} \right] \\ & = \frac{{u\left( {t_{0} } \right)\left( {t_{k + 1} - t_{0} } \right)^{ - \alpha } }}{{\Gamma \left( {1 - \alpha } \right)}} + \frac{{u^{\prime}\left( {t_{0} } \right)\left( {t_{k + 1} - t_{0} } \right)^{1 - \alpha } }}{{\Gamma \left( {2 - \alpha } \right)}} + \mathop \sum \limits_{j = - 1}^{k + 1} W_{j} u\left( {t_{k + 1 - j} } \right) \\ \end{aligned}$$
(34)

where \(b_{j} = \left( {j - 1} \right)^{2 - \alpha } - j^{2 - \alpha }\) and \(\left\{ {W_{j} } \right\}_{j = - 1}^{k + 1}\) can be expressed by \(\left\{ {b_{j} } \right\}_{j = 0}^{k}\) by defining \(u^{\prime\prime}\left( {t_{k + 1} - s} \right)\) in subinterval [\(t_{j, } t_{kj + 1} ]\) in the form:

$$u^{\prime\prime}\left( {t_{k + 1} - s} \right) \approx \frac{{u\left( {t_{k - j - 1} } \right) - u\left( {t_{k - j} } \right) + u\left( {t_{k + 2 - j } } \right) - u\left( {t_{k + 1 - j} } \right)}}{{2\Delta t^{2} }}$$

A new scheme is obtained, namely, \(L_{2}\)C in the form:

$$\begin{aligned} D_{{t_{0} ,t }}^{\alpha } {\check{u}}\left( {t_{k + 1} } \right) & = \frac{{u\left( {t_{0} } \right)\left( {t_{k + 1} - t_{0} } \right)^{ - \alpha } }}{{\Gamma \left( {1 - \alpha } \right)}} + \frac{{u^{\prime}\left( {t_{0} } \right)\left( {t_{k + 1} - t_{0} } \right)^{1 - \alpha } }}{{\Gamma \left( {2 - \alpha } \right)}} + \frac{{\Delta t^{ - \alpha } }}{{2\Gamma \left( {3 - \alpha } \right)}}[u\left( {t_{k - j - 1} } \right) - u\left( {t_{k - j} } \right) + u\left( {t_{k + 2 - j } } \right) - u\left( {t_{k + 1 - j} } \right)] \\ & = \frac{{u\left( {t_{0} } \right)\left( {t_{k + 1} - t_{0} } \right)^{ - \alpha } }}{{\Gamma \left( {1 - \alpha } \right)}} + \frac{{u^{\prime}\left( {t_{0} } \right)\left( {t_{k + 1} - t_{0} } \right)^{1 - \alpha } }}{{\Gamma \left( {2 - \alpha } \right)}} + \mathop \sum \limits_{j = - 1}^{k + 2} W_{j} u\left( {t_{k + 1 - j} } \right) \\ \end{aligned}$$
(35)

When \(\alpha = 1\), the scheme \(L_{1}\) in Eq. (28) is reduced to the back forward difference, \(L_{2}\) in Eq. (31) is reduced to the forward difference method and \(L_{2}\) C in Eq. (32) is reduced to the centered difference method, see [32,33,34]:

3.2 Validation

Table 1 shows comparisons of the average Nusselt for varies values of \(Ra \left( {Ra = 100,1000,100{,}00} \right)\) with many published results (Baytas and Pop [3], Walker and Homsy [35], Bejan [36], Gross et al. [37] and Manole and Lage [31]) in case of the ordinary derivatives α = 1. It is noted that there are good harmony between the results. Also, it is worth mentioned that a home FORTRAN code is used and, approximately, 5 min CPU time is the time of each computation.

Table 1 Comparisons of the average Nusselt number at A = 1 and \(\Phi\) = 0
Full size table

4 Results and discussion

The obtained results are shown in terms of contours of the isotherms and streamlines. Also, profiles of the Nusselt and average Nusselt number at the hot wall. In this simulation, orders of the fractional derivatives take the range from 0.7 to 1, the walls inclination angle is varied from 0 to \(45^{^\circ }\), values of Rayleigh number are between \(10^{2}\) and \(10^{4}\) and the aspect ratio is fixed at \(A = 1\).

Table 2 presents results of the average Nusselt for some values of the fractional derivatives orders α and \(\beta\) at \(Ra = 100, 1000, 100{,}00\). It is observed that the decrease in time fractional derivatives order \(\beta\) gives a small reduction in values of Nu. This behavior is observed only in case of Ra = 100 but in other cases (\(Ra = 1000, 100{,}00\)) the average Nusselt number is insensitive with variations of \(\beta\). In addition, the variations of α are more dominant on behaviors of Nu than \(\beta\). A very good enhancement in values of Nu is noted as α decreases from 1 to 0.9.

Table 2 Results of average Nusselt number for various values of \(\alpha , \beta\) and \(Ra\)
Full size table

Figures 2, 3 and 4 display contours of the isotherms and streamlines for various values the fractional derivatives orders α and \(\beta\) in cases of \({\Phi} = 0\), \({\Phi} = 30^{^\circ }\) and \({\Phi} = 45^{^\circ }\) respectively. In all these figures, the Rayleigh number is fixed at \(Ra = 1000\). The results revealed that, in general, the streamlines show a large clockwise circular cell inside the enclosure with limited increment between the minimum value of \(\varPsi_{min}\) at the boundaries and maximum value \({\Psi}_{max}\). Also, the isotherms are distributed with equal distances from the greatest value of temperature of the hot wall to the lowest value of temperature of the cold wall. In addition, the decrease in the derivatives orders α and \(\beta\) accelerates the fluid flow and enhances the thermal boundary layer near the left wall. On the contrary, the increase in the inclination angle \({\Phi}\) acts as a retarding force to the fluid movement. It reduces the maximum values the stream function as \({\Phi}\) decreases. Also, the thermal boundary layer near the heated wall is diminished with the growing of \({\Phi}\). Physical, when \({\Phi}\) is increased the geometry of the enclosure become more complex and consequently the natural convection is reduced.

Fig. 2
figure 2

Streamlines and isotherms for various values of α and β at A = 1, \(\Phi\)  = 0°, Ra = 103

Full size image
Fig. 3
figure 3

Streamlines and isotherms for various values of α and β at A = 1, \(\Phi\) = 30°, Ra = 103

Full size image
Fig. 4
figure 4

Streamlines and isotherms for various values of α and β at A = 1, \(\Phi\) = 45°, Ra = 103

Full size image

In Fig. 5a–c, profiles of the Nusselt numbers at the hot wall for variations of the fractional derivatives orders α and \(\beta\) are plotted. Also, these figures corresponds the cases of square enclosure \(({\Phi} = 0)\) and slanted enclosures (\({\Phi} = 30^{^\circ }\), \({\Phi} = 45^{^\circ }\)) respectively. It is found that the Nusselt number decreases monotonically as α and \(\beta\) decreases. Like effect of α and \(\beta\), the increases in \({\Phi}\) results in a reduction in the local Nusselt due to the decrease in the thermal boundary layer mentioned later. Moreover, as it be observed from Fig. 6 which show the average Nusselt number for variations of α, \(\beta\) and \({\Phi}\), a clear reduction in profiles of Nu is noted as either α and \(\beta\) or \({\Phi}\) decrease.

Fig. 5
figure 5

a Nusselt number at the hot wall for various values of α at \(\Phi\) = 0°, Ra = 103. b Nusselt number at the heated wall for various values of α at \(\Phi\) = 30°, Ra = 103. c Nusselt number at the heated wall for various values of α at \(\Phi\) = 45°, Ra = 103

Full size image
Fig. 6
figure 6

Average Nusselt number at the hot wall for various values of α and \(\Phi\) at Ra = 103

Full size image

With the help of Figs. 7, 8, 9 and 10, effects of variation the fractional derivatives α and \(\beta\) on the contours of the isotherms and streamlines at \(Ra = 10^{4}\). In these figures, values of the walls inclination angle \({\Phi}\) are taken to be equal \(0^{^\circ } ,15^{^\circ } ,30^{^\circ }\) and \(45^{^\circ }\), respectively. By comparing case of \(Ra = 10^{3}\) with the current case, one can observe that great enhancements in rate of the fluid flow are found in case of \(Ra = 10^{4}\) due to the increase in the buoyancy force. In addition, like case of \(Ra = 10^{3}\), the decrease in α and \(\beta\) enhances the minimum values the stream function indicating a good natural convective transport. But as the inclination angle increases, negative effects on the streamlines and temperature distributions are noted regardless values of the Ra, α and \(\beta\).

Fig. 7
figure 7

Streamlines and isotherms for different values of α and β at A = 1, \(\Phi\) = 0°, Ra = 104

Full size image
Fig. 8
figure 8

Streamlines and isotherms for various values of α and β A = 1, \(\Phi\) = 15°, Ra = 104

Full size image
Fig. 9
figure 9

Streamlines and isotherms for various values of α and β at A = 1, \(\Phi\) = 30°, Ra = 104

Full size image
Fig. 10
figure 10

Streamlines and isotherms for various values of α and β at A = 1, \(\Phi\) = 45°, Ra = 104

Full size image

Figures 11 and 12 show rate of transfer of heat represented by profiles of the local and average Nusselt numbers for some values of the fractional derivatives orders α and \(\beta\) and, also, for variations of the inclination angle in case of the high Rayleigh number \(\left( {Ra = 10^{4} } \right)\). It is clear that a significant reduction in both of the local and average Nusselt number is found as the fractional derivatives orders α and \(\beta\) decreases. Also, similar behaviors are noted as the inclination angle increases. Physically, these behaviors are due to the reduction in the thermal boundary layer near the left wall that is obtained as α and \(\beta\) decreases or \({\Phi}\) increases.

Fig. 11
figure 11

Nusselt number at the hot wall for various values of α and \(\Phi\) at Ra = 104

Full size image
Fig. 12
figure 12

Average Nusselt number at the hot wall for various values of α and \(\Phi\) at Ra = 104

Full size image

5 Conclusion

The unsteady fluid flow and free convection in a slanted cavity containing a porous medium has been discussed under effect of the conformable fractional derivative. The finite differences method is used to solve the conformable fractional partial differential equations. In the ordinary case at α and β equal 1, the results very agree with the previous result from the open literatures. The following conclusions are summarized from the current study:

  • In both cases of the low Rayleigh number and high Rayleigh number, values of the fractional derivatives orders less than 1 enhances the flow rate while they reduce rate of the heat transfer.

  • The natural convection in case of the high Rayleigh number is the best comparing by the low Rayleigh number.

  • The increase in the walls inclination angle gives a clear reduction in both the fluid flow and heat transfer.