1 Introduction

Micro-electro mechanical systems (MEMS) may have complex geometries superimposed with surface micro-structures in the form of textures and protruding ridges which can affect the flow locally in a non-trivial manner. The effect of ridges therefore cannot be neglected especially in rarefied gas flows. Most of the analytical, experimental and computational work deals with randomly distributed rough micro-structures, micro-cavities, textured, furrowed or wavy microchannels, but work on structured micro-ridges protruding outward from the channel wall surface is minimal [1]. In the current numerical investigation, it is found that the influence of ridges and rarefaction on Poiseuille number (fRe where f is friction factor and Re is Reynolds number) on gas flow in microchannels is vigorously coupled.

There is a necessity of numerically studying the intricacies of ridge effects at micro-scale in slip flow regime. Mahulikar et al. [2] concluded that the effect of slip is to flatten the velocity distribution and reduce f as compared to continuum flow. Compressibility leads to a non-linear axial pressure variation, while rarefaction decreases the curvature in pressure distribution. Therefore, the pressure distribution becomes linear again in the free-molecular flow regime [3]. Croce et al. [4] found that rarefaction has a significant impact on fRe, even at an exit Kn as low as 0.0083. Numerical tool is preferred for such a study as the geometry of the flow passage and flow conditions are clearly known in this approach unlike in experiments. Two-dimensional (2D) approximation is insufficient to describe the real microchannel. The 2D approximation can enhance the strength of the vortices inside the ridges. In actual three-dimensional (3D) ridge elements, the flow may turn around the valley rather than filling it. Hence, 2D schematisation could be inappropriate for modelling the friction factor of a 3D microchannel. Our 3D simulations focus on external ridge elements aligned normal to the flow direction, to understand the friction resistance to the flow in such cases.

Since flow in microchannel can also be viewed as wavy channels, we briefly review the relevant literature based on numerical studies available for wavy and furrowed microchannels. Khan et al. [5] demonstrated better thermal–hydraulic performance for wavy as compared to straight channel based on printed circuit heat exchanger for three angles of zigzag bend with helium as the working fluid. Sarkar and Sharma [6] also found a monotonic increase in the ratio of f and Nusselt number (Nu = hDh/k, where h is the convective heat transfer coefficient, Dh is the hydraulic diameter and k is the thermal conductivity of the flow medium), of a furrowed sinusoidal wavy channel with that of plane channel, with rising Re. The area goodness factor of a wavy channel as compared to a plane channel is found to decrease with increasing amplitude and remains almost constant with increasing wavelength of wavy channel. Harikrishnan and Tiwari [7] numerically studied effect of different skewness angles and wave amplitudes of a sinusoidal wavy channel. They found that both Nu and f increase up to a certain skewness angle, beyond which these parameters decrease.

Ridges are a form of micro-structures protruding outward from the channel wall surface, while cavities sink into the surface. A physical geographical analogy is that ridges are like hills on the Earth’s surface and cavities are similar to valleys. Ridges and cavities appear together. In the present work, the height of a ridge is equal to the depth of a cavity. Ridges and cavities exist in applications like fuel cell devices, micro-heat sinks and exchangers, micro-mixers, pumps, turbines, valves and reactors. Cavities also appear at unwanted drag-increasing gaps between segments of aircraft skin, slots between moveable parts of control surfaces, ship hulls and slotted walls of transonic wind-tunnels [8]. Difficulties like store separation, optical distortion and structural damage can arise due to severe acoustic loading and self-sustained oscillations inside a cavity. According to Bres and Colonius [9], instabilities in the shear layer interact with the downstream corner in compressible flows. This creates acoustic waves propagating upstream and generating additional disturbances in the shear layer. This mechanism of cavity oscillations is called flow-acoustic resonance. Motivation for cavity research comes from noise reduction and substitution of active flow control devices with their passive counterparts. Bres and Colonius [9] carried out complete 3D global instability analysis over rectangular cavity for compressible flows. Shear-driven cavity incompressible flows have been investigated by Horner et al. [10], Vicente et al. [11], Romanò and Kuhlmann [12]. Vicente et al. [11] noted that spanwise dynamics occur in the recirculating flow in both shear and lid-driven cavities; this makes 3D flows significantly more complex than their 2D counterparts.

The numerical benchmark problem of lid-driven cavity has been a paradigm for solving vortex dynamics problems in closed systems [13]. Prior to this recent review on lid-driven cavity [13] is a two-decade old review by Shankar and Deshpande [14]. Mohammadzadeh et al. [15] studied circulation in lid-driven cavities and concluded that increment of non-equilibrium effects decreases the vortex strength as well as the propagation of downstream information. Reducing the wall velocity decreases the flow temperature and the induced shear forces by the driven lid to the flow. Naris and Valougeorgis [16] studied the rarefied gas flow in rectangular cavity driven by upper wall. They observed growing and collating of corner counter-rotating vortices on incrementing the cavity depth. Alkhalidi et al. [17] numerically investigated buoyancy driven rarefied gas inside a conjugate cavity of uniform wall temperature and found that the average Nu is inversely proportional to Kn. Gat et al. [18] focussed on extending the analysis of Arkilic et al. [19] for compressible viscous flows to configurations with symmetric constriction or cavity. The present work also uses the analysis of Arkilic et al. [20] for the validation of our simulations. Yu et al. [21] used experimental and numerical techniques to study pressure driven gas and liquid flow in micro-cavities. According to them, the pressure gradient first decreases due to flow divergence into the cavity and then increases due to flow convergence into the main channel. The mass flow rate increases in multi-cavity channel due to reduction in drag locally along every cavity. This local cavity effect on pressure distribution could be detected only computationally because it is generally smaller than the experimental error. This establishes the necessity of numerical work to explore the local cavity and ridge effect.

Since pressure drop characteristics along the microchannels with ridges is crucial to arrive at an optimum structural size of a micro-device, the objectives of the current work are to (i) simulate flow over three-dimensional external ridge elements located on the side walls of a microchannel, (ii) investigate the effect of Reynolds number and ridge geometry on the frictional resistance in slip flow regime, (iii) explore the effect of rarefaction and TMAC on fRe, and (iv) uncover the flow physics inside the micro-ridge.

2 Methodology

Micro-ridge effect on fRe in the slip flow regime has been investigated using numerical simulations in this work (Fig. 1). The simulations are performed using Ansys Fluent 15.0. A pressure based solver with absolute velocity formulation and steady time is employed. Viscous laminar model with low pressure boundary slip (LPBS) option is applied.

Fig. 1
figure 1

a Entire front view of 3-D microchannel with sixteen transverse ridges simulated with mass flow inlet and pressure outlet boundary conditions, b magnified view highlighting first three ridges

Full size image

Important parameters are defined in Eqs. 1, 2 and 3. Knudsen number (Kn) is the ratio of mean free path (λ) to the characteristic scale of gas flow, which is hydraulic diameter (Dh = 4Ac/P). Here, Ac is area of cross-section and P is perimeter. Note that Dh is calculated on the basis of the main channel inlet cross-section and not the ridge cross-section.

$$Kn = \frac{\lambda }{{D_{h} }} = \frac{\mu }{{PD_{h} }}\sqrt {\frac{\pi RT}{2}}$$
(1)
$$Re = \frac{{\dot{m}D_{h} }}{{\mu A_{c} }}$$
(2)
$$fRe = 2 \frac{\Delta P}{L}\frac{{D_{h}^{2} A_{c} \rho }}{{\dot{m}\mu }}$$
(3)

where μ is viscosity of ideal gas, air (μ = 1.7894 × 10−5 kg/m-s) taken at temperature (T) set as 300 K, P is the pressure, R is the specific gas constant, Re is the Reynolds number, ṁ is the specified mass flow rate, fRe is the Poiseuille number, ΔP is the pressure drop of the channel, and ρ is density of ideal gas.

Five parameters, exit Knudsen number (4.44 × 10−4 < Kn < 2.07 × 10−2), Reynolds number (0.10 < Re < 50.31), tangential momentum accommodation coefficient (0.10 < TMAC < 0.926), ridge fraction (0 < δ < 1) and ridge height ratio (0.05 < h/H < 1) are varied to explore their influence on fRe. A large number of simulations (about 700) were therefore conducted as part of this study.

2.1 Governing equations

The governing equations include mass conservation,

$$\nabla .\left( {\rho \vec{V}} \right) = 0,$$
(4)

and momentum equations in x, y and z directions for compressible flow and energy equation are given by

$$\rho \left( {\vec{V}.\nabla } \right)u = - \frac{\partial p}{\partial x} + \mu \nabla^{2} u + \frac{\mu }{3}\frac{\partial }{\partial x} \left( {\nabla .\vec{V}} \right),$$
(5)
$$\rho \left( {\vec{V}.\nabla } \right)v = - \frac{\partial p}{\partial y} + \mu \nabla^{2} v + \frac{\mu }{3}\frac{\partial }{\partial y} \left( {\nabla .\vec{V}} \right),$$
(6)
$$\rho \left( {\vec{V}.\nabla } \right)w = - \frac{\partial p}{\partial z} + \mu \nabla^{2} w + \frac{\mu }{3}\frac{\partial }{\partial z} \left( {\nabla .\vec{V}} \right),$$
(7)
$$\nabla .\left( {\vec{V}\left( {\rho E + p} \right)} \right) = \nabla .\left( {k\nabla T} \right)$$
(8)

We have used the default Maxwell’s model (Fluent Inc. Theory guide, 2010). Slip velocity is given by Eq. 9 and temperature jump is given by Eq. 10.

$$u_{w} - u_{g} = \left( {\frac{{2 - \alpha_{v} }}{{\alpha_{v} }}} \right)Kn\frac{\partial u}{\partial n}$$
(9)
$$T_{w} - T_{g} = 2\left( {\frac{{2 - \alpha_{T} }}{{\alpha_{T} }}} \right)Kn\frac{\partial T}{\partial n}$$
(10)

where \(\vec{V}\) is the velocity vector with u, v and w being the velocity components in streamwise, cross-streamwise and spanwise directions. The subscripts g and w represent gas and wall respectively. n is the normal to the wall. αv is TMAC of the gas taken as 0.1, 0.3, 0.5, 0.7 and 0.926. The last value is suggested by Agrawal and Prabhu [22] based on a detailed survey of experimental data. T is the temperature, ρ is density, E is energy (E = h − p/ρ + V2/2), h is sensible enthalpy, p is pressure, k is thermal conductivity of fluid, and αT is the thermal accommodation coefficient with a value of 0.9137. Viscous dissipation term is included in the energy equation for the highest and lowest values of TMAC, Mach number, Knudsen number, Reynolds number of all ridge fractions, and Poiseuille number (fRe) is compared to that without inclusion of viscous dissipation. The per cent deviation in fRe is found to be less than 1%. Therefore, viscous heating is negligible in our work.

2.2 Geometry and boundary conditions

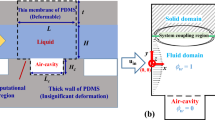
Figure 1a depicts the front view of three dimensional microchannel with transverse ridges, where first three ridges are highlighted. A zoomed view with all the prescribed boundary conditions is illustrated schematically in Fig. 1b. Microchannel is simulated with mass flow inlet and pressure outlet boundary conditions. Since, the flow is compressible, a flow development length of 800 μm is provided, which is double of that required at the maximum value of Re considered in this study.

A parameter, ridge fraction (δ) is defined as the ratio of length (s) of a protruded ridge to the pitch of the ridges (L) (Fig. 1b). For fixed L = 200 µm, s is varied as 0, 50, 100 and 150 µm. Therefore, δ values of 0, 0.25, 0.5 and 0.75 are obtained. δ = 0 corresponds to smooth microchannel without ridges. These are simulated to compare the ridge effect on fRe with baseline case of smaller straight channel. Sixteen ridges of each ridge fraction for a given length are modelled. The height (2H, due to symmetry) of channel is 200 µm and width (W) is 100 µm, making the aspect ratio (α = W/2H) of the channel as 0.5. The width of the protruded ridge is same as the width of the main channel (W) as shown in Fig. 1b. The height (h) of the ridge is varied as 100, 50, 40, 30, 20, 10 and 5 µm. Height of the ridge is non-dimensionalised by half the height of the channel (h/H).

Air is assumed to behave as an ideal gas. At the bottom surface, symmetry boundary condition [4, 23] is applied. Mass flow inlet boundary condition is applied at the inlet of the microchannel with mass flow rate varying from 1.35 × 10−10 to 2.25 × 10−7 kg/s. At the exit of microchannel, pressure outlet boundary condition is allocated in order to fix Knudsen number from 4.44 × 10−4 to 2.07 × 10−2.

The SIMPLE scheme is employed with least square cell based spatial discretisation and second order upwind for better accuracy. The convergence of continuity, momentum and energy equations is checked with residuals of the order of 10−9. Pressure drop calculations are performed for each δ, Re, Kn and TMAC case and converted into Poiseuille number (fRe) as given by Eq. 3 [4, 23, 24].

2.3 Grid independence test

Maximum Knudsen number (Kn = 2.07 × 10−2), Reynolds number (Re = 50.31) and ridge fraction (δ = 0.75) cases are chosen for performing grid independence test for four ridges. This case is chosen since it has the maximum influence on fRe, as indicated in Fig. 6e (presented later). In Table 1 (in bold), it is observed that a hexahedral mesh size of 4 µm gives a deviation of 0.76% as compared to a mesh size of 2 µm. Even 5 µm mesh size gives a deviation within 1%. Hence, 4 µm size is selected for all the simulations with ridge height of 20 μm and above to save computational time and power (Fig. 4a; presented later). For shorter ridge heights of 0.5, 5 and 10 μm, the grid is drastically refined up to 0.05 μm in the cross-streamwise direction leading to mesh volumes up to 1,313,500 to ensure the solution is grid independent.

Table 1 Grid independence test
Full size table

2.4 Validation of results with analytical solution and DSMC data

The validation of simulations performed by benchmarking against two-dimensional channel solution for compressible flow is presented in this section. A parallel plate microchannel of height 1 μm and length 10 μm is taken. The centre-line pressure distribution is compared with the analytical solution of non-linear pressure distribution reported by Arkilic et al. [20]. The present predictions are also compared with the DSMC data of compressible flow provided by Gavasane et al. [25] on Argon gas for Kn = 0.124 at channel outlet, as illustrated in Fig. 2a. The mass flow rate specified at inlet of this geometry has been computed from the solved DSMC data. The results obtained for the absolute pressure are in good agreement with the analytical solution as well as the DSMC data. The centre-line velocity distribution obtained by the present simulation matches well with that of DSMC data (Fig. 2b). Centre-line static temperature distribution (Fig. 2c) obtained in streamwise direction matches with DSMC data, hence the energy equation is validated. Any minor difference in comparison is due to use of pressure inlet boundary condition in DSMC and mass flow inlet boundary condition in Fluent. This difference is insignificant to comprehend the flow physics further away from channel boundaries. Similarly, the slip velocity in streamwise direction plotted at cell adjacent to the wall is in good agreement with DSMC (Fig. 2d). The cross-streamwise velocity distribution plotted at half of the channel length (x/L = 0.5) is in excellent agreement with that of DSMC data (Fig. 2e) as well as analytical solution for first and second-order slip boundary conditions given by Karniadakis et al. [26]. Hence, the boundary conditions used are validated.

Fig. 2
figure 2

A comparison between variations of a centre-line pressure distribution along streamwise direction obtained in present simulation with analytical solution of Arkilic et al. [20] and DSMC data of Gavasane et al. [25], b centre-line velocities along streamwise direction, c centre-line static temperature distribution along streamwise direction, d slip velocity adjacent to the wall along streamwise direction, e cross-streamwise velocity profile obtained at half length of the channel, obtained in simulation, DSMC data [25], analytical solution of Karniadakis et al. [26] for first and second-order slip boundary conditions

Full size image

The incompressible flow results for three-dimensional straight channel of with aspect ratio, α = 0.5 are compared with analytical solution reported by Morini et al. [27] (Eq. 11).

$$fRe = \frac{62.192}{1 + 8.571 Kn }$$
(11)

Poiseuille number (fRe) of straight channel reported by them is 61.956, and that obtained in this work is 61.698 which give a percentage difference of 0.4%. There is an excellent agreement with the corresponding analytical solution at all Re in the continuum regime, where Kn = 4.44 × 10−4. Validation in the slip regime has been performed at four different Knudsen numbers (Table 2). At highest Kn = 2.07 × 10−2, deviation of fRe from analytical solution is minimum (in bold), trusting us with working in the rarefied gas flow regime. Since, fRe of straight channel is matching very well with the analytical solution [27]; this gives us the confidence to introduce the ridges in the straight channel.

Table 2 Validation of fRe for straight microchannel (α = 0.5) with analytical solution of Morini et al. [27]
Full size table

3 Results and discussion

The hydraulic diameter (Dh) is 133.33 μm for all the ridge fractions. Kn at the outlet of channel and Re are calculated based on Dh according to Eqs. 1 and 2 respectively. The mass flow rate is specified from 1.35 × 10−10 kg/s (Re = 0.10), 1.35 × 10−8 kg/s (Re = 10.06), 3.375 × 10−8 kg/s (Re = 25.15), 5.40 × 10−10 kg/s (Re = 40.24) and 6.75 × 10−8 kg/s (Re = 50.31). The exit Kn and Re are kept same for all δ. Table 3 gives the combination of all the specific parameters used for about 700 three-dimensional simulations conducted. The flow characteristics inside ridges with mass flow inlet and pressure outlet boundary conditions are depicted for the highest exit Knudsen number of this study, Kn = 2.07 × 10−2. In the later subsections, the combined effect of Re, δ and Kn on fRe is extensively explained.

Table 3 Specific values of parameters simulated
Full size table

3.1 Effect of Reynolds number on the flow characteristics inside a ridge

The flow characteristics inside ridges of δ = 0.75 are depicted by streamtraces, absolute pressure, x-velocity, y-velocity and vorticity at Kn = 2.07 × 10−2 (Fig. 3). These contours are compared at minimum and maximum Reynolds numbers (Re = 0.10 and 50.31) to investigate the influence of Re. All the contours are drawn at the mid-plane along z–direction, which is located at z/H = 0.5 for δ = 0.75. This ridge fraction is chosen because it gives the lowest fRe value of 44.02 in the investigated range of Kn, Re and δ, as described in subsequent Sect. 3.2. The velocity profiles are qualitatively similar at the entrance of each ridge, once the gas passes through the flow development length. The flow characteristics depicted for sixteen ridges are zoomed in the 8th, 9th, 10th and 11th ridges for clarity. The dimensions of the channel in x, y and z coordinates are non-dimensionalised by hydraulic diameter. Overall, it can be observed that flow is behaving in a periodic manner. The same flow pattern is repeating after every ridge, indicating that the periodicity is same as the pitch length.

Fig. 3
figure 3

Comparison of flow characteristics of δ = 0.75 for minimum and maximum Re, at exit Kn = 2.07 × 10−2; left column Re = 0.1, right column Re = 50.31. a, b Streamtraces for 16 ridges; c, d streamtraces in magnified view of 8th, 9th, 10th and 11th ridges; e, f absolute pressure variation; g, h streamwise velocity variation; i, j cross-streamwise velocity variation; k, l vorticity variation

Full size image

Figure 3a, b shows the comparison of streamtraces in all sixteen ridges at Re = 0.10 and 50.31. Figure 3c, d depicts the magnified view of streamtraces of 8th, 9th, 10th and 11th ridges. Upon examining the pattern in Fig. 3c, the streamlines move very smoothly inside the ridges at low Re = 0.10, whereas Fig. 3d depicts the presence of trapped vortices at Re = 50.31. This indicates that there is an exchange of momentum from the main channel to the ridge, which is more pronounced for Re = 50.31. A counter-clockwise vortex is trapped in every ridge. This phenomenon of creation of eddies is also observed by Naris and Valougeorgis [16].

The absolute pressure in Fig. 3e, f is non-dimensionalised by pressure at the outlet of the channel. At Re = 0.10, low pressure is seen at ridges due to extremely low flow rate of 1.35 × 10−10 kg/s. At Re = 50.31, the magnitude of lowest pressure is more than the highest pressure at Re = 0.10. Overall, the range of absolute pressures and pressure drop in ridges is higher at Re = 50.31 compared to that at Re = 0.10.

Figure 3g shows the streamwise velocity distribution at Re = 0.10. All the velocities are normalised with respect to the average velocity at the inlet of the main channel. At y = 0, there is higher x-velocity, which gradually reduces as the flow approaches the mouth of the ridge (located at y = H), and further reduces till the topmost wall of the ridge. As the streamlines enter the ridge mouth, the area for the flow increases which leads to a reduction in velocity according to mass conservation. The magnitudes of x-velocity are higher at Re = 50.31 (Fig. 3h) as opposed to those at Re = 0.10. As apparent from the velocity contours, the flow is not symmetric along the vertical centre-line of the ridge. The velocity peaks rather drift slightly towards the right side of the centre-line. However, notice from Fig. 3g that the flow is symmetric along vertical centre-line at Re = 0.10. This indicates that there is a phenomenon happening inside the ridge, which is leading to this drift of velocity peaks, upon increasing the Reynolds number. This observation becomes clear upon examining the streamline pattern in Fig. 3b, d which depicts the presence of trapped vortices. At Re = 50.31, due to the presence of vortex, all the velocity peaks are drifted slightly away from the vertical centre-line of the ridge and the flow becomes non-symmetric, unlike symmetric flow observed at Re = 0.01. Moreover, the vortex is itself not symmetric, as it is clinging towards the left corner. This could be because of the flow entering the ridge at an angle from the left corner. While exiting from the ridge, flow hits the right corner, thus vortex gets drifted away from the right corner.

Figure 3i, j depicts a comparison of the cross-streamwise velocities. At Re = 0.10 and Re = 50.31, a high positive magnitude of y-velocity is observed at the left corner of the ridge and high negative magnitude is seen at the right corner of the ridge, because of the flow impacting the wall before exiting the right corner of the ridge. In between these two corners, the y-velocity variation from positive to negative is more gradual at Re = 50.31 (Fig. 3j) compared to that at Re = 0.10 (Fig. 3i).

Figure 3k, l shows vorticity contours orthogonal to streamwise and cross-streamwise directions. The vorticity is multiplied by Dh and divided by inlet velocity to make it non-dimensional. The z-vorticity magnitude is higher in the corners of the ridge compared to other regions. At Re = 0.10, z-vorticity is symmetric along the vertical centre-line of the ridge, but not at Re = 50.31. Similar phenomenon is reported for incompressible flow in lid-driven cavity flow by Kuhlmann and Romanò [13] as well as in shear-driven cavity flow by Romanò and Kuhlmann [12]. At Re = 1, streamlines are almost symmetrical due to symmetries of Navier–Stokes equation in Stokes flow limit of Re tending to zero. At greater Re, inertia terms in incompressible Navier–Stokes equations deteriorate the reflectional symmetry in the flow direction [13]. Horner et al. [10] also observed asymmetry in manifold structure of shear-driven cavity for incompressible flows due to inertia. Moreover, at Re = 50.31, the z-vorticity is lower at right corner as compared to that at left corner (Fig. 3l). This is because of flow hitting the right corner before exiting the ridge. This creates higher pressure and lower velocity gradients at right corner, leading to lower vorticity.

Figure 4a shows the 3D view of two locations, s0 which is the entrance of ridge expansion region and s1/2 which is the ridge vertical centre-line. Figure 4b represents 2D view of s0 and s1/2 where normalised cross- streamwise velocity variation is plotted for Re = 0.10 and Re = 50.31. The velocity is normalised with the average velocity at the inlet of the straight channel (δ = 0) after a flow development length of 800 μm (Fig. 4a). One of the middle ridges (thirteenth) is chosen for plotting the velocity variation to avoid any effect of boundary conditions. In Fig. 4b, c, the two curves meet at a point where the velocity at s1/2 becomes equal to velocity at s0. This point is christened as ‘intersection point’ which is the point where the velocities are equal for the flow just entering the ridge expansion region and ridge vertical centre-line. This helps in identifying the position at which momentum exchange is expected. Intersection point is located below the ridge mouth (y = H). Hence, there is an exchange of momentum from the main channel to the ridge at intersection point below the ridge mouth. This momentum exchange is more rapid for Re = 50.31, since the two curves intersect much earlier, at about y/H = 0.25 and again at about y/H = 0.8 (Fig. 4d).

Fig. 4
figure 4

a Three-dimensional representation of hexahedral mesh of size 4 µm representing two locations, entrance of ridge expansion (s0) and ridge vertical centre-line (s1/2), b two-dimensional representation of s0 and s1/2, where comparison of cross-streamwise velocity profiles obtained for Kn = 2.07 × 10−2 at c Re = 0.10 and d Re = 50.31

Full size image

Figure 5a depicts a comparison of the normalised streamwise velocities in the slip and continuum regimes at Re = 0.10, obtained at the mouth of the ridge (y = H). The velocities are normalised with respect to the average velocity at the inlet of the straight channel after flow development length (Fig. 1b). There is a strong effect of slip seen at Kn = 2.07 × 10−2. The magnitude of streamwise velocity at Kn = 2.07 × 10−2 is lower than that at Kn = 4.44 × 10−4 at Re = 0.10. A curious dip is seen at the velocity profile near the top wall of the ridge, which is explained by the streamline pattern in Fig. 3a. As the streamlines enter the ridge mouth, the area for the flow increases which leads to a reduction in velocity according to mass conservation. However, at Re = 50.31, the velocity magnitude at Kn = 2.07 × 10−2 is comparatively much greater than that at Kn = 4.44 × 10−4 (Fig. 5b).

Fig. 5
figure 5

Comparison of velocity profile obtained at the mouth of the ridge (located at y = H) in slip and continuum regime at a Re = 0.10 and b Re = 50.31

Full size image

This section helped in comparing of flow characteristics inside a micro-ridge for low and high Re at a specific Kn. The key point is the formation of vortices at Re = 50.31 for Kn = 2.07 × 10−2, which are absent at Re = 0.10. This understanding of the influence of Re on micro-ridge flow physics provides a vivid picture for further understanding of Re influence on fRe, which is another key objective of this work. Since, this section focussed on flow characteristics of only a specific Kn and δ value, later sections explain Re influence on fRe over wide ranges on Kn and δ.

3.2 Effect of Reynolds number and ridge fraction on Poiseuille number

In this subsection, fRe for a wide range of Re is plotted for the ridges in Fig. 6a–c for exit Kn = 4.44 × 10−4, 4.61 × 10−3 and 2.07 × 10−2, respectively. As explained in Sect. 2.4, fRe results for straight microchannel of aspect ratio, α = 0.5 are validated with fRe value reported by Morini et al. [27].

Fig. 6
figure 6

Effect of Reynolds number on Poiseuille number at all ridge fractions, compared to straight channel at exit Knudsen number a 4.44 × 10−4, b 4.61 × 10−3, c 1.01 × 10−2, d 1.50 × 10−2 and e 2.07 × 10−2

Full size image

In the continuum regime (Fig. 6a), the value of fRe is nearly constant for δ = 0.25, whereas fRe increases slightly with Re for δ values 0.50 and 0.75. The increase is more prominent for higher δ. It is interesting to note that none of the four graphs intersect each other. In case of δ = 0.75, even after exhibiting a noteworthy climb of fRe with increase in Re, the plot does not touch the other plots in the investigated range. At lowest Re = 0.10, fRe of δ = 0.75 is 15.5% less than fRe of δ = 0 while fRe of δ = 0.50 is 6.8% less than that of δ = 0. Therefore, at low Re, fRe is quite low, indicating less distortion of streamlines and penetrability into the ridges due to expansion and contraction cycles. As Re increases, streamlines distort and gas penetrates more, leading to a higher frictional resistance.

At exit Kn = 4.61 × 10−3, 1.01 × 10−2, 1.50 × 10−2 and 2.07 × 10−2 (Fig. 6b, c), fRe value at low Re has reduced for all microchannels with ridges, as compared to continuum regime, indicating that fRe decreases with Kn. At Kn = 4.61 × 10−3, δ = 0.50 and lowest Re = 0.10, fRe has decreased by 6.68% with respect to δ = 0 while at highest Re = 50.31, fRe has decreased by 5.70%. For δ = 0.75, at Re = 0.10, fRe has decreased to 15.22% with respect to δ = 0 and decreased to 11.99% at Re = 50.31. At higher Kn values, fRe increases with Re. The reason for increase in fRe with Re is due to formation of vortices inside the ridges and distortion of streamlines, as shown in Fig. 3d. At Kn = 1.01 × 10−2 and Re = 0.10, fRe has decreased by 6.40% for δ = 0.50 and 14.83% for δ = 0.75, whereas at Re = 50.31, has decreased by 5.82% for δ = 0.50 and 12.21% for δ = 0.75 with respect to δ = 0 (Fig. 6c). Similarly at Kn = 1.50 × 10−2, fRe has decreased by 6.13% for δ = 0.50 and 14.45% for δ = 0.75 at Re = 0.10, whereas at Re = 50.31, has decreased by 5.83% for δ = 0.50 and 12.17% for δ = 0.75 with respect to δ = 0 (Fig. 6d).

At Kn = 2.07 × 10−2 (Fig. 6e), for δ = 0.50, at lowest Re = 0.10, fRe has decreased by 5.80% compared to that of δ = 0 while at Re = 50.31, fRe has similarly decreased by 5.79%. For δ = 0.75, at Re = 0.10, fRe has decreased by 14.01% compared to that of δ = 0 and decreased by 12.01% at Re = 50.31. Dorari et al. [23] found recirculation zones due to pressure vibration, which are considered as dead zones with slip velocities almost zero, hindering the upstream gas flow and causing increase in flow resistance.

3.3 Effect of rarefaction on Poiseuille number

In Fig. 5 of Sect. 3.1, rarefaction highly influenced the streamwise velocity profile obtained at the ridge mouth. Thus arises the need for focussing upon the effect of Kn on fRe. Figure 7 shows the trend of fRe with Kn at five different Reynolds numbers. The present straight channel plot for δ = 0 and δ = 0.25 are quite close to each other for all Re values. In Fig. 7a, b, fRe for δ = 0.5 and 0.75 is less compared to fRe for δ = 0.25 and reduces further as Kn increases for Re = 0.10 and 10.03. The behaviour of inverse proportionality of fRe with Kn is also reported by Morini et al. [27]. In Fig. 7c at Re = 25.15, fRe reduces up to Kn = 4.61 × 10−3 and becomes nearly constant with increasing Kn for all ridge fractions. In Fig. 7d at Re = 40.24, fRe reduces up to Kn = 4.61 × 10−3 and starts increasing with Kn for all ridge fractions. Hence, rarefaction beyond threshold Kn = 4.61 × 10−3, there is a direct proportionality of fRe with Kn observed after a threshold Re = 25.15.

Fig. 7
figure 7

Effect of Knudsen number on Poiseuille number at various ridge fractions, compared to straight channel at Reynolds number a 0.10, b 10.06, c 25.15, d 40.24 and e 50.31

Full size image

Figure 7e shows the trend of fRe with Kn at highest Re = 50.31. As Kn increases, fRe increases. This reflects the strong effect of Re on fRe. The present work elaborates about decrease in fRe of δ = 0.5 and 0.75 compared to straight channel (δ = 0), on increasing δ is much stronger on gas flow with lower Kn. For instance, at Re = 0.1, δ = 0.5, the decrease is 6.68% at Kn = 4.61 × 10−3 and 5.8% at Kn = 2.07 × 10−2 as seen in Fig. 6a. Similarly at Re = 0.1, δ = 0.75, the decrease is 15.22% at Kn = 4.61 × 10−3, whereas 14.1% for Kn = 2.07 × 10−2 (Fig. 6c). Therefore, the ridge elements assist the upstream gas flow and decrease fRe due to increment in flow area.

Figure 8 compares the streamtraces of ridges of δ = 0.75 at minimum and maximum exit Kn and same Re = 50.31. As observed in Fig. 8, the size of vortex is smaller at Kn = 4.61 × 10−3 as compared to that at Kn = 2.07 × 10−2. On the increment of vortex size at higher Kn, flow area is expected to reduce due to which fRe is more compared to lower Kn (Fig. 7d–e). This might be the reason for the increasing trend of fRe with Kn noticed at high Re.

Fig. 8
figure 8

Comparison of streamtraces for 16 ridges of δ = 0.75 at Re = 50.31; left column Kn = 4.61 × 10−3, right column Kn = 2.07 × 10−2. a, b entire 16 ridges; c, d magnified view of 8th, 9th, 10th and 11th ridges

Full size image

3.4 Effect of TMAC on Poiseuille number

Tangential momentum accommodation coefficient (TMAC) is the fraction of tangential momentum lost when by a molecule on colliding a surface. For specular reflection, TMAC is zero signifying no accommodation, whereas for diffuse reflection, its value is 1, signifying total accommodation. In present work, TMAC is varied as 0.1, 0.3, 0.5, 0.7 and 0.926 as shown in Fig. 9. It is varied for across five different Re of this study at maximum exit Kn of 2.07 × 10−2. In Eq. 9, inserting low values of TMAC increases the slip velocity, even for small values of Kn [2]. The more the value of TMAC, the more is the tangential momentum lost by a molecule on hitting the surface and less is the slip velocity. Hence, the gas molecules would slip less on the surface, leading to higher flow friction. This reflects the strong effect of slipping in reducing the Poiseuille number.

Fig. 9
figure 9

Effect of TMAC on Poiseuille number at various ridge fractions, compared to straight channel at Reynolds number a 0.10, b 10.06, c 25.15, d 40.24 and e 50.31

Full size image

The dependence of Poiseuille number on TMAC is tremendously affected by modifying the surface topography using micro-ridges. In straight channel (δ = 0), fRe is minimum at lowest value of TMAC = 0.1 for all Re values. On contrary at highest TMAC = 0.926, fRe is maximum for δ = 0. The role of ridges in reducing friction becomes effective after a threshold TMAC value. At lowest Re = 0.10, this threshold TMAC is less than 0.5, whereas at highest Re = 50.31, the threshold TMAC is less than 0.3. Hence, the threshold TMAC decreases with increase in Reynolds number. Below the threshold TMAC, there is high slipping already, which is enough for reduction of flow resistance. Introduction of ridges below this threshold TMAC is not helping at all in reducing the friction, since gas molecules are hardly able to appreciate the surface topography. After TMAC is more than a certain threshold, the loss of momentum of molecules increases and slipping decreases. This brings the need of changing the topography with ridges, which supports in drag reduction. The more is the ridge fraction, the less is the Poiseuille number. The results with shortest ridge length (δ = 0.25) are almost overlapping with results with straight channel (δ = 0). Longer ridge lengths (δ = 0.5 and δ = 0.75) are actually aiding in reduction of drag at high TMAC values. The reason is the increase in ridge length leading to increase in flow area, leading to less frictional resistance. Since, flow area is playing a major role in reducing friction, next we concentrate on changing the height of the ridge and studying its effect on fRe.

3.5 Effect of ridge height ratio on Poiseuille number

Ridge height ratio is the height of the ridge divided by half the height of channel (h/H). The height of the ridge is varied for each ridge fraction and influence of ridge height ratio on the Poiseuille number is studied in detail. Figures 10, 11, 12 and 13 signify that fRe decreases as the ridge height increases, up to a certain critical height (hc), after which fRe becomes almost constant for a specific Re and Kn. Maximum fRe is observed in the case of lowest height. Beyond the ridge height of 100 µm (h/H = 1), there would not be any further considerable decrease in fRe. Hence, 100 μm height is chosen to explain the effect of Re, Kn and TMAC at all ridge fractions in the above sections and to calculate the critical height.

Fig. 10
figure 10

Effect of height of ridge on Poiseuille number at ridge fraction 0.75 at various exit Knudsen number a 4.44 × 10−4, b 4.61 × 10−3, c 1.01 × 10−2, d 1.50 × 10−2 and e 2.07 × 10−2

Full size image
Fig. 11
figure 11

Streamlines at maximum exit Kn = 2.07 × 10−2 and maximum Re = 50.31 at different ridge heights of a 5 µm, b 10 µm, c 20 µm, d 30 µm, e 40 µm, f 50 µm and g 100 µm

Full size image
Fig. 12
figure 12

Effect of height of ridge on Poiseuille number at ridge fraction 0.50 at various exit Knudsen number a 4.44 × 10−4, b 4.61 × 10−3, c 1.01 × 10−2, d 1.50 × 10−2 and e 2.07 × 10−2

Full size image
Fig. 13
figure 13

Effect of height of ridge on Poiseuille number at ridge fraction 0.25 at various exit Knudsen number a 4.44 × 10−4, b 4.61 × 10−3, c 1.01 × 10−2, d 1.50 × 10−2 and e 2.07 × 10−2

Full size image

If a horizontal line is drawn at 1% increment of fRe obtained at h/H = 1, wherever it intersects fRe versus h/H curve, gives us the critical ridge height ratio (hc/H). One should not take anything less than 1% because that would be within numerical uncertainty. The concept of critical height would be significant for designing low friction channels. Ridge height chosen must be greater than the critical height for achieving low fRe. Therefore, greater is the value of critical height, more is the fabrication flexibility in choosing the ridge height without being concerned of increased flow friction. The detailed elucidation of critical height attained for each ridge fraction is provided in the following subsections.

3.5.1 Critical height for ridge fraction 0.75

The height of the ridge is varied as 5, 10, 20, 30, 40, 50 and 100 µm for δ = 0.75. As height increases up to 100 µm, fRe decreases up to height 50 µm, after which fRe is almost same at height 100 µm. In Fig. 10a, in the continuum regime, at heights of 5, 10 and 20 µm, there is no change in fRe with respect to Re. In Fig. 10b–e, as Kn increases, the effect of Re on fRe is prominent even at lower ridge heights. The range over which fRe varies with Re widens as the flow becomes more rarefied. fRe is inversely proportional to Kn and directly proportional to Re. After a certain ridge height ratio (h/H), there is no decrease in fRe at a specific Re value. Critical height (hc) is found by intersection of a line drawn at 1% increment of fRe obtained at h/H = 1 with the fRe versus h/H curve. Such lines are drawn for all Re at a specific Kn. It is deduced from Fig. 10, at Re = 0.1, 30 μm < hc< 40 μm for all slip regimes. In continuum regime, lowest Kn = 4.44 × 10−4, 40 μm < hc < 50 μm. At Re = 10.06, 30 μm < hc < 40 μm; whereas at Re = 25.25, 40.25 and 50.31, 20 μm < hc < 30 μm for all Kn. Therefore, ridge critical height reduces with increase in Re.

Figure 11 compares the streamline pattern for all the heights simulated for δ = 0.75 at Kn = 2.07 × 10−2 and Re = 50.31. It is observed that vortex formation is absent for lower ridge heights of 5 and 10 µm. At 20 µm height, streamlines begin to curl at the left corner of the ridge, forming a counter-rotating vortex. The size of this vortex increases with increment in ridge height. Naris and Valougeorgis [16] too reported the growth of counter-clockwise corner vortex on increasing the depth of a cavity in a compressible rarefied gas flow. Figure 11c, d depicts that left corner vortex size is the smallest for the range of critical height (20 μm < hc < 30 μm). Beyond hc, the size of vortex increases upon incrementing the ridge height resulting in no significant reduction in fRe. The flow is asymmetric along the vertical centre-line of the ridge. According to Kuhlmann and Romanò [13], reflectional symmetry in x-direction is ruined at higher Re. Figure 3j depicts the z-vorticity to be lower at the right corner as compared to the left corner for the same flow conditions. This is because of the flow hitting the right corner before exiting the ridge. This creates higher pressure and lower velocity gradients at the right corner, leading to lower vorticity. This also explains the creation of vortex at left corner and not at the right corner in Fig. 11c–g. Interestingly, a trapped asymmetric vortex is created on further increasing the ridge height to 100 µm. This vortex hinders the penetration of streamlines into ridges and reduces the area available for flow expansion. In fact, there is a slight increment of 0.21% in fRe at 100 µm height with respect to fRe at 50 µm. This value might be within the numerical uncertainty, but at least there is no further decrement in fRe. This establishes the redundancy in further increasing the ridge height.

3.5.2 Critical height for ridge fraction 0.5

The height of the ridge is varied as 5, 10, 20, 50 and 100 µm for ridge fraction of 0.5 (Fig. 12). Since fRe obtained at 20, 50 and 100 μm heights are almost the same, there is no need of simulating heights 30 µm and 40 μm, unlike δ = 0.75. Therefore, the effect of height at δ = 0.5 is not as strong as seen in δ = 0.75. In the continuum regime, at heights of 5 and 10 µm, there is no change in fRe with respect to Re (Fig. 12a). Similar to δ = 0.75, fRe decreases with increasing Kn and increases with incrementing Re (Fig. 12b–e). There is no change in fRe as h/H increases beyond hc/H. It is deduced from Fig. 12, for each Kn and Re, 10 μm < hc < 20 μm. The magnitudes of hc obtained for δ = 0.5 is less than hc obtained at δ = 0.75 at any specific Re and Kn.

3.5.3 Critical height for ridge fraction 0.25

For ridge fraction 0.25, the effect of height seen is the least (Fig. 13). The height of the ridge is varied as 0.5, 5, 10, 20, 50 and 100 µm for δ = 0.25. Figure 13a indicates the overlapping of all fRe versus h/H curves indicating no effect of Re in the continuum regime. As Re decreases and Kn increases, fRe decreases. A slight decrease in fRe is observed till h/H = 0.1, beyond which fRe value is almost the same at any specific Re and Kn. It is deduced from Fig. 13, for each Kn and Re, 0.5 μm < hc < 5 μm. The magnitudes of hc obtained for δ = 0.25 is less than hc obtained at δ = 0.5 and δ = 0.75 at any specific Re and Kn.

The range of hc has been provided in this study for all δ, Kn and Re; its exact value could be found in future studies. If the value of hc is higher, then there are more choices of ridge heights that could be fabricated without being concerned about an increase in flow friction. As the ridge fraction increases, ridge critical height increases at any specific Re and Kn. This indicates that the effect of increasing the ridge height for reducing the friction factor is most prominent in longest ridge length. The reason could be more area for the flow to expand, once it enters the ridge and then contract once it exits the ridge. The ability of the flow to penetrate into the ridge could be limited by the critical height. Beyond hc/H, the streamlines might not be penetrating further, leading to a saturation of fRe value.

The above results certainly indicate that the presence of micro-ridges reduce the frictional resistance in rarefied gas flow.

4 Conclusions

The present three-dimensional numerical investigation of micro-scale gas flows through microchannel with ridges has led to the following conclusions:

  1. 1.

    Cuboidal micro-ridges play a significant role in reducing the frictional resistance in rarefied gas flows.

  2. 2.

    Poiseuille number reduces as the length and height of the ridge increases.

  3. 3.

    In all ridge fraction microchannels, fRe increases with Re in the slip flow regime.

  4. 4.

    fRe is inversely proportional to Kn at low Re and interestingly, fRe becomes directly proportional to Kn at high Re values.

  5. 5.

    fRe is directly proportional to the tangential momentum accommodation coefficient. The role of ridges in reducing the frictional resistance becomes effective at higher values of TMAC.

  6. 6.

    Critical height (hc) of ridge is a major factor in deciding the ridge geometry which provides the least fRe value. The critical height is smallest for δ = 0.25, followed by δ = 0.50 and δ = 0.75 at a specific Re and Kn.

  7. 7.

    Re = 0.1 and Kn = 2.07 × 10−2 provides the minimum fRe value of 44.02, obtained at δ = 0.75 and h/H = 1. This is the lowest frictional resistance micro-ridge design recommended.

Present work sets no restriction in extending the height of ridge elements, since ridges protrude outward from the surface. Here, the height of highest ridge is of same order as the channel height and helps in drastic drag reduction. The existing literature on micro-cavities focuses more on shear driven [9,10,11,12] and lid-driven [13,14,15,16] liquid flows [24, 28] and not from the perspective of reducing friction in rarefied gas flows.

Our study concludes that ridges assist the upstream flow and decrease fRe due to increase in flow area for a specific Re, Kn, TMAC, δ and h/H range. The influence of threshold TMAC in reducing frictional resistance inside microchannels has been studied for the first time. The concept of choosing the ridge height greater than critical height would be significant for designing low friction channels. Contours of non-dimensional pressure, velocity, vorticity and streamtraces inside a micro-ridge are depicted to understand the dynamics of the flow. We recommend that care must be taken while selection of the ridge length and height for the working range of Re, Kn and TMAC. As a future work, the effect of ridges at higher Kn for a variety of shapes, orientations, number density and pitch can be studied.