1 Introduction

The precise estimation of hydrodynamic pressure on water retaining structures such as concrete gravity dam is considered to be the major issue in design of these structures. Westergaard [1] evaluated hydrodynamic pressure on the vertical upstream face of dam. Thus, a lot of research work was carried out in this area. A group researcher [2,3,4,5,6] used displacement-based finite element method to obtain hydrodynamic pressure. Another group of researchers [7,8,9,10] used Eulerian approach as the number of unknowns per node reduces to one and the critical irrotational condition of fluid motion is satisfied automatically. Again, in finite element analysis of reservoir adjacent to concrete gravity dam, difficulties arise mainly due to the infinite extend of reservoir. The first radiation boundary condition in fluid domain was proposed by Sommerfeld [11]. Similarly, Sharan [12] proposed another boundary condition considering the effect of absorption of presser wave at reservoir bottom. Maity and Bhattacharya [13] incorporated a nonreflecting condition at the artificial boundary of infinite reservoir. However, this condition cannot be defined for the case when the exciting frequency is greater than the fundamental frequency of the reservoir. Gogoi and Maity [7] proposed similar frequency-dependent absorbing boundary condition for the analysis of infinite reservoir. The hydrodynamic pressure acting on concrete gravity dam depends on several parameters such as characteristic of reservoir bottom, compressibility of water in the reservoir and the inclination of upstream face of dam. In most of the cases, the reservoir bottom is considered to be rigid and the hydrodynamic pressure on adjacent dam obtained from such cases is overestimated. Lotfi [14] studied the effect of sediment layer at reservoir bottom on the performance of reservoir. In this study, the sediment layer is considered to be viscoelastic and almost incompressible. Some researchers [12, 15, 16] implemented a damping boundary condition at the reservoir bottom to simulate the reservoir bottom absorption. In some cases, the reservoir is considering water to be incompressible [17,18,19]. On the other hand, Maity and Bhattacharya [13], Gogoi and Maity [7], Mirzabozorg et al. [8]. Mandal and Maity [9, 10, 20], Adhikary and Mandal [21] considered water to be compressible.

It is apparent from the literatures referred above that for precise estimation of hydrodynamic pressure on concrete gravity dam, finite element analysis is considered to be an efficient numerical tool in which water in the reservoir can be modelled as either compressible or incompressible fluid. Several truncation boundary conditions are available in the existing literatures. However, the suitability of these boundary conditions is not explained. In the present study, a computer code in MATLAB environment has been developed to compare existing boundary conditions. Further, the study is extended to observe the effect of compressibility of water and the inclination of dam upstream face.

2 Theoretical formulation

The state of stress for a Newtonian fluid is defined by an isotropic tensor as

$$T_{ij} = - p\delta_{ij} + T_{ij}^{'}$$
(1)

where \(T_{ij}^{{}}\) is total stress. \(T_{ij}^{'}\) is viscous stress tensor which depends only on the rate of deformation in such a way that the value becomes zero when the fluid is under rigid body motion or rest. The variable p is defined as hydrodynamic pressure whose value is independent explicitly on the rate of deformation, and \(\delta_{ij}\) is Kronecker delta. For isotropic linear elastic material, the most general form of \(T_{ij}^{'}\) is

$$T_{ij}^{'} = \lambda \Delta \delta_{ij} + 2\mu D_{ij}$$
(2)

where μ and λ are two material constants. μ is known as first coefficient of viscosity or viscosity and (λ + 2μ/3) is second coefficient of viscosity or bulk viscosity. \(D_{ij}^{{}}\) is the rate of deformation tensor and is expressed as

$$D_{ij} = \frac{1}{2}\text{(}\frac{{\partial v_{i} }}{{\partial y_{j} }} + \frac{{\partial v_{j} }}{{\partial x_{i} }})\,\,\,\,\,\,\,\,\,\text{and}\,\,\,\,\,\,\,\Delta = D_{11} + D_{22} + D_{33}$$
(3)

Thus, the total stress tensor becomes

$$T_{ij} = - p\delta_{ij} + \lambda\Delta \delta_{ij} + 2\mu D_{ij}$$
(4)

For compressible fluid, bulk viscosity (λ + 2μ/3) is zero. Thus, Eq. (4) becomes

$$T_{ij} = - p\delta_{ij} - \frac{2\mu }{3}\Delta \delta_{ij} + 2\mu D_{ij}$$
(5)

If the viscosity of fluid is neglected, Eq. (5) becomes

$$T_{ij} = - p\delta_{ij}$$
(6)

Generalized Navier–Stokes equations of motion are given by

$$\rho \left(\frac{{\partial v_{i} }}{\partial t} + v_{j} \frac{{\partial v_{i} }}{{\partial x_{j} }}\right) = \frac{{\partial T_{ij} }}{{\partial x_{j} }} + \rho B_{i}$$
(7)

where Bi is the body force and ρ is the mass density of fluid.Substituting Eq. (6) in Eq. (7), the following relations are obtained.

$$\rho \left(\frac{{\partial v_{i} }}{\partial t} + v_{j} \frac{{\partial v_{i} }}{{\partial x_{j} }}\right) = \rho B_{i} - \frac{\partial p}{{\partial x_{i} }}$$
(8)

If u and v are the velocity components along x and y axes, respectively, and fx and fy are body forces along x and y direction, respectively, and if the convective terms are neglected, the equation of motion may be written as

$$\frac{1}{\rho }\frac{\partial p}{\partial x} + \frac{\partial u}{\partial t} = f_{x}$$
(9)
$$\frac{1}{\rho }\frac{\partial p}{\partial y} + \frac{\partial v}{\partial t} = f_{y}$$
(10)

Neglecting the body forces, Eqs. (9) and (10) become

$$\frac{1}{\rho }\frac{\partial p}{\partial x} + \frac{\partial u}{\partial t} = 0$$
(11)
$$\frac{1}{\rho }\frac{\partial p}{\partial y} + \frac{\partial v}{\partial t} = 0$$
(12)

The continuity equation of fluid in two dimensions is expressed as

$$\frac{\partial p}{\partial t} + \rho c^{2} \left(\frac{\partial u}{\partial x} + \frac{\partial v}{\partial y}\right) = 0$$
(13)

where c is the acoustic wave speed in fluid. Now, differentiating Eqs. (11) and (12) with respect to x and y, respectively, the following relations are obtained.

$$\frac{1}{\rho }\frac{{\partial^{2} p}}{{\partial x^{2} }} + \frac{\partial }{\partial x}\left( {\frac{\partial u}{\partial t}} \right) = 0$$
(14)
$$\frac{1}{\rho }\frac{{\partial^{2} p}}{{\partial y^{2} }} + \frac{\partial }{\partial y}\left( {\frac{\partial v}{\partial t}} \right) = 0$$
(15)

Adding Eqs. (14) and (15), the following expression is finally arrived.

$$\frac{1}{\rho }\frac{{\partial^{2} p}}{{\partial x^{2} }} + \frac{1}{\rho }\frac{{\partial^{2} p}}{{\partial y^{2} }} + \frac{\partial }{\partial x}\left( {\frac{\partial u}{\partial t}} \right) + \frac{\partial }{\partial y}\left( {\frac{\partial v}{\partial t}} \right) = 0$$
(16)

Differentiating Eq. (13) with respect to time, the following expression can be obtained.

$$\frac{{\partial^{2} p}}{{\partial t^{2} }} + \rho c^{2} \left\{ {\frac{\partial }{\partial x}\left( {\frac{\partial u}{\partial t}} \right) + \frac{\partial }{\partial y}\left( {\frac{\partial v}{\partial t}} \right)} \right\} = 0$$
(17)

Thus, from Eqs. (16) and (17), one can find the following expression:

$$\frac{1}{\rho }\frac{{\partial^{2} p}}{{\partial x^{2} }} + \frac{1}{\rho }\frac{{\partial^{2} p}}{{\partial y^{2} }} - \frac{1}{{\rho c^{2} }}\left( {\frac{{\partial^{2} p}}{{\partial t^{2} }}} \right) = 0$$
(18)

Simplifying Eq. (18), the equation for compressible fluid may be obtained

$$\nabla^{2} p(x,\;y,\;t) = \frac{1}{{c^{2} }}\ddot{p}(x,\;y,\;t)$$
(19)

If the compressibility of fluid is neglected, Eq. (19) will be modified as

$$\nabla^{2} p(x,\;y,\;t) = 0$$
(20)

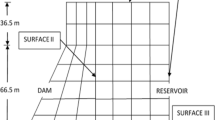
The pressure distribution in the fluid domain may be obtained by solving Eq. (19) with the following boundary conditions. A typical geometry of tank–water system is shown in Fig. 1.

Fig. 1
figure 1

A typical geometry of dam–reservoir system

Full size image
  1. (i)

    At surface I

Considering the effect of surface wave of the fluid, the boundary condition of the free surface is taken as

$$\frac{1}{g}\ddot{p} + \frac{\partial p}{\partial y} = 0$$
(21a)

And if the surface weave is neglected, the condition becomes

$$p(H,\;x) = 0$$
(21b)
  1. (ii)

    At surface II

At water–tank wall interface, the pressure should satisfy

$$\frac{\partial p}{\partial n}(0, y, t) = \rho_{f} ae^{i\omega \,t}$$
(22)

where \(ae^{i\omega \,t}\) is the horizontal component of the ground acceleration in which \(\omega\) is the circular frequency of vibration and \(i = \sqrt { - 1}\). n is the outwardly directed normal to the element surface along the interface. \(\rho_{f}\) is the mass density of the fluid.

  1. (iii)

    At surface III

If this surface is considered as rigid, then pressure should satisfy the following condition

$$\frac{\partial p}{\partial n}\left( {x,\;0,\;t} \right) = 0.0$$
(23a)

And if the reservoir bottom absorption is considered, Eq. (23a) is modified as [16]

$$\frac{\partial p}{\partial n}\left( {x,\;0,\;t} \right) = - q\dot{p}(x,\;0,\;t)$$
(23b)

where

$$q = \frac{1}{c}\left( {\frac{1 - \alpha }{1 + \alpha }} \right)$$
(23c)

\(\alpha\) is the frequency-independent reflection coefficient.

  1. (iii)

    At surface IV

The specification of the far-boundary condition is one of the most important features in the FE analysis of a semi-infinite or infinite reservoir. This is due to the fact that the developed hydrodynamic pressure, which affects the response of the structure, is dependent on the truncation boundary condition. Application of Sommerfeld [11] radiation condition at the truncation boundary leads to

$$\frac{\partial p}{\partial n} = 0$$
(24a)

L represents the distance between the structure and the truncation boundary. Incorporating the effect of reservoir bottom absorption, Sharan [12] has incorporated the following condition.

$$\frac{\partial p}{\partial n} = - \frac{\varPi }{2H}p - \frac{1}{c}\dot{p}$$
(24b)

According to Maity and Bhattacharya [13] and Gogoi and Maity [7], the following boundary condition at truncation surface is proposed.

$$\frac{\partial p}{\partial n} = \left( {\mathop \zeta \nolimits_{m} - \frac{1}{c}} \right) \dot{p}$$
(24c)

According to Maity and Bhattacharya [13],

$$\mathop \zeta \nolimits_{m} = - \frac{{{\mathop \varSigma \nolimits_{m = 1}^{\infty } {{\left[ {( - 1)^{m + 1} /(2m - 1)} \right]}\mathop e\nolimits^{{\left( {\mathop { - f}\nolimits_{m} x/H} \right)}} \;\text{cos}(\lambda_{m} y/H)}}}}{{{\mathop \varSigma \nolimits_{m = 1}^{\infty } {{\left[ {( - 1)^{m + 1} /(2m - 1)\mathop f\nolimits_{m} } \right]}\mathop e\nolimits^{{\left( {\mathop { - f}\nolimits_{m} x/H} \right)}} \;\text{cos}(\lambda_{m} y/H)}}}}$$
(25a)

And from Gogoi and Maity [7],

$$\mathop \zeta \nolimits_{m} = - \frac{{i{\mathop \varSigma \nolimits_{m = 1}^{\infty } {{\frac{{\lambda \,_{m}^{2} I_{m} }}{{\beta_{m} }}}\mathop e\nolimits^{{\left( {\mathop { - k}\nolimits_{m} x} \right)}} \left( {\varPsi_{m} } \right)}}}}{{{\varOmega^{\prime}c\mathop \varSigma \nolimits_{m = 1}^{\infty } {{\frac{{\lambda \,_{m}^{2} I_{m} }}{{\beta_{m} \mathop k\nolimits_{m} }}}\mathop e\nolimits^{{\left( {\mathop { - k}\nolimits_{m} x} \right)}} \left( {\varPsi_{m} } \right)}}}}$$
(25b)

2.1 Finite element formulation for fluid domain

By using Galerkin approach and assuming pressure to be the nodal unknown variable, the discretized form of Eq. (19) may be written as

$$\int\limits_{\varOmega } {N_{rj} \left[ {\nabla^{2} \sum {N_{ri} p_{i} - \frac{1}{{c^{2} }}\sum {N_{ri} \ddot{p}_{i} } } } \right]} \,{\text{d}}\varOmega = 0$$
(26)

where Nrj is the interpolation function for the reservoir and Ω is the region under consideration. Using Green’s theorem, Eq. (26) may be transformed to

$$- \int\limits_{\varOmega } {\left[ {\frac{{\partial N_{rj} }}{\partial x}\sum {\frac{{\partial N_{ri} }}{\partial x}p_{i} + \frac{{\partial N_{rj} }}{\partial y}\sum {\frac{{\partial N_{ri} }}{\partial y}p_{i} } } } \right]\,{\text{d}}\varOmega } - \frac{1}{{c^{2} }}\int\limits_{\varOmega } {N_{rj} } \sum {N_{ri} \,{\text{d}}\varOmega } \,\,\ddot{p}_{i} + \int\limits_{\varGamma } {N_{rj} \sum {\frac{{\partial N_{rj} }}{\partial n}} } \,{\text{d}}\varGamma \,\,p_{i} = \,0$$
(27)

in which i varies from 1 to total number of nodes and Γ represents the boundaries of the fluid domain. The last term of the above equation may be written as

$$\left\{ F \right\} = \int\limits_{\varGamma } {N_{rj} } \frac{\partial p}{\partial n}\,{\text{d}}\varGamma \,$$
(28)

The whole system of Eq. (27) may be written in a matrix form as

$$\left[ {\bar{E}} \right]\left\{ {\ddot{P}} \right\} + \left[ {\bar{G}} \right]\left\{ P \right\} = \left\{ {F{}_{{}}} \right\}$$
(29)

where

$$\left[ {\bar{E}} \right] = \frac{1}{{C^{2} }}\sum {\int\limits_{\varOmega } {\left[ {N_{r} } \right]^{T} } } \left[ {N_{r} } \right]{\text{d}}\varOmega$$
(30)
$$\left[ {\bar{G}} \right] = \sum {\int\limits_{\varOmega } {\left[ {\frac{\partial }{\partial x}\left[ {N_{r} } \right]^{T} \frac{\partial }{\partial x}\left[ {N_{r} } \right] + \frac{\partial }{\partial y}\left[ {N_{r} } \right]^{T} \frac{\partial }{\partial y}\left[ {N_{r} } \right]} \right]} } {\text{d}}\varOmega$$
(31)
$$\left[ F \right] = \sum {\int\limits_{\varGamma } {\left[ {N_{r} } \right]^{T} } } \frac{\partial p}{\partial n}{\text{d}}\varGamma = \left\{ {F_{\text{f}} } \right\} + \left\{ {F_{\text{fs}} } \right\} + \left\{ {F_{\text{fb}} } \right\} + \left\{ {F_{\text{t}} } \right\}$$
(32)

Here the subscripts f, fs, fb and t stand for the free surface, fluid–structure interface, fluid–bed interface and truncation surface, respectively. For surface wave, Eq. (21a) may be written in finite element form as

$$\left\{ {F_{\text{f}} } \right\} = - \frac{1}{g}\left[ {R_{\text{f}} } \right]\,\left\{ {\ddot{p}} \right\}$$
(33)

in which

$$\left[ {R_{\text{f}} } \right] = \sum {\int\limits_{{\varGamma_{\text{f}} }} {\left[ {N_{r} } \right]} }^{T} \left[ {N_{r} } \right]\,{\text{d}}\varGamma$$
(34)

At the dam–reservoir interface, if {a} is the vector of nodal accelerations of generalized coordinates, {Ffs} may be expressed as

$$\left\{ {F_{\text{fs}} } \right\} = - \rho \left[ {R_{\text{fs}} } \right]\left\{ a \right\}$$
(35)

in which

$$\left[ {R_{fs} } \right] = \sum {\int\limits_{{\varGamma_{\text{fs}} }} {\left[ {N_{r} } \right]^{T} \left[ T \right]} } \left[ {N_{\text{d}} } \right]{\text{d}}\varGamma$$
(36)

where [T] is the transformation matrix at fluid structure interface and Nd is the shape function of dam. At reservoir–bed interface,

$$\left\{ {F_{\text{fd}} } \right\} = 0$$
(37)

And at the truncation boundary:

$$\left\{ {F_{\text{t}} } \right\} = \zeta_{m} \left[ {R_{\text{t}} } \right]\left\{ p \right\} - \frac{1}{C}\left[ {R_{\text{t}} } \right]\left\{ {\dot{p}} \right\}$$
(38)
$$\left[ {R_{\text{t}} } \right] = \sum {\int\limits_{{\varGamma_{\text{t}} }} {\left[ {N_{r} } \right]^{T} } } \left[ {N_{r} } \right]{\text{d}}\varGamma$$
(39)

After substitution all terms, Eq. (29) becomes

$$\left[ E \right]\left\{ {\ddot{P}} \right\} + \left[ A \right]\left\{ {\dot{P}} \right\} + \left[ G \right]\left\{ P \right\} = \left\{ {F_{r} } \right\}$$
(40)

where

$$\left[ E \right] = \left[ {\bar{E}} \right] + \frac{1}{g}\left[ {R_{f} } \right]$$
(41)
$$\left\{ {F_{r} } \right\} = - \rho \left[ {R_{fs} } \right]\left\{ a \right\}$$
(42)
$$\left[ A \right] = \frac{1}{C}\left[ {R_{\text{t}} } \right]$$
(43)
$$\left[ G \right] = \left[ {\bar{G}} \right] + \zeta_{m} \left[ {R_{t} } \right]$$
(44)

For any given acceleration at the fluid–structure interface, Eq. (40) is solved to obtain the hydrodynamic pressure within the fluid.

2.2 Time history analysis of dynamic equilibrium equation

Dynamic equilibrium equation of fluid can be expressed as

$$\left[ E \right]\left\{ {\ddot{P}} \right\} + \left[ A \right]\left\{ {\dot{P}} \right\} + \left[ G \right]\left\{ P \right\} = \left\{ {F_{r} } \right\}$$
(45)

In a linear dynamic system, these values remain constant throughout the time history analysis. The force vector is given by {Fr}. To obtain the transient response at time tN, the time axis can be discretized into N equal time intervals (\(t_{N} = \sum\nolimits_{j = 1}^{N} {j\Delta t}\)). The choice of method for time history analysis is strongly problem dependent. Various direct time integration methods exist for time history analysis that are expedient for structural dynamics and wave propagation problem. Amongst these, the Newmark family of methods is most popular and is given by

$$\left\{ p \right\}_{j + 1} = \,\left\{ p \right\}_{j} +\Delta t\left\{ {\dot{p}} \right\}_{j} + \frac{{\Delta t^{2} }}{2}\left[ {\left( {1 - 2\vartheta } \right)\left\{ p \right\}_{j} + 2\vartheta \left\{ {\ddot{p}} \right\}_{j + 1} } \right]$$
(46)
$$\left\{ {\dot{p}} \right\}_{j + 1} = \,\left\{ {\dot{p}} \right\}_{j} +\Delta t\left[ {\left( {1 - \gamma } \right)\left\{ {\ddot{p}} \right\}_{j} + \gamma \left\{ {\ddot{p}} \right\}_{j + 1} } \right]$$
(47)

Here, \(\vartheta\) and \(\gamma\) are chosen to control stability and accuracy. It is evident from the literature that the integration scheme is unconditionally stable if \(2\vartheta \ge \gamma \ge 0.5\).

3 Results and discussions

3.1 Validation of the algorithm

In order to validate the algorithm, a benchmark problem is considered. The results are compared with an existing literature [22] for reservoir adjacent to the Pine Flat Dam. The reservoir is truncated at a distance of 200.0 m, and Sommerfeld [11] boundary condition is implemented at this truncation surface. In this case, the geometric and material properties are as considered by Sami and Lotfi [22]. The first five natural frequencies of reservoir are summarized in Table 1. The results obtained from the developed algorithm almost match with the results obtained by Sami and Lotfi [22]. Slight discrepancies in results are observed due to different meshing of reservoir domain.

Table 1 First five natural frequencies of the reservoir
Full size table

3.2 Comparison of various truncation boundary conditions for infinite reservoir

In this section, results from different boundary conditions (Sommerfeld [11]; Sharan [12]; Maity Bhattacharya [13]; Gogoi and Maity [7]) are compared with the closed-form solutions obtained by Bouaanani et al. [23] to study the effectiveness of these boundary conditions for finite element analysis of infinite reservoir. The water in the present case considered is linearly compressible, inviscid and of small amplitude of motion. Here, the depth of the reservoir (H) is considered as 70 m. The mass density and acoustic speed of water are considered as 1000 kg/m3 and 1440 m/sec, respectively. The reservoir bottom refection coefficient is taken as 0.95. The study is carried out for different values of Tc/H, i.e. 1, 4 and 100. The amplitude of the external sinusoidal excitation, i.e. a, is assumed to be equal to the gravitational acceleration 1.0 g. The pressure coefficients at the heel of the rigid dam (cp =  P/ρaH) are determined for different boundary conditions and presented in Table 2. It is noted that the pressure coefficient obtained from all the boundary conditions are almost equal to those obtained from closed-form solution when the truncation of infinite reservoir is at a distance of 3.0H. For Tc/H = 4, the Sharan boundary [12] gives exact pressure coefficient for reservoir length equal or greater than (L) 0.5H. However, for Tc/H = 1 and 100, the results are almost equal to the exact results for L ≥ 1.0H. On the other hand, for all Tc/H values and all truncation lengths, the hydrodynamic pressure obtained from Gogoi and Maity boundary condition [7] is equal to those obtained from closed-form solution. Thus, the remaining study associates with infinite reservoir, Gogoi and Maity boundary [7] condition is implemented at the truncation surface and the infinite reservoir is truncated at a distance of 0.5H from the upstream face of the dam.

Table 2 Comparison of truncation boundary conditions
Full size table

3.3 Analysis of infinite reservoir with different inclinations of upstream face for compressible fluid

In this section, the hydrodynamic pressure at the upstream face of concrete gravity dam having different inclinations is computed against harmonic excitations of different frequencies and earthquake excitation. For this, the geometric and material properties of reservoir are as considered in Sect. 3.2 and the water is considered to be compressible. The hydrodynamic pressure distribution along the reservoir–structure interface having different inclinations of the upstream face is presented in graphical form (Figs. 2, 3, 4, 5). Here, the reflection coefficient at the reservoir bottom is considered as 0.95 and results are presented for three different slopes of the fluid–structure interface, i.e. θ = 30°, 45° and 60°. From these plots, it is evident that with the increase in inclination the pressure coefficient (cp) is also increased. It is also clear that the distribution for Tc/H = 4100 (Figs. 3, 4) is almost parabolic, but in case of Tc/H = 1 (Fig. 2) the distribution is slightly different. For earthquake excitation (Koyna earthquake), the distribution of hydrodynamic pressure (Fig. 5) along the face of the dam follows almost similar pattern for all angles of inclination. However, the maximum hydrodynamic pressure occurs when the angle of inclination is 60°.

Fig. 2
figure 2

Distribution of hydrodynamic pressure coefficient along an inclined surface for Tc/H = 1

Full size image
Fig. 3
figure 3

Distribution of hydrodynamic pressure coefficient along an inclined surface for Tc/H = 4

Full size image
Fig. 4
figure 4

Distribution of hydrodynamic pressure coefficient along an inclined surface for Tc/H = 100

Full size image
Fig. 5
figure 5

Distribution of hydrodynamic pressure coefficient along an inclined surface for Koyna earthquake

Full size image

The time history of hydrodynamic pressure at point A (Fig. 1) is also plotted for different excitations. Here the reflection coefficient is considered as 0.95 in case of sinusoidal acceleration (Figs. 6, 7, 8) and 0.95 and 0.5 (Figs. 9, 10) for earthquake excitation for better understandings the responses of reservoir under earthquake excitations. For sinusoidal acceleration with different frequencies, the maximum hydrodynamic pressures at point A occur when θ = 60° and this difference is comparatively higher when Tc/H = 1.0. Similarly, for earthquake excitation, the hydrodynamic pressure increases with the increase in angle of inclination, the maximum hydrodynamic pressure occurs when the angle of the upstream face of the dam is 60° and this increase is more when the reflection coefficient is 0.95.

Fig. 6
figure 6

Variation of hydrodynamic pressure at point A for Tc/H = 1

Full size image
Fig. 7
figure 7

Variation of hydrodynamic pressure at point A for Tc/H = 4

Full size image
Fig. 8
figure 8

Variation of hydrodynamic pressure at point A for Tc/H = 100

Full size image
Fig. 9
figure 9

Variation of hydrodynamic pressure at point A for reflection coefficient 0.95 for Koyna earthquake

Full size image
Fig. 10
figure 10

Variation of hydrodynamic pressure at point A for reflection coefficient 0.5 for Koyna earthquake

Full size image

3.4 Analysis of infinite reservoir with different inclinations of upstream face for incompressible fluid

In the present section, the compressibility effect of water is neglected. The geometry of infinite reservoir is as considered in Sect. 3.2. The mass density of water is considered as 1000 kg/m3. Similar to Sect. 3.3, the study is carried out for different upstream slopes and hydrodynamic pressure at point A (Fig. 1) is determined against sinusoidal acceleration of different frequencies (Figs. 11, 12, 13). It is clear from these figure that the variation of hydrodynamic pressure with upstream slope of hydrodynamic pressure is almost similar to the trend obtained in case of compressible fluid, i.e. the hydrodynamic pressure increases with the increases in upstream slope and maximum hydrodynamic pressure occurs when the upstream slope is 60° and the variation of hydrodynamic pressure coefficient with Tc/H is not so much significant when the compressibility of water is neglected.

Fig. 11
figure 11

Variation of hydrodynamic pressure coefficient on at heel for Tc/H = 1

Full size image
Fig. 12
figure 12

Variation of hydrodynamic pressure coefficient on at heel for Tc/H = 4

Full size image
Fig. 13
figure 13

Variation of hydrodynamic pressure coefficient on at heel for Tc/H = 100

Full size image

4 Conclusions

The characteristics of hydrodynamic pressures on concrete gravity dam are studied for different exciting frequencies. The governing equation for water is expressed in terms of the pressure variable and is discretized by the finite element method. In finite element modelling of reservoir, a simple but effective boundary condition at the truncation surface of the infinite reservoir is used in the present study. The present far-boundary condition has capable of taking care of reservoir bottom absorption effects. It is observed from the results that the present far-boundary condition produces accurate results for all ranges of excitation frequencies. The results also show that the unbounded reservoir domain may be truncated even at a relatively smaller distance away from the dam, resulting in great computational advantages. The variation of hydrodynamic with different excitations of various frequencies is not significant, i.e. hydrodynamic pressure on dam remains independent of exciting frequency when the water is modelled as incompressible one. On the other hand, the hydrodynamic pressure coefficient very much depends on the frequency of excitation for compressible water. Similarly, the effect of reservoir bottom absorption is found to be small for lower values of excitation frequencies. However, this effect may not be neglected if the excitation frequency becomes equal or more than the fundamental frequency of the reservoir. The hydrodynamic pressure increases with the increase in the slope of the upstream face of the rigid dam. The distribution of hydrodynamic pressure also varies with this slope. The variation is almost parabolic for vertical upstream face, and the maximum pressure occurs at the heel of the dam. However, for other upstream slope the distribution is something different and maximum hydrodynamic pressure occurs just above the hell of rigid dam.