Abstract
A new three-wave method is efficient and well-developed approach to solve nonlinear partial differential equation. In this paper, a (3+1)-dimensional Jimbo–Miwa equation is investigated by using this approach. Some periodic wave solutions and kink solutions are obtained through the Hirota bilinear form. Furthermore, figures of some special periodic wave solutions and kink solutions are presented to illustrate the dynamical features of these solutions.
Similar content being viewed by others
1 Introduction
As we all know, there are many nonlinear partial differential equation (NLPDEs) especially soliton equations in the fields of physics, chemistry, biology and mechanics. We explain the phenomena and dynamic processes in these fields by solving the exact solutions of NLPDEs. Naturally, searching exact solutions of NLPDEs becomes an important work. In recent years, many methods have been proposed to find the exact solutions of the NLPDEs, such as Hirota bilinear method [1,2,3,4], homogeneous balance method [5], multiple exp-function method [6, 7], the Bäcklund transformation [8]. The Hirota bilinear method is considered as a useful method to obtain exact solutions of nonlinear evolution equations. We find that a lot of integrable equations can be transformed into Hirota bilinear forms by different dependent variable transformations such as the KP equation and BKP equation, subsequently, different types of solutions can be successfully achieved, such as soliton solutions, compacton solutions, Wronskian forms of N-soliton soultions, rational solutions (which usually contain rogue waves and lump solutions) and periodic solutions [9,10,11,12,13,14,15,16]. Among them, the periodic solution is the one of more important solutions to understand some of the natural phenomena. A lot of scholars have constructed periodic soliton solutions by using Hirota bilinear forms with the aid of symbolic computation [17,18,19]. Furthermore, some double periodic solutions and quasi-periodic wave solutions have been also investigated [20, 21].
In this paper, we will consider the (3+1)-dimensional Jimbo–Miwa equation [22], which reads
under the dependent variable transformation
Equation (1.2) can be transformed into the following bilinear form
or, equivalently
where \(f=f(x,y,z,t)\) is also real function with respect to variables x, y, z and t. \(D_x^3{D_y}\), \(D_t{D_y}\) and \(D_{x}D_{z}\) are called Hirota bilinear operators [23] defined by
Many papers focus on analyzing the exact solutions of Eq. (1.1). For example, its exact solutions were explicitly given by transformed rational function method [24], the soliton solutions and Wronskian determinant solutions have been obtained by Hirota bilinear forms and Wronskian technique [25,26,27], the Bäcklund transformations and Lax system were discussed by Bell-polynomials theory [28], the lump and lump-type solutions have been derived by Hirota bilinear method [29,30,31,32,33,34,35,36] and some periodic wave solutions also have been found in Refs. [37,38,39].
This paper mainly aims at studying periodic wave solutions of (3+1)-dimensional Jimbo–Miwa equation by using the Hirota bilinear form and new three-wave method. Through various forms of graphic illustration, we would give a better understanding on the evolution of solutions of waves.
2 Describe the new three-wave method
Here, we briefly show the new three-wave method [40, 41].
- Step 1::
-
Taking the Cole–Hopf transformation \(u=2(ln f)_{x}\), the Eq. (1.1) is transformed into the proper bilinear form
$$\begin{aligned} H(D_{x}, D_{y},D_{z},D_{t},\cdots )f f=0, \end{aligned}$$(2.1)where \(f=f(x,y,z,t)\) and the derivatives \(D_{x}, D_{y}, D_{z},D_{t}\) are the Hirota operators.
- Step 2: :
-
Based on the Hirota bilinear of Eq. (2.1), we assume that the solution can be expressed in the form
$$\begin{aligned} \begin{aligned} f&=a_{{1}}\cosh \left( c_{{1}}t+k_{{1}}x+l_{{1}}y+b_{{1}}z \right) +a_{ {2}}\cos \left( c_{{2}}t+k_{{2}}x+l_{{2}}y+b_{{2}}z \right) \\&\quad+a_{{3}}\cosh \left( c_{{3}}t+k_{{3}}x+l_{{3}}y+b_{{3}}z \right) , \end{aligned} \end{aligned}$$(2.2)where \(a_{i}, b_{i}, c_{i}, l_{i},k_{i}, (i=1,2,3)\) are real parameters to be determined.
- Step 3: :
-
Substituting (2.2) into (1.3), with the help of maple, collecting all the coefficients about \(\cosh \left( c_{{1}}t+k_{{1}}x+l_{{1}}y+b_{{1}}z \right),\) \(\cos \left( c_{{2}}t+k_{{2}}x+l_{{2}}y+b_{{2}}z \right),\) \(\cosh \left( c_{{3}}t+k_{{3}}x+l_{{3}}y+b_{{3}}z \right),\) \(\sinh \left( c_{{1}}t+k_{{1}}x+l_{{1}}y+b_{{1}}z \right)\), \(\sin \left( c_{{2}}t+k_{{2}}x+l_{{2}}y+b_{{2}}z \right)\) and \(\sinh \left( c_{{3}}t+k_{{3}}x+l_{{3}}y+b_{{3}}z \right)\), whose coefficients become zero, we can obtain a set of determining equations for \(a_{i}, b_{i}, c_{i}, l_{i},k_{i}, (i=1,2,3)\). By the transformation (1.2), we will find the solutions of Eq. (1.1).
3 Periodic wave solutions of the (3+1)-dimensional Jimbo–Miwa equation
According to the new three-wave method of the above stated in Sect. 2, we assume that Eq. (1.1) has the following type solutions. That is
where \(a_{i}, b_{i}, c_{i}, l_{i},k_{i}, (i=1,2,3)\) are arbitrary real constants.
In order to get the periodic wave solutions, substituting (3.1) into (1.3), collecting the coefficients about \(\cosh \left( c_{{1}}t+k_{{1}}x+l_{{1}}y+b_{{1}}z \right)\), \(\cos \left( c_{{2}}t+k_{{2}}x+l_{{2}}y+b_{{2}}z \right)\), \(\cosh \left( c_{{3}}t+k_{{3}}x+l_{{3}}y+b_{{3}}z \right)\), \(\sinh \left( c_{{1}}t+k_{{1}}x+l_{{1}}y+b_{{1}}z \right)\), \(\sin \left( c_{{2}}t+k_{{2}}x+l_{{2}}y+b_{{2}}z \right)\) and \(\sinh \left( c_{{3}}t+k_{{3}}x+l_{{3}}y+b_{{3}}z \right)\), we can obtain a system of algebraic system in \(a_{i}, b_{i}, c_{i}, l_{i},k_{i}, (i=1,2,3)\). Solving this system of equations with the help of symbolic computation, we get the following solutions of parameters:
Case 1.
where \(a_{i}(i=2,3), b_{1}, c_{j}(j=1,2),k_{p}(p=1,2,3)\) and \(l_{q}(q=1,3)\) are arbitrary real constants.
Case 2.
where \(a_{i}(i=1,2), b_{3}, c_{j}(j=1,3),k_{p}(p=1,2,3)\) and \(l_{q}(q=2,3)\) are arbitrary real constants.
Case 3.
where \(a_{i}(i=1,2,3), c_{1}, k_{p}(p=1,2)\) and \(l_{q}(q=2,3)\) are arbitrary real constants.
Case 4.
where \(a_{i}(i=1,3), b_{2}, c_{j}(j=1,2), k_{p}(p=1,2,3)\) and \(l_{q}(q=2,3)\) are arbitrary real constants.
Thus, from Case 1, the f is given by
So we obtain one solution of Eq. (1.1), that is
where k, l is defined by
From Case 2, by the same calculation, we can obtain another solution, that is
where f, m, n are defined by
From Case 3, similarly, we can get the third solution, that is
where f, h, r, s are given by
From Case 4, similarly, we can get the fourth solution, that is
where f, v, w are given by
Now we depict the dynamic behaviors of some special periodic wave solutions in each Case.
In Case 1, we take the parameters as
get
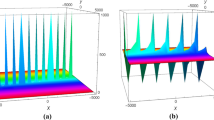
Its plot when \(z=0, t=0\) is showed in Fig. 1 and the wave along different axis is depicted in Fig. 2.
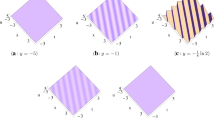
The periodic wave solution of Eq. (3.16) with \(z=0, t=0\). a Perspective view of the wave. b Contour plot
The periodic wave solution of Eq. (3.16) with \(z=0, t=0\). a x-curve with \(y=0\) (red), \(y=1\) (blue) and \(y=-1\) (green). b y-curve with \(x=0\) (red), \(x=1\) (blue) and \(x=-1\) (green)
In Case 2, we take the parameters as
get
Their plots when \(z=0\) and \(t=10, 30\) are respectively depicted in Figs. 3 and 4.
The periodic wave solution of Eq. (3.18) with \(z=0, t=10\). a Perspective view of the wave. b Contour plot
The periodic wave solution of Eq. (3.18) with \(z=0, t=30\). a Perspective view of the wave. b Contour plot
In Case 3, we take the parameters as
get
Their plots when \(t=0\) and \(y=0, z=0\) are showed in Figs. 5 and 6, respectively.
The periodic wave solution of Eq. (3.20) with \(y=0, t=0\). a Perspective view of the wave. b Contour plot
The periodic wave solution of Eq. (3.20) with \(z=0, t=0\). a Perspective view of the wave. b Contour plot
In Case 4, we take the parameters as
get
Their plots when \(z=0\) and \(t=0, z=0\) are showed in Figs. 7 and 8, respectively.
The kink solution of Eq. (3.22) with \(z=0, t=0\). a Perspective view of the wave. b Contour plot
The kink solution of Eq. (3.22) with \(x=0, z=0\). a Perspective view of the wave. b Contour plot
4 Conclusions
In this paper, associating with the Hirota bilinear form of the (3+1)-dimensional Jimob-Miwa equation, we construct the periodic wave solutions and kink solutions through the new three-wave method. Some special solutions are shown graphically in order to demonstrate that the method is quite effective for handling nonlinear evolution equations. Meanwhile, the solutions obtained in this paper can effectively explain more phenomena in fluid or plasma mechanics.
References
Hirota R (2004) The direct method in soliton theory. Cambridge University Press, Cambridge
Wazwaz AM (2007) Multiple-soliton solutions for the KP equation by Hirota’s bilinear method and by the tanh–coth method. Appl Math Comput 190(1):633–640
Wazwaz AM (2008) The Hirota’s bilinear method and the tanh-coth method for multiple-soliton solutions of the Sawada–Kotera–Kadomtsev–Petviashvili equation. Appl Math Comput 200(1):160–166
Ma WX, Zhou R, Gao L (2009) Exact one-periodic and two-periodic wave solutions to Hirota bilinear equations in (2+1) dimensional. Mod Phys Lett A 24(21):1677–1688
Abdel Rady AS, Osman ES (2010) The homogeneous balance method and its application to the Benjamin–Bona–Mahoney (BBM) equation. Appl Math Comput 217(4):1385–1390
Ma WX, Huang T, Zhang T (2010) A multiple exp-function method for nonlinear differential equations and its application. Phys Scr 82(6):5468–5478
Ma WX, Zhu Z (2012) Solving the (3+1)-dimensional generalized KP and BKP equations by the multiple exp-function algorithm. Appl Math Comput 218(24):11871–11879
Bai CL (2002) Extended homogeneous balance method and Lax Pairs, Bäcklund transformation. Commun Theor Phys 37:1–6
Yan Z, Bluman G (2002) New compacton soliton solutions and solitary patterns solutions of nonlinearly dispersive Boussinesq equations. Comput Phys Commun 149(1):11–18
Geng X, Ma Y (2007) N-soliton solution and its Wronskian form of a (3+1)-dimensional nonlinear evolution equation. Phys Lett A 369(4):285–289
Ma WX (2015) Lump solutions to the Kadomtsev–Petviahvili equation. Phys Lett A 379(36):1975–1978
Zhang Y, Ma WX (2015) Rational solutions to a KdV-like equation. Appl Math Comput 256:252–256
Yang JY, Ma WX (2016) Lump solutions to the BKP equation by symbolic computation. Internat J Mod Phys B 30(28):16402–16428
Ma HC, Deng AP (2016) Lump solution of (2+1)-dimensional Boussinesq equation. Commun Theor Phys 65(5):546
Feng LL, Fian TS, Wang XB (2017) Rogue waves, homoclinic breather waves and soliton waves for the (2+1)-dimensional B-type Kadomtsev–Petviashvili equation. Appl Math Lett 65:90–97
Belmekki M, Nieto J (2009) Existence of periodic solution for a nonlinear fractional differential equation. Bound Value Probl 2009(1):324561
MasayoshiTajiri YW (1997) Periodic soliton solutions as imbricate series of rational solitons: solutions to the Kadomtsev–Petviashvili equation with positive dispersion. J Math Phys 4(3–4):350–357
Dai Z, Li S (2007) Singular periodic soliton solutions and resonance for the Kadomtsev–Petviashvili equation. Chaos Solitons Fractals 34(4):1148–1153
Wei L (2011) Multiple periodic-soliton solutions to Kadomtse–Petviashvili equation. Appl Math Comput 218(2):368–375
Fan E, Hon BYC (2002) Double periodic solutions with Jacobi elliptic functions for two generalized Hirota–Satsuma coupled KdV systems. Phys Lett A 292(6):335–337
Date E, Jimbo M (2009) Quasi-periodic solutions of the orthogonal KP equation. Publ Res Inst Math Sci 18(3):409–423
Jimbo M, Miwa T (1983) Solitons and infinite-dimensional Lie algebras. Publ Res Inst Math Sci 19:943–1001
Hirota R (1986) Reduction of soliton equations in bilinear form. Phys D Nonlinear Phenom 18(s1–3):161–170
Ma WX (2009) A transformed rational function method and exact solutions to the (3+1) dimensional Jimbo–Miwa eqnution. Chaos Solitons Fractals 42:1356–1363
Hu XB, Wang DL (1999) Soliton solutions to the Jimbo–Miwa and the Fordy–Gibbors–Jimbo–Miwa equation. Phys Lett A 262(4–5):310–320
Tang Y (2011) Wronskian determinant solutions of the (3+1)-dimensional Jimbo–Miwa eqnution. Appl Math Comput 217:8722–8730
Tang Y (2013) Pfaffian solutions and extended Pfaffian solutons to (3+1)-dimensional Jimbo–Miwa equation. Appl Math Model 37(10–11):6631–6638
Msingh RK (2016) Gupta, Bäcklund transformations, Lax system, conservation laws and multisoliton solutions for Jimbo–Miwa equation with Bell-polynomials. Commun Nonlinear Sci Numer Simul 37:362–373
Yang JY, Ma WX (2017) Abundant lump-type solutions of the Jimbo–Miwa equation in (3+1)-dimensions. Comput Math Appl 73(2):220–225
Sun HQ, Chen AH (2017) Lump and lump–kink solutions of the (3+1)-dimensional Jimbo–Miwa and two extended Jimbo–Miwa equations. Appl Math Lett 68:55–60
Ma WX (2018) Abundant lumps and their interaction solutions of (3+1)-dimensional linear PDEs. J Geom Phys 133:10–16
Ma WX (2018) Lump and interaction solutions of linear PDEs in (3+1)-dimensions. East Asian J Appl Math 8:224–232
Yang JY, Ma WX, Qin Z (2018) Lump and lump-soliton solutions to the(2+1)-dimensional Ito equation. Anal Math Phys 8(3):427–436
Chen ST, Ma WX (2018) Lump solutions of a generalized Calogero–Bogoyavlenskii–Schiff equation. Comput Math Appl 76(7):1680–1685
Chen ST, Ma WX (2018) Lump solutions to a generalized Bogoyavlensky–Konopelchenko equation. Front Math China 13:525–534
Ma WX, Li J, Khalique CM (2018) A study on lump solutions to a generalized Hirota–Satsuma–Ito equation in (2+1)-dimensions. Complexity 2018:9059858
Li Zhaqilao ZB (2008) Multiple periodic soliton solutions for (3+1)-dimensional Jimbo–Miwa equation. Commun Theor Phys 50(11):1036–1040
Dai Z (2008) Periodic kink-wave and kinky periodic-wave solutions for the Jimbo–Miwa equation. Phys Lett A 372(38):5984–5986
Lu B, Zhang HQ (2010) Quasi-periodic wave solutions of (3+1)-dimensional Jimbo–Miwa equation. Int J Nonlinear Sci 4:452–461
Liu J, Mu ZD (2016) Spatiotemporal deformation of multi-soliton to (2+1)-dimensional KdV equation. Nonlinear Dyn 83(1–2):355–360
Jiangen L, Pinxia W, Zhang Y et al (2017) New periodic wave solutions of (3+1)-dimensional soliton equation. Thermal Sci 21:S169–S176
Acknowledgements
This study was funded by National Natural Science Foundation of China (Grant Number 41504032).
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflicts of interest
The authors declare that they have no conflicts of interest. Disclosure of potential conflicts of interest Research involving Human Participants.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Zhang, S. New periodic wave solutions of a (3+1)-dimensional Jimbo–Miwa equation. SN Appl. Sci. 1, 201 (2019). https://doi.org/10.1007/s42452-019-0198-9
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s42452-019-0198-9