A new iterative method based solution for fractional Black–Scholes option pricing equations (BSOPE)

Abstract

In this manuscript, a new expansion technique namely residual power series method is used for finding the analytical solution of the Fractional Black–Scholes equation with an initial condition for European option pricing problem. The Black–Scholes formula is important for estimating European call and put option on a non-dividend paying stock in particular when it contains time-fractional derivatives. The fractional derivative is defined in Caputo sense. This technique is based on fractional power series expansion. The convergence analysis of the present method is also deliberated. Example problems are given to examine the efficacy of the proposed method. Obtained solutions are compared with exact solutions solved by other techniques which demonstrate that the present method is robust and easy to implement for other fractional problems arising in science and engineering.

1 Introduction

Pricing of options is a critical element of mathematical finance problems. The important thought of their examinations is that one did not have to evaluate the regular return of a stock with a specific end goal to value an option written on that stock. In 1973, the familiar theoretical widespread valuation formula for options was derived with the aid of Fischer Black and Myron Scholes [1] which received them the 1997 Nobel Prize in Economics. The FBSE which is a second-order parabolic equation deals with the estimation of financial derivatives. Such equations support the usage of the no-arbitrage principle also. Hence, the BS equation is utilized for estimating call and put options on a paying stock [2]. In this association, various researchers have performed innovative work which includes Hilfer [3], Podlubny [4], Caputo [5], Miller and Ross [6], Kilbas et al. [7], Heydari et al. [8, 9] and others.

As such in this article, fractional BSOPE is considered as

$$\frac{{\partial^{\alpha } w}}{{\partial t^{\alpha } }} + \frac{{\sigma^{2} x^{2} }}{2}\frac{{\partial^{2} w}}{{\partial x^{2} }} + s\left( t \right)\,x\frac{\partial w}{\partial x} - s\left( t \right)w = 0,\quad \left( {x,t} \right) \in R^{ + } \times \left( {0,T} \right),$$

(1)

where $w\left( {x,t} \right),\,s\left( t \right),\,\,\sigma \left( {x,t} \right),\,\,T\,and\,\,t$ denote the European call option price, interest rate, volatility function, maturity and time respectively. The payoff functions are

$$w_{call} \left( {x,t} \right) = \hbox{max} \left( {0,\,x - E} \right),\quad w_{put} \left( {x,t} \right) = \hbox{max} \left( {0,\,E - x} \right),$$

(2)

where $w_{call} \left( {x,t} \right)$ and $w_{put} \left( {x,t} \right)$ signify the values of European call and put option respectively. $E$ represents the expiration price of the option. The fractional BSOPE has been examined with the help of various techniques such as Laplace Transform Method (LTM) [10], Homotopy Perturbation Method (HPM) [11], Homotopy Analysis Method (HAM) [11], Sumudu Transform Method (STM) [12], Projected Differential Transformation Method (PDTM) [13], Adomian Decomposition Method (ADM) with conformal derivative and Modified Homotopy Perturbation Method (MHPM) [14], Multivariate Padé Approximation [15] and ADM [16]. Recently fractional order European Vanilla option pricing model has also been studied by Yavuz and Özdemir [17]. These methods have their particular limits and inadequacies. Also, these methods require tremendous computational work and take high running time. As regards, RPSM is found to be an efficient and effective method initially recommended by the mathematician Abu Arqub [18]. The RPSM has been implemented in the generalized Lane-Emden equation [19], fractional KdV-Burgers equation [20] and fractional foam drainage equation [21]. Moreover, RPSM has also been effectively applied to the time–space-fractional Benny-Lin equation [22].

In this article, RPSM has been implemented for solving the fractional BS European option pricing equation. The performance and precision of the present method are studied by comparing the solution of the titled problem solved by RPSM and other analytical methods. However, to the best of the authors’ information, the time-fractional BS equation has not yet been solved by RPSM.

2 Preliminaries of fractional calculus and RPSM

Definition 2.1 [4, 6]

The Abel–Riemann (A–R) fractional derivative operator $D^{\alpha }$ of order $\alpha$ is defined as

$$D^{\alpha } u(x) = \left\{ {\begin{array}{*{20}l} {\frac{{d^{m} }}{{dx^{m} }}u\left( x \right),} \hfill & {\alpha = m,} \hfill \\ {\frac{1}{\varGamma (m - \alpha )}\frac{d}{{dx^{m} }}\int\limits_{0}^{x} {\frac{u(t)}{{(x - t)^{\alpha - m + 1} }}} dt,} \hfill & {m - 1 < \alpha < m.} \hfill \\ \end{array} } \right.$$

(3)

where $m \in Z^{ + } ,$ $\alpha \in R^{ + }$.

Definition 2.2 [4, 6]

The integral operator $J^{\alpha }$ in A–R sense is defined as

$$J^{\alpha } u\left( x \right) = \frac{1}{\varGamma \left( \alpha \right)}\int\limits_{0}^{x} {\left( {x - t} \right)^{\alpha - 1} u\left( t \right)} \,dt,\quad t > 0,\quad \alpha > 0.$$

(4)

Following Podlubny [4] we may have

$$J^{\alpha } t^{m} = \frac{{\varGamma \left( {m + 1} \right)}}{{\varGamma \left( {m + \alpha + 1} \right)}}t^{m + \alpha } .$$

(5)

$$D^{\alpha } t^{m} = \frac{{\varGamma \left( {m + 1} \right)}}{{\varGamma \left( {m - \alpha + 1} \right)}}t^{m - \alpha } .$$

(6)

Definition 2.3 [4, 5]

The Caputo fractional derivative operator $D^{\alpha }$ is well-defined as

$${}^{C}D^{\alpha } u(x) = \left\{ {\begin{array}{*{20}l} {\frac{1}{\varGamma (m - \alpha )}\int\limits_{0}^{x} {\frac{{u^{m} (t)}}{{(x - t)^{\alpha - m + 1} }}} dt,} \hfill & {m - 1 < \alpha < m,} \hfill \\ {\frac{{d^{m} }}{{dt^{m} }}u\left( x \right),} \hfill & {\alpha = m.} \hfill \\ \end{array} } \right.$$

(7)

Definition 2.4 [4,5,6]

• (a)
  $$D_{t}^{\alpha } J_{t}^{\alpha } g\left( t \right) = g\left( t \right),$$

  (8)
• (b)
  $$J_{t}^{\alpha } D_{t}^{\alpha } g\left( t \right)\, = g\left( t \right) - \sum\limits_{k = 0}^{m} {g^{\left( k \right)} \left( {0^{ + } } \right)} \frac{{t^{k} }}{k!},\quad {\text{for}}\quad m - 1 < \alpha \le m\,, \quad {\text{and}}\quad t > 0.$$

  (9)

Definition 2.5

A series of the form

$$\sum\limits_{k = 0}^{\infty } {a_{k} \left( {t - t_{0} } \right)^{k\alpha } = a_{0} + a_{1} \left( {t - t_{0} } \right)^{\alpha } + } a_{2} \left( {t - t_{0} } \right)^{2\alpha } + \cdots \quad {\text{for}}\quad 0 \le n - 1 < \alpha \le n,\;t \ge t_{0} ,$$

(10)

is called FPSE at $t = t_{0} ,$ where $a_{k}$ is the coefficient of series.

Theorem 2.1

If $f\left( t \right) = \sum\nolimits_{k = 0}^{\infty } {a_{k} \left( {t - t_{0} } \right)^{k\alpha } }$ and $D^{k\alpha } f\left( t \right) \in C\left( {t_{0} ,\,t_{0} + R} \right)$ for $k = 0,\,1,\,2, \ldots$ then the value of $a_{k}$ in Eq. (10) is given by $a_{k} = \frac{{D^{k\alpha } f\left( {t_{0} } \right)}}{{\varGamma \left( {k\alpha + 1} \right)}}$.

Definition 2.6

An FPSE about $t = t_{0}$ of the form $\sum\nolimits_{k = 0}^{\infty } {b_{k} (x)\left( {t - t_{0} } \right)^{k\alpha } }$ is called multiple FPSE about $t = t_{0}$, where $b_{k}$’s are coefficients of the series.

3 RPS solution for FBSE

Let us consider the FBSE as [23]

$$D_{t}^{\alpha } w = D_{x}^{2} w + \left( {k - 1} \right)D_{x} w - kw,\quad 0 < \alpha \le 1,$$

(11)

with IC

$$w\left( {x,0} \right) = \hbox{max} \left( {e^{x} - 1,0} \right).$$

(12)

3.1 Procedure of RPS solution

Step 1 Let us assume that FPSE of Eq. (11) with IC Eq. (12) about the point $t = t_{0}$ is written as

$$w\left( {x,t} \right) = \sum\limits_{k = 0}^{\infty } {b_{k} \left( x \right)\frac{{t^{\alpha k} }}{{\varGamma \left( {\alpha k + 1} \right)}}} ,\quad 0 < \alpha \le 1,\;\;0 \le t.$$

(13)

In order to evaluate the value of $w\left( {x,t} \right)$, let $w_{m} \left( {x,t} \right)$ signifies the mth truncated series of $w\left( {x,t} \right)$ as

$$w_{m} \left( {x,t} \right) = \sum\limits_{k = 0}^{m} {b_{k} \left( x \right)\frac{{t^{\alpha k} }}{{\varGamma \left( {\alpha k + 1} \right)}}} ,\quad 0 < \alpha \le 1,\;\;0 \le t.$$

(14)

For $m = 0$, the 0th RPS solution of $w\left( {x,t} \right)$ may be written as

$$w_{0} \left( {x,t} \right) = b_{0} \left( x \right) = \hbox{max} \left( {0,\,e^{x} - 1} \right).$$

(15)

Using Eqs. (15) and (14) can be modified as

$$w_{m} \left( {x,t} \right) = b_{0} \left( x \right) + \sum\limits_{k = 1}^{m} {b_{k} \left( x \right)\frac{{t^{\alpha k} }}{{\varGamma \left( {\alpha k + 1} \right)}}} ,\quad 0 < \alpha \le 1,\;\;0 \le t,\;\;m = 1,\,2,\,3, \ldots$$

(16)

So mth RPS solution can be evaluated after obtaining all $b_{k} \left( x \right)$, $k = 1,\,2, \ldots ,m$.

Step 2 Let us consider the residual function (RF) of Eq. (11) as

$$res\left( {x,t} \right) = D_{t}^{\alpha } w - D_{x}^{2} w - \left( {k - 1} \right)D_{x} w + kw,$$

(17)

and mth RF may be written as

$$res_{m} \left( {x,t} \right) = \frac{{\partial^{\alpha } w_{m} \left( {x,t} \right)}}{{\partial t^{\alpha } }} - \frac{{\partial^{2} w_{m} \left( {x,t} \right)}}{{\partial x^{2} }} - \left( {k - 1} \right)\frac{{\partial w_{m} \left( {x,t} \right)}}{\partial x} + kw_{m} \left( {x,t} \right),\quad m = 1,\,2,\,3, \ldots$$

(18)

Some useful results about $res_{m} \left( {x,t} \right)$ have been included in [21, 22] which are given below

• i.
  $$res\left( {x,t} \right) = 0.$$
• ii.
  $$\mathop {Lim}\limits_{m \to \infty } \,\,res_{m} \left( {x,t} \right) = res(x,t).$$
• iii.
  $$D_{t}^{i\alpha } res\left( {x,0} \right) = D_{t}^{i\alpha } res_{m} \left( {x,0} \right) = 0,\quad i = 0,1,2, \ldots ,m.$$

  (19)

Step 3 Putting Eq. (16) into Eq. (18) and calculating $D_{t}^{{\left( {k - 1} \right)\alpha }} res_{m} \left( {x,t} \right),\quad k = 1,2, \ldots$ at $t = 0$, together with the above three results, we have the following algebraic systems

$$D_{t}^{{\left( {k - 1} \right)\alpha }} res_{m} \left( {x,0} \right),\quad 0 < \alpha \le 1,\quad k = 1,2, \ldots$$

(20)

Step 4 By solving Eq. (20), we can get the coefficients $b_{k} \left( x \right),\quad k = 1,2, \ldots ,m$. Thus mth RPS approximate solution is derived.

4 Convergence analysis

Lemma 1 [4]

If $f\left( x \right)$ is a continuous function and $\alpha ,\,\beta > 0$ then

$$I_{c}^{\alpha } I_{c}^{\beta } f\left( x \right) = I_{c}^{\alpha + \beta } f\left( x \right) = I_{c}^{\beta } I_{c}^{\alpha } f\left( x \right).$$

(21)

Theorem 4.1

• (a) If the FPS of the form $\sum\nolimits_{n = 0}^{\infty } {a_{n} x^{n\alpha } } ,\quad x \ge 0$ converges at $x = x_{1}$, then it converges absolutely $\forall$$x$ satisfying $\left| x \right| < \left| {x_{1} } \right|$.

• (b) If the FPS diverges at $x = x_{1}$, then it will diverge $\forall$$x$ such that $\left| x \right| > \left| {x_{1} } \right|$.

Theorem 4.2 [22]

For $0 \le n - 1 < \alpha \le n,$ suppose $D_{t}^{r + k\alpha } ,D_{t}^{r + (k + 1)\alpha } \in C\left[ {R,t_{0} } \right] \times \left[ {R,t_{0} + R} \right]$,

$$\left( {I_{t}^{r + k\alpha } D_{t}^{r + k\alpha } u} \right)\left( {x,t} \right) - \left( {I_{t}^{r + (k + 1)\alpha } D_{t}^{r + (k + 1)\alpha } u} \right)\,\left( {x,t} \right) = \frac{{\left( {t - t_{0} } \right)^{r + k\alpha } }}{{\varGamma \left( {r + k\alpha + 1} \right)}}D_{t}^{r + k\alpha } u\left( {x,t_{0} } \right),$$

(22)

where $D_{t}^{r + k\alpha } = \mathop {\left( {D_{t} D_{t} D_{t} \ldots } \right)}\limits_{r - times} \mathop {\left( {D_{t}^{\alpha } D_{t}^{\alpha } D_{t}^{\alpha } \ldots } \right)}\limits_{k - times}$.

Proof

Using Lemma 1,

$$\left( {I_{t}^{r + k\alpha } D_{t}^{r + k\alpha } u} \right)\left( {x,t} \right) - \left( {I_{t}^{r + (k + 1)\alpha } D_{t}^{r + (k + 1)\alpha } u} \right)\,\left( {x,t} \right) = I_{t}^{r + k\alpha } \left( {\left( {D_{t}^{r + k\alpha } u} \right)\,\left( {x,t} \right) - \left( {I_{t}^{\alpha } D_{t}^{r + (k + 1)\alpha } u} \right)\,\left( {x,t} \right)} \right) = I_{t}^{r + k\alpha } \left( {\left( {D_{t}^{r + k\alpha } u} \right)\,\left( {x,t} \right) - \left( {I_{t}^{\alpha } D_{t}^{\alpha } } \right)\left( {D_{t}^{r + k\alpha } u} \right)\,\left( {x,t} \right)} \right) = I_{t}^{r + k\alpha } \left( {\left( {D_{t}^{r + k\alpha } u} \right)\left( {x,t_{0} } \right)} \right) = \frac{{\left( {t - t_{0} } \right)^{r + k\alpha } }}{{\varGamma \left( {r + k\alpha + 1} \right)}}D_{t}^{r + k\alpha } u\left( {x,t_{0} } \right).$$

(23)

$\square$

Theorem 4.3 [22]

Let $w\left( {x,t} \right),\,\,D_{t}^{k\alpha } w\left( {x,t} \right) \in C\left[ {R,t_{0} } \right] \times \left[ {R,t_{0} + R} \right]$ where $k = 0,1,2, \ldots ,N + 1$ and $j = 0,1,2, \ldots ,n - 1.$ Also $D_{t}^{k\alpha } w\left( {x,t} \right)$ may be differentiated $n - 1$ times concerning “$t$”. Then

$$w\left( {x,t} \right) \cong \sum\limits_{j = 0}^{n - 1} {\sum\limits_{i = 0}^{N} {W_{j + i\alpha } \left( x \right)\left( {t - t_{0} } \right)^{j + i\alpha } ,} }$$

(24)

where $W_{j + i\alpha } \left( x \right) = \frac{{D_{t}^{j + i\alpha } w\left( {x,t_{0} } \right)}}{{\varGamma \left( {j + i\alpha + 1} \right)}}.$ Also, $\exists$ a value $\varepsilon ,\,\,0 \le \varepsilon \le t$, the error term has the term as follows,

$$\left\| {E_{N} \left( {x,t} \right)} \right\| = \mathop {\sup }\limits_{{t \in \,\left[ {0,\,T} \right]}} \left| {\sum\limits_{j = 0}^{n - 1} {\left[ {\frac{{D^{{j + \left( {N + 1} \right)\alpha }} w\left( {x,\varepsilon } \right)}}{{\varGamma \left( {\left( {N + 1} \right)\alpha + j + 1} \right)}}t^{{\left( {N + 1} \right)\alpha + j}} } \right]} } \right|.$$

(25)

Proof

From Eq. (23),

$$\sum\limits_{j = 0}^{n - 1} {\sum\limits_{i = 0}^{N} {\left( {\left( {I_{t}^{j + i\alpha } D_{t}^{j + i\alpha } w} \right)\,\,\left( {x,t} \right) - \left( {I_{t}^{j + (i + 1)\alpha } D_{t}^{j + (i + 1)\alpha } w} \right)\,\,\left( {x,t} \right)} \right)} } = \sum\limits_{j = 0}^{n - 1} {\sum\limits_{i = 0}^{N} {\frac{{\left( {t - t_{0} } \right)^{j + i\alpha } }}{{\varGamma \left( {j + i\alpha + 1} \right)}}} } D_{t}^{j + i\alpha } w\left( {x,t_{0} } \right) = \sum\limits_{j = 0}^{n - 1} {\sum\limits_{i = 0}^{N} {W_{j + i\alpha } \left( x \right)\left( {t - t_{0} } \right)^{j + i\alpha } } } .$$

(26)

That is,

$$w\left( {x,t} \right) - \sum\limits_{j = 0}^{n - 1} {\left[ {\left( {I_{t}^{{j + \left( {N + 1} \right)\alpha }} D_{t}^{{j + \left( {N + 1} \right)\alpha }} w} \right)\left( {x,t} \right)} \right]} = \sum\limits_{j = 0}^{n - 1} {\sum\limits_{i = 0}^{N} {W_{j + i\alpha } \left( x \right)\left( {t - t_{0} } \right)^{j + i\alpha } } } .$$

(27)

Considering the second term of Eq. (27), we have

$$\sum\limits_{j = 0}^{n - 1} {\left[ {\left( {I_{t}^{{j + \left( {N + 1} \right)\alpha }} D_{t}^{{j + \left( {N + 1} \right)\alpha }} w} \right)\left( {x,t} \right)} \right]} = \sum\limits_{j = 0}^{n - 1} {\left[ {\frac{1}{{\varGamma \left( {\left( {N + 1} \right)\alpha + j} \right)}}\int\limits_{0}^{t} {\frac{{D^{{j + \left( {N + 1} \right)\alpha }} w\left( {x,\varepsilon } \right)}}{{\left( {t - \tau } \right)^{{1 - \left( {j + \left( {N + 1} \right)\alpha } \right)}} }}d\tau } } \right]} ,\quad = \sum\limits_{j = 0}^{n - 1} {\left[ {\frac{{D^{{j + \left( {N + 1} \right)\alpha }} w\left( {x,\varepsilon } \right)}}{{\varGamma \left( {\left( {N + 1} \right)\alpha + j + 1} \right)}}t^{{\left( {j + \left( {N + 1} \right)\alpha } \right)}} } \right]} .\left( {Mean \, value \, theorem \, for \, integral} \right)$$

(28)

From Eqs. (27) and (28),

$$w\left( {x,t} \right) - \sum\limits_{j = 0}^{n - 1} {\sum\limits_{i = 0}^{N} {W_{j + i\alpha } \left( x \right)\left( {t - t_{0} } \right)^{j + i\alpha } } } = \sum\limits_{j = 0}^{n - 1} {\left[ {\frac{{D^{{j + \left( {N + 1} \right)\alpha }} w\left( {x,\varepsilon } \right)}}{{\varGamma \left( {\left( {N + 1} \right)\alpha + j + 1} \right)}}t^{{\left( {j + \left( {N + 1} \right)\alpha } \right)}} } \right]}$$

Now the error term is

$$\left\| {E_{N} \left( {x,t} \right)} \right\| = \left\| {w\left( {x,t} \right) - \sum\limits_{j = 0}^{n - 1} {\sum\limits_{i = 0}^{N} {W_{j + i\alpha } \left( x \right)\,\left( {t - t_{0} } \right)^{j + i\alpha } } } } \right\|,\quad =\left\| {\sum\limits_{j = 0}^{n - 1} {\left[ {\frac{{D^{j + (N + 1)\alpha } w(x,\varepsilon )}}{\varGamma ((N + 1)\alpha + j + 1)}t^{(j + (N + 1)\alpha )} } \right]} } \right\| \Rightarrow \left\| {E_{N} \left( {x,t} \right)} \right\| = \mathop {\sup }\limits_{{t \in \left[ {0,T} \right]}} \left| {\sum\limits_{j = 0}^{n - 1} {\left[ {\frac{{D^{{j + \left( {N + 1} \right)\alpha }} w\left( {x,\varepsilon } \right)}}{{\varGamma \left( {\left( {N + 1} \right)\alpha + j + 1} \right)}}t^{{\left( {j + \left( {N + 1} \right)\alpha } \right)}} } \right]} } \right|,$$

As $N \to \infty ,\,\,\left\| {E_{N} \left( {x,t} \right)} \right\| \to 0$, thus $w\left( {x,t} \right)$ can be estimated as follows$w\left( {x,t} \right) \cong \sum\nolimits_{j = 0}^{n - 1} {\sum\nolimits_{i = 0}^{N} {W_{j + i\alpha } \left( x \right)\left( {t - t_{0} } \right)^{j + i\alpha } } }$, with the error term in Eq. (25).$\square$

5 Numerical examples

Example 1

Consider Eqs. (12) and (13)

According to the RPSM,$w_{0} \left( {x,t} \right) = \hbox{max} (0,\,e^{x} - 1)$ and the infinite series solution of Eq. (12) can be written as

$$w\left( {x,t} \right) = \hbox{max} (0,\,e^{x} - 1) + \sum\limits_{k = 1}^{\infty } {b_{k} \left( x \right)\frac{{t^{\alpha k} }}{{\varGamma \left( {\alpha k + 1} \right)}}} .$$

(29)

mth truncated series solution of $w\left( {x,t} \right)$ becomes

$$w_{m} \left( {x,t} \right) = \hbox{max} (0,e^{x} - 1) + \sum\limits_{k = 1}^{m} {b_{k} \left( x \right)\frac{{t^{\alpha k} }}{{\varGamma \left( {\alpha k + 1} \right)}}} ,\quad m = 1,\,2,\,3, \ldots ,$$

(30)

For $m = 1$, 1st RPS solution for Eq. (11) may be written as

$$w_{1} \left( {x,t} \right) = \hbox{max} (0,e^{x} - 1) + b_{1} \left( x \right)\frac{{t^{\alpha } }}{{\varGamma \left( {\alpha + 1} \right)}}.$$

(31)

To determine the value of $b_{1} \left( x \right)$, we substitute Eq. (31) in the 1st residual function of Eq. (18) $res_{1} \left( {x,t} \right) = \frac{{\partial^{\alpha } w_{1} \left( {x,t} \right)}}{{\partial t^{\alpha } }} - \frac{{\partial^{2} w_{1} \left( {x,t} \right)}}{{\partial x^{2} }} - \left( {k - 1} \right)\frac{{\partial w_{1} \left( {x,t} \right)}}{\partial x} + kw_{1} \left( {x,t} \right)$, this gives

$$res_{1} \left( {x,t} \right) = b_{1} \left( x \right) - e^{x} - b_{1}^{\prime \prime } \left( x \right)\frac{{t^{\alpha } }}{{\varGamma \left( {\alpha + 1} \right)}} - (k - 1)\left( {e^{x} + b_{1}^{\prime } \left( x \right)\frac{{t^{\alpha } }}{{\varGamma \left( {\alpha + 1} \right)}}} \right) + k\left( {\hbox{max} \left( {0,\,e^{x} - 1} \right) + b_{1} \left( x \right)\frac{{t^{\alpha } }}{{\varGamma \left( {\alpha + 1} \right)}}} \right).$$

(32)

Using (iii) of Eq. (19) for $i = 0$ that is $res\left( {x,0} \right) = res_{1} \left( {x,0} \right) = 0$, we get

$$res_{1} \left( {x,0} \right) = b_{1} \left( x \right) - ke^{x} + k\hbox{max} \left( {e^{x} - 1,0} \right) = 0.$$

$${\text{So}}\,b_{1} \left( x \right) = ke^{x} - k\hbox{max} \left( {e^{x} - 1,0} \right).$$

(33)

For $m = 2$, 2nd RPS solution for Eq. (11) can be written as

$$w_{2} \left( {x,t} \right) = \hbox{max} (e^{x} - 1,0) + \left( {ke^{x} - k\hbox{max} \left( {e^{x} - 1,0} \right)} \right)\frac{{t^{\alpha } }}{{\varGamma \left( {\alpha + 1} \right)}} + b_{2} \left( x \right)\frac{{t^{2\alpha } }}{{\varGamma \left( {2\alpha + 1} \right)}}.$$

(34)

To find the value of $b_{2} \left( x \right)$, Eq. (34) is substituted in the 2nd residual function of Eq. (18) $res_{2} \left( {x,t} \right) = \frac{{\partial^{\alpha } w_{2} \left( {x,t} \right)}}{{\partial t^{\alpha } }} - \frac{{\partial^{2} w_{2} \left( {x,t} \right)}}{{\partial x^{2} }} - \left( {k - 1} \right)\frac{{\partial w_{2} \left( {x,t} \right)}}{\partial x} + kw_{2} \left( {x,t} \right).$ Then we have

$$res_{2} (x,t) = ke^{x} - k\hbox{max} \left( {0,e^{x} - 1} \right) + b_{2} \left( x \right)\frac{{t^{\alpha } }}{{\varGamma \left( {\alpha + 1} \right)}} - e^{x} - b_{2}^{\prime \prime } \left( x \right)\frac{{t^{2\alpha } }}{{\varGamma \left( {2\alpha + 1} \right)}} - \left( {k - 1} \right)\left[ {e^{x} + b_{2}^{\prime } \left( x \right)\frac{{t^{2\alpha } }}{{\varGamma \left( {2\alpha + 1} \right)}}} \right] + k\left[ {\hbox{max} (e^{x} - 1,0) + \left( {ke^{x} - k\hbox{max} \left( {e^{x} - 1,0} \right)} \right)\frac{{t^{\alpha } }}{{\varGamma \left( {\alpha + 1} \right)}} + b_{2} \left( x \right)\frac{{t^{2\alpha } }}{{\varGamma \left( {2\alpha + 1} \right)}}} \right]$$

(35)

Using (iii) of Eq. (19) for $i = 1$ that is $D_{t}^{\alpha } res\left( {x,0} \right) = D_{t}^{\alpha } res_{2} \left( {x,0} \right) = 0$, we get

$$b_{2} \left( x \right) = k^{2} \hbox{max} \left( {0,\,e^{x} - 1} \right) - k^{2} e^{x} .$$

(36)

For $m = 3$, 3rd RPS solution for the Eq. (11) can be written as

$$w_{3} \left( {x,t} \right) = \hbox{max} (0,\,e^{x} - 1) + \left( {ke^{x} - k\hbox{max} \left( {0,\,e^{x} - 1} \right)} \right)\frac{{t^{\alpha } }}{{\varGamma \left( {\alpha + 1} \right)}} + \left( {k^{2} \hbox{max} \left( {e^{x} - 1,0} \right) - k^{2} e^{x} } \right)\frac{{t^{2\alpha } }}{{\varGamma \left( {2\alpha + 1} \right)}} + b_{3} \left( x \right)\frac{{t^{3\alpha } }}{{\varGamma \left( {3\alpha + 1} \right)}}.$$

(37)

Putting Eq. (37) in the 3rd residual function of Eq. (18) we obtain $res_{3} \left( {x,t} \right) = \frac{{\partial^{\alpha } w_{3} \left( {x,t} \right)}}{{\partial t^{\alpha } }} - \frac{{\partial^{2} w_{3} \left( {x,t} \right)}}{{\partial x^{2} }} - \left( {k - 1} \right)\frac{{\partial w_{3} \left( {x,t} \right)}}{\partial x} + kw_{3} \left( {x,t} \right)$, we have

$$res_{3} (x,t) = ke^{x} - k\hbox{max} \left( {e^{x} - 1,0} \right) + \left( {k^{2} \hbox{max} \left( {e^{x} - 1,0} \right) - k^{2} e^{x} } \right)\frac{{t^{\alpha } }}{{\varGamma \left( {\alpha + 1} \right)}} + b_{3} \left( x \right)\frac{{t^{2\alpha } }}{{\varGamma \left( {2\alpha + 1} \right)}} - e^{x} - b_{3}^{\prime \prime } \left( x \right)\frac{{t^{3\alpha } }}{{\varGamma \left( {3\alpha + 1} \right)}} - \left( {k - 1} \right)\left[ {e^{x} + b_{3}^{\prime } \left( x \right)\frac{{t^{3\alpha } }}{{\varGamma \left( {3\alpha + 1} \right)}}} \right] + k\left[ \begin{aligned} \hbox{max} (0,\,e^{x} - 1) + \left( {ke^{x} - k\hbox{max} \left( {0,\,e^{x} - 1} \right)} \right)\frac{{t^{\alpha } }}{{\varGamma \left( {\alpha + 1} \right)}} \hfill \\ + \left( {k^{2} \hbox{max} \left( {0,\,e^{x} - 1} \right) - k^{2} e^{x} } \right)\frac{{t^{2\alpha } }}{{\varGamma \left( {2\alpha + 1} \right)}} + b_{3} \left( x \right)\frac{{t^{3\alpha } }}{{\varGamma \left( {3\alpha + 1} \right)}} \hfill \\ \end{aligned} \right].$$

(38)

Using Eq. (19) for $i = 2$ that is $D_{t}^{2\alpha } res\left( {x,0} \right) = D_{t}^{2\alpha } res_{3} \left( {x,0} \right) = 0$, it follows that

$$b_{3} \left( x \right) = k^{3} e^{x} - k^{3} \hbox{max} \left( {e^{x} - 1,0} \right).$$

(39)

Continuing this way, one may find the values of $b_{4} \left( x \right)$, $b_{5} \left( x \right)$,……So the solution of Eq. (11) may be written as

$$w\left( {x,t} \right) = \hbox{max} (0,\,e^{x} - 1) + \left( {ke^{x} - k\hbox{max} \left( {0,\,e^{x} - 1} \right)} \right)\frac{{t^{\alpha } }}{{\varGamma \left( {\alpha + 1} \right)}} + \left( {k^{2} \hbox{max} \left( {0,\,e^{x} - 1} \right) - k^{2} e^{x} } \right)\frac{{t^{2\alpha } }}{{\varGamma \left( {2\alpha + 1} \right)}} + \left( {k^{3} e^{x} - k^{3} \hbox{max} \left( {0,\,e^{x} - 1} \right)} \right)\frac{{t^{3\alpha } }}{{\varGamma \left( {3\alpha + 1} \right)}} + \cdots ,$$

(40)

$$= \hbox{max} \left( {e^{x} - 1,0} \right)\left[ {1 - \frac{{kt^{\alpha } }}{{\varGamma \left( {1 + \alpha } \right)}} + \frac{{k^{2} t^{2\alpha } }}{{\varGamma \left( {1 + 2\alpha } \right)}} - \frac{{k^{3} t^{3\alpha } }}{{\varGamma \left( {1 + 3\alpha } \right)}} + \cdots } \right] + e^{x} \,\left[ {\frac{{kt^{\alpha } }}{{\varGamma \left( {1 + \alpha } \right)}} - \frac{{k^{2} t^{2\alpha } }}{{\varGamma \left( {1 + 2\alpha } \right)}} + \frac{{k^{3} t^{3\alpha } }}{{\varGamma \left( {1 + 3\alpha } \right)}} - \cdots } \right]\,,$$

(41)

$$= \hbox{max} \left( {e^{x} - 1,0} \right)E_{\alpha } \left( { - kt^{\alpha } } \right) + e^{x} \left( {1 - E_{\alpha } \left( { - kt^{\alpha } } \right)} \right).$$

(42)

where $E_{\alpha } \left( t \right) = \sum\nolimits_{n = 0}^{\infty } {\frac{{t^{n} }}{{\varGamma \left( {1 + n\alpha } \right)}},}$ is Mittag–Leffler function. Equation (42) is the analytical solution of Eq. (11) which is same as [10,11,12,13].

Case 1

Considering the vanilla call option [25] for $\alpha = 1$, $\sigma = 0.2,\,r = 0.04,\,\tau = 0.5.$ years then $k = 2.$ The solution of Eq. (11) for this case is $w\left( {x,t} \right) = \hbox{max} \left( {0,\,e^{x} - 1} \right)\,e^{ - 2t} + e^{x} \left( {1 - e^{ - 2t} } \right)$.

Case 2

For vanilla call option [25] with parameter $\sigma = 0.2,\,r = 0.01,\,\alpha = 1,\tau = 1\,$ year then $k = 5$.In this example, we obtain the solution of Eq. (11) as $w\left( {x,t} \right) = \hbox{max} \left( {0,\,e^{x} - 1} \right)\,e^{ - 5t} + e^{x} \left( {1 - e^{ - 5t} } \right)\,.$

Example 2

Let us consider the generalized BS equation [24]

$$\frac{{\partial^{\alpha } w}}{{\partial t^{\alpha } }} + 0.08\left( {2 + \sin x} \right)^{2} x^{2} \frac{{\partial^{2} w}}{{\partial x^{2} }} + 0.06x\frac{\partial w}{\partial x} - 0.06w = 0,\quad 0 < \alpha \le 1,$$

(43)

with IC

$$w\left( {x,0} \right) = \hbox{max} \left( {0,\,x - 25e^{ - 0.06} } \right).$$

(44)

According to the RPSM, $w_{0} \left( {x,t} \right) = \hbox{max} \left( {0,\,x - 25e^{ - 0.06} } \right)$, and the FPS solution of Eq. (43) can be written as

$$w\left( {x,t} \right) = \hbox{max} (x - 25e^{ - 0.06} ,0) + \sum\limits_{k = 1}^{\infty } {b_{k} \left( x \right)\frac{{t^{\alpha k} }}{{\varGamma \left( {\alpha k + 1} \right)}}} .$$

(45)

In consideration of the present method, mth truncated series solution of $w\left( {x,t} \right)$ becomes

$$w_{m} \left( {x,t} \right) = \hbox{max} (0,\,x - 25e^{ - 0.06} ) + \sum\limits_{k = 1}^{m} {b_{k} \left( x \right)\frac{{t^{\alpha k} }}{{\varGamma \left( {\alpha k + 1} \right)}}} ,\quad m = 1,\,2,\,3, \ldots ,$$

(46)

and mth residual function of Eq. (43) may be written as

$$res_{m} \left( {x,t} \right) = \frac{{\partial^{\alpha } w_{m} \left( {x,t} \right)}}{{\partial t^{\alpha } }} + 0.08\left( {2 + \sin x} \right)^{2} x^{2} \frac{{\partial^{2} w_{m} \left( {x,t} \right)}}{{\partial x^{2} }} + 0.06x\frac{{\partial w_{m} \left( {x,t} \right)}}{\partial x} - 0.06w_{m} \left( {x,t} \right),\quad m = 1,\,2,\,3, \ldots ,$$

(47)

For $m = 1$, 1st RPS solution for the Eq. (43) can be written as

$$w_{1} \left( {x,t} \right) = \hbox{max} (x - 25e^{ - 0.06} ,0) + b_{1} \left( x \right)\frac{{t^{\alpha } }}{{\varGamma \left( {\alpha + 1} \right)}}.$$

(48)

By substituting Eq. (48) into the 1st residual function of Eq. (47) as

$$res_{1} \left( {x,t} \right) = \frac{{\partial^{\alpha } w_{1} \left( {x,t} \right)}}{{\partial t^{\alpha } }} + 0.08\left( {2 + \sin x} \right)^{2} x^{2} \frac{{\partial^{2} w_{1} \left( {x,t} \right)}}{{\partial x^{2} }} + 0.06x\frac{{\partial w_{1} \left( {x,t} \right)}}{\partial x} - 0.06w_{1} \left( {x,t} \right),$$

(49)

We get

$$res_{1} \left( {x,t} \right) = b_{1} \left( x \right) + 0.08\left( {2 + \sin x} \right)^{2} x^{2} b_{1}^{\prime \prime } \left( x \right)\frac{{t^{\alpha } }}{{\varGamma \left( {1 + \alpha } \right)}} + 0.06x\left( {1 + b_{1}^{\prime } \left( x \right)\frac{{t^{\alpha } }}{{\varGamma \left( {1 + \alpha } \right)}}} \right) - 0.06\left( {\hbox{max} (x - 25e^{ - 0.06} ,0) + b_{1} \left( x \right)\frac{{t^{\alpha } }}{{\varGamma \left( {\alpha + 1} \right)}}} \right)\,\,.$$

(50)

Using (iii) of Eq. (19) for $i = 0$ that is $res\left( {x,0} \right) = res_{1} \left( {x,0} \right) = 0$, we get

$$b_{1} (x) + 0.06x - 0.06\hbox{max} \left( {x - 25e^{ - 0.06} ,0} \right) = 0.$$

$$b_{1} (x) = 0.06\hbox{max} \left( {x - 25e^{ - 0.06} ,0} \right) - 0.06x.$$

(51)

For $m = 2$, 2nd RPS solution for the Eq. (43) is written as

$$w_{2} \left( {x,t} \right) = \hbox{max} (0,\,x - 25e^{ - 0.06} ) + \left( {0.06\hbox{max} \left( {0,\,x - 25e^{ - 0.06} } \right) - 0.06x} \right)\frac{{t^{\alpha } }}{{\varGamma \left( {\alpha + 1} \right)}} + b_{2} \left( x \right)\frac{{t^{2\alpha } }}{{\varGamma \left( {2\alpha + 1} \right)}},$$

(52)

To find out the value of $b_{2} \left( x \right)$, substitute Eq. (52) into the 2nd residual function of Eq. (47) as $res_{2} \left( {x,t} \right) = \frac{{\partial^{\alpha } w_{2} \left( {x,t} \right)}}{{\partial t^{\alpha } }} + 0.08\left( {2 + \sin x} \right)^{2} x^{2} \frac{{\partial^{2} w_{2} \left( {x,t} \right)}}{{\partial x^{2} }} + 0.06x\frac{{\partial w_{2} \left( {x,t} \right)}}{\partial x} - 0.06w_{2} \left( {x,t} \right),$ we get

$$res_{2} \left( {x,t} \right) = 0.06{\text{max}}\left( {x - 25e^{{ - 0.06}} ,0} \right) - 0.06x + b_{2} \left( x \right)\frac{{t^{\alpha } }}{{\Gamma \left( {1 + \alpha } \right)}} + 0.08\left( {2 + \sin x} \right)^{2} x^{2} \left( {b_{2}^{{\prime \prime }} \left( x \right)\frac{{t^{{2\alpha }} }}{{\Gamma \left( {1 + 2\alpha } \right)}}} \right) + 0.06x\left( {1 + b_{2}^{\prime } \left( x \right)\frac{{t^{{2\alpha }} }}{{\Gamma \left( {2\alpha + 1} \right)}}} \right) - 0.06\left( \begin{gathered} {\text{max}}(x - 25e^{{ - 0.06}} ,0) + \left( {0.06{\text{max}}\left( {x - 25e^{{ - 0.06}} ,0} \right) - 0.06x} \right)\frac{{t^{\alpha } }}{{\Gamma \left( {\alpha + 1} \right)}} \hfill \\ + b_{2} \left( x \right)\frac{{t^{{2\alpha }} }}{{\Gamma \left( {2\alpha + 1} \right)}} \hfill \\ \end{gathered} \right).$$

(53)

Using (iii) of Eq. (19) for $i = 1$ that is $D_{t}^{\alpha } res\left( {x,0} \right) = D_{t}^{\alpha } res_{2} \left( {x,0} \right) = 0$, we get

$$b_{2} \left( x \right) - 0.06\left( {0.06\hbox{max} \left( {x - 25e^{ - 0.06} ,0} \right) - 0.06x} \right) = 0.$$

$$b_{2} \left( x \right) = 0.06\left( {0.06\hbox{max} \left( {0,\,x - 25e^{ - 0.06} } \right) - 0.06x} \right) = \left( {0.06} \right)^{2} \hbox{max} \left( {0,\,x - 25e^{ - 0.06} } \right) - \left( {0.06} \right)^{2} x.$$

(54)

For $m = 3$, 3rd RPS solution for the Eq. (43) is reduced as

$$w_{3} \left( {x,t} \right) = \hbox{max} (x - 25e^{ - 0.06} ,0) + \left( {0.06\hbox{max} \left( {0,\,x - 25e^{ - 0.06} } \right) - 0.06x} \right)\frac{{t^{\alpha } }}{{\varGamma \left( {\alpha + 1} \right)}} + \left( {\left( {0.06} \right)^{2} \hbox{max} \left( {0,\,x - 25e^{ - 0.06} } \right) - \left( {0.06} \right)^{2} x} \right)\frac{{t^{2\alpha } }}{{\varGamma \left( {2\alpha + 1} \right)}} + b_{3} \left( x \right)\frac{{t^{3\alpha } }}{{\varGamma \left( {3\alpha + 1} \right)}}.$$

(55)

To determine the value of $b_{3} \left( x \right)$, putting Eq. (55) into the 3rd residual function of Eq. (47) as $res_{3} \left( {x,t} \right) = \frac{{\partial^{\alpha } w_{3} \left( {x,t} \right)}}{{\partial t^{\alpha } }} + \left( {2 + \sin x} \right)^{2} x^{2} 0.08\frac{{\partial^{2} w_{3} \left( {x,t} \right)}}{{\partial x^{2} }} + 0.06x\frac{{\partial w_{3} \left( {x,t} \right)}}{\partial x} - 0.06w_{3} \left( {x,t} \right),$ one may get

$$\begin{aligned} res_{3} \left( {x,t} \right) & = 0.06\max \left( {0,\,x - 25e^{{ - 0.06}} } \right) - 0.06x + \left( {\left( {0.06} \right)^{2} \max \left( {0,\,x - 25e^{{ - 0.06}} } \right) - \left( {0.06} \right)^{2} x} \right)\frac{{t^{\alpha } }}{{\Gamma \left( {1 + \alpha } \right)}} \\ & \quad + b_{3} \left( x \right)\frac{{t^{{2\alpha }} }}{{\Gamma \left( {1 + 2\alpha } \right)}} + \left( {2 + \sin x} \right)^{2} 0.08x^{2} \left( {b_{3} ^{{\prime \prime }} \left( x \right)\frac{{t^{{3\alpha }} }}{{\Gamma \left( {1 + 3\alpha } \right)}}} \right) + 0.06x\left( {1 + b_{3} ^{\prime } \left( x \right)\frac{{t^{{3\alpha }} }}{{\Gamma \left( {3\alpha + 1} \right)}}} \right) \\ & \quad - 0.06\left( {\begin{array}{ll} {\max (0,\,x - 25e^{{ - 0.06}} ) + \left( {0.06\max \left( {0,\,x - 25e^{{ - 0.06}} } \right) - 0.06x} \right)\frac{{t^{\alpha } }}{{\Gamma \left( {\alpha + 1} \right)}}} \\ { + \left( {\left( {0.06} \right)^{2} \max \left( {0,\,x - 25e^{{ - 0.06}} } \right) - \left( {0.06} \right)^{2} x} \right)\frac{{t^{{2\alpha }} }}{{\Gamma \left( {2\alpha + 1} \right)}} + b_{3} \left( x \right)\frac{{t^{{3\alpha }} }}{{\Gamma \left( {3\alpha + 1} \right)}}} \\ \end{array} } \right). \\ \end{aligned}$$

(56)

By Eq. (19) for $i = 2$ that is $D_{t}^{2\alpha } res\left( {x,0} \right) = D_{t}^{2\alpha } res_{3} \left( {x,0} \right) = 0$, it follows that

$$b_{3} \left( x \right) - 0.06\left( {\left( {0.06} \right)^{2} \hbox{max} \left( {0,\,x - 25e^{ - 0.06} } \right) - \left( {0.06} \right)^{2} x} \right) = 0.$$

$$b_{3} \left( x \right) = \left( {0.06} \right)^{3} \hbox{max} \left( {0,\,x - 25e^{ - 0.06} } \right) - \left( {0.06} \right)^{3} x.$$

(57)

Continuing as above, one may obtain the values of $b_{4} \left( x \right)$, $b_{5} \left( x \right)$,……,So the solution of Eq. (43) may be written as

$$\begin{aligned} w\left( {x,t} \right) & = \hbox{max} \left( {0,\,x - 25e^{ - 0.06} } \right) + \left( {0.06\hbox{max} \left( {0,\,x - 25e^{ - 0.06} } \right) - 0.06x} \right)\frac{{t^{\alpha } }}{{\varGamma \left( {\alpha + 1} \right)}} + \left( {\left( {0.06} \right)^{2} \hbox{max} \left( {0,\,x - 25e^{ - 0.06} } \right) - \left( {0.06} \right)^{2} x} \right)\frac{{t^{2\alpha } }}{{\varGamma \left( {2\alpha + 1} \right)}} + \left( \begin{aligned} \left( {0.06} \right)^{3} \hbox{max} \left( {0,\,x - 25e^{ - 0.06} } \right) - \hfill \\ \left( {0.06} \right)^{3} x \hfill \\ \end{aligned} \right)\frac{{t^{3\alpha } }}{{\varGamma \left( {3\alpha + 1} \right)}} + \cdots , \\ & = \hbox{max} \left( {0,\,x - 25e^{ - 0.06} } \right)\,\left[ {1 + \frac{{0.06t^{\alpha } }}{{\varGamma \left( {1 + \alpha } \right)}} + \frac{{\left( {0.06} \right)^{2} t^{2\alpha } }}{{\varGamma \left( {1 + 2\alpha } \right)}} + \frac{{\left( {0.06} \right)^{3} t^{3\alpha } }}{{\varGamma \left( {1 + 3\alpha } \right)}} + \cdots } \right] + x\left[ { - \frac{{0.06t^{\alpha } }}{{\varGamma \left( {1 + \alpha } \right)}} - \frac{{\left( {0.06} \right)^{2} t^{2\alpha } }}{{\varGamma \left( {1 + 2\alpha } \right)}} - \frac{{\left( {0.06} \right)^{3} t^{3\alpha } }}{{\varGamma \left( {1 + 3\alpha } \right)}} - \cdots } \right] \\ & = \hbox{max} \left( {0,\,x - 25e^{ - 0.06} } \right)\,E_{\alpha } \left( {0.06\,t^{\alpha } } \right) + x\,\left( {1 - E_{\alpha } \left( {0.06\,t^{\alpha } } \right)} \right). \\ \end{aligned}$$

(58)

Equation (58) is the exact solution of Eq. (43) which is the same as given in [11]. For $\alpha = 1$, we have $w\left( {x,t} \right) = \hbox{max} \left( {x - 25e^{ - 0.06} ,0} \right)\,e^{0.06t} + x\,\left( {1 - e^{0.06\,t} } \right)$. This is an analytical solution of fractional BS Eq. (43).

6 Conclusion

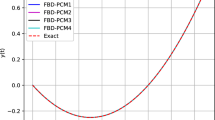
In this study, a new iterative technique namely RPSM is effectively applied for finding the exact solution of FBSE with high accuracy. The convergence analysis is also described to validate the efficacy and powerfulness of the present technique. Solution plots of Eqs. (42) and (58) have been illustrated in Figs. 1, 2, 3, 4, 5 and 6 for different values of $\alpha$. It is clear from the figures that the European option prices increase with the decrease of $\alpha$. Moreover at $\alpha = 0.2$ it is seen that option is overpriced. The solutions in special cases achieved from the proposed method are in good agreement with the other methods described in [10,11,12,13] which shows that the method is effective, convenient and gives closed form solution in the series form.

Fig. 1

The plot of Eq. (42) represents the surface $w\left( {x,t} \right)$ at a $\alpha = 1$, b $\alpha = 0.2$, c $\alpha = 0.5$, d $\alpha = 0.6$ and e $\alpha = 0.8$

Fig. 2

The solution plots of Eq. (42) for different values of $\alpha$ at a $x = 0.2$, b $x = 0.5$

Fig. 3

The plot represents the surface $w\left( {x,t} \right)$ at $\alpha = 1$ and $k = 2$

Fig. 4

The plot represents the surface $w\left( {x,t} \right)$ at $\alpha = 1$ and $k = 5$

Fig. 5

The plot of Eq. (58) represents the surface $w\left( {x,t} \right)$ at a $\alpha = 1$, b $\alpha = 0.2$, c $\alpha = 0.4$, d $\alpha = 0.6$ and e $\alpha = 0.8$

Fig. 6

The solution plots of Eq. (58) for different values of $\alpha$ at a $x = 0.2$ and b $x = 0.5$