Skip to main content
SpringerLink
Log in

Parametric Analysis of a Rotational Piezoelectric-Coupled Tapered-Bimorph Structure with Various Boundary Conditions Under Transient Axial Loading

  • Original Paper
  • Published:
Journal of Vibration Engineering & Technologies Aims and scope Submit manuscript

Abstract

Purpose

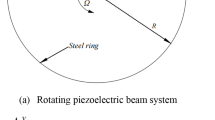
The steady-state parametric analysis of a piezoelectric-coupled rotating tapered-bimorph system consists of a central host beam and two piezoelectric ceramic patches above and below it, tapering along positive X-direction and rotating in the X–Y plane, subjected to axial dynamic as well as static loading at its one end is done. The influence of three boundary conditions and various system parameters are also studied.

Methods

The mathematical modeling of the rotating tapered-bimorph system is formulated with the help of Hamilton's equation. The parametric analysis of the axially loaded system is done for clamped-free (C-F), pinned-pinned (P-P), and clamped-pinned (C-P) boundary conditions. A number of parametric instability regions along with static buckling load plots are obtained and analyzed for various values of the piezoelectric patches to the host beam thickness ratio, taper parameter, and rotational frequency using MATLAB software and depicted through a series of diagrams.

Results

The results illustrate that the principal modal frequencies of the tapered-bimorph rotating system are increased rapidly with an increase in the thickness ratio, whereas increase less significantly with a rise in taper parameter and spinning speed for both the static and dynamic loading conditions.

Conclusion

The lowest first modal frequency is observed for the P-P system under any given system configurations and operating conditions, which can be used for low-frequency rotational vibration energy harvester over the orthodoxly used C-F system. Designing low-frequency rotational vibration energy harvester and rotor blades can be done by selecting appropriate dimensions and parameters presented in this article.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12

Similar content being viewed by others

Abbreviations

\(A_{p} \left( x \right)\) :

Cross-sectional area of the PZT patch

\(A_{h} \left( x \right)\) :

Cross-sectional area of the substrate beam

b :

Widths of the structure at the hub side

\(b\left( x \right)\) :

Widths of the structure at \(x^{\prime} = B_{0} + x\)

\(B_{0}\) :

Radius of the revolving hub

\(E_{h}\) :

Young's modulus of the substrate material

\(E_{p}\) :

Young's modulus of the PZT patch

\(I_{h} \left( x \right)\) :

Area moment of inertia of the substrate beam at standard section

\(I_{p} \left( x \right)\) :

Area moment of inertia of the PZT patch at standard section

l :

Total span of the beam

N :

Spinning speed of the system

P :

Maximum amplitude of the transient load

\(P_{s}\) :

Static load

\(t_{p}\) :

Thickness of the PZT patches

\(t_{h}\) :

Thickness of the host beam

T :

Total kinetic energy of the system

U :

Total potential energy of the system

\(W_{e}\) :

Work-done due to external axial load

\(W_{c}\) :

Work-done due to centrifugal force

\(w\left( {x,t} \right)\) :

The transverse displacement

\(\eta\) :

\(= {x \mathord{\left/ {\vphantom {x l}} \right. \kern-\nulldelimiterspace} l}\)

\(\zeta\) :

\(= {w \mathord{\left/ {\vphantom {w l}} \right. \kern-\nulldelimiterspace} l}\)

\(\alpha\) :

Taper parameter

\(\rho_{h}\) :

Mass density of the host beam

\(\rho_{p}\) :

Mass density of the PZT patches

\(\omega\) :

Driving frequency

\(\omega_{n}\) :

System natural frequency

References

  1. Abbas BAH (1986) Dynamic stability of a rotating Timoshenko beam with a flexible root. J Sound Vib 108:25–32. https://doi.org/10.1016/S0022-460X(86)80308-X

    Article  Google Scholar 

  2. Al-Ansary MD (1998) Flexural vibrations of rotating beams considering rotary inertia. Comput Struct 69:321–328. https://doi.org/10.1016/S0045-7949(98)00134-5

    Article  MATH  Google Scholar 

  3. Anton SR, Sodano HA (2007) A review of power harvesting using piezoelectric materials (2003–2006). Smart Mater Struct. https://doi.org/10.1088/0964-1726/16/3/R01

    Article  Google Scholar 

  4. Auciello NM, Ercolano A (2004) A general solution for dynamic response of axially loaded non-uniform Timoshenko beams. Int J Solids Struct 41:4861–4874. https://doi.org/10.1016/j.ijsolstr.2004.04.036

    Article  MATH  Google Scholar 

  5. Banerjee JR, Sobey AJ (2005) Dynamic stiffness formulation and free vibration analysis of a three-layered sandwich beam. Int J Solids Struct 42:2181–2197. https://doi.org/10.1016/j.ijsolstr.2004.09.013

    Article  MATH  Google Scholar 

  6. Carnegie W (1959) Vibrations of Pre-twisted cantilever blading. Proc Inst Mech Eng 173:343–374. https://doi.org/10.1243/pime_proc_1959_173_038_02

    Article  MATH  Google Scholar 

  7. Chand RR, Behera PK, Pradhan M (2019) Study of static and dynamic stability of an exponentially tapered revolving beam exposed to a variable temperature grade under axial loading. Int J Acoust Vib 24:504–510. https://doi.org/10.20855/ijav.2019.24.31357

    Article  Google Scholar 

  8. Chand RR, Behera PK, Pradhan M, Dash PR (2019) Parametric stability analysis of a parabolic-tapered rotating beam under variable temperature grade. J Vib Eng Technol 7:23–31. https://doi.org/10.1007/s42417-018-0071-y

    Article  Google Scholar 

  9. Dawson B, Carnegie W (1969) Modal curves of pre-twisted beams of rectangular cross-section. J Mech Eng Sci. https://doi.org/10.1243/jmes_jour_1969_011_003_02

    Article  Google Scholar 

  10. Hoa SV (1979) Vibration of a rotating beam with tip mass. J Sound Vib 67:369–381. https://doi.org/10.1016/0022-460X(79)90542-X

    Article  MATH  Google Scholar 

  11. Lee HP (1995) Dynamic response of a rotating timoshenko shaft subject to axial forces and moving loads. J Sound Vib 181:169–177. https://doi.org/10.1006/jsvi.1995.0132

    Article  Google Scholar 

  12. Lenci S, Clementi F (2012) Effects of shear stiffness, rotatory and axial inertia, and interface stiffness on free vibrations of a two-layer beam. J Sound Vib 331:5247–5267. https://doi.org/10.1016/j.jsv.2012.07.004

    Article  Google Scholar 

  13. Lin CY, Chen LW (2003) Dynamic stability of a rotating beam with a constrained damping layer. J Sound Vib 267:209–225. https://doi.org/10.1016/S0022-460X(02)01427-X

    Article  Google Scholar 

  14. Mead DJ, Tarantol RAD (1972) Resonance response criteria of a damped three-layered beam. J Manuf Sci Eng Trans ASME 94:174–180. https://doi.org/10.1115/1.3428108

    Article  Google Scholar 

  15. Nayak S, Bisoi A, Dash PR, Pradhan PK (2014) Static stability of a viscoelastically supported asymmetric sandwich beam with thermal gradient. Int J Adv Struct Eng 6:1–7. https://doi.org/10.1007/s40091-014-0065-2

    Article  Google Scholar 

  16. Nayfeh AH, Mook DT (1995) Nonlinear oscillations. Wiley, New Jersey

    Book  Google Scholar 

  17. Parida R, Dash P (2016) Dynamic stability analysis of a circularly tapered rotating beam subjected to axial pulsating load and thermal gradient under various boundary conditions. Int J Acoust Vib 21:137–144. https://doi.org/10.20855/ijav.2016.21.2402

    Article  Google Scholar 

  18. Pradhan M, Dash PR (2016) Stability of an asymmetric tapered sandwich beam resting on a variable Pasternak foundation subjected to a pulsating axial load with thermal gradient. Compos Struct. https://doi.org/10.1016/j.compstruct.2016.01.010

    Article  MATH  Google Scholar 

  19. Pradhan M, Dash PR, Pradhan PK (2016) Static and dynamic stability analysis of an asymmetric sandwich beam resting on a variable pasternak foundation subjected to thermal gradient. Meccanica. https://doi.org/10.1007/s11012-015-0229-6

    Article  MathSciNet  MATH  Google Scholar 

  20. Rao DK, Stühler W (1977) Frequency and loss factors of tapered symmetric sandwich beams. J Appl Mech Trans ASME 44:511–513. https://doi.org/10.1115/1.3424117

    Article  MATH  Google Scholar 

  21. Rao JS, Banerjee S (1977) Coupled bending-torsional vibrations of rotating cantilever blades-method of polynomial frequency equation. Mech Mach Theory. https://doi.org/10.1016/0094-114X(77)90003-9

    Article  Google Scholar 

  22. Sabuncu M, Evran K (2005) Dynamic stability of a rotating asymmetric cross-section Timoshenko beam subjected to an axial periodic force. Finite Elem Anal Des 41:1011–1026. https://doi.org/10.1016/j.finel.2004.12.004

    Article  MATH  Google Scholar 

  23. Saito H, Otomi K (1979) Parametric response of viscoelastically supported beams. J Sound Vib. https://doi.org/10.1016/0022-460X(79)90874-5

    Article  MATH  Google Scholar 

  24. Saito H, Otomi K (1979) Vibration and stability of elastically supported beams carrying an attached mass under axial and tangential loads. J Sound Vib. https://doi.org/10.1016/0022-460X(79)90025-7

    Article  Google Scholar 

  25. Sodano HA, Inman DJ, Park G (2004) A review of power harvesting from vibration using piezoelectric materials. Shock Vib Dig 36:197–205. https://doi.org/10.1177/0583102404043275

    Article  Google Scholar 

  26. Tekinalp O, Ulsoy AG (1989) Modeling and finite element analysis of drill bit vibrations. J Vib Acoust Trans ASME 111:148–155. https://doi.org/10.1115/1.3269835

    Article  Google Scholar 

  27. Wei K, Meng G, Zhou S, Liu J (2006) Vibration control of variable speed / acceleration rotating beams using smart materials. J Sound Vib 298:1150–1158. https://doi.org/10.1016/j.jsv.2006.05.033

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Mechanical Engineering Department, Indian Institute of Technology (BHU), Varanasi, 221005, India

    R. R. Chand & A. Tyagi

Authors
  1. R. R. Chand
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. A. Tyagi
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to R. R. Chand.

Ethics declarations

Conflict of Interest

On behalf of all authors, the corresponding author states that there is no conflict of interest.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Chand, R.R., Tyagi, A. Parametric Analysis of a Rotational Piezoelectric-Coupled Tapered-Bimorph Structure with Various Boundary Conditions Under Transient Axial Loading. J. Vib. Eng. Technol. 9, 907–917 (2021). https://doi.org/10.1007/s42417-020-00272-9

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s42417-020-00272-9

Keywords

Search

Navigation