Skip to main content
SpringerLink
Log in

Determination of Dynamic Coefficients of Air-Ring Bearings

  • Original Paper
  • Published:
Journal of Vibration Engineering & Technologies Aims and scope Submit manuscript

Abstract

Purpose

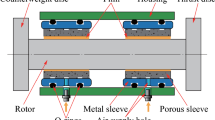
An externally-pressurized journal air bearing (AB) with an air-ring (AR), or air-ring bearing (ARB), for a balanced, rigid and light-weight rotor is studied. An elastic structure in the form of an AR is provided between the bearing-bushing and the casing. The ARB is analyzed to determine the dynamic coefficients (DC) at various angular velocities and angular frequencies of vibration of the journal in its range of operation. These DC can then be used to predict the dynamic stability of the rotor ARB system against self-excited (SE) vibration. A numerical simulation procedure is followed to determine the DC.

Methods

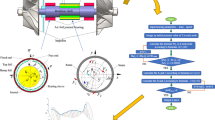
The ARB is modeled as a two-degrees of freedom system. During the simulation, the journal follows a prescribed harmonic motion. Self-exciting forces due to flow dynamics inside an ARB induce this motion. Three-dimensional (3-D) flow equations are solved on a moving/deformable grid using ANSYS®, to compute the pressure (p) distribution in the ARB. Unlike in previous studies, in this study the bushing displacement is determined by the instantaneous p-distribution in the ARB. DC of both AB and AR are determined simultaneously by considering the interaction between the AR and the AB regions through the feed-holes in the bushing.

Results

Time-dependent displacement, velocity, and load-carrying capacity obtained by numerical simulation are used to evaluate the DC.

Conclusion

Incorporation of an AR around an AB can prevent SE vibration due to positive values of direct damping coefficients of AR. A 3-D flow analysis can reveal the realistic nature of flow in an ARB.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16
Fig. 17
Fig. 18
Fig. 19
Fig. 20
Fig. 21

Similar content being viewed by others

Abbreviations

AB:

Air-bearing

AR:

Air-ring

ARB:

Air-ring bearing

CG:

Geometric center

CFD:

Computational fluid dynamics

DC:

Dynamic coefficients

FC:

Face centroid

FH:

Feed-hole

GCI:

Grid convergence indicator

LHS:

Left-hand side

RARBS:

Rotor air-ring bearing system

RE:

Reynolds equation

RHS:

Right-hand side

RPM:

Revolutions per minute

SE:

Self-excited

SEP:

Static equilibrium position

SHM:

Simple harmonic motion

SSS:

Steady-state simulation

TSS:

Transient-state simulation

UDF:

User-defined function

1-DOF:

Single-degree of freedom

2-DOF:

Two-degrees of freedom

A :

Amplitude of vibration (m)

a :

A coefficient (see Eq. 5)

b :

Reference cell size (m); time step size (s); a coefficient (see Eq. 6)

C :

Damping coefficient (N s m−1)

c :

Radial clearance (m); specific heat (J kg−1 K−1)

D :

Diameter (m)

d :

Diameter (m)

E :

Discretization error

e :

Eccentricity (m)

F :

Absolute dynamic load-carrying capacity (N)

f :

Incremental dynamic load-carrying capacity (N)

g :

Acceleration due to gravity (m s−2)

h :

Axial length (m)

K :

Stiffness coefficient (N m−1)

k :

Thermal conductivity (W m−1 K−1)

L :

Bearing length (m)

m :

Mass (kg)

N :

Number of time steps; rotational speed of the rotor (RPM)

n :

Number of feed-holes per row (see Table 1); an index

P :

Static load (N)

p :

Static pressure (Pa)

R :

Gas constant (J kg−1 K−1)

r :

Radial coordinate (m); number of rows of feed-holes (see Table 1)

S :

Absolute displacement (m)

\(\dot{S}\) :

Absolute velocity (m s−1)

s :

Incremental displacement (m)

\(\dot{s}\) :

Incremental velocity (m s−1)

T :

Temperature (K); time period of vibration (s)

t :

Time (s)

U :

A target quantity of interest

u :

Fluid velocity component (m s−1)

x :

A coordinate (m)

y :

A coordinate (m)

z :

A coordinate (m)

α :

Attitude angle (rad)

β :

Angular position of baffle (rad) (see Fig. 1)

γ :

Angular width of baffle (rad) (see Fig. 1)

δ :

Radial distance (across film thickness) measured from bushing surface (m)

\(\epsilon\) :

(= e/c) Eccentricity ratio

θ :

Angle coordinate (rad)

λ :

Rate of reduction of truncation error

μ :

Dynamic viscosity (kg m−1 s−1)

ν :

Angular frequency (rad s−1)

ρ :

Density (kg m−3)

ω :

Angular velocity (rad s−1)

AB:

Air-bearing

AR:

Air-ring

B:

Bushing

dm:

Dynamic mesh

i :

Grid-level

J:

Journal

max:

Maximum

v :

At constant volume

r :

Radial

rel:

Relative

s:

Supply

z :

Axial

θ :

Circumferential

i :

An index

j :

An index

x :

x-Component

y :

y-Component

F :

Absolute dynamic load-carrying capacity (N)

f :

Incremental dynamic load-carrying capacity (N)

r :

Position vector (m)

S :

Absolute displacement (m)

\(\dot{\mathbf{S}}\) :

Absolute velocity (m s−1)

s :

Incremental displacement (m)

\(\dot{\mathbf{s}}\) :

Incremental velocity (m s−1)

\(\ddot{\mathbf{s}}\) :

Acceleration (m s−2)

u :

Velocity (m s−1); orthonormal vector

v :

Orthogonal vector

w :

A vector

τ :

Viscous stress tensor (N m−2)

ω :

Angular velocity vector (rad s−1)

References

  1. Moore MJ (2002) Micro-turbine generators. Professional Engineering Publishing, London

    Google Scholar 

  2. Gao Q, Chen W, Lu L, Huo D, Cheng K (2019) Aerostatic bearings design and analysis with the application to precision engineering: state-of-the-art and future perspectives. Tribol Int 135:1–17

    Article  Google Scholar 

  3. Czołczyński K (1996) How to obtain stiffness and damping coefficients of gas bearings. Wear 201(1–2):265–275

    Article  Google Scholar 

  4. Pan CHT, Sternlicht B (1962) On the translatory whirl motion of a vertical rotor in plain cylindrical gas-dynamic journal bearings. ASME J Basic Eng 84(1):152–158

    Article  Google Scholar 

  5. Gross WA (1962) Investigation of whirl in externally pressurized air-lubricated journal bearings. ASME J Basic Eng 84(1):132–138

    Article  Google Scholar 

  6. Fuller DD (1969) A review of the state-of-the-art for the design of self-acting gas-lubricated bearings. ASME J Lubr Technol 91(1):1–16

    Article  Google Scholar 

  7. Chu TY, McCabe JT, Elrod HG (1968) Stability considerations for a gas-lubricated tilting-pad journal bearing–Part 1: analytical methods. ASME J Lubr Technol 90(1):162–172

    Article  Google Scholar 

  8. Kai F, Minghui S, Tao G, Yuanyuan L, Jie Z (2017) A novel squeeze-film air bearing with flexure pivot-tilting pads: numerical analysis and measurement. Int J Mech Sci 134:41–50

    Article  Google Scholar 

  9. Jiang S, Lin S, Xu C (2018) Static and dynamic characteristics of externally pressurized porous gas journal bearing with four degrees-of-freedom. ASME J Tribol 140(1):011702

    Article  Google Scholar 

  10. Bhore SP, Darpe AK (2019) Nonlinear transient stability analysis of meso-scale rotor supported on gas foil journal bearings. J Vib Eng Technol 7(4):399–406

    Article  Google Scholar 

  11. Arghir M, Hassini MA, Balducchi F, Gauthier R (2016) Synthesis of experimental and theoretical analysis of pneumatic hammer instability in an aerostatic bearing. ASME J Eng Gas Turbines Power 138(2):021602

    Article  Google Scholar 

  12. Lund JW (1965) The stability of an elastic rotor in journal bearings with flexible, damped supports. ASME J Appl Mech 32(4):911–920

    Article  Google Scholar 

  13. Powell JW, Tempest MC (1968) A study of high speed machines with rubber stabilized air bearings. ASME J Lubr Technol 90(4):701–708

    Article  Google Scholar 

  14. Majumdar BC (1975) Stability characteristics of gas-lubricated bearings supported on rubber ‘O’ rings. Tribol Int 8(3):127–129

    Article  Google Scholar 

  15. Belforte G, Colombo F, Raparelli T, Viktorov V (2008) High-speed rotor with air bearings mounted on flexible supports: test bench and experimental results. ASME J Tribol 130(2):021103

    Article  Google Scholar 

  16. Brzeski L, Kazimierski Z (1979) High stiffness bearing. ASME J Lubr Technol 101(4):520–525

    Article  Google Scholar 

  17. Kazimierski Z, Trojnarski J (1980) Investigations of externally pressurized gas bearings with different feeding systems. ASME J Lubr Technol 102(1):59–64

    Article  Google Scholar 

  18. Czołczyński K, Brzeski L, Kazimierski Z (1993) High stiffness gas journal bearing under the step force. Wear 167(1):49–58

    Article  Google Scholar 

  19. Czołczyński K, Kapitaniak T, Marynowski K (1996) Stability of rotors supported in gas bearings with bushes mounted in air rings. Wear 199(1):100–112

    Article  Google Scholar 

  20. Czołczyński K (1997) Stability of the rotor supported in gas journal bearings with a chamber feeding system. Wear 210(1-2):220–236

    Article  Google Scholar 

  21. Czołczyński K (1999) Rotor dynamics of gas-lubricated journal bearing systems. Springer-Verlag, New York

    Book  Google Scholar 

  22. Muruganandam M, Ramamurthy S, Nadarajan S (2005) Design of air bearing for a high-speed micro gas turbine. In: Proceedings of the 5th national seminar and exhibition on aerospace and related mechanisms, ISRO Satellite Centre, Bangalore, India, pp 269–277

  23. Muruganandam M, Thyageswaran S, Aswin V, Rajakumaran T (2017) Analysis of load-carrying abilities in rotor-bearing systems. In: 13th international conference on vibration problems, Indian Institute of Technology, Guwahati, India, P 38

  24. Burton TD (1994) Introduction to dynamic systems analysis. Mc Graw Hill, New York

    Google Scholar 

  25. Den Hartog JP (1984) Mechanical vibrations. Dover Publications, New York

    MATH  Google Scholar 

  26. Friedberg SH, Insel AJ, Spence LE (2013) Linear algebra, 4th edn. PHI Learning Private Limited, New Delhi

    MATH  Google Scholar 

  27. Ueberhuber CW (1997) Numerical computation–2 (methods, software, and analysis). Springer-Verlag, Berlin

    MATH  Google Scholar 

  28. Byron Bird R, Stewart WE, Lightfoot EN (2012) Transport phenomena, 2nd edn. Wiley India Private Limited, New Delhi

    Google Scholar 

  29. Hirsch C (2007) Numerical computation of internal and external flows, the fundamentals of computational fluid dynamics, 2nd edn. Butterworth-Heinemann, Oxford

    Google Scholar 

  30. San Andrés L (2010) Gas film lubrication. Notes 15. In: Modern lubrication theory. Texas A & M University Digital Libraries. https://repository.tamu.edu/handle/1969.1/93197. Accessed 26 Aug 2015

  31. FLUENT Theory Guide. ANSYS®, Inc. Canonsburg, PA. https://ansyshelp.ansys.com/account/secured?returnurl=/Views/Secured/corp/v190/flu_th/flu_th_dynam_mesh_cons_eqns.html. Accessed 10 Feb 2020

  32. Versteeg HK, Malalasekera W (2009) An introduction to computational fluid dynamics, the finite volume method, 2nd edn. Pearson Education, Harlow

    Google Scholar 

  33. Khonsari MM, Booser ER (2001) Applied tribology, bearing design and lubrication. Wiley, New York

    Google Scholar 

  34. Wang B, Sun Y, Ding Q (2020) Free fluid-structure interaction method for accurate nonlinear dynamic characteristics of the plain gas journal bearings. J Vib Eng Technol 8(1):149-161

    Article  Google Scholar 

Download references

Acknowledgements

The corresponding author wishes to thank J-U. Friemann, X. Wang and P. Zamankhan, of ANSYS® Inc. for their guidance in writing UDFs for moving/deformable mesh in the transient-state simulations using ANSYS® FLUENT.

Funding

This research did not receive any grant from funding agencies in the public, commercial, or not-for-profit sectors.

Author information

Authors and Affiliations

  1. Department of Mechanical Engineering, Coimbatore Institute of Technology, Coimbatore, 641 014, India

    Muruganandam Muthanandam & Sridhar Thyageswaran

Authors
  1. Muruganandam Muthanandam
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Sridhar Thyageswaran
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Muruganandam Muthanandam.

Ethics declarations

Conflict of interest

The authors declare that they have no conflict of interest.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Muthanandam, M., Thyageswaran, S. Determination of Dynamic Coefficients of Air-Ring Bearings. J. Vib. Eng. Technol. 9, 1–21 (2021). https://doi.org/10.1007/s42417-020-00207-4

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s42417-020-00207-4

Keywords

Search

Navigation