Abstract
Longitudinal clustering techniques are widely deployed in computational social science to delineate groupings of subjects characterized by meaningful developmental trends. In criminology, such methods have been utilized to examine the extent to which micro places (such as streets) experience macro-level police-recorded crime trends in unison. This has largely been driven by a theoretical interest in the longitudinal stability of crime concentrations, a topic that has become particularly pertinent amidst a widespread decline in recorded crime. Recent studies have tended to rely on a generic implementation k-means to unpick this stability, with little consideration for its theoretical suitability. This study makes two methodological contributions. First, it demonstrates the application of k-medoids to study longitudinal crime concentrations, and second, it develops a novel ‘anchored k-medoids’ (ak-medoids), a bespoke clustering method specifically designed to meet the theoretical requirements of micro-place investigations into long-term stability. Using both simulated data and 15-years of police-recorded crime data from Birmingham, England, we compare the performances of k-medoids against ak-medoids. We find that both methods highlight instability in the exposure to crime over time, but the consistency and contribution of cluster solutions determined by ak-medoids provide insight overlooked by k-medoids, which is sensitive to short-term fluctuations and subject starting points. This has important implications for the theories said to explain longitudinal crime concentrations, and the law enforcement agencies seeking to offer an effective and equitable service to the public.
Similar content being viewed by others
Introduction
Across developed polities there is widespread evidence of a long-term decline in place-based recorded crime [1,2,3]. Research examining the crime drop in cities has consistently demonstrated that the crime trajectories of a small proportion of micro places (such as streets) tend to drive citywide trends [4], with the vast majority of areas exhibiting stable crime profiles [5, 6]. That some micro places appear to have benefited more than others during the crime drop is suggestive of shifting spatial inequality in the exposure to crime, a finding of significant theoretical and policy interest. These investigations into the relative longitudinal (in)stability of crime concentrations have tended to rely on generic implementations of longitudinal clustering methods, such as k-means, to delineate groupings characterized by distinct developmental trends, rather than deploy bespoke, theoretically-driven methods.
Set against this context, our paper makes a substantive methodological contribution to support the investigation of crime in micro places. We provide the first implementation of k-medoids (partitioning around medoids (PAM)) for measuring longitudinal (in)stability of crime concentration. We then introduce a novel longitudinal clustering technique, termed anchored k-medoids. A variant of k-medoids clustering, the development of anchored k-medoids has been informed by recognition of the typical stability and / or slow changing character of the crime profiles of micro places, and the theoretical interest in long-term directional change. Thus, and in contrast to k-medoids, which clusters trajectories based on the scale of distances between observations, such that trajectories with similar directional changes are likely to end up in separate clusters [7], anchored k-medoids has been specifically designed to identify cluster solutions characterized by within-group directional homogeneity. We demonstrate the merits of the technique using simulated data and 15-years of police-recorded property crime data from Birmingham (UK). Further, we provide access to an R package user manual to enable standardized replication of this technique in future research [8].
The paper is structured in the following fashion. First, we provide a brief justification for the deployment of longitudinal clustering in the study of crime in micro places, as well as an overview of existing methods, their reported implementation and consequent qualities of the derived clustering solutions. Second, we provide a detailed outline of how both k-medoids and anchored k-medoids are operationalized. Third, we describe the simulated data and 15-years of recorded property crime from Birmingham used to demonstrate the methods, and the analytical strategy deployed to assess the distinctions between anchored k-medoids and k-medoids. Thereafter, we present and discuss the results of the simulated data and Birmingham case study, prior to offering a conclusion.
Background
The motivation for deploying longitudinal clustering methods in spatial criminology rests on the empirical evidence of, and the theoretical plausibility for, distinct and (relatively) stable crime or offender concentrations over time. Here, the groundbreaking work of Shaw and McKay [9] in Chicago is of note as they found areas with high rates of offenders tended to persist through time, irrespective of the turnover of area populations. Such stability was interpreted as theoretically likely, following social disorganization theory, due to the economic deprivation, high-level of resident turnover and ethnic heterogeneity of these areas [10, 11]. Whilst later studies [12, 13] corroborated the stability of the spatial patterning of offender and crime concentrations, others did not. For example, and in part replication and extension of Shaw and McKay’s Chicago study, Bursik and Webb found that through time, changes in area population characteristics held association with changes in area offender rates [11, 14]. Recognizing the potential for longer-term change, Schuerman and Kobrin [15] demonstrated, in a study of Los Angeles, that small geographic areas did not necessarily mimic citywide crime trends but rather exhibited crime profiles that could be characterized as emergent, transitional or enduring. Similarly, a study of Sheffield (UK), identified that residential areas, just like individuals, could hold crime careers [16].
Informed by a desire to explore individual life-course offending patterns, a major breakthrough in longitudinal clustering methodologies was made by Nagin and Land [17] who developed group-based trajectory modelling (GBTM). GBTM is a semi-parametric method that aims to simplify longitudinal data through clustering observations based on the similarity of their trajectories. Weisburd et al. [5] were the first to deploy GBTM to examine the stability of crime concentrations in micro places, in a study of Seattle. They found subgroups of micro places, or street segments, with comparable crime levels through time, with only a small number of street segments being evidenced as driving the overall crime drop in Seattle between 1989 and 2002. These findings have been interpreted as consistent with social disorganization theory, which posits linear and slow change over time [18]. Weisburd et al. [5] also argued that their findings could be explained by routine activities theory [19] given that the supply of capable guardians, motivated offenders and suitable targets in any given micro place is also only thought to change over an extensive time period. GBTM has since become the most widely used method for examining the longitudinal clustering of crime and offending across street segments [6, 19,20,21,22,23] and larger spatial scales, such as those approximating neighbourhoods [18, 23,24,25,26]. Collectively, these studies continue to report that citywide crime drops tend to be driven by a small number of areas, with the majority exhibiting stable crime profiles.
The implementation of GBTM does not lend itself to a bespoke adjustment prompted by theoretical or empirical insight. Rather, the statistical assumptions underpinning GBTM demand repeated measurement and spatially proximate units be treated as independent of one another. To avoid such statistical assumptions, Curman et al. [27] and Andresen et al. [4] have deployed a non-parametric alternative to GBTM, namely, k-means clustering [28]. Unlike GBTM, k-means is not limited by polynomial terms and is therefore capable of capturing short-term fluctuations and outliers in longitudinal data. This is of significant value when seeking to explore phenomena, such as homicide and handgun availability, that may be subject to rapid change [18]. However, such sensitivity may impede the identification of clusters based on underlying, or longer-term, trends, as posited by social disorganization and, in many contexts, routine activities theory.
The default implementation of k-means follows a random and therefore exploratory initialization process. Thereafter, the expectation–maximization algorithm iterates until clusters become stable, with the centroid of each cluster being calculated using the mean, which is why the cluster solutions are sensitive to outliers [29]. Given that existing research does not report otherwise [4, 27], it must be assumed that it has utilized the default implementation of k-means. However, the outlier problem can be addressed using medoids (i.e. the most centrally placed object of the cluster) instead of centroids. This gives rise to a variant of k-means called k-medoids. Both k-means and k-medoids are malleable techniques that can be tailored to disentangle pre-defined, theoretically driven, functional forms. As the existing research on crime in micro places has evidenced, there are clear theoretical and empirical grounds to stipulate initialization points to enable the algorithm to better delineate long-term stability and/or slow changing trajectories in cluster solutions. In particular, studies have demonstrated an interest in disentangling clusters characterized by directional (i.e. increasing, decreasing) homogeneity, along with stable clusters that might remain constant even amidst wider macro-level change [4, 5, 27]. However, no attempt has been made to develop a bespoke implementation of either k-means or k-medoids to meet these requirements. In other fields, utilizing bespoke initialization points has been shown to optimize the final cluster solution and provide greater computational efficiency [29,30,31,32], though these demonstrations have largely relied only on synthetic data. That no attempt has been made to deploy non-random initialization points, or to tailor the k-means or k-medoids algorithm to support investigation of the longitudinal clustering of crime in micro places, provides the motivation for this paper.
Definitions
K-means and K-medoids algorithm
Given an integer k(k < n) and a set of longitudinal observations \({y}_{it}\)(i = 1, …, n; t = 1, …,T) in Euclidean space, the k-means algorithm defines a set of centroid estimates (means) \({\mu }_{k}\) (\({\mu }_{1t}\), \({\mu }_{2t}\), …, \({\mu }_{kt}\)), |\(\mu\)|= k in the space, such that \({y}_{it}\) can be partitioned into k corresponding clusters \({C}_{1}\), \({C}_{2}\),…,\({C}_{k}\), by assigning each observation in \({y}_{it}\) to its closest centre \({\mu }_{it}\). Mathematically, the objective function of k-means algorithm is given as:
which represents the sum of the squares of the distances of each observation to its assigned centroid \({\mu }_{k}\). For each observation \({y}_{it}\), a corresponding set of binary indicator variable \({w}_{ik}\in \{0, 1\}\) is created, where \(k=1,\dots ,K\) describes which cluster the observation is assigned to, such that \({w}_{ik}=1\) if \({y}_{it}\) belongs to cluster \(k\); otherwise, \({w}_{ik}=0.\) The goal of k-means is to find values of \({w}_{ik}\) and \({\mu }_{k}\) so as to minimize \(J\). Randomly setting some initial values for \({\mu }_{k}\), clusters are formed through an iterative procedure involving two successive steps, E(expectation) and M(maximization) steps, corresponding to successive optimizations with respect to the \({w}_{ik}\) and the \({\mu }_{k}\) [32,33,35].
The E-step minimizes \(J\) with respect to \({w}_{ik}\) keeping \({\mu }_{k}\) fixed, and then updates cluster assignments. The E-step can be solved as follows:
In other words, assign the observation \({y}_{it}\) to the closest cluster judged by the Euclidean distance from the cluster’s centroid. The M-step minimizes \(J\) with respect to \({\mu }_{k}\) and recompute the centroids. The M-step can be solved as:
In other words, the centroid of each cluster is recomputed to reflect the new assignment. Both E-step and M-step are solved iteratively until the objective function (Eq. 1) converges (or until some maximum number of iterations is exceeded). As Eq. 3 ensures the maximal distance between the centroids \({\mu }_{k}\) (means) and the observations of the cluster represented by the centroids, k-means is sensitive to the presence of outliers. Further, k-means has been found to be sensitive to starting points as well as short-term changes.
From the above, if we first order the observations based on distance proximity relative to a chosen baseline (typically the x-axis), and partition the observation into an equal-sized pre-defined number of groups, the medoids of each group can be set as the starting points [33, 34]. The subsequent steps can proceed as described for the k-means above. This variant of k-means is called k-medoids [32,33,34,35]. To the best of our knowledge, k-medoids have never been applied in the longitudinal clustering of crime datasets.
The proposed anchored K-medoids (Ak-medoids)
Ak-medoids, in harmony with the k-medoids, follows the same formulation. However, with the ambition of identifying cluster solutions informed by longer-term changes, we propose two fundamental modifications to the aforementioned default implementation: a functional linear approximation of observations [36] to minimize the impact of short-term trajectory fluctuations, and an elimination of the starting levels observations. We now describe the steps involves in the design of ak-medoids, and their significance. We also provide an R package to enable standardized replication of the technique (Anonymous).
Step one: Trajectory approximation
A linear ordinary least squares (OLS) regression line, \({y}_{it}={m}_{i}t+{b}_{i}\), is fitted to the trajectory of each observation \(i\), where \(m\) represents the gradient, \(t\) the time steps and, \({b}_{i}\) the initial level. Having eliminated the bias due to the population denominator,Footnote 1 we can drop the initial level \({b}_{i}\) across all observations with the aim to model only the longer-term trend of the observation \({y}_{it}^{^{\prime}}={m}_{i}t\). This enables subsequent focus on the varying directional change of a trajectory over time.
Step two: Non-random initialization
The next step is to deploy a non-random initialization through ordering of the gradients \({m}_{i}\left(i=1,\dots ,n\right)\), creating \(k\) equal-interval partition \(Y\)={\({Y}_{1}, \dots , {Y}_{k}\)}, and then select the subset \(\mathcal{K}\subset \{1,\dots .,k\}\), where its elements are pointers to the medoids estimates \(c({c}_{1}, \dots , {c}_{k})\) of the partitions. In other words, we select amongst the estimated regression lines to initialize the clustering process as oppose to random initial values. These medoid estimates are used as the ‘anchors’ to enable the clustering to begin. The purpose behind this step is to provide the algorithm with clearly delineated starting points, guided by the interest in generating clusters characterized by varying degrees of directional change, and with the purpose of ensuring that heterogenous longer-term trends occupy different clusters [37, 38]. The corresponding dissimilarity measure between the estimates and the medoids can be expressed as \({d}_{ik}= {\Vert {y}_{it}^{^{\prime}}-{c}_{kt}\Vert }^{2}.\)
Step three: Bespoke E-M steps
Once the initial anchors have been set, the E-M steps is executed as follow:
-
1.
Repeat until convergence {
-
2.
E-step: Assign estimates to cluster \({C}_{i}^{^{\prime}}\) using the rule
-
3.
M-step: Update the medoids and compute J
The Eq. 4 implies that estimate \(i\) is assigned to the least dissimilar medoid from the set \(\mathcal{K}\), while Eq. 5 states that for a set of estimates sharing a common medoid, we select the new medoid such that the estimate for which the sum of dissimilarities to other estimates of the cluster is lowest. The use of medoids by ak-medoids as oppose to the mean marks another key difference from k-means [39]. Just like the standard usage of k-medoids is isolation, ak-medoids tends to be more robust to outliers and produces a more balanced cluster solution. The resulting clusters based on the approximated functional linear estimates are eventually mapped onto the actual observations,\(f:{C}^{^{\prime}}\to C\), to derive the final cluster solution. In all, the result is the partition of trajectories into clusters characterized by within-group directional homogeneity, but between-group directional heterogeneity, relative to a reference direction (typically the horizontal axis). The expectation is that this approach will generate more theoretically meaningful cluster solutions according to the longer-term directional change over time [4].
Applications to artificial and real data sets
Construction of artificial data sets
We first use simulated data to demonstrate the key distinctions between ak-medoids and k-means, under a scenario in which the goal is to capture pre-defined clusters characterized by their within-group directional homogeneity. The demonstration showcases the relative robustness of ak-medoids, in comparison to k-means, to the scale of variability (in starting values and subsequent longitudinal volatility) between the observations. Existing studies in the crime concentrations literature that have compared longitudinal clustering methods have only done so using police-recorded crime data in isolation [25, 27]. Here, the simulated data is comprised of three distinct groups whose long-term directional change is classified as increasing, decreasing or stable, a common classification in crime concentration research [4]. The success of the clustering method in capturing these pre-defined clusters can be assessed by comparing the pre-defined and the identified clusters.
In essence, a groupm is conceived as a theoretical trajectory defined by a baseline polynomial function \({f}_{m}\left(t\right)=b+{a}_{1}t+\dots +{a}_{n}{t}^{n}\), where b is the baseline intercept, \({a}_{1}, \dots {a}_{n}\) the coefficients, \(t\) the time, and \(n\) the order of the polynomial [28]. We consider both the linear (\({1}^{st}-order)\) and the quadratic \(({2}^{nd}-order)\) forms of the polynomial function (Fig. 1). We simulate samples of large (N = 250), medium (N = 100) and small sizes (N = 75), for the groups experiencing stable (B), decreasing (A) and increasing (C) directional change, respectively.Footnote 2 Figure 1 shows three selected data samples with varying levels of longitudinal variations (overlaps) between the groups for each polynomial type. The baseline trajectories of each group are defined as follow:
-
(i)
‘Linear groups’: \({f}_{A}\left(t\right)=10 -0.5t\); \({f}_{B}\left(t\right)=3\);\({f}_{C}\left(t\right)=0.5t\), with \(t\) in\([0 : 20]\).
-
(ii)
‘Quadratic groups’: \({f}_{A}\left(t\right)=9+0.55t-0.05{t}^{2}\); \({f}_{B}\left(t\right)=2+t- 0.05{t}^{2}\); \({f}_{C}\left(t\right)=1.17t-0.035{t}^{2}\) with \(t\) in\(\left[0 : 20\right]\).
The baseline functions were chosen to produce three clearly identifiable clusters. The variation of individual members within a group is defined in terms of two parameters: the intercept deviation \(\tau ,\) and the errors (fluctuations) \(\epsilon\), over time. For the linear group A, for example, an individual member i within the group is defined by \({f}_{A, i}\left(t\right)=10+{\tau }_{i}-0.5t+{\epsilon }_{i}\left(t\right)\) [28, 40]. We define the intercept deviations as gamma-distributed \(\tau \sim\Gamma (\alpha ,1/\beta )\) [17, 40], in which the shape parameter \(\alpha\) is kept constant (\(\alpha =2\)), while the scale parameter \((\beta )\), henceforth referred to as variability, ranges from 1 to 8, by steps of 0.02, to produce the variation of groups for each consecutive data set. With \(\alpha =2\) the distribution of the intercepts in each data set is similarly skewed, but become more spread out as \(\beta\) increases, giving rise to an increasingly large mean. To ensure proportional longitudinal errors for different levels of intercepts, we define \(\epsilon\) as a function of the intercept using normal law \({\epsilon }_{i}(t)\) \(\mathcal{N}(0, {\tau }^{2}\)). This specification ensures that low intercept trajectories have proportionally low errors (fluctuation) over time and vice versa for the higher intercept trajectories. The intercept error distribution at the \(\beta\) values 1, 3 and 8, and the corresponding longitudinal error distribution can be seen in the Appendix. At \(\beta =1\), we have easily identifiable and directionally-homogeneous clusters, whereas \(\beta =8\) gives overtly overlapping groups whose overall mean directions are not easily discernable. The result of this simulation process are groups defined by directional homogeneity, rather than within-group distance similarity [28, 41]. Overall, 700 simulated data sets were created, comprising 350 variances for each functional form (linear and quadratic).
Real data set
Study location
The city of Birmingham is located in the metropolitan county of the West Midlands, England, UK. It is the largest urban conurbation in the county, which contains six other districts including the cities of Wolverhampton and Coventry. Birmingham city is spread over 268km2 and contains around 1.1 million residents. It is served by West Midlands Police Force and has the highest crime rate in the region. Birmingham has a disproportionately large number of deprived communities and is one of the most ethnically diverse cities in the country [42].
Unit of analysis
To date, the majority of research examining the longitudinal stability or instability of crime in and across micro places has been North American, though notable exceptions exist [43]. Following Weisburd et al. [5], this research has typically defined micro places as street segments. Due to the grid-based networks of many North American cities, street segments offer the advantage of being fine-grained, yet large enough to minimize geocoding inaccuracies, and are comparable in spatial scale. Utilizing fine-grained spatial units, such as street segments, holds clear benefit in unmasking variation in crime concentrations that would otherwise be hidden within larger aggregations [44, 45]. Further, street segments have been argued to hold ontological meaning in the fabric of the urban space [13], therefore constituting theoretically relevant behaviour settings [20].
In this study, however, we deploy Output Areas, of which there are 3,223 in the city of Birmingham as defined by the 2011 census of England and Wales. We deploy Output Areas on two key grounds. First, our study area of the city of Birmingham does not have a grid-based street network. As such, its street segments vary significantly in scale and population size. In these terms, it is unlikely that street segments in Birmingham hold comparable ontological significance to those in North America or in other settings that have grid-based street networks. Output areas are the smallest spatial scale at which census information is collected and contain socially homogenous populations [46] and their boundaries recognize major physical features on the ground, such as main roads [47]. In these terms, we think it plausible that Output Areas hold ontological meaning. Further, the scale of Output Areas, comprising approximately 120 households, is comparable to that of the street segments deployed by Weisburd et al. [5] in their study of Seattle, which comprised approximately 99 street addresses. Second, in the UK, data on resident populations is not available for street segments, but it is at the Output Area level, on an annual basis. Being able to capture accurate population data enables the research to explore and control for variance in the crime profile of Output Areas arising from distinctions in population size.
Police recorded data
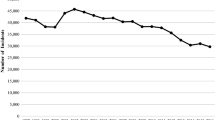
We use police-recorded property crime data for the city of Birmingham for the years 2001 to 2016. A single crime type was selected for the analysis to counter for the potential that different crime types might exhibit distinct trends [48] and in recognition of research that has demonstrated such disparities when undertaking longitudinal clustering [4]. Data is aggregated by yearly time points running from April to March, so the earliest crime report is dated 1 April 2001 and latest on 31 March 2016. Raw property crime counts were aggregated to Output Area level and then adjusted by the annual resident population estimates to create a rate per 100 people.Footnote 3 In overview, the 15-year study period witnessed the property crime rate fall by 69% (see Fig. 2a).
Dependent variable
A relative crime exposure measure was generated from the rates data to perform clustering (Fig. 2b). This measure represents the proportion of total (population adjusted) property crime occurring in any given Output Area for the year. The percentage attributable to each Output Area is thus the relative exposure of each unit. This application enables clear identification of the strongest and weakest performing clusters given the overall (citywide) trend. It is important to note that the assessment of relative crime exposure opens the possibility that a cluster experiencing increasing relative exposure to crime might also be experiencing a decline in absolute exposure to crime, but doing so at a slower rate than the wider area trend. And, of course, vice versa. We return to this issue in the results and discussion sections, in which both relative (proportional) and absolute (rates) are reported.
Analytical strategy
Given that this study seeks to advance a novel adaptation of k-medoids, namely ak-medoids, with the intention of demonstrating its capability of delineating trajectories according to their directional change over time, and in doing so also demonstrate the first application of k-medoids in crime concentration research, it is necessary to highlight the key distinction between the ak-medoids, k-medoids and k-means using the simulated data set. The real-life implications of these distinctions will then be demonstrated using the police-recorded property crime data aggregated to micro places (Output Areas) in Birmingham, UK. To these ends, the research adopts the following analytical strategy.
Application to simulated data set
The simulated data set was created to test the ability of ak-medoids, k-medoids and k-means to identify three known directionally homogeneous clusters characterized by their increasing, decreasing and stable trajectories. Both Ak-medoids and k-medoids are implemented in R, using the ak-medoids package (Anonymous). We deploy the default implementation of k-means, using the Kml package [28, 39]. This is the package used to deploy longitudinal k-means in previous research [4, 27]. Options regarding the random initialization points and expectation–maximization were kept as default. The performance of each method was evaluated using the Adjusted Rand Index (aRand) [49]. The aRand is a measure of agreement between two clustering results. The index takes a value between 0 and 1, for which a value of 0 is synonymous to random agreement and a value of 1 is perfect agreement between two clustering results. Here, the aRand index is utilized to compare the clustering results C of each method with respect to the pre-defined known clusters R. With the simulated data, a judgement of the relative performance of each method in identifying known underlying clusters can be made at differing degrees of variation in trajectory starting points and longitudinal fluctuation. Further, we deploy the index to examine the level of similarity between the clustering results of each pair of methods. The process is repeated for both the linear and quadratic dataset.
Application to real data set
Here, only ak-medoids and k-medoids are deployed on the police-recorded property crime data at Output Area level in Birmingham. As demonstrated later, this decision was made due to the similarity in performance of k-medoids and k-means using simulated data. The deployment of ak-medoids and k-medoids on police-recorded crime data permits an assessment of performance in a situation where the underlying latent clusters and their characteristics are unknown. We deploy both methods on the relative crime exposure variable outlined earlier and report findings using both this relative measure and the absolute property crime rate. We determine the optimal cluster solution of each method using the Average Silhouette width index [50].
To support the systematic comparison of clustering solutions, the results of these analytical steps will be visualized and presented alongside a descriptive table detailing the size of each cluster, the percentage of trajectories which have positive or negative slopes and a classification of whether the cluster is ‘decreasing’, ‘increasing’ or ‘stable’ for each method, similar to existing research [4, 5]. The cluster solutions for each are then plotted as a proportion of total crime to examine the contribution of each cluster to the crime drop, a technique used in recent research [21]. Maps visualizing the spatial patterning of cluster solutions are also reported for context and further comparison.
Results
The findings are presented in two parts, reflecting the analytical strategy.
Comparison of ak-medoids, k-medoids and k-means using simulated data
The performance of ak-medoids, k-medoids and k-means with respect to the pre-defined (known) solution is shown in Fig. 3a and b, representing the linear and quadratic datasets, respectively. The aRand scores are plotted with a smoothed line of best fit, a representation of clustering agreement against the variability, \(\beta\) (i.e., the degree of individual variations within each group). It is evident that the three methods perform well when the clusters are characterized by low variation (at \(\beta =1\)), with scores between 0.7–0.9. This suggests that the methods are largely successful in identifying the underlying increasing, decreasing and stable clusters, though ak-medoids performs better. As the individual variations increase, however, the performance of the three methods decline, with that of k-medoids and k-means declining at a faster rate compared to ak-medoids. At a variability of 3.7, the performance of both k-medoids and k-means reduces to a random level, whilst ak-medoids is still able to attain a moderate level of accuracy through achieving aRand scores of between 0.42 and 0.45 for both linear and quadratic data sets. The performance of k-medoids and k-means are similar, and the randomness of their cluster solutions at high variability (> 3.7) demonstrates their sensitivity to the distribution of the starting points and subsequent volatility of trajectories. This sensitivity results in trajectories within the same group holding dissimilar long-term directional trends, contrary to a fundamental aim in crime concentration research [4].
The next step is to examine the similarities between methods, holding k-means as the baseline method for comparison. The aRand scores at all variabilities is computed in similar fashion as above. The result is shown in Fig. 3c and d, representing the linear and quadratic datasets, respectively. At low variations (\(\beta <2\)) in which each method produces relatively accurate results (from Fig. 3a and b), the performance of k-medoids is found to be very similar to k-means. This is evidenced by the slowly falling aRand scores which start from 0.80 at the \(\beta =0.02\) (the lowest variability) to drop to 0.62 at \(\beta =2\). At \(\beta\) > 3.7, at which point the actual performances of both methods with respect to the true solution becomes random (see Fig. 3a and b), the aRand scores remain high and steady, indicating two random solutions broadly matching each other in terms of accuracy. In contrast, the performance of ak-medoids with respect to k-means is found to dissipate rapidly, dropping to aRand score of 0.32 at \(\beta =2\). This demonstrates the distinctness of the two methods. At \(\beta\) > 3.7, when the actual performance of k-means has become random, ak-medoids remains relatively accurate.
The accuracy of each method can be described for specific values of the variability. For instance, with a reasonable amount of individual variation (\(\beta =2\)) ak-medoids correctly identifies 98% of observations as belonging to cluster A (decreasing). In contrast, k-medoids and k-means correctly identifies only 32% and 34%, respectively, of observations as belonging to cluster A, with the remaining being erroneously assigned to cluster B (stable). Largely due to this misassignment to cluster B, k-medoids and k-means only identifies 78% and 72%, respectively, of observations in cluster B correctly, whereas ak-medoids manages to achieve an accuracy level of 90%. For cluster C (increasing), both ak-medoids and k-means achieve 93% accuracy, while k-medoids only achieves 84% accuracy. These findings are comparable when quadratic clusters are used. Detailed findings of this descriptive analysis are presented in the Appendix. In overview, and through the use of simulated data, the performance of k-medoids and k-means are very similar, but are distinct from that of ak-medoids when seeking to determine the long-term directional similarity of clusters. We now proceed to deploy only ak-medoids and k-medoids on the real police-recorded crime data with unknown latent clusters.
Comparison of ak-medoids and k-medoids on real data set
For the police-recorded property crime data in Birmingham, the Average Silhouette score criterion suggested a five-cluster solution as optimal for k-medoids, and a five-cluster solution as optimal for ak-medoids. These results are presented in Fig. 4, showing individual trajectories belonging to each group with their respective mean trajectory. Clusters representing a high proportion of total crime are indicated as ‘‘high’ clusters, whilst the remaining clusters are indicated as ‘low’ clusters, with matching Y-axis for comparison. A slope classification threshold was deployed to categorise mean relative trajectories as decreasing, increasing and stable, in the spirit of existing research examining micro-place exposure to an absolute measure of crime [4, 5, 27]. Clusters were deemed stable if the group slope deviated less than ± 25% from the maximum slope of the citywide trend line, permitting some variability around the reference point. The slope classification and descriptive statistics for each cluster solution are reported in Table 1.
Table 1 reveals that k-medoids generates similar cluster sizes to ak-medoids. This might be attributed to the fact that they both attempt to minimize the impact of outliers. However, it is clear from Fig. 3, which visually represents the clusters, that the character and quality of cluster solutions for each method are remarkably distinct.
Of the five clusters generated by k-medoids, cluster A and B are decreasing, while the remaining three, comprising 92.6% of all trajectories, are considered stable. The mean trajectory of this cluster A shows undulating change over time. The cluster comprising high magnitude trajectories, numbering 33 in total, experienced a steady decreasing inequality trajectory from 2001/02 to 2018/19, then increased rapidly to plateau in the last two years. The mean proportion of total property crime occurring in each Output Area in cluster A was approximately 0.3%. Cluster B is a slowly decreasing cluster with the mean proportion of total crime occurring in Output Areas being approximately 0.05%. We now provide a brief description of the stable clusters. Cluster C (green) contains Output Areas (N = 813) experiencing a lower average exposure to property crime of 0.011%. Cluster D (dark purple), comprising 836 Output Areas has an average exposure to property crime of 0.008%. Lastly, Cluster E (orange), the largest cluster (N = 1334), has a mean proportion of approximately 0.004%.
We turn now to consider the ak-medoids cluster solution. Cluster A (light red) experienced a sharp decreasing relative trajectory. In 2001/02, the mean proportion of total property crime for Output Areas in this cluster was found to be 0.6%, but by 2015/16 this had declined to 0.08%. The decline was more dramatic than those observed in the k-means decreasing clusters A and B (dark red and dark blue). Cluster B (khaki green), comprising 796 Output Areas, also experienced a decreasing relative trajectory, but much less steep in character (0.04% in 2001/02 and 0.03% in 2015/2016). Cluster C (teal) exhibited a stable relative trajectory. This was the largest group identified by the ak-medoid cluster solution (N = 1,428) but much smaller in size than the largest group identified by k-means. This group had an average exposure to property crime of 0.021%, which is comparable to 0.024% for the largest (stable) group of the k-means. Cluster D (light blue), comprising 819 Output Areas, exhibited an increasing relative trajectory, with the mean proportion of total property crime being 0.018% in 2001/02 rising to 0.033% in 2015/2015. It is interesting to note that Clusters C and D held similar relative exposure to property crime in the first year of the study, prior to adopting divergent trajectories. Finally, and in key distinction to the k-means cluster solution, ak-medoids identified a group characterised by a steep increasing relative trajectory. Cluster E (light purple), comprising 137 Output Areas, increased in relative exposure to property crime to more than double (from 0.067% to 0.17%) in the 15-year study period.
In overview, k-medoids and ak-medoids have delivered clearly distinct cluster solutions. K-medoids identified three stable clusters and two decreasing clusters, but no increasing cluster, whilst ak-medoids identified one stable cluster, two decreasing clusters and two increasing clusters. Moreover, the membership of the k-medoids and ak-medoids cluster solutions also exhibit variation. As might be expected, in the largest stable k-medoids and ak-medoids clusters, given that the ± 25% membership threshold permits some degree of variability, there are a mix of decreasing (positive) and increasing (negative) relative trajectories. Of keynote, however, are the membership profiles of the remaining k-medoids and ak-medoids clusters. Neither decreasing cluster identified by k-medoids was characterised by directional homogeneity, and neither were especially steep declines. Although the majority of Output Areas in these clusters had declining slopes, the composition was relatively mixed, with around 34.3% of Output Areas actually having positive trajectories. In contrast, the membership of all decreasing and increasing ak-medoids clusters were homogenous.
Comparing relative and absolute measures
The k-medoids and ak-medoids cluster solutions were deployed on the relative exposure measure. To highlight the differences between visualizing relative and absolute measures of crime, these same clusters are visualised in Fig. 5 using the absolute property crime rate measure.
All k-medoids clusters exhibited decreasing absolute property crime rate trajectories. Out of the four clusters which exhibited a stable relative exposure to crime, only cluster A (dark red) shows a dramatic decline in absolute crime exposure, while the three remaining clusters, i.e. clusters C (green), D (dark purple) and E (orange), are characterized by a steady decline in absolute crime exposure. With a combined size of 93.6% of all Output Areas in Birmingham, these clusters can be considered to have benefitted from the drop in police-recorded property crime at a similar rate to the city as a whole. Despite exhibiting a decreasing relative exposure to crime, Cluster B (dark blue) is also characterised by a steady decline in absolute property crime rates. However, the declining relative trend in this cluster indicates that its Output Areas benefitted disproportionately from the citywide drop in property crime (i.e. outstripping the citywide trend).
All k-medoids clusters exhibited decreasing absolute property crime rate trajectories. The three clusters which exhibited a stable relative exposure to crime are characterised by a steady decline in absolute crime exposure. Comprising 92.5% of all Output Areas in Birmingham, this cluster benefitted from the drop in police-recorded property crime at a similar rate to the city as a whole. In contrast, cluster A (dark red) is characterised by a sharp decline in absolute property crime rates. The declining relative trend in this cluster indicates that its Output Areas benefitted disproportionately from the citywide drop in property crime (i.e. outstripping the citywide trend).
The ak-medoids cluster solution, also expressed as absolute changes in the rate per 100 residents, delivers a similar story. All clusters benefitted from an absolute fall in their property crime rate during the study period. Thus, the rapidly decreasing cluster A holds similarly shaped relative and absolute measure trajectories, with a sharp fall evident at the commencement of the study period. Cluster B also experienced a decreasing exposure to property crime rate. Whilst the slope of decline was less severe than that of cluster A, the fall was spread over a number of years. The absolute decline in the property crime rates of clusters A and B were in excess of the citywide average. Cluster D’s increase in relative property crime exposure is reflected in its shallow decline in absolute property crime rates. Although Output Areas in this cluster benefitted from the crime drop in absolute terms, their decline was so immaterial that they lost out relative to the city as a whole. Cluster C, which held a stable relative trajectory, experienced a steadily decreasing absolute exposure to property crime. This group, representing approximately half of the sample of Output Areas included in the study, benefitted from the crime drop at a similar rate to that of the city as a whole, and is therefore comparable to k-medoids’ clusters C and D and E. Cluster E, which held an increasing relative trajectory, steadily increased throughout the study period, exhibited a decreasing absolute trajectory. This pattern was not identified by k-medoids.
The proportion of total property crime attributable to each k-medoids and ak-medoid cluster is visualized in Fig. 6. Had every cluster held similar experience (i.e. rate of decline) of the crime drop, then the proportion of total property crime that each cluster is exposed to would be the same at the commencement and end of the study period: the boundaries between clusters would be represented by horizontal lines across the X-axis. However, Fig. 6 confirms the existence of shifting inequalities in the exposure to crime during the property crime drop in Birmingham using both k-medoids and ak-medoids. Although, ak-medoids shows a stronger capability for revealing those shifting inequalities. This is evident by the share of total crime captured in each group at the start (2001/02) as compared to the end (2015/16) of the study period. The high decreasing group identified with ak-medoids (cluster A in light red) benefitted most from the crime drop. Having started with a large share of total crime 2001/02, accounting for 26% of all property crime, by 2015/16 these same Output Areas accounted for only 3.4% of all property crime in Birmingham. In contrast, the equivalent high decreasing cluster identified by k-medoids (cluster A in dark red) accounted for only 11% of all property crime in 2001/02 and 7% of all property crime in 2015/16. Whilst the larger cluster B (in dark blue) accounted for 30% of total property crime in 2001/02, this fell to 21% by 2015/16. Here, it should be noted that both methods identified clusters which contributed disproportionally to the crime drop, but groups with the most dramatic falls were generated by ak-medoids.
The spatial patterning of crime exposure at the micro areas
To understand the spatial character of the clusters identified by ak-medoids and k-medoids, we map the geographic distribution of their groups using hexograms [51] as shown in Fig. 7. Hexograms are utilized rather than the actual Output Area boundaries to help ensure anonymity whilst accurately conveying the spatial character (e.g. clustering) of units [52]. Figure 7a and b represents the results of k-medoids and ak-medoids, respectively, with the colour of each group matching those used in the representation of their respective group trajectories (e.g. Figure 4). We delineate (in black) those areas designated as the city centre, consisting of Output Areas with the highest number of commercial land uses. The rest of the city is predominantly suburban and residential.
From Fig. 7a and b, there is clear evidence of spatial patterning of clusters identified by each method. For k-medoids, the two high clusters, Cluster A (dark red) and Cluster B (dark blue) represent Output Areas found mostly in the city centre, while the three low clusters, Cluster C (in green), Cluster D (in dark purple), and Cluster E (in orange), represent Output Areas generally found in the suburbs. The distinction in the relative exposure to crime between the city centre and the suburbs is consistent with opportunity theories of crime [19, 53]. The elevated level of activity in the city centre and the high number of commercial outlets make it a lucrative (and plentiful) location for property crime victimization. Given the character of the k-medoids clusters outlined earlier, the clusters represent groups of communities largely characterized by distinct outright levels of exposure to property crime.
For ak-medoids, Cluster A (light red) which represents Output Areas with the most dramatic drop in the relative exposure to crime are also found to concentrate in the city centre, while Cluster E (in light blue), a steadily decreasing cluster is found to dominate the north-eastern part of the city. Conversely, both increasing clusters, D (in light blue) and E (in light purple), are mostly found in the southern parts of the city. The character of ak-medoids clusters, namely, Output Areas grouped by similarity in their long-term trajectories (rather than outright levels) in relative crime exposure, thus generate distinct spatial patterns compared to k-medoids. In particular, we can identify Output Areas characterized by a slow increase in relative crime exposure.
Discussion
The findings from the deployment of ak-medoids, k-medoids and k-means on simulated data highlight key distinctions between each method. Whilst the three methods successfully identified the three pre-defined clusters characterized by directional homogeneity with a reasonable degree of accuracy, ak-medoids was able to distinguish the known clusters more precisely. Further, the drop-off in performance as variability in the starting levels and longitudinal volatility increased was less marked for ak-medoids, which maintained a higher degree of precision. A one-on-one comparison between methods shows that k-medoids and k-means are very similar, but distinct from ak-medoids. The sensitivity of k-medoids and k-means to both starting levels and subsequent fluctuation inhibits their ability to accurately disentangle clusters characterized by their within-group directional homogeneity. Consequently, they were more likely to identify clusters that did not exist in the simulated data. This demonstration might, at least in part, explain the findings of previous research utilizing k-means, in which clusters appear to be harnessed to the starting level (intercepts) alone [4, 27]. This being said, the sensitivity of k-medoids and k-means to starting levels and short-term fluctuation is not necessarily problematic, depending on the objective of the study. However, given the focus of the crime concentrations literature on long-term stability and directional change, the findings from the simulated data analyses suggest that ak-medoids can deliver valuable insights that would remain hidden by the deployment of either k-medoids or k-means in isolation. The similarities between the performance of k-medoids and k-means then prompt us to focus on k-medoids and ak-medoids for the remaining parts of the analysis.
In one sense, the results generated using police-recorded property crime data using k-medoids and ak-medoids are comparable in nature, with both delivering evidence in accordance with existing research on the longitudinal stability of crime concentrations and trajectories at fine-grained spatial scales [4,5,6, 27]. A small number of Output Areas have been shown to hold a disproportionately large impact on the decline in police-recorded property crime in Birmingham (UK) between 2001/2002 and 2015/2016, whilst the majority of Output Areas can be characterized as having exhibited gradual and moderate change over time, in alignment with the citywide trend. On the other hand, there are key distinctions in the consistency and scale of clusters generated by each method. Whether these issues matter will rest upon the methodological, theoretical and empirical ambition of the research. We now deal with each of these issues in turn.
Beyond the observation that the overarching split of the qualities (decreasing, stable, increasing) of the ak-medoids and k-medoids cluster solutions are different, it is in the consistency of their cluster membership that more significant distinctions emerge. Four of the ak-medoids clusters were identified as either increasing or decreasing, and comprised homogenous relative trajectories. In contrast, k-medoids identified two decreasing clusters, neither comprising of homogenous relative trajectories. Given that a key aim of longitudinal cluster analysis in the crime concentration literature has been to identify meaningful subgroups, based on their within-group similarity [54], and the interest in long-term trend classifications in crime concentration literature [4], these distinctions are noteworthy. That the four increasing or decreasing ak-medoids clusters comprised homogenous relative trajectories opens prospect of advancing theoretical consideration and empirical assessment of the place-based drivers of, in this case, the long-term drop in recorded property crime in Birmingham. The potential value of such an exercise is informed, at least in part, by the scale and contribution of the clusters to the crime drop.
The ak-medoids and k-medoids cluster solutions identified two decreasing clusters, but their scale differed markedly. A total of just 240 Output Areas (from a total of 3,223) comprised the membership of the two decreasing k-medoids clusters (with the remaining 2,983 Output Areas being classified as stable), whilst 839 Output Areas comprised the membership of the ak-medoids decreasing clusters. One of the k-medoids decreasing clusters, whose relative trajectory was characterized by some undulation, only contained 33 Output Areas (1% of the sample). Here, it is plausible that disparities in the scale of clusters impact on the stability of their trajectories, given that small clusters are more sensitive to each observation’s contribution to the cluster. Distinctions in scale further manifest in the change through time in the proportion of total property crime in Birmingham attributable to these clusters. Here, the two decreasing k-medoids clusters experienced a fall from 46.4 to 34.3% in the proportion of total property crime, a drop of 12.1%. In contrast, the two decreasing ak-medoids clusters experienced a fall from 55.4 to 24.7% in the proportion of property crime experienced, a drop of 30.7%. Not only did the average Output Area in the decreasing k-medoids clusters experience a less intense drop in their relative exposure to crime compared to those in the decreasing ak-medoids clusters, but the decreasing ak-medoids clusters collectively experienced a greater drop in their proportional contribution to total property crime. It is also noteworthy that ak-medoids was capable of disentangling clusters with a similar initial exposure to crime, but which diverge through time (Clusters C and D). This is consistent with the findings of the simulated data analysis, which suggested that k-means is sensitive to delineations apparent at the first time point.
Further insight and geographic context was given to the clusters generated by ak-medoids and k-medoids by visualizing their spatial patterning. Both methods created clusters with distinct geographic patterns, largely characterized by the clustering of Output Areas with similar trajectories. k-medoids clusters revealed the disparity in crime levels between the city centre and the suburbs. This can largely be attributed to long-standing differences in the opportunity structure of city centres and residential areas, rather than change over time. However, k-medoids (like k-means) is well-suited to unpicking short-term fluctuations in crime brought about by rapid changes in opportunity structures (e.g. target hardening, directed police patrols). In contrast, ak-medoids clusters continued to demonstrate some disparity between the city centre and the suburbs, but by design, the character of the ak-medoids groupings showcased long-term processes consistent with similarly glacial urban processes, consistent with suburbanization and social disorganization of residential areas.
Turning to consider the application of these findings, should such an assessment determine that homogenous trajectories are informed by common factors (e.g. lack of capable guardians in the city centre), a crime reduction strategy whether motivated by efficiency or legitimacy should focus upon the increasing clusters. In this scenario, findings suggest that k-medoids would be ill-suited for marking areas for intervention, since clusters lacked an increasing classification, whereas ak-medoids would prove invaluable, having identified a large (N = 956) increasing cluster. That said, retrospective evaluations of short-term interventions, such as hotspot policing strategies, would be best carried out using k-medoids, due to its ability to unpick volatility.
The development of ak-medoids was informed by theoretical and empirical recognition of the typical stability and slowly changing character of place-based crime profiles, and the interest in long-term directional change. The findings reported, based on an assessment of both simulated and police-recorded property crime data, demonstrate that ak-medoids can provide valuable insights in the study of long-term exposure to crime across micro areas. These insights are not capable of being discerned using k-medoids (or k-means), which appears sensitive to variations in the starting levels of trajectories and their short-term fluctuation. But, this does not render k-medoids (or k-means) redundant. Rather, unrestricted by linear functional forms, the identification of small outlier groupings characterized by short-term volatility in crime trajectories can be of substantive theoretical interest and policy relevance [18]. In these terms, the selection of ak-medoids or k-medoids (or k-means) as the preferred methodology requires being informed by the research problem under investigation. Indeed, we can envision grounds in which both might be applied, particularly in the endeavour to disentangle and describe both short and long-term exposure to crime across micro places. It remains to be evaluated whether ak-medoids holds distinction in its outcomes to group-based trajectory modelling (GBTM). Although ak-medoids, as an adaptation of k-medoids, holds a number of benefits over GBTM, such as computational efficiency, it is currently only capable of clustering around linear slopes. Studies deploying GBTM have tended to report better model fits using more complex, non-linear polynomials, although there are some exceptions [27]. The degree to which one would expect linear or non-linear trends may be dependent on the crime type and context-specific factors in the study region, and we would encourage future studies to explore more complex non-linear trends using an implementation of ak-medoids.
Conclusion
This paper has sought to make a substantive methodological contribution in support of research seeking to explore the longitudinal stability of crime in micro places. It has introduced the first implementation of k-medoids for the longitudinal clustering of crime, as well as a novel longitudinal clustering technique, termed ‘anchored k-medoids’ (ak-medoids). A variant of k-medoids, ak-medoids has been specifically designed to identify cluster solutions based on the long-term directional change of crime trajectories of micro places. In support of the wider application of this technique, the paper also provides access to an R package user manual to enable standardized replication of this technique in future research. The value of this methodological contribution is assessed through systematic comparison of the cluster solutions derived by ak-medoids, k-medoids and k-means (the existing approach) using both simulated and real-life police-recorded data. The empirical findings resonate with existing research that finds the crime profiles of the majority of micro places to remain stable through time, with a small proportion of such places evidenced to hold a disproportionately large impact on citywide crime trends. That said, ak-medoids cluster solutions demonstrate higher in-group consistency and are of a greater scale than those generated by k-medoids (or k-means) cluster solutions. Ak-medoids also proves more adept in identifying pre-defined clusters in synthetic data, for which the within-group characteristic is one of directional homogeneity. Evidently, ak-medoids and k-medoids (or k-means) hold differing merits. To gain a comprehensive picture of the stability of crime concentrations across micro places, we recommend the use of ak-medoids and k-medoids (or k-means) in concert. We contend that these findings open prospect of theoretical development in the field as well as policy advance centred on questions of the efficiency, effectiveness and legitimacy of crime prevention interventions.
Notes
Converting crime counts to rates (i.e. count divided by the population) eliminates the bias due to the variances in population distribution over time.
These group sizes were chosen to reflect common findings in existing research, namely, that most micro places are characterised by a flat, stable relative trend. However, it is worth emphasising that findings were insensitive to the grouping balances selected.
A number of Output Areas were identified as potential outliers based on high values of property crime rates. For the purposes of this demonstration these OA were retained, and as such, analysis was undertaken on all 3,223 OA in Birmingham.
References
Aebi, M.F., & Linde, A. (2016). Long-term trends in crime: continuity and change. In P. Knepper, & A. Johansen (Eds.) The Oxford Handbook of the History of Crime and Criminal Justice, (pp. 57–87). Oxford University Press.
Tseloni, A., Mailley, J., Farrell, G., & Tilley, N. (2010). Exploring the international decline in crime rates. European Journal of Criminology, 7(5), 375–394.
Farrell, G., Tilley, N., Tseloni, A., & Mailley, J. (2010). Explaining and sustaining the crime drop: clarifying the role of opportunity-related theories. Crime Prevention and Community Safety, 12(1), 24–41.
Andresen, M. A., Curman, A. S., & Linning, S. J. (2017). The trajectories of crime at places: understanding the patterns of disaggregated crime types. Journal of Quantitative Criminology, 33(3), 427–449.
Weisburd, D., Bushway, S., Lum, C., & Yang, S. (2004). Trajectories of crime at places: a longitudinal study of street segments in the city of Seattle. Criminology, 42(2), 283–322.
Groff, E., Weisburd, D., & Morris, N. (2009). Where the action is at places: examining Spatio-Temporal patterns of juvenile crime at places using trajectory analysis and GIS. In D. Weisburd, W. Bernasco, & G. J. N. Bruinsma (Eds.), Putting crime in its place: Units of analysis in geographic criminology (pp. 61–87). New York: Springer.
Eze, J. I., Innocent, G. T., Adam, K., Huntley, S., & Gunn, G. J. (2019). Exploring the longitudinal dynamics of herd BVD antibody test results using model-based clustering. Scientific Reports, 9(11353), 1–10.
Adepeju, M., Langton, S., & Bannister, J. (2020). Akmedoids R package for generating directionally-homogeneous clusters of longitudinal datasets. Journal of Open Source Software, 5(56), 2379.
Shaw, C. R., & McKay, H. D. (1942). Juvenile delinquency and urban areas. Chicago: University of Chicago Press.
Kornhauser, R. R. (1978). Social sources of delinquency: an appraisal of analytic models. Chicago: University of Chicago Press.
Bursik, R. J., Jr. (1986). Ecological stability and the dynamics of delinquency. Crime Justice, 8, 35–66.
Schmidt, C. F. (1960). Urban crime areas. Part II. American Sociological Review, 1, 527–542.
Taylor, R. B. (1999). Crime, grime, fear, and decline: A longitudinal look. Office of Justice Programs, National Institute of Justice: US Department of Justice.
Bursik, R. J., Jr., & Webb, J. (1982). Community change and patterns of delinquency. American Journal of Sociology, 88(1), 24–42.
Schuerman, L., & Kobrin, S. (1986). Community careers in crime. Crime Justice, 8, 67–100.
Bottoms, A. E., & Wiles, P. (1986). Housing tenure and residential community crime careers in Britain. Crime Justice, 8, 101–162.
Nagin, D. S., & Land, K. C. (1993). Age, criminal careers and population heterogeneity: specification and estimation of a nonparametric, mixed Poisson model. Criminology, 31(3), 327–362.
Griffiths, E., & Chavez, J. M. (2004). Communities, street guns and homicide trajectories in Chicago, 1980–1995: merging methods for examining homicide trends across space and time. Criminology, 42(4), 941–978.
Cohen, L. E., & Felson, M. (1979). Social change and crime rate trends: a routine activities approach. American Sociology Review, 44(4), 588–608.
Weisburd, D., Morris, N. A., & Groff, E. R. (2009). Hot spots of juvenile crime: a longitudinal study of arrest incidents at street segments in Seattle. Washington. Journal of Quantitative Criminology, 25(4), 443–467.
Wheeler, A. P., Worden, R. E., & McLean, S. J. (2016). Replicating group-based trajectory models of crime at microplaces in Albany, NY. Journal of Quantitative Criminology, 32(4), 589–612.
Hibdon, J., Telep, C. W., & Groff, E. R. (2017). The concentration and stability of drug activity in Seattle, Washington, using police and emergency medical services data. Journal of Quantitative Criminology, 33(3), 497–517.
Favarin, S. (2018). This must be the place (to commit a crime). Testing the law of crime concentration in Milan, Italy. European Journal of Criminology, 15(6). 702–729.
Chavez, J. M., & Griffiths, E. (2009). Neighborhood dynamics of urban violence: Understanding the immigration connection. Homicide Studies, 13(3), 261–273.
Yang, S. M. (2010). Assessing the spatial–temporal relationship between disorder and violence. Journal of Quantitative Criminology, 26, 139–163.
Bannister, J., Bates, E., & Kearns, A. (2017). Local variance in the crime drop: A longitudinal study of neighbourhoods in greater Glasgow, Scotland. British Journal of Criminology, 58(1), 177–199.
Curman, A. S. N., Andresen, M. A., & Brantingham, P. J. (2015). Crime and place: a longitudinal examination of street segment patterns in Vancouver, BC. Journal of Quantitative Criminology, 31(1), 127–147.
Genolini, C., & Falissard, B. (2011). KmL: A package to cluster longitudinal data. Computer Methods and Programs in Biomedicine, 104(3), e112–e121.
Wang, J., & Su, X. (2011). An improved K-Means clustering algorithm. In 3rd International Conference on Communication Software and Networks IEEE (pp. 44–46).
Bradley, P.S., & Fayyad, U.M. (1998). Refining initial points for k-means clustering. In Proc International Conference on Machine Learning, 9 (pp. 91–99).
Su, T., & Dy, J. (2004). A deterministic method for initializing k-means clustering. In 16th IEEE International Conference on Tools with Artificial Intelligence IEEE (pp. 784–786).
Aldahdooh, R. T., & Ashour, W. M. (2013). DIMK-means: distance-based initialization method for K-means clustering algorithm. International Journal of Intelligent Systems and Applications, 2, 41–51.
Rousseeuw, P. J., & Kaufman, L. (1990). Finding groups in data (p. 1). Hoboken: Wiley Online Library.
Wierzchoń, S. T., & Kłopotek, M. (2018). Modern algorithms of cluster analysis. Berlin, Germany: Springer.
Park, H. S., & Jun, C. H. (2009). A simple and fast algorithm for K-medoids clustering. Expert systems with applications, 36(2), 3336–3341.
Heggeseth, B. (2013). Longitudinal Cluster Analysis with Applications to Growth Trajectories. UC Berkeley.
Khan, S. S., & Ahmad, A. (2004). Cluster center initialization algorithm for k-means clustering. Pattern Recognition Letters, 25(11), 1293–1302.
Steinley, D., & Brusco, M. J. (2007). Initializing k-means batch clustering: a critical evaluation of several techniques. Journal of Classification, 24(1), 99–121.
Genolini, C., Alacoque, X., Sentenac, M., & Arnaud, C. (2015). kml and kml3d: R Packages to Cluster Longitudinal Data. Journal of Statistical Software, 65(4), 1–34.
Skardhamar, T. (2010). Distinguishing facts and artifacts in group-based modeling. Criminology, 48(1), 295–320.
Genolini, C., Ecochard, R., Benghezal, M., Driss, T., Andrieu, S., & Subtil, F. (2016). kmlShape: an efficient method to cluster longitudinal data (time-series) according to their shapes. Plos one, 11(6).
Wessendorf, S. (2019). Migrant belonging, social location and the neighbourhood: Recent migrants in East London and Birmingham. Urban Studies, 56(1), 131–146.
Vandeviver, C., & Steenbeek, W. (2019). The (in) stability of residential burglary patterns on street segments: The case of Antwerp, Belgium 2005–2016. Journal of Quantitative Criminology, 35(1), 111–133.
Steenbeek, W., & Weisburd, D. (2016). Where the Action is in Crime? An Examination of Variability of Crime Across Different Spatial Units in The Hague, 2001–2009. Journal of Quantitative Criminology, 32(3), 449–469.
Schnell, C., Braga, A. A., & Piza, E. L. (2017). The influence of community areas, neighborhood clusters, and street segments on the spatial variability of violent crime in Chicago. Journal of Quantitative Criminology, 33(3), 469–496.
Martin, D. (2002). Geography for the 2001 Census in England and Wales. Population Trends, 108(7), 7–15.
Cockings, S., Harfoot, A., Martin, D., & Hornby, D. (2011). Maintaining existing zoning systems using automated zone-design techniques: methods for creating the 2011 Census output geographies for England and Wales. Environment and Planning A, 43, 2399–2418.
Andresen, M. A., & Linning, S. J. (2012). The (in) appropriateness of aggregating across crime types. Applied Geography, 35(1–2), 275–282.
Hubert, L., & Arabie, P. (1985). Comparing partitions. Journal of Classification, 2(1), 193–218.
Rousseeuw, P. J. (1987). Silhouettes: a graphical aid to the interpretation and validation of cluster analysis. Journal of Computational and Applied Mathematics, 20, 53–65.
Harris, R., Charlton, M., & Brunsdon, C. (2018). Mapping the changing residential geography of White British secondary school children in England using visually balanced cartograms and hexograms. Journal of Maps, 14(1), 65–72.
Langton, S. H., & Solymosi, R. (2019). Cartograms, hexograms and regular grids: Minimising misrepresentation in spatial data visualisations (p. 2399808319873923). Environment and Planning B: Urban Analytics and City Science.
Cornish, D.B., & Clarke, R.V. (eds. 2014). The reasoning criminal: Rational choice perspectives on offending. Transaction Publishers.
Nagin, D.S. (2005). Group-based modeling of development. Harvard University Press.
Acknowledgements
We gratefully acknowledge the Economic and Social Research Council (ESRC), who funded the Understanding Inequalities project (Grant Reference ES/P009301/1) through which this research was conducted.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
None to declare.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary Information
Below is the link to the electronic supplementary material.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Adepeju, M., Langton, S. & Bannister, J. Anchored k-medoids: a novel adaptation of k-medoids further refined to measure long-term instability in the exposure to crime. J Comput Soc Sc 4, 655–680 (2021). https://doi.org/10.1007/s42001-021-00103-1
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s42001-021-00103-1