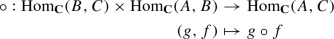Abstract
We formalize the notion of the dependency structure of a collection of multiple signals, relevant from the perspective of information theory, artificial intelligence, neuroscience, complex systems and other related fields. We model multiple signals by commutative diagrams of probability spaces with measure-preserving maps between some of them. We introduce the asymptotic entropy (pseudo-)distance between diagrams, expressing how much two diagrams differ from an information-processing perspective. If the distance vanishes, we say that two diagrams are asymptotically equivalent. In this context, we prove an asymptotic equipartition property: any sequence of tensor powers of a diagram is asymptotically equivalent to a sequence of homogeneous diagrams. This sequence of homogeneous diagrams expresses the relevant dependency structure.
Similar content being viewed by others
1 Introduction
According to usual modeling assumptions in information theory, a discrete signal is cut into a collection of long words of length n, whose particular representation is irrelevant (each word is considered as an atomic object without inner structure), and small errors are allowed. If the signal is modeled as a sequence of independently, identically distributed random variables, there is only one relevant variable determining the signal, namely the entropy: the exponential growth rate of the number of typical words of length n. We elaborate on this point of view below in Sect. 1.1.
Similarly, if one probes a measure-preserving dynamical system at a discrete sequence of times with a finite-output measurement device and counts measurement trajectories of length n, while discarding rarely appearing, untypical ones, one arrives at the notion of entropy of a system-measurement pair. Entropy, in this case, is the exponential growth rate of the number of typical trajectories with respect to the length n. The supremum of such entropies over varying measurement devices is the Kolmogorov–Sinai entropy of a measure-preserving dynamical system. According to a theorem of Ornstein [17], the entropy is the only invariant of the isomorphism classes of certain types of dynamical systems (Bernoulli shifts).
In information theory, but also in artificial intelligence, neuroscience and the theory of complex systems, one usually studies multiple signals at once. Likewise, a dynamical system is often observed with multiple measurement devices simultaneously. In these cases, one assumes in addition that the relations between the signals are essential. In this article we characterize, under these modeling assumptions, the relevant invariants in multiple signals, that are obtained as i.i.d. samples from random variables. We explain this in more detail in Sects. 1.3 and 1.4.
We will now explain our point of view on entropy for a single signal, that is, for a single probability space.
1.1 Probability spaces and their entropy
First we consider a finite probability space \(X = (S, p)\), where S is a finite set, and p is a probability measure on S. For simplicity, assume for now that the measure p has full support. Next, we consider the, so-called, Bernoulli sequence of probability spaces
where \(S^n\) denotes the n-fold Cartesian product of S, and \(p^{\otimes n}\) is the n-fold product measure.
The entropy of X is the exponential growth rate of the observable cardinality of tensor powers of X. The observable cardinality, loosely speaking, is the cardinality of the set \(X^{n}\) after the biggest possible subset of small measure has been removed. It turns out that the observable cardinality of \(X^{n}\) might be much smaller than \(|S|^{n}\), the cardinality of the whole of \(X^{n}\), in the following sense.
The Asymptotic Equipartition Property states that for every \(\varepsilon >0\) and \(n\gg 0\) one can find a, so-called, typical subset \(A^{(n)}_{\varepsilon }\subset S^{n}\), defined as a subset that takes up almost all of the mass of \(X^{n}\) and the probability distribution on \(A^{(n)}_{\varepsilon }\) is almost uniform on the normalized logarithmic scale, as stated in the following theorem, see [8].
Theorem 1.1
(Asymptotic equipartition property) Suppose \(X=(S,p)\) is a finite probability space. Then, for every \(\varepsilon >0\) and every \(n\gg 0\) there exists a subset \(A^{(n)}_{\varepsilon }\subset X^{n}\) such that
-
1.
\(p^{\otimes n}(A^{(n)}_{\varepsilon })> 1-\varepsilon \)
-
2.
For any \(a,a'\in A^{(n)}_{\varepsilon }\) holds
$$\begin{aligned} \left| \frac{\ln p^{\otimes n}(a)}{n} - \frac{\ln p^{\otimes n}(a')}{n} \right| < \varepsilon . \end{aligned}$$
Moreover, if \(A^{(n)}_{\varepsilon }\) and \(B^{(n)}_{\varepsilon }\) are two subsets of \(X^{n}\) satisfying the two conditions above, then their cardinalities satisfy
The cardinality \(|A^{(n)}_{\varepsilon }|\) may be much smaller than \(|S|^{n}\), but it will still grow exponentially with n. Even though there are generally many choices for such a set \(A^{(n)}_\varepsilon \), in view of the property (1) in Theorem 1.1, the exponential growth rate with respect to n is well-defined up to \(2\varepsilon \).
The limit of the growth rate as \(\varepsilon {\mathop {\rightarrow }\limits ^{}}0+\) is called the entropy of X
This point of view on entropy goes back to the original idea of Boltzmann [3, 4], according to which entropy is the logarithm of the number of equiprobable states, that a system, comprised of many identical weakly interacting subsystems, may take on. It was further developed and applied to Information Theory by Shannon [19], and in the context of dynamical systems by Kolmogorov and Sinai [12, 13, 21].
Entropy is especially easy to evaluate if the space is uniform, since for any finite probability space with the uniform distribution the observable cardinality is equal to the cardinality of the whole space and therefore
For non-uniform spaces, the entropy can be evaluated by the well-known formula
1.2 Asymptotic equivalence
If \(X_1\) and \(X_2\) are probability spaces with the same entropy, there is a bijection between their typical sets of sequences of length n, for the plain reason that they can be chosen to have the same cardinality. It means that up to a change of code (of representation) and an error that becomes small as n gets large, the spaces \(X_1^n\) and \(X_2^n\) are equivalent. In the same sense, both \(X_1^n\) and \(X_2^n\) are equivalent to a uniform measure space with cardinality \({\mathbf{e}}^{{n}{\textsf {Ent}}{(X_i)}}\).
In [10], Gromov formalized this concept of asymptotic equivalence. With his definition, two Bernoulli sequences of measure spaces \(X_1^n\) and \(X_2^n\) are asymptotically equivalent if there exists an “almost-measure-preserving” “almost-bijection”

Even though we were greatly influenced by ideas in [10], we found that Gromov’s definition does not extend easily to situations in which multiple signals are processed at the same time, or when a dynamical system is probed with several measurement devices at once.
1.3 Diagrams of probability spaces
We model multiple signals by diagrams of probability spaces. By a diagram of probability spaces we mean a commutative diagram of probability spaces and measure-preserving maps between some of them. We will give a precise definition in Sect. 2.4, but will now consider particular examples of diagrams called two-fans.
A two-fan
is a triple of probability spaces \(X = (\underline{X}, p_X), Y = (\underline{Y}, p_Y)\) and \(U = (\underline{U}, p_U)\), and two measure-preserving maps \(\pi _X\) and \(\pi _Y\). We will restrict ourselves for now to the case in which the underlying set of U is the Cartesian product of the underlying sets of X and Y, \(\underline{U} = \underline{X} \times \underline{Y}\), and \(\pi _X\) and \(\pi _Y\) are the ordinary projections. Such a situation arises, for example, when a complex dynamical system, such as a living cell or a brain, is observed via two measuring devices.
Generalizing from the case of single signals, we might want to say that two-fans
are asymptotically equivalent if for large n there exist almost measure-preserving, almost-bijections

Without additional assumptions, asymptotic equivalence classes for two-fans would be completely determined by the entropies of the constituent spaces.
However, such an asymptotic equivalence relation would be too coarse. Consider the three examples of two-fans are shown in Fig. 1, which is to be interpreted in the following way. Each of the spaces \(X_{i}\) and \(Y_{i}\), \(i=1,2,3\), have cardinality six and a uniform distribution, where the weight of each atom is \(\frac{1}{6}\). The spaces \(U_{i}\) have cardinality 12 and the distribution is also uniform with all weights being \(\frac{1}{12}\). The support of the measure on \(U_{i}\)’s is colored grey on the pictures. The maps from \(U_{i}\) to \(X_{i}\) and \(Y_{i}\) are coordinate projections.
In view of Eq. (3) we have for each \(i=1,2,3\),
However, common information-processing techniques can still differentiate between the two-fans, by calculating solutions to information-optimization problems. This observation is sometimes expressed by saying that mutual information does not capture the full dependency structure that is relevant from an information-processing perspective. Information-optimization problems play an important role in information theory [25], causal inference [18], artificial intelligence [23], information decomposition [5], robotics [1], and neuroscience [9].
The additional assumption that the relations between the signals is relevant and should be preserved by the asymptotic equivalence results in the requirement that the following diagram commutes

However, with this generalization of an asymptotic equivalence to diagrams, we were not able to prove a corresponding Asymptotic Equipartition Property or even to prove the transitivity of the relation.
1.4 The entropy distances and asymptotic equivalence for diagrams
Instead of finding an almost measure-preserving bijection between large parts of the two spaces, we consider a stochastic coupling (transportation plan, joint distribution) between a pair of spaces and measure its deviation from being an isomorphism of probability spaces (a measure-preserving bijection). Such a measure of deviation from being an isomorphism then leads to the notion of intrinsic entropy distance, and its stable version—the asymptotic entropy distance, as explained in Sect. 3. We say two sequences of diagrams are asymptotically equivalent if the asymptotic entropy distance between them vanishes.
The intrinsic entropy distance is an intrinsic version of a distance between random variables going by many different names, such as entropy distance, shared information distance and variation of information. It was reinvented many times by different people, among them Shannon [20], Kolmogorov, Sinai and Rokhlin. It appears in the proof of the theorem about generating partitions for ergodic systems by Kolmogorov and Sinai, see for example [22].
The intrinsic version of the entropy distance between probability spaces was introduced by Kovacevic et al. [14] and by Vidyasagar [24]. They showed that the involved minimization problem is NP-hard. Methods to find approximate solutions are discussed in [6, 11].
1.5 Asymptotic equipartition property
With the notion of asymptotic equivalence induced by the asymptotic entropy distance, we can prove an asymptotic equipartition property for diagrams. Whereas the asymptotic equipartition property for single probability spaces states that high tensor powers of probability spaces can be approximated by uniform measure spaces, the Asymptotic Equipartition Property Theorem for diagrams, Theorem 6.1, states that sequences of successive tensor powers of a diagram can be approximated in the asymptotic entropy distance by a sequence of homogeneous diagrams.
Homogeneous diagrams have the property that the symmetry group acts transitively on the support of the measures of the constituent spaces. Two-fans shown on Fig. 1 are particular examples of homogeneous diagrams.
Homogeneous probability spaces are just uniform probability spaces, while homogeneous diagrams are, unlike homogeneous probability spaces, rather complex objects. Nonetheless, they seem to be simpler than arbitrary diagrams of probability spaces for the types of problems that we would like to address.
In a subsequent article we show that the optimal values in Information-Optimization problems only depend on the asymptotic class of a diagram and that they are continuous with respect to the asymptotic entropy distance; in many cases, the optimizers are continuous as well. The Asymptotic Equipartition Property implies that for the purposes of calculating optimal values and approximate optimizers, one only needs to consider homogeneous diagrams and this can greatly simplify computations.
Summarizing, the Asymptotic Equipartition Property and the continuity of Information-Optimization problems are important justifications for the choice of asymptotic equivalence relation and the introduction of the intrinsic and asymptotic Kolmogorov–Sinai distances.
1.6 Definitions and results in random variable context
In this article, we use the language of probability spaces and their commutative diagrams rather than the language of random variables, because we often encounter situations in which their joint distributions are not defined, are variable, or even do not exist.
Some relations between the probability spaces can be easily represented by commutative diagrams of probability spaces, such as by a diamond diagram, Sect. 2.5.5, while the description with random variables is complex and not easily interpretable. The diagrams also provide a geometric overview of various entropy identities and inequalities.
Since the language of random variables will be more familiar to many readers, we now present our main result in these terms.
For random variables \(\textsf {X}, \textsf {Y}, \textsf {Z}\) etc., we denote by \(\underline{X}, \underline{Y}, \underline{Z}\) the target sets, and by X, Y, Z the probability spaces with the induced distributions.
In general, there is a relation between k-tuples of random variables and diagrams of a certain type, involving a space for every subset \(I \subset \{1, \dots , k\}\).
For example, a pair of random variables \(\textsf {X}, \textsf {Y}\) (defined on the same probability space) gives rise to a two-fan,
where X, Y and \(X\times Y\) are the target spaces of the random variables \(\textsf {X}\), \(\textsf {Y}\) and \((\textsf {X},\textsf {Y})\) endowed with their respective laws (i.e. the pushforward of the probability measure).
However, not every type of diagram corresponds to a tuple of random variables.
The entropy distance between two k-tuples \(\textsf {X} = (\textsf {X}_1, \dots , \textsf {X}_k)\) and \(\textsf {Y} = (\textsf {Y}_1, \dots , \textsf {Y}_k)\) is defined by
A random k-tuple \((\textsf {H}_1, \dots , \textsf {H}_k)\) is called homogeneous if for every two elements
there exists a k-tuple of invertible maps \(f_1: {\underline{H}}_1 {\mathop {\rightarrow }\limits ^{}}{\underline{H}}_1, \dots , f_k:{\underline{H}}_k{\mathop {\rightarrow }\limits ^{}}{\underline{H}}_k\) such that \((f_1 \circ \textsf {H}_1, \dots , f_k \circ \textsf {H}_k)\) is equal to \((\textsf {H}_1, \dots , \textsf {H}_k)\) in distribution and \(f_i (h_i) = h_i'\). This condition is strictly stronger than the requirement that all the distributions are uniform.
Given n random k-tuples
we can naturally construct the k-tuple
defined by
It is difficult to formulate our main result, Theorem 6.1, in full generality using the language of random variables. However, the following theorem is an immediate corollary.
Theorem 1
Let \((\textsf {X}(i): i \in {\mathbb {N}})\) be a sequence of i.i.d. random tuples defined on a standard probability space.
Define random k-tuples \(\textsf {Y}(n)\) by
Then, there exists a sequence of homogeneous random k-tuples \(\textsf {H}(n) = ( \textsf {H}_1(n), \dots , \textsf {H}_k(n)),\) where \(\textsf {H}_i(n)\) takes values in \({\underline{X}}_i^n,\) such that
2 Category of probability spaces and diagrams
In this section we present the basic setup used throughout the article. We will start by explaining how probability spaces and (equivalence classes) of measure-preserving maps between them form a category. This point of view on probability theory was already advocated in [2, 10].
Category theory yields simple definitions of diagrams of probability spaces and morphisms between them and allows for precise and relatively short proofs. The setup is also convenient when couplings (joint distributions) between probability spaces are absent or variable.
2.1 Categories
Below we briefly review elementary category theory. We refer the reader to the first chapter of [15] for a more extensive introduction.
A category \(\mathbf{C}\) is an abstract mathematical structure that captures the idea of a collection of spaces and structure-preserving maps between them, such as groups and homomorphisms, vector spaces and linear maps, and topological spaces and continuous maps. Categories consist of a collection of objects (which need not to be sets), a collection of morphisms (which need not to be maps), and a rule for composing morphisms.
More formally a category consists of
-
A class of objects \(\text {Obj}_{\mathbf{C}}\);
-
A class of morphisms \(\text {Hom}_{\mathbf{C}}(A,B)\) for every pair of objects \(A,B\in \text {Obj}_{\mathbf{C}}\). For a morphism \(f\in \text {Hom}_{\mathbf{C}}(A,B)\) one usually writes \(f:A{\mathop {\rightarrow }\limits ^{}}B\). Object A will be called the domain and B the target of f, and we say that f is a morphism from A to B;
-
For each triple of objects A, B and C, a binary, associative operation, called composition,
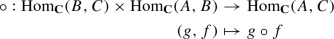
-
For every object \(A \in \text {Obj}_{\mathbf{C}}\) an identity morphism \(\mathbf{1 }_{A}:A {\mathop {\rightarrow }\limits ^{}}A\), with the property that for every \(f: A {\mathop {\rightarrow }\limits ^{}}B\) and every \(g:B {\mathop {\rightarrow }\limits ^{}}A\),
$$\begin{aligned} f \circ \mathbf{1 }_{A} = f, \quad \mathbf{1 }_{A} \circ g = g. \end{aligned}$$
A morphism \(f:A {\mathop {\rightarrow }\limits ^{}}B\) is an isomorphism if there exists a morphism \(g:B{\mathop {\rightarrow }\limits ^{}}A\) such that \(f \circ g = \mathbf{1 }_{B}\) and \(g \circ f = \mathbf{1 }_{A}\).
Category theory becomes a very powerful tool when functors and their natural transformations are considered. Functors can be seen as homomorphisms between categories. In turn, natural transformations are homomorphisms between functors.
A (covariant) functor \(\mathscr {X}:\mathbf{C} {\mathop {\rightarrow }\limits ^{}}\mathbf{D}\) between two categories \(\mathbf{C}\) and \(\mathbf{D}\), maps objects and morphisms in \(\mathbf{C}\) to objects and morphisms in \(\mathbf{D}\), respectively. It satisfies the following additional properties: For every morphism \(f:A {\mathop {\rightarrow }\limits ^{}}B\) in \(\mathbf{C}\) the image \(\mathscr {X}(f)\) is a morphism from \(\mathscr {X}(A)\) to \(\mathscr {X}(B)\) in \(\mathbf{D}\) and composition is preserved,
for any pair of morphisms \(f:A {\mathop {\rightarrow }\limits ^{}}B\) and \(g:B {\mathop {\rightarrow }\limits ^{}}C\).
A natural transformation between functors \(\mathscr {X},\mathscr {Y}:\mathbf{C} {\mathop {\rightarrow }\limits ^{}}\mathbf{D}\) is a family \(\eta \) of morphisms in category \(\mathbf{D}\), indexed by objects in \(\mathbf{C}\): For every \(A \in \text {Obj}_{\mathbf{C}}\), there is a morphism \(\eta _{A}:\mathscr {X}(A) {\mathop {\rightarrow }\limits ^{}}\mathscr {Y}(A)\), such that for every morphism \(f:A {\mathop {\rightarrow }\limits ^{}}B\) the diagram

commutes, that is
2.2 Probability spaces and reductions
We will now describe the category \({{\mathrm{\mathbf {Prob}}}}\). The objects in \({{\mathrm{\mathbf {Prob}}}}\) are finite probability spaces. A finite probability space X is a pair (S, p), where S is a (not necessarily finite) set and \(p:2^{S} {\mathop {\rightarrow }\limits ^{}}[0,1]\) is a probability measure, such that there is a finite subset of S with full measure. We denote by \(\underline{X}=\text {supp}\,p\) the support of the measure and by \(|X|:=|\text {supp}\,p_{X}|\) its cardinality. Slightly abusing the language, we call this quantity the cardinality of X. We will no longer explicitly mention that the probability spaces we consider are finite. We will also write \(p_X\) where we truly mean its density with respect to the counting measure.
We say that a map \(f:X {\mathop {\rightarrow }\limits ^{}}Y\) between two probability spaces X and Y is measure-preserving if the push-forward \(f_{*} p_X\) equals \(p_Y\). This means that for every \(A \subset Y\),
We say that two measure-preserving maps \(f:X {\mathop {\rightarrow }\limits ^{}}Y\) are equivalent if they agree on a set of full measure. We call an equivalence class of measure-preserving maps from X to Y a reduction.
The morphisms in the category \({{\mathrm{\mathbf {Prob}}}}\) are exactly the reductions between finite probability spaces. At this stage one might want to check that \({{\mathrm{\mathbf {Prob}}}}\) is indeed a category, and this is guaranteed as the composition of two reductions is again a reduction.
2.3 Isomorphisms, automorphisms and homogeneity
Now that we have organized probability spaces and reductions into a category, we get concepts such as isomorphism for free: Two probability spaces X and Y are isomorphic in the category \({{\mathrm{\mathbf {Prob}}}}\) if and only if there exists a measure-preserving bijection between the supports of the measures on X and Y. If X and Y are isomorphic, they have the same cardinality. The automorphism group \(\text {Aut}(X)\) is the group of all self-isomorphisms of X.
A probability space X is called homogeneous if the automorphism group \(\text {Aut}(X)\) acts transitively on the support \(\underline{X}\) of the measure. For the category \({{\mathrm{\mathbf {Prob}}}}\), this turns out to be a complicated way of saying that the measure on X is uniform on its support, but when we consider diagrams later, there will be no such simple implication. Homogeneity is an isomorphism invariant and we will denote the subcategory of homogeneous spaces by \({{\mathrm{\mathbf {Prob}}}}_\mathbf{h}\).
There is a product in \({{\mathrm{\mathbf {Prob}}}}\) (which is not a product in the sense of category theory!) given by the Cartesian product of probability spaces, that we will denote by \(X\otimes Y:=(\underline{X}\times \underline{Y},p_{X}\otimes p_{Y})\), where \(p_{X} \otimes p_{Y}\) is the (independent) product measure. There are canonical reductions \(X\otimes Y{\mathop {\rightarrow }\limits ^{}}X\) and \(X\otimes Y{\mathop {\rightarrow }\limits ^{}}Y\) given by projections to factors. For a pair of reductions \(f_{i}:X_{i}{\mathop {\rightarrow }\limits ^{}}Y_{i}\), \(i=1,2\) their tensor product is the reduction \(f_{1}\otimes f_{2}:X_{1}\otimes X_{2}{\mathop {\rightarrow }\limits ^{}}Y_{1}\otimes Y_{2}\), which is equal to the class of the Cartesian product of maps representing \(f_{i}\)’s. The product leaves the subcategory of homogeneous spaces invariant. If one of the factors in the product is replaced by an isomorphic space, then the product stays in the same isomorphism class.
We close this section with a technical remark. The category \({{\mathrm{\mathbf {Prob}}}}\) is not a small category. However it has a small full subcategory, that contains an object for every isomorphism class in \({{\mathrm{\mathbf {Prob}}}}\) and for every pair of objects in it, it contains all the available morphisms between them and is closed under the product. From now on we imagine that such a subcategory was chosen and fixed and replaces \({{\mathrm{\mathbf {Prob}}}}\) in all considerations below.
2.4 Diagrams of probability spaces
Essentially, a diagram \(\mathscr {X}=\left\{ X_{i};f_{ij}\right\} \) is a commutative diagram in \({{\mathrm{\mathbf {Prob}}}}\) consisting of a finite number of probability spaces and reductions between some of them. We have seen an example of the two-fan diagram in the introduction
Another example is the diamond diagram

We require the diagram to be commutative, that is
A morphism \(\rho :\mathscr {X}{\mathop {\rightarrow }\limits ^{}}\mathscr {Y}\) between two diagrams \(\mathscr {X}=\left\{ X_{i};f_{ij}\right\} \) and \(\mathscr {Y}=\left\{ Y_{i};g_{ij}\right\} \) of the same shape is a collection of reductions between corresponding individual objects \(\rho _{i}:X_{i}{\mathop {\rightarrow }\limits ^{}}Y_{i}\), that commute with the reductions within each diagram, \(\rho _{j}\circ f_{ij}=g_{ij}\circ \rho _{i}\).
We need to keep track of the combinatorial structure of the collection of reductions within a diagram. There are several possibilities for doing so:
-
the reductions form a directed, acyclic graph which is transitively closed;
-
the spaces in the diagram form a poset;
-
the underlying combinatorial structure could be recorded as a finite category.
The last option seems to be most convenient since it has many operations, that are necessary for our analysis, already built-in. Besides, we need at times to iterate the construction of commutative diagrams, to create diagrams of diagrams, which is readily available in the category-theory framework but is cumbersome in the other contexts.
A (finite) poset category \(\mathbf{G}\) is a finite category such that for every two objects \(O_1\) and \(O_2\) there is at most one morphism between them in either direction:
For instance, the poset category \(\varvec{\varLambda }_{2}\),

is a category with three objects \(\left\{ O_{1},O_{12},O_{2}\right\} \) and two non-identity morphisms \(\pi _1:O_{12}{\mathop {\rightarrow }\limits ^{}}O_{1}\) and \(\pi _2:O_{12}{\mathop {\rightarrow }\limits ^{}}O_{2}\).
A two-fan is then a diagram indexed by \(\varvec{\varLambda }_{2}\): we assign to each object in \(\varvec{\varLambda }_{2}\) a probability space and to each morphism in \(\varvec{\varLambda }_2\) a reduction.
In general, then, a diagram of probability spaces indexed by a poset category \(\mathbf{G}\) is a functor \(\mathscr {X}:\mathbf{G} {\mathop {\rightarrow }\limits ^{}}{{\mathrm{\mathbf {Prob}}}}\). The requirement that \(\mathscr {X}\) is a functor and not just a map between objects and morphisms (combined with the assumption that there is only one morphism between objects), is exactly the requirement that the diagrams should be commutative.
The collection of all diagrams of probability spaces indexed by a fixed poset category \(\mathbf{G}\) forms the so-called category of functors
The objects of \({{\mathrm{\mathbf {Prob}}}}\langle \mathbf{G} \rangle \) are diagrams, that is functors from \(\mathbf{G}\) to \({{\mathrm{\mathbf {Prob}}}}\), while morphisms in \({{\mathrm{\mathbf {Prob}}}}\langle \mathbf{G} \rangle \) are natural transformations between them. We will refer to the morphisms in \({{\mathrm{\mathbf {Prob}}}}\langle \mathbf{G} \rangle \) as reductions as well.
Let us go through the simple example of two-fans: we look at a reduction \(\eta :{\mathscr {X}} {\mathop {\rightarrow }\limits ^{}}{\mathscr {Y}}\) between two-fan diagrams \({\mathscr {X}}, {\mathscr {Y}}:\varvec{\varLambda }_2 {\mathop {\rightarrow }\limits ^{}}{{\mathrm{\mathbf {Prob}}}}\). The reduction \(\eta \), being a natural transformation between \(\mathscr {X}\) and \(\mathscr {Y}\), is illustrated by the commutative diagram

Thus, a reduction of a two-fan is a family of reductions of probability spaces indexed by the objects in the poset category \(\varvec{\varLambda }_2\) such that the diagram commutes.
For a diagram \(\mathscr {X}\in {{\mathrm{\mathbf {Prob}}}}\langle \mathbf{G} \rangle \), the poset category \(\mathbf{G}\) will be called the combinatorial type of \(\mathscr {X}\). For a poset category \(\mathbf{G}\) or a diagram \(\mathscr {X}\in {{\mathrm{\mathbf {Prob}}}}\langle \mathbf{G} \rangle \) we denote by  the number of objects in the category \(\mathbf{G}\).
the number of objects in the category \(\mathbf{G}\).
An object O in a poset category \(\mathbf{G}\) will be called a source, if it is not a target of any morphism except for the identity. Likewise a sink object is not a domain of any morphism, except for the identity morphism. If a category contains a unique source object, the object is called the initial object and such a category will be called complete.
The above terminology transfers to diagrams indexed by \(\mathbf{G}\): A source space in \(\mathscr {X}\in {{\mathrm{\mathbf {Prob}}}}\langle \mathbf{G} \rangle \) is one that is not a target space of any reduction within the diagram, a sink space is not the domain of any non-trivial reduction and \(\mathscr {X}\) is called complete if \(\mathbf{G}\) is, i.e. if it has a unique source space.
The tensor product of probability spaces extends to a tensor product of diagrams. For \(\mathscr {X},\mathscr {Y}\in {{\mathrm{\mathbf {Prob}}}}\langle \mathbf{G} \rangle \), such that \(\mathscr {X}=\left\{ X_{i};f_{ij}\right\} \) and \(\mathscr {Y}=\left\{ Y_{i};g_{ij}\right\} \) define
The construction of the category of commutative diagrams could be applied to any category, not just \({{\mathrm{\mathbf {Prob}}}}\). Two additional cases will be of interest to us.
Denote by \({{\mathrm{\mathbf {Set}}}}\) the category of finite sets and surjective maps. Then all of the above constructions could be repeated for sets instead of probability spaces. Thus we could talk about the category of diagrams of sets \({{\mathrm{\mathbf {Set}}}}\langle \mathbf{G} \rangle \).
Given a reduction \(f:X{\mathop {\rightarrow }\limits ^{}}Y\) between two probability spaces, the restriction \(\underline{f}:\underline{X}{\mathop {\rightarrow }\limits ^{}}\underline{Y}\) is a well-defined surjective map. Given a diagram \(\mathscr {X}=\left\{ X_{i};f_{ij}\right\} \) of probability spaces, there is an underlying diagram of sets, obtained by taking the supports of measures on each level and restricting reductions on these supports. We will denote it by \(\underline{\mathscr {X}}=\left\{ \underline{X}_{i};\underline{f}_{ij}\right\} \), where \(\underline{X}_{i}:=\text {supp}\,p_{X_{i}}\). Thus we have a forgetful functor
We could also repeat the construction of commutative diagrams to form a category of diagrams of diagrams. Thus given two poset categories \(\mathbf{G}\) and \(\mathbf{H}\) we can form a category \({{\mathrm{\mathbf {Prob}}}}\langle \mathbf{G},\mathbf{H} \rangle :={{\mathrm{\mathbf {Prob}}}}\langle \mathbf{G} \rangle \langle \mathbf{H} \rangle \). We will rarely need anything beyond a two-fan of diagrams. There is a natural isomorphism
Thus, for example, a two-fan of \(\mathbf{G}\)-diagrams could be equivalently considered as a \(\mathbf{G}\)-diagram of two-fans, see also Sect. 2.5.3.
2.5 Examples of diagrams
We now consider some examples of poset categories and corresponding diagrams, that will be important in what follows.
2.5.1 Singleton
We denote by \(\bullet \) the poset category with a single object. Clearly diagrams indexed by \(\bullet \) are just probability spaces and we have \({{\mathrm{\mathbf {Prob}}}}\equiv {{\mathrm{\mathbf {Prob}}}}\langle \bullet \rangle \).
2.5.2 Chains
The chain \(\mathbf{C}_{n}\) of length \(n\in \mathbb {N}\) is a category with n objects \(\left\{ O_{i}\right\} _{i=1}^{n}\) and morphisms from \(O_{i}\) to \(O_{j}\) whenever \(i\ge j\). A diagram \(\mathscr {X}\in {{\mathrm{\mathbf {Prob}}}}\langle \mathbf{C}_{n} \rangle \) is a chain of reductions
2.5.3 Two-fan
The two-fan \(\varvec{\varLambda }_{2}\) is a category with three objects \(\left\{ O_{1},O_{12},O_{2}\right\} \) and two non-identity morphisms \(O_{12}{\mathop {\rightarrow }\limits ^{}}O_{1}\) and \(O_{12}{\mathop {\rightarrow }\limits ^{}}O_{2}\). A diagram indexed by a two-fan will also be called a two-fan.
Essentially, a two-fan \((X{\mathop {\leftarrow }\limits ^{}}Z{\mathop {\rightarrow }\limits ^{}}Y)\) is a triple of probability spaces and a pair of reductions between them.
A reduction of a two-fan \(\mathscr {F}=(X{\mathop {\leftarrow }\limits ^{}}Z{\mathop {\rightarrow }\limits ^{}}Y)\) to another two-fan \(\mathscr {F}'=(X'{\mathop {\leftarrow }\limits ^{}}Z'{\mathop {\rightarrow }\limits ^{}}Y')\) is a triple of reductions \(Z{\mathop {\rightarrow }\limits ^{}}Z'\), \(Y{\mathop {\rightarrow }\limits ^{}}Y'\) and \(X{\mathop {\rightarrow }\limits ^{}}X'\) that commute with the reductions within each fan, so that the diagram on Fig. 2a is commutative.
A two-fan \((X{\mathop {\leftarrow }\limits ^{}}Z{\mathop {\rightarrow }\limits ^{}}Y)\) is called minimal if for any super-diagram \(\left\{ X,Y,Z,Z'\right\} \) shown on Fig. 2b the reduction \(m:Z{\mathop {\rightarrow }\limits ^{}}Z'\) must be an isomorphism. Minimal two-fans are also called couplings in probability theory.
For any two-fan \((X{\mathop {\leftarrow }\limits ^{}}Z{\mathop {\rightarrow }\limits ^{}}Y)\) of probability spaces there always exist a unique (up to isomorphism), minimal two-fan \((X{\mathop {\leftarrow }\limits ^{}}Z'{\mathop {\rightarrow }\limits ^{}}Y)\), that can be included in the diagram shown on Fig. 2b. The minimization can be constructed by taking \(Z':=\underline{X}\times \underline{Y}\) as a set and considering a probability distribution on \(Z'\) induced by a map \(Z{\mathop {\rightarrow }\limits ^{}}Z'\), that is the Cartesian product of the reductions \(\underline{Z}{\mathop {\rightarrow }\limits ^{}}\underline{X}\) and \(\underline{Z}{\mathop {\rightarrow }\limits ^{}}\underline{Y}\) in the original two-fan. Thus, the inclusion of a pair of probability spaces X and Y as sink vertices in a minimal two-fan is equivalent to specifying a joint distribution on \(\underline{X}\times \underline{Y}\).
Note that minimality of a two-fan is defined in purely categorical terms. Even though the definition applies to two-fans of morphisms in any category, the minimization need not to exist. However as the next proposition asserts, if minimization of any two-fan exists in a category \(\mathbf{C}\), then it also exists in a category of diagrams over \(\mathbf{C}\).
Proposition 2.1
Let \(\mathbf{G}\) be a poset category, and let \(\mathscr {X}= \{X_i; a_{ij} \}\), \(\mathscr {Y}= \{Y_i; b_{ij}\}\) and \(\mathscr {Z}= \{Z_i; c_{ij}\}\) be three \(\mathbf{G}\)-diagrams. Then
-
1.
A two-fan \(\mathscr {F}=(\mathscr {X}{\mathop {\leftarrow }\limits ^{}}\mathscr {Z}{\mathop {\rightarrow }\limits ^{}}\mathscr {Y})\in {{\mathrm{\mathbf {Prob}}}}\langle \mathbf{G},\varvec{\varLambda }_{2}\rangle \) of \(\mathbf{G}\)-diagrams is minimal if and only if the constituent two-fans of probability spaces \(\mathscr {F}_{i}=(X_{i}{\mathop {\leftarrow }\limits ^{}}Z_{i}{\mathop {\rightarrow }\limits ^{}}Y_{i})\) are all minimal.
-
2.
For any two-fan \(\mathscr {F}=(\mathscr {X}{\mathop {\leftarrow }\limits ^{}}\mathscr {Z}{\mathop {\rightarrow }\limits ^{}}\mathscr {Y})\) of \(\mathbf{G}\)-diagrams its minimal reduction exists, that is, there exists a minimal two-fan \(\mathscr {F}'=(\mathscr {X}{\mathop {\leftarrow }\limits ^{}}\mathscr {Z}'{\mathop {\rightarrow }\limits ^{}}\mathscr {Y})\) included in the following diagram

The proof of Proposition 2.1 can be found on page 38.
2.5.4 Co-fan
A co-fan \(\mathbf{V}\) is a category with three objects and morphisms
2.5.5 A diamond diagram
A “diamond” diagram is indexed by a diamond category \(\varvec{\diamond }\), that consists of a two-fan and a co-fan, as shown on Fig. 3.
Of course, there is also a morphism \(O_{12}{\mathop {\rightarrow }\limits ^{}}O_{\bullet }\), which lies in the transitive closure of the given four morphisms. We will often skip writing morphisms that are implied by the transitive closure.
A diamond diagram will be called minimal if the top two-fan in it is minimal.
2.5.6 “Two-tents” diagram
The “two-tents” category \(\mathbf{M}_{2}\) consists of five objects, of which two are sources and three are sinks, and morphisms are as in Fig. 3b.
Thus, a typical two-tents diagram consists of five probability spaces and reductions as in
The probability spaces U and V are sources and X, Y and Z are sinks.
2.5.7 Full diagram
The full category \(\varvec{\varLambda }_{n}\) on n objects is a category with objects \(\left\{ O_{I}\right\} _{I\in 2^{\left\{ 1,\ldots ,n\right\} }\setminus \left\{ \emptyset \right\} }\) indexed by all non-empty subsets \(I\in 2^{\left\{ 1,\ldots ,n\right\} }\) and a morphism from \(O_{I}\) to \(O_{J}\), whenever \(J\subseteq I\).
A diagram \(\mathscr {X}\) indexed by a full category will be called minimal, if for every two-fan in it, it also contains a minimal two-fan with the same sink vertices. If \(\mathscr {X}\in {{\mathrm{\mathbf {Prob}}}}\langle \varvec{\varLambda }_n\rangle \) is minimal full diagram of probability spaces, then the set \(\underline{\mathscr {X}(O_{I})}\) can be considered as a subset of the product \(\prod _{i\in I}\underline{\mathscr {X}(O_{i})}\), while reductions are just coordinate projections.
For an n-tuple of random variables \(\textsf {X}_{1},\ldots ,\textsf {X}_{n}\) one may construct a minimal full diagram \(\mathscr {X}\in {{\mathrm{\mathbf {Prob}}}}\langle \varvec{\varLambda }_{n}\rangle \) by considering all joint distributions and “marginalization” reductions. We denote such a diagram by \(\langle \textsf {X}_{1},\ldots ,\textsf {X}_{n}\rangle \). On the other hand, the reductions from the initial space to the sink vertices of a full diagram can be viewed as random variables on the domain of definition given by the (unique) initial space.
Suppose \(\mathscr {X}\in {{\mathrm{\mathbf {Prob}}}}\langle \varvec{\varLambda }_{n}\langle \) is a minimal full diagram with sink vertices \(X_{1},\ldots ,X_{n}\). It is convenient to view \(\mathscr {X}\) as a distribution on the Cartesian product of the underlying sets of the sink vertices:
where \(\varDelta S\) stands for the space of all probability distribution on a finite set S.
Once the underlying sets of the sink spaces are fixed, there is a one-to-one correspondence between the full minimal diagrams and distributions as above.
As a corollary of Proposition 2.1 we also obtain the following characterization of minimal full diagrams of any \(\mathbf{G}\)-diagrams of probability spaces.
Corollary 2.2
Let \(\mathbf{G}\) be an arbitrary poset category. Then
-
1.
A full diagram \(\mathscr {F}\) of \(\mathbf{G}\)-diagrams is minimal, if and only if the constituent full diagrams of probability spaces \(\mathscr {F}_{i}\) are all minimal.
-
2.
For any full diagram \(\mathscr {F}\in {{\mathrm{\mathbf {Prob}}}}\langle \mathbf{G},\varvec{\varLambda }_{n}\rangle \) of \(\mathbf{G}\)-diagrams there exists another minimal full diagram \(\mathscr {F}'\in {{\mathrm{\mathbf {Prob}}}}\langle \mathbf{G},\varvec{\varLambda }_{n}\rangle \) with the same sink entries and a reduction \(\mu :\mathscr {F}{\mathop {\rightarrow }\limits ^{}}\mathscr {F}',\) such that \(\mu \) restricts to an isomorphism on sink entries of \(\mathscr {F}\). Moreover, \(\mathscr {F}'\) is unique upto isomorphism.
2.6 Constant diagrams
Suppose X is a probability space and \(\mathbf{G}\) is a poset category. One may form a constant \(\mathbf{G}\)-diagram by considering a functor that maps all objects in \(\mathbf{G}\) to X and all the morphisms to the identity morphism \(X{\mathop {\longrightarrow }\limits ^{\text {Id}}} X\). We denote such a constant diagram by \(X^{\mathbf{G}}\) or simply by X, when \(\mathbf{G}\) is clear from the context. Any constant diagram is automatically minimal.
If \(\mathscr {Y}=\left\{ Y_{i};f_{ij}\right\} \) is another \(\mathbf{G}\)-diagram, then a reduction \(\rho :\mathscr {Y}{\mathop {\rightarrow }\limits ^{}}X^{\mathbf{G}}\) (which we write sometimes simply as \(\rho :\mathscr {Y}{\mathop {\rightarrow }\limits ^{}}X\)) is a collection of reductions \(\rho _{i}:Y_{i}{\mathop {\rightarrow }\limits ^{}}X\), such that
Let \(\mathscr {X}=\left\{ X_{i};f_{ij}\right\} \) be a complete diagram with the initial space \(X_{0}\). Then there is a canonical reduction
with components
By \(\left\{ \bullet \right\} \) we denote a one-point probability space. The constant \(\mathbf{G}\)-diagram \(\left\{ \bullet \right\} ^{\mathbf{G}}\) is a unit with respect to the product in \({{\mathrm{\mathbf {Prob}}}}\langle \mathbf{G} \rangle \).
2.7 Homogeneous diagrams
A diagram \(\mathscr {X}\in {{\mathrm{\mathbf {Prob}}}}\langle \mathbf{G} \rangle \) indexed by some poset category \(\mathbf{G}\) is called homogeneous if its automorphism group \(\text {Aut}(\mathscr {X})\) acts transitively on every probability space in \(\mathscr {X}\). Three examples of homogeneous diagrams were given in the introduction. The subcategory of all homogeneous diagrams indexed by \(\mathbf{G}\) will be denoted \({{\mathrm{\mathbf {Prob}}}}\langle \mathbf{G} \rangle _\mathbf{h}\).
In fact, for \(\mathscr {X}\) to be homogeneous it is sufficient that the \(\text {Aut}(\mathscr {X})\) acts transitively on every source space in \(\mathscr {X}\). Thus, if \(\mathscr {X}\) is complete with initial space \(X_{0}\), to check homogeneity it is sufficient to check the transitivity of the action of the symmetries of \(\mathscr {X}\) on \(X_{0}\).
Any subdiagram of a homogeneous diagram is also homogeneous. In particular, all the individual spaces of a homogeneous diagram are homogeneous
However homogeneity of the whole of the diagram is a stronger property than homogeneity of the individual spaces in the diagram, thus in general
Two examples of non-homogeneous two-fans are shown in Fig. 4. The pictures are to be interpreted in the same way as the pictures in Fig. 1.
A single probability space is homogeneous if and only if there is a representative in its isomorphism class with uniform measure and the same holds true for chain diagrams, for the co-fan or any other diagram that does not contain a two-fan. However, for more complex diagrams, for example for two-fans, no such simple description is available.
2.7.1 Universal construction of homogeneous diagrams
Examples of homogeneous diagrams could be constructed in the following manner. Suppose \(\varGamma \) is a finite group and \(\left\{ H_{i}\right\} \) is a collection of subgroups. Consider a collection of sets \(\underline{X}_{i}:=\varGamma /H_{i}\) and consider a natural surjection \(f_{ij}:\underline{X}_{i}{\mathop {\rightarrow }\limits ^{}}\underline{X}_{j}\) whenever \(H_{i}\) is a subgroup of \(H_{j}\). Equipping each \(\underline{X}_{i}\) with the uniform distribution one can turn the diagram of sets \(\left\{ \underline{X}_{i};f_{ij}\right\} \) into a homogeneous diagram of probability spaces. It will be complete if there is a smallest subgroup (under inclusion) among \(H_{i}\)’s.
Such a diagram will be complete and minimal, if together with any pair of groups \(H_{i}\) and \(H_{j}\) in the collection, their intersection \(H_{i}\cap H_{j}\) also belongs to the collection \(\left\{ H_{i}\right\} \).
In fact, any homogeneous diagram arises this way. Suppose diagram \(\mathscr {X}= \left\{ X_i ; f_{ij} \right\} \) is homogeneous, then we set \(\varGamma = \text {Aut}(\mathscr {X})\) and choose a collection of points \(x_i \in X_i\) such that \(f_{ij} (x_i) = x_j\) and denote by \(H_i := {\text {Stab}}(x_i) \subset \varGamma \). Then, if one applies the construction of the previous paragraph to \(\varGamma \), with the collection of subgroups \(\left\{ H_i\right\} \), one recovers the original diagram \(\mathscr {X}\) upto isomorphism.
2.8 Conditioning
Suppose a diagram \(\mathscr {X}\) contains a fan
Given a point \(x\in X\) with a non-zero weight one may consider conditional probability distributions \(p_Z(\;\cdot \;\lfloor x)\) on \(\underline{Z}\), and \(p_Y( \; \cdot \;\lfloor x)\) on \(\underline{Y}\). The distribution \(p_Z(\; \cdot \; \lfloor x)\) is supported on \(f^{-1}(x)\) and is defined by the property that for any function \(f:Z{\mathop {\rightarrow }\limits ^{}}\mathbb {R}\) holds
and is given by
The distribution \(p_Y(\;\cdot \;\lfloor x)\) is the pushforward of \(p_Z( \; \cdot \; \lfloor x)\) under g
Recall that if \(\mathscr {F}\) is minimal, the underlying set of Z can be assumed to be the product \(\underline{X} \times \underline{Y}\). In that case
We denote the corresponding space \(Y\lfloor x:=\big (\underline{Y},p_Y(\;\cdot \;\lfloor x)\big )\).
Under some assumptions it is possible to condition a whole sub-diagram of \(\mathscr {X}\). More specifically, if a diagram \(\mathscr {X}\) contains a sub-diagram \(\mathscr {Y}\) and a probability space X satisfying the condition that there exists a space Z in \(\mathscr {X}\) that reduces to all the spaces in \(\mathscr {Y}\) and to X, then we may condition the whole of \(\mathscr {Y}\) on \(x \in X\) given that \(p_X(x)>0\).
For \(x\in X\) with positive weight we denote by \(\mathscr {Y}\lfloor x\) the diagram of spaces in \(\mathscr {Y}\) conditioned on \(x\in X\). The diagram \(\mathscr {Y}\lfloor x\) has the same combinatorial type as \(\mathscr {Y}\) and will be called the slice of \(\mathscr {Y}\) over \(x\in X\). Note that the space X itself may or may not belong to \(\mathscr {Y}\). The conditioning \(\mathscr {Y}\lfloor x\) may depend on the choice of a fan between \(\mathscr {Y}\) and X, however when \(\mathscr {X}\) is complete the conditioning \(\mathscr {Y}\lfloor x\) is well-defined and is independent of the choice of fans.
Suppose now that there are two subdiagram \(\mathscr {Y}\) and \(\mathscr {Z}\) in \(\mathscr {X}\) and in addition \(\mathscr {Z}\) is a constant diagram, \(\mathscr {Z}=Z^{\mathbf{G}'}\) for some poset category \(\mathbf{G}'\). Let \(z\in \underline{Z}\), then \(\mathscr {Y}\lfloor z\) is well defined and is independent of the choice of the space in \(\mathscr {Z}\), the element of which z is to be considered.
If \(\mathscr {X}\) is homogeneous, then \(\mathscr {Y}\lfloor x\) is also homogeneous and its isomorphism class does not depend on the choice of \(x\in \underline{X}\).
2.9 Entropy
We define entropy by the limit in Eq. 2. Entropy satisfies the so-called Shannon inequality, see for example [8]. Namely for any minimal diamond diagram

the following inequality holds,
Furthermore, entropy is additive with respect to the tensor product, that is, for a pair of probability spaces \(X,Y\in {{\mathrm{\mathbf {Prob}}}}\) holds
Conditional entropy \(\textsf {Ent}(X\lfloor Y)\) is defined for a pair X, Y of probability spaces included in a minimal two-fan \((X{\mathop {\leftarrow }\limits ^{}}Z{\mathop {\rightarrow }\limits ^{}}Y)\) as
The above quantity is always non-negative in view of Shannon inequality (5). Moreover, the following identity holds, see [8]
For a \(\mathbf{G}\)-diagram \(\mathscr {X}=\left\{ X_{i};f_{ij}\right\} \) define the entropy homomorphism

It will be convenient for us to equip the target  with the \(\ell ^{1}\)-norm. Thus
with the \(\ell ^{1}\)-norm. Thus

If \(\mathscr {X}\) is a complete \(\mathbf{G}\)-diagram with initial space \(X_{0}\), then by Shannon inequality (5) there is an obvious estimate

3 The entropy distance
We turn the space of diagrams into a pseudo-metric space by introducing the intrinsic entropy distance and asymptotic entropy distance. The intrinsic entropy distance is obtained by taking an infimum of the entropy distance over all possible joint distributions on two probability spaces.
3.1 Entropy distance and asymptotic entropy distance
3.1.1 Entropy distance in the case of single probability spaces
For a two-fan \(\mathscr {F}=(X{\mathop {\leftarrow }\limits ^{}}Z{\mathop {\rightarrow }\limits ^{}}Y)\) define a “distance” \(\text {kd}(\mathscr {F})\) between probability spaces X and Y with respect to \(\mathscr {F}\) by
If a two-fan \(\mathscr {F}\) satisfies \(\text {kd}(\mathscr {F})=0\), then both reductions in \(\mathscr {F}\) are isomorphisms. Thus, essentially \(\text {kd}(\mathscr {F})\) is some measure of the deviation of the statistical map defined by \(\mathscr {F}\) from being a deterministic bijection between X and Y.
The minimal reduction \(\mathscr {F}'\) of \(\mathscr {F}\) satisfies
For a pair of probability spaces X, Y define the intrinsic entropy distance as
The optimization takes place over all two-fans with sink spaces X and Y. In view of inequality (8) one could as well optimize over the space of minimal two-fans, which we will also refer to as couplings between X and Y. The tensor product of X and Y trivially provides a coupling and the set of couplings is compact, therefore an optimum is always achieved and it is finite.
The bivariate function \(\mathbf k :{{\mathrm{\mathbf {Prob}}}}\times {{\mathrm{\mathbf {Prob}}}}{\mathop {\rightarrow }\limits ^{}}\mathbb {R}_{\ge 0}\) defines a notion of pseudo-distance and it vanishes exactly on pairs of isomorphic probability spaces. This follows directly from the Shannon inequality (5), and a more general statement will be proven in Proposition 3.1 below.
3.1.2 Entropy distance for complete diagrams
The definition of entropy distance for complete diagrams repeats almost literally the definition for single spaces. We fix a complete poset category \(\mathbf{G}\) and will be considering diagrams from \({{\mathrm{\mathbf {Prob}}}}\langle \mathbf{G} \rangle \).
Consider three such diagrams \(\mathscr {X}=\left\{ X_{i},f_{ij}\right\} \), \(\mathscr {Y}=\left\{ Y_{i},g_{ij}\right\} \) and \(\mathscr {Z}=\left\{ Z_{i},h_{ij}\right\} \) from \({{\mathrm{\mathbf {Prob}}}}\langle \mathbf{G} \rangle \). Recall that a two-fan \(\mathscr {F}=(\mathscr {X}{\mathop {\leftarrow }\limits ^{}}\mathscr {Z}{\mathop {\rightarrow }\limits ^{}}\mathscr {Y})\) can also be viewed as a \(\mathbf{G}\)-diagram of two-fans
Define
The quantity \(\text {kd}(\mathscr {F})\) vanishes if and only if the fan \(\mathscr {F}\) provides isomorphisms between all individual spaces in \(\mathscr {X}\) and \(\mathscr {Y}\) that commute with the inner structure of the diagrams, that is, it provides an isomorphism between \(\mathscr {X}\) and \(\mathscr {Y}\) in \({{\mathrm{\mathbf {Prob}}}}\langle \mathbf{G} \rangle \).
The intrinsic entropy distance between diagrams is defined in analogy with the case of single probability spaces
where the infimum is over all two-fans of \(\mathbf{G}\)-diagrams with sink vertices \(\mathscr {X}\) and \(\mathscr {Y}\).
The following proposition records that the intrinsic entropy distance is in fact a pseudo-distance on \({{\mathrm{\mathbf {Prob}}}}\langle \mathbf{G} \rangle \), provided \(\mathbf{G}\) is a complete poset category (that is when \(\mathbf{G}\) has a unique initial space).
Proposition 3.1
Let \(\mathbf{G}\) be a complete poset category. Then the bivariate function
is a pseudo-distance on \({{\mathrm{\mathbf {Prob}}}}\langle \mathbf{G} \rangle \).
Moreover, two diagrams \(\mathscr {X}, \mathscr {Y}\in {{\mathrm{\mathbf {Prob}}}}\langle \mathbf{G} \rangle \) satisfy \(\mathbf k (\mathscr {X},\mathscr {Y})=0\) if and only if \(\mathscr {X}\) is isomorphic to \(\mathscr {Y}\) in \({{\mathrm{\mathbf {Prob}}}}\langle \mathbf{G} \rangle \).
The idea of the proof is very simple. In the case of single probability spaces X, Y, Z a coupling between X and Z can be constructed from a coupling between X and Y and a coupling between Y and Z by adhesion on Y, see [16]. The triangle inequality then follows from Shannon inequality. However, since we are dealing with diagrams the combinatorial structure requires careful treatment. Therefore, we provide a detailed proof on page 40.
It is important to note, that the proof uses the fact that \(\mathbf{G}\) is complete. In fact, even though the definition of \(\mathbf k \) could be easily extended to some bivariate function on the space of diagrams of any fixed combinatorial type, it fails to satisfy the triangle inequality in general, because the composition of couplings requires completeness of \(\mathbf{G}\).
3.1.3 The asymptotic entropy distance
Let \(\mathbf{G}\) be a complete poset category. We will show in Corollary 3.5 below, that the sequence
is sublinear and therefore the following limit exists.
We call it’s value, \({\varvec{\upkappa }}( \mathscr {X}, \mathscr {Y})\), the asymptotic entropy distance between two diagrams \(\mathscr {X}, \mathscr {Y}\in {{\mathrm{\mathbf {Prob}}}}\langle \mathbf{G}\rangle \).
As a corollary of Proposition 3.1 and definition (10) we immediately obtain that the asymptotic entropy distance is a homogeneous pseudo-distance on \({{\mathrm{\mathbf {Prob}}}}\langle \mathbf{G} \rangle \).
Corollary 3.2
Let \(\mathbf{G}\) be a complete poset category. Then the bivariate function
is a pseudo-distance on \({{\mathrm{\mathbf {Prob}}}}\langle \mathbf{G} \rangle \) satisfying the following properties : for any pair of diagrams \(\mathscr {X},\mathscr {Y}\in {{\mathrm{\mathbf {Prob}}}}\langle \mathbf{G} \rangle \)
-
1.
\({\varvec{\upkappa }}(\mathscr {X},\mathscr {Y})\le \mathbf k (\mathscr {X},\mathscr {Y})\)
-
2.
for any \(n\in \mathbb {N}_{0}\) holds \( {\varvec{\upkappa }}(\mathscr {X}^{n},\mathscr {Y}^{n})=n\cdot {\varvec{\upkappa }}(\mathscr {X},\mathscr {Y}) \).
We will see later that there are instances when \({\varvec{\upkappa }}<\mathbf k \), moreover there are pairs of non-isomorphic diagrams with vanishing asymptotic entropy distance between them.
In the next subsection we derive some elementary properties of the intrinsic entropy distance and the asymptotic entropy distance.
3.2 Properties of (asymptotic) entropy distance
3.2.1 Tensor product
We show that the tensor product on the space of diagrams is 1-Lipschitz. Later this will allow us to give a simple description of tropical diagrams, that is, of points in the asymptotic cone of \({{\mathrm{\mathbf {Prob}}}}\langle \mathbf{G} \rangle \), as limits of certain sequences of “classical” diagrams, as will be discussed in a subsequent article.
Proposition 3.3
Let \(\mathbf{G}\) be a complete poset category. Then with respect to the Kolmogorov distance on \({{\mathrm{\mathbf {Prob}}}}\langle \mathbf{G} \rangle \) the tensor product
is 1-Lipschitz in each variable, that is, for every triple \(\mathscr {X}, \mathscr {Y}, \mathscr {Y}' \in {{\mathrm{\mathbf {Prob}}}}\langle \mathbf{G} \rangle \) the following bound holds
This statement is a direct consequence of additivity of entropy with respect to the tensor product. Details can be found on page 42.
It follows directly from definition (10) and Proposition 3.3, that the asymptotic entropy distance enjoys a similar property.
Corollary 3.4
Let \(\mathbf{G}\) be a complete poset category. Then with respect to the asymptotic entropy distance on \({{\mathrm{\mathbf {Prob}}}}\langle \mathbf{G} \rangle \) the tensor product
is 1-Lipschitz in each variable.
As another corollary we obtain the subadditivity properties of the intrinsic entropy distance and asymptotic entropy distance.
Corollary 3.5
Let \(\mathbf{G}\) be a complete poset category and let \(\mathscr {X}, \mathscr {Y}, \mathscr {U}, \mathscr {V}\in {{\mathrm{\mathbf {Prob}}}}\langle \mathbf{G} \rangle ,\) then
and
It implies in particular that shifts are non-expanding maps in \(({{\mathrm{\mathbf {Prob}}}}\langle \mathbf{G} \rangle ,\mathbf k )\) or \(({{\mathrm{\mathbf {Prob}}}}\langle \mathbf{G} \rangle ,{\varvec{\upkappa }})\).
Corollary 3.6
Let \(\mathbf{G}\) be a complete poset category and \(\varvec{\delta }=\mathbf k ,{\varvec{\upkappa }}\) be either intrinsic entropy distance or asymptotic entropy distance on \({{\mathrm{\mathbf {Prob}}}}\langle \mathbf{G} \rangle \). Let \(\mathscr {U}\in {{\mathrm{\mathbf {Prob}}}}\langle \mathbf{G} \rangle \). Then the shift map
is a non-expanding map with respect to either intrinsic entropy distance or asymptotic entropy distance.
Less obvious is the fact that \({\varvec{\upkappa }}\) is, in fact, translation invariant and in particular, \(({{\mathrm{\mathbf {Prob}}}}\langle \mathbf{G} \rangle ,{\varvec{\upkappa }})\) satisfies the cancellation property. This is the subject of Proposition 3.7 below, which was communicated to us by Tobias Fritz.
Proposition 3.7
For any triple of diagrams \(\mathscr {X},\mathscr {Y},\mathscr {U}\) holds
The proof of the lemma can be found on page 43.
3.2.2 Entropy
Recall that we defined the entropy function

by evaluating the entropy of all individual spaces in a \(\mathbf{G}\)-diagram. The target space  will be endowed with the \(\ell ^{1}\)-norm with respect to the natural coordinate system. With such a choice, the entropy function is 1-Lipschitz with respect to the Kolmogorov distance on \({{\mathrm{\mathbf {Prob}}}}\langle \mathbf{G} \rangle \).
will be endowed with the \(\ell ^{1}\)-norm with respect to the natural coordinate system. With such a choice, the entropy function is 1-Lipschitz with respect to the Kolmogorov distance on \({{\mathrm{\mathbf {Prob}}}}\langle \mathbf{G} \rangle \).
Proposition 3.8
Suppose \(\mathbf{G}\) is a complete poset category and \(\varvec{\delta }=\mathbf k ,{\varvec{\upkappa }}\) is either intrinsic entropy distance or asymptotic entropy distance on \({{\mathrm{\mathbf {Prob}}}}\langle \mathbf{G} \rangle \). Then the entropy function

is 1-Lipschitz.
Again, the proof of the proposition above is an application of Shannon’s inequality, see page 44 for details.
3.3 The Slicing Lemma
The Slicing Lemma, Proposition 3.9 below, allows to estimate the intrinsic entropy distance between two diagrams with the integrated intrinsic entropy distance between “slices”, which are diagrams obtained by conditioning on another probability space. It turned out to be a very powerful tool for estimation of the intrinsic entropy distance and will be used below on several occasions.
As described in Sect. 2.6, by a reduction of a diagram \(\mathscr {X}=\left\{ X_{i},f_{ij}\right\} \) to a single space U we mean a collection of reductions \(\left\{ \rho _{i}:X_{i}{\mathop {\rightarrow }\limits ^{}}U\right\} \) from the individual spaces in \(\mathscr {X}\) to U, that commute with the reductions within \(\mathscr {X}\)
Alternatively, whenever a single probability space appears as a domain or a target of a morphism to or from a \(\mathbf{G}\)-diagram, it should be replaced by a constant \(\mathbf{G}\)-diagram.
Proposition 3.9
(Slicing Lemma) Suppose \(\mathbf{G}\) is a complete poset category and we are given \(\mathscr {X},{\hat{\mathscr {X}}},\mathscr {Y},{\hat{\mathscr {Y}\in {{\mathrm{\mathbf {Prob}}}}}} \langle \mathbf{G} \rangle \)—four \(\mathbf{G}\)-diagrams and \(U,V,W\in {{\mathrm{\mathbf {Prob}}}}\)—three probability spaces, that are included into the following three-tents diagram

such that the two-fan \((U{\mathop {\leftarrow }\limits ^{}}W{\mathop {\rightarrow }\limits ^{}}V)\) is minimal. Then the following estimate holds

The idea of the proof of the Slicing Lemma (page 45) is as follows. For every pair \((u,v)\in \underline{W}\) we consider an optimal two-fan \(\mathscr {G}_{uv}\) coupling \(\mathscr {X}\lfloor u\) and \(\mathscr {Y}\lfloor v\). These fans have the same underlying diagram of sets. Then we construct a coupling between \(\mathscr {X}\) and \(\mathscr {Y}\) as a convex combination of distributions of \(\mathscr {G}_{uv}\)’s weighted by \(p_{W}(u,v)\). The estimates on the resulting two-fan then imply the proposition.
Various implications of the Slicing Lemma are summarized in the next corollary.
Corollary 3.10
Let \(\mathbf{G}\) be a complete poset category, \(\mathscr {X},\mathscr {Y}\in {{\mathrm{\mathbf {Prob}}}}\langle \mathbf{G} \rangle \) and \(U\in {{\mathrm{\mathbf {Prob}}}}\).
-
1.
Given a “two-tents” diagram
$$\begin{aligned} \mathscr {X}{\mathop {\leftarrow }\limits ^{}}{\hat{\mathscr {X}}}{\mathop {\rightarrow }\limits ^{}}U{\mathop {\leftarrow }\limits ^{}}{\hat{\mathscr {Y}}}{\mathop {\rightarrow }\limits ^{}}\mathscr {Y}\end{aligned}$$the following inequality holds

-
2.
Given a fan
$$\begin{aligned} \mathscr {X}{\mathop {\leftarrow }\limits ^{}}{\hat{\mathscr {X}}}{\mathop {\rightarrow }\limits ^{}}U \end{aligned}$$the following inequality holds

-
3.
Let \(\mathscr {X}{\mathop {\rightarrow }\limits ^{}}U\) be a reduction, then

-
4.
For a co-fan \(\mathscr {X}{\mathop {\rightarrow }\limits ^{}}U{\mathop {\leftarrow }\limits ^{}}\mathscr {Y}\) holds
$$\begin{aligned} \mathbf k (\mathscr {X},\mathscr {Y}) \le \int _{U}\mathbf k (\mathscr {X}\lfloor u,\mathscr {Y}\lfloor u)\hbox {d}\,p_{U}(u). \end{aligned}$$
4 Distributions and types
In this section we recall some elementary inequalities for (relative) entropies and the total variation distance for distributions on finite sets. Furthermore, we generalize the notion of a probability distribution on a set to a distribution on a diagram of sets. Finally, we give a perspective on the theory of types, and also introduce types in the context of complete diagrams.
4.1 Distributions
4.1.1 Single probability spaces
For a finite set S we denote by \(\varDelta S\) the collection of all probability distributions on S. It is a unit simplex in the real vector space \(\mathbb {R}^S\). We often use the fact that it is a compact, convex set, whose interior points correspond to fully supported probability measures on S.
For \(\pi _{1},\pi _{2}\in \varDelta S\) denote by \(|\pi _{1}-\pi _{2}|_1\) the total variation of the signed measure \((\pi _{1}-\pi _{2})\) and define the entropy of the distribution \(\pi _{1}\) by
If, in addition, \(\pi _{2}\) lies in the interior of \(\varDelta S\) define the relative entropy by
The entropy of a probability space is often defined through formula (11). It is a standard fact, and can be verified with the help of Lemma 4.2 below, that for \(\pi \in \varDelta S\) holds
which justifies the name “entropy” for the function \(h:\varDelta S{\mathop {\rightarrow }\limits ^{}}\mathbb {R}\).
Define a divergence ball of radius \(\varepsilon >0\) centered at \(\pi \in \text {Interior}\varDelta S\) as
For a fixed \(\pi \) and \(\varepsilon \ll 1\) the ball \(B_{\varepsilon }(\pi )\) also lies in the interior of \(\varDelta S\).
The total variation norm and relative entropy are related by the following inequality.
Lemma 4.1
Let S be a finite set, then for any \(\pi _{1},\pi _2\in \varDelta S\), Pinsker’s inequality holds
The claim of the Lemma, Pinsker’s inequality, is a well-known inequality in for instance information theory, and a proof can be found in [8].
4.1.2 Distributions on diagrams
A map \(f:S{\mathop {\rightarrow }\limits ^{}}S'\) between two finite sets induces an affine map \(f_{*}:\varDelta S{\mathop {\rightarrow }\limits ^{}}\varDelta S'\).
For a diagram of sets \(\mathscr {S}=\left\{ S_{i};f_{ij}\right\} \) we define the space of distributions on the diagram \(\mathscr {S}\) by
Essentially, an element of \(\varDelta \mathscr {S}\) is a collection of distributions on the sets \(S_i\) in \(\mathscr {S}\) that is consistent with respect to the maps \(f_{ij}\). The consistency conditions \((f_{ij})_* \pi _i = \pi _j\) form a collection of linear equations with integer coefficients with respect to the standard convex coordinates in \(\prod \varDelta S_i\). Thus, \(\varDelta \mathscr {S}\) is a rational affine subspace in the product of simplices. In particular, \(\varDelta \mathscr {S}\) has a convex structure.
If \(\mathscr {S}\) is complete with initial set \(S_{0}\), then specifying a distribution \(\pi _{0}\in \varDelta S_{0}\) uniquely determines distributions on all of the \(S_{i}\)’s by setting \(\pi _{i}:=(f_{0i})_{*}\pi _{0}\). In such a situation we have
If \(\mathscr {S}\) is not complete and \(S_{0},\ldots ,S_{k}\) is a collection of its source sets, then \(\varDelta \mathscr {S}\) is isomorphic to an affine subspace of the product \(\varDelta S_{0}\times \dots \times \varDelta S_{k}\) cut out by linear equations with integer coefficients corresponding to co-fans in \(\mathscr {S}\) with source sets among \(S_{0},\ldots ,S_{k}\).
To simplify notation, for a probability space X or a diagram \(\mathscr {X}\) we will write
4.2 Types
We now discuss briefly the theory of types. Types are special subspaces of tensor powers that consist of sequences with the same “empirical distribution” as explained in details below. For a more detailed discussion the reader is referred to [7, 8]. We generalize the theory of types to complete diagrams of sets and complete diagrams of probability spaces.
The theory of types for diagrams, that are not complete, is more complex and will be addressed in a subsequent article.
4.2.1 Types for single probability spaces
Let S be a finite set. For \(n\in \mathbb {N}\) denote also
a collection of rational points in \(\varDelta S\) with denominator n. (We say that a rational number \(r\in \mathbb {Q}\) has denominator \(n\in \mathbb {N}\) if \(r\cdot n\in \mathbb {Z}\))
Define the empirical distribution map \(\mathbf{q}:S^{n}{\mathop {\rightarrow }\limits ^{}}\varDelta S\), that sends \((s_{i})_{i=1}^{n}=\mathbf{s}\in S^{n}\) to the empirical distribution \(\mathbf{q}(\mathbf{s})\in \varDelta S\) given by
Clearly the image of \(\mathbf{q}\) lies in \({\varDelta ^{^{(n)}}} S\).
For \(\pi \in {\varDelta ^{^{(n)}}} S\), the space \(T^{n}_{\pi }S:=\mathbf{q}^{-1}(\pi )\) equipped with the uniform measure is called a type over \(\pi \). The symmetric group \(\mathbb {S}_{n}\) acts on \(S^{n}\) by permuting the coordinates. This action leaves the empirical distribution invariant and therefore could be restricted to each type, where it acts transitively. Thus, for \(\pi \in {\varDelta ^{^{(n)}}} S\) the probability space \((T^{n}_{\pi }S,u)\) with u being a uniform (\(\mathbb {S}_{n}\)-invariant) distribution, is a homogeneous space.
Suppose \(X=(\underline{X},p)\) is a probability space. Let \(\tau _{n}\) be the pushforward of \(p^{\otimes n}\) under the empirical distribution map \(\mathbf{q}:\underline{X}^{n}{\mathop {\rightarrow }\limits ^{}}\varDelta X\). Clearly \(\text {supp}\,\tau _{n}\subset \varDelta ^{^{(n)}}X\), thus \((\varDelta X,\tau _{n})\) is a finite probability space. Therefore we have a reduction
which we call the empirical reduction. If \(\pi \in \varDelta ^{^{(n)}}X\) is such that \(\tau _{n}(\pi )>0\), then
In particular, it follows that the right-hand side does not depend on the probability p on X as long as \(\pi \) is “compatible” to it.
The following lemma records some standard facts about types, which can be checked by elementary combinatorics and found in [8].
Lemma 4.2
Let X be a probability space and \({\mathbf{x}}\in X^{n},\) then
-
1.
\(|\varDelta ^{^{(n)}}X| = \genfrac(){0.0pt}0{n+|X|}{|X|} \le {\mathbf{e}}^{|X| \cdot \ln (n+1)} = {\mathbf{e}}^{\textsf {O}(|X| \cdot \ln n)}\)
-
2.
\(p^{\otimes n}(\mathbf{x}) = \mathbf{e}^{-n\big [h(\mathbf{q}(\mathbf{x}))+D(\mathbf{q}(\mathbf{x})\,||\,p)\big ]}\)
-
3.
\(\mathbf{e}^{n \cdot h(\pi ) - |X| \cdot \ln (n+1)}\le |T^{n}_{\pi } \underline{X}| \le \mathbf{e}^{n\cdot h(\pi )}\) or\(|T^{n}_{\pi } \underline{X}|=\mathbf{e}^{n\cdot h(\pi )+\textsf {O}(|X|\cdot \ln n)}\)
-
4.
\(\mathbf{e}^{-n\cdot D(\pi \,||\,p)-|X| \cdot \ln (n+1)} \le \tau _n(\pi )=p^{\otimes n}(T^{n}_{\pi } \underline{X}) \le \mathbf{e}^{-n\cdot D(\pi \,||\,p)}\) or\(\tau _n(\pi )= \mathbf{e}^{-n\cdot D(\pi \,||\,p)+\textsf {O}(|X|\cdot \ln n)}\)
If \(X=(\underline{X},p_{X})\) is a probability space with rational probability distribution with denominator n, then the type over \(p_{X}\) will be called the true type of X
As a corollary to Lemma 4.2 and equation (12) we obtain the following.
Corollary 4.3
For a finite set S and \(\pi \in {\varDelta ^{^{(n)}}} S\) holds
Also, for a finite probability space \(X=(S,p)\) with a rational distribution p with denominator n holds
In particular,
The following important theorem is known as Sanov’s theorem. It can be easily derived from Lemma 4.2 or a proof can be found in [8].
Theorem 4.4
(Sanov’s Theorem) Let \(X=(S,p)\) be a finite probability space and let \(\mathbf{q}:X^{n} {\mathop {\rightarrow }\limits ^{}}(\varDelta X, \tau _n)\) be the empirical reduction. Then for every \(r>0,\)
where \(B_r(p)\) is the divergence ball (relative entropy ball) defined in (13).
Combining the estimate in Theorem 4.4 with the Pinsker’s inequality in 4.1 we obtain the following corollary.
Corollary 4.5
For a finite probability space \(X=(S,p)\) holds
4.3 Types for complete diagrams
In this subsection we generalize the theory of types for diagrams indexed by a complete poset category. The theory for a non-complete diagrams is more complex and will be addressed in our future work. Before we describe our approach we need some preparatory material.
Suppose we have a reduction \(f:X{\mathop {\rightarrow }\limits ^{}}Y\) between a pair of probability spaces. Then for any \(n\in \mathbb {N}\) there is an induced reduction \(f_{*}:(\varDelta X,\tau _{n}){\mathop {\rightarrow }\limits ^{}}(\varDelta Y,\tau _{n})\) that can be included in the following diamond diagram

that satisfies certain special condition, namely, the sides of the diamond are independent conditioned on the bottom space

In particular, for any \(\pi \in \varDelta X\) with \(\tau _{n}(\pi )>0\) and \(\pi '=f_{*}\pi \in \varDelta Y\) holds
and there is a well-defined reduction
for any \(\pi \in \varDelta ^{^{(n)}}X\) and \(\pi '=f_{*}\pi \in \varDelta ^{^{(n)}}Y\).
Now we are ready to give the definitions of types. Let \(\mathscr {X}\in {{\mathrm{\mathbf {Prob}}}}\langle \mathbf{G} \rangle \) be a complete diagram, \(\mathscr {X}=\left\{ X_{i};f_{ij}\right\} \) with initial space \(X_{0}\) and let \(\pi \in \varDelta ^{^{(n)}}\mathscr {X}\).
Define the type \(T^{n}_{\pi }\underline{\mathscr {X}}\) as the \(\mathbf{G}\)-diagram, whose individual spaces are types of the individual spaces of \(\mathscr {X}\) over the corresponding push-forwards of \(\pi \)
Consider a symmetric group \(\mathbb {S}_{n}\) acting on \(\mathscr {X}^{n}\) by automorphisms permuting the coordinates. The action leaves the types \(T^{n}_{\pi }\underline{\mathscr {X}}\) invariant and it is transitive on the initial space \(T^{n}_{\pi }X_{0}\). Thus, each type \(T^{n}_{\pi }\underline{\mathscr {X}}\) is a homogeneous diagram.
4.3.1 The empirical two-fan
Unlike in the cases of single probability spaces there is no empirical reduction from the power of \(\mathscr {X}\) to \(\varDelta \mathscr {X}\). It will be convenient for us to see the types as the power of the diagram conditioned on a distribution. This is achieved by including the power of diagram into a empirical two-fan.
Given a \(\mathbf{G}\)-diagram \(\mathscr {X}\) with initial space \(X_{0}\) we construct the associated empirical two-fan with sink vertices \(\mathscr {X}^{n}\) and \((\varDelta \mathscr {X},\tau _{n})^{\mathbf{G}}\) as the “composition” of the canonical reduction \((X_{0})^{\mathbf{G}}{\mathop {\longrightarrow }\limits ^{}}\mathscr {X}\), Eq. (4) in Sect. 2.6, and the empirical reduction \(X_{0}^{n}{\mathop {\longrightarrow }\limits ^{}}\varDelta X_{0}\cong \varDelta \mathscr {X}\) in Eq. (14).

The two-fan \(\mathscr {Q}_{n}\) is not necessarily minimal, but its minimal reduction can be constructed using Lemma 2.2 on page 15.
Let \(\pi _{0} \in (\varDelta \mathscr {X}, \tau _n)\) with \(\tau _n(\pi ) > 0\) and \(\pi _{i}=f_{0i}\pi _{0}\). Then within \(\mathscr {Q}_{n}\) holds
by Eq. (15) and therefore
For every \(n\in \mathbb {N}\) and \(\pi \in \varDelta ^{^{(n)}}\underline{X}_{0}\) the type \(T^{n}_{\pi }\mathscr {X}\) is a homogeneous diagram. Suppose that a complete diagram \(\mathscr {X}\) is such that the probability distribution \(p_{0}\) on the initial set is rational with the denominator n, then we call \(T^{n}_{p}\underline{\mathscr {X}}\) the true type of \(\mathscr {X}\) and denote
5 Distance between types
Our goal in this section is to estimate the intrinsic entropy distance between two types over two different distributions \(\pi _{1},\pi _{2}\in \varDelta ^{^{(n)}}\mathscr {S}\) in terms of the total variation distance \(|\pi _{1}-\pi _{2}|_1\).
For this purpose we use a “lagging” technique which is explained below. Practically, we couple different types by randomly removing and inserting the appropriate amount of symbols to pass from a trajectory of the one type to a trajectory of the other.
5.1 The lagging trick
Let \(\varLambda _\alpha \) be a binary probability space,
and let \(\mathscr {X}=\left\{ (\underline{X}_{i},p_{i});f_{ij}\right\} \), \(\mathscr {Z}=\left\{ (\underline{Z}_{i},q_{i});g_{ij}\right\} \) be two diagrams indexed by a complete poset category \(\mathbf{G}\) and included in a minimal two-fan, i.e a coupling,
Assume further that the distribution q on \(\mathscr {Z}\) is rational with denominator \(n\in \mathbb {N}\), that is \(q \in \varDelta ^{^{(n)}}\underline{\mathscr {Z}}\). It follows that p and \(p_{\varLambda _\alpha }\) are also rational with the same denominator n.
We construct a lagging two-fan
as follows. The right leg \(T\rho \) of \(\mathscr {L}\) is induced by the right leg \(\rho \) of the original two-fan. The left leg
is obtained by erasing symbols that reduce to \(\blacksquare \) and applying \(\rho \) to the remaining symbols. The target space for the reduction l is the true type of \(\mathscr {X}\lfloor \square \) which is “lagging” behind \(T^{n} \mathscr {Z}\) by a factor of \((1-\alpha )\). More specifically, the reduction l is constructed as follows.
Let \(\lambda _{j}:Z_{j}{\mathop {\rightarrow }\limits ^{}}\varLambda _\alpha \) be the components of the reduction \(\lambda :\mathscr {Z}{\mathop {\rightarrow }\limits ^{}}\varLambda _\alpha \). Given \(\bar{z}=(z_{i})_{i=1}^{n}\in T^{n}Z_{j} \) define the subset of indices
and define the jth component of l by
By equivariance each \(l_{j}\) is a reduction of homogeneous spaces, since the inverse image of any point has the same cardinality. Moreover the reductions \(l_{j}\) commute with the reductions in \(T^{n}\mathscr {Z}\) as explained in Sect. 4.3 and therefore l is a reduction of diagrams.
The next lemma uses the lagging two-fan to estimate the intrinsic entropy distance between its sink diagrams.
Lemma 5.1
Let \(\mathscr {X},\mathscr {Z}\in {{\mathrm{\mathbf {Prob}}}}\langle \mathbf{G} \rangle \) be two diagrams indexed by a complete poset category \(\mathbf{G}\) and included in a minimal two-fan
where distribution on \(\mathscr {Z}\) is rational with denominator \(n\in \mathbb {N}\). Then

It is an immediate consequence of the Slicing Lemma, in particular Corollary 3.10 part (2) that

By the subadditivity of the intrinsic entropy distance,

This bound is almost the estimate in Lemma 5.1, except Lemma 5.1 estimates the distance between types rather than tensor powers. We will soon see that tensor powers and types are very close in the intrinsic entropy distance. However, for the purpose of the proof of Lemma 5.1, it suffices to know that their entropies are close, an estimate that is provided by Corollary 4.3.
Proof of Lemma 5.1
We will use the lagging two-fan constructed in Eq. (17), namely
as a coupling to estimate the intrinsic entropy distance
Recall that by Corollary 4.3 for a probability space X with a rational distribution we have
Thus we can estimate \(\text {kd}(\mathscr {L})\) as follows

By minimality of the original two-fan and Shannon inequality (5) we have a bound
The second part in the sum can be estimated using relation (7) as follows
Combining all of the above we obtain the estimate in the conclusion of the lemma. \(\square \)
5.2 Distance between types
In this section we use the lagging trick as described above to estimate the distance between types over two different distributions in \(\varDelta \mathscr {S}\) where \(\mathscr {S}\) is a complete diagram of sets.
Proposition 5.2
Suppose \(\mathscr {S}\) is a complete \(\mathbf{G}\)-diagram of sets with initial set \(S_{0}\). Suppose \(p, q \in \varDelta ^{^{(n)}}\mathscr {S}\) and let \(\alpha =\frac{1}{2}|p_0-q_0|_1\). Then

The idea of the proof is to write p and q as a convex combination of a common distribution \({\hat{p}}\) and “small amounts” of \(p^{+}\) and \(q^{+}\), respectively. Then we use the lagging trick to estimate distances between types over p and \({\hat{p}}\), as well as between types over q and \({\hat{p}}\). We now present details of the proof.
Proof of Proposition 5.2
Recall that for a complete diagram \(\mathscr {S}\) with initial set \(S_{0}\) we have
Our goal now is to write p and q as the convex combination of three other distributions \({\hat{p}}\), \(p^{+}\) and \(q^{+}\) as in
We could do it the following way. Let \(\alpha :=\frac{1}{2}|p_{0}-q_{0}|_1\). If \(\alpha =1\) then the proposition follows trivially by constructing a tensor-product fan, so from now on we assume that \(\alpha <1\). Define three probability distributions \({\hat{p}}_{0}\), \(p_{0}^{+}\) and \(q_{0}^{+}\) on \(S_{0}\) by setting for every \(x\in S_{0}\)
Denote by \({\hat{p}},p^{+},q^{+}\in \varDelta \mathscr {S}\) the distributions corresponding to \({\hat{p}}_{0},p_{0}^{+},q_{0}^{+}\in \varDelta S_{0}\) under the affine isomorphism (18). Thus we have
Now we construct a pair of two-fans of \(\mathbf{G}\)-diagrams
by setting
The reductions in (19) are given by coordinate projections. We have the following isomorphisms
To estimate the distance between types we now apply Lemma 5.1 to the fans in (19)

\(\square \)
6 Asymptotic equipartition property for diagrams
Below we prove that any Bernoulli sequence of complete diagrams can be approximated by a sequence of homogeneous diagrams. This is essentially the Asymptotic Equipartition Theorem for diagrams.
Theorem 6.1
Suppose \(\mathscr {X}\in {{\mathrm{\mathbf {Prob}}}}\langle \mathbf{G} \rangle \) is a complete diagram of probability spaces. Then there exists a sequence \({\bar{\mathscr {H}}}=(\mathscr {H}_{n})_{n=0}^{\infty }\) of homogeneous diagrams of the same combinatorial type as \(\mathscr {X}\) such that for all \(n \ge |X_0|\)

where \(X_0\) is the initial space of \(\mathscr {X}\) and  is a constant only depending on \(|X_0|\) and
is a constant only depending on \(|X_0|\) and  .
.
Proof
Denote by \(\mathscr {S}= \underline{\mathscr {X}}\) the underlying diagram of sets and by \(p_\mathscr {X}\) the true distribution on \(\mathscr {S}\), such that
We will construct the approximating homogeneous sequence by taking types over rational approximations of \(p_\mathscr {X}\) in \(\varDelta \mathscr {S}\), that converge sufficiently fast to the true distribution \(p_{\mathscr {X}}\).
More specifically, we select rational distributions \(p_n \in \varDelta ^{^{(n)}}\mathscr {S}\) such that
As homogeneous spaces \(\mathscr {H}_n\) we set \(\mathscr {H}_n = T_{p_{n}}^{n}\mathscr {S}\). We will show that the intrinsic entropy distance between \(\mathscr {H}_n\) and \(\mathscr {X}^{n}\) satisfies the required estimate (20).
First we apply slicing along the empirical two-fan
defined in Sect. 4.3, Eq. (16) on page 30.
For the estimate below we use the fact that
By slicing (see Corollary 3.10(2)) along the empirical two-fan we have

To estimate the integral we split the domain into a small divergence ball \(B_{\varepsilon _n} = B_{\varepsilon _n}(p_\mathscr {X})\) around the “true” distribution and its complement
and we set the radius \(\varepsilon _n\) equal to
To estimate the first integral on the right-hand side of equality (22) note that the distance between two types over the same diagram of sets can always be crudely estimated by

Moreover, by Sanov’s theorem, Theorem 4.1, we can estimate the empirical measure of the complement of the divergence ball
where we used the definition of \(\varepsilon _n\) to conclude the last inequality. Therefore we obtain

Define
if the right-hand side is smaller than 1 and set \(\alpha _n=1\) otherwise. Then every \(\pi \in B_{\varepsilon _n}(p_\mathscr {X})\) satisfies \(|p_n - \pi | \le 2 \alpha _n\) by Pinsker’s inequality (Lemma 4.1), and the triangle inequality. Consequently, by the estimate on the distance between types in Proposition 5.2

Using the definition of \(\alpha _n\) and \(\varepsilon _n\) we find that
and hence combining the above estimates
A more precise check shows that for \(n \ge |S_0|\), the constants appearing in \(\textsf {O}\) only depend on \(|S_0|\) and  . \(\square \)
. \(\square \)
7 Technical proofs
This section contains some proofs that did not make it into the main text. The numbering of the claims in this section coincides with the numbering in the main text. Lemma that first appear in this section are numbered within section.
Proposition 2.1
Let \(\mathbf{G}\) be a poset category, and let \(\mathscr {X}= \{X_i; a_{ij} \},\) \(\mathscr {Y}= \{Y_i; b_{ij}\}\) and \(\mathscr {Z}= \{Z_i; c_{ij}\}\) be three \(\mathbf{G}\)-diagrams. Then
-
1.
A two-fan \(\mathscr {F}=(\mathscr {X}{\mathop {\leftarrow }\limits ^{}}\mathscr {Z}{\mathop {\rightarrow }\limits ^{}}\mathscr {Y})\in {{\mathrm{\mathbf {Prob}}}}\langle \mathbf{G},\varvec{\varLambda }_{2} \rangle \) of \(\mathbf{G}\)-diagrams is minimal if and only if the constituent two-fans of probability spaces \(\mathscr {F}_{i}=(X_{i}{\mathop {\leftarrow }\limits ^{}}Z_{i}{\mathop {\rightarrow }\limits ^{}}Y_{i})\) are all minimal.
-
2.
For any two-fan \(\mathscr {F}=(\mathscr {X}{\mathop {\leftarrow }\limits ^{}}\mathscr {Z}{\mathop {\rightarrow }\limits ^{}}\mathscr {Y})\) of \(\mathbf{G}\)-diagrams its minimal reduction exists, that is, there exists a minimal two-fan \(\mathscr {F}'=(\mathscr {X}{\mathop {\leftarrow }\limits ^{}}\mathscr {Z}'{\mathop {\rightarrow }\limits ^{}}\mathscr {Y})\) included in the following diagram

Before we go to the proof of Proposition 2.1, we will need the following lemma.
Lemma 7.1
Suppose we are given a pair of two-fans of probability spaces
such that \(\mathscr {F}''\) is minimal. Let
be a minimal reduction of \(\mathscr {F}\). Then for any reduction \(\rho :\mathscr {F}{\mathop {\rightarrow }\limits ^{}}\mathscr {F}''\), there exists a reduction \(\rho ':\mathscr {F}'{\mathop {\rightarrow }\limits ^{}}\mathscr {F}''\) such that \(\rho =\rho '\circ \mu \).
Proof of Lemma 7.1
We define \(\rho '\) on the sink spaces of \(\mathscr {F}'\) to coincide with \(\rho \).
To prove the lemma we just need to provide a dashed arrow that makes the following diagram commutative

The reduction \(\rho '\) is constructed by simple diagram chasing and by using the minimality of \(\mathscr {F}''\). Suppose \(z'\in \underline{Z'}\) and \(z_{1},z_{2}\in \underline{Z}\) are such that \(z' = \mu (z_{1})=\mu (z_{2})\). By commutativity of the solid arrows in the diagram above, we have
Similarly
Thus by minimality of \(\mathscr {F}''\) it follows that \(\rho (z_{1})=\rho (z_{2})\). Hence, \(\rho '\) can be constructed by setting \(\rho '(z') = \rho (z_1)\). This finishes the proof of Lemma 7.1. \(\square \)
Proof of Proposition 2.1
First we address claim (1) of the Proposition. Let \(\mathbf{G}=\left\{ O_{i};m_{ij}\right\} \) be a poset category, \(\mathscr {X},\mathscr {Y},\mathscr {Z}\in {{\mathrm{\mathbf {Prob}}}}\langle \mathbf{G} \rangle \) be three \(\mathbf{G}\)-diagrams and \(\mathscr {F}=(\mathscr {X}{\mathop {\leftarrow }\limits ^{}}\mathscr {Z}{\mathop {\rightarrow }\limits ^{}}\mathscr {Y})\) be a two-fan. Recall that it can also be considered as a \(\mathbf{G}\)-diagram of two-fans
Any minimizing reduction
induces reductions
for all i in the index set I. It follows that if all \(\mathscr {F}_{i}\)’s are minimal, then so is \(\mathscr {F}\).
Now we prove the implication in the other direction. Suppose \(\mathscr {F}\) is minimal. We have to show that all \(\mathscr {F}_{i}\) are minimal as well. Suppose there exist a non-minimal fan among \(\mathscr {F}_{i}\)’s. For an index \(i \in I\) let
Choose an index \(i_{0}\) such that
-
1.
\(\mathscr {F}_{i_{0}}\) is not minimal
-
2.
for any \(j\in {\hat{J}}(i_{0}) \backslash \{ i_0 \}\) the two-fan \(\mathscr {F}_{j}\) is minimal.
Consider now the minimal reduction \(\mu :\mathscr {F}_{i_{0}}{\mathop {\rightarrow }\limits ^{}}\mathscr {F}'_{i_{0}}\) and construct a two-fan \(\mathscr {G}=\left\{ \mathscr {G}_{i};g_{ij}\right\} \) of \(\mathbf{G}\)-diagrams by setting
and
where \(f'_{i_{0}j}\) is the reduction provided by the Lemma 7.1 applied to the diagram

We thus constructed a non-trivial reduction \(\mathscr {F}{\mathop {\rightarrow }\limits ^{}}\mathscr {G}\) which is identity on the sink \(\mathbf{G}\)-diagrams \(\mathscr {X}\) and \(\mathscr {Y}\). This contradicts the minimality of \(\mathscr {F}\).
To address the second assertion of the Lemma 2.1 observe that the argument above gives an algorithm for the construction of a minimal reduction of any two-fan of \(\mathbf{G}\)-diagrams. \(\square \)
Proposition 3.1
Let \(\mathbf{G}\) be a complete poset category. Then the bivariate function
is a pseudo-distance on \({{\mathrm{\mathbf {Prob}}}}\langle \mathbf{G} \rangle \).
Moreover, two diagrams \(\mathscr {X}, \mathscr {Y}\in {{\mathrm{\mathbf {Prob}}}}\langle \mathbf{G} \rangle \) satisfy \(\mathbf k (\mathscr {X},\mathscr {Y})=0\) if and only if \(\mathscr {X}\) is isomorphic to \(\mathscr {Y}\) in \({{\mathrm{\mathbf {Prob}}}}\langle \mathbf{G} \rangle \).
Proof
The symmetry of \(\mathbf k \) is immediate. The non-negativity of \(\mathbf k \) follows from the fact that entropy of the target space of a reduction is not greater then the entropy of the domain, which is a particular instance of the Shannon inequality (5).
We proceed to prove the triangle inequality. We will make use of the following lemma
Lemma 7.2
For a minimal full diagram of probability spaces

holds
The Lemma 7.2 follows immediately from Shannon inequality.
Suppose for now that \(\mathbf{G}=\bullet \) and we are given three probability spaces X, Y, Z together with the optimal couplings \(\mathscr {U}=(X{\mathop {\leftarrow }\limits ^{}}U{\mathop {\rightarrow }\limits ^{}}Y)\) and \(\mathscr {V}=(Y{\mathop {\leftarrow }\limits ^{}}V{\mathop {\rightarrow }\limits ^{}}Z)\) in the sense of optimization problem (9). Together they form a two-tents diagram \(\mathscr {T}=(X{\mathop {\leftarrow }\limits ^{}}U{\mathop {\rightarrow }\limits ^{}}Y{\mathop {\leftarrow }\limits ^{}}V{\mathop {\rightarrow }\limits ^{}}Z)\). If we can extend \(\mathscr {T}\) to a minimal full diagram \(\mathscr {Q}\) as in the assumption of Lemma 7.2, the triangle inequality would follow. The diagram \(\mathscr {Q}=\mathbf ad (\mathscr {T})\) can be constructed by the so called adhesion, as explained below.
As explained in Sect. 2.5.7, to construct a minimal full diagram with sink vertices X, Y and Z it is sufficient to provide a distribution on \(\underline{Q}:=\underline{X}\times \underline{Y}\times \underline{Z}\) with the correct push-forwards. We do this by setting
It is straightforward to check that the appropriate restriction of the full diagram defined in the above manner is indeed the original two-tents diagram. Essentially, to extend we need to provide a relationship (coupling) between spaces X and Z and we do it by declaring X and Z independent conditioned on Y. This is an instance of operation called adhesion, see [16]. Thus we have shown that \(\mathbf k :{{\mathrm{\mathbf {Prob}}}}\times {{\mathrm{\mathbf {Prob}}}}{\mathop {\rightarrow }\limits ^{}}\mathbb {R}\) is a pseudo-distance.
Assume now that \(\mathbf{G}\) is an arbitrary complete poset category. Suppose \(\mathscr {X}= \left\{ X_i ; f_{ij}\right\} \), \(\mathscr {Y}= \left\{ Y_i; g_{ij}\right\} \) and \(\mathscr {Z}= \left\{ Z_i; h_{ij}\right\} \) are \(\mathbf{G}\)-diagrams, with initial spaces being \(X_{0}\), \(Y_{0}\) and \(Z_{0}\), respectively. Let
be two optimal minimal two-fans.
Recall that each two-fan of \(\mathbf{G}\)-diagrams is a \(\mathbf{G}\)-diagram of two-fans between the individual spaces, that is

We construct a coupling \({\hat{\mathscr {W}}}\) between \(\mathscr {X}\) and \(\mathscr {Z}\) in the following manner. Starting with the two-tents diagram between the initial spaces, we use adhesion to extend it to a full diagram, thus constructing a coupling between \(X_{0}\) and \(Z_{0}\). This full diagram could then be “pushed down” and provides full extensions of two-tents on all lower levels. Thus we could “compose” couplings \({\hat{\mathscr {U}}}\) and \({\hat{\mathscr {V}}}\) and use a Shannon inequality to establish the triangle inequality for the intrinsic entropy distance. Details are as follows.
Consider a two-tents diagram
and extend it by adhesion, as described above, to a \(\varvec{\varLambda }_{3}\)-diagram

Together with the reductions
explained in Sect. 2.6, it gives rise to a \(\varvec{\varLambda }_{3}\)-diagram of \(\mathbf{G}\)-diagrams

The diagram above is not necessarily minimal and we now consider the “minimization” of the \(\varvec{\varLambda }_{3}\)-diagram (23), as provided by Lemma 2.2

Applying Lemma 7.2 to each

which is minimal by Lemma 2.2(1), we obtain the required inequality, concluding the proof of the triangle inequality.
Finally, if \(k(\mathscr {X}, \mathscr {Y}) = 0\), then there is a two-fan \(\mathscr {F}\) of \(\mathbf{G}\)-diagrams between \(\mathscr {X}\) and \(\mathscr {Y}\) with \(\text {kd}(\mathscr {F})= 0\), from which it follows that \(\mathscr {X}\) and \(\mathscr {Y}\) are isomorphic. \(\square \)
Proposition 3.3
Let \(\mathbf{G}\) be a complete poset category. Then with respect to the Kolmogorov distance on \({{\mathrm{\mathbf {Prob}}}}\langle \mathbf{G} \rangle \) the tensor product
is 1-Lipschitz in each variable, that is, for every triple \(\mathscr {X}, \mathscr {Y}, \mathscr {Y}' \in {{\mathrm{\mathbf {Prob}}}}\langle \mathbf{G} \rangle \) the following bound holds
Proof
The claim follows easily from the additivity of entropy in equation (6). Suppose that \(\mathscr {X}=\left\{ X_{i};f_{ij}\right\} \), \(\mathscr {Y}=\left\{ Y_{i};g_{ij}\right\} \) and \(\mathscr {Y}'=\left\{ Y'_{i};g'_{ij}\right\} \) are three \(\mathbf{G}\)-diagrams and
is an optimal fan, so that
Consider the fan
Then, by additivity of entropy, in equation (6), we have
and, therefore,
Thus, the tensor product of probability spaces is 1-Lipschitz with respect to each argument. \(\square \)
Proposition 3.7
For any triple of diagrams \(\mathscr {X},\mathscr {Y},\mathscr {U}\) holds
Proof
Define a translation-invariant bivariate function \({\varvec{\upkappa }}'\) on \({{\mathrm{\mathbf {Prob}}}}\langle \mathbf{G} \rangle \) by setting for a pair \(\mathscr {A},\mathscr {B}\in {{\mathrm{\mathbf {Prob}}}}\langle \mathbf{G} \rangle \)
Clearly, function \({\varvec{\upkappa }}'\) is translation invariant and satisfies \({\varvec{\upkappa }}'\le {\varvec{\upkappa }}\). Our task now is to show that \({\varvec{\upkappa }}'\ge {\varvec{\upkappa }}\).
Fix \(\mathscr {X},\mathscr {Y}\in {{\mathrm{\mathbf {Prob}}}}\langle \mathbf{G} \rangle \). Choose some \(\varepsilon >0\) and take \(\mathscr {Z}\in {{\mathrm{\mathbf {Prob}}}}\langle \mathbf{G} \rangle \) such that
Since translations are non-expanding, it holds also for any \(\mathscr {U}\in {{\mathrm{\mathbf {Prob}}}}\langle \mathbf{G} \rangle \)
Then for any \(n\in \mathbb {N}\) we can estimate
For \(i=0,\ldots ,n\) we set \(\mathscr {T}_{i}=\mathscr {X}^{n-i}\otimes \mathscr {Y}^{i}\otimes \mathscr {Z}\). Then we have \(\mathscr {T}_{0}=\mathscr {X}^{n}\otimes \mathscr {Z}\) and \(\mathscr {T}_{n}=\mathscr {Y}^{n}\otimes \mathscr {Z}\). Also for each \(i=0,\ldots ,n-1\) the pair \((\mathscr {T}_{i},\mathscr {T}_{i+1})\) is a translation of the pair \((\mathscr {X}\otimes \mathscr {Z},\mathscr {Y}\otimes \mathscr {Z})\) by \(\mathscr {X}^{n-i-1}\otimes \mathscr {Y}^{i}\), therefore
Now we continue the estimate
Since n is arbitrarily large, the first summand in the right-hand-side could be dropped and then by choosing \(\varepsilon >0\) arbitrarily small we obtain the required inequality. \(\square \)
Proposition 3.8
Suppose \(\mathbf{G}\) is a complete poset category and \(\varvec{\delta }=\mathbf k ,{\varvec{\upkappa }}\) is either intrinsic entropy distance or asymptotic entropy distance on \({{\mathrm{\mathbf {Prob}}}}\langle \mathbf{G} \rangle \). Then the entropy function

is 1-Lipschitz.
Proof
Let \(\mathscr {X},\mathscr {Y}\in {{\mathrm{\mathbf {Prob}}}}\langle \mathbf{G} \rangle \) and let
be an optimal fan with components
For a fixed index i we can estimate the difference of entropies
By symmetry we then have
Adding above inequalities for all i we have
By the additivity of entropy we also obtain the 1-Lipschitz property of the entropy function with respect to the asymptotic entropy distance \({\varvec{\upkappa }}\). \(\square \)
Proposition 3.9
(Slicing Lemma) Suppose \(\mathbf{G}\) is a complete poset category and we are given \(\mathscr {X},{\hat{\mathscr {X}}},\mathscr {Y},{\hat{\mathscr {Y}\in {{\mathrm{\mathbf {Prob}}}}}} \langle \mathbf{G} \rangle \)—four \(\mathbf{G}\)-diagrams and \(U,V,W\in {{\mathrm{\mathbf {Prob}}}}\)—three probability spaces, that are included into the following three-tents diagram

such that the two-fan \((U{\mathop {\leftarrow }\limits ^{}}W{\mathop {\rightarrow }\limits ^{}}V)\) is minimal. Then the following estimate holds

Proof
Since the two-fan \((U{\mathop {\leftarrow }\limits ^{}}W{\mathop {\rightarrow }\limits ^{}}V)\) is minimal the probability space W could be considered having underlying set to be a subset of the Cartesian product of the underlying sets of U and V. For any pair \((u,v)\in \underline{W}\) with a positive weight consider an optimal two-fan
where \(\mathscr {Z}_{uv}=\left\{ Z_{uv,i};\rho _{ij}\right\} \). Let \(p_{uv,i}\) be the probability distributions on \(Z_{uv,i}\)—the individual spaces in the diagram \(\mathscr {Z}_{uv}\). The next step is to take a convex combination of distributions \(p_{uv,i}\) weighted by \(p_{W}\) to construct a coupling \(\mathscr {X}{\mathop {\leftarrow }\limits ^{}}\mathscr {Z}{\mathop {\rightarrow }\limits ^{}}\mathscr {Y}\).
First we extend the 7-vertex diagram to a full \(\varvec{\varLambda }_{4}\)-diagram of \(\mathbf{G}\)-diagrams, such that the top vertex has the distribution
as described in the Sect. 2.5.7.
If we integrate over y, we obtain
Equation (24) implies that \((\pi _{\mathscr {X},i})_{*}p_{uv,i}=p_{X_i}(\,\cdot \,\lfloor u)\) and therefore
In the same way,
It follows that
and
The extended diagram contains a two-fan of diagrams \(\mathscr {F}=(\mathscr {X}{\mathop {\leftarrow }\limits ^{}}\mathscr {Z}{\mathop {\rightarrow }\limits ^{}}\mathscr {Y})\) with sink vertices \(\mathscr {X}\) and \(\mathscr {Y}\). We call its initial vertex \(\mathscr {Z}=\left\{ XY_{i},f_{ij}\right\} \).
The following estimates conclude the proof the Slicing Lemma. First we use the definitions of intrinsic entropy distance \(\mathbf k \) and of \(\text {kd}(\mathscr {F})\) to estimate
Next, we apply the definition of the conditional entropy to rewrite the right-hand side
We now use (26) and rearrange terms to obtain
By the integral formula for conditional entropy (7) applied to the first three terms we get
However, because of (25) this simplifies to
Therefore,

\(\square \)
References
Ay, N., Bertschinger, N., Der, R., Güttler, F., Olbrich, E.: Predictive information and explorative behavior of autonomous robots. Eur. Phys. J. B 63(3), 329–339 (2008)
Baez, J.C., Fritz, T., Leinster, T.: A characterization of entropy in terms of information loss. Entropy 13(11), 1945–1957 (2011)
Boltzmann, L.: über die mechanische Bedeutung des zweiten Hauptsatzes der Wärmetheorie. Wiener Berichte 53, 195–220 (1866)
Boltzmann, L.: Vorlesungen über Gastheorie, vols. I, II. J.A. Barth, Leipzig (1896)
Bertschinger, N., Rauh, J., Olbrich, E., Jost, J., Ay, N.: Quantifying unique information. Entropy 16(4), 2161–2183 (2014)
Cicalese, F., Gargano, L., Vaccaro, U.: How to find a joint probability distribution of minimum entropy (almost) given the marginals. In: 2017 IEEE International Symposium on Information Theory (ISIT), pp. 2173–2177. IEEE, New York (2017)
Csiszár, I.: The method of types. IEEE Trans. Inf. Theory, 44(6):2505–2523 (1998) (Information theory: 1948–1998)
Cover, T.M., Thomas, J.A.: Elements of Information Theory. Wiley Series in Telecommunications. A Wiley-Interscience Publication, Wiley, New York (1991)
Friston, K.: The free-energy principle: a rough guide to the brain? Trends Cogn. Sci. 13(7), 293–301 (2009)
Gromov, M.: In a search for a structure, part 1: on entropy (2012). Preprint. https://www.ihes.fr/~gromov/wp-content/uploads/2018/08/structre-serch-entropy-july5-2012.pdf and https://math.mit.edu/~dspivak/teaching/sp13/gromov--EntropyViaCT.pdf. Accessed 08 Oct 2018
Kocaoglu, M., Dimakis, A.G., Vishwanath, S., Hassibi, B.: Entropic causality and greedy minimum entropy coupling (2017). arXiv preprint. arXiv:1701.08254
Kolmogorov, A.N.: New metric invariant of transitive dynamical systems and endomorphisms of Lebesgue spaces. Dokl. Russ. Acad. Sci. 119(5), 861–864 (1958)
Kolmogorov, A.N.: New metric invariant of transitive dynamical systems and endomorphisms of Lebesgue spaces. Dokl. Russ. Acad. Sci. 124, 754–755 (1959)
Kovacevic, M., Stanojevic, I., Senk, V.: On the hardness of entropy minimization and related problems. In: Information Theory Workshop (ITW). 2012 IEEE, pp. 512–516. IEEE, New York (2012)
MacLane, S.: Categories for the Working Mathematician. Graduate Texts in Mathematics, vol. 5. Springer, New York (1971)
Matus, F.: Infinitely many information inequalities. In: IEEE International Symposium on Information Theory, 2007. ISIT 2007, pp. 41–44. IEEE, New York (2007)
Ornstein, D.: Bernoulli shifts with the same entropy are isomorphic. Adv. Math. 4, 337–352 (1970)
Steudel, B., Ay, N.: Information-theoretic inference of common ancestors. Entropy 17(4), 2304–2327 (2015)
Shannon, C.E.: A mathematical theory of communication. Bell Syst. Tech. J. 27(3), 379–423 (1948)
Shannon, C.: The lattice theory of information. Trans. IRE Prof. Group Inf. Theory 1(1), 105–107 (1953)
Sinai, Ya G.: On the notion of entropy of a dynamical system. Dokl. Russ. Acad. Sci. 124, 768–771 (1959)
Sinai, Y.G.: Introduction to Ergodic Theory. Princeton University Press, Princeton (1976) (Translated by V. Scheffer Mathematical Notes, vol. 18)
Van Dijk, S.G., Polani, D.: Informational constraints-driven organization in goal-directed behavior. Adv. Complex Syst. 16(02n03), 1350016 (2013)
Vidyasagar, M.: A metric between probability distributions on finite sets of different cardinalities and applications to order reduction. IEEE Trans. Autom. Control 57(10), 2464–2477 (2012)
Yeung, R.W.: A First Course in Information Theory. Springer Science & Business Media, Berlin (2012)
Acknowledgements
Open access funding provided by Max Planck Society. We would like to thank Tobias Fritz, František Matúš, Misha Movshev and Johannes Rauh for inspiring discussions. We are grateful to the participants of the Wednesday Morning Session at the CASA group at the Eindhoven University of Technology for valuable feedback on the introduction of the article. Finally, we thank the Max Planck Institute for Mathematics in the Sciences, Leipzig, for its hospitality.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Matveev, R., Portegies, J.W. Asymptotic dependency structure of multiple signals. Info. Geo. 1, 237–285 (2018). https://doi.org/10.1007/s41884-018-0013-5
Received:
Revised:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s41884-018-0013-5