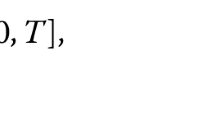Abstract
In this paper we prove local existence of solutions to the nonlinear heat equation \(u_t = \Delta u +a |u|^\alpha u, \; t\in (0,T),\; x=(x_1,\ldots , x_N)\in {\mathbb {R}}^N,\; a = \pm 1,\; \alpha >0;\) with initial value \(u(0)\in L^1_{\mathrm{{loc}}}({\mathbb {R}}^N{\setminus }\{0\}),\) anti-symmetric with respect to \(x_1,\; x_2,\ldots , x_m\) and \(|u(0)|\le C(-1)^m\partial _{1}\partial _{2}\cdots \partial _{m}(|x|^{-\gamma })\) for \(x_1>0,\ldots , x_m>0,\) where \(C>0\) is a constant, \(m\in \{1, 2,\ldots , N\},\) \(0<\gamma <N\) and \(0<\alpha <2/(\gamma +m).\) This gives a local existence result with highly singular initial values. As an application, for \(a=1,\) we establish new blowup criteria for \(0<\alpha \le 2/(\gamma +m),\) including the case \(m=0.\) Moreover, if \((N-4)\alpha <2,\) we prove the existence of initial values \(u_0 = \lambda f,\) for which the resulting solution blows up in finite time \(T_{\max }(\lambda f),\) if \(\lambda >0\) is sufficiently small. We also construct blowing up solutions with initial data \(\lambda _n f\) such that \(\lambda _n^{[({1\over \alpha }-{\gamma +m\over 2})^{-1}]}T_{\max }(\lambda _n f)\) has different finite limits along different sequences \(\lambda _n\rightarrow 0.\) Our result extends the known “small lambda” blow up results for new values of \(\alpha\) and a new class of initial data.
Similar content being viewed by others
References
Bandle, C., Levine, H.A.: On the existence and nonexistence of global solutions of reaction–diffusion equations in sectorial domains. Trans. AMS 316, 595–622 (1989)
Brézis, H.: Functional Analysis, Sobolev Spaces and Partial Differential Equations. Universitext. Springer, New York (2011)
Brézis, H., Friedman, A.: Nonlinear parabolic equations involving measures as initial conditions. J. Math. Pures Appl. 62, 73–97 (1983)
Cazenave, T., Dickstein, F., Escobedo, M., Weissler, F.B.: Self-similar solutions of a nonlinear heat equation. J. Math. Sci. Univ. Tokyo 8, 501–540 (2001)
Cazenave, T., Dickstein, F., Weissler, F.B.: Universal solutions of the heat equation in \({\mathbb{R}}^{N}\). Discrete Contin. Dyn. Syst. 9, 1105–1132 (2003)
Cazenave, T., Dickstein, F., Weissler, F.B.: Multi-scale multi-profile global solutions of parabolic equations in \({\mathbb{R}}^{N}\). Discrete Contin. Dyn. Syst. Ser. S 5, 449–472 (2012)
Dickstein, F.: Blowup stability of solutions of the nonlinear heat equation with a large life span. J. Differ. Equ. 223, 303–328 (2006)
Fermanian Kammerer, C., Merle, F., Zaag, H.: Stability of the blow-up profile of nonlinear heat equations from the dynamical system point of view. Math. Ann. 317, 347–387 (2000)
Ghoul, T.: An extension of Dickstein’s “small lambda” theorem for finite time blowup. Nonlinear Anal. T.M.A. 74, 6105–6115 (2011)
Giga, Y., Matsui, S., Sasayama, S.: Blow up rate for semilinear heat equations with subcritical nonlinearity. Indiana Univ. Math. J. 53, 483–514 (2004)
Giga, Y., Matsui, S., Sasayama, S.: On blow up rate for sign-changing solutions in a convex domain. Math. Methods Appl. Sci. 27, 1771–1782 (2004)
Gui, C., Wang, X.: Life span of solutions of the Cauchy problem for a semilinear heat equation. J. Differ. Equ. 115, 166–172 (1995)
Kavian, O.: Remarks on the large time behaviour of a nonlinear diffusion equation. Ann. I. H. Poincaré Anal. Non Linéaire 4, 423–452 (1987)
Lee, T.Y., Ni, W.M.: Global existence, large time behavior and life span of solutions of a semilinear parabolic Cauchy problem. Trans. Am. Math. Soc. 333, 365–378 (1992)
Levine, H.A., Meier, P.: The value of the critical exponent for reaction–diffusion equations in cones. Arch. Ration. Mech. Anal. 109, 73–80 (1990)
Meier, P.: Existence et non-existence de solutions globales d’une équations de la chaleur semi-linéaire: extention d’un théoreme de Fujita. C. R. Acad. Sci. Paris Ser. I(303), 635–637 (1986)
Meier, P.: Blow up of solutions of semilinear parabolic differential equations. Z. Angew. Math. Phys. 39, 135–149 (1988)
Mizoguchi, N., Yanagida, E.: Blowup and life span of solutions for a semilinear parabolic equation. SIAM J. Math. Anal. 29, 1434–1446 (1998)
Molinet, L., Tayachi, S.: Remarks on the Cauchy problem for the one-dimensional quadratic (fractional) heat equation. J. Funct. Anal. 269, 2305–2327 (2015)
Mouajria, H., Tayachi, S., Weissler, F.B.: The heat equation on sectorial domains, highly singular initial values and applications. J. Evol. Equ. 16, 341–364 (2016)
Mueller, C.E., Weissler, F.B.: Single point blow-up for a general semilinear heat equation. Indiana Univ. Math. J. 34, 881–913 (1985)
Quittner, P., Souplet, Ph: Superlinear Parabolic Problems. Blow-Up, Global Existence and Steady States. Birkhäuser, Basel (2007)
Ribaud, F.: Semilinear parabolic equations with distributions as initial values. Discrete Contin. Dyn. Syst. 3, 305–316 (1997)
Rouchon, P.: Blow-up of solutions of nonlinear heat equations in unbounded domains for slowly decaying initial data. ZAMP 52, 1017–1032 (2001)
Souplet, Ph, Weissler, F.B.: Self-similar sub-solutions and blow-up for nonlinear parabolic equations. J. Math. Anal. Appl. 212, 60–74 (1997)
Tayachi, S., Weissler, F.B.: The nonlinear heat equation with high order mixed derivatives of the Dirac delta as initial values. Trans. AMS 366, 505–530 (2014)
Tayachi, S., Weissler, F.B.: Some remarks on life span results (in preparation)
Weissler, F.B.: Existence and nonexistence of global solutions for a semilinear heat equation. Isr. J. Math. 38, 29–40 (1981)
Weissler, F.B.: \(L^p\)-energy and blow-up for a semilinear heat equation. Proc. Symp. Pure Math. 45(Part 2), 545–551 (1986)
Wu, J.: Well-posedness of a semilinear heat equation with weak initial data. J. Fourier Anal. Appl. 4, 629–642 (1998)
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Tayachi, S., Weissler, F.B. The nonlinear heat equation involving highly singular initial values and new blowup and life span results. J Elliptic Parabol Equ 4, 141–176 (2018). https://doi.org/10.1007/s41808-018-0014-5
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s41808-018-0014-5