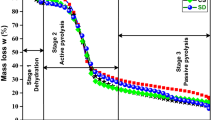
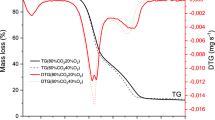
Abstract
Reutilizing the shavings of willow wood (Salix alba), a waste biomass from cricket bat manufacturing units of Kashmir (India) through pyrolysis, would prove to be a promising way for bioenergy production. The thermal degradation of this waste biomass was carried out under inert atmosphere using thermogravimetric analysis (TGA), at three different heating rates of 10, 25, and 50 K min−1. The kinetic and thermodynamic analyses were performed using isoconversional models of Kissenger-Akahira-Sunrose (KAS) and Ozawa-Flynn-Wall (OFW). The heating value of the willow wood shavings was found to be 18.03 MJ kg−1. The values of activation energy were found to be in the range of around 41.5 to 167.8 kJ mol−1 through conversion points of 0.2 to 0.8. The average value of change in Gibbs free energy were calculated to be of the order of 183.2 and 182 kJ mol−1 using KAS and OFW models, respectively. The thermal degradation reaction mechanism was predicted using Coats-Redfern method which showed that the one-dimensional diffusion model and first-order kinetic reaction model were best suited to represent the degradation process involving both exothermic and endothermic reactions. The thermodynamic parameters including pre-exponential factor, changes in enthalpy, and entropy reflect an enormous potential of the Salix alba shavings as low-cost waste biomass for bioenergy production.





Similar content being viewed by others
Abbreviations
- A:
-
Pre-exponential factor (s−1)
- CR:
-
Coats-Redfern
- D:
-
Diffusion-based reactor mechanism
- DSC:
-
Differential scanning calorimetry
- DTA:
-
Differential thermal analysis
- DTG:
-
Differential thermogravimetry
- Ea :
-
Activation energy (kJ mol−1)
- F:
-
Chemical reaction-based mechanism
- ∆G:
-
Gibbs free energy (kJ mol−1)
- ∆H:
-
Change in enthalpy (kJ mol−1)
- HHV:
-
High heating value (MJ g−1)
- KAS:
-
Kissinger-Akahira-Sunrose
- k (T):
-
Reaction rate constant
- Kb :
-
Boltzman constant (1.381× 10−23 J K−1)
- OFW:
-
Ozawa-Flynn-Wall
- R:
-
Gas constant (8.314 J K−1 mol−1)
- ∆S:
-
Change in entropy (kJ mol−1)
- T:
-
Temperature (K)
- Tp :
-
Peak temperature of DTG curve (K)
- TGA:
-
Thermogravimetric analyzer/analysis
- WWS:
-
Willow wood shavings
References
Acikalm K (2011) Thermogravimetric analysis of walnut shell as pyrolysis feedstock. J Therma Anal Calorim 105:145–150
Ahmad MS, Mehmood MA, Taqvi STH, Elkamel A, Liu C, Xu J, Rahimuddin SA, Gull M (2017) Pyrolysis, kinetics analysis, thermodynamics parameters and reaction mechanism of Typha latifolia to evaluate its bioenergy potential. Bioresour Technol 245:491–501
Ahmaruzzaman M (2008) Proximate analyses and predicting HHV of chars obtained from co-craking of petroleum vacuum residue with coal, plastics and biomass. Bioresour Technol 99:5043–5044
ASTME1534–93 (Reapproved 2013) Standard test method for determination of ash content of particulate wood fuels
ASTME1755-01 (2007) Standard test method for ash in biomass. ASTM International, West Conshohocken
ASTME871–72 (Reapproved 2013) Standard test method for moisture analysis of particulate wood fuels
ASTME872–82 (Reapproved 2013) Standard test method for volatile matter in the analysis of particulate wood fuels
Braga RM, Melo DM, Aquino FM, Frietas JC, Melo MA, Baros JM, Fontes MS (2014) Characterization and comparative study of pyrolysis kinetics of the rice husk and elephant grass. J Therm Anal Calorim 115(2):1915–1920
Bridgwater AV (2012) Review of fast pyrolysis of biomass and product upgrading. Biomass Bioenergy 38:68–94
Buryan P, Staff M (2008) Pyrolysis of the waste biomass. J Thermal Anal Calorim 93(2):637–640
Butler E, Devlin G, Meier D, Mc Donnell K (2013) Fluidized bed pyrolysis of lignocellulosic biomasses and comparison of bio-oil and micropyrolyser pyrolysate by GC/MS-FID. J Anal App Pyrolysis 103:96–101
Ceylan S, Kazan D (2015) Pyrolysis kinetics and thermal characteristics of microalgae Nannochloropsisaculata and Tetraselmis sp. Bioresour Technol 187:1–5
Ceylan S, Topcu Y (2014) Pyrolysis kinetics of hazelnut husk using thermogravimetric analysis. Bioresour Technol 156:182–188
Doyle CD (1965) Series approximations to the equations of thermogravimetric data. Nature 207:290–291
El-Sayed SA, Mostafa ME (2015) Kinetic parameters determination of biomass pyrolysis fuels using TGA and DTA techniques. Waste Biomass Valoriz 6:401–415
Haq IU, Dar BA, Thoker IA (2013) Impact of disturbances on cricket bat manufacturing industry in Kashmir valley. Inter J Research Soc Sci 3:175–183
Heo HS, Park HJ, Park YK, Ryu C, Suh DJ, Suh YW, Yim JH, Kim SS (2010) Bio-oil production from fast pyrolysis of waste furniture sawdust in a fluidized bed. Bioresour Technol 101:591–596
Khawam A, Flanagan DR (2006) Solid-state kinetic models: basics and mathematical fundamentals. J Phys Chem B 110:17315–17328
Kim YS, Kim YS, Kim SH (2010) Investigations of thermodynamic parameters in the thermal decomposition of plastic waste-waste lube oil compounds. Environ Sci Technol 44(13):5313–5317
Li D, Chen L, Chen S, Zhang X, Chen F, Ye N (2012) Comparative evolution of the pyrolytic and kinetic characteristics of a macro alga (Sargassum thumbergii) and a fresh water plant (Potamageton cripsus). Fuel 96:185–191
Maia AAD, de-Morais LC (2016) Kinetic parameters of red pepper waste as biomass to solid bio fuel. Bioresour Technol 204:157–163
Mehmood MA, Ye G, Luo H, Liu C, Malik S, Afzal I, Xu J, Ahmad MS (2017) Pyrolysis and kinetic analyses of Camel grass (Cymbopogon schoenanthus) for bio energy. Bioresour Technol 228:18–24
Monti A, Di Virgilio N, Venturi G (2008) Mineral composition and ash content of six major energy crops. Biomass Bioenergy 32(3):216–223
Mythili R, Venkatachalam P, Subramanian P, Uma D (2013) Characterization of bioresidues for biooil production through pyrolysis. Bioresour Technol 138:71–78
Nhuchhen DR, Salam PA (2012) Estimation of higher heating value of biomass from proximate analysis: a new approach. Fuel 99:55–63
Ningbo G, Baoling L, Aimin L, Juanjuan L (2015) Continuous pyrolysis of pine sawdust at different pyrolysis temperatures and solid residence times. J Anal Appl Pyrol 114:155–162
Popescu MC, Popescu CM, Lisa G, Sakata Y (2011) Evaluation of morphological and chemical aspects of different wood species by spectroscopy and thermal methods. J Mol Structure 988(1):65–72
Poskrobko S (2012) Biofuels Krol D, Part II. Thermogravimetric research of dry composition. J Thermal Anal Calorim 109:629–638
Rath J, Staudinger G (2001) Cracking reactions of tar from pyrolysis of spruce wood. Fuel 80(10):1379–1389
Saqib A, Tabbssum MR, Rashid U, Ibrahim M, Gill SS, Mehmood MA (2013) Marine macro algae Ulva: a potential feed-stock for bio-ethanol and biogas production. Asian J Agri Biol 1:155–163
Shen J, Zhu S, Liu X, Zhang H, Tan J (2010) The prediction of elemental composition of biomass based on proximate analysis. Energy Conservs Manag 51:983–987
Skevas T, Swinton SM, Hayden NJ (2014) What type of land owner would supply marginal land for energy crops. Biomass Bioenergy 67:252–259
Slopiecka K, Bartocci P, Fantozzi F (2012) Thermogravimetric analysis and kinetic study of poplar wood pyrolysis. Appl Energy 97:491–497
Vyazovkin S, Wight CA (1997) Kinetics in solids. Annu Rev Phy Chem 48:125–149
White JE, Catallo WJ, Legendre BL (2011) Biomass pyrolysis kinetics: a comparative critical review with relevant agricultural residue case studies. J Anal Appl Pyrolysis 91:1–33
Yahiaoui M, Hadoun H, Toumert I, Hassani A (2015) Determination of kinetic parameters of Phlomis Bovei de Noé using thermogravimetric analysis. Bioresour Technol 196:441–447
Yan HL, Zong ZM, Li ZK, Kong J, Zheng QX, Li Y, Wei XY (2017) Sweet sorghum stalk liquefaction in supercritical methanol: effects of operating conditions on product yields and molecular composition of soluble fraction. Fuel Process Technol 155:42–50
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of Interest
The authors declare that they have no conflict of interest.
Rights and permissions
About this article
Cite this article
Rasool, T., Srivastava, V.C. & Khan, M.N.S. Bioenergy Potential of Salix alba Assessed Through Kinetics and Thermodynamic Analyses. Process Integr Optim Sustain 2, 259–268 (2018). https://doi.org/10.1007/s41660-018-0040-7
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s41660-018-0040-7