Skip to main content
SpringerLink
Log in

Neural networks-based model predictive control for precision motion tracking of a micropositioning system

  • Regular Paper
  • Published:
International Journal of Intelligent Robotics and Applications Aims and scope Submit manuscript

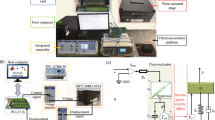
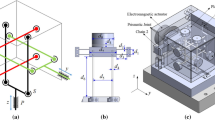
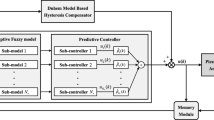
Abstract

Micropositioning systems are widely employed in industrial applications. Nonminimum-phase (NMP) is a normal phenomenon in micropositioning system, which leads to a great challenge for control system design. Model predictive control (MPC) is effective in handling the NMP problem. However, the parameter tuning of MPC is quite complicated and time-consuming using traditional methods for motion tracking control implementation. In this paper, an efficient neural networks (NN) model is established to optimize the MPC controller parameters including the prediction horizon, control horizon, and weighting factor. With the developed NN model, the motion tracking process of the micropositioning system is more intelligent and adaptive. The effectiveness of the presented novel NN-MPC control strategy has been verified by conducting extensive simulation studies. Furthermore, the results demonstrate that the NN-MPC scheme has good robustness under model parameter variation and noise condition.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16
Fig. 17

Similar content being viewed by others

References

  • Ali A., Ahmed, S.F., Joyo, M.K., Kushsairy K.: Mpc-pid comparison for controlling therapeutic upper limb rehabilitation robot under perturbed conditions. In: Proc. of 2017 IEEE 3rd International Conference on Engineering Technologies and Social Sciences (ICETSS), 2017, pp. 1–5

  • Chen, Z., Zheng, J., Zhang, H., Ding, H.: Tracking of piezoelectric actuators with hysteresis: a nonlinear robust output regulation approach. Int J Robust Nonlinear Control 27(15), 2610–2626 (2017)

    MathSciNet  MATH  Google Scholar 

  • Cheng, L., Liu, W., Hou, Z., Yu, J., Tan, M.: Neural-network-based nonlinear model predictive control for piezoelectric actuators. IEEE Trans Ind Electron 62(12), 7717–7727 (2015)

    Google Scholar 

  • Dong, R., Tan, Y., Xie, Y., Janschek, K.: Recursive identification of micropositioning stage based on sandwich model with hysteresis. IEEE Trans Control Syst Technol 25(1), 317–325 (2017)

    Google Scholar 

  • Elmali, H., Olgac, N.: Sliding mode control with perturbation estimation (SMCPE): a new approach. Int J Control 56(4), 923–941 (1992)

    MathSciNet  MATH  Google Scholar 

  • Hauser, J., Sastry, S., Meyer, G.: Nonlinear control design for slightly non-minimum phase systems: application to v/stol aircraft. Automatica 28(4), 665–679 (1992)

    MathSciNet  MATH  Google Scholar 

  • Hoagg, J.B., Bernstein, D.S.: Nonminimum-phase zeros—much to do about nothing—classical control—revisited part ii. IEEE Control Syst Mag 27(3), 45–57 (2007)

    Google Scholar 

  • Kapur J.N., Kesavan H.K.: Entropy optimization principles and their applications. In: Entropy and Energy Sissipation in Water Resources. Springer, 1992, pp. 3–20

  • Liu, W., Cheng, L., Hou, Z., Yu, J., Tan, M.: An inversion-free predictive controller for piezoelectric actuators based on a dynamic linearized neural network model. IEEE/ASME Trans Mech 21(1), 214–226 (2016)

    Google Scholar 

  • Mohammadzaman I., Sedigh, A.K., Nasirian, M.: Predictive control of non-minimum phase motor with backlash in an earth station antenna. In: Proc. of 2006 Chinese Control Conference (CCC 2006), 2006, pp. 900–905

  • Park, K., Desai, J.P.: Micropositioning and control of an underactuated platform for microscopic applications. IEEE/ASME Trans Mech 21(6), 2635–2646 (2016)

    Google Scholar 

  • Qin, S.J., Badgwell, T.A.: A survey of industrial model predictive control technology. Control Eng Pract 11(7), 733–764 (2003)

    Google Scholar 

  • Rana, M.S., Pota, H.R., Petersen, I.R.: Performance of sinusoidal scanning with mpc in afm imaging. IEEE/ASME Trans Mech 20(1), 73–83 (2015)

    Google Scholar 

  • Rawlings, J.B.: Tutorial overview of model predictive control. IEEE Control Syst Mag 20(3), 38–52 (2000)

    Google Scholar 

  • Richalet, J.: Industrial applications of model based predictive control. Automatica 29(5), 1251–1274 (1993)

    MathSciNet  Google Scholar 

  • Rossiter, J.A.: Model-based predictive control: a practical approach. CRC Press, Boca Raton (2017)

    Google Scholar 

  • Sin, G., De Pauw, D.J., Weijers, S., Vanrolleghem, P.A.: An efficient approach to automate the manual trial and error calibration of activated sludge models. Biotechnol Bioeng 100(3), 516–528 (2008)

    Google Scholar 

  • Wan, S., Xu, Q.: Design and analysis of a new compliant xy micropositioning stage based on roberts mechanism. Mech Mach Theory 95, 125–139 (2016)

    Google Scholar 

  • Wang P., Xu Q.: Model predictive control design of a flexure-based micropositioning system. In: Proc. of 2016 Chinese Control and Decision Conference (CCDC), 2016, pp. 5232–5236

  • Wang L.: Model predictive control system design and implementation using MATLAB®. Springer, 2009

  • Wills, A.G., Bates, D., Fleming, A.J., Ninness, B., Moheimani, S.O.R.: Model predictive control applied to constraint handling in active noise and vibration control. IEEE Trans Control Syst Technol 16(1), 3–12 (2008)

    Google Scholar 

  • Wojsznis, W., Gudaz, J., Blevins, T., Mehta, A.: Practical approach to tuning mpc. ISA Trans 42(1), 149–162 (2003)

    Google Scholar 

  • Xiao, H., Li, Z., Yang, C., Zhang, L., Yuan, P., Ding, L., Wang, T.: Robust stabilization of a wheeled mobile robot using model predictive control based on neurodynamics optimization. IEEE Trans Ind Electron 64(1), 505–516 (2017)

    Google Scholar 

  • Xu, Q.: New flexure parallel-kinematic micropositioning system with large workspace. IEEE Trans Robot 28(2), 478–491 (2012)

    Google Scholar 

  • Xu, Q.: Digital integral terminal sliding mode predictive control of piezoelectric–driven motion system. IEEE Trans Ind Electron 63(6), 3976–3984 (2016)

    Google Scholar 

  • Yan Y., Xu Q.: Neural networks-based pid precision motion control of a piezo-actuated microinjector. In: Intelligent Robotics and Applications. ICIRA 2019, H. Yu, J. Liu, L. Liu, Z. Ju, Y. Liu, D. Zhou, Eds., Springer, 2019, Lecture Notes in Computer Science 11745, ISBN: 978-3-030-27528-0, pp. 407-418

  • Zhang, R., Gao, F.: Multivariable decoupling predictive functional control with non-zero-pole cancellation and state weighting: application on chamber pressure in a coke furnace. Chem Eng Sci 94, 30–43 (2013)

    Google Scholar 

  • Zhang, X., Xu, Q.: Design and testing of a new 3-DOF spatial flexure parallel micropositioning stage. Int J Precis Eng Manuf 19(1), 109–118 (2018)

    Google Scholar 

  • Zhang, Y., Yu, L.-C.: Single-cell microinjection technology in cell biology. Bioessays 30(6), 606–610 (2008)

    Google Scholar 

  • Zhang, H., Hu, B., Li, L., Chen, Z., Wu, D., Xu, B., Huang, X., Gu, G., Yuan, Y.: Distributed hammerstein modeling for cross-coupling effect of multiaxis piezoelectric micropositioning stages. IEEE/ASME Trans Mech 23(6), 2794–2804 (2018)

    Google Scholar 

  • Zou, Q., Leang, K., Sadoun, E., Reed, M., Devasia, S.: Control issues in high-speed afm for biological applications: collagen imaging example. Asian J Control 6(2), 164–178 (2004)

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Electromechanical Engineering, University of Macau, Avenida da Universidade, Taipa, Macau, China

    Yizheng Yan & Qingsong Xu

Authors
  1. Yizheng Yan
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Qingsong Xu
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Qingsong Xu.

Ethics declarations

Conflict of interest

The authors declare that they have no conflict of interest.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

This work was funded in part by National Natural Science Foundation of China (File No. 51575545), The Science and Technology Development Fund, Macau SAR (File Nos. 0008/2020/A, 0153/2019/A3 and 0022/2019/AKP) and University of Macau (File Nos. MYRG2018-00034-FST and MYRG2019-00133-FST).

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Yan, Y., Xu, Q. Neural networks-based model predictive control for precision motion tracking of a micropositioning system. Int J Intell Robot Appl 4, 164–176 (2020). https://doi.org/10.1007/s41315-020-00134-3

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s41315-020-00134-3

Keywords

Search

Navigation