Abstract
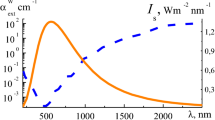
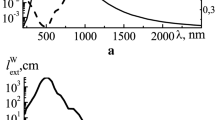
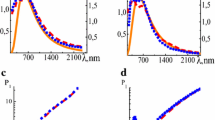
Absorption of solar radiation by nanoparticles and their heating are applied in light-to-heat conversion, in solar thermal devices, photocatalysis, solar cells, etc. The purpose of this investigation is the modeling of the heating dynamics of single homogeneous and core–shell nanoparticles, their assemblies and surrounding medium (fluid) by solar radiation allowing to select their parameters for effective applications. The properties of homogeneous metallic (titanium Ti and aurum Au) nanoparticles and titanium core–its oxide shell (Ti–TiO2) nanoparticles with the radii in the range 25–125 nm have been investigated for the spectral interval 200–2500 nm of solar radiation. Novel temporal dependencies of the temperatures of single nanoparticles, their assemblies and ambient medium under solar irradiation have been investigated. The influence of the concentrations, sizes and other parameters of nanoparticles on dynamics and the results of solar heating have been established. Metallic Ti and core–shell Ti–TiO2 nanoparticles with the radii in the range 75–125 nm and maximal values of energetic \( q_{0} r_{0}^{2} \), \( q_{1} r_{1}^{2} \) and optical P1 ≥ 1 parameters can be used for effective absorption of solar radiation and heating of nanoparticles and nanofluids in the spectral interval 200–1100 nm in volumetric water absorber and in the spectral interval 1100–2500 nm in surface absorbing layer of water. Presented results can be used for increase in efficiency of solar absorption by nanofluids and can be applied for the development of novel working nanofluids and their heating in solar collectors. Selection of suitable nanoparticles and nanofluids for effective absorption of solar radiation and their heating includes the choice of nanoparticles structure (homogeneous, core–shell, etc.), material (metal, oxide, etc.), size (their radii, thicknesses of shells), their concentrations and the simultaneous use of appropriate values of parameters realizing effective heating of nanoparticles and surrounding medium. These results are highlighting the importance of the use of established remarkable approaches that can improve current solar thermal technologies in near future.




Similar content being viewed by others
References
Kalogirou SA (2013) Solar energy engineering processes and systems. Academic Press, Cambridge
Wang Z, Qiu F, Yang W, Zhao X (2015) Applications of solar water heating system with phase change material. Renew Sustain Energy Rev 52:645–652
Jebasingh VK, Herbert GM (2016) A review of solar parabolic trough collector. Renew Sustain Energy Rev 54:1085–1091
Toygar EM, Bayram T, Daş O, Demir A (2016) The design and development of solar flat mirror (Solarux) system. Renew Sustain Energy Rev 54:1278–1284
Pandey KM, Chaurasiya R (2017) A review on analysis and development of solar flat plate collector. Renew Sustainable Energy Rev 67:641–650
Phelan P, Otanicar T, Taylor R, Tyagi H (2013) Trends and opportunities in direct absorption solar thermal collectors. J Therm Sci Eng Appl 5:021003
Masud M, Khan K, Chowdhury AA, Sayeed Hassan NM (eds) (2017) Application of thermo-fluid processes in energy systems: key issues and recent developments for a sustainable future. Springer, Berlin
Shrivastava RL, Kumara V, Untawale SP (2017) Modeling and simulation of solar water heater: a TRNSYS perspective. Renew Sustain Energy Rev 67:126–143
Saidur R, Meng TC, Said Z, Hasanuzzaman M, Kamyar A (2012) A evaluation of the effect of NF-based absorbers on direct solar collector. Int J Heat Mass Transfer 55:5899–5907
Tang Y, Vlahovic B (2013) Metallic nanoparticles for trapping light. Nanoscale Res Lett 8:65–72
Kameya Y, Hanamura K (2011) Enhancement of solar radiation absorption using NP suspension. Sol Energy 85:299–307
He Q, Wang S, Zeng S, Zheng Z (2013) Experimental investigation on photothermal properties of nanofluids for direct absorption solar thermal energy systems. Energy Conver Manag 73:150–157
Reddy KS, Kamnapure NR, Srivastava S (2017) Nanofluid and nanocomposite applications in solar energy conversion systems for performance enhancement: a review. Int J Low Carbon Technol 12:1–23
Hussein AK (2016) Applications of nanotechnology to improve the performance of solar collectors—recent advances and overview. Renew Sustain Energy Rev 62:767–792
Verma SK, Tiwari AK (2015) Progress of nanofluid application in solar collectors: a review. Renew Sustain Energy Rev 100:324–346
Leong K, Ong HC, Amer NH, Norazrina MJ, Risby MS (2016) An overview on current application of nanofluids in solar thermal collector and its challenges. Renew Sustain Energy Rev 53:1092–1095
Verma SK, Tiwari AK, Chauhan DS (2017) Experimental evaluation of flat plate solar collector using nanofluids. Energy Conver Manag 134:103–115
Hashemi SM, Choi J-W, Psaltis D (2014) Solar thermal harvesting for enhanced photocatalytic reactions. Phys Chem Chem Phys 16:5137–5141
Ba-Abbad M, Kadhum AA, Mohamad AB, Takriff MS, Sopian K (2012) Synthesis and catalytic activity of Ti–TiO2 nanoparticles for photochemical oxidation of concentrated chlorophenols under direct solar radiation. Int J Electrochem Sci 7:4871–4888
Yadav D, Banerjee R (2016) A review of solar thermochemical processes. Renew Sustain Energy Rev 54:497–532
Villesen TF, Uhrenfeldt C, Johansen D, Larsen AN (2013) Self-assembled Al nanoparticles on Si and fused silica, and their application for Si solar cells. Nanotechnology 24:275606
Paris A, Vaccari A, Lesina AC, Serra E, Calliari L (2012) Plasmonic scattering by metal nanoparticles for solar cells. Plasmonics 7:525–534
Bohren CF, Huffman DR (1983) Absorption and scattering of light by small nanoparticles. Wiley, New York
Ishii S, Sugavaneshwar RP, Chen K, Dao TD, Nagao T (2016) Solar water heating and vaporization with silicon nanoparticles at Mie resonances. Opt Mater Express 6:640–648
Amjad M, Razaa G, Xinc Y, Pervaiza S, Xuc J, Duc X, Wen D (2017) Volumetric solar heating and steam generation via gold nanofluids. Appl Energy 206:393–400
Gorji TB, Ranjbar A (2016) A numerical and experimental investigation on the performance of a low-flux direct absorption solar collector (DASC) using graphite, magnetite and silver nanofluids. Sol Energy 135:493–505
Pustovalov VK, Astafyeva LG, Fritzsche W (2015) Analysis of optical properties of spherical metallic nanoparticles for effective absorption of solar radiation and their heating. Sol Energy 122:1334–1341
Chen M, He Y, Zhu J, Shuai Y, Jiang B, Huang Y (2015) An experimental investigation on sunlight absorption characteristics of silver nanofluids. Sol Energy 115:85–94
Gorji TB, Ranjbar AA (2017) A review on optical properties and application of nanofluids in direct absorption solar collectors (DASCs). Renew Sustain Energy Rev 72:10–32
Astafyeva LG, Pustovalov VK (2016) Efficiency of absorption of solar radiation by liquids containing metallic nanoparticles. J Appl Spectrosc 83:218–224
Xuan Y, Duan H, Li Q (2014) Enhancement of solar energy absorption using plasmonic NF based on TiO2/Ag composite nanoparticles. RSC Adv 4:16206–16213
Pustovalov V, Astafyeva L, Fritzsche W (2017) Light-absorption selection of nanoparticles and nanofluids containing nanoparticles for their effective heating by solar radiation. Nanotechnol Environ Eng 2:7–13
Wang Z, Zhang ZM, Quan X, Cheng P (2018) A numerical study on effects of surrounding fluid, material, and geometry of nanoparticles on solar absorption efficiencies. Int J Heat Mass Transf 116:825–832
Pustovalov VK, Astafyeva LG (2017) Spectral properties of nanofluids with homogeneous and bilayer nanoparticles for efficient absorption of solar radiation. Opt Spectrosc 123:158–163
Qin Z, Wang Y, Randrianaliso J, Raeesi V, Chan W, Lipiński W, Bischof J (2016) Quantitative comparison of photothermal heat generation between gold nanospheres and nanorods. Sci Rep 6:29836
Zhang H, Chen H-J, Du X, Wen D (2014) Photothermal conversion characteristics of gold nanoparticle dispersions. Sol Energy 100:141–147
Chen M, He Y, Zhu J, Kim DR (2016) Enhancement of photo-thermal conversion using gold nanofluids with different particle sizes. Energy Convers Manag 112:21–30
Guo A, Fu Y, Wang G, Wang X (2017) Diameter effect of gold nanoparticles on photothermal conversion for solar steam generation. RSC Adv 7:4815–4822
Pustovalov VK (2016) Light-to-heat conversion and heating of single nanoparticles, their assemblies, and surrounding fluid under laser pulses. Review. RSC Adv 6:81266–81289
Jin H, Lin G, Bai L, Amjad M, Filho E, Wen D (2016) Photothermal conversion efficiency of nanofluids: an experimental and numerical study. Sol Energy 139:278–289
Pustovalov VK, Smetannikov AS (2014) Analytical and computer modeling of thermal processes of laser interaction with single nanoparticle. RSC Adv 4:55760–55772
Pustovalov VK, Astafyeva LG (2013) Investigation of thermo-optical characteristics of the interaction processes of laser radiation with silver nanoparticles. Laser Phys 23:065901
Zhang D, Gökce B, Barcikowski S (2017) Laser synthesis and processing of colloids: fundamentals and applications. Chem Rev 117:3990–4103
Neumann O, Urban AS, Day J, Lal S, Halas NJ (2012) Solar vapor generation enabled by nanoparticles. ACS Nano 7:42–49
ASTM G173 - 03 (2012) Standard tables for reference solar spectral irradiances: direct normal and hemispherical on 37° tilted surface
Born M, Wolf E (1964) Principles of optics. Pergamon Press, Oxford
Kreith F, Black WZ (1980) Basic heat transfer. Harper and Row, New York
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Rights and permissions
About this article
Cite this article
Pustovalov, V.K. Heating of single nanoparticles, their assemblies and ambient medium by solar radiation. Nanotechnol. Environ. Eng. 3, 7 (2018). https://doi.org/10.1007/s41204-018-0036-0
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s41204-018-0036-0