Lorentzian causality theory

Abstract

I review Lorentzian causality theory paying particular attention to the optimality and generality of the presented results. I include complete proofs of some foundational results that are otherwise difficult to find in the literature (e.g. equivalence of some Lorentzian length definitions, upper semi-continuity of the length functional, corner regularization, etc.). The paper is almost self-contained thanks to a systematic logical exposition of the many different topics that compose the theory. It contains new results on classical concepts such as maximizing curves, achronal sets, edges, horismos, domains of dependence, Lorentzian distance. The treatment of causally pathological spacetimes requires the development of some new versatile causality notions, among which I found particularly convenient to introduce: biviability, chronal equivalence, araying sets, and causal versions of horismos and trapped sets. Their usefulness becomes apparent in the treatment of the classical singularity theorems, which is here considerably expanded in the exploration of some variations and alternatives.

1 Introduction

Let us consider a differentiable manifold M and a convex sharp cone distribution $x\rightarrow C_x\subset T_xM\backslash 0$. Causality theory is the study of the global qualitative properties of the differential inclusion

$$\begin{aligned} \dot{x}(t)\in C_{x(t)} \end{aligned}$$

where $x\rightarrow C_x$ is upper semi-continuous and x(t) is absolutely continuous. This rather abstract point of view does a good job in mathematically framing Causality Theory but provides little insights on the motivations that brought researchers from mathematical relativity to its study.

Causality theory really developed within general relativity. Here the spacetime is a time oriented Lorentzian manifold (M, g), with g a metric of Lorentzian signature, i.e. $(-,+,\ldots , +)$. The cone $C_x$ is then the future causal cone, namely a connected component of the double cone $\{y\in T_xM\backslash 0:g(y,y)\le 0\}$ and so it is really round (it has ellipsoidal section). In general relativity g is usually assumed to be $C^2$ in such a way that the Riemannian curvature is continuous. Often, depending on the application, stronger assumptions are contemplated. Since this work aims to introduce causality theory to the reader interested in general relativity we shall stick to the $C^2$ Lorentzian metric case in the whole work.

1.1 History and peculiarities of causality theory

We can identify the birth of Lorentzian causality theory with the publication of the paper “Conformal treatment of null infinity” by Penrose (1964) and most notably with his landmark paper “Gravitational collapse and space-time singularities” (Penrose 1965a) (see also the review by Senovilla and Garfinkle 2015). In it Penrose employed global methods from differential geometry to predict the formation of singularities in the universe. Relevant but less geometrical ideas were contained in previous work by Raychaudhuri (1955). In short Penrose showed that if the geometry of spacetime is so bent that lightlike geodesics issued normally from a closed codimension two surface converge, then the spacetime develops a future geodesic singularity. Such special surfaces were termed trapped by Penrose.

In Penrose’s theorem there appeared many ingredients that today are recognized as characteristics of causality arguments entering singularity theorems (Senovilla 1998): an energy condition (the null convergence condition); a causality condition (global hyperbolicity); some special (hyper)surface which is believed to form under sufficient concentration of mass-energy (trapped surface).

Hawking soon realized that the approach could be adapted to study the singularities of the Universe as a whole, by replacing the trapped surface with a Cauchy hypersurface with diverging normal vector field (Hawking 1966b). This condition of expansion of the universe was indeed justified by the observed validity of the local Hubble law. His theorem predicted that under suitable energy conditions there had to be an initial singularity at the beginning of the Universe. The result caused a sensation in the public and in the subsequent years mathematical relativity began to develop at a fast pace. This early development is associated to the names of Penrose, Hawking, Geroch and Tipler. Within few years most relevant concepts, from global hyperbolicity to conformal completions, were identified and in fact, after only seven years from Penrose’s theorem, Penrose’s book (Penrose 1972; Lerner 1972) and the classic book by Hawking and Ellis (1973) signaled that mathematical relativity had transitioned to a mature theory.

It must be said that most of the community of theoretical physicists looked at these developments with interest but a bit from a distance. The tools from global differential geometry were at the time perceived as far too new and technical to be shared by large communities of researchers. The subsequent results by Bekenstein, Hawking and others on the thermodynamical interpretation of black holes attracted much more interest as they bridged different fields of physics. In fact, methods familiar from quantum field theory such as Bogoliubov transformations could be employed. Many theoretical physicists began to investigate the physics of black holes, as they were regarded as the new atoms of the late twentieth century: they could give hints on the unification between gravity and the other fundamental forces of nature.

Meanwhile smaller communities of mathematical physicists and mathematicians began to systematize mathematical relativity. In fact, the early heroic years had been a bit too frenetic. Some subtle issues, most notably those connected with differentiability of Cauchy hypersurfaces and horizons, had been incompletely or incorrectly treated. Several variations of singularity theorems were explored. Topology change and formation of closed timelike curves were studied. Analysts, in particular, began to obtain significant results on the Cauchy problem for general relativity, and Penrose’s conjectured inequality led to a flourishing of results broadly belonging to geometrical analysis. This phase really continues up to this day.

However, only a few of the mentioned developments pertain to causality theory as this theory mostly focuses on cones. It is easy to prove that the distribution of cones determines the Lorentzian metric only up to a conformal factor. To give an example, of the previous ingredients entering Penrose’s theorem, neither the energy condition nor the notion of trapped surface is really conformally invariant. In fact neither are Einstein’s equations, thus although mathematically one might try to identify causality theory with the body of conformally invariant results of mathematical relativity, it is often the case that it becomes impossible to disentangle causality theory from non-conformally invariant results, and for one good reason: the latter are necessary to make contact with Physics and so to motivate the very study of causality theory.

Though it is a bit difficult to draw the boundary of causality theory within mathematical relativity, by working in causality theory one ends up recognizing some features which distinguish this topic.

Inequalities are more important than equalities: in causality theory Einstein’s equations are seldom used, what are important are really the energy inequalities deduced from those. As a consequence, causality theory is rather robust and largely independent of the dynamical equations of gravity. One might suppose that the Einstein equations should have some implications on causality, but in fact, they are not particularly restrictive. This was recognized long ago with the Gödel solution, and while the causality conditions were refined, many exact solutions with specific causality properties or violations were found (the exact gravitational waves provide a nice laboratory). What is true is that the mentioned energy inequalities restrict the development of causal pathologies provided the Universe starts from causally well behaved conditions.

Causality theory is the least Riemannian among the subjects pertaining to mathematical relativity: while tensorial analogies are useful and might serve to translate results from Riemannian to Lorentzian geometry, the presence of cones and their orientation really leads to a qualitative dynamics which has no analog in the Riemannian world. In fact, it is generically incorrect to regard Lorentzian geometry as a minor, perhaps annoying, variation of Riemannian geometry, as Lorentzian geometry is in fact richer than Riemannian geometry. In fact, it is easy to prove that Riemannian geometry is contained within Lorentzian geometry. Let $(S,g_R)$ be a Riemannian manifold. The product manifold $M=\mathbb {R} \times S$ endowed with the direct sum metric

$$\begin{aligned} g=-\mathrm{d}t^2+g_R \end{aligned}$$

is a Lorentzian manifold (M, g) which encodes all the information of $(S,g_R)$. For instance, geodesics on M project to geodesics on S and every geodesic on S comes from such a projection. In practice in Lorentzian geometry the Riemannian manifolds can be identified with instances of product spacetimes (hence static). The converse inclusion does not hold since Riemannian manifolds do not encode any cone dynamics, i.e. any causality theory.

This review aims to give an updated account of causality theory. For each result we tried to present the strongest version, often improving those available in the literature. As for previous references, the most important books containing extensive discussions are Penrose (1972), Lerner (1972), Hawking and Ellis (1973), O’Neill (1983), Wald (1984b), Joshi (1993), Beem et al. (1996) and Kriele (1999). Other more specific review papers with an objective similar to our own are Senovilla (1998), García-Parrado and Senovilla (2005), Minguzzi and Sánchez (2008) and Chruściel (2011).

Since the subject is extensive we could not include the proofs of all the presented results, however, we tried to include almost all proofs with a causality flavor. For instance, we omitted some proofs on the exponential map, Gauss lemma or on the existence of convex neighborhoods. We made this choice because the proofs are lengthy and pertain more to the field of Analysis. They really use analytic arguments and tools that do not show up again in the study of causality theory.

Some specific or technical topics of causality theory have not been discussed in this review. I give a list here pointing the reader to some literature

• Chronology violation (time machines) and topology change (Geroch 1967; Tipler 1974, 1977; Yodzis 1972, 1973; Galloway 1983b, 1995; Kriele 1989; Hawking 1992; Ori 1993, 2007; Borde 1997, 2004; Krasnikov 1995, 2002; Minguzzi 2015a, 2016a; Larsson 2015; Lesourd 2018).

• Spacetime boundaries (Penrose 1964, 1965c; Schmidt 1971a, b; Geroch et al. 1972; Sachs 1973; Budic and Sachs 1974; Geroch 1977a; Szabados 1987, 1988; Rácz 1987, 1988; Kuang and Liang 1988, 1992; Scott and Szekeres 1994; Harris 1998, 2000, 2004, 2017; Marolf and Ross 2003; García-Parrado and Senovilla 2005; Low 2006; Flores 2007; Flores and Sánchez 2008; Flores and Harris 2007; Sánchez 2009; Chruściel 2010; Flores et al. 2011; Minguzzi 2013; Whale et al. 2015).

• Horizons and lightlike hypersurfaces (including regularity issues, area theorem, splitting) (Moncrief and Isenberg 1983; Borde 1984; Isenberg and Moncrief 1985; Kupeli 1987; Chruściel and Isenberg 1993, 1994; Beem and Królak 1998; Friedrich et al. 1999; Galloway 2000; Budzyński et al. 1999, 2001, 2003; Chruściel and Galloway 1998; Chruściel 1998; Chruściel et al. 2001, 2002; Minguzzi 2014, 2015a; Krasnikov 2014; Moncrief and Isenberg 2018).

Hopefully, they will be covered in future versions of this work.

For what concerns the study of singularities, the literature is so vast that we decided to present just a few results beyond the classical ones. Nevertheless, we devoted some space to the exploration and improvement of the classical theorems, for instance we were able to weaken considerably the assumptions in Penrose’s theorem, cf. Theorem 6.33. The new theorem could be useful in the study of black hole evaporation. We have also obtained a singularity theorem sufficiently versatile to be applicable in astrophysics and cosmology, cf. Theorem 6.52.

The review introduces some new causality concepts which we found particularly convenient e.g.: biviability, chronal equivalence, araying sets, causal versions of horismos and trapped sets (Sect. 2.17).

As for the prerequisites, the reader is assumed to be familiar with basic results on differential geometry and on the notion of (pseudo-)Riemannian space, hence with the notions of metric, affine connection, curvature tensor, Lie differentiation, exterior forms and integration over manifolds.

1.2 Notation and terminology

Greek indices run from 0 to n, where $n+1$ is the dimension of the spacetime manifold M. Latin indices run from 1 to n. We might use the notation $\mathbf {x}:=(x^1,\ldots ,x^n)$. The Lorentzian signature is $(-,+,\ldots ,+)$. The Minkowski metric is denoted by $\eta$, so in canonical coordinates $\eta _{00}=-1$, $\eta _{ij}=\delta _{ij}$ for $i,j=1,\ldots , n$, $\eta _{0 i}=0$, for $i=1,\ldots , n$. Sometimes for brevity we set $F(v)=\sqrt{-g(v,v)}$ and $L=-F^2/2$. Terminologically we might not distinguish between a curve and its image, the intended meaning will be clear from the context. Often, given a sequence $x_n$, a subsequence $x_{n_k}$ might simply be denoted $x_k$. The boundary of a set S can be denoted $\dot{S}$ or $\partial S$, the latter choice being sometimes less ambiguous but also less compact. The subset symbol is reflexive, $S\subset S$. The index placement for the notable tensors is consistent with Misner et al. (1973), the convention on the wedge product is $\alpha \wedge \beta =\alpha \otimes \beta -\beta \otimes \alpha$ where $\alpha$ and $\beta$ are 1-forms (i.e. that of Spivak 1979, which is different from that of Kobayashi and Nomizu 1963). (Sub)manifolds, e.g. hypersurfaces, do not have boundary unless otherwise stated.

1.3 The notion of spacetime

Let V be an $n+1$-dimensional vector space, and let $g:V\times V\rightarrow \mathbb {R}$ be a scalar product of Lorentzian signature, that is $(-,+,\ldots ,+)$. We can find a basis $\{e_\alpha , \alpha =0,1,\ldots , n\}$ of V and associated (canonical) coordinates $\{v^\alpha \}$ so that if $v=v^\alpha e_\alpha$ the scalar product reads

$$\begin{aligned} g(v,w)=-v^0 w^0+\varSigma _i v^i w^i=\eta _{\alpha \beta } v^\alpha w^\beta \end{aligned}$$

where $\eta _{\alpha \beta }=0$ if $\alpha \ne \beta$, $\eta _{00}=-1$ and $\eta _{ii}=1$. A vector is called¹

Causal vectors might also be called nonspacelike, though this terminology is less common. The coordinate expression for g clarifies that the timelike locus is the union of two disjoint open cones, one in the region $v^0>0$ and the other in the region $v^0<0$. We say that V is time-oriented, and simply denoted (V, g), if a choice of cone, termed future, has been made. The other cone is called past. In this case we assume that the above coordinates have been chosen so that the future cone lies in $v^0>0$ (if this is not the case just redefine $v^0\rightarrow -v^0$). The causal vectors are now future or past (directed) depending on the sign of $v^0$, either positive or negative.

The observer space or indicatrix is

$$\begin{aligned} \mathcal {I}=\{v\in V:g(v,v)=-1, v^0>0\} \end{aligned}$$

and geometrically is a hyperboloid $\mathbb {H}^n$.

Definition 1.1

The Minkowski space is the pair (V, g) understood as time oriented.

The Minkowski space serves as a model for the tangent space of a spacetime.

A Lorentz map is an endomorphism $\varLambda :V\rightarrow V$ which preserves g, i.e. for every $v,w\in V$,

$$\begin{aligned} g(\varLambda v,\varLambda w)=g(v,w). \end{aligned}$$

If $\varLambda$ sends the future timelike cone into the future timelike cone then it is said to be orthochronous. If V has an orientation and $\varLambda$ preserves the orientation then $\varLambda$ is said to be proper.

1.4 Reverse triangle and Cauchy–Schwarz inequalities

In this section $F:C\rightarrow [0,\infty )$, where $F(v):=\sqrt{-g(v,v)}$. The following results really extend by continuity to include the case with $v_1=0$ or $v_2=0$.

Theorem 1.2

(Reverse Cauchy–Schwarz inequality) Let (V, g) be Minkowski space and $C\subset V$ the future causal cone. If $v_1,v_2\in C$ then

$$\begin{aligned} -g(v_1,v_2)\ge F(v_1) F(v_2) \end{aligned}$$

where equality holds iff $v_1$ and $v_2$ are proportional.

Proof

Let $v_1\in C$ be timelike and let us choose canonical coordinates such that $e_0\propto v_1$, then

$$\begin{aligned} -g(v_1,v_2)=v_1^0v_2^0 \ge F(v_1) F(v_2). \end{aligned}$$

where equality holds only if $v_2^i=0$ for all $i\ge 1$, that is, only if $v_2$ is proportional to $v_1$. The inequality for $v_1$ lightlike follows by continuity. It remains to prove that $v_1$ and $v_2$ are proportional if they are both lightlike and the inequality holds with the equality sign, i.e., $g(v_1,v_2)=0$. Let us choose the canonical coordinates so that $v_1=a (e_0+e_1)$, $a>0$, then $g(v_1,v_2)=0 \Rightarrow v^0_2=v^1_2$, and since $v_2$ is lightlike $v_2^k=0$ for $k\ge 2$, that is, $v_2 \propto v_1$. $\square$

Theorem 1.3

(Reverse triangle inequality) Let (V, g) be Minkowski space and $C\subset V$ the future causal cone. For every $v_1,v_2\in C$ we have

$$\begin{aligned} F(v_1+v_2)\ge {F}(v_1)+{F}(v_2), \end{aligned}$$

(1.1)

with equality if and only if $v_1$ and $v_2$ are proportional.

Proof

Let $v=v_1+v_2$; since v is twice the average of $v_1,v_2\in C$ and C is strictly convex we have that $v\in \mathrm {Int} C$ unless $v_1$ and $v_2$ are proportional and lightlike. In the latter case the inequality is clear so let us suppose that such case does not apply and hence that v is timelike. We have

$$\begin{aligned} F^2(v)=-g(v,v)=-g(v,v_1)-g(v,v_2) \end{aligned}$$

Dividing by F(v) we get

$$\begin{aligned} F(v) = \frac{-g(v,v_1)}{F(v)}+\frac{-g(v,v_2)}{F(v)}\ge F(v_1)+F(v_2), \end{aligned}$$

where we used the reverse Cauchy–Schwarz inequality. Now notice that if equality holds and v is timelike then in this chain of inequalities the only way of obtaining a final equality is with the Cauchy–Schwarz inequalities used with the equality sign, which means $v\propto v_1$ and $v \propto v_2$, which implies that $v_1$ and $v_2$ are proportional. If v is instead lightlike we have already shown that $v_1$ and $v_2$ are proportional and lightlike. $\square$

Notice that F is positive homogeneous: for every $a>0$, $F(av)=a F(v)$. We have also

Corollary 1.4

Function $F:C\rightarrow [0,\infty )$ is concave.

Proof

In fact if $a,b\in [0,1]$, $a+b=1$, $F(av_1+bv_2)\ge F(av_1)+F(bv_2)=a F(v_1)+bF(v_2)$. $\square$

It is also easy to prove that the properties of positive homogeneity and concavity imply the reverse triangle inequality (Minguzzi 2019, Proposition 3.4).

1.5 Manifolds

In this work we shall assume the reader to be familiar with the notion of real smooth manifold (Lee 2012). It is also understood that the definition of manifold includes the properties Hausdorff and second countability. All our manifolds will be without boundary unless otherwise specified. Since every real manifold is locally homeomorphic with an open subset of $\mathbb {R}^{n+1}$, with $n+1$ the dimension of the manifold, it is also locally compact.

It is useful to recall a few definitions and results from topology (Willard 1970). A topological space is Hausdorff if the open sets separate points. A Hausdorff space is regular if points and disjoint closed sets are separated by open sets. A topological space is metrizable if there is a distance function that induces the topology.

A Hausdorff locally compact space is regular (in fact completely regular). Moreover, every Hausdorff second-countable regular space is metrizable, thus every manifold is metrizable. Every locally compact Hausdorff second-countable space is paracompact, thus every manifold is paracompact.

It is worth to recall that a topological space is paracompact if every open cover admits a locally finite refinement. A Hausdorff topological space is paracompact if and only if it admits a partition of unity, thus manifolds admit partitions of unity. Partitions of unity are really important, for instance they help to define integration over manifolds or to obtain continuous selections of convex bundles over manifolds.

A Lorentzian manifold is just a pair (M, g), where M is a smooth manifold and $g:M\rightarrow T^*M\otimes _M T^*M$ is a $C^2$ metric of Lorentzian signature.

The assumptions within the definition of manifold are rather reasonable for our purposes. Suppose second countability and paracompactness were dropped. Due to a theorem by Marathe (1972) paracompactness would be recovered from the assumption of the existence of a pseudo-Riemannian metric or of a connection, ingredients which are clearly necessary for Lorentzian geometry, see also Palomo and Romero (2006). Paracompactness would imply the existence of a partition of unity and hence that of a Riemannian metric, and from here the metrizability of the topological space. Finally, a result in topology states that any connected and locally compact metrizable space is second countable, so both properties are recovered.

1.6 Auxiliary Riemannian metrics

A Riemannian manifold has a definition similar to that of Lorentzian manifold, where now the metric h has Euclidean signature. Given a metric the length of the $C^1$ curve $x:[0,1]\rightarrow M$, $t\mapsto x(t)$, is

$$\begin{aligned} l^h(x)=\int _0^1 \sqrt{h(\dot{x},\dot{x})} \mathrm{d}t, \end{aligned}$$

while the distance between two points is the infimum over the connecting curves

$$\begin{aligned} d^h(p,q)=\inf _x l^h(x). \end{aligned}$$

Sometimes we might denote them $l_0$ and $d_0$. The topology of the manifold coincides with the topology induced by $d^h$, in particular $d^h$ can be shown to be continuous. The Hopf–Rinow theorem gives some equivalent characterizations for the completeness of (M, h), i.e., in terms of the completeness of $d^h$-Cauchy sequences, compactness of closed balls, and completeness of geodesics (Klingenberg 1982; Gallot et al. 1987).

In Lorentzian geometry several constructions make use of an auxiliary Riemannian metric h. This approach might seem unnatural, however Riemannian metrics, particularly complete ones, are indeed useful when it comes to express results which are local, i.e. which hold only over compact sets. To this end the following theorem by Nomizu and Ozeki (1961) is handy

Theorem 1.5

Let M be a connected (second countable) differentiable manifold, then it admits a complete Riemannian metric. If every Riemannian metric is complete then M must be compact.

Since the bundle of Riemannian metrics over M is convex, and since every point admits a Riemannian metric in its neighborhood (as it is clear by using the Euclidean metric in local coordinates), the use of a partition of unity immediately gives that every manifold admits a Riemannian metric. The proof then really shows that for every Riemannian metric there is a complete Riemannian metric in the same conformal class.

1.7 Time orientation

A Lorentzian manifold is said to be time orientable if at every point we can make a choice of future cone for $(T_xM,g_x)$ in such a way that the choice is continuous in $x\in M$. Here continuity can be understood in several equivalent ways. Let $C_x\subset T_xM\backslash 0$ be the causal future cone at x, then $C=\cup _x C_x$ is a continuous cone bundle, that is $\partial C\backslash 0$ is a continuous hypersurface of the slit tangent bundle $TM\backslash 0$. Equivalently, it is possible to find a continuous (global) timelike vector field $x\mapsto v(x)$. With it we can call future that half of the timelike double cone which contains v.

Notice, that in every Lorentzian manifold we can find a local timelike vector field. In fact, given ${\bar{x}} \in M$, we can find a local chart $\{x^\alpha \}$ in a neighborhood of ${\bar{x}}$ such that $g(\partial _\alpha ,\partial _\beta )\vert _{{\bar{x}}}=\eta _{\alpha \beta }$. Then, by continuity, $\partial _0$ is timelike in a neighborhood of ${\bar{x}}$. Since we have a partition of unity at our disposal we could hope to patch together the local fields to get a global timelike vector field. In general this is not possible the obstruction being precisely the condition of time orientability. Nevertheless, every Lorentzian manifold admits a (at most double) covering which is time orientable. Over a connected component it is constructed as follows (Geroch 1970). Let $p_0\in M$ be a reference point, and consider the family of pairs

$$\begin{aligned} \mathcal {F}=\{(p,\gamma ):p\in M, \gamma \text { continuous curve from } p_0 \text { to } p\} \end{aligned}$$

Let us introduce the equivalence relation $(p,\gamma )\sim (p',\gamma ')$ if $p=p'$ and a timelike vector at p, when continuously transferred from p to $p_0$ along $\gamma$ and then back to p along $\gamma '$, does not reverse its time direction. The set of equivalence classes defines a new manifold, called by Geroch the Lorentzian covering. It is really a double covering of the original Lorentzian manifold (M, g). Moreover, it is really M if the Lorentzian manifold is time orientable.

A time orientable Lorentzian manifold is said to be time oriented if a choice of time orientation has been made.

Definition 1.6

A spacetime is a connected non-compact time oriented Lorentzian smooth manifold. It is still denoted (M, g).

It can be noticed that the tangent space $(T_xM,g_x)$ to a spacetime is a Minkowski space. The simplest spacetime is Minkowski spacetime: M admits a single chart whose image is the whole $\mathbb {R}^{n+1}$, and in the coordinates $\{x^\mu \}$ of $\mathbb {R}^{n+1}$,

$$\begin{aligned} g=-(\mathrm{d}x^0)^2+\varSigma _i (\mathrm{d}x^i)^2, \end{aligned}$$

and $\partial _0$ is future directed. In other words, the Minkowski spacetime is an affine space modeled over the Minkowski space. The mentioned coordinates are the canonical coordinates for the Minkowski spacetime. Sometimes the notions of Minkowski space and Minkowski spacetime are not distinguished terminologically though the former is a vector space while the latter is an affine space endowed with a translationally invariant metric.

Compact time-oriented Lorentzian manifolds will be referred to as compact spacetimes while, unless otherwise specified, a spacetime will always be non-compact. The physics community has been oriented towards this definition of spacetime by the simple result that compact spacetimes contain closed timelike curves (time travel), cf. Proposition 4.18. It is unlikely that they could represent our actual Universe. Nevertheless, many mathematicians have investigated compact spacetimes. They have some interesting mathematical peculiarities. The reader is referred to the works by Tipler (1979), Galloway (1984, 1986a), Guediri (2002, 2003, 2007), Romero and Sánchez (1995), Sánchez (1997, 2006) and references therein.

Remark 1.7

We recall the famous words of Minkowski: “Henceforth space by itself, and time by itself, are doomed to fade away into mere shadows, and only a kind of union of the two will preserve an independent reality”. This union is the spacetime, which terminologically, in our opinion, should be written as a single word, and not as space-time, precisely due the fact that spacetime cannot be canonically split as the union of space and time. The very word of spacetime reminds us of the main accomplishment of relativity theory, the unification of space and time.

1.8 Existence of Lorentzian metrics

We have recalled that every manifold admits a Riemannian metric. We wish to find conditions that guarantee the existence of a Lorentzian metric.

A continuous line field is a continuous distributions of lines. Let h be a Riemannian metric, then a line field is locally determined by a continuous h-unit vector field v (or $-v$) which generates the line.

A manifold M which admits a continuous line field admits a Lorentzian metric. Indeed, $g=h-2v^\flat \otimes v^\flat$, with $v^\flat (\cdot )=h(v,\cdot )$, is Lorentzian, for as a quadratic form it is positive on the hyperplane h-orthogonal to v and negative on v. Notice that it does not depend on the sign of v.

The converse holds true as well. If the manifold admits a Lorentzian metric g then it admits a double covering which is time orientable. Thus over the double covering we have a timelike (hence non-vanishing) global vector field v. Let $x_1$ and $x_2$ be the counterimages of the point $x\in M$, and let $v_1$ and $v_2$ be the values of v at these points, so that their projections to M belong to different halves of the timelike double cone. The assignment at x of the line generated by the vector $v_1-v_2$ provides a line field on M (notice that it is independent of which counterimage is called $x_1$) .

Similarly, a slight modification of the above argument proves that the existence of a non-vanishing continuous vector field is equivalent to the existence of a spacetime structure (Lorentzian metric plus time orientation), for in the above construction the vector field v is timelike with respect to g.

In fact, the equivalence can be further improved as follows (Steenrod 1970, Theorem 39.7; O’Neill 1983, Proposition 37; Palomo and Romero 2006).

Theorem 1.8

For a smooth manifold M the following properties are equivalent:

• 1. existence of a Lorentzian metric,

• 2. existence of a continuous line field,

• 3. existence of a non-vanishing continuous vector field,

• 4. existence of a spacetime structure,

• 5. either M is non-compact, or M is compact and has zero Euler characteristic.

It is worth to recall that a compact manifold whose dimension $n+1\ge 2$ is odd has zero Euler characteristic.

Fig. 1

Examples of non-orientable (no) or non-time orientable (nto) 2-dimensional Lorentzian manifolds. The curly line indicates that the edges have to be twisted and identified. The future cone is the white one

Example 1.9

(A non-time orientable Lorentzian manifold) Consider $\mathbb {R}^2$ with Cartesian coordinates (x, y) and metric

$$\begin{aligned} g=-\alpha \otimes \beta , \quad \alpha =\cos \theta \mathrm{d}x+ \sin \theta \mathrm{d}y, \quad \beta =-\sin \theta \mathrm{d}x+ \cos \theta \mathrm{d}y, \quad \theta = \pi x/2. \end{aligned}$$

Then $M=[0,1]\times (-1,1)$ where the segment $\{0\}\times (-1,1)$ is glued to the segment $\{1\}\times (-1,1)$ with a twist (see Fig. 1), and where the metric is the induced one provides the example we were looking for. This example is really non-orientable. To get an orientable example, glue $\{0\}\times (-1,1)$ to $\{2\}\times (-1,1)$ without a twist.

Example 1.10

(A non-orientable spacetime) Start with $(\mathbb {R}^2,g)$ as before but this time let $M=[0,3]\times (-1,1)$ and the segment $\{0\}\times (-1,1)$ is glued to the segment $\{3\}\times (-1,1)$ with a twist. The topology is that of a Möbius strip.

One can ask whether a non-compact manifold admits Lorentzian metrics with stronger properties, say existence of continuous increasing functions (time functions) or bounds on the Ricci tensor of physical relevance. The strongest result in this direction is due to Kokkendorff (2002). The proof makes use of Gromov’s h-principle.

Theorem 1.11

Any noncompact manifold can be given a spacetime structure admitting a time function and such that the sectional curvature is negative over every timelike plane, so in particular $R(v,v) >0$ for every timelike tangent vector.

1.9 Cone distributions and conformal invariance

In this section we clarify the connection between causal structure and conformal invariance. We need a simple algebraic result (Wald 1984b, Appendix D).

Proposition 1.12

Let V be an $n+1$-dimensional vector space, $n\ge 1$, and let g and ${\bar{g}}$ be two Lorentzian bilinear forms over it. The forms g and ${\bar{g}}$ induce the same (double) cone of causal vectors if and only if there is a constant $\varOmega ^2>0$ such that ${\bar{g}}=\varOmega ^2 g$.

Proof

The if part is obvious, so let us assume that g and ${\bar{g}}$ induce the same (double) cone of causal vectors, and hence the same double cone of lightlike vectors. There is a basis $\{e_\mu \}$ of V such that $g(e_\mu , e_\nu )=\eta _{\mu \nu }$. For every i, $e_0 \pm e_i$ is g-lightlike, thus

$$\begin{aligned} 0={\bar{g}}(e_0 \pm e_i,e_0 \pm e_i)={\bar{g}}(e_0,e_0)+{\bar{g}}(e_i,e_i)\pm 2 {\bar{g}}(e_0,e_i) , \end{aligned}$$

which implies ${\bar{g}}(e_i,e_i)=-{\bar{g}}(e_0,e_0)$, ${\bar{g}}(e_0,e_i)=0$, where ${\bar{g}}(e_0,e_0)<0$ since $e_0$ is g-timelike and hence ${\bar{g}}$-timelike. Moreover, for $i\ne j$, $e_0 +\frac{1}{\sqrt{2}} (e_i+e_j)$ is lightlike, thus

$$\begin{aligned} 0={\bar{g}}\big (e_0 +\tfrac{1}{\sqrt{2}} (e_i+e_j),e_0 +\tfrac{1}{\sqrt{2}} (e_i+e_j)\big )={\bar{g}}(e_i,e_j). \end{aligned}$$

In summary ${\bar{g}}(e_\mu ,e_\nu )=[-{\bar{g}}(e_0,e_0)] \eta _{\mu \nu }$, which concludes the proof. $\square$

It has the following important consequence.

Corollary 1.13

Two spacetimes (M, g), $(M,{\bar{g}})$ based on the same manifold M share the same causal cones if and only if there is a function $\varOmega :M\rightarrow (0,\infty )$ such that ${\bar{g}}=\varOmega ^2 g$, i.e. ${\bar{g}}$ and g are conformally related.

Every non-degenerate bilinear form g on an oriented vector space V induces an alternating multilinear form given by

$$\begin{aligned} \mu (X_0,X_1, \ldots , X_n)=\epsilon \sqrt{ \vert \det g(X_i,X_j)\vert } \end{aligned}$$

where $\epsilon =1$ if the n-ple $(X_0, X_1, \ldots , X_n)$ is positively oriented, and $\epsilon =-1$ if it is negatively oriented (the determinant on the right-had side vanishes if it is not a basis).

If V is identified with the tangent space to the spacetime manifold $T_xM$, $\mu$ is called the volume form associated to the metric g. It can be observed that if ${\bar{g}}=\varOmega ^2 g$ then ${\bar{\mu }}=\varOmega ^{n+1} \mu$, so by fixing the volume form we fix the conformal factor.

Corollary 1.14

Two spacetimes (M, g), $(M,{\bar{g}})$ based on the same oriented manifold M share the same causal cones and the same volume form if and only if ${\bar{g}}= g$, that is, iff they are actually the same spacetime.

This result establishes that a Lorentzian spacetime is nothing but a distribution of round cones and a volume form.

It is interesting to compare the connection, geodesics and curvature for conformally related metrics, ${\bar{g}}=\varOmega ^2 g$. This detailed study can be found in Wald (1984b, Appendix D). Here we just mention the fact that unparametrized lightlike geodesics are really independent of the conformal factor while the affine parameter changes as follows

$$\begin{aligned} \frac{\mathrm{d}{\bar{\lambda }} }{\mathrm{d}\lambda }=c \varOmega ^2 \end{aligned}$$

where c is a constant. It can be observed that the exponent does not coincide with that entering the transformation of proper time: $\frac{\mathrm{d}{\bar{\tau }} }{\mathrm{d}\tau }=\varOmega$.

1.10 Abstract relations

A relation on M is a subset of the Cartesian product: $R\subset M\times M$. The relation is closed if it is closed in the product topology and similarly for open. Given two relations $R_1$ and $R_2$ the composition is

$$\begin{aligned} R_2\circ R_1=\{(p,q): \text { there is } r\in M \text { such that } (p,r)\in R_1 \text { and } (r,q)\in R_2\}. \end{aligned}$$

A relation is transitive if $R\circ R\subset R$ and idempotent if $R\circ R=R$. The diagonal $\varDelta :=\{(p,p):p\in M\}$ acts as an identity for the composition $\varDelta \circ R=R\circ \varDelta =R$. We say that R is reflexive if $\varDelta \subset R$. A reflexive and transitive relation is called a preorder and it is idempotent. The inverse or transpose relation is $R^{-1}:=\{(p,q):(q,p)\in R\}$. A relation is antisymmetric if

$$\begin{aligned} (p,q)\in R \text { and } (q,p)\in R\Rightarrow p=q \end{aligned}$$

or equivalently $R\cap R^{-1}=\varDelta$. An order or a partial order is an antisymmetric preorder. A total order is an order for which any two elements are comparable: $R\cup R^{-1}=M\times M$. We also define the increasing hull or R-future of a point by

$$\begin{aligned} R^+(p)=\{q\in M:(p,q)\in R\}, \end{aligned}$$

and the decreasing hull or R-past of a point by

$$\begin{aligned} R^-(p)=\{q\in M:(q,p)\in R\}. \end{aligned}$$

They extend to the R-future (past) of a set as follows

$$\begin{aligned} R^\pm (S)=\cup _{p\in S} R^\pm (p). \end{aligned}$$

(1.2)

An R-diamond is a set of the form $R^+(p)\cap R^-(q)$ for some $p,q\in M$.

1.11 Causality relations

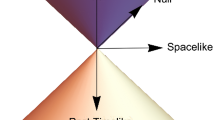
In Sect. 1.3 we have given the definition of causal, timelike and lightlike vector. A piecewise $C^1$ curve $x:I \rightarrow M$, $t \mapsto x(t)$, $I\subset \mathbb {R}$ an interval of the real line, is said to be causal, timelike or lightlike if the tangent vector has the corresponding future causal character at every point. Notice that by our definition of causal vector we have $\dot{x} \ne 0$ at every point of differentiability, i.e. causal curves are regular. Notice also that all our causal curves will be future directed unless otherwise specified. The concatenation of causal curves gives a causal curve, and similarly in the timelike or lightlike cases.

On spacetime we can define relations connected to the notions of causal or timelike curves. They are the causal relation

$$\begin{aligned} J=\{(p,q):\text { there is a causal curve connecting } p \text { to } q \text { or } p=q\}, \end{aligned}$$

(1.3)

and the chronological relation

$$\begin{aligned} I=\{(p,q):\text { there is a timelike curve connecting } p \text { to } q \}. \end{aligned}$$

Clearly, $I\cup \varDelta \subset J$. As an example, the chronological relation for Minkowski spacetime is given by the open set

$$\begin{aligned} I=\{(x,y)\in \mathbb {R}^4\times \mathbb {R}^4:y^0-x^0>0, (y^0-x^0)^2>(y^1-x^1)^2+\cdots +(y^n-x^n)^2 \} \end{aligned}$$

while the causal relation is obtained by replacing > with $\ge$.

The horismos relation is the difference $\mathcal {E}=J\backslash I$. We shall also write

• $p\le q$ for $(p,q)\in J$,

• $p<q$ for “$p\le q$ and $p\ne q$”,

• $p\ll q$ for $(p,q)\in I$, and

• $p\rightarrow q$ for $(p,q)\in J\backslash I$.

For the relation J the J-future and J-past of a point are denoted $J^\pm (p)$ and we speak of causal future (past) of the point. Similarly $I^+(p)$ denotes the chronological future of p, and $E^+(p):=J^+(p)\backslash I^+(p)=\mathcal {E}^+(p)$ denotes the future horismos of p. We stress that given a set S, we write

$$\begin{aligned} E^+(S):=J^+(S)\backslash I^+(S) \, {\varvec{\ne }}\, \mathcal {E}^+(S)= \cup _{p\in S} \mathcal {E}^+(p)=\cup _{p\in S} {E}^+(p). \end{aligned}$$

We introduced a calligraphic notation for the relation $J\backslash I$ precisely to avoid conflicts with the general notation introduced in Eq. (1.2).

Lemma 1.15

Let S be any set then $E^{+}(S) \subset \mathcal {E}^+(S)$.

Proof

If $q \in E^{+}(S)\subset J^{+}(S)$ then there is $p\in S$ such that $q \in J^{+}(p)$, but we cannot have $q \in I^{+}(p)$, as it would imply $q \in I^{+}(S)$. Thus $q \in E^{+}(p)$. $\square$

The J-diamonds, i.e. the sets of the form $J^+(p)\cap J^{-}(q)$ for $p,q\in M$, are also called causal diamonds.

Sometimes we might need to consider the causal relation for a subset $U\subset M$, which is defined as above but with the causal curves having image in U. Such a causal relation is denoted $J_U$ or $J_{(U,g)}$ and must not be confused with $J\cap (U\times U)$. Also $J^+_U(p)$ might be denoted $J^+(p, U)$ and similarly in the past and chronological cases. Sometimes we might need to consider different metrics $g'$, in which case we might write $J_{g'}$ or $J_{(M,g')}$ for the corresponding causal relation.

Given two Lorentzian metrics over M we write $g\le g'$ if at every point the future causal cone of g is included in the future causal cone of $g'$, and we write $g<g'$ if the future causal cone of g is included in the future timelike cone of $g'$.

Proposition 1.16

The causal relation J is transitive and reflexive. The chronological relation I is transitive and open.

Notice that the openness of I implies that of $I^+(p)$ and $I^-(p)$ for every point p and hence that of $I^+(S)$ and $I^-(S)$ for every subset $S\subset M$.

Proof

The only non-trivial statement is the openness of I. Let $(p,q)\in I$ then there is a timelike curve $\gamma$ from p to q. Let $v={\dot{\gamma }}\in T_q M$ be the tangent to the curve at q. Let us introduce local coordinates in a neighborhood U of q such that $g_q=-(\mathrm{d}x^0)^2+\sum _i (\mathrm{d}x^i)^2$, and let ${\bar{g}}=-(1-\epsilon )(\mathrm{d}x^0)^2+\sum _i (\mathrm{d}x^i)^2$ where $\epsilon >0$ is so small that v is both g-timelike and ${\bar{g}}$-timelike. By continuity, in a neighborhood $V\subset U$ of q, ${\dot{\gamma }}$ is ${\bar{g}}$-timelike and the ${\bar{g}}$-causal cone is contained in the g-timelike cone, i.e. ${\bar{g}}<g$. As shown previously, the chronological relation is open in a Minkowski spacetime, thus taking $r\in \gamma \cap V\backslash \{q\}$, the points of a whole neighborhood $U_q$ of q can be reached from r with ${\bar{g}}$-timelike (and hence g-timelike) curves. The argument can be repeated time-dually for p, by taking $r'$ sufficiently close to p so that $(r',r)\in I$. Then by concatenating the timelike curves we conclude $U_p\times U_q\subset I$. $\square$

Fig. 2

The causal relation is not necessarily closed, $(p,q)\in {\bar{J}}\backslash J$. Here (M, g) is Minkowski $1+1$ spacetime with a point removed

The causal relation is not necessarily closed (cf. Fig. 2), a fact which ultimately is responsible for the variety of different causality conditions that can be placed on a spacetime. Later on we shall introduce two closed and transitive relations, namely the Seifert’s relation $J_S$ and Sorkin and Woolgar’s K relation.

1.12 Non-decreasing functions

We introduce families of non-decreasing functions over causal curves which will be useful in what follows.

Definition 1.17

A function $t:M\rightarrow \mathbb {R}$ which satisfies $p\le q \Rightarrow t(p)\le t(q)$ is said to be isotone or causal.

The notion of isotone function might be defined for any relation R on M, not just $R=J$. One says that the function t is a R-utility if it is R-isotone and additionally: $(p,q)\in R$ and $(q,p)\notin R$ $\Rightarrow t(p)<t(q)$.

Proposition 1.18

If an isotone function is differentiable at p, then $\nabla t(p)$ is past directed causal or zero.

Proof

If $w=-\nabla t(p)$ is non zero and not future directed causal then we can find a future directed timelike vector v such that $g(w,v)> 0$, hence $-\mathrm{d}t(v)=-g(\nabla t,v)> 0$, which contradicts the fact that t cannot decrease over timelike curves with tangent v at p. $\square$

Monotone functions on the real line are known to be (Fréchet-)differentiable almost everywhere. An analogous result holds true for isotone functions.

Theorem 1.19

Every isotone function $f:M\rightarrow \mathbb {R}$ on (M, g) is almost everywhere continuous and almost everywhere differentiable. Moreover, it is differentiable at $p\in M$ iff it is Gâteaux–differentiable at p. Finally, if $x:I\rightarrow M$ is a timelike curve, the isotone function f is upper/lower semi-continuous at $x_0=x(t_0)$ iff $f\circ x$ has the same property at $t_0$.

A similar result is contained in Rennie and Whale (2016) but, unfortunately, the proof of the non-trivial almost differentiability statement is incorrect² (cf. their Lemma A.4-5). The proof below takes advantage of a previous proof on the product order of $\mathbb {R}^k$ by Chabrillac and Crouzeix (1987). Notice that our proof remains unaltered for continuous distributions of closed cones with non-empty interior as considered in Minguzzi (2019). Also we might replace in the statement the isotone assumption with the weaker condition $p\ll q \Rightarrow f(p)\le f(q)$.

Proof

It is sufficient to prove the result in a neighborhood of a chosen point $q\in M$. Let $\{e_a\}$ be a holonomic basis of future directed timelike vector fields, where $e_a=\partial /\partial x^a$, $x^a(q)=0$, $a=0,1,\ldots , n$. By using these coordinates we can identify a neighborhood of q with a neighborhood of $O\ni 0$, $O\subset \mathbb {R}^{n+1}$. At every point the future timelike cone contains the cone $K=\{v^a e_a: v^a \ge 0, a=0,\ldots , n\}$, thus the spacetime isotone function $f:O \rightarrow \mathbb {R}$ is isotone also for the canonical product order $(x_0, \ldots , x_n) \le (y_0,\ldots , y_n)$ iff $x_a\le y_a$ for every a. The main statement is now a consequence of the results in Chabrillac and Crouzeix (1987), Theorems 6 and 14. The proof of the last statement is as in Proposition 5 of the mentioned reference, it is sufficient to replace $\le$ with the causal order and $f(x_0+td)$ with f(x(t)). $\square$

Definition 1.20

A continuous function $t:M\rightarrow \mathbb {R}$ such that $p\ll q \Rightarrow t(p)<t(q)$ is a semi-time function.

We shall see later (Theorem 2.27) that $J\subset {\bar{I}}$, thus by continuity we have that the semi-time functions are isotone. Semi-time functions were introduced by Seifert (1977), see also Ehrlich and Emch (1992b).

Definition 1.21

A continuous function $t:M\rightarrow \mathbb {R}$ which satisfies $p< q \Rightarrow t(p)<t(q)$ is a time function.

Every time function is a semi-time function, hence isotone.

Definition 1.22

A $C^1$ function $t:M\rightarrow \mathbb {R}$ such that $\mathrm{d}t$ is positive over the future causal cone (equivalently $\nabla t$ is past directed) is called temporal function.

Temporal functions are time functions.

Theorem 1.23

For a function t differentiable at $p\in M$ the inequalities at p

• (a) for every future directed causal vector v, $\mathrm{d}t(v) \ge \sqrt{-g(v,v)}$,

• (b) $-g(\nabla t,\nabla t)\ge 1$, and $\nabla t$ is past directed (clearly timelike).

are equivalent.

I mention that in Finslerian theories (a) $\Rightarrow$ (b) does not necessarily hold without conditions on the behavior of the Finsler function at the boundary of the causal cone.

Proof

(b) $\Rightarrow$ (a). Let v be future directed causal, then by the reverse Cauchy-Schwarz inequality

$$\begin{aligned} \mathrm{d}t(v)=-g(-\nabla t, v) \ge \sqrt{-g(\nabla t,\nabla t)} \sqrt{-g(v,v)}, \end{aligned}$$

thus if $-g(\nabla t,\nabla t)\ge 1$ then t satisfies (a).

(a) $\Rightarrow$ (b). Condition (a) implies that f is isotone so $\nabla f$ is past directed causal or zero. Moreover, over future directed timelike vectors (a) implies $\mathrm{d}f \ne 0$. Suppose that $w=-\nabla f(p)$ is lightlike, so that $\mathrm{d}f(w)=0$. Let n be a null vector such that $g(n,w)=-1/2$, then the vector $v(s)=w+sn$, $g(v,v)=-s$, for $s\ge 0$, is causal, thus by the steep condition $s \mathrm{d}f(n)=\mathrm{d}f(v(s))\ge \sqrt{s}$, which is impossible for sufficiently small s. We conclude that $\nabla f$ is past directed timelike. Now, $\mathrm{d}t(v)\ge \sqrt{-g(v,v)}$ holds also for $v=-\nabla t$, which, using the fact that $\nabla t$ is timelike, gives $-g(\nabla t,\nabla t) \ge 1$. $\square$

Definition 1.24

A function t which satisfies the equivalent conditions in the previous theorem is steep at p. A $C^1$ function $t:M\rightarrow \mathbb {R}$ which is steep at every point is a steep function.

Steep functions first appeared in a work by Parfionov and Zapatrin (2000) on the Lorentzian analog of Connes distance formula though the terminology comes from Müller and Sánchez (2011). These functions also proved useful in the study of the isometric embedding problem (Müller and Sánchez 2011; Minguzzi 2019).

Proposition 1.25

An isotone function $f:M\rightarrow \mathbb {R}$ is almost everywhere steep iff

$$\begin{aligned} {{\,\mathrm{ess\,inf}\,}}{ \sqrt{-g(\nabla f,\nabla f)}} \ge 1. \end{aligned}$$

(1.4)

Proof

If f is almost everywhere steep then for almost every p, $\sqrt{-g(\nabla f,\nabla f)}(p)$ $\ge 1$, that is, Eq. (1.4). Conversely, if f is isotone and Eq. (1.4) holds, then by Proposition 1.18 and Theorem 1.19 f is differentiable almost everywhere with past directed causal or zero gradient, but by Eq. (1.4) it satisfies $-g(\nabla t,\nabla t)\ge 1$ almost everywhere thus it has a.e. past directed timelike gradient, and hence it is almost everywhere steep. $\square$

The remainder of the section uses the notion of Lorentzian distance and some of its basic properties, c.f. Sect. 2.9.

Definition 1.26

A function $f:M\rightarrow \mathbb {R}$ which satisfies for every $(p,q)\in I$

$$\begin{aligned} f(q)\ge f(p)+d(p,q), \end{aligned}$$

(1.5)

is a rushing function. A rushing time function is a rushing time.

If a rushing function exists then the spacetime is chronological because d is finite.

The codomain of f could be extended to $[-\infty , +\infty ]$, but the previous statement would not hold. In order to simplify the following statements we shall not consider this generalization.

Our terminology here comes from the fact that given a proper time–parameterized timelike curve $\gamma :I \rightarrow M$, introduced the f-time $f(\gamma (t))$, we have for every $t_1\le t_2$, $f(\gamma (t_2))\ge f(\gamma (t_1))+ \varDelta t$, i.e. the f-clock is faster than the physical proper time clock. So we are just asking the f-time to be rushing for every observer. Clearly, rushing functions are isotone hence almost everywhere continuous and differentiable.

Proposition 1.27

For a $C^0$ rushing function Eq. (1.5) holds for $(p,q)\in {\bar{J}}$.

Proof

Let $(p,q)\in \bar{J}$, let $p_n\ll p$, $p_{n+1}\gg p_n$, be a sequence such that $p_n\rightarrow p$, and similarly, let $q_n\gg q$, $q_{n+1}\ll q_n$, be a sequence such that $q_n\rightarrow q$. Since I is open, $(p_n,q_n)\in I$ (here we are making use of Theorem 2.24 that shall be proved later on), thus $f(q_n)-f(p_n)\ge d(p_n,q_n)$, so $f(p)-f(q)=\liminf _n [f(q_n)-f(p_n)]\ge \liminf _n d(p_n,q_n) \ge d(p,q)$. $\square$

A theorem analogous to the following one can be found in Rennie and Whale (2016). We give this version because theirs uses a different ‘norm’ and because their proof runs into some problems (see the previous footnote).

Theorem 1.28

The rushing functions are precisely the isotone almost everywhere steep functions. The $C^1$ rushing functions are precisely the steep functions. The $C^0$ rushing functions are precisely the $C^0$ almost everywhere steep functions.

Notice that it is not true that the almost everywhere steep functions are isotone (just suitably change a $C^1$ steep function at some points).

Proof

Let f be rushing and let p be a differentiability point of t. We have already proved that (M, g) is chronological thus $d(p,p)=0$. Let C be a convex neighborhood of p, let $d^C$ be the Lorentzian distance of $(C,g\vert _C)$, and let $v\in T_pM$ be future directed timelike, then

$$\begin{aligned} \mathrm{d}f(v)&= \lim _{\epsilon \rightarrow 0} [f(\exp _p ( \epsilon v))-f(p)]\ge \lim _{\epsilon \rightarrow 0} \frac{1}{\epsilon } d(p,\exp _p ( \epsilon v) ) \\&\ge \lim _{\epsilon \rightarrow 0} \frac{1}{\epsilon } d^C(p,\exp _p ( \epsilon v) )=\lim _{\epsilon \rightarrow 0} \frac{1}{\epsilon } \int _0^\epsilon \sqrt{-g(x',x')} \, \mathrm{d}s=\sqrt{-g(v,v)} \end{aligned}$$

where $s\mapsto x(s)$ is the geodesic starting from p with velocity v, and where we used the fact that $d\vert _{C\times C}\ge d^C$. By continuity the inequality extends to v lightlike, thus the inequality proves that f is an almost everywhere steep function.

For the converse, let $(p,q)\in I$, by the lower semi-continuity of the Lorentzian distance for every $\epsilon >0$ there are open neighborhoods $U\ni p$, $V\ni q$, such that for every $(p',q')\in U\times V$, $d(p',q')\ge d(p,q)-\epsilon$, if d(p, q) is finite, or $d(p',q')>1/\epsilon$ if d(p, q) is infinite. Let ${\bar{p}}\in I^+(p,U)$ and ${\bar{q}}\in I^-(q,V)$, be such that $({\bar{p}},{\bar{q}})\in I$. Let $\epsilon >0$ and let $x:[0,1] \rightarrow M$, $x(0)={\bar{p}}$, $x(1)={\bar{q}}$, be a $C^1$ timelike curve such that $\ell (x)> d({\bar{p}},{\bar{q}})-\epsilon$, if $d({\bar{p}},{\bar{q}})$ is finite, or $\ell (x)>1/\epsilon -\epsilon$ if $d({\bar{p}},{\bar{q}})$ is infinite. So if d(p, q) is infinite we have $\ell (x)>1/\epsilon -\epsilon$ independently of the finiteness of $d({\bar{p}},{\bar{q}})$.

Let us construct a tubular neighborhood of x, of coordinates $(t,{\varvec{x}})$, having the topology $C:=[0,1]\times B$ of a cylinder, where $B\subset \mathbb {R}^n$ is a ball. We can find the radius of the ball so small that $\partial _t$ is timelike over the cylinder and the balls $t=0$ and $t=1$, namely the bases of the cylinder, are contained in $I^+(p,U)$ and $I^-(q,V)$. Let $x(t,{\varvec{x}})$ be the point determined by the coordinates $(t,{\varvec{x}})$. We regard f as a function over the coordinated cylinder. The curves $t\mapsto x_{{\varvec{x}}}(t)=x(t, {\varvec{x}})$ (we have a curve for any choice of constants ${\varvec{x}}$) that thread the cylinder are timelike, start from $I^+(p,U)$ and end in $I^-(q,V)$. Notice that $\partial _t$ is continuous so the length of the curves is a continuous function of $\mathbf{x}$. The radius of the ball can be chosen so small that they all have length larger than $\ell (x)-\epsilon$. Now, let E be the subset of the cylinder at which f is differentiable, and for every ${\varvec{x}}\in B$, let $E_{{\varvec{x}}}\subset [0,1]$ be the set of those s, such that f is differentiable at $x_{{\varvec{x}}}(s)$. Then the coordinate volume of the cylinder coincides with the volume of E, a condition which by Fubini-Tonelli reads $\int _B \mathrm{d}x^1 \ldots \mathrm{d}x^n[\int _{E_{{\varvec{x}}}} \mathrm{d}t-1]=0$, so for almost every $\mathbf{x}$, $E_{{\varvec{x}}}$ has full measure 1. So there is a timelike curve $s \mapsto {\tilde{x}}(s)$ with tangent $\partial _t$ over whose image f is differentiable almost everywhere. Let ${\tilde{p}}$ and ${\tilde{q}}$ be its endpoints. We have

$$\begin{aligned} f(q)-f(p){\ge } f({\tilde{q}}){-}f({\tilde{p}})= \!\!\int \! \mathrm{d}f( {\tilde{x}}') \,\mathrm{d}s \ge \! \int \!\sqrt{-g({\tilde{x}}',{\tilde{x}}')}\, \mathrm{d}s=\ell ({\tilde{x}}) \ge \ell (x)-\epsilon , \end{aligned}$$

where in the first inequality we used the fact that f is isotone (one can avoid to use the isotone property in the first inequality, provided one assumes continuity of f and takes U and V so small that the final inequality gets corrected by some $2\epsilon$. Proceeding in this one one proves the last statement of the theorem). But if d(p, q) is finite then $d({\bar{p}},{\bar{q}})$ is finite and we have

$$\begin{aligned} f(q)-f(p)\ge \ell (x)-\epsilon \ge d({\bar{p}},{\bar{q}})-2\epsilon \ge d(p,q)-3\epsilon , \end{aligned}$$

so by the arbitrariness of $\epsilon$ we get that $f(q)-f(p)\ge d(p,q)$. If instead, d(p, q) is infinite we get

$$\begin{aligned} f(q)-f(p)\ge \ell (x)-\epsilon \ge \frac{1}{\epsilon }-2\epsilon , \end{aligned}$$

so by the arbitrariness of $\epsilon$ we get that f cannot be finite. The contradiction proves that if there is an isotone almost everywhere steep function f, then the Lorentzian distance is finite and that the function f is rushing. $\square$

We have the following relative strengths for functions $f:M\rightarrow \mathbb {R}$

A last useful definition is

Definition 1.29

A Cauchy time function is a time function such that each of its level sets is intersected by every causal curve.

In particular, Cauchy time functions have image $\mathbb {R}$.

Other special time functions have been introduced in the literature, e.g. quasi-time functions (Ehrlich and Emch 1992b) and cosmological time functions (Andersson et al. 1998).

1.13 Recovering causality relations

We have seen that in a spacetime it is quite natural to define the triple of binary relations I, J and $\mathcal {E}$ (or $\ll$, $\le$ and $\rightarrow$). Since $\mathcal {E}$ is just the difference of the other two, it is clear that given two relations it is possible to recover the third.

Later on we shall prove that some causality conditions on spacetime guarantee that these binary relations can be recovered from just one causality relation of the triple. Kronheimer and Penrose (1967) suggested to define two new relations starting from a given one as follows.³

Definition 1.30

Let $\ll , \le , \rightarrow$ ($I, J, \mathcal {E}$) be binary relations on a set M (here the relations and M are abstract entities, possibly unrelated to a Lorentzian manifold). We define the associated relations

• 1. Starting from $\le$:

  • (a) $p\rightarrow ^{(\le )} q$ $\Leftrightarrow$ $p\le q$ and any proper subset $J^+(p')\cap J^-(q')$ of $J^+(p)\cap J^-(q)$ ordered by $\le$ is order homeomorphic to [0, 1].

  • (b) $p \ll ^{(\le )} q$ $\Leftrightarrow$ $p \le q$ and not $p \rightarrow ^{(\le )} q$.

• 2. Starting from $\rightarrow$:

  • (a) $p \le ^{(\rightarrow )} q$ $\Leftrightarrow$ $p=p_1 \rightarrow p_2 \dots \rightarrow p_{n-1}\rightarrow p_n=q$ for some finite sequence $p_1, \dots ,p_n \in M$.

  • (b) $p \ll ^{(\rightarrow )} q$ $\Leftrightarrow$ $p \le ^{(\rightarrow )} q$ and not $p \rightarrow q$.

• 3. Starting from $\ll$:

  • (a) $p \le ^{(\ll )} q$ $\Leftrightarrow$ $I^+(p) \supset I^+(q)$ and $I^-(p) \subset I^-(q)$.

  • (b) $p \rightarrow ^{(\ll )} q$ $\Leftrightarrow$ $p\le ^{(\ll )} q$ and not $p \ll q$.

It is worth to recall that the empty set admits just one relation (the empty set) which is a total order.

We anticipate the result which establishes under which causality conditions recovery of the triple is really possible. Notice that the causality condition in 2 has been improved with respect to the paper by Kronheimer and Penrose (1967) (and Minguzzi and Sánchez 2008) (they assumed strong causality).

Theorem 1.31

Let (M, g) be a (Lorentzian) spacetime and let $\ll ,\le ,\rightarrow$ be the usual chronological, causal, and horismos relations.

• 1. In a causal spacetime (Theorem 4.33)

  $$\begin{aligned} \rightarrow ^{(\le )}=\rightarrow , \qquad \ll ^{(\le )}=\ll . \end{aligned}$$

• 2. In a distinguishing spacetime (Theorem 4.66)

  $$\begin{aligned} \le ^{(\rightarrow )}=\le , \qquad \ll ^{(\rightarrow )}=\ll , \end{aligned}$$

• 3. In a causally simple spacetime

  $$\begin{aligned} \le ^{(\ll )} = \le , \qquad \rightarrow ^{(\ll )}=\rightarrow \end{aligned}$$

1.14 Causal convexity and first causality properties

Definition 1.32

Given two sets $U\subset V\subset M$, we say that U is causally convex in V (or simply causally convex if $V=M$) if every causal curve $x:[0,1]\rightarrow V$ such that $x(0),x(1)\in U$ has image contained in U.

Clearly, if U is causally convex in V, and V is causally convex in W then U is causally convex in W. Notice that if U is causally convex

$$\begin{aligned} J_U=J\cap U\times U. \end{aligned}$$

The converse does not hold: let M be $1+1$ Minkowski spacetime of coordinates $\{t,x\}$, and let $U=\{p:x(p)=0\}$.

We say that a point $p\in M$ admits an arbitrarily small neighborhood U with property P, if for every neighborhood $V\ni p$, we can find $U\subset V$, $p\in U$, satisfying property P.

Lemma 1.33

At every point $p\in M$ we can find local coordinates $\{x^\mu \}$ such that $x^\mu (p)=0$, $\{e_\mu :=\partial _\mu \}$ is a canonical basis of $(T_pM,g_p)$, i.e., $g(e_\mu , e_\nu )=\eta _{\mu \nu }$ with $e_0$ future directed, and defining $g^\epsilon =-(1+\epsilon ) (\mathrm{d}x^0)^2+ \mathrm{d}\mathbf {x}^2$, $\epsilon \in (-1,1)$, we can find $\epsilon _+>0$ and $\epsilon _-<0$, such that in a neighborhood of p, $g^{\epsilon _-}<g<g^{\epsilon _+}$. Moreover, in this neighborhood for every g-causal vector v

$$\begin{aligned} \sqrt{(\mathrm{d}x^0)^2+(\mathrm{d}\mathbf {x})^2}\, (v)< (2+\epsilon _+)^{1/2} \mathrm{d}x^0(v). \end{aligned}$$

(1.6)

Proof

The inclusion of the cones can be easily checked at p, so the validity in a neighborhood follows by continuity. Every g-causal vector is $g^{\epsilon _+}$-timelike, thus $(1+\epsilon _+) [\mathrm{d}x^0(v)]^2>(\mathrm{d}\mathbf {x})^2(v)$. $\square$

A closed causal curve $x:[0,1]\rightarrow M$ is one for which $x(0)=x(1)$ (possibly $\dot{x}(0)\ne \dot{x}(1)$). A similar definition holds in the timelike case. Clearly no point in a closed causal curve can admit arbitrarily small causally convex neighborhoods.

We need to define a few basic causality properties.

Definition 1.34

A spacetime is

• 1. chronological: if it does not admit any closed timelike curve,

• 2. causal: if it does not admit any closed causal curve,

• 3. strongly causal: if it admits arbitrarily small causally convex neighborhoods at every point.

Observe that the properties are ordered from the weakest to the strongest, and that in 3 arbitrarily small is important, for the set M is causally convex and a neighborhood for every point.

Theorem 1.35

Every point $p\in M$ admits a local basis $\{V_k, k\ge 1\}$, for the topology such that for every k

• (a) $\overline{V_{k+1}} \subset V_k$,

• (b) $V_{k+1}$ is causally convex in $V_k$ (and hence in $V_1$),

• (c) $(V_k,g)$ is strongly causal,

• (d) Let h be a Riemannian metric; on $(V_k,g)$ the h-arc length of any causal curve contained in $V_k$ is bounded by a positive constant c(k) which goes to zero for $k\rightarrow +\infty$,

• (e) $V_k$ is relatively compact.

Moreover, if (M, g) is strongly causal then $V_1$ can be chosen causally convex so all the elements of the local basis are causally convex.

Proof

Let $g^{\epsilon _+}$ be the metric in a neighborhood U of p mentioned in Lemma 1.33. Let $q_n$ be such that $x^0(q_n)=1/n$, $x^i(q_n)=0$, and similarly let $r_n$ be such that $x^0(r_n)=-1/n$, $x^i(r_n)=0$. Let

$$\begin{aligned} V_k=I_{g^{\epsilon _+}}^+(r_{N+k}) \cap I_{g^{\epsilon _+}}^-(q_{N+k}), \end{aligned}$$

(1.7)

then for sufficiently large N, $\partial V_k\cap \partial U=\emptyset$. The properties (a)-(c) are easily checked since if A is causally convex in B with respect to a metric g then the same holds using a metric $g'<g$. Property (d) follows from the inequality (1.6), from the fact that $\vert x^0\vert <1/n$ on $V_n$, and from the Lipschitz equivalence of Riemannian norms over compact sets.

If (M, g) is strongly causal then p admits a causally convex set W contained in $V_1$. For some sufficiently large k, $V_k\subset W$, and any causal curve $\sigma$ with endpoints in $V_k$ has endpoints in W thus $\sigma$ is contained in W and hence in $V_1$, but since $V_k$ is causally convex in $V_1$, $\sigma$ is contained in $V_k$, i.e. $V_k$ is causally convex. Now renumber the sequence starting from $V_k\rightarrow V_1$. $\square$

Remark 1.36

The construction appearing in the proof of this theorem contains much more information than is conveyed by the statement. For instance, it can be observed that the function $x^0:V_k \rightarrow \mathbb {R}$ is a continuous function which increases over every causal curve of $(V_k,g^{\epsilon _+})$ and hence of $(V_k,g)$ (we shall see later that this property is known as stable causality and that in fact, $(V_k,g)$ shares the strongest causality property according to the causal ladder of spacetimes, namely globally hyperbolicity).

2 Some preliminaries

In this section we explore the local properties of the exponential map and its consequences. Some of these results are really quite technical already in the $C^2$ case, in fact most proofs found in the literature are given for the $C^\infty$ metric case. A closer investigation shows that the results of this section really require just a $C^{1,1}$ assumption on the metric, so that most of causality theory can be generalized to this regularity class (Minguzzi 2015b; Kunzinger et al. 2014a, b). For most of the proofs we shall follow Minguzzi (2015b).

2.1 The exponential map

A geodesic is a stationary point of the functional (with a prime we denote differentiation, typically with respect to a parameter s, if the parameter is t we often use a dot)

$$\begin{aligned} S[x]=\int _{s_0}^{s_1} L(x,x')\, \mathrm{d}s , \qquad x:[s_0,s_1]\rightarrow M, x(s_0)=x_0, x(s_1)=x_1 , \end{aligned}$$

where $x\in C^1([s_0,s_1])$ and $L(x,v)=\frac{1}{2} g_x(v,v)$.

Let $x^\mu :U\rightarrow \mathbb {R}^{n+1}$ be a local chart where U is an open subset. Every chart induces a chart $(x^\mu , v^\mu ):\pi ^{-1}(U)\rightarrow \mathbb {R}^n\times \mathbb {R}^n$, on the tangent bundle $\pi : TU\rightarrow U$.

The Euler–Lagrange equations determining the geodesic read, in the local chart, as a second order ODE defined just over U

$$\begin{aligned} \frac{\mathrm{d}x^{\mu }}{ \mathrm{d}t}&=v^\mu , \end{aligned}$$

(2.1)

$$\begin{aligned} \frac{\mathrm{d}v^\mu }{\mathrm{d}t}&= - \varGamma _{\alpha \beta }^\mu (x) v^\alpha v^\beta , \end{aligned}$$

(2.2)

where $\varGamma _{\alpha \beta }^\mu$ is the Christoffel symbol for the Levi-Civita connection. Since g is $C^2$ the right-hand side is Lipschitz and so by the Picard–Lindelöf theorem for any given initial condition $x(0)=x_0$, $\dot{x}(0) = \dot{x}_0$ the solution exists and is unique. In fact, since $\varGamma$ is $C^1$ the geodesics are $C^3$ and the dependence on initial conditions is $C^1$.

The Lagrangian L is constant over the geodesics because, using the Euler–Lagrange equations and the positive homogeneity of degree two of L

$$\begin{aligned} \frac{\mathrm{d}L}{\mathrm{d}t}=\frac{\partial L}{\partial x^\mu }\, v^\mu + \frac{\partial L}{\partial v^\mu } \frac{\mathrm{d}v^\mu }{\mathrm{d}t}=\left( \frac{\mathrm{d}}{\mathrm{d}t}\frac{\partial L}{\partial v^\mu }\right) v^\mu + \frac{\partial L}{\partial v^\mu } \frac{\mathrm{d}v^\mu }{\mathrm{d}t}=\frac{\mathrm{d}}{\mathrm{d}t} \left( \frac{\partial L}{\partial v^\mu } v^\mu \right) =2\frac{\mathrm{d}L}{\mathrm{d}t}. \end{aligned}$$

Its constancy implies that the causal character of the tangent vector is preserved throughout the whole domain of definition of the geodesic, so geodesics are said to be timelike, lightlike or spacelike depending on the causal character of their tangent vector.

Let $v\in TM\backslash 0$, and let $\gamma _v(t)$ be the unique geodesic which starts from $\pi (v)$ with velocity v. The set $\varOmega$ is given by those v for which the geodesic exists at least for $t\in [0,1]$. The exponential map $\exp :\varOmega \rightarrow M\times M$ is given by

$$\begin{aligned} v \mapsto (\pi (v),\gamma _v(1)), \end{aligned}$$

while the pointed exponential map at $p \in M$, is $\exp _p:\varOmega _p \rightarrow M$, $\varOmega _p=\varOmega \cap \pi ^{-1}(p)$, $\exp _p v:=\gamma _v(1) =\pi _2(\exp v)$. By the homogeneity of degree two of $\varGamma ^\mu _{\alpha \beta } v^\alpha v^\beta$ on velocities we have

$$\begin{aligned} \gamma _{sv}(t)=\gamma _v(st), \end{aligned}$$

(2.3)

thus the set $\varOmega$ (and $\varOmega _p$) is star-shaped in the sense that if $v\in \varOmega$ then $s v\in \varOmega$ for every $s\in [0,1]$. Equation (2.3) clarifies that it makes sense to call affine the geodesic parameter, for any affine reparametrization of a geodesic gives a curve which solves the geodesic equation.

The following result is consequence of the inverse function theorem on the diagonal of $M\times M$.

Theorem 2.1

Let M be a manifold endowed with a $C^1$ connection.

$(\exp )$:

The set $\varOmega$ is open in the topology of TM. The exponential map $\exp :\varOmega \rightarrow M\times M$, $\varOmega \subset TM$, provides a $C^1$ diffeomorphism between an open star-shaped neighborhood of the zero section and an open neighborhood of the diagonal of $M\times M$.

$(\exp _p)$:

For every $p\in M$ the set $\varOmega _p$ is open in the topology of $T_pM$. The pointed exponential map $\exp _p:\varOmega _p \rightarrow M$, $\varOmega _p \subset T_pM$, provides a $C^1$ diffeomorphism from a star-shaped open subset of $\varOmega _p$ and an open neighborhood of p.

A proof can be found in Minguzzi (2015b).

2.2 Convex neighborhoods

Definition 2.2

An open neighborhood N of $p\in M$ is called normal if there is an open star-shaped subset $N_p\subset \varOmega _p$ such that $\exp _p:N_p \rightarrow {N}$ is a $C^1$ diffeomorphism.

Definition 2.3

An open set $C\subset M$ is called convex normal if it is a normal neighborhood of each of its points. We shall say that C is strictly convex normal if C is convex normal and any two points of $\bar{C}$ are connected by a unique geodesic contained in C but for the endpoints.

Theorem 2.4

Let M be a manifold endowed with a $C^1$ connection. Let O be an open neighborhood of $p\in M$. Then there is a strictly convex normal neighborhood C of p contained in O, such that $\exp$ establishes a $C^1$ diffeomorphism between an open star-shaped subset of TC and $C\times C$.

Moreover, for every chart $\{x^\mu \}$ defined in a neighborhood of p, C can be chosen equal to the open ball $B(p,\delta )$ for any sufficiently small $\delta$ (the ball is defined through the Euclidean norm induced by the coordinates).

The local length minimization property of geodesics in Riemannian spaces, or the local Lorentzian length maximization property of causal geodesics in Lorentzian manifolds, are proved passing through Gauss’ Lemma.

Definition 2.5

Let C be a convex normal set, let $p,q\in C$ and let $x: [0,1]\rightarrow C$, $x(0)=p$, $x(1)=q$, be the unique geodesic connecting them. The vector $\dot{x}(1)$ is denoted P(p, q) and called position vector.

Theorem 2.6

(Gauss’ Lemma) Let $p\in M$, let N be a normal neighborhood of p and let $v\in \exp _p^{-1}\!\! N\backslash 0$. Let $w\in T_p M\sim T_v(T_p M)$. Then

$$\begin{aligned} g_{\exp _p \!v}( (d \exp _p)_v v, (d \exp _p)_v w )=g_p(v,w). \end{aligned}$$

(2.4)

Moreover, the function $D^2_p:N \rightarrow \mathbb {R}$ defined by

$$\begin{aligned} D^2_p(q):= \,g_{p}(\exp _p^{-1}(q),\exp _p^{-1}(q)) \end{aligned}$$

(2.5)

is $C^{2}$ in q and

$$\begin{aligned} d D^2_p(q)= 2 g_{q} (P(p,q),\cdot ), \end{aligned}$$

(2.6)

where $P(p,q):= \gamma '_{\exp ^{-1}_p q}(1)$ is the position vector of q with respect to p. Thus the level sets of $D^2_p$ are orthogonal to the geodesics issued from p. Finally, on a convex normal set C the function $D^2:C\times C \rightarrow \mathbb {R}$ defined by

$$\begin{aligned} D^2 (p,q):= \,g_{p}(\exp _p^{-1}(q),\exp _p^{-1}(q)) \end{aligned}$$

(2.7)

is $C^2$ and its differential is

$$\begin{aligned} d D^2_p(q) (v_p,v_q)= 2 g_{q} (P(p,q),v_q)+2 g_{p} ({P}(q,p),v_p), \end{aligned}$$

where $v_p\in T_pM$, $v_q\in T_qM$.

A proof of the previous result can be found in Minguzzi (2015b, Theorem 5).

The following result was proved only recently in Minguzzi (2015b, Corollary 2). The proof is quite technical so it is omitted. In short it states that the topological basis can be chosen to have the best convexity and causality properties.

Theorem 2.7

The basis $\{V_k\}$ for the topology mentioned in Theorem 1.35 can really be chosen so that, additionally, the sets $V_k$ are strictly convex normal and globally hyperbolic.

Without this result one is forced to phrase some arguments by using a few nested neighborhoods, some convex and other globally hyperbolic, so as to get some desired property. This sort of involved construction is common in references devoted to causality theory. Thus, although this result is not necessary for the development of causality theory, it might be used to simplify some proofs.

2.3 Causal AC-curves

So far we considered only piecewise $C^1$ curves, but for what follows we need to weaken their differentiability properties so as to work with a family which is closed under a suitable notion of limit.

A curve $\sigma :[a,b]\rightarrow M$ will be called absolutely continuous (an AC-curve for short) if its components in one (and hence every) local chart are locally absolutely continuous. Equivalently, introducing a complete Riemannian metric on M, and denoting by $\rho$ the corresponding distance, $\sigma$ is absolutely continuous if it satisfies locally the usual definition of absolute continuity between (topological) metric spaces. Since every pair of Riemannian metrics over a compact set are Lipschitz equivalent, and M is locally compact, this definition does not depend on the metric chosen. Analogously, we can define the concept of Lipschitz curve.

We shall say that an AC-curve $\sigma :[a,b]\rightarrow M$, $t\mapsto \sigma (t)$, is a (future directed) causal AC-curve if ${\dot{\sigma }}$ is (future directed) causal almost everywhere. We do not need to define a notion of timelike AC-curve.

Remark 2.8

Lipschitz reparametrizations. Over every compact set $A\subset U$ we can find a constant $a>0$ such that for every $x\in A$, $y\in T_xM$, $\Vert y\Vert _h=\sqrt{h_{\alpha \beta } y^\alpha y^\beta } \le a \sum _\mu \vert y^\mu \vert$. As each component $x^\mu (t)$ is absolutely continuous, each derivative $\dot{x}^\alpha$ is integrable and so $\Vert \dot{x}\Vert _h$ is integrable. The integral

$$\begin{aligned} s(t)=\int _0^t \Vert \dot{x}\Vert _h(t') \mathrm{d}t' \, , \end{aligned}$$

is the Riemannian h-arc length. Observe that by definition causal vectors are not zero so the argument of the integral is positive almost everywhere so the map $t\mapsto s(t)$ is increasing and absolutely continuous. Its inverse $s\mapsto t(s)$ is differentiable wherever $t\mapsto s(t)$ is with $\dot{s}\ne 0$, in fact $t'= \dot{s}^{-1}=\Vert \dot{x}\Vert _h^{-1}$ at those points, where a prime denotes differentiation with respect to s. By Sard’s theorem for absolutely continuous functions (Montesinos et al. 2015) and by the Luzin N property of absolutely continuous functions, a.e. in the s-domain the map $s\mapsto t(s)$ is differentiable and $\dot{x}(t(s))\in C_{x(t(s))}$. At those points $x'= \dot{x}/\Vert \dot{x}\Vert _h^{-1}\in C_{x(t(s))}$ so $\Vert x'\Vert _h=1$ and the map $s \mapsto x(t(s))$ is really Lipschitz. The discussion shows that by a change of parameter we can pass from absolutely continuous causal curves to Lipschitz causal curves parametrized with respect to h-arc length (see also the discussion in Petersen 2006, Sect. 5.3).

2.4 Local maximization properties of geodesics

The Lorentzian length of a causal AC-curve is

$$\begin{aligned} l(\sigma )=\int _a^b\! \sqrt{-g({\dot{\sigma }},{\dot{\sigma }})} \,\, \mathrm{d}t . \end{aligned}$$

The integral is finite, in fact locally we can find coordinates $\{x^\mu \}$ and a constant $a>0$ such that over causal vectors $\sqrt{-g(v,v)}\le a v^0$, and moreover ${\dot{\sigma }}^0(t)$ belongs to to $L^1([a,b])$ as $\sigma (t)$ is absolutely continuous.

The proof of the following result is adapted from Minguzzi (2015b, Theorem 6). For an alternative proof of the first part see Chruściel (2011, Proposition 2.4.5).

Theorem 2.9

Let (M, g) be a spacetime for which g is $C^{2}$. Let N be a normal neighborhood of $p\in M$ and let $\sigma :[0,1]\rightarrow N$ be any future directed causal AC-curve starting from p, then $\exp ^{-1}(\sigma (s))$ is future directed causal for every $s>0$, and if $\exp ^{-1}(\sigma ({\hat{s}}))$ is lightlike then $\sigma \vert _{[0,\hat{s}]}$ coincides with a future directed lightlike geodesic segment up to parametrizations.

Finally, the Lorentzian length of $\sigma$ is smaller than that of the (unique) future directed causal geodesic connecting its endpoints, unless its image coincides with that of that geodesic. In this last case the affine parameter of the geodesic is absolutely continuous and increasing with s.

Proof

If q is a point such that $D^2_p(q)\le 0$, the Lorentzian length of the geodesic $\gamma$ connecting p to q is:

$$\begin{aligned} D^L_p(q):=\int \sqrt{-g({\dot{\gamma }},{\dot{\gamma }})} \mathrm{d}t=\sqrt{-g({\dot{\gamma }},{\dot{\gamma }})} \int \mathrm{d}t=\sqrt{-g({\dot{\gamma }},{\dot{\gamma }})} \end{aligned}$$

that is $D^L_p(q):=(- D^2_p(q))^{1/2}$. Since $D_p^2$ is $C^{2}$, $D^L_p$ is $C^{2}$ in the region $D_p^2< 0$.

Suppose that for some $\tilde{s}$, $D_p^2(\sigma (\tilde{s}))< 0$. By continuity the same inequality holds in an interval $[\tilde{s},s]$ provided s is sufficiently close to $\tilde{s}$, which implies that $P(p,\sigma (s'))$ is causal for $s'\in [{\tilde{s}},s]$. The function $D^L(\sigma (s))$ being the composition of a locally Lipschitz and an absolutely continuous function is absolutely continuous over $[\tilde{s},s]$. We have

$$\begin{aligned} D_p^L(\sigma (s))- D_p^L(\sigma (\tilde{s}))&=\int _{\tilde{s}}^s \frac{\mathrm{d}D_p^L(\sigma (s))}{\mathrm{d}s}\, \mathrm{d}s \nonumber \\&=- \int _{\tilde{s}}^s \frac{1}{D_p^L(\sigma (t))}\,g_{\sigma (s)}(P(p,\sigma (s)),\sigma '(s))\, \mathrm{d}s \nonumber \\&= -\int _{\tilde{s}}^s \,g_{\sigma (s)}(\hat{P}(p,\sigma (s)),\sigma '(s)) \, \mathrm{d}s \nonumber \\&\ge \int _{\tilde{s}}^s \, \sqrt{- g_{\sigma (s)}(\sigma '(s),\sigma '(s))} \,\mathrm{d}s = l[\sigma \vert _{[{\tilde{s}}, s]}], \end{aligned}$$

(2.8)

where ${\hat{P}}:=P/\sqrt{-g_{\sigma (s)}(P,P)}$. In the last inequality we used the reverse Cauchy–Schwarz inequality.

The inequality so obtained proves that once $\sigma$ enters the region with $D^2_p<0$ it remains in that region (this is the region of points reachable from p with a timelike geodesic in N) for the function $D^2_p$ can only decrease.

Now let $\eta :[-\epsilon ,0] \rightarrow C$, $\eta (0)=p$, be a small future directed timelike geodesic contained in a convex normal neighborhood of p, $p\in C\subset N$. For sufficiently small s, $\sigma (s)\in C$, and the curve obtained concatenating $\eta$ with $\sigma$ which connects $\eta (-\epsilon )$ to $\sigma (s)$ starts with a timelike geodesic, hence it enters the chronological future of $\eta (-\epsilon )$, and hence, by the above argument there is a future directed timelike geodesic $\nu ^{(\epsilon )}$ connecting $\eta (-\epsilon )$ to $\sigma (s)$. Letting $\epsilon \rightarrow 0$, and using the continuity of the exponential map $\exp$ at $\sigma (s)$ we infer the existence of a geodesic connecting p to $\sigma (s)$, which by the continuity of $g_{\sigma (s)}(v,v)$ at $T_{\sigma (s)}M$ must be future directed causal. As s is arbitrary we have shown that in a maximal closed interval $[0,b]\subset [0,1]$, $b>0$, we have $D^2_p(\sigma (s))\le 0$.

Let us prove that if for $a\in (0,b]$, $D^2_p(\sigma (a))=0$ then $\sigma \vert _{[0,a]}$ is a lightlike geodesic up to parametrizations and hence that $D^2_p=0$ over [0, a].

Observe that $D^2_p$ is Lipschitz, thus $D^2_p(\sigma (s))$ is absolutely continuous

$$\begin{aligned} D^2_p(\sigma (a))=\int _0^a \frac{\mathrm{d}D^2_p(\sigma (s))}{\mathrm{d}s}\, \mathrm{d}s=2 \int _0^a g_{\sigma (s)}(P(p,\sigma (s)), \sigma '(s))\, \mathrm{d}s. \end{aligned}$$

Since on the region $D^2_p\le 0$, we have $g_{\sigma (s)}(P(p,\sigma (s)), \sigma '(s))\le 0$ for almost every s (by the reverse Cauchy–Schwarz inequality since $\sigma '$ is future directed causal almost everywhere), thus we can have $D^2_p(\sigma (a))=0$ only if $\sigma '\propto P$ for almost every s in [0, a]. Let us introduce a Euclidean scalar product on $T_pM$, and associated spherical normal coordinates $(r,\theta _1,\ldots , \theta _{n})$ over N. As this coordinate chart is $C^1$ related to those of M, $\sigma$ is still absolutely continuous in this chart. Thus since $\sigma '\propto \partial _r$ almost everywhere, the angular coordinates cannot change over $\sigma$, otherwise since $\theta _i(\sigma (s))$ is the integral of its own derivative one would get that $\sigma '$ is not radial in a set of non-vanishing measure, a contradiction. Thus $\sigma \vert _{[0,a]}$ is an integral curve of P, hence a lightlike geodesic issued from p.

From now on let a be the maximum value of s for which $D^2_p(\sigma (s))=0$.

It remains only to prove that $b=1$. Suppose not then $a=b$ otherwise $D^2_p(b)<0$, which would imply the same inequality also in (b, 1], a contradiction to $b<1$. Set $p'=\sigma (b)$ and take a convex normal neighborhood $C'\ni p'$, $C'\subset N$. Arguing as above proves that for any sufficiently small $\delta$, $p'$ is connected to $\sigma (b+\delta )$ by a future directed causal geodesic $\eta : [0,1]\rightarrow C'$. This geodesic cannot be the prolongation of the lightlike geodesic $\sigma _{[0,b]}$ for we would get $D_p^2(\sigma (b+\alpha \delta ))\le 0$, $\alpha \in [0,1]$, a contradiction to the maximality of b. Thus the scalar product $g_{\eta (t)}(P(p,\eta (t)), \eta '(t))$ is negative for $t=0$ and hence in a neighborhood of $t=0$. Now, observe that $D^2_p$ is $C^1$, thus $D^2_p(\eta (t))$ is absolutely continuous and, for sufficiently small t,

$$\begin{aligned} D^2_p(\eta (t))=D^2_p(\sigma (b))+\int _0^t \frac{\mathrm{d}D^2_p(\eta (t))}{\mathrm{d}t}\, \mathrm{d}t=2 \int _0^t g_{\eta (t)}(P(p,\eta (t)), \eta '(t))\, \mathrm{d}t<0. \end{aligned}$$

As the concatenation of $\sigma _{\vert _{[0,b]}}$ with $\eta$ is a causal AC-curve and on it $D^2_p$ becomes negative at some point, and it remains so, we have at the endpoint $D^2_p(\sigma (b+\delta ))=D^2_p(\eta (1))<0$. As $\delta$ is arbitrary we get a contradiction to the maximality of b. The contradiction proves that $b=1$.

If $\sigma$ is a lightlike geodesic up to parametrization, then clearly its Lorentzian length vanishes and the inequality $D_p^L(\sigma (1))\ge l(\sigma )$ is satisfied. Suppose that $\sigma$ is not a lightlike geodesic up to parametrizations then $a<1$, and its Lorentzian length is given just by the contribution of $\sigma _{[a,1]}$. Let $\tilde{s}\in [a,1]$ so that $D^2_p(\sigma (\tilde{s}))<0$. By (2.8)

$$\begin{aligned} D^L_p(\sigma (1))\ge l(\sigma _{[\tilde{s},1]}) \end{aligned}$$

and taking the limit $\tilde{s}\rightarrow a$ we obtain $D^L_p(\sigma (1))\ge l(\sigma )$. This proves that $\sigma$ has a Lorentzian length no larger than that of the geodesic connecting its endpoints.

Now, suppose by contradiction that they have the same Lorentzian length and that $\sigma$ is not a causal geodesic up to parametrizations. Then necessarily $a<1$, for otherwise it would be a lightlike geodesic. But then from (2.8), for $\tilde{s}>a$,

$$\begin{aligned} D^L_p(\sigma (1))\ge D^L_p(\sigma (\tilde{s}))+ l(\sigma _{[\tilde{s},1]})\ge l(\sigma _{[0,\tilde{s}]})+l(\sigma _{[\tilde{s},1]})=l(\sigma ). \end{aligned}$$

Thus the equality implies that the first inequality is actually an equality, which implies the equality case for almost every $s\in [\tilde{s}, 1]$ in the reverse Cauchy–Schwarz inequality used to deal with $g_{\sigma (s)}(P(p,\sigma (s)),\sigma '(s))$ and hence, by the arbitrariness of $\tilde{s}$, $\sigma '\propto P$ for almost every $s\in [a,1]$. Introducing again spherical normal coordinates and arguing as above proves that the image of $\sigma \vert _{[a,1]}$ is an integral curve of P (and hence the prolongation of $\sigma \vert _{[0,a]}$ if $a\ne 0$), thus it is the image of a geodesic.

Finally, suppose that the image of $\sigma$ coincides with that of a causal geodesic $\eta$. Since the coordinates of the spherical normal chart are Lipschitz functions, the composition r(s) is absolutely continuous. By definition r is an affine parameter over the geodesic $\eta$. The map r(s) is necessarily increasing, for if $r(s_2)\le r(s_1)$ for $s_1<s_2$, then we would have $r'\le 0$ in a subset of measure different from zero on $[s_1,s_2]$, which would imply that $\frac{\mathrm{d}}{\mathrm{d}s } \sigma =(\frac{\mathrm{d}}{\mathrm{d}r } \eta ) r'$ is not future directed causal in a set of measure different from zero, a contradiction to the definition of future directed causal AC-curve. $\square$

Corollary 2.10

Let N be a normal neighborhood of p. Then for $v\in \exp _p^{-1} N\subset T_pM$:

• 1. $\exp _p \!v \in J_N^+(p)$ iff v is future directed causal or zero,

• 2. $\exp _p \!v \in I_N^+(p)$ iff v is future directed timelike,

• 3. $\exp _p \!v \in E_N^+(p)$ iff v is future directed lightlike or zero.

Proof

The if part of the first two statements is clear, for the geodesic connecting p to $q=\exp _p \!v$ is causal in case 1 and timelike in case 2. If $q=0$ then $v=0$ (recall that $\exp$ is one-to-one from $\exp _p^{-1} N$ to N), if $q \in J_N^+(p)\backslash 0$ then by the first part of Theorem 2.9 v is future directed causal. If $q\in I_N^+(p)$ then, as before, v is future directed causal, but by the second part of Theorem 2.9 the causal geodesic connecting p to q in N maximizes the Lorentzian length among the connecting causal curves in N, thus this length is positive and so v is timelike.

As for the last statement, if v is future directed lightlike by the last part of the first statement in Theorem 2.9 p is connected to q by no causal curve other than the unique lightlike geodesic generated by v, in particular $q\notin I_N^+(p)$, thus $q\in E_N^+(p)$. Conversely, if $q\in E_N^+(p)\backslash p$, then v is future directed causal by point 1, but non-timelike by point 2, thus v is lightlike. $\square$

Convex normal sets enjoy in a natural way some causality properties (Minguzzi and Sánchez 2008; Minguzzi 2015b).

Theorem 2.11

Let C be a convex normal set, then the causal relation $J_C$ of (C, g) is closed. Moreover, on (C, g) there is no closed causal curve.

As we shall see, these two properties taken jointly are known as causal simplicity.

Proof

Let T be the global timelike vector field which provides the time orientation. Let C be a convex normal subset, and let $f_1,f_2:C\times C \rightarrow \mathbb {R}$ be the functions $f_1(p,q):=g(\exp _p^{-1}q, \exp _p^{-1}q)$, $f_2(p,q):=g(\exp _p^{-1}q, T(p))$. Since $\exp ^{-1}$ and g are continuous $f_1$ and $f_2$ are continuous, and hence $J^{+}_C=f_1^{-1}((-\infty ,0])\cap f_2^{-1}((-\infty ,0])$ is closed.

Suppose that there are $p,q\in C$, $p\ne q$, such that $p\le _C q$ and $q\le _C p$. Let $\gamma _1$ be the future directed causal geodesic connecting p to q and let $\gamma _2$ be the future directed causal geodesic connecting q to p. Then the images of $\gamma _1$ and $\gamma _2$ differ (a causal curve cannot be both future and past directed), and hence there are two geodesics connecting p to q, a contradiction to the uniqueness of the connecting geodesic in convex normal sets (Theorem 2.4). $\square$

2.5 Continuous causal curves

A future directed continuous causal curve⁴ is a continuous map $x:[a,b]\rightarrow M$ such that for every open convex normal set C intersecting x, whenever $x([t_1,t_2])\subset C$, $t_1<t_2$, the points $x(t_1)$ and $x(t_2)$ are connected by a future directed causal geodesic contained in C.

Theorem 2.12

Let I be an interval of the real line. Every future directed causal AC-curve $x:I\rightarrow M$ is a future directed continuous causal curve. Every future directed continuous causal curve $x:I\rightarrow M$ once suitably parametrized (e.g. with respect to the arc-length of a Riemannian metric, or with respect to the local time coordinate $x^0$ mentioned in Remark 1.36) becomes a future directed causal locally Lipschitz curve.

Remark 2.13

It is not true that every continuous causal curve is a causal AC-curve. For instance, consider the timelike geodesic of Minkowski spacetime which satisfies $x^i=0$, $i\ge 1$, and which is parametrized by $x^0$. Consider the parametrization $t=f_s^{-1}(x^0)$ where $f_s$ is a singular monotone continuous function (Rudin 1970, Example 8.20), so that $\dot{f}_s=0$ almost everywhere.

Most of the results of causality theory that shall follow are expressed in terms of continuous causal curves, unless the parameter has some relevance, in which case causal AC or Lipschitz curves are used.

Proof

It is sufficient to prove it for $I=[a,b]$. Suppose that x is a future directed causal AC-curve, let C be a convex normal set intersecting x, and let $t_1<t_2$ be such that $x([t_1,t_2]) \subset C$. The set C is a normal neighborhood for $p:=x(t_1)$, thus by Theorem 2.9 the geodesic connecting $x(t_1)$ and $x(t_2)$ is (future directed) causal.

Conversely, suppose that $x:I\rightarrow M$ is a future directed continuous causal curve and let $\bar{t}\in I$. By Lemma 1.33 we can find coordinates $x^\mu$ in a convex neighborhood C of $p:=x(\bar{t})$ such that for some $\epsilon _+>0$, the Lorentzian metric $g^+=-(1+\epsilon _+)(\mathrm{d}x^0)^2+ (\mathrm{d}x^1)^2+\cdots (\mathrm{d}x^{n-1})^2$ satisfies $g<g^+$ throughout C.

The function $x^0(t)$ must be increasing in a neighborhood of $\bar{t}$. Indeed, for $t_1,t_2$ belonging to a sufficiently small neighborhood of $\bar{t}$, $x(t_1), x(t_2)\in C$. By assumption there is a future directed causal g-geodesic connecting $x(t_1)$ with $x(t_2)$, which is, in particular, a future directed $g^+$-causal $C^1$ curve. But $x^0$ is increasing over this type of curve since $x^0$ is the rescaled time coordinate for a subset $(C,g^+)$ of Minkowski spacetime, which proves the claim.

Once parametrized with respect to $x^0$ the curve becomes Lipschitz because of the condition of g-causality, which implies $g^+$-causality, which reads $\Vert \mathbf {x}(t_2)-\mathbf {x}(t_1)\Vert \le (1+\epsilon _+)^{1/2} \vert x^0(t_2)-x^0(t_1)\vert$. Clearly, if s is an arc-length parameter induced by the Euclidean coordinate metric $(\mathrm{d}x^0)^2+(\mathrm{d}\mathbf {x})^2$ then $x^0(s)$ is 1-Lipschitz, and so x(s) is locally Lipschitz. As all Riemannian metrics are Lipschitz equivalent over compact sets, x is locally Lipschitz whenever parametrized with respect to Riemannian arc-length. $\square$

Remark 2.14

Observe that if x is a continuous causal curve connecting two points p and q, then, as it can be covered by a finite number of convex normal neighborhoods, p and q are also connected by a (piecewise $C^1$) causal curve. So the definition (1.3) of the causal relation J can equivalently make use of continuous causal curves.

Remark 2.15

The definition of continuous timelike curve given by Hawking and Ellis (1973, Sect. 6.2), has not proved to be equally important, in fact they never used the concept. Notice that every lightlike curve $x:I \rightarrow M$ for which $D_{\dot{x}} \dot{x}\not \propto \dot{x}$ at every point would be a continuous timelike curve according to their definition, a circumstance which makes their terminology questionable.

2.6 Inextendibility and Riemannian length

Definition 2.16

A continuous causal curve $\gamma :(a,b)\rightarrow M$ is future inextendible if $\gamma (t)$ does not converge to any point for $t\rightarrow b$. A similar definition is given in the past case. A continuous causal curve which is both future and past inextendible is said to be inextendible.

The following lemma can be found, in one direction, in Beem et al. (1996, Lemma 3.65) and in the other direction at the end of the proof of Beem et al. (1996, Proposition 3.31). This last step is given here a different, shorter proof (Minguzzi 2008c).

Lemma 2.17

Let (M, g) be a spacetime and let h be a complete Riemannian metric on M. A continuous causal curve $\gamma$ once parametrized with respect to h-arc length has a domain unbounded from above iff future inextendible and unbounded from below iff past inextendible.

Proof

Let (a, b) be the interior of a domain obtained by parametrizing the curve with respect to h-arc length, with possibly $b=+\infty$ and $a=-\infty$. Assume $\gamma$ future inextendible and let $p= \gamma (t)$, $t \in (a,b)$, and consider the balls $B_n(p)=\{q:d_0(p,q)\le n\}$. They are compact because of the Hopf–Rinow theorem. If $\gamma \vert _{[t,b)}$ is not entirely contained in $B_n(p)$ for any n, then $b-t=l_0(\gamma \vert _{[t,b)}) \ge n$ for all n, thus $b=+\infty$. Otherwise, $\gamma \vert _{[t,b)}$ is contained in a compact set and there is a sequence $t_k \in (a,b)$, $t_k \rightarrow b$, such that $\gamma (t_k) \rightarrow q$. But since q can’t be a limit point there are $\bar{t}_k \in (a,b)$, $\bar{t}_k \rightarrow b$, such that $\gamma (\bar{t}_k) \notin B_{1/n}(q)$ for some n. For sufficiently large k, $\gamma (t_k) \in B_{1/(2n)}(q)$, and hence $\gamma \vert _{[t,b)}$ enters $B_{1/(2n)}(q)$ and escapes $B_{1/n}(q)$ infinitely often, and thus has infinite length, $b-t=l_0(\gamma \vert _{[t,b)})=+\infty$ $\Rightarrow b=+\infty$.

Assume $b=+\infty$ then if, by contradiction, $\gamma$ has a future endpoint x there is a neighborhood V as in Lemma 1.33, and a constant $t \in (a,+\infty )$ such that $\gamma \vert _{[t,+\infty )} \subset V$. But there is also a constant $K>0$ such that for $n>t$, $1=l_0(\gamma \vert _{[n,n+1]}) \le K \vert x^{0}(\gamma (n+1))-x^{0}(\gamma (n))\vert$, thus it is impossible that $x^{0}(\gamma (n)) \rightarrow x^{0}(x)$, and hence that $\gamma (n) \rightarrow x$, a contradiction. $\square$

Corollary 2.18

No future or past inextendible curve can be contained in the basis neighborhoods mentioned in Theorem 1.35.

2.7 Maximization properties of continuous causal curves

A continuous causal curve with endpoints is maximizing if it has the maximum Lorentzian length among the continuous causal curves with the same endpoints. More generally, it might miss some endpoints, in which case it is maximizing if any of its segments is maximizing. We anticipate that in terms of the Lorentzian distance d, to be introduced in Sect. 2.9, a continuous causal curve $\gamma :I\rightarrow M$ is maximizing if for every $t,t'\in I$, $t<t'$,

$$\begin{aligned} l(\gamma \vert _{[t,t']})=d(\gamma (t),\gamma (t')). \end{aligned}$$

A continuous causal curve with endpoints $p\in S$ and q is future S-maximizing or simply S-maximizing if it has the maximum Lorentzian length among the continuous causal curves which start from S and end at q. More generally, it might miss the future endpoint in which case it is S-maximizing if any of its segments starting from S is maximizing. Clearly, every S-maximizing continuous causal curve is maximizing. Defining

$$\begin{aligned} d(S,q)=\sup _{p\in S} d(p,q), \end{aligned}$$

a continuous causal curve $\gamma :I \rightarrow M$, with $I=[0,a)$ or $I=[0,a]$, $\gamma (0)\in S$, is S-maximizing if for every $t\in I$

$$\begin{aligned} l(\gamma \vert _{[0,t]})=d(S,\gamma (t)). \end{aligned}$$

Definition 2.19

A subset $S\subset M$ is achronal if no two points are connected by a timelike curve, that is $I^+(S)\cap S=\emptyset$.

Theorem 2.20

Every maximizing continuous causal curve is a causal geodesic (up to parametrizations). Every causal geodesic $\gamma :I\rightarrow M$ is locally maximizing, in the sense that for every $t\in I$ we can find some neighborhood O of $\gamma (t)$ and some connected neighborhood ${\tilde{I}}$ of t, $\gamma \vert _{{\tilde{I}}}\subset O$, such that $\gamma \vert _{{\tilde{I}}}$ is maximizing on (O, g). In particular, lightlike geodesics are locally achronal.

Proof

Let $\gamma$ be a maximizing continuous causal curve, let $p\in \gamma$ and let C be a convex normal neighborhood of p. The connected piece $\sigma$ of $\gamma$ contained in C is necessarily maximizing on the spacetime (C, g), thus by Theorem 2.9 $\sigma$ is a geodesic. As p is arbitrary, $\gamma$ suitably parametrized satisfies the geodesic equation. Conversely, let $\gamma$ be a causal geodesic, let $p\in \gamma$ and let C be a convex normal neighborhood of p. The connected piece $\sigma$ of $\gamma$ contained in C is a causal geodesic hence maximizing on the spacetime (C, g) by Theorem 2.9. $\square$

In our terminology hypersurfaces are $C^1$ codimension one submanifolds without boundary.

Proposition 2.21

Let S be a spacelike hypersurface, then every S-maximizing continuous causal curve is a timelike geodesic orthogonal to S.

Proof

By the previous result the continuous causal curve is a causal geodesic. It has to be orthogonal and hence timelike, due to Eq. (2.6) (in the time dual version) applied on a convex neighborhood of the starting point $q\in S$, where $p\gg q$ is chosen in the geodesic but not on S. $\square$

Theorem 2.22

Let $\gamma$ be a continuous causal curve connecting p to $q\ne p$. There is a timelike curve $\sigma$ connecting p to q such that $l(\sigma )>l(\gamma )$, or $\gamma$ is a maximizing geodesic (up to parametrizations). In particular, if there are no timelike curves connecting p to q then $\gamma$ is an achronal lightlike geodesic (up to parametrizations).

It is clear that every maximizing lightlike geodesic is achronal. The theorem proves that every achronal lightlike geodesic is maximizing, and so that the notions of maximizing lightlike geodesic and achronal lightlike geodesic coincide.

This theorem is particularly useful if we take a neighborhood V of $\gamma$ and regard (V, g) as the spacetime M of the theorem. For instance, if $\gamma$ is not maximizing in (V, g) no matter how small V is (for instance, this is the case if $\gamma$ is a causal geodesic with conjugate points in its interior), then a longer timelike curve connecting the same endpoints can be found in any arbitrarily small neighborhood of $\gamma$.

Proof

Assume $(p,q)\notin I$ and let $\gamma : [0,1]\rightarrow M$ be a future directed continuous causal curve such that $\gamma (0)=p$ and $\gamma (1)=q$. Since the image of $\gamma$ is compact there is a finite covering with convex normal neighborhoods $\{U_i\}$. We can assume $U_i\cap U_{i+1}\ne \emptyset$ and that there is an increasing sequence $t_i$, $t_0=0$, $t_1=1$, such that the points $p_i=\gamma (t_i)$ are such that for every i, $p_i,p_{i+1}\in U_{i+ 1}$. Since $\gamma$ is a continuous causal curve, $(p_i,p_{i+1}) \in J_{U_{i+1}}$, thus $p_i$ and $p_{i+1}$ are joined by a geodesic $\eta _i$ in $U_{i+1}$ and, by Theorem 2.9, this geodesic coincides with the segment $\gamma _i$ of $\gamma$ between the same points or it is timelike and $l(\eta _i)>l(\gamma _i)$.

Let us show that the presence of one timelike segment $\eta _i$ implies $(p,q)\in I$. This is so because from the curve made of geodesic segments $\eta _i$ one can construct a piecewise curve made of timelike geodesic segments. Indeed, one starts from $\eta _i$ and translates slightly the final point of $\eta _{i-1}$ along $\eta _i$ so that the new connecting $\eta '_{i-1}$ becomes timelike (as the Lorentzian distance between the new endpoints is necessarily positive). Analogously, one translates slightly the starting point of $\eta _{i+1}$ along $\eta _i$ so that the new connecting $\eta '_{i+1}$ becomes timelike. Then one continues in this way by taking as reference the timelike geodesic segments $\eta '_{i-1}$ or $\eta '_{i+1}$. In fact, at each step of this construction we have replaced a two-segment geodesic in a convex normal neighborhood with a maximizing geodesic segment, so either at each step our replacement did not change the curve, for the two segments joined smoothly, or the Lorentzian length got increased (remember that by Theorem 2.9 the maximizing causal curve over the convex normal neighborhood is unique and a geodesic, hence $C^1$), thus in the end of the process either we are left with the original curve, which so was a timelike geodesic, or with a timelike curve $\eta$ such that $l(\eta )>l(\gamma )$. In the former case, if the geodesic is not maximizing then we can find another causal curve connecting p and q, necessarily timelike in some open set. Then by repeating the process to the new curve we find a longer timelike curve connecting p and q.

Also note that if all the segments $\eta _i$ are lightlike but do not join smoothly then one can, arguing as above, replace one lightlike segment with one causal geodesic segment by moving slightly the starting endpoint along the previous segment. Once again the new segment is maximizing and it cannot coincide with the original two-segment portion for it is $C^1$, so by Theorem 2.9 its Lorentzian length must be positive and so the new segment must be timelike. The process of the previous paragraph can then be applied.

Thus if $(p,q)\notin I$ the continuous causal curve must be coincident with a lightlike geodesic connecting p to q. This geodesic must be achronal, otherwise there is a timelike curve $\sigma$ connecting $p',q'\in \gamma$. The continuous causal curve connecting p to $p'$ following $\gamma$, $p'$ to $q'$ following $\sigma$, and $q'$ to q following $\gamma$ is, by the just proved result, a lightlike geodesic, which is impossible since $\sigma$ is timelike. The contradiction proves that $\gamma$ is achronal. $\square$

Proposition 2.23

If a continuous causal curve $\gamma$ connects two points p and q and $l(\gamma )>0$, then $p\ll q$.

Proof

If $\gamma$ is a geodesics it must be timelike since at some point $g({\dot{\gamma }},{\dot{\gamma }})>0$. If it is not a geodesic then by Theorem 2.22 we can find a timelike curve connecting the two points. $\square$

An important consequence of the previous theorem is:

Theorem 2.24

If $p\ll r$ and $r \le q$ then $p \ll q$. If $p\le r$ and $r\ll q$ then $p\ll q$. Equivalently, in terms of causal relations, $I\circ J\cup J\circ I\subset I$.

The last property jointly with causality is the defining condition of Kronheimer and Penrose causal spaces, see Sect. 4.2.3.

Proof

It follows from the fact that the composition of a timelike and a causal curve, in whatever order, gives a causal curve which is not a lightlike geodesic as at some points it is timelike. $\square$

Definition 2.25

A line is a maximizing inextendible continuous causal curve. A future ray is a maximizing future inextendible continuous causal curve (and similarly in the past case). A future S-ray is a future S-maximizing future inextendible continuous causal curve (and similarly in the past case).

Clearly, by Theorem 2.22 these curves are causal geodesics. Notice that a future lightlike ray $\gamma$ starting at p is contained in $E^+(p)$, in fact if there where $q\in \gamma \cap I^+(p)$ then the timelike curve connecting p to q would be longer than the lightlike segment of $\gamma$ joining p to q. Similarly, a future lightlike S-ray is contained in $E^+(S)$.

Theorem 2.26

On a causal spacetime if $q\in E^+(p)$ then every proper subset $J^+(p')\cap J^-(q')\subset J^+(p)\cap J^-(q)$ is totally ordered by $\le$ (in fact it is either empty, the single point $p'$, or the image of an achronal lightlike geodesic).

Proof

Let us suppose that $J^+(p')\cap J^-(q')$ is empty. Over this set the only order is the empty relation which is a total order. Similarly, if $p'=q'$, $J^+(p')\cap J^-(q')=\{p'\}$, and $\le$ is a total order over it. Next, suppose that it is non-empty and let $p'\ne q'$, $p\le p' < q'\le q$, where $p'\ne p$ or $q'\ne q$. Let us assume the former case, the latter being analogous. Let $\sigma ^p$ be a causal curve connecting p to $p'$, and $\sigma ^q$ a causal curve connecting q to $q'$ (the latter might degenerate to a point). If $p'\ll q'$ then $p\ll q$, a contradiction, thus $q'\in E^+(p')$ and hence every causal curve connecting $p'$ to $q'$ is actually a lightlike geodesic. There cannot be two such geodesics $\eta _1$, $\eta _2$, for the compositions $\sigma ^q\circ \eta _1\circ \sigma ^p$, $\sigma ^q\circ \eta _2\circ \sigma ^p$ cannot both be smooth at $p'$ and $q'$, hence $p\ll q$ by Theorem 2.22, a contradiction. We conclude that $J^+(p')\cap J^-(q')$ is the image of an achronal lightlike geodesic hence totally ordered by $\le$. $\square$

Theorem 2.27

We have the identities ${\bar{J}}={\bar{I}}$, $\partial J=\partial I$, $I=\mathrm {Int} J$, and for every subset $S \subset M$, $\overline{J^+(S)}=\overline{I^+(S)}$, $\partial J^+(S)=\partial I^+(S)$, $I^+(S)=\mathrm {Int} J^+(S)$, and analogously in the past case.

Proof

Since $I\subset J$, we have ${\bar{I}} \subset {\bar{J}}$. Let $(p,q)\in J$ and let us take $p',q'$ such that $p'\ll p$, $q\ll q'$. Then $(p',q')\in I$, and since $p'$ and $q'$ can be chosen arbitrarily close to p and q respectively, we have $(p,q)\in {\bar{I}}$. Thus $J\subset {\bar{I}}$, which implies ${\bar{J}}\subset {\bar{I}}$. We proved ${\bar{J}}={\bar{I}}$. The inclusion $I\subset J$ implies $I\subset \text {Int} J$. For the converse, let $(p,q)\in \text {Int} J$, and let $q'\ll q$ be sufficiently close to q that $(p,q')\in J$, then $p\le q'\ll q$, hence $(p,q)\in I$. We proved $I=\mathrm {Int} J$ and hence also $\partial J=\partial I$. The proofs for the subset versions are similar. $\square$

Theorem 2.28

Let $S\subset M$ and let $q\in E^+(S)$, then there is an achronal lightlike geodesic entirely contained in $E^+(S)$ which connects S to q.

Proof

Since $q\in J^+(S)\backslash I^+(S)$ there is a causal curve connecting S to q. No point of this causal curve can belong to $I^+(S)$, otherwise by Theorem 2.24 $q\in I^+(S)$, a contradiction. Thus the causal curve is contained in $E^+(S)$. It is achronal otherwise, again by Theorem 2.24, some of its points would belong to $I^+(S)$, thus it is a lightlike geodesic. $\square$

2.8 Rounding off the corners

The following result is due to Penrose (Lerner 1972).

Theorem 2.29

Let $\gamma :[a,b]\rightarrow M$ be a piecewise timelike geodesic, then the discontinuity points for ${\dot{\gamma }}$ (corners, joints) can be rounded off, thereby obtaining a $C^1$ timelike curve connecting $\gamma (a)$ to $\gamma (b)$.

Each corner can be rounded off by perturbing the curve just in an arbitrarily small neighborhood of the corner so that the perturbation of the Lorentzian length can be controlled and made arbitrarily small.

Proof

Let C be a convex normal neighborhood of the corner $\gamma ({\bar{t}})$, and let it be chosen so small that it does not contain any other corner. The curve $\sigma (t)=\exp _p^{-1} \gamma (t)$, consists, for t close to ${\bar{t}}$, of two straight segments in $T_pM$ with timelike tangents $v_1$ and $v_2$. Let $\eta _p$ be a Minkowski metric on $T_pM$ chosen so that $\eta _p<g_p$, and $v_1,v_2$ are $\eta _p$-timelike. Recall that the exponential map is $C^1$ (even at the origin) so the distribution of cones on C pulled back to $T_pM$ by $\exp _p^{-1}$ is continuous. By shrinking C, if necessary, we obtain by continuity that $\exp _p^{-1} (g) >\eta$, that is the metric g pulled back to $T_pM$ has cones wider that $\eta$. Now, we can find on $(T_pM,\eta )$ a $C^1$ $\eta$-causal curve which rounds off the corner in such a flat spacetime (this is just a coordinate exercise). The so deformed curve pushed with $\exp _p$ provides the desired g-timelike curve. $\square$

Corollary 2.30

In the definition of the chronological relation I we might equivalently use $C^1$ timelike curves (or piecewise timelike geodesics). In the definition of the causal relation J we might equivalently use $C^1$ causal curves (or piecewise causal geodesics).

The reader can check also Remark 2.14 for a result of this type.

Proof

The definition of chronological relation involved piecewise $C^1$ curves with timelike tangents. We have now learned to smooth the corners, so such curves can be replaced by $C^1$ timelike curves with the same endpoints. As for the causal case, the definition of the causal relation involved piecewise $C^1$ curves with causal tangents. By Theorem 2.22 if $p< q$ then either $p\ll q$, and hence there is a $C^1$ timelike (hence causal) curve connecting the endpoints, or p and q are connected by a geodesic, which is $C^1$, so whenever $p<q$, p and q are connected by a $C^1$ curve with causal tangents.

The statement in parenthesis follows immediately from Corollary 2.10 and from the fact that the curve can be covered by convex neighborhoods. $\square$

Remark 2.31

Given a causal or timelike curve $\gamma$ one can apply the previous result to the spacetime (V, g) where V is an arbitrary open neighborhood of $\gamma$. Then we get that the $C^1$ and piecewise geodesic curve replacements can be found inside any arbitrarily small neighborhood of $\gamma$.

2.9 The Lorentzian distance

The Lorentzian distance $d:M\times M \rightarrow [0,\infty ]$ between p and q is given by

$$\begin{aligned} d(p,q)=\sup _\gamma l(\gamma ) \end{aligned}$$

for $p\le q$, where $\gamma$ belongs to the family of continuous causal curves connecting p to q, and by zero for $p\nleq q$.

Notice that the Lorentzian distance is not a distance, much in the same way as a reverse triangle inequality is not a triangle inequality. Words like Lorentzian, pseudo, reverse point out that there is an analogy with the Riemannian world which is just that, an analogy, not an identity. Some authors that don’t want to evoke any analogy call the Lorentzian distance the time separation function. We do not recommend this terminology since there are indeed many analogies between the Lorentzian and the Riemannian worlds, e.g. the (Lorentzian/Riemannian) distance formula, which might be missed due to a terminology that does not suggest them.

Theorem 2.32

The Lorentzian distance is lower semi-continuous and satisfies the reverse triangle inequality: if $p\le q$ and $q\le r$ then

$$\begin{aligned} d(p,q)+d(q,r)\le d(p,r). \end{aligned}$$

(2.9)

Proof

Lower semi-continuity at (p, q) such that $d(p,q)=0$ is obvious, so let us assume $d(p,q)>0$. Suppose that d(p, q) is finite. Let $\epsilon$ be such that $0<3\epsilon <d(p,q)$, and let $\gamma$ be a continuous causal curve connecting p to q such that $l(\gamma )>d(p,q)-\epsilon >0$. We can assume that $\gamma$ is timelike, for if not we can apply Theorem 2.22 to find a connecting timelike curve satisfying the same inequality. Let $p'\in \gamma$ be a point chosen sufficiently close to p that the Lorentzian length of the portion of $\gamma$ between p and $p'$ is less than $\epsilon$. Similarly, let $q'\in \gamma$ be a point chosen sufficiently close to q that the Lorentzian length of the portion of $\gamma$ between $q'$ and q is less than $\epsilon$. Then the portion of $\gamma$ between $p'$ and $q'$ has Lorentzian length larger than $l(\gamma )-2 \epsilon >d(p,q)-3\epsilon$. Since $p\in I^{-}(p')=:O_p$ and $q\in I^+(q')=:O_q$, where the sets $O_p$ and $O_q$ are open, for every $({\bar{p}},{\bar{q}})\in O_p\times O_q$, we have $d({\bar{p}},{\bar{q}})>d(p,q)-3\epsilon$ which, by the arbitrariness of $\epsilon$, means that d is lower semi-continuous at (p, q).

The case with $d(p,q)=+\infty$ is similar. For every $N>0$, let $\gamma$ be a continuous causal curve connecting p to q such that $l(\gamma )>N$. Let $\epsilon >0$, and construct $p'$ and $q'$ as above, so that the portion of $\gamma$ between $p'$ and $q'$ has Lorentzian length larger than $l(\gamma )-2 \epsilon >N-2\epsilon$. Thus for every $({\bar{p}},{\bar{q}})\in O_p\times O_q$, we have $d({\bar{p}},{\bar{q}})>N-2\epsilon$ which, by the arbitrariness of N and $\epsilon$, means that d is lower semi-continuous at (p, q).

Now, suppose $p\le q$ and $q\le r$. If d(p, q) or d(q, r) are not finite it is easy to construct by concatenation of curves continuous causal curves of abitrarily large Lorentzian length connecting p to r, thus $d(p,q)=\infty$ and the inequality is satisfied with the equality sign. So we can assume that both d(p, q) and d(q, r) are finite. Let $\epsilon >0$ and let $\gamma$ be a continuous causal curve connecting p to q such that $l(\gamma )>d(p,q)-\epsilon$. Similarly, let $\sigma$ be a continuous causal curve connecting q to r such that $l(\sigma )>d(q,r)-\epsilon$. The curve $\eta$ obtained concatenating $\gamma$ and $\sigma$ satisfies $d(p,r)\ge l(\eta )>d(p,q)+d(q,r)-2 \epsilon$. Since $\epsilon$ is arbitrary the reverse triangle inequality holds true. $\square$

We recall that for a set S we define $d(S,q)=\sup _{p\in S} d(p,q)$, so that $d(S,q)=0$ for $q\notin I^+(S)$.

Proposition 2.33

The function $d(S,\cdot )$ is lower semi-continuous.

Proof

This follows from the general fact that the supremum of a family of lower semi-continuous functions is lower semi-continuous. $\square$

Theorem 2.34

On a convex normal set C regarded as a spacetime, the Lorentzian distance $d_C:C\times C \rightarrow [0,\infty ]$, is finite, continuous and $C^2$ on I.

Proof

This is a consequence of Theorems 2.6 and 2.9. The former clarifies the regularity properties of $D^2 (p,q)= \,g_{p}(\exp _p^{-1}(q), \exp _p^{-1}(q))$ while the latter shows that on $J_C$, $\vert D(p,q)\vert$ is the Lorentzian distance between p and q. $\square$

Theorem 2.35

On a causally convex set C contained in a convex normal set, the Lorentzian distance $d_C:C\times C \rightarrow [0,\infty ]$, is finite, continuous, $C^2$ on I, and coincident with $d\vert _{C\times C}$.

Proof

Let $(p,q)\in C\times C$. All the causal curves connecting p to q have image in C due to the causal convexity of this set, thus $d_C= d\vert _{C\times C}$. Let $V\supset C$, be a convex normal set, then by the same argument $d_C=d_V\vert _{C\times C}$, and the other statements follow from the previous theorem. $\square$

2.10 The Lorentzian length functional

In this section we study the properties of the Lorentzian length functional. It assigns the total proper time to a continuous causal curve.

Lemma 2.36

Let $f:I\rightarrow \mathbb {R}^m$ be a continuous function which is differentiable at $t\in I$, then

$$\begin{aligned} \dot{f}(t)=\lim _{(t_1,t_2)\rightarrow (t,t), t_1<t<t_2} \frac{f(t_2)-f(t_1)}{t_2-t_1}. \end{aligned}$$

Proof

Let $p=\dot{f}(t)$, we have the identity

$$\begin{aligned} \tfrac{f(t_2)-f(t_1)}{t_2-t_1}-p= \tfrac{t_2-t}{t_2-t_1} \big (\tfrac{f(t_2)-f(t)}{t_2-t} -p\big )+\tfrac{t-t_1}{t_2-t_1} \big (\tfrac{f(t)-f(t_1)}{t-t_1} -p\big ). \end{aligned}$$

Since f is differentiable at t, for every $\epsilon >0$ there is $\delta >0$ such that for every s satisfying $\vert s-t\vert <\delta$, the inequality $\vert \tfrac{f(s)-f(t)}{s-t}-p\vert <\epsilon$ holds. Thus for $0<t_2-t<\delta$ and $0<t-t_1<\delta$

$$\begin{aligned} \vert \tfrac{f(t_2)-f(t_1)}{t_2-t_1}-p\vert&\le \tfrac{t_2-t}{t_2-t_1} \vert \tfrac{f(t_2)-f(t)}{t_2-t} -p\vert +\tfrac{t-t_1}{t_2-t_1} \vert \tfrac{f(t)-f(t_1)}{t-t_1} -p\vert \\&\le \tfrac{t_2-t}{t_2-t_1} \epsilon + \tfrac{t-t_1}{t_2-t_1} \epsilon \le \epsilon . \end{aligned}$$

$\square$

We defined the length of a continuous causal curve $\gamma :[0,1] \rightarrow M$ as

$$\begin{aligned} l(\gamma )=\int _\gamma \! \sqrt{-g({\dot{\gamma }},{\dot{\gamma }})} \, \mathrm{d}t. \end{aligned}$$

where the parameter can be chosen so as to get a causal Lipschitz curve.

We now present one of those folklore results whose proof is nowhere to be found, while everybody is convinced it should have been published somewhere. Since I claimed its validity in Minguzzi (2008c, p. 3) Greg Galloway asked if I knew any reference with detailed proof, I did not, so I offered the following proof which I had used to convince myself.⁵

The result establishes the equivalence of our (integral) definition of Lorentzian length with that based on interpolating piecewise geodesics chiefly used by Penrose (1972) (so it shows how to recover the Lorentzian length from the local Lorentzian distance). It also implies the equivalence between our definition of Lorentzian length and that given by Hawking and Ellis (1973, Sect. 6.7), cf. Remark 2.43. Given a continuous causal curve $\gamma$, an interpolating piecewise causal geodesic is a piecewise causal geodesic with the same endpoints of $\gamma$ in which each geodesic piece has endpoints in $\gamma$.

Theorem 2.37

The Lorentzian length of a continuous causal curve satisfies

$$\begin{aligned} l(\gamma )=\inf _{\sigma } l(\sigma ), \end{aligned}$$

(2.10)

where $\sigma$ runs over the interpolating piecewise causal geodesics in which each geodesic segment is contained in a convex normal neighborhood together with the segment of $\gamma$ that it interpolates.

The last requirement is important, otherwise there are simple counterexamples due to the fact that the causal curve $\gamma$, starting from p, can escape every convex normal neighborhood and then return to a point $q\in I^+(p)$ very close to p, so that p and q are connected by a timelike geodesic whose Lorentzian length is shorter than that of $\gamma$.

The proof really shows that there is a sequence of interpolating piecewise causal geodesics $\gamma ^s$ which, in a suitable parametrization, converges uniformly to $\gamma$ and in such a way that a.e. ${\dot{\gamma }}^s \rightarrow {\dot{\gamma }}$.

Proof

For any point $p\in \gamma$ we can find $K>0$ such that $\sqrt{-g(v,v)}< K v^0$ over every causal vector, so that, by continuity, the same inequality holds in a neighborhood U of p. Thus $\gamma$ can be covered by a finite number of neighborhoods $U_i$, associated with some constants $K_i>0$. The curve $\gamma$ can also be covered by a finite number of neighborhoods $V_k$ constructed as in Theorem 1.35, each one contained in some $U_{i(k)}$. Finally, it can also be covered by convex normal neighborhoods $C_j$ each one contained in some $V_{k(j)}$. As a consequence we can, without loss of generality, assume that $\gamma$ is contained in a convex normal set $C\subset V$ where V is an open neighborhood as in Theorem 1.35 and hence (Remark 1.36) endowed with a time coordinate $x^0:V\rightarrow \mathbb {R}$ which is a time function for $(V,g^{\epsilon _+})$, where $g^{\epsilon _+}>g$. Moreover, there is a constant K such that on V $\sqrt{-g(v,v)}< K v^0$ over every causal vector. By Theorem 2.12 we can parametrize $\gamma$ and the interpolating geodesics with $x^0$, so that they become Lipschitz curves. For these curves the tangent vector v, where it exists, satisfies $v^0=1$, thus the argument of the Lorentzian length integral is bounded by K.

Let $\gamma :[a,b]\rightarrow C$ and let $\gamma ^s:[a,b]\rightarrow C$ be a sequence of interpolating piecewise causal geodesics parametrized with respect to $x^0$ and such that $l(\gamma ^s) \rightarrow \inf _{\sigma } l(\sigma )$. Notice that for any given s we can enlarge the number of non-$C^1$ points (joints) in $\gamma ^s$ for this operation has the only effect of decreasing the Lorentzian length of $\gamma ^s$ (cf. Theorem 2.9). Thus we can assume that for every s, $\gamma ^{s+1}$ has at least the same joints of $\gamma ^s$ and that every point of the segment [a, b] of the form $N/2^{s+1}$, with N integer is a joint. At this point we need only to prove that ${\dot{\gamma }}^s\rightarrow {\dot{\gamma }}$ a.e., for it implies $\sqrt{-g({\dot{\gamma }}^s,{\dot{\gamma }}^s)}\rightarrow \sqrt{-g({\dot{\gamma }},{\dot{\gamma }})}$ and by the Lebesgue dominated convergence theorem $\lim _{s\rightarrow \infty } l(\gamma ^s)=l(\gamma )$.

Let N, $N^s$ be the set of non-differentiability points for $\gamma$ and $\gamma ^s$, respectively. Since $N^s$ is finite, and $\gamma$ is almost everywhere differentiable, $D:=[a,b]\backslash (N\cup \cup _s N^s)$ has full measure.

Let $t\in D$. We are going to prove that ${\dot{\gamma }}^s(t)\rightarrow {\dot{\gamma }}(t)$. In what follows we identify some objects in C with those on TC by using the affine structure induced by the coordinates. Let us consider the geodesic segment $\sigma ^s$ of $\gamma ^s$ which contains the point with parameter t. Its endpoints $a^s$ and $b^s$ stay in $\gamma$ and cannot be at a time parameter farther than $1/2^s$ from t. Let $\eta ^s$ be the coordinate-straight segment connecting $a^s$ to $b^s$, which in general is different from $\sigma ^s$. If we parametrize $\eta ^s$ with $x^0$ we conclude by Lemma 2.36 that the tangent ${\dot{\eta }}^s$ converges to ${\dot{\gamma }}(t)$. It remains only to prove that the difference between the tangents ${\dot{\sigma }}^s(t)$ and ${\dot{\eta }}^s(t)$ becomes negligibly small with s and so that the former also converge to ${\dot{\gamma }}(t)$. The geodesic ODE satisfied by $\sigma ^s$ (parametrized with respect to an affine parameter) implies, by the continuity of the connection coefficients, $\vert \frac{\mathrm{d}^2 x^0}{\mathrm{d}\lambda ^2}\vert \le K(\frac{\mathrm{d}x^0}{\mathrm{d}\lambda })^2$, $\vert \frac{\mathrm{d}^2 \mathbf {x}}{\mathrm{d}\lambda ^2}\vert \le K(\frac{\mathrm{d}x^0}{\mathrm{d}\lambda })^2$, where $K>0$ is a constant independent of the geodesic considered in C (we have also used the causality of the curve, which implies $\vert \mathrm{d}\mathbf {x} /\mathrm{d}x^0\vert <(1+\epsilon _+)^{1/2}$).

The identity

$$\begin{aligned} \frac{\mathrm{d}^2 \mathbf {x}}{\mathrm{d}(x^0)^2}=\big (\frac{\mathrm{d}x^0}{\mathrm{d}\lambda }\big )^{-2}\big [- \frac{\mathrm{d}^2 x^0}{\mathrm{d}\lambda ^2} \frac{\mathrm{d}\mathbf {x}}{\mathrm{d}x^0}+\frac{\mathrm{d}^2 \mathbf {x}}{\mathrm{d}\lambda ^2}\big ], \end{aligned}$$

implies using the previous inequalities

$$\begin{aligned} \left| \frac{\mathrm{d}^2 \mathbf {x}}{\mathrm{d}(x^0)^2}\right| \le K \left[ \left| \frac{\mathrm{d}\mathbf {x}}{\mathrm{d}x^0}\right| ^2 +1\right] ^{1/2}\le K(2+\epsilon _+)^{1/2}=:{\tilde{K}}. \end{aligned}$$

For every $i=1,\ldots , n$, by the mean value theorem $({\dot{\sigma }}^s)^i$ coincides at some time with $({\dot{\eta }}^s)^i$, but for any other time, in particular for $x^0=t$, it differs from this value by at most ${\tilde{K}} /2^{s-1}$ (the range of the parameter $x^0$ over $\sigma ^s$ is no larger than $1/2^{s-1}$) hence $\vert \dot{\mathbf {\sigma }}^s -\dot{\mathbf {\eta }}^s \vert \le {\tilde{K}} /2^{s-1}$, and hence ${\dot{\sigma }}^s(t)$ and ${\dot{\eta }}^s(t)$ have the same limit. $\square$

The previous result will be used in a moment to prove the upper semi-continuity of the length functional, see Theorem 2.41. However, it has also the following interesting consequence, which is worth pointing out as it shows that the Lorentzian length can be recovered from the Lorentzian distance. This result has also appeared in a recent paper by Kunzinger and Sämann (2018) where they provide a different elegant proof. I notice that their argument can likely be localized to offer a different proof of Theorem 2.37.

Theorem 2.38

Let (M, g) be a strongly causal spacetime and let $x:[a,b] \rightarrow M$ be a continuous causal curve. Then

$$\begin{aligned} l(x)=\inf \sum _i d(x(t_i), x(t_{i+1})), \end{aligned}$$

(2.11)

where the infimum is over all the partitions $a=t_0<t_1<\cdots <t_n=b$.

Proof

The image of the curve can be covered by a finite number of causally convex neighborhoods $\{C_i\}$, where each $C_i$ is contained in some convex neighborhood. For some partition the consecutive points $\{x(t_i),x(t_{i+1})\}$ belong to $C_{j(i)}$ and so can be joined by a causal geodesic segment $\sigma _i$ included in $C_j$. All the causal curves joining the endpoints of $\sigma _i$ stay in $C_i$ by causal convexity, thus $d(x(t_i),x(t_{i+1})=l(\sigma _i)$ (recall Theorems 2.9 and 2.35). The infimum in Eq. (2.10) can be restricted to piecewise geodesics for which the consecutive corners belong to some $C_k$, for by increasing the number of corners to a piecewise geodesic one can only decrease the Lorentzian length (due to the reverse triangle inequality). Thus Eq. (2.10) proves the theorem. $\square$

Definition 2.39

Let h be a Riemannian metric on M and let $d_0$ be the associated Riemannian distance. We say that $\gamma _n:I \rightarrow M$ converges h-uniformly to $\gamma :I \rightarrow M$ if for every $\epsilon >0$ there is $N>0$, such that for $n>N$, and for every $t \in I$, $d_0(\gamma (t),\gamma _n(t)) <\epsilon$.

Remark 2.40

Actually, the h-uniform convergence, if on compact subsets, is independent of the Riemannian metric h chosen. The reason is that if the domain of $\gamma :[a,b] \rightarrow M$ is compact then the same is true for its image so $\gamma ([a,b])$ admits a compact neighborhood K. On K, for every Riemannian metric $h'$, there are constants m and M such that $m h'<h <M h'$.

The proof of the upper semi-continuity of the length functional goes as in Penrose (1972) and hence uses the definition of Lorentzian length based on the infimum of the lengths of the interpolating piecewise causal geodesics. Other proofs are possible that do not make use in any way of the notion of convex neighborhood (Minguzzi 2019).

Theorem 2.41

Let $\gamma :[a,b] \rightarrow M$, be a continuous causal curve in the spacetime (M, g) and let h be a Riemannian metric on M. If the sequence of continuous causal curves $\gamma _n:[a,b] \rightarrow M$ converges h-uniformly to $\gamma$, then

$$\begin{aligned} \limsup l(\gamma _n) \le l(\gamma ) . \end{aligned}$$

The proof really provides a stronger result, namely the upper semi-continuity of the map $\gamma \rightarrow l(\gamma )$, where $\gamma$ belongs to the family of AC-causal curves $\gamma _n:[a,b] \rightarrow M$ endowed with a distance between curves induced by the h-distance $d_0$, i.e. $d(\gamma ,\sigma )=\sup _t d_0(\gamma (t),\sigma (t))$.

Proof

Given $\varepsilon >0$ a partition of [a, b] can be found into intervals $[t_i,t_{i+1}]$, $1\le i \le m-1$, $t_i\in [a,b]$, $t_1=a$, $t_m=b$, $t_i<t_{i+1}$, so that there are convex sets $U_i$, $1\le i \le m-1$, covering $\gamma$ such that $\gamma \vert _{[t_i,t_{i+1}]} \subset U_i$ and $x_i=\gamma (t_i)$, $x_i \in U_{i-1}\cap U_i$. Moreover, the interpolating piecewise causal geodesic $\eta$ passing through the events $x_i$, has a length $l(\eta )\le l(\gamma )+\varepsilon /2$.

For every i let events $y_i,z_i \in U_{i-1}\cap U_i$ be chosen such that $y_i\ll _{U_i} x_i \ll _{U_{i-1}} z_i$. By Theorem 2.34 the Lorentzian distance $d_i:U_i\times U_i \rightarrow [0,+\infty ]$ is finite and continuous for each i. Thus the events $y_i,z_{i+1}\in U_i$ can be chosen close enough to $x_i$ and $x_{i+1}$ so that $d_i(y_i,z_{i+1})<d_i(x_i,x_{i+1})+\varepsilon /(2m)$. Since the image of $\gamma$ is compact and the convergence is uniform, it is possible to find $N>0$, such that for $n>N$, $\gamma _{n} \subset A= \bigcup ^{m-1}_{i=1} U_i$ and $\gamma _n(t_i) \in I_{U_i}^{+}(y_i)\cap I_{U_{i-1}}^{-}(z_i)$ for $2\le i\le m-1$, $\gamma _n(t_1) \in I_{U_1}^{+}(y_1)$, $\gamma _n(t_m) \in I_{U_{m-1}}^{-}(z_m)$. The curves $\gamma _n$ split into curves $\gamma _n^{i}=\gamma _n\vert _{[t_i,t_{i+1}]}$ contained in $U_i$. Now, note that the curve $\gamma ^{i}_n$ can be considered as the segment of a longer causal curve that connects $y_i$ to $z_{i+1}$ entirely contained in $U_i$, thus $l(\gamma ^i_n)\le d_i(y_i,z_{i+1})$. Finally,

$$\begin{aligned} l(\gamma _n)\le \sum _{i=1}^{m-1} d_i(y_i,z_{i+1})\le \sum _{i=1}^{m-1} d_i(x_i,x_{i+1})+ \frac{\varepsilon }{2} =l(\eta )+\frac{\varepsilon }{2} \le l(\gamma )+\varepsilon . \end{aligned}$$

$\square$

Remark 2.42

This theorem can be generalized in various directions. One is to consider the domains dependent on n but curves parametrized with respect to h-arc length, so $\gamma _n:[a_n,b_n]\rightarrow M$, where $a_n\rightarrow a$ and $b_n\rightarrow b$. The other is to consider $\gamma _n$ to be a continuous $g_n$-causal curve where $g_n>g_{n+1}$, $g_n\rightarrow g$ pointwise. The reader is referred to Minguzzi (2008c, Theorem 2.4) and Minguzzi (2019, Theorem 2.122) for these variations.

Remark 2.43

Hawking and Ellis (1973, Sect. 6.7) prove the upper semi-continuity of the length functional just for $C^1$ causal curves, then they define the length of a continuous causal curve in such a way that the upper semi-continuity of the length functional is preserved (their upper semi-continuity uses the $C^0$ topology on causal curves (Beem et al. 1996, Definition 3.33) and a strongly causal assumption on spacetime), thus as follows

$$\begin{aligned} l_H(\gamma )=\inf _{W \ni \gamma , U \ni \gamma (0), V \ni \gamma (1)} \sup _{W \ni \sigma , \sigma (0) \in U, \sigma (1) \in V} l(\sigma ), \end{aligned}$$

where $\gamma :[0,1] \rightarrow M$, is a continuous causal curve, $\sigma :[0,1]\rightarrow M$ are $C^1$ causal curves and U, V are, respectively, neighborhoods of $\gamma (0)$ and $\gamma (1)$, while W is a neighborhood of $\gamma$.

A consequence of this definition is that there is a sequence $\gamma _n$ of $C^1$ causal curves such that $\limsup l_H(\gamma _n)= l_H(\gamma )$. The curve $\gamma$ can be covered with convex normal neighborhoods endowed with time functions (Lemma 1.36), and these time functions can be used to partition into parametrized segments the curves, then the convergence in the $C^0$ topology implies that in the uniform topology, thus $l_H(\gamma )=\limsup l_H(\gamma _n) =\limsup l(\gamma _n) \le l(\gamma )$. For the other direction, if we find a sequence of $C^1$ causal curves $\gamma _n$ such that $\lim _n l(\gamma _n)=l(\gamma )$ and $\gamma _n \rightarrow \gamma$ in the $C^0$ topology then $l(\gamma )=\limsup _n l(\gamma _n)=\limsup _n l_H(\gamma _n)\le l_H(\gamma )$. We constructed such a sequence in the proof of Theorem 2.37, for there the obtained sequence was only piecewise $C^1$ but the corners can be rounded off (cf. Sect. 2.8) with the effect of perturbing the Lorentzian length of a quantity which can be made negligible in the limit.

In conclusion, all the definitions of Lorentzian length found in the literature really coincide. The most natural definition is that adopted in this work. Penrose, and Hawking and Ellis used more involved definitions likely because they wanted to get an easy proof of the upper semi-continuity of the length functional without passing from the proof of Theorem 2.37.

2.11 Limit curve theorems

The purpose of this section is to introduce various versions of the limit curve theorem of Lorentzian geometry. It is likely the strongest tool available in causality theory. The main reference for this section is Minguzzi (2008c).

A sequence of functions $f_n:[a,b]\rightarrow \mathbb {R}^m$ is uniformly bounded if there is $M>0$ such that $\vert f_n\vert <M$ for all n, and equicontinuous if for every $\epsilon >0$ and for every $t\in [a,b]$ there exists a $\delta (t,\epsilon )>0$ such that

$$\begin{aligned} \vert f_n(t')-f_n(t)\vert <\epsilon \end{aligned}$$

for all n whenever $\vert t'-t\vert <\delta$.

Theorem 2.44

(Ascoli–Arzelà) Every uniformly bounded and equicontinuous sequence $f_n:[a,b]\rightarrow \mathbb {R}^m$ admits a subsequence that converges uniformly.

Remark 2.45

If all the elements in the sequence are Lipschitz, relative to a common Lipschitz constant K, then the sequence is equicontinuous (just take $\delta =\epsilon /K$). Whenever the theorem applies there is a subsequence $f_{n_k}$ which converges uniformly to some (necessarily continuous) function f. Notice that by taking the limit $k\rightarrow \infty$ of $\vert f_{n_k}(t')-f_{n_k}(t)\vert \le K \vert t'-t\vert$ we get $\vert f(t')-f(t)\vert \le K \vert t'-t\vert$, thus the limit function is also K-Lipschitz.

Suppose now that $f_n=x_n:[a,b]\rightarrow V$, are continuous causal curves, where V is a relatively compact coordinate neighborhood as in Theorem 1.35 hence endowed with a time function $x^0$, and where the parametrization is chosen to be $x^0$ so that the curves are Lipschitz (Remark 1.36, Theorem 2.12). The bounds provided by the shape of the cones and by the parametrization are really common to all the curves, that is, the maps $x_n$ are equi-Lipschitz. By the previous remark there is a subsequence $x_{n_k}$ that converges uniformly (in the coordinate Euclidean distance, and hence, equivalently, in the distance of any Riemannian metric) to some continuous function $x:[a,b]\rightarrow V$. Let $t\in [a,b]$ and let C be a convex neighborhood of x(t), then for $t_1<t_2$ so close to t that $x(t_1),x(t_2)\in C$, we have for sufficiently large k, $x_{n_k}([t_1,t_2])\subset C$, hence $x_{n_k}(t_1) \le _C x_{n_k}(t_2)$, which, taking the limit $k\rightarrow \infty$ and using the fact that the causal relation is closed on convex neighborhoods (Theorem 2.11), gives $x(t_1) \le _C x(t_2)$. By Corollary 2.10 x is a continuous causal curve.

This local argument suitably generalized leads to more general limit curve theorems in Lorentzian geometry. Since we have given the idea of proof, we present here just the statement of the results, while referring to Minguzzi (2008c) for details. There one can also find a discussion of the history of limit curve theorem results in Lorentzian geometry. In fact, many authors contributed to their formulation, e.g. Hawking and Ellis (1973), Penrose (1972), Beem et al. (1996), Galloway (1986b), Eschenburg and Galloway (1992) and Minguzzi (2008c).

We stress that we are giving the strongest versions available. The classical references (Hawking and Ellis 1973; Beem et al. 1996) contain versions that are weaker in several respects, most notably they might impose global causality conditions, such as strong causality, or the deduced convergence might be weak, e.g. in the $C^0$ topology on curves.

We recall that if h is a Riemannian metric on M and $d_0$ is the associated Riemannian distance then $\gamma _n:I \rightarrow M$ converges uniformly to $\gamma :I \rightarrow M$ if for every $\epsilon >0$ there is $N>0$, such that for $n>N$, and for every $t \in I$, $d_0(\gamma (t),\gamma _n(t)) <\epsilon$. For the next applications this definition is too restrictive and must be generalized to the case in which the domains of $\gamma _n$ differ.

Definition 2.46

(In this definition $a_n, b_n, a, b$, may take an infinite value) Let h be a Riemannian metric on M and let $d_0$ be the associated Riemannian distance. The sequence of curves $\gamma _n:[a_n,b_n] \rightarrow M$ converges h-uniformly to $\gamma :[a,b] \rightarrow M$ if $a_n \rightarrow a$, $b_n \rightarrow b$, and for every $\epsilon >0$ there is $N>0$, such that for $n>N$, and for every $t \in [a,b]\cap [a_n,b_n]$, $d_0(\gamma (t),\gamma _n(t)) <\epsilon$.

The sequence of curves $\gamma _n:[a_n,b_n] \rightarrow M$ converges h-uniformly on compact subsets to $\gamma :[a,b] \rightarrow M$ if for every compact interval $[a',b'] \subset [a,b]$, there is a choice of sequences $a'_n ,b'_n \in [a_n,b_n]$, $a'_n <b'_n$, such that $a'_n \rightarrow a'$, $b'_n \rightarrow b'$, and for any such choice $\gamma _n\vert _{[a'_n,b'_n]}$ converges h-uniformly to $\gamma \vert _{[a',b']}$.

Remark 2.47

Clearly, if $\gamma _n:[a_n,b_n] \rightarrow M$ converges h-uniformly to $\gamma :[a,b] \rightarrow M$ then $\gamma _n$ converges h-uniformly on compact subsets to $\gamma$. Conversely, if $\gamma _n:[a_n,b_n] \rightarrow M$ converges h-uniformly on compact subsets to $\gamma :[a,b] \rightarrow M$, [a, b] is compact and $a_n \rightarrow a$, $b_n \rightarrow b$, then $\gamma _n$ converges h-uniformly to $\gamma$.

Remark 2.48

Actually, the h-uniform convergence on compact subsets is independent of the Riemannian metric h chosen. The reason is that if the domain of $\gamma :[a,b] \rightarrow M$ is compact then the same is true for its image and it is possible to find a open set O of compact closure containing $\gamma ([a,b])$. Then on $\bar{O}$, given a different Riemannian metric $h'$, there are positive constants m and M such that $m h'<h <M h'$.

As the reader will soon notice, the next limit curve theorems contemplate the case in which the sequence $x_k$ consists of continuous $g_k$-causal curves, where $g_k$, $k\ge 1$, is a sequence of Lorentzian metrics such that, $g_{k+1}\le g_k$, $g_k\rightarrow g$ pointwise. It is important to keep this generalization for results connected to stable causality. In fact the usual $g_k=g$ case implies such generalization as the proof of the following result shows.

Theorem 2.49

On (M, g) let $g_k$, $k\ge 1$, be a sequence of Lorentzian metrics such that, $g_{k+1}\le g_k$, $g_k\rightarrow g$ pointwise, and let h be a Riemannian metric on M. If the continuous $g_k$-causal curves $x_k:I_k \rightarrow M$ parametrized with respect to h-arc length converge h-uniformly on compact subsets to $x:I \rightarrow M$ then x is a continuous g-causal curve.

Proof

The proof in the case $g_k=g$ makes use of the Ascoli-Arzelà theorem as shown previously. As for the generalization, observe that for every s the sequence $x_k$ consists of continuous $g_s$-causal curves for $k\ge s$, thus the limit curve x is a continuous $g_s$-causal curve. So for every s, $\dot{x}$ is $g_s$-causal a.e., which implies $\dot{x}$ is g-causal a.e., namely x is a continuous g-causal curve. $\square$

Theorem 2.50

On (M, g) let h be a Riemannian metric. Let $K\subset M$ be a compact set and let $x_k:[0,L]\rightarrow K$ be a sequence of h-arc length parametrized continuous causal curves, then there is a subsequence converging uniformly on [0, L] to a continuous causal curve x (whose parametrization is not necessarily the h-arc length parametrization).

The bound on the h-arc length of $x_k$ is necessary, without it counterexamples can easily be found on the 2-dimensional spacetime $\mathbb {R}\times S^1$ whose metric is $g=-\mathrm{d}t\mathrm{d}\theta$.

The following limit curve result for sequences of inextendible continuous causal curves (i.e. $(a_n,b_n)=(-\infty , +\infty )$) is sometimes called the Limit curve lemma (Galloway 1986b; Beem et al. 1996, Lemma 14.2). For the definition of uniform convergence on compact subsets see Definition 2.39.

Theorem 2.51

(Limit curve theorem. One accumulation point case) On (M, g) let $g_k$, $k\ge 1$, be a sequence of Lorentzian metrics such that, $g_{k+1}\le g_k$, $g_k\rightarrow g$ pointwise, and let h be a complete Riemannian metric.

Let $x_n:(a_n,b_n) \rightarrow M$, be a sequence of inextendible continuous causal curves parametrized with respect to h-arc length (possibly $a_n=-\infty$, $b_n=+\infty$ for some n), such that $a_n \rightarrow -\infty$ and $b_n\rightarrow +\infty$, and suppose that $p\in M$ is an accumulation point of the sequence $x_n(0)$. There is an inextendible continuous causal curve $x:(-\infty ,+\infty ) \rightarrow M$, such that $x(0)=p$ and a subsequence $x_k$ which converges h-uniformly on compact subsets to x (once again the parametrization of x is not necessarily the h-arc length parametrization).

Remark 2.52

A similar version with $x_n:[0,b_n) \rightarrow M$, $b_n \rightarrow +\infty$, holds true where, of course, the limit curve $x:[0,\infty )\rightarrow M$ is future inextendible and starting from $x(0)=p$.

Fig. 3

An illustration of Theorem 2.53 case (ii). Here (M, g) is Minkowski $1+1$ dimensional spacetime with a spacelike half-line removed. The continuous causal curves $x_n$ here are obtained by joining a lightlike and a timelike geodesic. We have two limit curves (dashed) namely $x^p$ and $x^q$, the former being future inextendible and the latter being past inextendible. An important piece of information is that for every $p'\in x^p$ and $q'\in x^q$, $(p',q')\in {\bar{J}}$

The version for curves with endpoints introduced in Minguzzi (2008c) is often more useful, see Fig. 3 for an illustration.

Theorem 2.53

(Limit curve theorem. Two accumulation points (the endpoints) case) On (M, g) let $g_k$, $k\ge 1$, be a sequence of Lorentzian metrics such that, $g_{k+1}\le g_k$, $g_k\rightarrow g$ pointwise, and let h be a complete Riemannian metric. Let $x_n:[0,a_n] \rightarrow M$ be a sequence of h-arc length parametrized continuous $g_n$-causal curves with endpoints $p_n\rightarrow p$, and $q_n\rightarrow q$. Provided the curves $x_n$ do not contract to a point (which is the case if $p\ne q$) we can find either

• (i) a continuous g-causal curve $x:[0,a] \rightarrow M$ to which a subsequence $x_k$, $a_k\rightarrow a$, converges uniformly on compact subsets,

or

• (ii) a future inextendible parametrized continuous g-causal curve $x^p:[0,+\infty ) \rightarrow M$ starting from p, and a past inextendible parametrized continuous g-causal curve $x^q:(-\infty ,0] \rightarrow M$ ending at q, to which some subsequence $x_k(t)$ (resp. $x_k(t+a_k)$) converges uniformly on compact subsets. Moreover, for every $p'\in x^p$ and $q'\in x^q$, $(p',q')\in \cap _n {\bar{J}}_n$.

It can be observed that in the constant metric case, $g_n=g$, the last inclusion reads $(p',q') \in {\bar{J}}$. As another observation, in case (ii) with $q=p$ the curves $x^q$ and $x^p$ actually join to form an inextendible continuous causal curve passing through p.

Remark 2.54

As we shall see a fairly weak causality condition is non-total imprisonment: no future or past inextendible continuous causal curve is contained in a compact set. Under this condition if every element in the sequence $x_n$ has image contained in the same compact set K then $x^p$ and $x^q$ are contained in K, a contradiction with their inextendibility. Thus case (ii) does not really apply in such a circumstance and so, due to (i), there exists a limit continuous causal curve connecting p to q. We shall meet this type of argument in the proof of the geodesic connectedness of globally hyperbolic spacetimes.

A first simple application of Theorem 2.51 is the following

Theorem 2.55

Let h be an auxiliary Riemannian metric. If (M, g) is non-totally imprisoning then for every compact set K we can find a constant $c(K)>0$ such that the h-arc length and the Lorentzian length of any continuous causal curve contained in K is bounded by c.

Proof

$\Rightarrow$. Since any two Riemannian metrics are Lipschitz equivalent over a compact set we may choose the Riemannian metric as we desire. In particular, we can choose it in such a way that on TK the unit balls of h do not intersect the indicatrices of g. As a consequence, for every causal vector on TK, $\sqrt{-g(v,v)}\le \sqrt{h(v,v)}$ and hence for every continuous causal curve contained in K, $l(\gamma )\le l_0(\gamma )$ where $l_0$ is the h-arc length. Thus we need only to show that the h-arc length is bounded. Suppose it is not then we can find a sequence of continuous causal curves parametrized with respect to h-arc length $x_n:[a_n,b_n]\rightarrow K$, such that $a_n\rightarrow -\infty$, $b_n\rightarrow \infty$ and $x_n(0)\rightarrow p\in K$. Then by Theorem 2.51 there is an inextendible limit continuous causal curve contained in K, a contradiction. $\square$

As a simple application of Theorem 2.53 we complement Theorem 2.28 with the following result.

Theorem 2.56

For any subset $S\subset M$ we have the identity $\dot{J}^+(S)\backslash E^+(S)=\dot{J}^+(S)\backslash J^+(S)$. Moreover, if S is closed and $q\in \dot{J}^+(S)\backslash E^+(S)$, then there is a past inextendible achronal lightlike geodesic ending at q and entirely contained in $\dot{J}^+(S)\backslash E^+(S)$.

Proof

Let $q\in \dot{J}^+(S)\backslash E^+(S)$ and suppose, by contradiction, that $q\in J^+(S)$, then if $q\notin I^+(S)$ we have $q\in E^+(S)$, which is a contradiction with $q\notin E^+(S)$, while if $q\in I^+(S)=\mathrm {Int} J^+(S)$ we have again a contradiction as $q\in \dot{J}^+(S)$, thus $\dot{J}^+(S)\backslash E^+(S)\subset \dot{J}^+(S)\backslash J^+(S)$. Conversely, if $q\in \dot{J}^+(S)\backslash J^+(S)$ then $q\notin J^+(S)$ and hence $q\notin E^+(S)$ since $E^+(S)\subset J^+(S)$, thus $\dot{J}^+(S)\backslash J^+(S)\subset \dot{J}^+(S)\backslash E^+(S)$.

Let $\gamma _n$ be a sequence of causal curves with endpoints $p_n\in S$, and $q_n\rightarrow q$. Since $q\notin S\subset J^+(S)$ the curves $\gamma _n$ do not contract to q. By the limit curve theorem 2.53, case (i) cannot apply otherwise $q \in J^+(S)$, which is a contradiction. Thus case (ii) applies and hence there is a past inextendible continuous causal curve $x^q$ ending at q, which being the limit of a subsequence of $\gamma _n$ is entirely contained in $\overline{ J^+(S)}$. But no point of $x^q$ can belong to $J^+(S)$ otherwise $q\in J^+(S)$, which is a contradiction, thus $x^q\subset [\overline{J^+(S)}\backslash I^+(S)] \backslash J^+(S)= \dot{J}^+(S)\backslash J^+(S)$. The curve $x^q$ is really achronal, for if not there would be two points $a,b\in x^q$, $a\ll b$, but a would be an accumulation point for the converging subsequence $\gamma _{n_k}$, thus, since I is open, for sufficiently large k, $p_{n_k} \ll b\le q$ and hence $q\in I^+(S)$, a contradiction. $\square$

2.12 Some existence results for maximizing geodesics

We have already defined the notion of maximizing continuous causal curve. In this section we make use of the following important concept.

Definition 2.57

A sequence of continuous causal curves $\gamma _n:I_n\rightarrow M$, is limit maximizing if defining

$$\begin{aligned} \epsilon _n=\sup _{t,t'\in I_n, t<t'}[d(\gamma _n(t),\gamma _n(t'))-l(\gamma _n\vert _{[t,t']})]\ge 0 \end{aligned}$$

we have $\epsilon _n\rightarrow 0$.

The formulation of the following result is taken from Minguzzi (2008c) but it is really standard (Beem et al. 1996, Sect. 8).

Theorem 2.58

Let h be an auxiliary Riemannian metric on M. If the sequence of continuous causal curves $\gamma _n:I_n \rightarrow M$ is limit maximizing, the curves are parametrized with respect to h-length and the sequence converges h-uniformly on compact subsets to the curve $\gamma :I \rightarrow M$, then $\gamma$ is a maximizing continuous causal curve. Moreover, given $[a,b] \subset I$ there are $[a_n,b_n] \subset I_n$, such that $a_n \rightarrow a$, $b_n \rightarrow b$ and for any such choice

$$\begin{aligned} \lim l(\gamma _n\vert _{[a_n,b_n]})= \lim d(\gamma _n(a_n),\gamma _n(b_n))=l(\gamma \vert _{[a,b]}) = d(\gamma (a),\gamma (b)). \end{aligned}$$

(2.12)

Proof

The curve $\gamma$ is a continuous causal curve by Theorem 2.49. Let $[a,b] \subset I$, then there are $[a_n,b_n] \subset I_n$, such that $a_n \rightarrow a$, $b_n \rightarrow b$, and $\gamma _n \vert _{[a_n,b_n]}$ converges h-uniformly to $\gamma _{[a,b]}$. By the limit maximization property of the sequence $d(\gamma _n(a_n),\gamma _n(b_n))-l(\gamma _n\vert _{[a_n,b_n]})\le \epsilon _n$, with $\epsilon _n \rightarrow 0$. Using the upper semi-continuity of the length functional (Remark 2.42) and the lower semi-continuity of the distance we get

$$\begin{aligned} d(\gamma (a),\gamma (b))&\le \liminf d(\gamma _n(a_n),\gamma _n(b_n)) \le \limsup d(\gamma _n(a_n),\gamma _n(b_n)) \\&\le \limsup l(\gamma _n\vert _{[a_n,b_n]}) \le l(\gamma \vert _{[a,b]}) \le d(\gamma (a),\gamma (b)) \end{aligned}$$

hence $d(\gamma (a),\gamma (b))=l(\gamma \vert _{[a,b]})$, which concludes the proof. $\square$

The following consequence is immediate (the assumed convergence is again uniform on compact subsets).

Corollary 2.59

The continuous causal curves which are limits of a sequence of maximizing continuous causal curves are also maximizing. The continuous causal curves which are limits of achronal geodesics are also achronal geodesics.

Given a subset S, there are analogous S-maximization versions (see also Sect. 2.7).

Definition 2.60

A sequence of continuous causal curves $\gamma _n:I_n\rightarrow M$, $I_n=[0,a_n)$ or $I_n=[0,a_n]$, $\gamma _n(0)\in S$, is limit S-maximizing if defining

$$\begin{aligned} \epsilon _n=\sup _{t\in I_n}[d(S,\gamma _n(t))-l(\gamma _n\vert _{[0,t]})]\ge 0 \end{aligned}$$

we have $\epsilon _n\rightarrow 0$.

Theorem 2.61

Let h be an auxiliary Riemannian metric on M. If the sequence of continuous causal curves $\gamma _n:I_n \rightarrow M$ is limit S-maximizing, the curves are parametrized with respect to h-length and the sequence converges h-uniformly on compact subsets to the curve $\gamma :I \rightarrow M$ starting from S, then $\gamma$ is an S-maximizing continuous causal curve. Moreover, given $[0,b] \subset I$ there are $[0,b_n] \subset I_n$, such that $b_n \rightarrow b$ and for any such choice

$$\begin{aligned} \lim l(\gamma _n\vert _{[0,b_n]})= \lim d(S,\gamma _n(b_n))=l(\gamma \vert _{[0,b]}) = d(S,\gamma (b)). \end{aligned}$$

(2.13)

Proof

The curve $\gamma$ is a continuous causal curve by Theorem 2.49. Let $[0,b] \subset I$, then there are $[0,b_n] \subset I_n$, such that $b_n \rightarrow b$, and $\gamma _n \vert _{[0,b_n]}$ converges h-uniformly to $\gamma _{[0,b]}$. By the limit maximization property of the sequence $d(S,\gamma _n(b_n))-l(\gamma _n\vert _{[0,b_n]})\le \epsilon _n$, with $\epsilon _n \rightarrow 0$. Using the upper semi-continuity of the length functional (Remark 2.42) and the lower semi-continuity of $d(S,\cdot )$ (cf. Proposition 2.33) we get

$$\begin{aligned} d(S,\gamma (b))&\le \liminf d(S,\gamma _n(b_n)) \le \limsup d(S,\gamma _n(b_n)) \\&\le \limsup l(\gamma _n\vert _{[0,b_n]}) \le l(\gamma \vert _{[0,b]}) \le d(S,\gamma (b)) \end{aligned}$$

hence $d(S,\gamma (b))=l(\gamma \vert _{[0,b]})$, which concludes the proof. $\square$

The S-maximizing curves which are lightlike might be called S-achronal. Clearly, they lie in $E^+(S)$ and so they are geodesic generators for this set. The following consequence is immediate (the assumed convergence is again uniform on compact subsets).

Corollary 2.62

The continuous causal curves which are limits of a sequence of S-maximizing continuous causal curves are also S-maximizing. The continuous causal curves which are limits of S-achronal geodesics are also S-achronal geodesics.

We present three results on the existence of maximizing causal curves which are respectively, geodesic segments, rays and lines. They all hold under a non-totally imprisoning condition on the spacetime.

Proposition 2.63

Let (M, g) be non-totally imprisoning. Assume that $p,q\in M$ are such that $J^{+}(p)\cap J^{-}(q)$ is compact, then d(p, q) is finite and there is a maximizing causal curve (necessarily a geodesic) connecting p to q.

Proof

Since every continuous causal curve connecting p to q is contained in the compact set $K=J^{+}(p)\cap J^{-}(q)$ , by Theorem 2.55, d(p, q) is finite. Let $\gamma _n$ be a sequence of connecting causal curves such that $l(\gamma _n) \rightarrow d(p,q)$. By the non-imprisonment condition the limit curve theorem 2.53 applies in case (i), for case (ii) would lead to the existence of a future inextendible continuous causal curve starting from p and entirely contained in K, in contradiction to non-total imprisonment. Thus there exists a connecting limit continuous causal curve $\sigma$. By the upper semi-continuity of the length functional $l(\sigma )\le d(p,q) = \limsup l(\gamma _{n_k})\le l(\sigma )$. In particular, since $\sigma$ is maximizing it is a geodesic. $\square$

We now obtain an interesting existence result for rays. In Beem et al. (1996, Theorem 8.10) this result is obtained through a longer proof and under the assumption of strong causality, here replaced by the weaker non-imprisoning property.

Theorem 2.64

Let (M, g) be non-totally imprisoning. For every $p\in M$ there exists a future causal ray with starting point p (and analogously in the past case).

Proof

Let h be a complete Riemannian metric on M, and let $C_k={\bar{B}}(p,k)$ be the closed ball of h-radius k with center p. Clearly $p\in C_1$, $C_k\subset \mathrm {Int} C_{k+1}$ for every k, $\cup _k C_k=M$. There is a future inextendible causal curve starting from p, for instance any timelike geodesic. As this curve cannot be contained in a compact set we can find $q_k\in C_{k}\backslash \mathrm {Int} C_{k-1}\cap J^+(p)$. Let $d_k:C_k\times C_k\rightarrow [0,\infty ]$ be the Lorentzian distance on $C_k$, namely the two-point function defined through the supremum of the Lorentzian lengths of causal curves entirely contained in $C_k$. By Theorem 2.55 $d_k$ is bounded, thus we can find a continuous causal curve $\sigma _k$ entirely contained in $C_k$ and connecting p to $q_k$ such that $d_k(p,q_k)-l(\sigma _k)<1/k$. By the limit curve theorem 2.51 and Remark 2.52 we can assume without loss of generality (otherwise pass to a subsequence) that there is a future inextendible continuous causal curve $\sigma :[0,\infty )\rightarrow M$ starting from p to which $\sigma _k$ converges uniformly on compact subsets. But for every compact subset [0, b] in the domain of $\sigma$, the image $\sigma ([0,b])$ is contained in some $\mathrm {Int} C_k$ for sufficiently large k, thus for sufficiently large $j>k$, $\sigma _j([0,b])\subset \mathrm {Int} C_k$. The curves ${\tilde{\sigma }}_j=\sigma _j\vert _{[0,b]}$ are limit maximizing on the spacetime $\mathrm {Int} C_k$ due to $d_{\mathrm {Int} C_k}\le d_j$ and the reverse triangle inequality (2.9)

$$\begin{aligned} d_{\mathrm {Int} C_k}(p, {\tilde{\sigma }}_j(b))-l({\tilde{\sigma }}_j)&\le d_j(p,\sigma _j(b))-l(\sigma _j\vert _{[0,b]})+d_j(\sigma _j(b),q_j)-l(\sigma _j\vert _{>b})\\&\le d_j(p,q_j)-l(\sigma _j)<{1}/{j}. \end{aligned}$$

By Theorem 2.58 $\sigma \vert _{[0,b]}$ is maximizing on $\mathrm {Int} C_k$. Now it must be maximizing, for any other continuous causal curve connecting p to some point of $\sigma$ must be contained in $\mathrm {Int} C_k$ for sufficiently large k. $\square$

We have also the following result whose proof is obtained from the previous one by replacing p with S, and maximizing with S-maximizing.

Theorem 2.65

Let (M, g) be non-totally imprisoning. For every compact set $S\subset M$ there exists a future causal S-ray (and analogously in the past case).

The following concept, first introduced in Beem et al. (1996) (see also Beem and Ehrlich 1977; Ehrlich and Easley 2004), will play an important role in the study of Hawking and Penrose’s singularity theorem.

Definition 2.66

A spacetime is causally disconnected by a compact set K if there are sequences $p_n$ and $q_n$, $p_n<q_n$, going to infinity (i.e. escaping every compact set) such that for each n every continuous causal curve connecting $p_n$ to $q_n$ intersects K.

The following result improves Beem et al. (1996, Theorem 8.14) in that strong causality is weakened to non-total imprisonment.

Proposition 2.67

Any non-totally imprisoning spacetime which contains a lightlike line is causally disconnected.

Proof

Let $\gamma :\mathbb {R} \rightarrow M$, be the lightlike line. We claim that the set $K=\{r\}$, $r=\gamma (0)$, causally disconnects the spacetime. By non-total imprisonment we can find sequences $s_{n+1}<s_{n}<0$, $s_n\rightarrow -\infty$, $0<t_n<t_{n+1}$, $t_n\rightarrow +\infty$, such that the sequences $p_n=\gamma (s_n)$, $q_n=\gamma (t_n)$ escape every compact set. No causal curve $\sigma$ can connect $p_n$ to $q_n$ without intersecting K for if so one could go from $p_{n+1}$ to $q_{n+1}$ following a segment of $\gamma$ up to $p_n$, then $\sigma$ up to $q_n$, and then a segment of $\gamma$ up to $q_{n+1}$. This causal curve is not a geodesic, for it has a segment belonging to $\gamma$ so if it were a geodesic it would coincide with $\gamma$ and would pass through r, which is not the case by the assumption on $\sigma$. Thus by Theorem 2.22 there is a timelike curve from $p_{n+1}$ to $q_{n+1}$, which contradicts the achronality of $\gamma$. $\square$

The following result improves Beem et al. (1996, Theorem 8.13) (or Beem and Ehrlich 1979a) in that strong causality is once again weakened to non-total imprisonment. It must be said that many classical results of causality theory can be improved in this direction. It is now understood that the strong causality condition has been overestimated in the literature, as this condition can often be replaced by the weaker non-imprisoning property (cf. Theorem 2.80). As previously recalled, most limit curve theorems in the old standard references were developed under the assumption of strong causality though this condition could be removed. As a result many classical causality results are non-optimal as they impose too strong assumptions.

Theorem 2.68

Let (M, g) be a non-totally imprisoning space-time. If (M, g) is causally disconnected by a compact set K, then there is a causal line which intersects K. As a consequence, the Lorentzian distance is finite valued on the line.

Proof

By assumption we can find a sequence $p_k<q_k$ such that $p_k,q_k\rightarrow \infty$ and any continuous causal curve connecting $p_k$ to $q_k$ intersects K. Let $\gamma _k$ be one of those causal curves. Let h be a complete Riemannian metric on M, and let $C_k={\bar{B}}(K,n_k)=\overline{\cup _{q \in K} B(q,n_k)}$, where the increasing sequence $n_k$ is chosen in such a way that $\gamma _k\subset \mathrm {Int} C_k$. Clearly $K\subset C_1$, $C_k\subset \mathrm {Int} C_{k+1}$ for every k, $\cup _k C_k=M$. Let $d_k:C_k\times C_k\rightarrow [0,\infty ]$ be the Lorentzian distance on $C_k$, namely the two-point function defined through the supremum of the Lorentzian lengths of causal curves entirely contained in $C_k$. Since $\gamma _k\subset \mathrm {Int} C_k$, we have $(p_k,q_k)\in J_{\mathrm {Int} C_k}$. By Theorem 2.55 $d_k$ is bounded, thus we can find a continuous causal curve $\sigma _k$ connecting $p_k$ to $q_k$ and entirely contained in $C_k$ such that $d_k(p_k,q_k)-l(\sigma _k)<1/k$. By the causal disconnection assumption $\sigma _k$ intersects K, so let $r_k$ be a point in the intersection. By the limit curve theorem 2.51, we can without loss of generality (otherwise pass to a subsequence) assume that $r_k\rightarrow r\in K$ and $\sigma _k$ converges uniformly on compact subsets to an inextendible continuous causal curve $\sigma$ passing through r. But for every compact subset $[-b,b]$ in the domain of $\sigma$, the image $\sigma ([-b,b])$ is contained in some $\mathrm {Int} C_k$ for sufficiently large k, thus for sufficiently large $j>k$, $\sigma _j([-b,b])\subset \mathrm {Int} C_k$. The curves ${\tilde{\sigma }}_j=\sigma _j\vert _{[-b,b]}$ are limit maximizing on the spacetime $\mathrm {Int} C_k$ due to $d_{\mathrm {Int} C_k}\le d_k\le d_j$ and the reverse triangle inequality (2.9)

$$\begin{aligned} d_{\mathrm {Int} C_k}({\tilde{\sigma }}_j(-b), {\tilde{\sigma }}_j(b))-l({\tilde{\sigma }}_j)&\le d_j( \sigma _j(-b),\sigma _j(b))-l(\sigma _j\vert _{[-b,b]})+d_j(\sigma _j(b),q_j)\\&\quad -l(\sigma _j\vert _{>b})+d_j(p_j,\sigma _j(-b))-l(\sigma _j\vert _{<-b})\\&\le d_j(p_j,q_j)-l(\sigma _j)<{1}/{j}. \end{aligned}$$

By Theorem 2.58 $\sigma \vert _{[-b,b]}$ is maximizing on $\mathrm {Int} C_k$. Now it must be maximizing, for any other continuous causal curve connecting two of its points must be contained in $\mathrm {Int} C_k$ for sufficiently large k. $\square$

Notice that these theorems do not tell us if the causal ray and line are lightlike or timelike.

Sometimes negative causality properties imply the existence of lines, we shall see the strongest such result in Theorem 6.20.

By definition strong causality is violated at a point if that point does not admit arbitrarily small causally convex neighborhoods. The set of points at which strong causality is violated is called strong causality violating set.

Theorem 2.69

Suppose that strong causality fails at $p\in M$, then through p passes an inextendible continuous causal curve $\sigma$ over which strong causality is violated and (*): for every $a,b\in \sigma$, we have $(a,b)\in {\bar{J}}$. Moreover, if (M, g) is chronological this curve is a lightlike line and it is the only lightlike geodesic passing though p with the property (*).

For another theorem similar to this result see Penrose (1972, Theorem 4.31).

Proof

Let $\{V_k\}$ be a basis for the topology at p, as in Theorem 1.35. Since strong causality fails, for sufficiently large k they are not causally convex, though they are causally convex as subsets of $V_1$. Thus there is a sequence of causal curves $\sigma _k:[0,1]\rightarrow M$ which start and end in $V_k$ but escape $V_1$. In particular they do not contract to a point, thus by the limit curve theorem 2.53, either there is a closed causal curve passing through p (necessarily a lightlike line if (M, g) is chronological) which can be regarded as inextendible and would imply violation of strong causality over the curve, or there is a future inextendible causal curve $\sigma ^+$ starting from p and a past inextendible causal curve $\sigma ^-$ ending at p, such that for every $a\in \sigma ^+$ and $b\in \sigma ^-$, $(a,b)\in {\bar{J}}$. Defining $\sigma =:\sigma ^+\circ \sigma ^-$ the same holds for arbitrary $a,b\in \sigma$. This is clear for $a\le b$. If $a>b$ and $a,b\in \sigma ^+$, take $b_n\gg b$, $b_n\rightarrow b$, so that $p\in I^-(b_n)$, and since $(a,p)\in {\bar{J}}$ we infer $(a,b_n)\in {\bar{J}}$ and hence $(a,b)\in {\bar{J}}$. An analogous argument applies for $a,b\in \sigma ^-$.

If (M, g) is chronological there cannot be $a,b\in \sigma$ such that $b\ll a$ for jointly with $(a,b) \in {\bar{J}}$ gives, by the openness of I, the existence of closed timelike curves, thus $\sigma$ is a line. Strong causality is violated at any point $q\in \sigma$, for no neighborhood U of q contained in a convex normal neighborhood can be causally convex, it is sufficient to take $a,b\in U$ with a after b over the line and use $(a,b)\in {\bar{J}}$ and Theorem 2.11.

There cannot be a second lightlike geodesic $\gamma$ with property $(*)$. For let $p_1,p_2 \in \sigma$ be points before and after p on $\sigma$, and let $q_1,q_2\in \gamma$ be points before and after p on $\gamma$. Since $\sigma$ and $\gamma$ are transverse at p, $(q_1,p_2)\in I$, $(p_2,p_1)\in {\bar{J}}$, $(p_1,q_2)\in I$, $(q_2,q_1)\in {\bar{J}}$, which, by the openness of I, implies that there is a closed timelike curve, a contradiction. $\square$

This theorem tells us that the strong causality violating set is biviable according to the definition of the next section. It also tells us that under chronology over the strong causality violating set there is a natural lightlike vector field uniquely defined up to a multiplicative function.

2.13 Imprisoned curves

The application of the limit curve theorem 2.53 often leads, through case (ii), to inextendible curves $x^p$, $x^q$ that might be imprisoned in a compact set. The purpose of this section is to study continuous causal curves imprisoned in a compact set K and consequences thereof.

Since K is compact there will be some future accumulation point $p\in K$ for $\gamma$. In fact we can prove much more, namely, that there is another imprisoned continuous causal curve $\alpha$ which consists of accumulation points of $\gamma$ and which accumulates on every point of itself. The existence of these almost closed curves will be important for clarifying the relative strength of some causality conditions.

Much of the discussion of this section is based on Minguzzi (2008d, 2019), see also Kay et al. (1997) for related results.

Definition 2.70

A future inextendible continuous causal curve $\gamma :I \rightarrow M$, is totally future imprisoned in the compact set K if there is $t \in I$, such that for every $t'>t$, $t' \in I$, $\gamma (t') \in K$, i.e. if it enters and remains in K. It is partially future imprisoned if for every $t \in I$, there is $t'>t$, $t' \in I$, such that $\gamma (t') \in K$, i.e. if it does not remain in the compact set, it continually returns to it. The curve escapes to infinity in the future if it is not partially future imprisoned in any compact set. Analogous definitions hold in the past case.

Definition 2.71

Let $\gamma :\mathbb {R} \rightarrow M$ be a causal curve. Denote by $\varOmega _f(\gamma )$ and $\varOmega _p(\gamma )$ the following sets

$$\begin{aligned} \varOmega _f(\gamma )&= \bigcap _{t \in \mathbb {R}} \overline{\gamma _{[t,+\infty )}} \end{aligned}$$

(2.14)

$$\begin{aligned} \varOmega _p(\gamma )&= \bigcap _{t \in \mathbb {R}} \overline{\gamma _{(-\infty ,t]}} \end{aligned}$$

(2.15)

They give, respectively, the set of accumulation points in the future of $\gamma$ and the set of accumulation points in the past of $\gamma$. The sets $\varOmega _f$ and $\varOmega _p$ are well known from the study of dynamical systems (Perko 1991, Sect. 3.2). The points of $\varOmega _f(\gamma )$ are called $\omega$-limit points of $\gamma$, while the points of $\varOmega _p(\gamma )$ are called $\alpha$-limit points of $\gamma$. Note, however, that the analogy with dynamical systems is not complete because so far no flow has been defined on M.

Proposition 2.72

Let $\gamma :\mathbb {R} \rightarrow M$ be an inextendible causal curve.

• (a) The set $\varOmega _f(\gamma )$ is closed.

• (b) The curve $\gamma$ is partially future imprisoned in a compact set iff $\varOmega _f(\gamma ) \ne \emptyset$.

• (c) The curve $\gamma$ is totally future imprisoned in a compact set K iff $\varOmega _f(\gamma ) \ne \emptyset$ and $\varOmega _f(\gamma )$ is compact. In this case

  • (i) $\varOmega _f(\gamma )$ is the intersection of all the compact sets in which $\gamma$ is totally future imprisoned,

  • (ii) $\gamma$ is totally future imprisoned on every compact neighborhood of $\varOmega _f(\gamma )$,

  • (iii) $\varOmega _f(\gamma )$ is connected.

• (d) For every causal curve $\gamma$, the closure of its image is given by $\overline{\gamma }=\varOmega _p(\gamma )\cup \gamma \cup \varOmega _f(\gamma )$.

Analogous statements hold in the past case.

Notice that by (cii) a future totally imprisoned continuous causal curve $\gamma$ is attracted in the future by $\varOmega _f(\gamma )$.

Proof

The property of being closed is a consequence of the definition as intersection of closed sets.

If $\gamma$ is partially future imprisoned in the compact set K then for every $n \in \mathbb {N}$ there is $t_n \in \mathbb {R}$ such that $x_n=\gamma (t_n) \in K$ and $t_n>n$. If $x \in K$ is an accumulation point for $x_n$, there is a subsequence $x_{n_k}= \gamma (t_{n_k})$ such that $x_{n_k} \rightarrow x$. Choose $t \in \mathbb {R}$ then every neighborhood $U\ni x$ contains $x_{n_k}$ for sufficiently large k, thus $x \in \overline{\gamma _{[t,+\infty )}}$ and since t is arbitrary $x \in \varOmega _f(\gamma )$. For the converse, assume $\varOmega _f(\gamma )$ is non-empty, and take $x \in \varOmega _f(\gamma )$. Let $K\ni x$ be a compact neighborhood, then $\gamma$ is partially future imprisoned in K.

Assume $\gamma$ is totally future imprisoned in a compact set K. Since T can be chosen so large that $\gamma _{[T,+\infty )} \subset K$, we have $\varOmega _f(\gamma )\subset K$, and in particular $\varOmega _f(\gamma )$ is compact. Call I the intersection of all the compact sets totally future imprisoning $\gamma$, then since $\varOmega _f(\gamma )\subset K$ holds for any such compact set K, $\varOmega _f(\gamma )\subset I$.

Now, assume only that $\varOmega _f(\gamma )$ is non-empty and compact. Let h be an auxiliary complete Riemannian metric on M, and let $d_0$ be the corresponding continuous distance function. By the Hopf–Rinow theorem any closed and bounded set of (M, h) is compact. Thus $\varGamma _\epsilon =\{y \in M: d_0(y,\varOmega _f(\gamma )) \le \epsilon \}$ is compact and $\bigcap _{\epsilon >0} \varGamma _\epsilon = \varOmega _f(\gamma )$. But $\gamma$ is totally future imprisoned in each $\varGamma _\epsilon$, $\epsilon >0$. Indeed, if not there is some $\epsilon >0$ such that $\gamma$ intersects indefinitely the set $S_{\epsilon /2}=\{y \in M: d_0(y,\varOmega _f(\gamma ))=\epsilon /2\}$, which is compact and thus there would be an accumulation point $z \in S_{\epsilon /2} \cap \varOmega _f(\gamma )$ a contradiction since $S_{\epsilon /2} \cap \varOmega _f(\gamma )=\emptyset$. Thus $\gamma$ is totally future imprisoned in a compact set iff $\varOmega _f(\gamma )$ is non-empty and compact. From $\bigcap _{\epsilon >0} \varGamma _\epsilon = \varOmega _f(\gamma )$, it follows that $I\subset \varOmega _f(\gamma )$, and using the other inclusion, $I=\varOmega _f(\gamma )$. Also notice that if B is a compact neighborhood of $\varOmega _f(\gamma )$ then there is some $\epsilon >0$ such that $\varGamma _\epsilon \subset B$, and since $\gamma$ is totally future imprisoned in $\varGamma _\epsilon$ it is also totally future imprisoned in B.

As for the connectedness of $\varOmega _f(\gamma )$, without loss of generality we can assume $\gamma$ entirely contained in the compact set K, and we already know that $\varOmega _f(\gamma ) \subset K$. If there are two disjoint non-empty closed sets A and B such that $\varOmega _f=A\cup B$, then there are two open sets $A'\supset A$, $B'\supset B$, such that $\overline{A'}\cap \overline{B'}=\emptyset$. Since, by definition of $\varOmega _f$, $\gamma$ is partially imprisoned in $\overline{A'}$ and $\overline{B'}$ it crosses infinitely often both sets and there is a sequence of points $z_r=\gamma (t_r) \in \gamma \subset K$, $t_r \rightarrow +\infty$, $z_r \notin \overline{B'}\cup \overline{A'}$. Thus there is an accumulation point $z \in K\backslash (A \cup B)$ a contradiction since $z \in \varOmega _f(\gamma )$. The proof in the past case is analogous.

For the last statement let $\gamma$ have domain (a, b) (finiteness of a or b is irrelevant), and let $x \in \overline{\gamma }$. For some sequence $t_n \in (a,b)$, $\gamma (t_n) \rightarrow x$. Either $t_n$ admits a subsequence which converges to $t_0 \in (a,b)$, in which case by continuity $x=\gamma (t_0)\in \gamma$, or there is a subsequence which converges to b, in which case $x \in \varOmega _f(\gamma )$ or finally, there is a subsequence which converges to a, in which case $x \in \varOmega _p(\gamma )$. $\square$

We continue the analysis through the notion of biviable set introduced in Minguzzi (2019). For a similar approach which passes through the notion of invariant set see Minguzzi (2008d).

Definition 2.73

We say that a non-empty set C is biviable if for every point of C there is an inextendible continuous causal curve passing through the point which is contained in C.

Lemma 2.74

For a future inextendible continuous causal curve $\gamma$, the set $\varOmega _f(\gamma )$ if non-empty is biviable, and analogously in the past case.

Proof

Let $p\in \varOmega _f(\gamma )$ and let us parametrize $\gamma$ with h-arc length where h is a complete Riemannian metric. Let us set $p_k=\gamma (2t_k)$, where the sequence $t_k\rightarrow +\infty$ is chosen so that $p_k\rightarrow p$. Applying the limit curve theorem 2.51 to $\gamma ([t_k,3t_k])$ (with translated domain, so that 0 corresponds to $p_k$, $a_k=-t_k$ and $b_k=t_k$) we get the existence of an inextendible continuous causal curve $\sigma$ contained in $\varOmega _f(\gamma )$ and passing through p. $\square$

The key result is the following.

Theorem 2.75

Let $\gamma$ be a future inextendible continuous causal curve imprisoned in a compact set K, then inside $\varOmega _f(\gamma ) \subset K$ there is a minimal biviable closed subset B. For every point $p\in B$ there is an inextendible continuous causal curve $\alpha \subset B$ passing through p which satisfies $B={\overline{\alpha }}=\varOmega _f(\alpha )=\varOmega _p(\alpha )$. In particular, any two points of B share the same chronological future and the same chronological past.

So the existence of an imprisoned continuous causal curve implies the existence of a continuous causal curve which accumulates on every point of itself.

Proof

By Lemma 2.74 there is an inextendible continuous causal curve $\sigma$ contained in K. By the identity ${\bar{\sigma }}=\varOmega _p(\sigma )\cup \sigma \cup \varOmega _f(\sigma )$, ${\bar{\sigma }}$ is biviable. Let us consider the family $\mathscr {A}$ of all closed biviable subsets of ${\bar{\sigma }}$. This family is non-empty since it contains ${\bar{\sigma }}$. Let us order it through inclusion. By Hausdorff’s maximum principle (equivalent to Zorn’s lemma and the axiom of choice) there is a maximal chain of closed biviable sets $\mathscr {C} \subset \mathscr {A}$. Since M is second countable it is hereditarily Lindelöf (Willard 1970, 16E), thus $\cap \mathcal {C}=\cap _k A_k$ where $\{A_k\}\subset \mathscr {C}$ is a countable subfamily. Notice that $\cap \mathscr {C}$ is non-empty being the intersection of a nested family of non-empty compact sets (they have the finite intersection property). Every $p\in \cap \mathscr {C}$ belongs to $A_k$ so through it there passes an inextendible continuous causal curve $\eta _k$ contained in $A_k$. Since the $A_k$ are closed, by the limit curve theorem the limit curve $\eta$ passing through p belongs to $A_k$ for every k and hence belongs to $\cap \mathscr {C}$. Thus $B:=\cap \mathscr {C}$ is a non-empty closed biviable set which must be minimal otherwise the chain $\mathscr {C}$ would not be maximal. If $p\in B$ through it there passes an inextendible continuous causal curve $\alpha$ contained in B, but since both $\varOmega _f(\alpha )$ and $\varOmega _p(\alpha )$ are biviable and contained in B, $\varOmega _f(\alpha )=\varOmega _p(\alpha )=B\supset \alpha$, which due to ${\bar{\alpha }}=\alpha \cup \varOmega _f(\alpha ) \cup \varOmega _p(\alpha )$ implies ${\bar{\alpha }} =\varOmega _f(\alpha )=\varOmega _p(\alpha )$.

Let $p,q\in B$ and let $r\gg p$. Let $\alpha \subset B$ be an inextendible continuous causal curve passing through q, then $\varOmega _f(\alpha )=B\ni p$, in particular there will be some point of $\alpha$ in the future of q which intersects $I^-(r)$, thus $q\in I^{-}(r)$, which implies $r\gg q$. This proves $I^+(p)\subset I^+(q)$. The other inclusion is obtained reversing the roles of p and q, and the version with the minus sign is obtained by using the time dual argument. $\square$

Definition 2.76

The chronology violating set $\mathcal {C}$ is the set of points through which there passes a closed timelike curve. In other words,

$$\begin{aligned} \mathcal {C}=\{p\in M: p\ll p\}. \end{aligned}$$

Clearly, $\mathcal {C}$ is open because if $p\in \mathcal {C}$ and q is such that $p\ll q\ll p$ then $I^+(q)\cap I^{-}(q)\subset \mathcal {C}$ is a neighborhood of p. In fact, the relation $p\sim q$ iff $p\ll q\ll p$ is an equivalence relation and so $\mathcal {C}$ is really the union of open equivalence classes (Carter 1968; Hawking and Ellis 1973). If $p\in \mathcal {C}$ we denote by [p] the class which contains p.

We recall that a lightlike line is an achronal inextendible continuous causal curve hence a lightlike geodesic.

Theorem 2.77

Under the assumptions of the previous theorem, if $\gamma \cap \mathcal {C}=\emptyset$ then we have, additionally, that B is achronal, through every point of B there passes just one continuous causal curve $\alpha$ contained in B, and this curve is actually a lightlike line.

In other words the minimal biviable closed set is generated by lightlike lines. The reader is referred to Corollary 2.150 for more information on these sets.

Proof

Since $\mathcal {C}$ is open ${\bar{\gamma }}\cap \mathcal {C}=\emptyset$. Suppose that we can find $p,q\in B$ with $p\ll q$, and let $\alpha$ be an inextendible continuous causal curve contained in B such that $q=\alpha (0)$ (which exists by biviability). We know that ${\bar{\alpha }}=\varOmega _f(\alpha )=B\subset {\bar{\gamma }}$, thus for some $t>1$, $\alpha (t)$ is so close to p that $\alpha (t) \in I^-(q)$. As a consequence $q \le \alpha (t) \ll q$, hence $q\in \mathcal {C}$, a contradiction which proves that B is achronal and hence that $\alpha$ is a lightlike line.

There cannot be two distinct continuous causal curves $\alpha _1,\alpha _2$ passing through some point $p\in B$ and contained in B, for they would have to be lightlike lines, hence geodesics with different tangents at p. But then we could construct a different continuous causal curve $\alpha _3$ contained in B by taking the half-line of $\alpha _1$ up to p and the half-line of $\alpha _2$ starting from p. However, the curve $\alpha _3$ would not be a lightlike geodesic (and hence would not be a lightlike line) due to the corner at p, which gives a contradiction. $\square$

Theorem 2.78

If two achronal minimal biviable closed subsets $\varOmega _1$, $\varOmega _2$, intersect, then they coincide.

By achronality these sets do not intersect $\mathcal {C}$ and so neither do the continuous causal curves contained in these sets.

Proof

Let $p\in \varOmega _1\cap \varOmega _2$ and let $\gamma _1$ and $\gamma _2$ be the generators passing through p belonging respectively to $\varOmega _1$ and $\varOmega _2$. If the generators coincide for every p then $\varOmega _1\cap \varOmega _2$ is biviable closed set thus $\varOmega _1=\varOmega _1\cap \varOmega _2=\varOmega _2$ as both $\varOmega _1$ and $\varOmega _2$ are minimal. Let us show that there cannot be p such that $\gamma _1$ and $\gamma _2$ do not coincide. Indeed, in this case their tangent vectors differ at p thus taking $r,q\in \gamma _1$ with r before p and q after p along $\gamma _1$ and $x,y\in \gamma _2$ with x before p and y after p along $\gamma _2$ then $x \ll q$, $r\ll y$. Since the chronological relation is open, $r\in \bar{\gamma }_1$ and $x \in \bar{\gamma }_2$ we conclude that $q\ll y\ll q$, which is a contradiction with the achronality of $\varOmega _1$. $\square$

Part of the following definition had been anticipated in Remark 2.54.

Definition 2.79

A spacetime (M, g) is non-totally imprisoning, or simply non-imprisoning, if no future inextendible continuous causal curve is totally future imprisoned in a compact set. A spacetime (M, g) is non-partial future imprisoning, if no future inextendible continuous causal curve is partially future imprisoned in a compact set (and dually in the past case); it is non-partially imprisoning if there are no partially imprisoned continuous causal curves (neither in the past nor in the future).

The reader can notice that we have given the definition of non-imprisoning spacetime by using future inextendible curves. The definition formulated with the past adjective would have given the same property since by Lemma 2.74 the imprisonment of a future inextendible or of a past inextendible causal curve implies that of an inextendible continuous causal curve. This fact was recognized by Beem (1976a).

In a next section we shall study in detail the relationship between the various causality conditions. However, the following result is already worth mentioning.

Theorem 2.80

A strongly causal spacetime is non-partially imprisoning. A non-partially imprisoning spacetime is non-totally imprisoning.

Proof

The latter statement is obvious. Let us prove the former statement. Let K be a compact set, then we can find a finite covering $\{V_a\}$ through causally convex neighborhoods as in Theorem 1.35. Let h be an auxiliary complete Riemannian metric, then every inextendible continuous causal curve $\gamma$ has infinite h-arc length (Lemma 2.17), but each causally convex neighborhood is intersected only in a connected parameter domain of $\gamma$ and only for a finite length, thus $\gamma$ is bound to escape a causally convex set of the covering possibly reentering subsequently a different one but finally escaping for good the union of the elements of the covering. Thus $\gamma$ cannot be partially imprisoned in K. $\square$

2.14 Achronal and future sets

In this section we investigate the properties of achronal and future sets.

We recall (Definition 2.19) that a set S is achronal if $I^{+}({S})\cap {S}=\emptyset$.

Proposition 2.81

Every continuous causal curve contained in an achronal set is a maximizing lightlike geodesic (up to parametrizations). Any two causal geodesic segments contained in an achronal set that intersect are either segments of the same geodesic or intersect at the endpoints.

Proof

The first statement follows from Theorem 2.22. The second statement is due to the fact that if a causal geodesic segment intersects a second causal geodesic segment in the domain of its interior and in such a way that the tangents at the intersection point are not proportional, then the starting point of the former segment can be connected to the ending point of the latter by a timelike curve (again by Theorem 2.22). $\square$

It can be useful to observe that, due to the openness of I for any set S we have $I^+(S)=I^+({\bar{S}})$. Again by the openness of I we have

Proposition 2.82

If $S_1\subset S_2$ and $S_2$ is achronal then $S_1$ is achronal. S is achronal iff $\bar{S}$ is achronal.

Definition 2.83

A set F is a future set if $I^{+}(F)\subset F$ (past sets are defined dually).

The definition of future set follows Hawking and Ellis (1973). In the literature the definition $I^{+}(F)=F$ can also be found (Beem et al. 1996).

Typical examples of future sets are $I^+(S)$, $J^+(S)$ and $\overline{J^+(S)}$ (see Proposition 2.84(a)), where $S\subset M$.

We give a few simple properties of future sets.

Proposition 2.84

The following properties hold true:

• 1. F is a future set iff $M\backslash F$ is a past set,

• 2. If F is a future set,

  • (a) $\bar{F}=\{q \in M: I^{+}(q) \subset F\}$, thus ${\bar{F}}$ is also a future set,

  • (b) $\bar{F}=\overline{I^{+}(F)}$, $\partial {F}=\partial {I^{+}(F)}$, and $\mathrm {Int} \,F=I^{+}(F)$,

  • (c) $J^{+}(\bar{F}) \subset \bar{F}$, thus $E^{+}(F)=J^{+}(F)\backslash I^{+}(F) \subset \partial {F}$,

  • (d) $\bar{F}=\partial {F}\cup I^{+}(F)$,

• 3. A future set is open iff $I^{+}(F)=F$.

Proof

• 1. Indeed $I^{-}(M\backslash F) \cap F \ne \emptyset$ (i.e. $M \backslash F$ is not a past set) iff $I^{+}(F) \cap (M\backslash F)\ne \emptyset$ (i.e. F is not a future set).

• 2.

  • (a) If $I^{+}(q) \subset F$, since $q \in \overline{I^{+}(q)}$, $q \in \bar{F}$. If $q \in \bar{F}$ and $p \in I^{+}(q)$ then, since $I^{-}(p)$ is open, $I^{-}(p)\cap F \ne \emptyset$, thus $p \in I^{+}(F)\subset F$.

  • (b) Since $I^{+}(F)\subset F$, we have $\overline{I^{+}(F)} \subset \bar{F}$. For the converse, if $p \in \bar{F}$ then by the previous point $I^{+}(p) \subset F$. Take $q \in I^{+}(p)$ then there is r, $p \ll r \ll q$, $r \in F$, and hence $q \in I^{+}(F)$. Now let $q \rightarrow p$ and conclude $p \in \overline{I^{+}(F)}$. Next $I^{+}(F) \subset \mathrm {Int} F$ is obvious from $I^+(F)\subset F$. For the converse, if $p\in \mathrm {Int} F$ we can find $r\ll p$, $r \in F$, thus $p\in I^+(r)\subset I^+(F)$. A a consequence, $\partial {F}=\partial {I^{+}(F)}$.

  • (c) If $q \in J^{+}(p)$, $p \in \bar{F}$, then taking $r \in I^{+}(q)$ it is $r \in I^{+}(p)$ and hence $r \in I^{+}(F)\subset F$ since $I^{+}$ is open and F is a future set. Taking $r \rightarrow q$ it follows $q \in \bar{F}$. For the last statement use $E^{+}(F)\subset \bar{F}\backslash I^{+}(F)= \bar{F}\backslash \mathrm {Int} F=\partial {F}$.

  • (d) Trivial from $\mathrm {Int} F=I^{+}(F)$.

• 3. This point follows again from $\mathrm {Int} F=I^{+}(F)$.

$\square$

Remark 2.85

Note that $\partial {F}=\partial ({M\backslash F})$, thus the results on $\partial {F}$ have a past version.

Definition 2.86

An achronal boundary is a set of the form $\partial F$ where F is a future set.

By Proposition 2.84, point 2(b), an achronal boundary can also be characterized as a set of the form $\partial F$ where F is an open future set. Clearly, in these characterizations future can be replaced by past. Of course, as the name suggests, an achronal boundary is achronal indeed, if $p\ll q$, $p,q \in \partial {F}$ then $q \in I^{+}(\bar{F})=I^{+}(F)=\mathrm {Int} F$, a contradiction.

A maximal achronal set is an achronal set not properly contained in another achronal set. The following result clarifies that every achronal set is really a subset of some topological hypersurface. We recall that a topological hypersurface is a manifold obtained by patching open sets of $\mathbb {R}^n$ through homeomorphisms.

Theorem 2.87

• (i) Every achronal set is contained in a maximal achronal set,

• (ii) Every maximal achronal sets is an achronal boundary (hence closed) $\partial F$, with F a future set such that $I^{+}(F) = I^{+}(\partial {F})$,

• (iii) Every achronal boundary is a locally Lipschitz topological hypersurface and it is intersected at most once by every timelike curve.

In general it is not true that for a future set F, $I^{+}(F) = I^{+}(\partial {F})$, consider for instance, $F=M$. The last step of the proof goes as in Hawking and Ellis (1973, Proposition 6.3.1).

Proof

Let A be an achronal set and let us consider the family $\mathscr {A}$ of all achronal sets which contain A. This family is non-empty since it contains A. Let us order it through inclusion. By Hausdorff’s maximum principle (equivalent to Zorn’s lemma and the axiom of choice) there is a maximal chain $\mathscr {C}$ of achronal sets, and the union of its elements $\bigcup \mathscr {C}$ is an achronal set which is necessarily maximal otherwise the chain would not be maximal.

Let A be a maximal achronal set then $F=I^+(A)$ is a future set and $\partial F$ is an achronal boundary. By Proposition 2.84 point 2(a), $A \subset \bar{F}$, but $A \cap F=\emptyset$ due to the achronality of A, hence $A\subset \partial F$. But A is a maximal achronal set, thus $\partial F=A$, namely A is an achronal boundary. As for the identity $I^+(F)=I^+(I^+(A))=I^+(A)=I^+(\partial F)$.

Since A is an achronal boundary, $A=\partial F$, where F is an open future set, hence such that $F=I^+(F)$. Let $q\in A$ then $I^+(q)\subset F$, and dually $I^-(q) \subset M\backslash {\bar{F}}$. Let $g'<g$ be a flat Minkowski metric in a neighborhood U of q, then we can find local coordinates $\{x^0,x^1,\ldots ,x^n\}$ such that $g'=-(\mathrm{d}x^0)^2+\sum _i (\mathrm{d}x^i)^2$, $\partial _0=V$ where V is a global future g-timelike vector field. Then every integral curve of $\partial _0$ which passes sufficiently close to q intersects $I^+_{g'}(q)\subset I^+(q)\subset F$ and $I^-_{g'}(q)\subset I^-(q)\subset M\backslash {\bar{F}}$ and so it intersects $\partial F$, precisely at a single point since $\partial F$ is achronal. We conclude that locally $\partial F$ is a graph $x^0=x^0(x^1,\ldots , x^n)$, where the graphing function is Lipschitz due to the g-achronality, and hence $g'$-achronality, of $\partial F$. The achronal boundary $\partial F$ can be covered with cylindrical coordinate neighborhoods $U_\alpha$. The local charts $(x^1,\ldots , x^n)_\alpha$ can be patched together so as to assign to $\partial F$ a $C^1$ atlas, then the embedding into M becomes Lipschitz. $\square$

Remark 2.88

A maximal achronal set exists whenever the chronology violating set does not coincide with the whole manifold (so called non-totally vicious spacetimes), in fact for them an achronal set, for instance a point, can be found. Of course, every achronal set does not intersect the chronology violating region.

Given an achronal set S for any point $q\in S$ there may not exist points $p,r \in S$, with $p \in E^{-}(q)\backslash q$, $r \in E^{+}(q)\backslash q$. It is customary (Hawking and Ellis 1973, Sect. 6.3) to write S as the disjoint union $S=S_N\cup S_+\cup S_-\cup S_0$ where the sets on the right-hand side are defined as follows (Fig. 4)

• $\exists p, \exists r \Rightarrow q \in S_N$,          $\not \exists p, \not \exists r \Rightarrow q \in S_0$,

• $\exists p, \not \exists r \Rightarrow q \in S_+$,          $\not \exists p, \exists r \Rightarrow q \in S_-$.

Fig. 4

The types of points on an achronal set S

Lemma 2.89

Let $S=\partial {F}$ with F a future set. If $p \in S_{N}\cup S_{+}\cup S_{-}$ then through p there passes a maximizing lightlike geodesic (possibly with endpoints) entirely contained in S which cannot be further extended without escaping S. If $p\in S_N$ there is only one lightlike geodesic with the above properties. In any case, if this geodesic has a future endpoint then the endpoint belongs to $S_{+}$, if it has past endpoint then the endpoint belongs to $S_{-}$. In particular if $p\in S_{+}$ then the future endpoint exists and is p itself. Analogously, if $p\in S_{-}$ then the past endpoint exists and is p itself. Finally, if $p\in S_0\cup S_{+}$ then $J^{+}(p)\backslash \{p\} \subset I^{+}(F)$ and analogously, if $p \in S_0 \cup S_{-}$ then $J^{-}(p)\backslash \{p\} \subset I^{-}(M\backslash F)$.

Proof

If $p \in S_{N}\cup S_{+}\cup S_{-}$ there is $q_{+} \in E^{+}(p)\backslash \{p\}\cap S$ or $q_{-} \in E^{-}(p)\backslash \{p\}\cap S$. Let us assume that the first possibility holds, the other case being analogous. There is a maximizing lightlike segment $\sigma \subset E^{+}(p)$ connecting p to $q_{+}$ (cf. Theorem 2.28). Since $p \in \bar{F}$, $I^{+}(p)\subset F$, and since $E^{+}(p) \subset \overline{I^{+}(p)}$, we have $\sigma \subset \bar{F}$, but no point of $\sigma$ can belong to $\mathrm {Int} F=I^{+}(F)$, as it would imply $q_{+}\in I^{+}(F)=\mathrm {Int} F$ in contradiction with $q_{+}\in \partial {F}$. We conclude that $\sigma \subset S$. Now $\sigma$ can be prolonged as a geodesic towards the future. As long as it remains in S it belongs to $E^{+}(p)$, indeed, if it enters $I^{+}(p)$ then it enters $I^{+}(\bar{F})=\mathrm {Int} F$ in contradiction with it being contained in ${S}=\partial F$. If it ever escapes $\partial {F}$ then the last point $p^{+}$ clearly belongs to $S_N\cup S_{+}$ as $p\in E^{-}(p^{+})\backslash \{p^{+}\}\cap S$, however it cannot belong to $S_{N}$. Indeed, otherwise there would be a point $p' \in E^{+}(p^{+})\backslash \{p^{+}\}\cap S$. The maximizing lightlike geodesic $\gamma$ connecting $p^{+}$ to $p'$ must be a prolongation of that connecting p to $p^{+}$ otherwise $p' \in I^{+}(p)\subset \mathrm {Int} F$, in contradiction with $p' \in \partial {F}$. Moreover, $\gamma \cap I^{+}(F)=\emptyset$ otherwise $p' \in I^{+}(F)$ in contradiction with $p'\in \partial {F}$. However, by the same argument used above $\gamma \subset \partial {F}$ in contradiction with $p^{+}$ being a point at which the prolongation of $\sigma$ escaped S.

With an analogous argument we can extend $\sigma$ in the past direction indefinitely or till it meets a last point in S which, then, necessarily belongs to $S_{-}$ (of course if $p\in S_{-}$ then p itself is this last point as it cannot have points in $E^{-}(p)\backslash \{p\}\cap S)$). The final lightlike geodesic cannot be extended anymore and being contained in S is achronal and hence maximizing.

If $p \in S_N$ there is only one lightlike geodesic segments with the property of the theorem. Indeed, the two lightlike segments would meet p in the interior of their domains, then if they do not coincide, by Proposition 2.81 there are chronologically related events in S, a contradiction.

For the last statement, let $p \in S_0\cup S_{+}$, $J^{+}(p)\subset J^{+}(\bar{F})\subset \bar{F}$, thus if there is $q \in J^{+}(p)\backslash \{p\}$ which does not belong to $I^{+}(F)=\mathrm {Int} F$ then $q \in \partial {F}$, and it does not belong to $I^{+}(p)$ since $I^{+}(p)\subset I^{+}(\bar{F})=I^{+}(F)$, thus $q \in E^{+}(p)\backslash \{p\}\cap S$, a contradiction. $\square$

Remark 2.90

The fact that there is only one maximizing lightlike geodesic passing through $p\in S$ with the properties of the lemma does not imply $p \in S_N$.

For the following result see also Hawking and Ellis (1973, Lemma 6.3.2). We provide a different proof.

Proposition 2.91

Let $S=\partial {F}$ with F a future set, and let W be a relatively compact neighborhood of $q \in S$ as in Theorem 1.35, then

• (i) $I^{+}(q) \subset I^{+}(F\backslash W) \Rightarrow q \in S_N\cup S_+$,

• (ii) $I^{-}(q) \subset I^{-}((M\backslash F)\backslash W) \Rightarrow q \in S_N\cup S_-$.

Proof

It is sufficient to prove (i) since S can also be regarded as the boundary of the past set $M\backslash F$. Let $x_n$ be a sequence of points in $I^{+}(q) \cap W$ which converges to q. If $I^{+}(q) \subset I^{+}(F\backslash W)$, there will be a timelike curve $\lambda _n$ from $F\backslash W$ to $x_n$. By the limit curve theorem, there is a limit curve $\lambda$ ending at q (it can be past inextendible) not entirely contained in W by Corollary 2.18. Take $r \in \lambda \backslash \{q\}\cap W^{C}$ and $y \in I^{+}(r)$. Since $I^{-}(y)$ is open and r is an accumultation point for $\lambda _n$, $I^{-}(y)\cap F\ne \emptyset$, thus $I^{+}(r) \subset F$, that is $r \in \bar{F}\backslash W$. We cannot have $r\ll q$, nor $r \in I^{+}(F)$ otherwise $q \in I^{+}(F)=\mathrm {Int} F$. We conclude $r \in S\cap [ E^{-}(q)\backslash \{q\}]$. $\square$

The following result jointly with Lemma 2.89 provides information similar to that given by Theorems 2.28 and 2.56.

Corollary 2.92

Let $S=\partial J^+(B)$, where B is a closed set, then $S\backslash B\subset S_N\cup S_+$, and analogously in the past case.

Proof

Let $q\in S\backslash B$ and let $F=J^+(B)$. Since F is a future set and $q\in {\bar{F}}$, $I^+(q)\subset F$, thus $I^+(q)\subset \mathrm {Int} F=I^+(B)$. Since B is closed there is a compact neighborhood $W\ni q$, as in Theorem 1.35, such that $W\cap B=\emptyset$. But $I^+(F\backslash W)\supset I^+(B)\supset I^+(q)$, thus $q\in S_N\cup S_+$. $\square$

Proposition 2.93

If S is an achronal boundary such that $S=S_N$ then $E^{+}(S)=E^{-}(S)=S$.

Proof

If $q \in E^{+}(S)\backslash S$ then $q \in E^{+}(p) \backslash \{p\}$ for some $p \in S$. Since $S=S_N$, there is $r \in E^{-}(p)\backslash \{p\}\cap S$. If the maximizing lightlike geodesics connecting r to p and p to q have non-proportional tangent vectors at p then $q \in I^{+}(r)\subset I^{+}(S)$ a contradiction. However, if they are proportional then the lightlike geodesic $\sigma$ passing through r and p once extended into the future must escape S before it reaches q. Since S is closed, the escaping point x would belong to S, and to $S_{+}$ because of Lemma 2.89, a contradiction which proves that q does not exist. $\square$

Remark 2.94

The assumption that S is the boundary of a future set is necessary. Take as S a sequence of disjoint lightlike closed segments on a lightlike geodesic of Minkowski spacetime.

Definition 2.95

A set S is acausal if there is no causal curve which starts and ends at S. An achronal boundary which is also acausal is an acausal boundary.

Proposition 2.96

Let S be an achronal set, then for every $p \in S_0$, $J^{+}(p)\cap S=\{p\}$. In particular, if the spacetime is causal or if S is an achronal boundary then the set $S_0$ is acausal.

Proof

Since S is achronal $I^{+}(S) \cap S=\emptyset$. If there are $q \in S$, $p \in S_0$, with $q \in J^{+}(p)\backslash \{p \}$, since $q \notin I^{+}(S)$ then $q\in E^{+}(p)$, which contradicts the definition of $S_0$. Thus for every $p \in S_0$, $J^{+}(p)\cap S=\{p\}$. The set $S_0$ is acausal because there cannot be a causal curve $\sigma$ starting from p and reaching another point in $S_0$ as this last point would have to be p and thus $\sigma$ would be a closed causal curve. This fact is in contradiction with both (i) the causality of (M, g), or (ii) the fact that S is an achronal boundary $S=\partial {F}$. The former case is obvious, for the latter take $r \in \sigma \backslash \{p\}$, then $p<r<p$, then $I^{+}(r)=I^{+}(p) \subset I^{+}(\partial {F})\subset F$ and $r \in \overline{I^{+}(r)} \subset \bar{F}$. We cannot have $r \in I^{+}(F)$ (as a consequence, we cannot have $r\in I^+(p)\subset I^+({\bar{F}})=I^+(F)$) as it would imply $p \in I^{+}(F)$, thus $r \in \partial {F}=S$ and $r \in E^{+}(p)\backslash \{p\}$ in contradiction with $p \in S_0$. $\square$

2.15 Local achronality and coverings

A set $S\subset M$ is locally achronal (locally acausal) if every point $p\in S$ admits an open neighborhood U such that $S\cap U$ is achronal (resp. acausal) in (U, g).

Theorem 2.97

In a simply connected spacetime every connected (hence path connected) locally achronal topological hypersurface S is achronal. A similar statement holds with acausal replacing achronal.

Proof

We proceed by contradiction. By definition of topological hypersurface S is closed. If S is not achronal then there is a timelike curve $\gamma$ with starting point $p \in S$ and ending point $q \in S$. In the domain of $\gamma$ the intersection points are isolated due to the local achronality of S. There is a point $q'$ which is the first (for S is closed) intersection of S with $\gamma$ starting from p. The segment of $\gamma$ joining p to $q'$ does not intersect S but at the endpoints and can be closed with a curve $\mu$ in S joining $q'$ to p (which degenerates to a point if $p=q'$).

If $p=q'$ the whole closed curve intersects S just once. If $p\ne q'$ the whole closed curve can be deformed by pushing towards the future the points in $\mu$ but $q'$ (e.g. use the flow of a timelike vector field which vanishes just at $q'$). Under a sufficiently small variation the varied curve intersects S only once at $q'$ (for a sufficiently small variation of the points of $\mu$ one cannot reach S, for S is locally achronal). Then, this closed curve cannot be contracted to a point because by keeping transversality with S the intersection number can only change by an even number, a contradiction. The proof in the acausal case is analogous. $\square$

Let T be a topological manifold. A covering manifold is defined as a second topological manifold $T'$ together with a continuous map $\varphi :T'\rightarrow T$ such that for every point p there is an open neighborhood $U\ni p$ such that $\varphi ^{-1}(U)$ is a disjoint union of open sets of $T'$, each one being homeomorphic to U. If T is a differentiable manifold then $\varphi$ shall have the differentiability degree of T.

We recall that the universal covering ${\tilde{M}}$ of M is constructed by choosing a reference point $o\in M$ and by identifying each point of ${\tilde{M}}$ with an ordered pair $(p,[\lambda ])$, where $p\in M$ and $[\lambda ]$ is an equivalence class of homotopic curves joining o to p.

Let S be a locally achronal connected topological hypersurface. If M is not simply connected we can consider the universal covering $\pi :{\tilde{M}}\rightarrow M$ endowed with the only metric that projects to g. Then by the previous theorem $\pi ^{-1}(S)$ is locally achronal and hence achronal. Unfortunately, the homotopies used to construct the universal covering probe the topology of S as well, thus if the latter is not simply connected the achronal hypersurface $\pi ^{-1}(S)$ would not be the disjoint union of homeomorphic copies of S. In particular, $\pi ^{-1}(S)$ would be non-compact even if S is compact. As it will turn out, compactness will be quite important in the study of singularity theorems so it is really important to preserve it. Fortunately, the problem can be solved by introducing smaller coverings constructed with homotopies that do not “feel” the topology of S.

There are two notable constructions, one by Hawking (1967) and Hawking and Ellis (1973) and the other by Geroch (1967), that unwrap the topology just in directions “transverse” to S. Alternatives to these constructions were considered by Carter (1971). Actually, as pointed out by Haggman et al. (1980), in Hawking’s papers there is a mistake so that in the covering not all connected components of $\pi ^{-1}(S)$ are homeomorphic to S as was originally intended, though there is certainly one component homeomorphic to it. Fortunately, this property is sufficiently good for most purposes.

• (1) Hawking’s covering $\pi _H:M_H\rightarrow M$. It can be characterized as the largest covering for which there is at least one connected component of $\pi ^{-1}(S)$ homeomorphic to S. Here $M_H$ is the set of pairs $(p,[\lambda ])$ where $[\lambda ]$ is an equivalence class of curves from S to p homotopic modulo S, that is, the starting point on S can slide around. It is for this reason that $[\lambda ]$ cannot entangle with the topology of S.

• (2) Geroch’s covering $\pi _G:M_G\rightarrow M$. It can be characterized as the smallest covering for which each connected component of $\pi ^{-1}(S)$ divides the covering into two parts. Here $M_G$ is the set of pairs $(p,[\lambda ])$ where $[\lambda ]$ is an equivalence class of curves from a reference point o to p. Two curves are equivalent if they cross S the same (finite) number of times, with crossings in the future direction being counted positive and crossings in the past direction being counted negative (the curves need not be homotopic).

Notice that in (2) it might be necessary to deform the curve to make it transverse to S so as to be able to count the intersections. This can be done by pushing slightly to the future any segment laying on S but for one of the endpoints, see also the proof of Theorem 2.97.

Observe that $M_H$ is a covering of $M_G$. The region between two copies of S on $M_G$ might be non-simply connected. The region between two connected components of $\pi ^{-1}(S)$ in $M_H$ is simply connected. We arrive at (see also O’Neill 1983, Proposition 14.48)

Theorem 2.98

Let S be a locally achronal connected topological hypersurface on a spacetime M (hence without edge). On $M_H$ the fiber over S contains at least one connected component homeomorphic to S, and all connected components are achronal. On $M_G$ the fiber over S is the union of disjoint homeomorphic copies of S which are achronal. If S is locally acausal then the connected components on the covering are acausal.

We give an example of a spacetime on whose covering $M_H$ only one connected component of $\pi ^{-1}((S)$ is homeomorphic to S: let $N:=\mathbb {R}\times S^1$ be endowed with the metric $-\mathrm{d}t^2+\mathrm{d}\theta ^2$, let $S=\{0\}\times S^1$ and let $q\in N\backslash S$, then (M, g) is $M=N\backslash \{q\}$ with the induced metric. The fiber over S, $\pi ^{-1}(S)$, is the disjoint union of connected components with the topology of the real line, but for one which is homeomorphic to S.

Proof

The fact that in $M_H$ the fiber over S contains a connected component homeomorphic to S follows from the fact that in $M_H$ a curve laying in S and reaching $p\in S$ is homotopic to zero. The fact that in $M_G$ the fiber over S is a disjoint union of homeomorphic copies of S follows from the fact that a curve lying in S and reaching $p\in S$ can be pushed forward so as to be in S just at the endpoints where it is transverse. However, the direction of transversality is opposite and sums to zero so by moving the endpoint and $\lambda$ over S we cannot change the class. The achronality follows from the fact that in both cases a timelike curve from $p\in S$ to $q\in S$, intersecting S just at the endpoints, is not homotopic to zero (due to the number of oriented intersections with S that can only change by even numbers).

The proof in the acausal case is similar. $\square$

We record here a result whose statement and proof will be completely clear only after the section on the causal ladder.

Theorem 2.99

Let $\pi :{\tilde{M}}\rightarrow M$ be a covering. If M is chronological (causal, non-totally imprisoning, future/past distinguishing, strongly causal, stably causal, globally hyperbolic) then ${\tilde{M}}$ has the same property.

The property of the causal relation being closed and the reflectivity property do not seem to pass to ${\tilde{M}}$.

Proof

The proof is rather easy and uses the following facts. The projection of a timelike (causal) curve is timelike (resp. causal). The projection of a compact set is a compact set. Let $p=\pi (P)$ and let U be an open neighborhood of p which contains a causally convex neighborhood C. If U is sufficiently small a connected component ${\tilde{U}}$ of $\pi ^{-1}(U)$ is isometric to U (so since causal curves project to causal curve ${\tilde{U}}$ is causally convex). A similar argument holds for distinguishing neighborhoods. If S is a Cauchy hypersurface on M then $\pi ^{-1}(S)$ is a Cauchy hypersurface on ${\tilde{M}}$. $\square$

2.16 Horismos, trapped sets and null araying sets

In this section we introduce the notion of trapped set and develop some related causality results. Trapped sets will be of fundamental importance in the study of geodesic singularities.

The following theorem develops an idea contained in Newman (1989, Theorem 2.1). It is much stronger than that result or of Senovilla (1998, Proposition 4.3) because null geodesic completeness or the null convergence condition are not assumed. Moreover, as we shall see, it is adapted to work directly with the general notion of trapped set (rather than with the more restrictive notion of trapped surface).

Note that for any set $E^{+}(S)\cap S=S\backslash I^{+}(S)$. Strong causality holds at $p\in M$ if p admits arbitrarily small causally convex neighborhoods.

Theorem 2.100

Let S be a non-empty compact set, then $E^{+}(S)\cap S \ne \emptyset$ or S intersects the chronology violating set of (M, g). In the former case, defining $A= E^{+}(S)\cap S$, A is non-empty, compact achronal and we have $I^{+}(A)\subset I^{+}(S)$, $J^{+}(A)\subset J^{+}(S)$ and $E^{+}(S)\subset E^{+}(A)$. Moreover, if strong causality holds on S the converse inclusions hold.

Proof

Clearly $S\subset J^{+}(S)$, thus $E^{+}(S)\cap S=S\backslash I^{+}(S)$ and $E^{+}(S)\cap S=\emptyset$ iff $S\subset I^{+}(S)$. Assume $S\subset I^+(S)$ and consider the family of open sets $\mathcal {A}=\{I^{+}(p), p \in S\}$. It provides a covering of the compact set S, thus there are points $p_1,\ldots , p_n \in S$ and a finite subcovering $\{I^{+}(p_1),\ldots , I^{+}(p_n)\}$. Each $p_i$ belongs to the chronological future of some $p_j$, and going backwards, since the subcovering is finite, one finally finds twice the same $p_k$, thus $p_k\ll p_k$.

Let us consider the case $E^{+}(S)\cap S \ne \emptyset$ and let us define $A= E^{+}(S)\cap S$. Since $A\subset S$, we have $I^{+}(A)\subset I^{+}(S)$, $J^{+}(A)\subset J^{+}(S)$. Let $q\in E^{+}(S)$, then there is a point $p \in S$, such that $p \le q$. We cannot have $p \in I^{+}(S)$ otherwise $q\in I^{+}(S)$, thus $p \in S\backslash I^{+}(S)=A$. As a consequence, $q \in J^{+}(A)$. Moreover, $q \notin I^{+}(A)$ otherwise $q \in I^{+}(S)$. We conclude $q \in E^{+}(A)$, and hence $E^{+}(S)\subset E^{+}(A)$.

For the reverse inclusions assume strong causality holds at S. Suppose by contradiction that $q \in I^{+}(S)\backslash I^+(A)$ (or $q \in J^{+}(S)\backslash J^+(A)$) then there is some $p_1 \in S$, $p_1 \ll q$ (resp. $p_1 \le q$). We cannot have $p_1\in A$, thus $p_1\in I^{+}(S)$ and there is $p_2\in S$ such that $p_2 \ll p_1$. Again necessarily $p_2\notin A$ otherwise $q\in I^+(A)$, so $p_2 \in I^+(S)$. We want to formalize what it means to “continue in this way”. Let h be a complete Riemannian metric, and let $l_1$ be the h-arc length of a timelike curve $\gamma _1$ connecting $p_2$ to $p_1$. The point $p_2$ and the timelike curve $\gamma _1$ might be chosen in many ways. It is chosen so that $l_1\ge \text {min}(d_1/2, 1)$ where $d_1$ is the supremum of $l_1$ for all the possible choices (possibly $d_1=\infty$). By imposing the same criterion for each step we obtain a sequence of timelike curves which can be joined to form a curve $\gamma$.

Let us show that we cannot have $0<a=\sum _i l_i<+\infty$. The convergence of the series implies that $p_k$ is a Cauchy sequence, thus converging to some point $r\in S$. Then the h-arc length parametrized continuous causal curve $\gamma :(-a,0] \rightarrow M$, $\gamma (0)=p_1$, becomes a continuous causal curve $\gamma :[-a,0] \rightarrow M$ by setting $\gamma (-a)=r$ (i.e. continuous and almost everywhere differentiable with causal tangent). Moreover, for some $\delta >0$, $\gamma (-a)\le \gamma (-a+\delta )\ll p_1\le q$, thus $\gamma (-a)\in I^{-}(q)$ so $\gamma (-a)\notin A$ and hence $\gamma (-a)\in I^+(S)$. Thus $\gamma$ could be extended to an h-arc length parametrized continuous causal curve ${\tilde{\gamma }}:[-a-\epsilon ,0]\rightarrow M$ with $\gamma (-a-\epsilon )\in S$. For sufficiently large i, $l_i<\epsilon /2$, which contradicts the definition of $l_i$.

The possibility $a=+\infty$ would imply that $\gamma$ is past inextendible and partially imprisoned in S, which is impossible because by strong causality on S, S is covered by a finite number of causally convex neighborhoods, each of them being intersected only once by $\gamma$ (see also Theorem 2.80).

We conclude that $I^+(S)=I^+(A)$ and $J^+(S)=J^+(A)$ and thus also $E^{+}(S)=E^{+}(A)$. $\square$

Proposition 2.101

Let S be any set, then $\dot{I}^{+}(S)$ is an achronal boundary and $E^{+}(S)$ is achronal. If S is also achronal $S \subset E^{+}(S)$ and $E^{+}(E^{+}(S))=E^{+}(S)$.

Proof

The first statement is obvious because $\dot{I}^{+}(S)$ is the boundary of the future set $F=I^{+}(S)$ and $E^{+}(S)=J^{+}(S)\backslash I^{+}(S) \subset \overline{I^{+}(S)} \backslash I^{+}(S)=\dot{I}^{+}(S)$ is just a subset. Let $p\in S$, clearly $p\in J^{+}(p)\subset J^{+}(S)$. There cannot be any timelike curve from S to p because S is achronal, thus $p\in E^+(S)$, and by the arbitrariness of p, $S \subset E^{+}(S)$.

In the last equation replace S with the achronal set $E^{+}(S)$ to get $E^{+}(S)\subset E^{+}(E^{+}(S))$. For the converse, note that since $E^{+}({\tilde{S}})\subset J^{+}({\tilde{S}})$ for any ${\tilde{S}}\subset M$ we have $E^{+}(E^{+}(S))\subset J^{+}(S)$. If $q \in E^{+}(E^{+}(S))\subset J^{+}(S)$ but $q \notin E^{+}(S)$, then there is $p\in S$ such that $q \in I^{+}(p)$. If $p \in E^{+}(S)$ we have $q \in I^{+}(E^{+}(S))$ in contradiction with $q \in E^{+}(E^{+}(S))$, thus $p \in S\cap I^{+}(S)$, in contradiction with the achronality of S. $\square$

Corollary 2.102

Let S be a non-empty compact set and let strong causality hold at S, then $E^+(E^+(S))=E^+(S)$.

Proof

By Theorem 2.100 $A=E^+(S)\cap S$ is non-empty and achronal and $E^+(S)=E^+(A)$. By Proposition 2.101 due to the achronality of A, $E^+(E^+(A))=E^+(A)$, thus $E^+(E^+(S))=E^+(S)$. $\square$

Remark 2.103

The identity $E^{+}(E^{+}(S))=E^{+}(S)$ does not hold for general S (see Fig. 5).

Fig. 5

A closed set S for which the identity $E^{+}(E^{+}(S))=E^{+}(S)$ does not hold. Of course, S is neither achronal nor compact since (M, g) is strongly causal

Lemma 2.104

For every set S, $E^{+}(S)\subset E^{+}(\bar{S})$. If S is achronal and $E^{+}(S)$ is closed then $E^{+}(\bar{S})=E^{+}(S)$.

Proof

Since $I^{+}$ is open, $I^{+}(\bar{S})=I^{+}(S)$, and since $J^{+}(S)\subset J^{+}(\bar{S})$, we get $E^{+}(S)\subset E^{+}(\bar{S})$. If S is achronal $S \subset E^{+}(S)$, and if the latter set is closed, $\bar{S} \subset E^{+}(S)$. Suppose, by contradiction, that there is $q \in E^{+}(\bar{S})\backslash E^{+}(S)$ then there is $p\in \bar{S}$ such that $q \in E^{+}(p)$. But $p\in \bar{S}\subset E^{+}(S)$ thus there is $r \in S$ such that $p \in E^{+}(r)$. Thus $q \in J^{+}(r)$ that is, $q \in J^{+}(S)$, and using $I^{+}(S)=I^{+}(\bar{S})$ it follows $q \in E^{+}(S)$, a contradiction. $\square$

Remark 2.105

If $E^{+}(S)$ is compact S need not be closed, for instance consider $1+1$ Minkowski spacetime $g=-\mathrm{d}t^2+\mathrm{d}x^2$ endowed with coordinates (t, x), with the line $x=0$ identified with the line $x=3$, and let $S=\{(s/2,s): s\in [0,2)\}$.

Remark 2.106

The set S can be achronal with a compact $\overline{E^{+}(S)}$ but this fact does not imply that $\overline{E^{+}(\bar{S})}$ is compact, consider a spacelike disk without border in Minkowski spacetime.

Definition 2.107

A non-empty set S is a future trapped set if $E^{+}(S)$ is non-empty and compact.

By Theorem 2.100 under chronology a non-empty compact set S is future trapped iff $E^+(S)$ is compact.

Note that the previous definition differs from Hawking and Ellis’ (1973) in that S is not assumed to be achronal (Fig. 6).

Fig. 6

An example of trapped set S. The spacetime (M, g) is obtained by removing from $1+1$ Minkowski spacetime four spacelike segments, and by identifying the lower edges of the two cuts above with the upper edges of the two cuts below. Of course, the endpoints of the cuts do not belong to M. The gray region is the future domain of dependence of $E^+(S)$. More detailed explanations will be given later on, where the existence of an inextendibe causal curve $\sigma$ inside this domain will be important (Corollary 6.39). This spacetime is stably causal (cf. Sect. 4)

In some applications involving the notion of trapped set the requirement “$E^{+}(S)$ compact” rather than “$\overline{E^{+}(S)}$ compact” might seem too strong. However, under some conditions the two requirements are equivalent.

Theorem 2.108

Let S be a non-empty compact set such that $\overline{E^{+}(S)}$ is compact, then either ${E^{+}(S)}$ is compact or there is a future lightlike S-ray (thus future totally imprisoned in $\overline{E^{+}(S)}$). In particular, if (M, g) is non-totally imprisoning then $E^+(S)$ is non-empty and compact, namely S is a future trapped set.

We recall that a lightlike S-ray is necessarily contained in $E^+(S)$.

Proof

Suppose that there is no future lightlike S-ray. Let $q \in \overline{E^{+}(S)}$, we want to find under what additional conditions $q\in E^{+}(S)$. If $q \in S$ we must have $q\in E^{+}(S)$ otherwise $q\in I^{+}(S)$ and as $I^{+}(S)$ is open, we cannot have $q \in \overline{E^{+}(S)}$, a contradiction. Thus assume $q \in \overline{E^{+}(S)}\backslash S$. As S is closed there are $q_n \in E^{+}(S)\backslash S$, $q_n \rightarrow q$ and points $p_n \in S$ such that $p_n$ is connected to $q_n$ by a causal curve not intersecting $I^{+}(S)$. Since S is compact we can assume $p_n\rightarrow p \in S$. By an application of the limit curve theorem either, (i) there is a causal curve connecting p to q, necessarily not intersecting $I^{+}(S)$ (otherwise for sufficiently large n, $q_n \in I^{+}(S)$, which is a contradiction), thus $q \in E^{+}(S)$ and we have finished; or (ii) there is a future inextendible causal curve $\sigma ^p$ issued from p entirely contained in the achronal compact set $\overline{E^{+}(S)}$. Actually, since it starts from S it is contained in $J^{+}(S)$ but it has no point in $I^{+}(S)$ otherwise for sufficiently large n, $q_n \in I^{+}(S)$, and hence it must be contained in $E^{+}(S)$. The achronality of $E^+(S)$ implies that $\sigma ^p$ is an achronal lightlike geodesic, hence a future lightlike S-ray. The contradiction proves that (ii) does not apply. The last statement follows from Theorem 2.100. $\square$

Proposition 2.109

If S is a non-empty achronal future trapped set then $S'=E^{+}(S)$ is a non-empty, compact achronal future trapped set such that $E^{+}(S')=S'$.

Proof

As S is achronal, $S\subset E^{+}(S)$. The remainder is a consequence of Proposition 2.101. $\square$

Remark 2.110

Thus if the spacetime admits an achronal future trapped set then without loss of generality we can assume that it is achronal and compact. Similarly, by Theorem 2.100 under strong causality at S the assumption of existence of a compact future trapped set implies the existence of an achronal and compact future trapped set.

Proposition 2.111

Under strong causality there is an achronal or compact future trapped set iff there is an achronal compact future trapped set.

Theorem 2.112

Let S be a non-empty compact set that does not intersect the chronology violating set (and hence $E^{+}(S)\cap S\ne \emptyset$, see Theorem 2.100). If S is not a future trapped set then there is a future lightlike S-ray. The converse holds provided the following circumstance does not occur (e.g. under non-total imprisonment or under acausality of S): there is an inextendible totally imprisoned lightlike line $\gamma \subset E^+(S)$ such that $\gamma \subset \varOmega _p(\gamma )\cap \varOmega _f(\gamma )$, which is partially past imprisoned in S.

Proof

If $E^{+}(S)$ is not compact then, either $E^{+}(S)$ is relatively compact, and we reach the conclusion thanks to Theorem 2.108, or $\overline{E^{+}(S)}$ is non compact and it is possible to find a sequence $q_n \in E^{+}(S)$ escaping every compact set. Thus, for sufficiently large n, $q_n \notin S$, as S is compact, and hence there is a corresponding sequence $p_n \in S$ such that $q_n \in E^{+}(p_n)$. Passing to a subsequence if necessary, we can assume $p_n \rightarrow p \in S$. Consider the maximizing lightlike segments connecting $p_n$ to $q_n$. By the limit curve theorem there is a future inextendible limit curve $\sigma$ starting from p, and it is actually a future lightlike ray by Corollary 2.59. Since $p \in S$, $\sigma \subset J^{+}(S)$, but no point of $\sigma$ can belong to $I^{+}(S)$ otherwise, as I is open and $\sigma$ is a limit curve, some point $q_n$ would belong to $I^{+}(S)$, hence $\sigma \subset E^{+}(S)$.

For the converse, suppose that there is such a lightlike S-ray and assume by contradiction that $E^+(S)$ is compact. If there is such a lightlike S-ray it is imprisoned in $E^+(S)$, thus, by Theorem 2.75 and the achronality of $E^+(S)$ (notice that a maximizing curve cannot intersect the chronology violating set), there is an inextendible lightlike geodesic $\gamma$ contained in $E^+(S)$ (possibly closed) such that $\gamma \subset \varOmega _p(\gamma )\cap \varOmega _f(\gamma )$. Let $\gamma :\mathbb {R}\rightarrow E^+(S)$ be a parametrization with respect to a Riemannian metric. Let $q\in \gamma \cap E^+(S)$, if $q\in S$ set $p:=q$. Otherwise there is an achronal lightlike segment $\eta$ with starting point p and ending point q entirely contained in $E^+(S)$. The curve $\gamma$ must be tangent to $\eta$ at q otherwise the points along $\gamma$ after q would belong to $I^+(S)$, which is impossible since $\gamma \subset E^+(S)$. But then $\eta$ is a segment of $\gamma$, thus in both cases we conclude that there is $p\in S\cap E^+(S)\cap \gamma$, $p\le q$. The arbitrariness of q implies that $\gamma$ is partially past imprisoned in S, in particular S is acausal. $\square$

Under weak causality conditions the notion of trapped set, introduced by Hawking and Penrose (1970), can be replaced by a related notion.

Definition 2.113

A set S is a future null raying set if there exists a future lightlike S-ray. It is a future null araying set if there are no future lightlike S-rays.

Theorem 2.100 implies

Theorem 2.114

Let S be a non-empty compact future null raying set that does not intersect the chronology violating set. Then $A=E^{+}(S)\cap S=S\backslash I^+(S)$ is an achronal subset with the same properties. If strong causality holds on S then raying can be replaced by araying.

Proof

The lightlike S-ray is contained in $E^+(S)$ and since $E^+(S)\subset E^+(A)$ it is a lightlike A-ray. Under strong causality on S, $E^+(S)=E^+(A)$ thus a lightlike A-ray would be a lightlike S-ray. $\square$

Corollary 2.115

Let S be a non-empty compact future null raying/araying set that does not intersect the strong causality violating set, then $A=E^+(S)\cap S$ is an achronal subset with the same properties.

Theorem 2.112 translates to

Theorem 2.116

Let S be a non-empty compact set that does not intersect the chronology violating set (and hence $E^{+}(S)\cap S\ne \emptyset$, see Proposition 2.100). If S is a future null araying set then it is a future trapped set. The converse holds provided the following circumstance does not occur (e.g. under non-total imprisonment or under acausality of S): there is an inextendible totally imprisoned lightlike line $\gamma \subset E^+(S)$ such that $\gamma \subset \varOmega _p(\gamma )\cap \varOmega _f(\gamma )$, which is partially past imprisoned in S.

Corollary 2.117

Let S be a non-empty compact set that does not intersect the strong causality violating set. The set S a is future null araying set iff it is a future trapped set.

The trapped sets share a stability property under perturbations of the set (they are also stable under perturbations of the metric, see Theorem 4.103). In fact this property is inherited under non-total imprisonment or acausality by a stability property for null araying sets.

Theorem 2.118

Let S be a compact future null araying set. There is a relatively compact neighborhood $O\supset S$ such that if the compact set ${\tilde{S}}$ is such that $S\subset {\tilde{S}}\subset {\bar{O}}$, then ${\tilde{S}}$ is a future null araying set.

Proof

Let h be a complete Riemannian metric and let $O_k$ be the set of points at h-distance from S less than 1 / k. If the conclusion of the theorem is false then for every k we can find a compact set $S_k$, $S\subset S_k\subset {\bar{O}}_k$ which is not future null araying, thus there is a future lightlike ray $\sigma _k$ starting from $S_k$ entirely contained in $E^{+}(S_k)$. Since $S\subset S_k$ we have $I^+(S)\subset I^+(S_k)$, thus the whole sequence $\sigma _k$ does not intersect $I^+(S)$. However, by the limit curve theorem, there is a limit lightlike ray $\sigma$, starting from S, which necessarily does not intersect the open set $I^+(S)$, thus $\sigma \subset E^+(S)$, a contradiction. $\square$

Proposition 2.119

If $S_1$ and $S_2$ are future null araying sets, then $S_1\cup S_2$ is a future null araying set.

Thus under non-total imprisonment if $S_1$ and $S_2$ are future trapped sets then $S_1\cup S_2$ is a future trapped set.

Proof

If $S=S_1\cup S_2$ admits a lightlike S-ray $\gamma$ then it has some starting point which belongs to S hence to $S_1$ or $S_2$. Let us suppose the former case. The curve $\gamma$ has no point in $I^+(S)$, thus it has no point in $I^+(S_1)$, hence $\gamma$ is a lightlike $S_1$-ray, a contradiction. $\square$

It is interesting to consider the family of compact null araying sets (trapped sets) contained in a given non-compact maximal achronal set N.

Definition 2.120

We say that N is asymptotically null raying if there is a complete Riemannian metric h on the hypersurface N, a point $c\in N$, and a radius $R>0$, such that the closed h-balls ${\bar{B}}(c,r)$ of center c and radius $r>R$, are such that through every point of $\partial _N {\bar{B}}(c,r)$ there starts a future lightlike ray entirely contained in $E^+({\bar{B}}(c,r))$.

We did not introduce the concept of asymptotically flat spacetime (Hawking and Ellis 1973) but one can expect that on it one can find Cauchy hypersurfaces which are asymptotically null raying.

Theorem 2.121

Let N be an asymptotically null raying maximal achronal set N. Then the union $T \subset N$ of all the compact future null araying subsets of N is an open relatively compact set of N. For every neighborhood $U\supset \partial _N T$, we can find a compact null araying set $S\subset T$, such that $T\backslash U\subset S$.

The set T could be called the araying region of N. It should be distinguished from the notion of trapped region, defined in Hawking and Ellis (1973, p. 319) by means of the notion of trapped surface.

Proof

Let $S\subset N$ be a compact future null araying set and let O be the neighborhood mentioned in Theorem 2.118. Let ${\tilde{O}}=O\cap N$, then by Theorem 2.118 for $q\in {\tilde{O}}\backslash S$, $S\cup \{q\}$ is a future null araying set. Thus the union of all the compact future null araying sets of N includes ${\tilde{O}}$, namely T is the union of the open sets associated to the null araying sets by Theorem 2.118 and hence open.

No compact future null araying set $K\subset N$ can have points outside ${\bar{B}}(c,R)$, for there would be a minimum value of r such that $K\subset {\bar{B}}(c,r)$, so that there would be $q\in K \cap \partial {\bar{B}}(c,r)$ and hence a future lightlike ray $\sigma$ starting from q and entirely contained in $E^+({\bar{B}}(c,r))$. But if so the ray does not intersect $I^+({\bar{B}}(c,r))$ and hence $I^+(K)$, namely the ray is contained in $E^+(K)$, a fact which contradicts the araying property for K. We conclude that $T\subset {\bar{B}}(c,R)$ so it is relatively compact.

The compact set $T\backslash U={\overline{T}}\backslash U$ is covered by the family of open sets mentioned in the first paragraph of this proof, thus by a finite subfamily $\{O^k\}$. But then by Theorem 2.118 ${\bar{O}}^k$ is compact and future null araying, thus $S:=\cup _k {\bar{O}}^k\supset T\backslash U$ is compact and future null araying. By definition of T, $S\subset T$, which concludes the proof. $\square$

2.17 Causal versions of horismos, trapped sets and araying sets

The following new concepts are useful and quite natural. We stress that although analogous to the notions introduced in the previous section, they are not conformally invariant, for they make use of the Lorentzian distance d. They will play an important role in the study of Hawking’s singularity theorem.

We define the causal horismos of a subset S

$$\begin{aligned} C^+(S)&=\{q:{\text {there exists a causal curve (possibly degenerate to a point) }} \sigma \\&\qquad \quad {\text { starting from }} S {\text { and ending at }} q {\text { such that }} l(\sigma )=d(S,q) \}. \end{aligned}$$

Of course, in the degenerate case it is understood that $l(\sigma )=0$. Observe that $q\in S$ does not imply $q\in C^+(S)$, and that in case $q\in S\cap C^+(S)$ we do not necessarily have $d(S,q)=0$. If we replace causal with lightlike we obtain the set $E^+(S)$, thus the usual horismos can be called lightlike horismos. Notice that $E^+(S)\subset C^+(S)\subset J^+(S)$, and if $\sigma$ is the curve mentioned in the defining property, by the reverse triangle inequality for the Lorentzian distance, every point of $\sigma$ belongs to $C^+(S)$.

Definition 2.122

A non-empty set S is a future causally trapped set if $C^+(S)$ is non-empty and compact.

If we replace causal with lightlike we obtain the set $E^+(S)$, thus a future trapped set might also be called future null trapped set.

Proposition 2.123

If S is a future causally trapped set then it is a future trapped set.

Proof

Let $C^+(S)$ be compact and let us prove that $E^+(S)$ is closed. Let $q_n\in E^+(S)$, $q_n\rightarrow q$. Since $C^+(S)$ is closed, $q\in C^+(S)\subset J^+(S)$. We cannot have $q\in I^+(S)$ otherwise $q_n\in I^+(S)$ for sufficiently large n, thus $q\in E^+(S)$. Let us prove $E^+(S)\ne \emptyset$. By assumption $C^+(S)\ne \emptyset$, thus there are two cases: either $q\in S\cap C^+(S)$, and so we are in a degenerate case with $d(S,q)=0$, which implies that $q\notin I^+(S)$; or $q\in C^+(S)\backslash S$, which implies that there is a causal curve $\gamma$ such that $l(\gamma )=d(S,q)$. Let p denote the starting point of $\gamma$ from S, then $p\notin I^+(S)$, otherwise we could find a causal curve longer than $\gamma$ connecting S to q, a contradiction. In both cases $E^+(S)\supset S\backslash I^+(S)\ne \emptyset$. $\square$

The following result is analogous to Theorem 2.108.

Proposition 2.124

Let S be a non-empty and compact set such that $\overline{C^{+}(S)}$ is compact, then either $C^{+}(S)$ is compact or there is a future causal S-ray (thus future totally imprisoned in $\overline{C^{+}(S)}$). In particular, if (M, g) is non-totally imprisoning then $C^+(S)$ is non-empty and compact, namely S is a future causally trapped set.

Notice that any future causal S-ray belongs to $C^+(S)$.

Proof

Suppose that there are no future causal S-rays. Let $q \in \overline{C^{+}(S)}$, we wish to prove that $q\in C^{+}(S)$. Since there are no future lightlike S-rays, by Theorem 2.108 $E^+(S)$ is closed, thus it is sufficient to prove that if $q_n\in C^+(S)\backslash E^+(S)$, $q_n\rightarrow q$, we have $q\in C^+(S)$. Let $\gamma _n$ be a causal curve connecting S to $q_n$ such that $d(S,q_n)=l(\gamma _n)$. We have already observed that $\gamma _n\subset C^+(S)$, thus the sequence of causal curves is contained in the compact set $\overline{C^+(S)}$. If the h-length of the curves goes to zero (which is only possible if $q\in S$), for any neighborhood $U\ni q$, for sufficiently large n, $\gamma _n\subset U$, and hence $l(\gamma _n)\rightarrow 0$. In this case we cannot have $q\in I^+(S)$ otherwise the curves $\gamma _n$ would not be maximizing, for the Lorentzian lengths would have to be bounded from below by a constant $\epsilon >0$. Thus $q\in E^+(S)\subset C^+(S)$, and we have finished.

If the h-lengths of the curves $\gamma _n$ (or of any subsequence) do not go to zero, the limit curve theorem and Theorem 2.62 give the existence of an S-maximizing causal curve $\gamma$ (hence contained in $C^+(S)$), which either is inextendible and hence a future causal S-ray, which has been excluded, or connects S to q and hence $q\in C^+(S)$. Under non-total imprisonment we know that $E^+(S)\ne \emptyset$ (cf. Theorem 2.100), so $C^+(S)\ne \emptyset$, and the last statement follows. $\square$

The following result is analogous to Theorem 2.125.

Theorem 2.125

Let S be a non-empty compact set that does not intersect the chronology violating set (and hence $E^{+}(S)\cap S\ne \emptyset$, see Proposition 2.100). If S is not a future causally trapped set, then there is a future causal S-ray. The converse holds provided the following circumstance does not occur (e.g. under non-total imprisonment or under acausality of S): there is an inextendible totally imprisoned lightlike line $\gamma \subset C^+(S)$ such that $\gamma \subset \varOmega _p(\gamma )\cap \varOmega _f(\gamma )$, which is partially past imprisoned in S.

Proof

If $C^{+}(S)$ is not compact then, either $C^{+}(S)$ is relatively compact, and we reach the conclusion thanks to Theorem 2.124, or $\overline{C^{+}(S)}$ is non compact and it is possible to find a sequence $q_n \in C^{+}(S)$ escaping every compact set. Thus, for sufficiently large n, $q_n \notin S$, as S is compact, and hence there is a corresponding sequence $p_n \in S$ and S-maximizing causal segments connecting $p_n$ to $q_n$. Passing to a subsequence if necessary, we can assume $p_n \rightarrow p \in S$. By the limit curve theorem there is a future inextendible limit curve $\sigma$ starting from p, and it is actually a future causal S-ray by Theorem 2.62, hence $\sigma \subset C^+(S)$.

For the converse, suppose that there is such a causal S-ray and assume by contradiction that $C^+(S)$ is compact. If there is such a causal S-ray $\alpha$ it is imprisoned in $C^+(S)$, thus by Theorem 2.77 (notice that $\alpha$ cannot intersect the chronology violating set, for in that case it could not be maximizing) there is a lightlike line $\gamma$ contained in $C^+(S)$ (possibly closed) such that $\gamma \subset \varOmega _p(\gamma )\cap \varOmega _f(\gamma )$. Let $\gamma :\mathbb {R}\rightarrow C^+(S)$ be a parametrization with respect to a Riemannian metric. By the reverse triangle inequality $d(S, \gamma (t_1))\le d(S,\gamma (t_2))$, for $t_1< t_2$, that is $t\mapsto d(S,\gamma (t))$ is non-decreasing. But $\gamma \subset \varOmega _p(\gamma )$, thus for any $\tau \in \mathbb {R}$, there are $t_n\rightarrow -\infty$, $t_n<\tau$, such that $\gamma (t_n)\rightarrow \gamma (\tau )$, and hence by the lower semi-continuity of $d(S,\cdot )$, $d(S,\gamma (\tau ))\le \liminf d(S,\gamma (t_n))$. Since $t_n<\tau$, $d(S,\gamma (t_n))\le d(S,\gamma (\tau ))$, thus $d(S,\cdot )$ is really constant over $\gamma$.

Let $q\in \gamma$, and hence $q\in C^+(S)$. If $q\in S$ set $p:=q$. If $q\notin S$ there is an S-maximizing causal segment $\eta$ with starting point $p\in S$ and ending point q entirely contained in $C^+(S)$. The curve $\gamma$ must be tangent to $\eta$ at q otherwise by Theorem 2.22 any point $q'$ along $\gamma$ after q would be such that $d(S,q')>l(\eta )=d(S,q)$ while we know that $d(S,\cdot )$ is constant over $\gamma$. So in both cases we can conclude that there is $p\in S\cap C^+(S)\cap \gamma$, $p\le q$. The arbitrariness of q implies that $\gamma$ is partially past imprisoned in S, in particular S is acausal. $\square$

Definition 2.126

A set S is future causal raying if there exists a future causal S-ray. It is future causal araying if there are no future causal S-rays.

Theorem 2.125 translates to

Theorem 2.127

Let S be a non-empty compact set that does not intersect the chronology violating set (and hence $E^{+}(S)\cap S\ne \emptyset$, see Proposition 2.100). If S is a future causal araying set, then it is a future causally trapped set. The converse holds provided the following circumstance does not occur (e.g. under non-total imprisonment or under acausality of S): there is an inextendible totally imprisoned lightlike line $\gamma \subset C^+(S)$ such that $\gamma \subset \varOmega _p(\gamma )\cap \varOmega _f(\gamma )$, which is partially past imprisoned in S.

Corollary 2.128

Let S be a non-empty compact set that does not intersect the strong causality violating set. The set S is a future causal araying set iff it is a future causally trapped set.

Clearly $d(S,\cdot )$ is finite over $C^+(S)$, however we have also (we shall not use this result)

Theorem 2.129

Let S be a compact causal araying set, then the function $d(S,\cdot )$ is continuous over $C^+(S)$.

Proof

We need only to prove the upper semi-continuity. Let $q_n\in C^+(S)$, $q_n\rightarrow q$. If the h-lengths of the S-maximizing curves $\gamma _n$ connecting S to $q_n$ go to zero, we can argue as in Proposition 2.124, thus $q\in S\cap E^+(S)$, so $d(S,q)=0$, and $l(\gamma _n)=d(S,q_n)\rightarrow 0$. If there is a subsequence, here denoted in the same way, whose h-lengths do not converge to zero, then we can apply the limit curve theorem and, using the fact that the limit of S-maximizing causal curves is S-maximizing, conclude that either there is a future causal S-ray, which is impossible, or the sequence converges to an S-maximizing causal curve $\gamma$ connecting S to q. By the upper semi-continuity of the Lorentzian length, $\limsup d(S,q_n)=\limsup l(\gamma _n)\le l(\gamma )=d(S,q)$. $\square$

2.18 The edge of an achronal set

With Theorem 2.87 we learned that every achronal set S is contained in some (non unique) maximal achronal topological hypersurface N. Let $\partial _N$ be the boundary operator according to the topology induced on N. The set $\partial _N S\subset N$ represents a kind of ‘edge’ or ‘border’ for S which, unfortunately, seems to depend on the choice of N. In this section we give a notion of edge which does not have this drawback and prove (Theorem 2.147), that it actually coincides with $\partial _N S$ for every possible choice for N. Meanwhile, we obtain some useful results on edges.

Definition 2.130

Given an achronal set S we define $\mathrm {edge}(S)$ as the set of points $q\in \bar{S}$ such that for every open set $U\ni q$ there are $p\in I^{-}(q ,U)$, $r\in I^{+}(q,U)$, necessarily not belonging to S, such that there is a timelike curve in U connecting p to r which does not intersect S.

The points p and r cannot belong to S, otherwise, since I is open and $q \in \bar{S}$, S would not be achronal.

Proposition 2.131

Let S be an achronal set. If $q \in \mathrm {edge}(S)$ then for every neighborhood $V\ni q$ all the points $p \in I^{-}(q,V)$, $r \in I^{+}(q,V)$ are such that there is a timelike curve in V connecting p to r which does not intersect S.

Proof

Take $U=I^{+}(p,V)\cap I^{-}(r,V)$, we have $q \in V$ then since $q \in \mathrm {edge}(S)$ there are $r',p' \in V$ such that $p'\in I^{-}(q ,U)$, $r'\in I^{+}(q,U)$ and there is a timelike curve in U and hence in V connecting $p'$ to $r'$ not intersecting S. In particular $p\ll _V p'\ll _V r' \ll _V r$, but the timelike curve connecting p to $p'$ cannot intersect S since $p'\ll q$ and S is achronal (recall that $I^{+}$ is open, thus $\bar{S}$ is achronal). Analogously, the timelike curve connecting $r'$ to r cannot intersect S, from which the claim follows. $\square$

Proposition 2.132

If S is an achronal set, then $\bar{S}\backslash S \subset \mathrm {edge}(S)\subset \bar{S}$. In particular, $S\cup \mathrm {edge}(S)=\bar{S}$ and if $\mathrm {edge}(S) \subset S$ then S is closed.

Proof

By definition $\mathrm {edge}(S)\subset \bar{S}$. Let $q \in \bar{S}\backslash S$, and let $U\ni q$, take $p \in I^{-}(q,U)$ and $r \in I^{+}(q,U)$. The timelike curve which connects p to q and which is contained in U cannot intersect S, otherwise, since $I^{+}$ is open and $q \in \bar{S}$, we would have a contradiction with the achronality of S. Thus repeating the argument with r in place of p and joining the two timelike curves we obtain a timelike curve joining p to r not intersecting S, thus $q\in \mathrm {edge}(S)$. $\square$

Proposition 2.133

Let S be an achronal set, then $\mathrm {edge}(S)$ is closed.

Proof

Let $q \in \overline{\mathrm {edge}(S)}$ and $U\ni q$ an open set. Take any $p\in I^{-}(q ,U)$ and $r\in I^{+}(q,U)$, then $V=I^{-}(r,U)\cap I^{+}(p,U)\subset U$ is an open set and $q\in V$. Thus there is $\tilde{q} \in \mathrm {edge}(S)\cap V$ and events $\tilde{p} \in I^{-}(\tilde{q} ,V)$ and $\tilde{r}\in I^{+}(\tilde{q},V)$, such that there is a timelike curve entirely contained in V connecting $\tilde{p}$ and $\tilde{r}$ that does not intersect S. Since $\bar{S}$ is achronal the timelike curve entirely contained in U which connects $\tilde{r}$ to r cannot intersect $\bar{S}$ as $\tilde{q} \in \bar{S}$, and $\tilde{q} \ll \tilde{r}$. Analogously, p and $\tilde{p}$ can be connected with a timelike curve entirely contained in U that does not intersect $\bar{S}$. Finally, p and r can be connected through a timelike curve entirely contained in U that does not intersect S, and using the arbitrariness of U, $q \in \mathrm {edge}(S)$. $\square$

In general, given an achronal set S, $\mathrm {edge}(S)$ need not be equal to $\mathrm {edge}(\bar{S})$, however, since the timelike curves that do not intersect $\bar{S}$ do not intersect S, it holds $\mathrm {edge}(\bar{S}) \subset \mathrm {edge}(S)$.

Proposition 2.134

If $S_1\subset S_2$ then $\mathrm {edge}(S_2)\cap \bar{S}_1 \subset \mathrm {edge}(S_1)$.

Proof

The timelike curves that do not intersect $S_2$ do not intersect $S_1$, thus the points in $\mathrm {edge}(S_2)$ that do belong to $\bar{S}_1$ are edge points for $S_1$. $\square$

Proposition 2.135

Let S be a closed achronal set then $\mathrm {edge}(\mathrm {edge}(S))=\mathrm {edge}(S)$.

Proof

Since the set $C=\mathrm {edge}(S)$ is closed, by Proposition 2.132$\mathrm {edge}(C) \subset C$, that is $\mathrm {edge}(\mathrm {edge}(S))\subset \mathrm {edge}(S)$. For the converse use Proposition 2.134 with $S_2=S$, $S_1= \mathrm {edge}(S)$. $\square$

Proposition 2.136

If S is an achronal boundary, then $\mathrm {edge}(S)=\emptyset$.

Proof

Let $S=\partial {F}=\partial ({M\backslash F})$ with F a future set and $M\backslash F$ a past set. Take $q \in \bar{S}$, $U\ni q$, $p\in I^{-}(q ,U)$ and $r\in I^{+}(q,U)$. Since $q \in \bar{F}$, $r \in F$, analogously, since $q \in \overline{M\backslash F}$, $p \in M\backslash F$, thus any timelike curve joining p to r has to intersect $\partial {F}=S$, thus $q \notin \mathrm {edge}(S)$. $\square$

Lemma 2.137

Let S be an achronal set and let $w \in E^{+}(S)\backslash S$, then there is $q \in S$ and a maximizing lightlike geodesic segment $\eta$ in $E^{+}(S)$ which connects q to w. If q is such that $\eta \cap S=\{q\}$ (a choice of q with this property is possible if S is closed or acausal) then $q \in \mathrm {edge}(S)$.

Proof

Since $w\in J^{+}(S)$ there must be $q\in S$, such that $w \in J^{+}(q)$, but we cannot have $w \in I^{+}(q)\subset I^{+}(S)$, thus $w \in E^{+}(q)$. Denote by $\eta$ a maximizing lightlike geodesic segment which connects q to w. Clearly, if S is closed we can replace q with the last point in S along $\eta$ so that by redefining $\eta$ with the new endpoints, $\eta \cap S=\{q\}$. If instead S is acausal clearly the intersection $\eta \cap S$ is given by a unique point q (the remainder of the proof does not assume that S is closed or acausal). No point in the lightlike geodesic segment $\eta$ can belong to $I^{+}(S)$ otherwise $w \in I^{+}(S)$, hence $\eta \subset E^{+}(S)$.

Let $U\ni q$, $r\in I^{+}(q,U)$ and $p \in I^{-}(q,U)$, thus $q \in I^{-}(r,U)$ and let $r' \in \eta \backslash \{q\} \cap I^{-}(r,U)\cap I^+(p,U)$ which exists because the chronological relation in U is open. Moreover, choose $r'$ sufficiently close to q so that the segment of $\eta$ between $r'$ and q is entirely contained in U. Let $\sigma$ be a timelike curve inside U which connects $r'$ to r. The curve $\sigma$ cannot intersect S, indeed by assumption the intersection point y cannot be $r'$ as $\eta \cap S=\{q\}$, and for any other $y \in \sigma$ there would be a timelike curve which connects q to y in contradiction with the achronality of S. Now note that since $r'\in I^{+}(p,U)$, there is in U a timelike curve $\gamma$ which connects p to $r'$ and this curve cannot intersect S otherwise we would have $r' \in I^{+}(S)$, in contradiction with $r' \in E^{+}(S)$. The timelike curve $\sigma \circ \gamma$ is contained in U and connects p to r without intersecting S. $\square$

Corollary 2.138

Let S be an achronal set. If $E^{+}(S)\ne S$ then S has non-empty edge.

Proof

If it is edgeless then it is closed, and Lemma 2.137 implies it has non-empty edge, a contradiction. $\square$

Theorem 2.139

If S is achronal then $\mathrm {edge}(S)=\overline{S}\cap \overline{\dot{I}^{+}(S)\backslash S}=\overline{S}\cap \overline{\dot{I}^{-}(S)\backslash S}$.

Proof

Let $q \in \overline{S}\cap \overline{\dot{I}^{+}(S)\backslash S}$. Take $q_n \in \dot{I}^{+}(S)\backslash S$, $q_n \rightarrow q \in \bar{S}$. Since $\dot{I}^{+}(S)$ is closed, $q \in \dot{I}^{+}(S)$. Let $U\ni q$, $r \in I^{+}(q,U)$, $p\in I^{-}(q,U)$. Then for large n, $q_n \in I^{+}(p,U)$, and the timelike curve in U which joins p to $q_n$, cannot intersect S otherwise $q_{n}\in I^{+}(S)\cup S$, in contradiction with $q_{n} \in \dot{I}^{+}(S)\backslash S$. Analogously, for large n, $q_n \in I^{-}(r,U)$ and the timelike curve in U which joins $q_n$ to r cannot intersect S otherwise $q_n \in I^{-}(S)\cup S$, which is impossible since $q_n \notin S$, and $q_n \in I^{-}(S)$ would imply, because of $q_{n}\in \overline{I^{+}(S)}$, that S is not achronal. Thus there is a timelike curve in U which joins p to r and does not intersect S, i.e. $q \in \mathrm {edge}(S)$.

For the converse, let $q \in \mathrm {edge}(S)$, $U\ni q$, $r \in I^{+}(q,U)$, $p\in I^{-}(q,U)$. Since $q \in I^{+}(p,U)$ and $q \in \bar{S}$, $p\in I^{-}(S)$. Analogously, $r \in I^{+}(S)$. Since S is achronal $I^{+}(S)$ and $I^{-}(S)$ are disjoint. Let $\sigma$ be a timelike curve in U joining p to r and not intersecting S. The intersection of this curve with $\dot{I}^{+}(S)$ gives a point $z\in \dot{I}^{+}(S)\backslash S$. Since U is arbitrary, it is possible to find a sequence $z_n \in \dot{I}^{+}(S)\backslash S$ such that $z_n \rightarrow q$, hence $q \in \overline{\dot{I}^{+}(S)\backslash S}$. $\square$

Proposition 2.140

Let S be an achronal set. We have $q\in \mathrm {edge}(S)$ iff $q\in \bar{S}$ and there is a sequence $q_n \rightarrow q$, such that $q_n \notin S\cup I^{+}(S)\cup I^{-}(S)$, that is

$$\begin{aligned} \mathrm {edge}(S)=\bar{S}\cap \overline{(S\cup I^{+}(S)\cup I^{-}(S))^{C}}. \end{aligned}$$

Proof

Assume $q\in \mathrm {edge}(S)$ then by Theorem 2.139 $q\in \bar{S}$ and there is a sequence $q_n \in \dot{I}^{+}(S)\backslash S$, such that $q_n \rightarrow q$. Clearly, $q_n \notin I^{+}(S)$, and since S is achronal $q_n \notin I^{-}(S)$, hence $q_n \notin S\cup I^{+}(S)\cup I^{-}(S)$.

For the converse, assume $q\in \bar{S}$ and there is such a sequence $q_n\notin S\cup I^{+}(S)\cup I^{-}(S)$, $q_n \rightarrow q$. Take $U\ni q$, $r \in I^{+}(q,U)$, $p \in I^{-}(q,U)$. For sufficiently large n, $q_n \in I^{+}(p,U)\cap I^{-}(r,U)$. Consider a timelike curve $\sigma : [-1,1] \rightarrow U$, such that $\sigma (-1)=p$, $\sigma (1)=r$, and $\sigma (0)=q_n$. Since $r \in I^{+}(S)$, $p\in I^{-}(S)$, and $q_n \notin S\cup I^{+}(S)\cup I^{-}(S)$, there is a maximal connected closed interval $[a,b]\subset [-1,1]$, $a \le 0\le b$, such that $\sigma ([a,b]) \subset (I^{+}(S)\cup I^{-}(S))^C$. S is achronal thus $I^{+}(S)$ and $I^{-}(S)$ are disjoint. Note that $\dot{I}^{-}(S)$ is achronal, thus if a timelike curve leaves $I^{-}(S)$ it can’t return to it, and analogously for $I^{+}(S)$, thus $\sigma (a)\in \dot{I}^{-}(S)$ and $\sigma (b) \in \dot{I}^{+}(S)$.

If $a=b$ then $\sigma (a) \notin S$, because $\sigma (a)=q_n$. If $a\ne b$ either $\sigma (a)$ or $\sigma (b)$ does not belong to S otherwise, S would not be achronal. As a result, since $\sigma (a) \in \dot{I}^{-}(S)$ and $\sigma (b) \in \dot{I}^{+}(S)$, and U is arbitrary we can find either a sequence $x_k \in \dot{I}^{-}(S)\backslash S$, $x_k \rightarrow q$, or a sequence $y_s \in \dot{I}^{+}(S)\backslash S$, $y_s \rightarrow q$, thus Theorem 2.139 implies $q \in \mathrm {edge}(S)$. $\square$

Corollary 2.141

Let S be an achronal set. If $p\in \bar{S}$ and $p \notin \mathrm {edge}(S)$ then there is a neighborhood $U\ni p$ such that $U \subset S\cup I^{+}(S)\cup I^{-}(S)$.

Corollary 2.142

A closed achronal set S is edgeless iff $S\cup I^{+}(S)\cup I^{-}(S)$ is open.

Proof

Assume S is edgeless, let $p \in S\cup I^{+}(S)\cup I^{-}(S)$ and we have to prove that there is a neighborhood $U\ni p$ contained in $S\cup I^{+}(S)\cup I^{-}(S)$. If $p \in I^{+}(S)\cup I^{-}(S)$, this fact is obvious. If $p \in S$ it follows from Corollary 2.141 because $p \notin \mathrm {edge}(S)$.

For the converse if $S\cup I^{+}(S)\cup I^{-}(S)$ is open, and $q \in \mathrm {edge}(S) \subset S$ then there is a neighborhood $U\ni q$, $U \subset S\cup I^{+}(S)\cup I^{-}(S)$ a contradiction because of Proposition 2.140. $\square$

A spacetime is causally simple if it is causal and J is closed, see Sect. 4.5.3. There are simple examples of causally simple spacetimes in which there is a closed spacelike edgeless hypersurface such that $\overline{J^{+}(S)}\ne J^{+}(S)$ (remove the half line $\gamma$: $x\le 0$, $t=0$, in $1+1$ Minkowksi spacetime and the set $J^{-}(\gamma )$, and take S as $x> 0$, $t=0$). Nevertheless, the following result holds true.

Proposition 2.143

If (M, g) is causally simple and S is a compact set then $J^{+}(S)$ is closed, $E^{+}(S)=\dot{I}^{+}(S)$ and finally $\text {edge}(E^{+}(S))=\emptyset$.

Proof

Let us show that $J^{+}(S)$ is closed. Let $q \in \overline{J^{+}(S)}$, there are $q_n \in J^{+}(S)$, $q_n \rightarrow q$. As a consequence there are $p_n \in S$, such that $(p_n,q_n) \in J$ and without loss of generality we can assume (pass to a subsequence) $p_n\rightarrow p\in S$, as S is compact. Hence $(p_n,q_n) \rightarrow (p,q)$, and since J is closed, $(p,q)\in J$, that is $q \in J^{+}(S)$. As a consequence, $E^{+}(S)=J^{+}(S)\backslash I^{+}(S)=\overline{J^{+}(S)}\backslash I^{+}(S)=\dot{I}^+(S)$, where we used Theorem 2.27. As $E^{+}(S)$ is an achronal boundary it has no edge (Proposition 2.136). $\square$

We recall that a set is generated by lightlike lines if through every point of the set there passes a lightlike line contained in the set.

Theorem 2.144

Let S be a closed set. $E^{+}(S)=E^{-}(S)=S$ iff S is achronal and $\mathrm {edge}(S)$ (possibly empty) is generated by lightlike lines.

Proof

$\Rightarrow$. $E^{+}(S)=S$ implies that S is achronal since $E^+(S)\subset \dot{I}^+(S)$. By Theorem 2.139$\mathrm {edge}(S)=S\cap \overline{\dot{I}^{-}(S)\backslash S}$. Let $p \in \mathrm {edge}(S)$ and let $p_n \in \dot{I}^{-}(S)\backslash S$, $p_n \rightarrow p$. By Theorem 2.56 (here we use $E^{-}(S)=S$) from $p_n$ starts a future lightlike ray $\sigma _n$ contained in $\dot{I}^{-}(S)\backslash S$. By the limit curve theorem and Corollary 2.59 from p starts a future lightlike ray $\sigma$. Since $\sigma$ is a limit curve for $\sigma _n$, $\sigma \subset \overline{\dot{I}^{-}(S)\backslash S}\subset \overline{I^{-}(S)}$. But $\sigma \subset J^{+}(S)$ because $p\in S$, and we cannot have $\sigma \cap I^{+}(S)\ne \emptyset$ because otherwise, as $I^{+}$ is open, S would not be achronal, thus $\sigma \subset E^{+}(S)=S$ and finally $\sigma \subset S\cap \overline{\dot{I}^{-}(S)\backslash S}=\mathrm {edge}(S)$. Thus from every point $p \in \mathrm {edge}(S)$ starts a future lightlike ray contained in $\mathrm {edge}(S)$. An analogous time reversed argument gives that at every point $p \in \mathrm {edge}(S)$ ends a past lightlike ray contained in $\mathrm {edge}(S)$. Once joined at p they must give a lightlike line otherwise $\mathrm {edge}(S)\subset S$ would not be achronal.

$\Leftarrow$. Assume that S is closed, achronal and with $\mathrm {edge}(S)$ generated by lightlike lines. If $p\in E^{+}(S)\backslash S$ then by Lemma 2.137 there is $q \in \mathrm {edge}(S)\subset S$ such that $p\in E^{+}(q)$. Through q there passes a lightlike line $\sigma _q$ contained in $\mathrm {edge}(S)$. Take $r \in \sigma _q$, $r<q$, then the maximizing lightlike segment joining q to p must be contained in $\sigma _q$ otherwise $p \in I^{+}(r)\subset I^{+}(S)$, a contradiction. But we cannot have $p\in \sigma _q \subset \mathrm {edge}(S) \subset S$, thus $E^{+}(S)=S$, and analogously $E^{-}(S)=S$. $\square$

Corollary 2.145

If S is achronal and $\mathrm {edge}(S)=\emptyset$ then S is closed, causally convex and $E^+(S)=E^-(S)=S$. If S is also compact then it is a (future and past) trapped set. Thus, compact achronal sets which are not future or past trapped sets necessarily have a non-empty edge.

Proof

Proposition 2.132 proves that S is closed; Theorem 2.144 proves $E^{\pm }(S)=S$; since $E^\pm (S)=S$ we have $J^\pm (S)=S\cup I^\pm (S)$, thus $J^+(S)\cap J^-(S)=S$ by achronality, an equality which expresses the causal convexity of S. If S is compact $E^{\pm }(S)=S$ is compact, thus the last statement follows. $\square$

Theorem 2.146

An achronal set S is a maximal achronal set iff

$$\begin{aligned} {S}\cup I^{+}({S})\cup I^{-}({S})=M. \end{aligned}$$

In this case S is closed, edgeless, and $E^{+}({S})=E^-(S)={S}$.

Proof

Let S be a maximal achronal set. It is closed for if not the closure is achronal (as $I^{+}$ is open) and would provide a larger achronal set in contradiction with the maximality. Recall that a set has empty boundary iff it is both open and closed (i.e. it is M or the empty set). If ${S}\cup I^{+}({S})\cup I^{-}({S})\ne M$ then there is $q \in \partial [{S}\cup I^{+}({S})\cup I^{-}({S})]$. Note that we cannot have $q \ll q$ otherwise either S is not achronal (in the case $q \in {S}$) or $q \in I^{+}({S})$ (in the case $q \in \overline{I^{+}({S})}\backslash {S}$) or $q \in I^{-}({S})$ (in the case $q \in \overline{I^{-}({S})}\backslash {S}$), which is a contradiction. Thus $S'={S}\cup \{q\}$ would be achronal and strictly larger than S a contradiction which proves ${S}\cup I^{+}({S})\cup I^{-}({S})=M$. Due to it and by Corollary 2.142, S is edgeless, and by Corollary 2.145 it is such that $E^{+}({S})=E^{-}({S})={S}$.

Finally, it is trivial that if an achronal set S is such that ${S}\cup I^{+}({S})\cup I^{-}({S})= M$ then it is maximal achronal for it is impossible to add any point to S while keeping achronality. $\square$

We recall that with Theorem 2.87 we learned that every achronal set is contained in a maximal achronal set N which, as a consequence, is an achronal boundary and a locally Lipschitz topological hypersurface.

Theorem 2.147

Let S be an achronal set and let N be an achronal maximal set containing S. Regard N as a topological space and let ${\partial }_N$ be the boundary operator in this space, then $\mathrm {edge}(S) \subset N$ and

$$\begin{aligned} \mathrm {edge}(S)=\partial _N S . \end{aligned}$$

Thus if S has no edge it is a connected component of N and hence a locally Lipschitz topological hypersurface.

Proof

Since $S \subset N$ and N is closed, $\mathrm {edge}(S) \subset \bar{S}\subset N$. Let $q \in \mathrm {edge}(S)$ and let $V_n$ be a neighborhood base in M for q. There are sequences $r_n\rightarrow q$, $r_n\gg q$, and $p_n\rightarrow q$, $p_n\ll q$, $r_n,p_n \in V_n$ and there are timelike curves $\sigma _n$ connecting $p_n$ to $r_n$ entirely contained in $V_n$ and not intersecting S. By Theorem 2.146, $M=N\cup I^{+}(N)\cup I^{-}(N)$ and $r_n \in I^{+}(\bar{S})\subset I^{+}(N)$, $p_n \in I^{-}(\bar{S})\subset I^{-}(N)$, the curves $\sigma _n$ intersect N at a point $q_n\in V_n\cap S^{C}$, and since $V_n$ is a base for the topology at q, we have $q_n \rightarrow q$, thus $q \in \partial _N S$.

Conversely, assume $q \in \partial _N S$ then every neighborhood of q contains points in S, thus $q \in \bar{S}$, and there is a sequence of points $q_n \in S^C\cap N$ such that $q_n \rightarrow q$. Since N is achronal $q_n \notin I^{+}(N)\cup I^{-}(N)$, thus $q_n \notin I^{+}(S)\cup I^{-}(S)\cup S$ from which it follows that $q \in \mathrm {edge}(S)$ by Proposition 2.140. $\square$

Corollary 2.148

In the definition of edge (Definition 2.130), timelike curve can be replaced by $C^1$ timelike curve.

Proof

It is clear that the definition with $C^1$ curves gives a set that is no larger. Let $q\in \mathrm {edge}(S)$, for every open set $U\ni q$ there are $p\in I^{-}(q ,U)$, $r\in I^{+}(q,U)$, necessarily not belonging to S, such that there is a timelike curve in U connecting p to r which does not intersect S. We have to show that we can find a $C^1$ timelike curve in U connecting p to r which does not intersect S. By Theorem 2.147, $\mathrm {edge}(S)=\partial _N S$ with N a topological achronal hypersurface, thus there is $x\in I^+(p,U)\cap I^-(r,U)\cap N\cap S^C$. Let $\sigma :[-1,1]\rightarrow U$, $\sigma (0)=x$, be a $C^1$ timelike segment sufficiently small to be contained in $I^+(p,U)\cap I^-(r,U)$, then $\sigma (1)$ can be connected to r with a $C^1$ timelike curve which stays in U (recall Corollary 2.30) and similarly p can be connected to $\sigma (-1)$ with a $C^1$ timelike curve which stays in U. The corner can be rounded at $\sigma (-1)$ and $\sigma (1)$, so giving the desired $C^1$ timelike curve. It cannot intersect $S\subset N$, since it already intersects the achronal set N at x. $\square$

Theorem 2.149

If S is achronal and $\text {edge}(S)=\emptyset$ then S is closed, $S=E^{+}(S)$, and $\dot{I}^{+}(S)\backslash S$ is closed. Since $\dot{I}^{+}(S)= S \cup [\dot{I}^{+}(S)\backslash S]$, $\dot{I}^{+}(S)$ is an achronal boundary which can be split into the two closed disjoint sets S and $\dot{I}^{+}(S)\backslash S$ which are therefore achronal locally Lipschitz topological hypersurfaces. In particular, S is an achronal boundary in the spacetime $N=[\dot{I}^{+}(S)\backslash S]^{C}$ with the induced metric.

Proof

We have only to show that $\dot{I}^{+}(S)\backslash S$ is closed, because the previous results guarantee that S is closed and $E^{+}(S)=S$. By Theorem 2.139 $S \cap \overline{\dot{I}^{+}(S)\backslash S}= \emptyset$. In other words the accumulation points of $\dot{I}^{+}(S)\backslash S$ do not belong to S, but they belong to $\dot{I}^{+}(S)$ as this set is closed, hence they belong to $\dot{I}^{+}(S)\backslash S$ which therefore is closed. The last statement follows from the fact that $I^{-}_N(S)=I^{-}(S)$, indeed the inclusion $I^{-}_N(S)\subset I^{-}(S)\cap N$ is obvious while the other direction follows from the fact that every timelike curve ending at S can not intersect $\dot{I}^{+}(S)\backslash S$ as $S\cup [\dot{I}^{+}(S)\backslash S]=\dot{I}^{+}(S)$ is achronal. Then the boundary of $I^{-}(S)$ in N is S. $\square$

The following result adds some information to Theorems 2.75 and 2.77.

Corollary 2.150

Let $\eta$ be a causal curve future totally imprisoned in a compact set and which does not intersect the chronology violating set $\mathcal {C}$. Denote by $B\subset \varOmega _f(\eta )$ a (non-empty) minimal biviable closed set (see Theorems 2.75 and 2.77). We have that $E^{+}(B)=E^{-}(B)=B$ and either B has empty edge or $\mathrm {edge}(B)= B$.

Proof

First let us prove that $E^{+}(B)=B$, the proof of $E^{-}(B)=B$ being analogous. Since B is achronal, $B\subset E^{+}(B)$. If $q \in E^{+}(B)\backslash B$ then there is $p \in B$ such that $q \in E^{+}(p)\backslash \{p\}$. But if the maximizing lightlike geodesic connecting p to q is a segment of the lightlike line passing through p and contained in B then $q \in B$, a contradiction. If it differs then taking $r<p$ in this same line, and rounding off the corner at p one gets $q \in I^{+}(r)\subset I^{+}(B)$, again a contradiction which proves the first claim. Note that $\mathrm {edge}(B)\subset B$ is closed and, by Theorem 2.144, generated by lightlike lines hence biviable. By the minimality of B, $\mathrm {edge}(B)= B$ or $\mathrm {edge}(B)=\emptyset$. $\square$

2.19 Chronal equivalence

In this section we introduce the notion of chronal equivalence for two achronal sets. It is a useful concept which will allow us to establish that any two achronal sets sharing the same closed Cauchy development share also the same edge.

Definition 2.151

Let S be an achronal set. The achronal set A is an achronal complement of S if S and A are disjoint and $S\cup A$ is maximal achronal.

By Theorem 2.87 every achronal set S is contained in a maximal achronal set N, hence it admits $N\backslash S$ as an achronal complement. If S is itself a maximal achronal set, then the achronal complement is the empty set.

Definition 2.152

The achronal sets $S_1$ and $S_2$ are chronally equivalent if there is a set A which is an achronal complement for both of them.

Theorem 2.153

The achronal sets $S_1$ and $S_2$ are chronally equivalent iff $S_1\cup I^{+}(S_1)\cup I^{-}(S_1)=S_2\cup I^{+}(S_2)\cup I^{-}(S_2)$. Moreover, in this case $\mathrm {edge}(S_1)=\mathrm {edge}(S_2)$. As a consequence of the first statement the chronal equivalence is an equivalence relation.

Proof

Proof of first statement. Let $p \in S_1\cup I^{+}(S_1)\cup I^{-}(S_1)$ and assume that it does not belong to $S_2\cup I^{+}(S_2)\cup I^{-}(S_2)$. Let us consider the case $p \in I^{-}(S_1)$. There is $p'\in S_1\cap I^{+}(p)$ and $p'\notin S_2 \cup I^{-}(S_2)$ for otherwise $p\in I^{-}(S_2)$. But $p' \notin A$ because $S_1$ and A are disjoint, moreover, $p'\notin I^{+}(A)\cup I^{-}(A)$, because $S_1 \cup A$ is achronal, thus since $S_2 \cup A$ is maximal achronal (Theorem 2.146)

$$\begin{aligned} M&=(S_2\cup A)\cup I^{+}(S_2\cup A) \cup I^{-}(S_2\cup A) \\&=[S_2\cup I^{+}(S_2)\cup I^{-}(S_2)]\cup [A\cup I^{+}(A)\cup I^{-}(A)] , \end{aligned}$$

we have $p' \in I^{+}(S_2)$. But $p \notin I^{+}(S_2)$ thus if $\sigma$ is a timelike curve connecting p to $p'$, there is $z \in \dot{I}^{+}(S_2)\cap \sigma$. Note that $z \ne p'$ but we can have $z=p$. Note also that $z\notin S_2$ because $p\notin S_2\cup I^{-}(S_2)$, and $z \notin I^{-}(S_2)$ because $z \in \overline{I^{+}(S_2)}$ and $S_2$ is achronal. Since $S_2 \cup A$ is maximal achronal and $z \notin S_2\cup I^{+}(S_2)\cup I^{-}(S_2)$ we have $z \in A\cup I^{+}(A)\cup I^{-}(A)$. However, we can’t have $z \in I^{-}(A)$ for $z \in \overline{I^{+}(S_2)}$ and $S_2\cup A$ is achronal, nor we can have $z \in A\cup I^{+}(A)$ for in this case $p' \in S_1\cap I^{+}(z)\subset S_1\cap I^{+}(A)$, which is impossible because $S_1\cup A$ is achronal. The contradiction proves that it can’t be $p \in I^{-}(S_1)$. An analogous contradiction is obtained assuming $p \in I^{+}(S_1)$. Let us consider the case $p \in S_1$. Since $S_1\cup A$ is achronal and $S_1\cap A=\emptyset$, we have $p \notin A\cup I^{+}(A)\cup I^{-}(A)$. In conjunction with $p\notin S_2\cup I^{+}(S_2)\cup I^{-}(S_2)$ this implies that $S_2 \cup A$ is not maximal achronal, a contradiction. In conclusion we have proved $S_1\cup I^{+}(S_1)\cup I^{-}(S_1)\subset S_2\cup I^{+}(S_2)\cup I^{-}(S_2)$, the other direction being similar.

Let us now prove that if $S_1$ and $S_2$ are achronal and $S_1\cup I^{+}(S_1)\cup I^{-}(S_1) = S_2\cup I^{+}(S_2)\cup I^{-}(S_2)$ then they are chronally equivalent. Let A be any achronal complement of $S_1$. Since $S_1\cup A$ is achronal and $S_1\cap A=\emptyset$ we have $[S_1\cup I^{+}(S_1)\cup I^{-}(S_1)]\cap A=\emptyset$ which reads $[S_2\cup I^{+}(S_2)\cup I^{-}(S_2)]\cap A=\emptyset$ which states that $S_2$ and A are disjoint and $S_2\cup A$ is achronal. If $S_2\cup A$ were not maximal achronal there would be a point outside $S_2\cup A$ not chronologically related to $S_2\cup A$. This point cannot belong to $S_1\cup I^{+}(S_1)\cup I^{-}(S_1)=S_2\cup I^{+}(S_2)\cup I^{-}(S_2)$ for otherwise it would be chronologically related to $S_2$, thus it is also disjoint from $S_1$ and chronologically unrelated to $S_1$, as we know that is is chronologically unrelated to A, we have that it is chronologically unrelated to $S_1\cup A$ in contradiction with the maximal achronality of $S_1\cup A$.

Proof of second statement. Let A be the achronal complement for both $S_1$ and $S_2$. Consider the maximal achronal set $N=S_1\cup A$, then $\mathrm {edge}(S_1)=\partial _N S_1$. But $\partial _N S_1=\partial _N A=\mathrm {edge}(A)$, and by analogous reasoning $\mathrm {edge}(S_2)=\mathrm {edge}(A)$, thus $\mathrm {edge}(S_1)=\mathrm {edge}(S_2)$.

The last statement is trivial. $\square$

Remark 2.154

Let S be achronal. The set $S\cup I^{+}(S)\cup I^{-}(S)$ is the set of points through which there passes an inextendible timelike curve which intersects S. As we shall see more thoroughly in the next section, the definition is similar to that of the (closed) domain of dependence $\tilde{D}(S)$, with the difference that in the last case one demands that every inextendible timelike curve passing through the point intersects S.

For chronally equivalent sets $S_1$ and $S_2$ we can have $\tilde{D}(S_1)\ne \tilde{D}(S_2)$, however we have the following interesting result.

Theorem 2.155

Let $S_1$ and $S_2$ be achronal sets. Assume $\tilde{D}(S_1)= \tilde{D}(S_2)$ then $S_1$ and $S_2$ are chronally equivalent (and hence have the same edge).

Proof

If $p \in S_1\cup I^{+}(S_1)\cup I^{-}(S_1)$ then there is an inextendible timelike curve $\gamma$ which passes through p and intersects $S_1\subset \tilde{D}(S_1)=\tilde{D}(S_2)$. Thus there is $q\in \tilde{D}(S_2)\cap \gamma$, and since $\gamma$ is an inextendible timelike curve passing through $q\in \tilde{D}(S_2)$ it must intersect $S_2$, thus from p there passes a timelike curve $\gamma$ which intersects $S_2$, that is $p \in S_2\cup I^{+}(S_2)\cup I^{-}(S_2)$. The other inclusion is proved similarly. $\square$

3 Domains of dependence

Historically the domain of dependence or Cauchy development of a set S has been introduced in two different versions, depending on whether timelike (Geroch 1970; Penrose 1972) or causal curves (Hawking and Ellis 1973; O’Neill 1983; Wald 1984b; Beem et al. 1996) were used in the definition. It turns out that for S closed the former version is the closure of the latter version (Proposition 3.10). For the reader’s convenience, we shall present how the other constructions, including Cauchy horizons, depend on both versions.

I tend to prefer the causal version, for in general causal curves are better behaved than timelike curves as the limit curve theorem illustrates.

3.1 The one-sided Cauchy development

In this section we study the future and past domains of dependence, in the next section we shall study their union.

Definition 3.1

Let S be any set. The future Cauchy development (future domain of dependence) of S is the set

$$\begin{aligned} D^{+}(S)=\{p\in M:\text {every past inext. causal curve through } p \text { itersects } S \}. \end{aligned}$$

The same name is used for the analogous set

$$\begin{aligned} \tilde{D}^{+}(S)=\{p\in M:{\text {every past inext. timelike curve through }} p {\text { itersects }} S \}. \end{aligned}$$

Remark 3.2

Note that $S\subset D^{+}(S)\subset \tilde{D}^{+}(S)$, thus $D^{+}(S)$ and $\tilde{D}^{+}(S)$ are empty only if S is empty.

We recall that causal and timelike curves are, by definition, piecewise $C^1$.

Proposition 3.3

Let S be an achronal or closed set and let $p\in M$. There is a past inextendible continuous causal curve that does not intersect S iff there is a past inextendible $C^1$ causal curve that does not intersect S. An analogous future version holds. There is an inextendible continuous causal curve that does not intersect S iff there is an inextendible $C^1$ causal curve that does not intersect S.

Proof

From the right to the left it is obvious since every causal curve is a continuous causal curve. Assume there is a past inextendible continuous causal curve $\gamma :(-a,0]\rightarrow M$ ending at p and not intersecting S.

If V is an open set containing $\gamma$, we can cover $\gamma$ with convex sets contained in V, then by the definition of continuous causal curve, we can replace it with a piecewise causal geodesic ending at p and contained in V, finally we can smooth the corners so finding a past inextendible $C^1$ causal curve $\tilde{\gamma }$ ending at p contained in V. Thus if $\gamma \cap \bar{S}=\emptyset$ just take $V=M\backslash \bar{S}$. The proof is concluded if S is closed or achronal with $\gamma \cap \bar{S}=\emptyset$.

Assume instead that S is only achronal and that $\gamma$ intersects $\bar{S}$ and hence $\mathrm {edge}(S)$ (Proposition 2.132).

Note that if $p\in I^{+}(\mathrm {edge}(S))$ then it is easy to construct a past inextendible $C^1$ timelike curve not intersecting S and ending at p. First connect a point $e \in \mathrm {edge}(S)$ to p with a $C^1$ timelike curve $\sigma$, take $y \in I^{+}(e)\cap \sigma$, $x \in I^{-}(e)$, join x to y with a $C^1$ timelike curve that does not intersect S (remember Corollary 2.148), and join the curve segment so obtained with a past inextendible $C^1$ timelike curve ending at x (necessarily not intersecting S otherwise if r is the intersection point, $r\ll e$, and since I is open, S would not be achronal). Finally, smooth out the corners at x and y by noting that this operation does not introduce points in S because $x,y \notin \bar{S}$ again by the achronality of S. (This paragraph read independently of the rest proves that $I^{+}(\mathrm {edge}(S))\cap {\tilde{D}}^+(S)=\emptyset$.)

Thus we can assume that $p\notin I^{+}(\mathrm {edge}(S))$ and that $\gamma$ intersects $\bar{S}$ and hence $\mathrm {edge}(S)$. If $r\in \mathrm {edge}(S)$ is one such intersection point then $\gamma$ between r and p is achronal, and hence a $C^1$ lightlike geodesic, otherwise $p\in I^{+}(\mathrm {edge}(S))$.

If $\gamma$ is partially past imprisoned in $\bar{S}$ (i.e. it returns to $\bar{S}$ indefinitely into the past, notice that we do not assume $\bar{S}$ compact) then we conclude that it is a lightlike ray (hence $C^1$), and we have finished.

If it is not partially past imprisoned in ${\bar{S}}$ a similar argument proves that between p and the last (in the past direction) intersection point r with $\bar{S}$ the curve $\gamma$ is an achronal lightlike geodesic, hence $C^1$. Finally we have only to continue $\gamma$ after r in a $C^1$ way but in the junction point where the tangent could be causal. The curve cannot intersect S again by achronality of S (i.e. $\bar{S}$). $\square$

Corollary 3.4

If the set S is closed or achronal, in the definition of $D^{+}(S)$ causal curve can be replaced with continuous causal curve or $C^1$ causal curve.

This corollary is important for applications of the limit curve theorem, which in most cases establish the existence of a limit continuous causal curve.

Example 3.5

Let (M, g) be $1+1$ Minkowski spacetime and let S be a full square without a non-piecewise $C^1$ continuous causal curve running from the bottom of the box to the top, then the domain of dependence is different depending on whether continuous causal curves or causal curves are used in the definition. See also Remark 5.2 of Penrose (1972).

Remark 3.6

The definition of $\tilde{D}^{+}(S)$ is given only in the piecewise $C^1$ version because there is no satisfactory notion of continuous timelike curve (Remark 2.15).

Proposition 3.7

If S is achronal, $I^{+}(\mathrm {edge}(S))\cap {\tilde{D}}^+(S)=\emptyset$.

Proof

This result is proved in the fourth paragraph of the proof of Theorem 3.3. $\square$

Lemma 3.8

If S is achronal, $\tilde{D}^{+}(S)\cap \tilde{D}^{-}(S)={D}^{+}(S)\cap {D}^{-}(S)=S$.

Proof

Since $S\subset D^{+}(S)\subset \tilde{D}^{+}(S)$, we have only to prove $\tilde{D}^{+}(S)\cap \tilde{D}^{-}(S)\subset S$. If $p \in [\tilde{D}^{+}(S)\cap \tilde{D}^{-}(S)]\backslash S$ then $p \in I^{+}(S)\cap I^{-}(S)$ that is S is not achronal. $\square$

Lemma 3.9

(Avoidance Lemma) Let S be a closed set, if $p \in D^{+}(S)^{C}$ then $I^{+}_{M\backslash S}(p) \subset \tilde{D}^{+}(S)^{C}$.

Proof

The argument is that of Hawking and Ellis (1973, Proposition 6.5.1), see also O’Neill (1983, p. 416, Lemma 30). Let $\gamma :(a,0]\rightarrow M$ be a past inextendible causal curve ending at p and not intersecting S. Let $p_n=\gamma (a_n)$, $a_{n+1}<a_n$, $n\ge 1$, be a sequence of points not converging to any point. They exist because $\gamma$ is past inextendible. Let h be an auxiliary complete Riemannian metric. Denote $p=p_0$, and let $q(=q_0) \in I^{+}_{M\backslash S}(p)$. Clearly $p_1\in I^{-}_{M\backslash S}(q_0)$, thus take $q_1$ so that it stays in the timelike curve connecting $p_1$ to $q_0$ and not intersecting S, so that its h-distance from $p_1$ is less then 1. Continue in this way by choosing $q_{n+1}$ in the timelike curve connecting $p_{n+1}$ to $q_n$ and not intersecting S, so that its h-distance from $p_{n+1}$ is less then $1/(n+1)$. This way we have constructed a timelike curve $\sigma$ joining the points $q_n$, that does not intersect S, which ends at q and which is past inextendible, indeed we cannot have $q_n \rightarrow r$, otherwise $p_n \rightarrow r$ a contradiction. Thus $q\in \tilde{D}^{+}(S)^{C}$. $\square$

Proposition 3.10

Let S be a closed set then $\overline{D^{+}(S)}=\tilde{D}^{+}(S)$, $\mathrm {Int}\, \tilde{D}^{+}(S)=\mathrm {Int}\, D^{+}(S)$ and $\dot{\tilde{D}}^{+}(S)=\dot{D}^{+}(S)$.

Proof

The proof of the first statement can also be found in Hawking and Ellis (1973, Proposition 6.5.1).

If $q \in M\backslash \tilde{D}^{+}(S)$ at q ends a past inextendible timelike curve $\eta$ not intersecting S. Let U be an open neighborhood of q that does not intersect S. For all the points $q'\in I^+(r, U)$ where $r \in \eta \backslash \{q\}\cap U$ we can find a past inextendible timelike curve $\eta '$ ending at $q'$ not intersecting S. As $I^+(r,U)$ is an open neighborhood of q, and $I^+(r,U) \subset M\backslash \tilde{D}^{+}(S)$, $\tilde{D}^{+}(S)$ is closed.

Suppose there were a point $p \in \tilde{D}^{+}(S)$ which had a neighborhood V which did not intersect $D^+(S)$ (and hence S). Choose a point $x \in I^{-}(p,V)$. Since $x \notin D^{+}(S)$ by Proposition 3.9 $p \notin \tilde{D}^{+}(S)$ a contradiction. Thus $\tilde{D}^{+}(S)=\overline{D^{+}(S)}$.

Since $D^{+}(S)\subset \tilde{D}^{+}(S)$, we have $\mathrm {Int}\, \tilde{D}^{+}(S)\supset \mathrm {Int}\, D^{+}(S)$. Let $p\in \mathrm {Int}\, \tilde{D}^{+}(S)$, and let $U\ni p$ be a neighborhood such that $U \subset \mathrm {Int}\, \tilde{D}^{+}(S)$. Take $q \in U$, if $q \notin D^{+}(S)$ then $q\notin S$ and any $r \in I^{+}(q,U\backslash S)$ is such that $r \notin \tilde{D}^{+}(S)$ (Lemma 3.9) a contradiction. Thus $U \subset D^{+}(S)$ and hence $\mathrm {Int}\, \tilde{D}^{+}(S)\subset D^{+}(S)$ from which it follows $\mathrm {Int}\, \tilde{D}^{+}(S)\subset \mathrm {Int}\, D^{+}(S)$. The equality of the boundaries is a trivial consequence of the previous ones. $\square$

Remark 3.11

Suppose that S is achronal and non-closed. Every past inextendible timelike curve ending at $p\in {\bar{S}}\backslash S$ cannot intersect S by the achronality of ${\bar{S}}$, thus $({\bar{S}}\backslash S)\cap {\tilde{D}}^+(S)=\emptyset$. Since $S\subset {\tilde{D}}^+(S)$, the result proves that ${\tilde{D}}^+(S)$ is not closed. Therefore, even under achronality the condition of S being closed cannot be dropped in Proposition 3.10.

Proposition 3.12

Let S be a closed set, it holds $I^{-}(D^{+}(S))=I^{-}(\tilde{D}^{+}(S))$.

Proof

Since $D^{+}(S)\subset \tilde{D}^{+}(S)$ $\Rightarrow I^{-}(D^{+}(S)) \subset I^{-}(\tilde{D}^{+}(S))$. Let $p \in I^{-}(\tilde{D}^{+}(S))$ then there is $q \in \tilde{D}^{+}(S)$, $p \ll q$. Since $\tilde{D}^{+}(S)=\overline{D^+(S)}$ and I is open we can find $q'\in D^+(S)$ such that $p\ll q'$, thus $I^{-}(\tilde{D}^{+}(S))\subset I^{-}( D^+(S))$. $\square$

Proposition 3.13

Let S be a closed set. The sets $P(S)=D^{+}(S)\cup I^{-}(S)$ and $\tilde{P}(S)=\tilde{D}^{+}(S)\cup I^{-}(S)$ are past sets. Moreover,

$$\begin{aligned} \mathrm {Int}\,P(S)&= \mathrm {Int}\,\tilde{P}(S)=I^{-}(P(S))=I^{-}(\tilde{P}(S))=I^{-}(D^{+}(S)), \\ \overline{P(S)}&=\overline{\tilde{P}(S)}=\overline{I^{-}(P(S))}=\overline{I^{-}(\tilde{P}(S))}=\overline{I^{-}(D^{+}(S))}, \\ \dot{P}(S)&=\dot{\tilde{P}}(S)=\partial ({I^{-}(D^{+}(S))}). \end{aligned}$$

Analogous results hold for the future sets $F(S)=D^{-}(S)\cup I^{+}(S)$ and $\tilde{F}(S)=\tilde{D}^{-}(S)\cup I^{+}(S)$.

Proof

Let us first prove that $D^{+}(S)\cup I^{-}(S)$ is a past set. If $p\in S\cup I^{-}(S)$ then $I^{-}(p) \subset I^{-}(S)\subset D^{+}(S)\cup I^{-}(S)$. Let $p \in D^{+}(S)\backslash S$, and consider $q \in I^{-}(p)$. If $q \in S \cup I^{-}(S)$ there is nothing to prove because $S\cup I^{-}(S)\subset D^{+}(S)\cup I^{-}(S)$. If $q \notin S \cup I^{-}(S)$ we are able to prove that every past-inextendible causal curve through q must intersect S. Suppose not. Recall $q \ll p$ and the (actually every) timelike curve which connects q to p cannot intersect S otherwise $q \in I^{-}(S)\cup S$. Thus, joining the two curves we get a past-inextendible causal curve through p which does not intersect S, a contradiction with $p \in D^{+}(S)\backslash S$. Thus $q \in D^{+}(S)\subset D^{+}(S)\cup I^{-}(S)$.

Let us prove that $\tilde{D}^{+}(S)\cup I^{-}(S)$ is a past set. This follows from $I^{-}(D^{+}(S))=I^{-}(\tilde{D}^{+}(S))$ and the fact that $D^{+}(S)\cup I^{-}(S)$ is a past set

$$\begin{aligned} I^{-}(\tilde{D}^{+}(S)\cup I^{-}(S))&=I^{-}(\tilde{D}^{+}(S))\cup I^{-}(S)=I^{-}(D^{+}(S))\cup I^{-}(S)\\&=I^{-}(D^{+}(S)\cup I^{-}(S))\subset D^{+}(S)\cup I^{-}(S)\\&\subset \tilde{D}^{+}(S)\cup I^{-}(S). \end{aligned}$$

The equations in display follow from $I^{-}(P(S))=I^{-}(\tilde{P}(S))=I^{-}(D^{+}(S))$ and from the already obtained results on past sets (Proposition 2.84). $\square$

Definition 3.14

Let S be a closed set. The future Cauchy horizon of S is the closed set

$$\begin{aligned} H^{+}(S)=\overline{D^{+}(S)}\,\backslash I^{-}(D^{+}(S))=\tilde{D}^{+}(S)\backslash I^{-}(\tilde{D}^{+}(S)). \end{aligned}$$

The latter equality follows from Propositions 3.10 and 3.12.

Proposition 3.15

The set $H^{+}(S)$ is achronal.

Proof

If $p,q \in H^{+}(S)$, $p\ll q$, then since $q \in \tilde{D}^{+}(S)$ we have $p \in I^{-}(\tilde{D}^{+}(S))$ which is impossible since $p \in H^{+}(S)=\tilde{D}^{+}(S)\backslash I^{-}(\tilde{D}^{+}(S))$. $\square$

Proposition 3.16

If S is achronal, then $\overline{D^{+}(S)}\cap I^{-}(S) =\emptyset$. If S is closed and achronal, then

$$\begin{aligned} \mathrm {Int} \, D^{+}(S)&=I^{+}(S)\cap I^{-}(D^{+}(S)), \end{aligned}$$

(3.1)

$$\begin{aligned} \dot{D}^{+}(S)&=S\cup H^{+}(S), \end{aligned}$$

(3.2)

$$\begin{aligned} S\backslash H^{+}(S)&=S\cap I^{-}(D^{+}(S)), \end{aligned}$$

(3.3)

$$\begin{aligned} H^{+}(S)\backslash S&=H^{+}(S)\cap I^{+}(S) , \end{aligned}$$

(3.4)

$$\begin{aligned} {\tilde{D}}^+(S)&=D^+(S)\cup H^+(S). \end{aligned}$$

(3.5)

Proof

First $I^{-}(S)\cap S=\emptyset$ because S is achronal. If $z \in D^{+}(S) \cap I^{-}(S)$ then there is through z a past-inextendible causal curve which intersects S, thus S is not achronal. The contradiction proves that $D^{+}(S) \cap I^{-}(S)=\emptyset$ and since $I^{-}(S)$ is open the equation $\overline{D^{+}(S)}\cap I^{-}(S) =\emptyset$ follows.

Let $p \in \mathrm {Int} \, D^{+}(S)$ and take $q \in I^{+}(p, \mathrm {Int} \, D^{+}(S))$, then $p\in I^{-}(q)\subset I^{-}(D^{+}(S))$. Analogously, taking $r \in I^{-}(p, \mathrm {Int} \, D^{+}(S))$ either $r \in S$ or there is a causal curve which connects S to r. In both cases $p \in I^{+}(S)$, thus $\mathrm {Int} \, D^{+}(S)\subset I^{+}(S)\cap I^{-}(D^{+}(S))$. For the converse, let $q\in I^{+}(S)\cap I^{-}(D^{+}(S))$ and let $p\in D^{+}(S)$ be the point such that $q\in I^{-}(p)$. The set $V=I^{+}(S)\cap I^{-}(p)$ is a neighborhood of q contained in $D^{+}(S)$. Indeed, if $z \in V\cap D^{+}(S)^{C}$ there is a past-inextendible causal curve through z which does not intersect S, hence every timelike curve which connects z to p must intersect S as $p \in D^{+}(S)$. But since $z \in I^{+}(S)$, S is not achronal. The contradiction proves that $V \subset D^{+}(S)$ and hence $I^{+}(S)\cap I^{-}(D^{+}(S)) \subset \mathrm {Int} \, D^{+}(S)$.

Let $q \in H^{+}(S)=\overline{D^{+}(S)}\,\backslash I^{-}(D^{+}(S))$ and let $U\ni q$ be an arbitrary neighborhood. Any point $r \in I^{+}(q,U)$ is such that $r \notin D^{+}(S)$ otherwise $q \in I^{-}(D^{+}(S))$, which is impossible. Since $q \in \overline{D^{+}(S)}$ and its neighborhoods contain points of $D^{+}(S)^C$ we have $q \in \dot{D}^{+}(S)$. If $q \in S\subset D^{+}(S)$, then $I^{-}(q)\subset D^{+}(S)^C$ (because $D^{+}(S)\cap I^{-}(S) =\emptyset$), which implies $q \in \overline{I^{-}(q)}\subset \overline{D^{+}(S)^C}$, thus $q \in \dot{D}^{+}(S)$. We conclude $H^{+}(S)\cup S\subset \dot{D}^{+}(S)$. For the converse we have to show that $\dot{D}^{+}(S)\subset S \cup H^{+}(S)$. If $q \in \dot{D}^{+}(S)\backslash \{S\cup H^{+}(S)\}$ then $q \in \tilde{D}^{+}(S)\backslash S$ and hence $q \in I^{+}(S)$. Moreover, $q \in \overline{D^{+}(S)}\backslash H^{+}(S)$ thus, by definition of $H^{+}(S)$, $q \in I^{-}(D^{+}(S))$ and hence $q\in I^{+}(S)\cap I^{-}(D^{+}(S))=\mathrm {Int}\, D^{+}(S)$ a contradiction because $q \in \dot{D}^{+}(S)$.

For Eq. (3.3), $S\cap I^{-}(D^{+}(S))\subset S\backslash H^{+}(S)$ is obvious. For the converse $S\backslash H^{+}(S)\subset D^+(S) \backslash H^{+}(S) \subset I^{-}(D^{+}(S))$, thus $S\backslash H^{+}(S) \subset S\cap I^{-}(D^{+}(S))$.

For Eq. (3.4), $H^{+}(S)\backslash S\subset \tilde{D}^{+}(S)\backslash S\subset I^{+}(S)$. For the converse, $H^{+}(S) \cap I^{+}(S)$ does not contain points in S because S is achronal, thus $H^{+}(S) \cap I^{+}(S)\subset H^{+}(S)\backslash S$.

The last equality follows from Proposition 3.10. $\square$

Remark 3.17

We can have $\partial \mathrm {Int} \, D^{+}(S)\ne \partial {D}^{+}(S)$, consider the case in which $S\cap H^{+}(S)\ne \mathrm {edge}(S)$, e.g. let S be a subset of $1+1$ Minkowski spacetime obtained by joining a spacelike geodesic segment to the future endpoint of a lightlike geodesic segment.

Corollary 3.18

Let S be a closed and achronal set. Then $\mathrm {Int} \,D^{+}(S)= \emptyset$ if and only if $H^{+}(S)=S$.

Proof

Assume $\mathrm {Int} D^{+}(S)=\emptyset$, that is, $\mathrm {Int} \tilde{D}^{+}(S)=\emptyset$. If $p\in H^{+}(S)\backslash S$, then $p \in \tilde{D}^{+}(S)\backslash S$ and thus there is a past-inextendible timelike curve $\sigma$ connecting a point $q \in S$ to p. Taking r between q and p on $\sigma$, $r \in I^{-}(\tilde{D}^{+}(S))\cap I^{+}(S)=\mathrm {Int} \tilde{D}^{+}(S)$, a contradiction.

If $H^{+}(S)=S$ and $p \in \mathrm {Int} \tilde{D}^{+}(S)$ then there is a past-inextendible timelike curve which intersects $q\in S$, thus $q \in I^{-}(p) \subset I^{-}(\tilde{D}^{+}(S))$, thus $q \notin H^{+}(S)$ while $q\in S$, a contradiction. $\square$

Proposition 3.19

For a closed and achronal set S we have

$$\begin{aligned} J^{+}(S)\cap I^{-}(D^{+}(S))= \mathrm {Int} D^{+}(S)\cup [S\backslash H^{+}(S)]. \end{aligned}$$

Proof

Let us prove the inclusion $J^{+}(S)\cap I^{-}(D^{+}(S))\subset \mathrm {Int} D^{+}(S)\cup [S\backslash H^{+}(S)]$. Let $r \in J^{+}(S)\cap I^{-}(D^{+}(S))$, there are $p\in S$ and $q \in D^{+}(S)$ such that $r \in J^{+}(p)\cap I^{-}(q)$. Join a causal curve connecting p to r with a timelike curve connecting r to q. Clearly $q\notin S$ because S is achronal. If $q \notin \mathrm {Int} D^{+}(S)$ then by Eq. (3.2) $q\in H^{+}(S)\backslash S$. Let $U\ni q$ be an open neighborhood not intersecting S, by Lemma 3.9 $I^{-}(q,U)\subset D^{+}(S)$ and since this is an open set $I^{-}(q,U)\subset \mathrm {Int} D^{+}(S)$. Thus there is $\tilde{q}\in I^{-}(q,U)\subset \mathrm {Int} D^{+}(S)$ such that $r \in J^{+}(p)\cap I^{-}(\tilde{q})$. In other words we can assume $q \in \mathrm {Int} D^{+}(S)$. Join the causal curve connecting p to r with the timelike curve connecting r to q. Starting from q in the past direction, this curve escapes $\mathrm {Int} D^{+}(S)$ (indeed it intersects S at p) at a first point $\tilde{p}$ necessarily belonging to S (it cannot belong to $H^{+}(S)$ as $\tilde{p} \in I^{-}(D^{+}(S)))$. If r comes before $\tilde{p}$ (in the past direction) $r \in \mathrm {Int} D^{+}(S)$, if it coincides with $\tilde{p}$ then $r \in S\backslash H^{+}(S)$ and we have finished. If r comes after $\tilde{p}$ then $\tilde{p}\ne p$. But since the curve joining r to q is timelike so is the segment joining r to $\tilde{p}$, thus $p \ll \tilde{p}$ against the achronality of S.

Given Proposition 3.16, the other direction is trivial. $\square$

The following corollary follow from the openness of $I^{-}(D^{+}(S))$.

Corollary 3.20

Let S be closed and achronal. Every causal curve starting from $S\backslash H^{+}(S)$ has an initial non-degenerate segment in $\mathrm {Int} D^{+}(S)\cup [S\backslash H^{+}(S)]\subset D^+(S)$, and every timelike curve starting from $S\backslash H^{+}(S)$ has an initial non-degenerate segment in $\mathrm {Int} D^{+}(S)$ (save for the starting point).

Proof

By Proposition 3.19 every point $p\in S\backslash H^{+}(S)$ belongs to $I^{-}(D^{+}(S))$ which is open, so the same is true for points on a causal curve passing through p provided they are sufficiently close to p. Using again Proposition 3.19 we get the first statement. The second statement is proved similarly. $\square$

Corollary 3.21

Let S be closed and achronal, then $H^{+}(S)=\emptyset$ if and only if $S\cup I^{+}(S)=\tilde{D}^{+}(S)$.

Proof

Assume $S\cup I^{+}(S)=\tilde{D}^{+}(S)$. Let $p\in \tilde{D}^{+}(S)$ and take any $q \in I^{+}(p)$, so that $q \in I^{+}(S)\subset \tilde{D}^{+}(S)$ and thus $p \in I^{-}(\tilde{D}^{+}(S))$, which implies $H^{+}(S)=\emptyset$.

Assume $H^{+}(S)=\emptyset$. The inclusion $\tilde{D}^{+}(S) \subset S\cup I^{+}(S)$ is obvious. We already know that $S\subset \tilde{D}^{+}(S)$, thus it is sufficient to prove that $I^+(S)\backslash \tilde{D}^{+}(S)$ is empty. If $q \in I^{+}(p)\backslash \tilde{D}^{+}(S)$, $p\in S$, then the timelike curve joining p to q must intersect $\tilde{D}^{+}(S)$ at a last point r, thus $r \in \dot{D}^{+}(S)=S\cup H^{+}(S)$. If $r \in S\backslash H^{+}(S)$, because of the achronality of S, $r=p$, which is impossible because every causal curve issued from $S\backslash H^{+}(S)$ has a non-degenerate segment contained in $D^{+}(S)$. We conclude $r \in H^{+}(S)$, a contradiction which proves $I^{+}(S)\subset \tilde{D}^{+}(S)$. $\square$

Proposition 3.22

For a closed achronal set S, $\mathrm {edge}( H^{+}(S))=\mathrm {edge} (S)$.

Proof

We have $\mathrm {edge} (S)\subset S\subset \tilde{D}^{+}(S)$. By Proposition 3.7 $I^{+}(\mathrm {edge}(S))\cap \tilde{D}^{+}(S)=\emptyset$, that is, $\mathrm {edge}(S) \cap I^{-}(\tilde{D}^{+}(S))=\emptyset$, thus

$$\begin{aligned} \mathrm {edge}(S)\subset \tilde{D}^{+}(S)\backslash I^{-}(\tilde{D}^{+}(S))=H^{+}(S). \end{aligned}$$

We have to show that actually $\mathrm {edge}(S)\subset \mathrm {edge}(H^{+}(S))$. If $q \in \mathrm {edge}(S)\subset H^{+}(S)$ for any open set $U\ni q$, and for every $p \in I^{-}(q,U)$, $r \in I^{+}(q,U)$ there is a timelike curve connecting p to r in U not intersecting S. But this curve cannot intersect $H^{+}(S)$ at a point y. – Indeed, assume it does intersect $H^{+}(S)$. It would be possible to connect p to y with a timelike curve $\sigma$ not intersecting S. If $\gamma$ is a past-inextendible timelike curve ending at p, then it cannot intersect S because otherwise the intersection point would be chronologically related to q in contradiction with the achronality of S. Thus $\sigma \circ \gamma$ is a past-inextendible timelike curve not intersecting S ending at $y \in H^{+}(S)\subset \tilde{D}^{+}(S)$ a contradiction. – Thus since U, p, r, are arbitrary and $q \in H^{+}(S)$, we have $q \in \mathrm {edge}(H^{+}(S))$.

For the converse let $q \in \mathrm {edge}(H^{+}(S))\subset H^+(S)$. For every $U\ni q$, $r\in I^{+}(q,U)$, $p \in I^{-}(q,U)$, there is a timelike curve $\sigma$ contained in U joining p to r which does not intersect $H^{+}(S)$. Clearly, $r \notin \tilde{D}^{+}(S)$ otherwise $q \in I^{-}(\tilde{D}^{+}(S))$, which is impossible. As a consequence $\sigma$ does not intersect $\mathrm {Int}\tilde{D}^{+}(S)\subset I^{+}(S)$ as it would have to escape from this set and since $\dot{\tilde{D}}^{+}(S)=S\cup H^{+}(S)$, and S is achronal, it would have to intersect $H^{+}(S)$ in the future of the intersection point. Nor can it intersect $S\backslash \mathrm {Int}\tilde{D}^{+}(S)$, because an intersection point y, necessarily before r, would imply that the points in $\sigma$ in the future of y belong to $I^{+}(S)$ and hence since they cannot belong to $\mathrm {Int}\tilde{D}^{+}(S)$ they belong to $I^{-}(\tilde{D}^{+}(S))^C$ (recall Eq. (3.1)), which being closed implies $y \in I^{-}(\tilde{D}^{+}(S))^C$ and hence $y \in S\backslash I^{-}(\tilde{D}^{+}(S))\subset H^{+}(S)$. We conclude that $\sigma$ does not intersect $\tilde{D}^{+}(S)=S \cup \mathrm {Int}\tilde{D}^{+}(S)\cup H^{+}(S)$. Using the fact that $\tilde{D}^{+}(S)\cup I^{-}(S)$ is a past set

$$\begin{aligned} I^{-}(q)\subset I^{-}(\tilde{D}^{+}(S))\subset \tilde{D}^{+}(S)\cup I^{-}(S), \end{aligned}$$

thus since $p\in \sigma$, we have $p \in I^{-}(S)$. Let $\gamma$ be a past-inextendible timelike curve ending at p. Since S is achronal it does not intersect S, but $q\in \tilde{D}^{+}(S)$ thus every timelike curve in U joining p to q intersects S. As U could be chosen arbitrarily small and S is closed, $q \in S$. Moreover, we proved that $\sigma$ does not intersect S hence $q \in \mathrm {edge}(S)$. $\square$

We recall that $P(S)=D^{+}(S)\cup I^{-}(S)$ is a past set, cf. Proposition 3.13.

Proposition 3.23

If S is closed and achronal, $\dot{P}(S)= H^{+}(S)\cup \{\dot{I}^{-}(S)\backslash S\}$ where the two sets on the right-hand side are disjoint. If S is also edgeless then $E^+(S)=E^-(S)=S$ and the sets $H^{+}(S)$, $\dot{I}^{-}(S)\backslash S$, are closed components of the achronal boundary $\dot{P}(S)$, hence achronal locally Lipschitz topological hypersurfaces. They can themselves be regarded as achronal boundaries in the spacetimes $\{\dot{I}^{-}(S)\backslash S\}^C$ or $H^{+}(S)^{C}$, with the induced metric.

Proof

By Proposition 3.13 P(S) is a past set. Moreover,

$$\begin{aligned} \dot{P}(S)&=\overline{D^{+}(S)\cup I^{-}(S)}\backslash I^{-}(D^{+}(S)) = [\overline{D^{+}(S)}\cup \overline{I^{-}(S)}]\backslash I^{-}(D^{+}(S))\\&= H^{+}(S)\cup \{\overline{I^{-}(S)} \backslash I^{-}(D^{+}(S))\}. \end{aligned}$$

Since $D^{+}(S)\supset S$, we have $I^{-}(D^{+}(S))\supset I^{-}(S)$. By Eq. (3.3) $S\backslash H^{+}(S) \subset I^{-}(D^{+}(S))$, which implies $S \subset I^{-}(D^{+}(S))\cup H^{+}(S)$, and hence $S\cup I^{-}(S) \subset I^{-}(D^{+}(S))\cup H^{+}(S)$. Thus

$$\begin{aligned} \dot{P}(S)&=H^{+}(S)\cup \overline{I^{-}(S)} \backslash \{ I^{-}(D^{+}(S))\cup H^{+}(S)\}\\&\subset H^{+}(S)\cup \overline{I^{-}(S)} \backslash \{I^{-}(S)\cup S\}\subset H^{+}(S)\cup \{ \dot{I}^{-}(S)\backslash S\} . \end{aligned}$$

Conversely, $H^{+}(S)=\tilde{D}^{+}(S)\backslash I^{-}(\tilde{D}^{+}(S))=\tilde{D}^{+}(S)\backslash \text {Int} P(S)$. Note that if $p \in \tilde{D}^{+}(S)$ then its past belongs to $I^{-}(\tilde{D}^{+}(S))\subset I^{-}( P(S))\subset P(S)$, thus since P(S) is a past set $p \in \overline{P(S)}$, that is, $\tilde{D}^{+}(S)\subset \overline{P(S)}$, and $H^{+}(S)=\tilde{D}^{+}(S)\backslash \text {Int} P(S)\subset \overline{P(S)}\backslash \text {Int} P(S)=\dot{P}(S)$. Now, note that $I^{-}(S) \subset P(S)=D^{+}(S)\cup I^{-}(S)$, thus $\overline{I^{-}(S)}\subset \overline{P(S)}$ and, since $\text {Int} P(S)=I^{-}(D^{+}(S))$, we have $\overline{I^{-}(S)}\backslash I^{-}(D^{+}(S))\subset \dot{P}(S)$. If $r\in I^{-}(D^{+}(S))$ then $r \in S \cup I^{+}(S)\cup I^{-}(S)$ because if not there would be a past inextendible causal curve from a point of $D^{+}(S)$ passing from r and not intersecting S. Note also that $\overline{I^{-}(S)}$ does not intersect $I^{+}(S)$ because of the achronality of S, hence $I^{-}(D^{+}(S)) \cap \overline{I^{-}(S)} \subset S \cup I^{-}(S)$ and $\dot{I}^{-}(S)\backslash S=\overline{I^{-}(S)}\backslash \{S\cup I^{-}(S)\}\subset \overline{I^{-}(S)}\backslash I^{-}(D^{+}(S)) \subset \dot{P}(S)$. The identity is proved.

Let us show that $H^{+}(S)$ and $\dot{I}^{-}(S)\backslash S$ are disjoint. Let $p\in H^{+}(S)$, if $p \in S$ then $p \notin \dot{I}^{-}(S)\backslash S$ and there is nothing to prove. If $p \in H^{+}(S)\backslash S\subset \tilde{D}^{+}(S)\backslash S$ then $p \in I^{+}(S)$ and hence $p\notin \dot{I}^{-}(S)$ otherwise, since I is open, S would not be achronal.

The last statement is a consequence of Theorem 2.149 which proves that $E^\pm (S)=S$ and that $\dot{I}^-(S)\backslash S$ is closed. $\square$

Theorem 3.24

Let S be a closed achronal set. Let $p\in H^{+}(S)\backslash \mathrm {edge}(S)$ then there is a maximizing lightlike geodesic with p as future endpoint which is entirely contained in $H^{+}(S)$ and is either past-inextendible or has past endpoint at $\mathrm {edge}(S)$. Moreover, the geodesic remains in S once it enters it (moving in the past direction).

Proof

The strategy is to prove that (A): at $p \in H^{+}(S)\backslash \mathrm {edge}(S)$ ends a causal curve entirely contained in $H^{+}(S)$. Assume we proved this result. By the achronality of $H^{+}(S)$ this causal curve is necessarily a maximizing lightlike geodesic. There is a maximal causal curve of this type which we denote $\sigma$. If it is past inextendible there is nothing to prove, if it has a last (in the past direction) point $q \in H^+(S)$ then this point must belong to $\mathrm {edge}(S)$ otherwise one can repeat the argument to infer that there is a segment of causal curve in $H^{+}(S)$ of endpoint q which, by the achronality of $H^{+}(S)$, is necessarily a prolongation of $\sigma$ in contradiction with the maximality of $\sigma$.

Let us prove (A). Let $p_n \rightarrow p$, with $p_n \gg p$, since $p \in H^{+}(S)$ none of the $p_n$ lies in $\tilde{D}^{+}(S)$ otherwise $p \in I^{-}(\tilde{D}^{+}(S))$. Therefore there is a corresponding sequence of past-inextendible timelike curves $\sigma _n$ ending at $p_n$ and not intersecting S. In particular they do not enter $\tilde{D}^{+}(S)$ otherwise they would be forced to intersect S. By the limit curve theorem through p there passes a past-inextendible causal curve $\sigma$ which belongs to $\overline{\tilde{D}^{+}(S)^C}$.

Now, let us consider the two cases $p \notin S$, and $p\in S$.

In the former case, since $p \in \tilde{D}^{+}(S)\backslash S$, we have $p\in I^{+}(S)$. The portion $\sigma '=\sigma \cap I^{+}(S)$ is contained in $H^{+}(S)$, indeed if $q \in \sigma '$ then it is possible to find $r \in I^{-}(q)\cap I^{+}(S)$, thus $r \in I^{-}(p)\cap I^{+}(S)\subset I^{-}(\tilde{D}^{+}(S))\cap I^{+}(S)=\text {Int}\, \tilde{D}^{+}(S)$. Taking $r \rightarrow q$ we conclude $q \in \overline{D^{+}(S)}$. But no point of $I^{+}(q)$ is in $\tilde{D}^{+}(S)$, for otherwise q would be in $I^{-}(\tilde{D}^{+}(S))\cap I^{+}(S)=\text {Int}\, \tilde{D}^{+}(S)$ and at least some $\sigma _n$ would enter $\tilde{D}^{+}(S)$. Thus $q \notin I^{-}(\tilde{D}^{+}(S))$ and hence $q \in H^{+}(S)$. Suppose that there is a first escaping point x of $\sigma$ from $I^+(S)$ (in the past direction), otherwise we have finished, then $x\in H^{+}(S) \subset {\tilde{D}}^+(S)$, thus we must have $x\in S$, otherwise $x\in I^+(S)$, which is a contradiction. If $x \in \mathrm {edge}(S)$ we have finished otherwise we argue as in the following paragraph with p replaced by x.

For the latter case recall that $\text {edge}(S)=S\cap \overline{\dot{I}{^{-}(S)}\backslash S}$, thus $p\in S\backslash \text {edge}(S)$ admits an open relatively compact non-imprisoning neighborhood V such that $V\cap [\dot{I}{^{-}(S)}\backslash S]=\emptyset$. Then the connected segments $\sigma '_n$, of the curves $\sigma _n$ in V which end at $p_n$, do not have any point in $I^{-}(S)\cap V$. Indeed, otherwise since $p_n \in I^{+}(p)\subset I^{+}(S)$ and S is achronal, there would be a point in $\dot{I}^{-}(S)$ necessarily not belonging to S (as it belongs to some $\sigma '_n$) i.e. we would have a point of $\dot{I}{^{-}(S)}\backslash S$ in V.

The segments $\sigma '_n$ belong to the future set $F=(\tilde{D}^{+}(S)\cup I^{-}(S))^{C}$ and have a past endpoint on the compact boundary of V. The limit curve $\sigma '$ has future endpoint p and past endpoint in the boundary $\dot{V}$. In the next paragraph we prove that there is a segment of this curve ending at p which is contained in S. From the second statement of Corollary 3.20 if some point of the segment were to belong to $S\backslash H^+(S)$, the curves $\sigma '_n$ would intersect $I^{-}(D^+(S))$. Since we know that they do not intersect $I^{-}(S)$, they would have to stay in $D^+(S)$, which is impossible. Hence the segment belongs to $S\cap H^+(S)$. As a consequence, there is a maximal segment $\eta \subset S\cap H^+(S)$ ending at p. If it has no starting point z we have finished, otherwise $z\in \mathrm {edge}(S)$ because if not the argument could be repeated getting a contradiction with maximality.

Suppose now that there is no segment of $\sigma '$ with endpoint p contained in S, and let $U\ni p$, $z\in I^{+}(p,U)$, $w\in I^{-}(p,U)$. We are going to prove that there is a timelike curve connecting w to z contained in U and not intersecting S, which due to the arbitrariness of U implies $p \in \text {edge}(S)$, a contradiction. No matter how small U is, there is a point $q\in \sigma ' \cap I^{+}(w,U)\cap S^{C}$ such that q comes before p along $\sigma '$, $q<p$. The point q can be reached from w with a timelike curve that necessarily does not intersect S (the intersection point must be different from q as $q \in S^{C}$, thus, the intersection point and p would be chronologically related in contradiction with the achronality of S). Let W be a neighborhood of q such that $W\subset I^{+}(w,U)\cap S^{C}$, and W is sufficiently small that every point in W can be reached from w with a timelike curve that does not intersect S and is contained in U. Since q and p are accumulation points for $\sigma '_n$ and the curves $\sigma '_n$ do not intersect $\tilde{D}^{+}(S)\supset S$, and converge to $\sigma$ uniformly on compact subsets, it is possible to reach from w any neighborhood of p with a timelike curve that does not intersect S and is entirely contained in U, by passing through a segment of $\sigma '_n$. Since $p \in I^{-}(z,U)$ this curve can be continued to z while remaining in U, and it cannot cross S as otherwise $\sigma '_n \cap I^{-}(S)\ne \emptyset$, which is impossible. $\square$

As a consequence, if S is closed and acausal

$$\begin{aligned} H^+(S)\cap S= \mathrm {edge}(S)=\mathrm {edge}(H^+(S)). \end{aligned}$$

(3.6)

Corollary 3.25

Let S be a closed achronal set. If $\text {edge}(S)$ vanishes, then $H^{+}(S)$, if non-empty, is an achronal Lipschitz hypersurface generated by past-inextendible lightlike geodesics.

Proof

It follows from Theorems 3.23 and 3.24. $\square$

Corollary 3.26

Let S be a closed and acausal edgeless set (partial Cauchy hypersurface, see Definition 3.35), then $D^+(S)\cap H^+(S)=\emptyset$ and $D^+(S)\backslash S$ is open.

Proof

It follows from Eq. (3.2) and Theorem 3.24 which implies $H^+(S)\cap D^+(S)=\emptyset$. $\square$

The following proposition is Lemma 6.6.4 of Hawking and Ellis’ book.

Proposition 3.27

Let S be any set. If $p \in D^{+}(S)\backslash H^{+}(S)$, then every past inextendible continuous causal curve ending at p intersects $I^{-}(S)$.

Proof

Let $p\in D^{+}(S)\backslash H^{+}(S)\subset I^{-}(D^{+}(S))$, and let $\gamma$ be a past inextendible continuous causal curve ending at p. There is $q \in D^{+}(S)\cap I^{+}(p)$ and a past inextendible timelike curve $\eta$ ending at q entirely contained in $I^{+}(\gamma )$ (construct it as in Lemma 3.9 and smooth out the corners). As $\eta$ will intersect S at some point x there will be a point $y \in \gamma$ such that $y\in I^{-}(x)\subset I^{-}(S)$. $\square$

Proposition 3.28

Let (M, g) be a non-totally imprisoning spacetime. Let S be compact and achronal. Let $p\in [S\cap H^{+}(S)]\backslash \text {edge}(S)$ then there is a maximizing null geodesic with p as future endpoint which is entirely contained in $H^{+}(S)$ and has past endpoint at $\text {edge}(S)$.

Proof

By Theorem 3.24 we know that there is a maximizing null geodesic with p as future endpoint which is entirely contained in $H^{+}(S)$ and is either past-inextendible or has past endpoint at $\text {edge}(S)$. In the latter case there is nothing to prove. In the former case, the past inextendible curve $\sigma$ must escape the compact set S, thus there is some point in $H^{+}(S)\backslash S\subset I^{+}(S)$ (see Proposition 3.16), and hence $p \in I^{+}(S)$ in contradiction with the achronality of S. $\square$

3.2 The two-sided Cauchy development

Definition 3.29

Let S be any set. The Cauchy development (domain of dependence) of S is the set

$$\begin{aligned} D(S)&=D^{+}(S)\cup D^{-}(S)\\&=\{p\in M: {\text {every inextendible causal curve through }} p {\text { itersects }} S \}. \end{aligned}$$

The same name is used for the analogous set

$$\begin{aligned} \tilde{D}(S)&=\tilde{D}^{+}(S)\cup \tilde{D}^{-}(S)\\&=\{p\in M: {\text {every inextendible timelike curve through }} p {\text { itersects }} S \}. \end{aligned}$$

Remark 3.30

The second definition of D(S) by means of inextendible curves works because if through $p\in M$ there passes a future inextendible causal curve which does not intersect S and a past inextendible causal curve that does not intersect S then their composition gives an inextendible causal curve that does not intersect S. Conversely, if through p there passes an inextendible causal curve which does not intersect S, then by restricting the domain we see that there pass also past inextendible and future inextendible causal curves not intersecting S. An analogous argument applies to ${\tilde{D}}(S)$.

Remark 3.31

Again by Proposition 3.3 for S achronal or closed, in the definition of D(S) causal curve can be replaced with continuous causal curve or $C^1$ causal curve.

Definition 3.32

Let S be any set. The Cauchy horizon of S is $H(S)=H^{+}(S)\cup H^{-}(S)$.

Clearly, $S\subset D(S)\subset {\tilde{D}}(S)$ and $H(S)\subset {\tilde{D}}(S)$.

Proposition 3.33

Let S be a closed set then $\overline{D(S)}=\tilde{D}(S)$. If S is closed and achronal:

$$\begin{aligned}&\displaystyle \tilde{D}^{+}(S)\cap \tilde{D}^{-}(S)=S, \end{aligned}$$

(3.7)

$$\begin{aligned}&\displaystyle \mathrm {Int} \tilde{D}(S)=\mathrm {Int} D(S)=\mathrm {Int} D^{+}(S)\cup \mathrm {Int} D^{-}(S)\cup S\backslash H(S)=\tilde{D}(S)\backslash H(S), \end{aligned}$$

(3.8)

$$\begin{aligned}&\displaystyle \dot{\tilde{D}}(S)=\dot{D}(S)=H(S), \end{aligned}$$

(3.9)

$$\begin{aligned}&\displaystyle \mathrm {Int} D(S) \cap I^{\pm }(S)= \mathrm {Int} D^{\pm }(S) \end{aligned}$$

(3.10)

Proof

The first statement follows from

$$\begin{aligned} \overline{D(S)}=\overline{D^{+}(S)\cup D^{-}(S)}=\overline{D^{+}(S)}\cup \overline{D^{-}(S)}=\tilde{D}^{+}(S)\cup \tilde{D}^{-}(S)=\tilde{D}(S). \end{aligned}$$

By Eq. (3.2) we have $H^{+}(S)\cap \text {Int}\, D^{+}(S)=\emptyset$, but also $H^{+}(S)\cap \text {Int}\, D^{-}(S)=\emptyset$, because by Eq. (3.1) $\text {Int}\, D^{-}(S) \subset I^{-}(S)$ and $\tilde{D}^{+}(S)\cap I^{-}(S)=\emptyset$ as S is achronal. An analogous conclusion holds for $H^{-}(S)$, thus we have proved

$$\begin{aligned}{}[\text {Int}\, D^{+}(S)\cup \text {Int}\, D^{-}(S)]\cap H(S)=\emptyset . \end{aligned}$$

If S is achronal the equation $\tilde{D}^{+}(S)\cap \tilde{D}^{-}(S)=S$ follows trivially.

Let S be closed and achronal. Since $D(S)\subset \tilde{D}(S)$, we have $\text {Int}\, {D}(S)\subset \text {Int}\, \tilde{D}(S)$. Let us prove the converse. Let $p\in \text {Int}\, \tilde{D}(S)$. Note that $\tilde{D}(S)\subset S \cup I^{+}(S) \cup I^{-}(S)$, thus there are three cases. Let us consider the three case. Let us prove that if $p\in I^{-}(S)$ then $p \in \text {Int}({D}^{-}(S))\subset \text {Int}(D(S))$. Indeed, if $p \in I^{-}(S)$ then $p \notin \tilde{D}^{+}(S)$ (by achronality of S), thus $p \in \tilde{D}^{-}(S)$. There are two subcases: if $p \in I^{+}(\tilde{D}^{-}(S))$ then $p\in I^{-}(S)\cap I^{+}(\tilde{D}^{-}(S))=\text {Int}(\tilde{D}^{-}(S))=\text {Int}({D}^{-}(S))\subset \text {Int}(D(S))$. If $p \notin I^{+}(\tilde{D}^{-}(S))$ then $p \in H^{-}(S)\cap I^{-}(S)$. But $p \notin \text {Int}\tilde{D}^{-}(S)$, thus the only way in which $p \in \text {Int}\tilde{D}(S)$ is that $p \in \overline{\tilde{D}^{+}(S)}=\tilde{D}^{+}(S)$, a contradiction, thus this last case cannot hold. The assumption $p \in I^{+}(S)$ leads to the analogous conclusion that necessarily $p \in \text {Int}({D}^{+}(S))\subset \text {Int}(D(S))$, and it remains to consider the case $p \in S$. If $p \notin \text {Int} D(S)$ then there is a sequence of points $p_n \notin D(S)$, $p_n \rightarrow p$. Since $p \in \text {Int} \tilde{D}(S)$, for sufficiently large n, $p_n \in \text {Int} \tilde{D}(S)$. Thus by the argument used above we cannot have $p_n \in I^{+}(S)\cup I^{-}(S)$ as one would get $p_n \in \text {Int}(D(S))$. Thus, since $\tilde{D}(S)\subset S \cup I^{+}(S) \cup I^{-}(S)$, we have $p_n \in S\subset D(S)$ a contradiction. Thus we have proved

$$\begin{aligned} \text {Int}\, \tilde{D}(S)=\text {Int}\, \tilde{D}^+(S)\cup \text {Int}\, \tilde{D}^-(S) \cup (\text {Int}\, \tilde{D}(S)\cap S) \subset \text {Int}\, D(S). \end{aligned}$$

and hence the equality $\text {Int}\, \tilde{D}(S)=\text {Int}\, D(S)$. Let us prove that $\text {Int}\, \tilde{D}(S) \cap S \subset S\backslash H(S)$. Let $p \in \text {Int}\, \tilde{D}(S) \cap S$. Assume $p \in \text {edge}(S)$ then by Proposition 2.140 there is sequence $p_k \in (I^{+}(S)\cup I^{-}(S)\cup S)^C$ such that $p_k \rightarrow p$. But $p_k \notin \tilde{D}(S)$ in contradiction with $p \in \text {Int}\, \tilde{D}(S)$, thus $p\notin \text {edge}(S)$. Assume $p\in H(S)\backslash \text {edge}(S)$ then there is a neighborhood $U\subset \text {Int}\tilde{D}(S)$ of p included in $S\cup I^{+}(S)\cup I^{-}(S)$. If $p \in H^{-}(S)$ (the future case being similar) taking $r \in I^{-}(p,U)$ it follows $p \in I^{+}(r,U)\subset I^{+}(\tilde{D}(S))$ in contradiction with $p \in H^{-}(S)$, thus $p \notin H(S)\backslash \text {edge}(S) \cup \text {edge}(S)=H(S)$. The claimed inclusion is proved.

Thus we have proved the inclusion $\text {Int}\, \tilde{D}(S)\subset \text {Int}\, D^{+}(S)\cup \text {Int}\, D^{-}(S)\cup S\backslash H(S)$. For the converse we have only to show that $S\backslash H(S) \subset \text {Int}\, \tilde{D}(S)$. Thus let $p \in S\backslash H(S)$, then since $p \notin H(S)$ we have $p \notin \text {edge}(S)$. Hence there is a neighborhood $U\ni p$ such that $U \subset I^{+}(S)\cup I^{-}(S)\cup S$ and we are going to show that there is a choice such that $U \subset \tilde{D}^{+}(S)$. Since $p \notin H(S)$ but $p \in S\subset \tilde{D}^{+}(S) \cap \tilde{D}^{-}(S)$ we have $p \in I^{-}(\tilde{D}^{+}(S))\cap I^{+}(\tilde{D}^{-}(S))$. Choose U so small that we have also $U \subset I^{-}(\tilde{D}^{+}(S))\cap I^{+}(\tilde{D}^{-}(S))$. Now, $U\cap S \subset \tilde{D}^{+}(S)$ because $S \subset \tilde{D}^{+}(S)$, while $U\cap I^{+}(S)\subset I^{-}(\tilde{D}^{+}(S)) \cap I^{+}(S)=\text {Int}\tilde{D}^{+}(S)$ and analogously, $U\cap I^{-}(S) \subset \text {Int}\tilde{D}^{-}(S)$, thus $U \subset \tilde{D}(S)$.

Finally, note that, because of Proposition 3.16, $\text {Int}\, {\tilde{D}}^{+}(S)\cup \text {Int}\, {\tilde{D}}^{-}(S)\cup S \cup H(S)=\tilde{D}(S)$. Now, $\text {Int}\, {\tilde{D}}^{+}(S) \subset I^+(S)$ so by achronality of S it has empty intersection with $H^{-}(S)$, and similarly $\text {Int}\, {\tilde{D}}^{-}(S)\cap H^+(S)=\emptyset$, thus we proved $\text {Int}\, {\tilde{D}}^{+}(S)\cup \text {Int}\, {\tilde{D}}^{-}(S)\cup S\backslash H(S)=\tilde{D}(S)\backslash H(S)$, thus finishing the proof of Eq. (3.8).

The equality $\dot{\tilde{D}}(S)=\dot{D}(S)=H(S)$ and the last one (which uses the achronality of S) are trivial consequences of the previous ones. $\square$

Corollary 3.34

Let S be closed and achronal. We have $\tilde{D}(S)=M$ iff $D(S)=M$ iff $H(S)=\emptyset$. In this case S is edgeless.

Proof

$\tilde{D}(S)=M$ iff $\tilde{D}(S)$ is not only closed but also open, that is iff $\dot{D}(S)=H(S)=\emptyset$. Moreover, in this case $M=\tilde{D}(S)=\text {Int} \tilde{D}(S)= \text {Int} D(S)$ from which it follows $D(S)=M$. Conversely, if $D(S)=M$ then D(S) equals its interior, thus $H(S)=\emptyset$. S is edgeless because $\text {edge}(S)=\text {edge}(H^{+}(S))\subset H^{+}(S)=\emptyset$. $\square$

Definition 3.35

An acausal edgeless (and hence closed) set is a partial Cauchy hypersurface. A Cauchy hypersurface is a closed acausal set S such that $D(S)=M$ (thus it is edgeless).

Due to Theorem 2.147 these sets are indeed locally Lipschitz topological hypersurfaces, and by Eq. (3.6) $H(S)\cap S=\emptyset$.

Notice also that by acausality a causal curve intersects a Cauchy hypersurface only once, and a partial Cauchy hypersurface at most once.

Corollary 3.36

Let S be a partial Cauchy hypersurface, then $D(S)\cap H(S)=\emptyset$, in particular D(S) is open and $H^{\pm }(S) \subset I^{\pm }(S)$.

Proof

Since S is edgeless if $p \in H^{+}(S)$ there is a past lightlike ray ending at p and contained in $H^{+}(S)$. Thus every point in $H^{+}(S)$ admits a past-inextendible causal curve that does not intersect S, i.e. $H^{+}(S)\cap D^{+}(S)=\emptyset$ and analogously for $H^{-}(S)$. Using $\tilde{D}^{+}(S)\cap \tilde{D}^{-}(S)=S$ we get that $D(S)\cap H(S)=\emptyset$, and hence D(S) is open. Since $H^{+}(S)\cap S=\emptyset$ and $H^{+}(S)\subset \tilde{D}^{+}(S)$ from the definition of $\tilde{D}^{+}(S)$ we infer $H^{+}(S)\subset I^{+}(S)$. $\square$

Proposition 3.37

If S is a Cauchy hypersurface then $M=S\cup I^{+}(S) \cup I^{-}(S)$, that is, S is maximal achronal.

Proof

Obvious because $M=D(S)=\text {Int}D(S)=\text {Int}D^{+}(S)\cup \text {Int}D^{-}(S)\cup S\subset I^{+}(S) \cup I^{-}(S)\cup S$ (see Eq. (3.8)). $\square$

Remark 3.38

The converse is not true, consider for instance the spacetime $\mathbb {R}\times (0,1)$, $g=-\mathrm{d}t^2+\mathrm{d}x^2$, and $S=t^{-1}(0)$.

A spacetime is stably non-totally vicious if it is possible to find a metric with wider cones $g'>g$ such that on $(M,g')$ there are still some points through which does not pass a closed $g'$-timelike curve (or equivalently, in the language of Definition 4.96, iff the stable recurrent set is not the whole spacetime, i.e. $vJ_S\ne M$). For instance, the spacetime of Fig. 10 is stably non-totally vicious while that Fig. 19 is not.

We shall see that stably causal spacetimes are stably non-totally vicious, as the former spacetimes are characterized by the equation $vJ_S=\emptyset$, however, the condition stably non-totally vicious will not fit into the causal ladder of spacetimes.

Theorem 3.39

Stably non-totally vicious spacetimes admit partial Cauchy hypersurfaces.

Proof

Let $g'>g$ be a metric such that $(M,g')$ is non-totally vicious, namely it admits some $p\in M$ through which does not pass a closed timelike curve. Since $\{p\}$ is an achronal set for $(M,g')$, we can find a maximal $g'$-achronal set A containing p. By Theorem 2.87 A is an achronal boundary for $(M,g')$ and hence for (M, g), because every future set for $(M,g')$ is a future set for (M, g), so A has no edge. The $g'$-achronality of A implies its g-acausality, thus A is a partial Cauchy hypersurface for (M, g). $\square$

The following theorem, here given a different proof, is due to Penrose (1968, 1972, Proposition 5.14) and Geroch (1970, Proposition 6). There is also a version by Galloway (1985) in which, among the other modifications, achronality is replaced by local achronality.

Theorem 3.40

A closed achronal set S is a Cauchy hypersurface iff every inextendible lightlike geodesic intersects S exactly at one point.

Proof

If S is a Cauchy hypersurface then it is obvious that every inextendible lightlike geodesic intersect S exactly once because S is acausal and $D(S)=M$.

For the converse, S must be acausal otherwise if $p,q \in S$, $p< q$ then necessarily $q \in E^{+}(p)$ because S is achronal. But then the inextendible lightlike geodesic passing through p and q intersects S at least at the two points p and q, a contradiction. Clearly, we have $M=S\cup J^{+}(S)\cup J^{-}(S)$, and since S is acausal $J^{+}(S)\cap J^{-}(S)=\emptyset$.

Actually, $J^{+}(S)=I^{+}(S)\cup S$, indeed otherwise there would be $r \in E^{+}(S)\backslash S$ and hence a segment of lightlike geodesic $\eta$ entirely contained in $E^{+}(S)\backslash S$ but for the starting point in S (no point in the segment can belong to S, otherwise S would not be causal). Let x, y and z, $x<y<z$, be three points in this segment, and let $\gamma$ be a lightlike geodesic passing through y but having tangent vector distinct from $\eta '$. The curve $\gamma$ intersects S at a point necessarily different from y. Due to the corner at y between $\eta$ and $\gamma$ we have that either $x \in I^{-}(S)$ or $z \in I^{+}(S)$. The former case is impossible because $x \in J^{+}(S)$ and S is achronal, the latter case is impossible because $z \in E^{+}(S)$. We conclude $M=S\cup I^{+}(S) \cup I^{-}(S)$, and by Proposition 2.140, S is edgeless.

By Corollary 3.36 $D(S)\cap H(S)=\emptyset$, and if $p\in H^{+}(S)$ then the generator of $H^{+}(S)$ is past inextendible and being contained in $H^{+}(S)$ it does not intersect S to the past of p, moreover, once extended into the future it cannot intersect S because it has a point in $H^{+}(S)\subset I^{+}(S)$, and thus the future intersection point would be in $I^{+}(S)$ whereas S is achronal. The contradiction proves that $H^{+}(S)=\emptyset$. An analogous argument proves that $H^{-}(S)=\emptyset$ $\square$

The following result is due to Budic and Sachs (1978), see also (Galloway 1985, Corollary 1). They assume that S is $C^1$ and spacelike but their proof work for locally acausal hypersurfaces as well.

Theorem 3.41

On a globally hyperbolic spacetime every compact, connected, locally acausal hypersurface S is a Cauchy hypersurface.

The following result is an improved version of the corollary after Hawking and Ellis’ Lemma 6.6.4.

Proposition 3.42

Let S be closed and achronal. If $p\in \text {Int} D(S)$ then every future inextendible continuous causal curve starting from p intersects $I^{+}(S)$ and every past inextendible continuous causal curve ending at p intersects $I^{-}(S)$.

Proof

Recall that $D(S) \subset \tilde{D}(S) \subset S\cup I^{+}(S)\cup I^{-}(S)$. If $p \in I^{+}(S)$ then (Proposition 3.33) $p \in \text {Int} D^{+}(S)$ and the claim follows from Proposition 3.27. An analogous conclusion is obtained if $p \in I^{-}(S)$. If $p \in S \subset D^{+}(S)$, as $p \notin H^{+}(S)$ we have that by Proposition 3.27 the past inextendible curve intersects $I^{-}(S)$. In the same way $p \in S \subset D^{-}(S)$, thus an analogous reasoning proves that the future inextendible curve intersects $I^{+}(S)$. $\square$

3.3 Causal convexity and other properties

The following result embodies the observation by Hanquin (1982) concerning the equivalence between the causal convexities of S and D(S). We recall that a set S which is achronal and edgeless is causally convex (Corollary 2.145).

Proposition 3.43

Let S be closed and achronal. The sets $\text {Int}\, D(S)$, $\text {Int}\, D^{+}(S)$ and $\text {Int}\, D^{-}(S)$ are all causally convex. Moreover, the causal convexity of one of the following four sets: S, D(S), $D^{+}(S)$ and $D^{-}(S)$, implies the causal convexity of the other three.

Proof

We have to prove that for any $p,q \in \text {Int} D(S)$, it holds $J^{+}(p) \cap J^{-}(q) \subset \text {Int} D(S)$. To this end take $\tilde{p}\in \text {Int} D(S)\cap I^{-}(p)$ and $\tilde{q}\in \text {Int} D(S)\cap I^{+}(q)$, we have $J^{+}(p) \cap J^{-}(q) \subset I^{+}(\tilde{p}) \cap I^{-}(\tilde{q})$ and we are going to prove that this last set is contained in $\text {Int} D(S)$. For if not there is $r \in I^{+}(\tilde{p}) \cap I^{-}(\tilde{q}) \cap [\text {Int} D(S)]^C$, and since I is open we can assume without loss of generality $r \notin \tilde{D}(S)$. There is a past inextendible timelike curve ending at r and not intersecting S (and an analogous future inextendible causal curve). Thus either (a): the timelike segment connecting r to $\tilde{q}$ intersect S (necessarily in a point different from r), in which case $\tilde{q}\in \text {Int} D^{+}(S)\cup S$ or (b): it does not in which case $\tilde{q} \in \text {Int} D^{-}(S)\subset I^{-}(S)$. Analogously, either (i): the timelike segment connecting $\tilde{p}$ to r intersects S, in which case $\tilde{p}\in \text {Int} D^{-}(S)\cup S$ or (ii): it does not in which case $\tilde{p} \in \text {Int} D^{+}(S)\subset I^{+}(S)$. Case (a)-(i) is impossible because S is achronal. Case (b)-(ii) is impossible again because S is achronal. Case (a)-(ii) is impossible because $\text {Int} D^{+}(S)$ is causally convex, and case (b)-(i) is impossible because $\text {Int} D^{-}(S)$ is causally convex. Indeed, take $\tilde{p}, \tilde{q} \in \text {Int} D^{+}(S)$, and construct $r \notin \tilde{D}^{+}$ as above. The timelike segment connecting r to $\tilde{q}$ intersects S, which implies $\tilde{p}\in I^{-}(S)$, which is impossible if $\tilde{p} \in \text {Int} D^{+}(S)\subset I^+(S)$, thus $\text {Int} D^{+}(S)$ is causally convex.

Let us come to the proof for the last three sets. Assume S is causally convex and let us prove the causal convexity of $D^{+}(S)$. Let $p,q\in D^{+}(S)$, if $J^{+}(p)\cap J^{-}(q)$ contains a point $r \notin D^{+}(S)$ then the causal curve $\eta$ connecting r to q must intersect S at a point z necessarily different from r, which implies $r \in [J^{+}(S)\cap J^{-}(S)] \backslash S$, a contradiction.

The causal convexity of $D^{-}(S)$ starting from that of S is analogous.

Assume S is causally convex and let us prove the causal convexity of D(S). Let $p \in D^{-}(S)$, $q\in D^{+}(S)$, if $J^{+}(p)\cap J^{-}(q)$ contains a point $r \notin D(S)$ then the causal curve $\eta$ connecting r to q must intersect S at a point z necessarily different from r. Analogously, the causal curve $\gamma$ connecting p to r must intersect S at a point necessarily different from r. Finally, $r \in [J^{+}(S)\cap J^{-}(S)] \backslash S$ a contradiction.

Conversely, assume one of $D^{+}(S)$, $D^{-}(S)$ or D(S), is causally convex. If $r \in [J^{+}(S)\cap J^{-}(S)] \backslash S$ then as S is a subset of a causally convex set among $D^{+}(S)$, $D^{-}(S)$ and D(S), we have that r belongs to this same causally convex set and thus $r \in D(S)\backslash S\subset I^{+}(S)\cup I^{-}(S)$, but as $r \in J^{+}(S)\cap J^{-}(S)$, S is not achronal, a contradiction. $\square$

Proposition 3.44

Let S be closed and achronal. The strong causality condition holds at the points of $\text {Int} D(S)$. If strong causality holds on $S\cap H(S)$ then it holds on D(S). If strong causality holds on $S\cap H^+(S)$ then it holds on $D^+(S)\backslash [S\backslash H^+(S)]$.

Proof

Assume strong causality does not hold at p, then by a standard application of the limit curve theorem 2.53-(ii) (see also the proof of Theorem 2.69) there is a limit inextendible continuous causal curve $\eta$ passing through p, such that for every pair $r,q \in \eta$ we have $(r,q) \in \bar{J}$ (the Case 2.53-(i) gives a closed limit curve which can also be regarded as inextendible by traversing the curve infinitely often). But by Proposition 3.42 it is possible to choose $r \in I^{+}(S)$ and $q \in I^{-}(S)$, and since I is open S is not achronal, a contradiction.

Assume that strong causality holds at $S\cap H(S)$. By Proposition 3.33 strong causality holds on $S\backslash H(S)$, thus if it holds on $S\cap H(S)$ then it holds on S. Strong causality holds at $p \in D(S)$ because otherwise by the limit curve theorem 2.53 through p passes an inextendible continuous causal curve along which strong causality is violated (Theorem 2.69). This curve intersects S, thus strong causality is violated at some point of S, a contradiction.

Assume that strong causality holds at $S\cap H^+(S)$. We already know that it holds on $\text {Int} D^+(S)$, so we need only to prove that it holds at $D^+(S)\cap H^+(S)$. If strong causality fails at $p\in D^+(S)\cap H^+(S)$ by the limit curve theorem 2.53 through p passes an inextendible continuous causal curve (possibly closed) at whose points strong causality is violated. This curve cannot enter $\text {Int}D^+(S)\subset \text {Int}D^+(S)$ for there strong causality holds, so it intersects S at a first point (in the past direction) $q\in S\cap H^+(S)$ where strong causality holds, a contradiction. $\square$

Theorem 3.45

Let S be closed and achronal. The open set $\text {Int} D(S)$, if non-empty, once endowed with the induced metric is a globally hyperbolic spacetime (strong causality and compactness of the causal diamonds).

Proof

Let $p,q \in \text {Int} D(S)$ and assume $\overline{J^{+}(p)\cap J^{-}(q)}$ is not compact, then there are points $r_n \in J^{+}(p)\cap J^{-}(q)$ with $r_n \rightarrow +\infty$ (i.e. escaping every compact set). Let $\sigma _n$ be a causal curve starting from p passing through $r_n$ and ending at q. By the limit curve theorem 2.53 there are a past inextendible causal curve $\sigma ^{q}$ ending at q, and a future inextendible causal curve $\sigma ^p$ starting from p, which are uniform limits of a subsequence of $\sigma _n$. By Proposition 3.42 there are $\tilde{p} \in \sigma ^p \cap I^{+}(S)$ and $\tilde{q} \in \sigma ^q \cap I^{-}(S)$. However, the limit curve theorem also states that $(\tilde{p},\tilde{q}) \in \bar{J}$, and since I is open we obtain that S is not achronal, a contradiction. Let us now prove that $J^{+}(p)\cap J^{-}(q)$ is closed, indeed, if it were not then there would be points $r_n \in J^{+}(p)\cap J^{-}(q)$ with $r_n \rightarrow r \in \overline{J^{+}(p)\cap J^{-}(q)}\backslash [J^{+}(p)\cap J^{-}(q)]$. The argument goes as above, in fact the limit curve cannot join p to q, that is Theorem 2.53-(i) cannot apply, otherwise r would belong to it and hence $r\in J^{+}(p)\cap J^{-}(q)$, a contradiction. Thus case (ii) of Theorem 2.53 applies and from here we reach the contradiction as above. We conclude that the causal diamonds $J^{+}(p)\cap J^{-}(q)$ are compact. These causal diamonds coincide with those of the spacetime $\text {Int} D(S)$ because of its causal convexity. $\square$

Theorem 3.46

Let S be closed and achronal and let $q \in \text {Int} D(S)$. The sets $J^{+}(S)\cap J^{-}(q)$ and $J^{+}(q)\cap J^{-}(S)$ are compact. The former set is non-empty iff $q \in D^{+}(S)$, the latter is non-empty iff $q \in D^{-}(S)$. Moreover, these sets are contained in $\mathrm {Int} D^{+}(S)\cup [S\backslash H^{+}(S)]$ for the former and in $\mathrm {Int} D^{-}(S)\cup [S\backslash H^{-}(S)]$ for the latter. Finally, $S\cap J^{-}(q)$ and $S\cap J^{+}(q)$ are compact.

If S is acausal by Eq. (3.6) $H^{\pm }(S)\cap S= \mathrm {edge}(S)$, which implies $S\backslash H^+(S)=S\backslash H(S)\subset \mathrm {Int} D(S)$ (Proposition 3.33), hence the sets of the theorem are contained in $\mathrm {Int} D(S)$.

Proof

Let us prove compactness. Assume $\overline{J^{+}(S)\cap J^{-}(q)}$ is not compact then there are $r_n \in J^{+}(S)\cap J^{-}(q)$ going to infinity. By an application of the limit curve theorem there is a past inextendible continuous causal curve $\sigma ^q$ ending at q. By Proposition 3.42 this curve intersects $I^{-}(S)$ and is the limit of causal curves issued from S, thus S is not achronal, a contradiction. The proof that ${J^{+}(S)\cap J^{-}(q)}$ is closed goes as above with the difference that $r_n \rightarrow r \in \overline{J^{+}(S)\cap J^{-}(q)} \backslash J^{+}(S)\cap J^{-}(q)$ (the limit curve may pass through r).

If the set $J^{+}(S)\cap J^{-}(q)$ is non-empty then $q \in D^{+}(S)$, for if $q \in D^{-}(S)\backslash S\subset I^{-}(S)$, S would not be achronal. The converse is obvious.

Assume $J^{+}(S)\cap J^{-}(q)$ is non-empty and let us prove that it is contained in $D^{+}(S)$. Since $q\in D^{+}(S)$ and $q\in \text {Int} D(S)$ either $q \in \text {Int} D^{+}(S)$ or $q \in S\backslash H(S)$, cf. Eq. (3.8). In the former case $J^{+}(S)\cap J^{-}(q) \subset J^{+}(S)\cap J^{-}(\text {Int} D^{+}(S))$ and since $\text {Int} D^{+}(S)$ is open $J^{+}(S)\cap J^{-}(q) \subset J^{+}(S)\cap I^{-}(\text {Int} D^{+}(S))\subset \mathrm {Int} D^{+}(S)\cup [S\backslash H^{+}(S)]$ where we used Proposition 3.19. In the latter case by Proposition 3.19, $q \in I^{-}(D^{+}(S))$, thus $J^{+}(S)\cap J^{-}(q) \subset J^{+}(S)\cap I^{-}(D^{+}(S))=\mathrm {Int} D^{+}(S)\cup [S\backslash H^{+}(S)]$, again by Proposition 3.19.

Note that $S\cap J^{-}(q)=S\cap [J^{+}(S)\cap J^{-}(q)]$, thus being the intersection of a closed and a compact set it is compact. $\square$

Corollary 3.47

Let S be closed and achronal. If $q \in \text {Int} D^{+}(S)$ then $d(S,q)<\infty$ and there is a causal geodesic which maximizes the Lorentzian length of the causal curves connecting S to q. Moreover, this curve is entirely contained in $D^{+}(S)$ and no other maximizing causal geodesic ${\tilde{\sigma }}$, $d(S,{\tilde{q}})=l({\tilde{\sigma }})$, can intersect $\sigma$ in the interior of its domain.

Thus the maximizing geodesics of the theorem can only intersect at the endpoints. After point q, the geodesic $\sigma$ may be no more maximizing while remaining inside $D^{+}(S)$.

Proof

Let $\gamma _n$ be a sequence of causal curves with starting point in $J^{-}(q)\cap S$ and ending point at q such that $l(\gamma _n) \rightarrow \sup _{\eta } l(\eta )=d(S,q)$ where $\eta$ is the generic causal curve with the same property. As $J^{-}(q)\cap S$ is compact we can assume without loss of generality that the sequence of starting points converges to some $p\in J^{-}(q)\cap S$. The sequence of causal curves must converge to a continuous causal curve $\sigma$ connecting p to q. Indeed, if not at q would end a past inextendible continuous causal curve intersecting $I^{-}(S)$ (Proposition 3.27) and limit of continuous causal curves issued from S, a contradiction with the achronality of S. Also by the upper semi-continuity of the length functional $d(S,q) \le l(\sigma )<\infty$ and hence $\sigma$ maximizes the Lorentzian length of the causal curves connecting S to q (so it maximizes the Lorentzian length of continuous causal curves connecting p to q and hence it is a causal geodesic, cf. Theorem 2.22). The curve $\sigma$ is entirely contained in $D^{+}(S)$ because $J^{+}(S)\cap J^{-}(q)$ is compact and contained in $D^{+}(S)$. Finally, there cannot be a similarly maximizing causal geodesic ${\tilde{\sigma }}$, $l({\tilde{\sigma }})=d(S,{\tilde{q}})$, intersecting $\sigma$ in a $\sigma$-domain interior point r. In fact, as they are both maximizing the respective segments from S up to r have the same length d(S, r), but then there would be a continuous causal curve $\gamma$ joining ${\tilde{p}}$ with q with length no shorter than $l(\sigma )$ but with a corner at r, which implies, by Theorem 2.22, that there is a continuous causal curve longer that $\sigma$ from ${\tilde{p}}$ (hence S) to q, a contradiction with the maximality of $\sigma$. $\square$

The following result contains Proposition 6.6.7 of Hawking and Ellis’ book as corrected by Hanquin (1982). The proof is different from Hawking and Ellis’.

Theorem 3.48

Let S be a closed, achronal, causally convex set such that strong causality holds on $S\cap H(S)$. Moreover, let S be either compact or acausal. We have that if $p,q\in D(S)$ then $J^{+}(p)\cap J^{-}(q)$ is compact and contained in D(S), and if $q \in D^{+}(S)$ then $J^{+}(S)\cap J^{-}(q)$ and $S\cap J^{-}(q)$ are compact and contained in $D^+(S)$.

The function $d(S,\cdot )$ is finite and continuous on $D^+(S)$, moreover for every $q\in D^{+}(S)\backslash S$ there is a geodesic segment $\gamma \subset D^+(S)$ connecting S to q for which $l(\gamma )=d(S,q)$.

Fig. 7

This closed achronal set S in Minkowski spacetime is either acausal (if the point r is removed from spacetime) or such that $J^{+}(S) \cap J^{-}(S)$ is compact (if r is kept). In either case $J^{+}(p)\cap J^{-}(q)$ is compact but in the latter case it is not contained in D(S), hence D(S) and S are not causally convex

The function $d(\cdot ,\cdot )$ is finite and continuous on $D(S)\times D(S)$, moreover for every $p,q\in D(S)$, $p\ne q$ there is a geodesic segment $\gamma \subset D(S)$ connecting p to q for which $l(\gamma )=d(p,q)$.

Note that strongly causality holds on D(S) by Proposition 3.44. If S is not causally convex, the causal diamonds are not contained in D(S), see Fig. 7 and Proposition 3.43.

Proof

The sets $D^{+}(S)$, $D^{-}(S)$ and D(S) are causally convex because of Proposition 3.43. By Proposition 3.44 strong causality holds at the points of D(S). We are going to prove that if $p,q\in D^{+}(S)$ (thus $p \in J^{+}(S)$) then $J^{+}(p)\cap J^{-}(q)$ and $J^{+}(S)\cap J^{-}(q)$ are compact. If one of these two sets has non-compact closure or has compact closure but is non-closed then by an application of the limit curve theorem 2.53 there is a past inextendible continuous causal curve $\sigma ^q$ ending at q which is the limit of continuous causal curves issued from S. If $\sigma ^q\cap \text {Int} D^{+}(S)\ne \emptyset$ then by Proposition 3.27 $\sigma ^q\cap I^{-}(S)\ne \emptyset$, thus as $I^{-}(S)$ is open, S is not achronal, a contradiction. Thus we can assume $\sigma ^q\subset \dot{D}^{+}(S)=S\cup H^{+}(S)$. The curve $\sigma ^q$ intersects S at a point $\tilde{q}$; from that point on (in the past direction) the curve belongs to S otherwise there would be a point $y<\tilde{q}$, $y \in H^{+}(S)\backslash S \cap \sigma ^q$. But $H^{+}(S)\backslash S \subset I^{+}(S)$ (Proposition 3.16), which gives a contradiction with the achronality of S. However, if $\sigma ^q$ after (in the past direction) $\tilde{q}$ is all contained in $S\cap H^+(S)$, we have that, on the one hand S is not acausal and, if strong causality holds at $S\cap H^+(S)$, S is not compact (Theorem 2.80), a contradiction. Since $S\cap J^{-}(q)=S\cap [J^{+}(S)\cap J^{-}(q)]$ this set being the intersection of a closed and a compact set is compact.

The case $p,q \in D^{-}(S)$ is analogous to the previous one.

If one of the points p, q belongs to S we are in one of the previous cases.

Let us consider the case $q \in D^{-}(S)\backslash S$, $p \in D^{+}(S)\backslash S$. We have $q \in \tilde{D}^{-}(S)\backslash S\subset I^{-}(S)$ and analogously, $p \in I^{+}(S)$, thus we have $J^{+}(p)\cap J^{-}(q)=\emptyset$, otherwise S would not be achronal.

Finally, let us consider the case $p \in D^{-}(S)\backslash S$, $q \in D^{+}(S)\backslash S$. Since $p \in I^{-}(S)$ and $q\in I^{+}(S)$ the causal curves which connect p to q, by the causal convexity of $D(S)\subset S\cup I^+(S)\cup I^-(S)$, must intersect S. Thus

$$\begin{aligned} J^{+}(p)\cap J^{-}(q)=[J^{+}(p)\cap J^{-}(S\cap J^{-}(q))] \cup [J^{+}(S\cap J^{+}(p))\cap J^{-}(q)]. \end{aligned}$$

The two sets in square brackets on the right-hand side are compact, for instance the proof that $J^{+}(S\cap J^{+}(p))\cap J^{-}(q)$ is compact is similar to the proof that $J^{+}(S)\cap J^{-}(q)$ is compact given above.

Let $q\in D^{+}(S)$ and let $\gamma _n$ be a sequence of causal curves with starting point in $J^{-}(q)\cap S$ and end point at q such that $l(\gamma _n) \rightarrow \sup _{\eta } l(\eta )=d(S,q)$ where $\eta$ is the generic causal curve with the same property. As $J^{-}(q)\cap S$ is compact we can assume the the sequence of first endpoints converges to some $p\in J^{-}(q)\cap S$. The sequence of causal curves must converge to a continuous causal curve $\gamma$ connecting $p\in S$ to q. Indeed, if not, at q would end a past inextendible continuous causal curve entirely contained in the compact set $J^{+}(S)\cap J^{-}(q)\subset D^{+}(S)$. Since strong causality holds on $D^{+}(S)$ this is impossible (Theorem 2.75). Also by the upper semi-continuity of the length functional $\sup _{\eta } l(\eta ) =\limsup l(\gamma _n)\le l(\gamma )$ and hence $d(S,q) = l(\gamma )<\infty$. In particular $\gamma$ maximizes the Lorentzian length of the causal curves connecting S (and hence p) to q, thus it is a causal geodesic. The curve $\gamma$ is contained in $D^{+}(S)$ because $J^{+}(S)\cap J^{-}(q)$ is compact and contained in $D^{+}(S)$.

Let us prove that $f=d(S,\cdot )$ is continuous on $D^+(S)$. By the achronality of S, $f\vert _S=0$, thus f is lower semi-continuous on S. If $q\in D^+(S)\backslash S$, then f is lower semi-continuous there, in fact there is some $p\in S$ and a maximizing curve $\gamma$ connecting p to q such that $d(p,q)=l( \gamma )=d(S,q)$. Let $q_n\rightarrow q$, and let similarly $p_n\in S$, and $\gamma _n$ such that $d(p_n,q_n)=l(\gamma _n)=d(S,q_n)$. By the lower semi-continuity of d, $d(S,q)=d(p,q)\le \liminf d(p_n,q_n)=\liminf d(S,q_n)$. It remains to prove the upper semi-continuity. Let $q\in D^+(S)$ and let $q_n,p_n,\gamma _n$ as above. Even if $q\in S$ we can assume without loss of generality $q_n\notin S$. Due to the compactness of $J^+(S)\cap J^-(q)$ and due to strong causality on this set, if $q\notin S$, there is a limit curve $\gamma$ connecting $p\in S$ to q. By the upper semi-continuity of the length functional $\limsup d(S,q_n)=\limsup l(\gamma _n)\le l(\gamma )\le d(S,q)$. If $q\in S$ the limit curve would be contained in $J^+(S)\cap J^-(q)\subset S$, which is impossible by the acausality of S, thus the sequence $\gamma _n$ really degenerates to the point q, thus $\limsup d(S,q_n)=\limsup l(\gamma _n)=0$.

Let $p,q\in D(S)$, $p\ne q$, and let $\gamma _n$ be a sequence of causal curves connecting p to q such that $l(\gamma _n) \rightarrow \sup _{\eta } l(\eta )=d(p,q)$ where $\eta$ is the generic causal curve with the same property. As $J^+(p)\cap J^{-}(q)$ is compact, the sequence of causal curves must converge to a continuous causal curve $\gamma$ connecting p to q. Indeed, if not, at q would end a past inextendible continuous causal curve entirely contained in the compact set $J^{+}(p)\cap J^{-}(q)$. Since strong causality holds on $D^{+}(S)$ this is impossible. Also by the upper semi-continuity of the length functional $\sup _{\eta } l(\eta ) =\limsup l(\gamma _n)\le l(\gamma )$ and hence $d(p,q) = l(\gamma )<\infty$. In particular $\gamma$ maximizes the Lorentzian length of the causal curves connecting p to q, thus it is a causal geodesic. The curve $\gamma$ is contained in D(S) because $J^{+}(p)\cap J^{-}(q)$ is compact and contained in D(S).

Let us prove that $f=d(\cdot ,\cdot )$ is continuous on $D(S)\times D(S)$. It is lower semi-continuous because d is lower semi-continuous. It remains to prove the upper semi-continuity. Let $p,q\in D$ and let $(q_n,p_n)\rightarrow (p,q)$. Even if $p=q$ we can assume without loss of generality $q_n\ne p_n$. Let $\gamma _n$ be such that $d(p_n,q_n)=l(\gamma _n)$. Due to the compactness of $J^+(p)\cap J^-(q)$ and due to strong causality on this set, if $p\ne q$, there is a limit curve $\gamma$ connecting p to q. By the upper semi-continuity of the length functional $\limsup d(p_n,q_n)=\limsup l(\gamma _n)\le l(\gamma )\le d(p,q)$. If $p=q$ the limit curve would be closed and contained in D(S), which is impossible by the strong causality in D(S), thus the sequence $\gamma _n$ really degenerates to the point q, thus $\limsup d(p_n,q_n)=\limsup l(\gamma _n)=0=d(p,q)$. $\square$

Example 3.49

We give an example of a (stably) causal spacetime in which there is an achronal, closed, edgeless set S such that there are points $p,q \in D(S)$ (actually in S) such that $J^{+}(p)\cap J^{-}(q)$ is closed but non compact. Let N be the spacetime given by the direct product between $\mathbb {R}$ (the time axis) and $S^2$ with the usual Riemannian metric. Let $p,q\in N$ be such that their projections are antipodal points in $S^2$ and they are causally but non timelike separated. The events p and q are joined by maximizing lightlike geodesic segments. Remove a point in the interior of one of these segments, then the obtained spacetime is the one we were looking for with $S=J^{+}(p)\cap J^{-}(q)$.

Theorem 3.50

Let S be closed and achronal, if $\text {Int} D(S)$ is non-empty then with the induced metric we already know that it is a globally hyperbolic spacetime (Theorem 3.45). If $S'$ is any Cauchy hypersurface for this spacetime then, once regarded as a hypersurface in M we have, $\text {Int} D(S)=\text {Int} D(S')$, $\tilde{D}(S)=\tilde{D}(S')$ and $\text {edge}(S)=\text {edge}(S')$. In particular S is edgeless iff $S'$ is edgeless. If S is a partial Cauchy hypersurface in M then one has also $D(S)= D(S')$.

Proof

If $p \in \text {Int} D(S)$ every inextendible causal curve passing through p, is also inextendible with respect to the spacetime $\text {Int} D(S)$ with the induced metric (it is the connected piece passing through p contained in this set), and thus intersects $S'$, thus $\text {Int} D(S)\subset D(S')$ and hence taking interior and closure we get $\text {Int} D(S)\subset \text {Int} D(S')$ and $\overline{D(S)}\subset \overline{D(S')}$.

Assume, by contradiction, the existence of $q\in D(S')\backslash D(S)$ then there is an inextendible causal curve $\gamma$ passing through q which does not intersect S. This curve intersects $S'$ at $r\in \text {Int} D(S)$, and the connected component of $\gamma$ containing r and included in $\text {Int} D(S)$ is inextendible when regarded as a causal curve on $\text {Int} D(S)$ with the induced metric. Thus it intersects S and hence $\gamma$ intersects S, a contradiction. We conclude $D(S')\subset D(S)$. Taking closure and interiors we finally get $\text {Int} D(S)= \text {Int} D(S')$ and $\overline{D(S)}= \overline{D(S')}$. The equality of the edges follows from Proposition 2.155.

If S is a partial Cauchy surface for (M, g) then the equality holds because $D(S)=\text {Int} D(S)=\text {Int} D(S')\subset D(S')$ while the converse inclusion has been proved above. $\square$

Remark 3.51

In the above theorem the equality ${D(S)}= {D(S')}$ does not necessarily hold if S is not a partial Cauchy hypersurface. For instance, let S be a unit disk in the slice $t=0$ in $2+1$ Minkowski spacetime. Whatever the choice of Cauchy hypersurface $S'$ for $\text {Int} D(S)$, we have that $S'$ does not include the boundary of the disk while S does, so D(S) is closed in M while $D(S')$ is open.

The following result is an improvement over Borde (1994, Lemma 5) where stable causality is assumed.

Theorem 3.52

Let (M, g) be a non-totally imprisoning spacetime and let S be a compact locally achronal (hence locally Lipschitz) topological hypersurface, then $\text {Int} \,D^{\pm }(S)\ne \emptyset$, $\text {Int} \,D(S)\ne \emptyset$.

Proof

Let us give the proof for $\text {Int} D^{+}(S)$. Consider a $C^1$ timelike complete vector field V over M, and define $S_\epsilon =\phi _\epsilon (S)$, where $\phi _t$ is the one parameter group of diffeomorphisms generated by V. Choose $\epsilon >0$ sufficiently small that $S_\epsilon$ and S do not intersect ($\epsilon$ exists by local achronality and compactness). Clearly $S_\epsilon$ being the continuous image of a compact set is compact and the compact set $C_\epsilon =\{p :p=\phi _t(r), r \in S, 0\le t\le \epsilon \}$ has as boundary the disjoint union $S\cup S_\epsilon$ (because the set $\{\phi _t(S), t\in (0,\epsilon )\}\subset C_\epsilon$ is indeed open due to the transversality of S with respect to V, that is, S can be locally expressed as a graph in which the direction of the ordinate is played by the integral lines of V, see e.g. the proof of Theorem 2.87). Since $S_\epsilon$ is compact and chronology holds there is a point $q\in S_\epsilon$ such that $q \notin I^{+}(S_\epsilon )$ (see Proposition 2.100). Let $\tilde{q}=\phi _{-{\tilde{\epsilon }}}(q)$, $0<{\tilde{\epsilon }}<\epsilon$, so that ${\tilde{q}}\in \mathrm {Int} C_\epsilon$, ${\tilde{q}}\ll q$.

The chronological past of ${\tilde{q}}$, at least in a sufficiently small open neighborhood U of ${\tilde{q}}$ is contained in $\text {Int}C_\epsilon$, i.e. $I_U^{-}(q)\subset \text {Int}C_\epsilon$, thus every past inextendible timelike curve ending at ${\tilde{q}}$ has a last segment in $\text {Int}C_\epsilon$, and since the spacetime is non-totally imprisoning, it escapes $C_\epsilon$ in the past direction somewhere on $\dot{C}_\epsilon =S\cup S_\epsilon$. However, the escaping point can not belong to $S_\epsilon$, because $q \notin I^{+}(S_\epsilon )$, thus every past inextendible timelike curve ending at q intersects S. As a consequence the same holds for points in the open set $I_U^{-}(q)$ which is therefore contained in $\text {Int} D^{+}(S)$. $\square$

4 The causal ladder

In this section we organize the causality properties into hierarchies. There are in fact two related hierarchies, the transverse ladder and the (main) causal ladder.

The causal ladder involves many properties at the center of which we find stable causality, Fig. 20.

Above stable causality the levels of the ladder impose limitations on the nasty influence of points at infinity on spacetime. The most important level in this respect is the strongest one, namely global hyperbolicity. Below stable causality the causality levels impose limitations on the causal pathologies which might arise due to the existence of almost closed causal curves. Likely the most important levels here are causality and non-total imprisonment, where the latter condition is not so well known among mathematical relativists.

The levels above and below stable causality are really connected by the properties of the transverse ladder. These transverse properties impose some relational or topological conditions on the causal relations. It is convenient to present the transverse ladder first, for the levels above stable causality are basically obtained from the levels below it by imposing some properties of the transverse ladder.

4.1 Reflectivity and transverse ladder

We need to introduce some interesting concepts. On a spacetime (M, g) let us introduce the relations (Minguzzi 2008a)

$$\begin{aligned} D_f&=\{(p,q):q\in \overline{J^+(p)}\}=\{(p,q):I^+(p) \supset I^+(q) \} , \end{aligned}$$

(4.1)

$$\begin{aligned} D_p&=\{(p,q):p\in \overline{J^-(q)}\}=\{(p,q):I^-(p) \subset I^-(q) \}. \end{aligned}$$

(4.2)

where f in $D_f$ stands for future and p in $D_p$ stands for past (we hope that it is not confused with a point). It is clear that they include J and are included in ${\bar{J}}$.

Proof of the equality in (4.1) and (4.2). Let us consider Eq. (4.1) the other being analogous. Proof of $\subset$: suppose (p, q) are such that $q\in \overline{J^+(p)}$ and let $r \in I^+(q)$, then $q\in I^-(r)$ and by the openness of I, $p\in I^-(r)$, which implies $r\in I^+(p)$, that is $I^+(q)\subset I^+(p)$. Proof of $\supset$: suppose (p, q) are such that $I^+(p) \supset I^+(q)$, then $q\in \overline{I^+(q)}\subset \overline{I^+(p)}$. $\square$

The following result was observed in Dowker et al. (2000) and Minguzzi (2008a, Theorem 3.3).

Proposition 4.1

On a spacetime (M, g) the relations $D_p$ and $D_f$ are reflexive and transitive.

Proof

It is clear that they contain the diagonal of $M\times M$, for they contain J, thus they are reflexive. The transitivity is immediate from the second characterization in Eqs. (4.1) and (4.2). $\square$

Since the relations $D_p$ and $D_f$ are transitive and satisfy the inclusions $J\subset D_p,D_f\subset {\bar{J}}$, the same properties hold for the relation

$$\begin{aligned} D:=D_p\cap D_f&=\{(p,q):q\in \overline{J^+(p)} \text { and } p\in \overline{J^-(q)}\}\\&=\{(p,q):I^+(p) \supset I^+(q) \text { and } I^-(p) \subset I^-(q) \} . \end{aligned}$$

The following definitions of inner/outer continuity and common future/past sets were introduced by Hawking and Sachs (1974).

Definition 4.2

A map $q \mapsto F(q)\subset M$ into the open subsets of M is said to be inner continuous at $p\in M$, if for every compact set $K\subset F(p)$ there is a neighborhood $U \ni p$ such that for every $q\in U$, $F(q)\supset K$. It is outer continuous at p if for for every compact set $K\subset M\backslash \overline{F(p)}$ there is a neighborhood $V\ni p$ such that for every $q\in V$, $K\subset M\backslash \overline{F(q)}$. We speak of inner continuity and outer continuity if the properties hold true for every p.

Proposition 4.3

The maps $p \mapsto I^-(p)$ and $p\mapsto I^+(p)$ are inner continuous.

Proof

We prove the inner continuity of $p \mapsto I^-(p)$, the other case being analogous. Let $K\subset I^-(p)$ be compact, then $\{I^-(r): r\in I^-(p)\}$ is an open covering. Choose $r_1,\ldots , r_k$ to determine a finite subcovering, then $U=\cap _{i=1}^k I^+(r_i)$ is the desired neighborhood of p. $\square$

Proposition 4.4

Let $\mu$ be a probability measure absolutely continuous with respect to the Lebesgue measures of the manifold charts. The volume function $p \mapsto t^+(p):=-\mu (I^+(p))$ is upper semi-continuous, while the volume function $p \mapsto t^-(p):=\mu (I^-(p))$ is lower semi-continuous.

Proof

Let us prove that $\mu (I^+(p))$ is lower semi-continuous. Indeed, for every $\epsilon >0$ by regularity of $\mu$ we can find a compact set K such that $\mu (I^+(p)\backslash K)<\epsilon$, and by inner continuity of $p \mapsto I^+(p)$ (Proposition 4.3) there is a neighborhood $U\ni p$ such that for every $q\in U$, $I^+(q)\supset K$, hence $\mu (I^+(q))\ge \mu (K)\ge \mu (I^+(p))-\epsilon$. $\square$

For $S\subset M$ let us introduce the common past $\downarrow \! S$ and common future $\uparrow \! S$

$$\begin{aligned} \downarrow \! S&= \text {Int} \Big \{\bigcap _{p\in S} I^-(p) \Big \}=I^-\Big (\bigcap _{p\in S} I^-(p)\Big ), \\ \uparrow \! S&= \text {Int} \Big \{\bigcap _{p\in S} I^+(p) \Big \}=I^+\Big (\bigcap _{p\in S} I^+(p) \Big ) . \end{aligned}$$

The equalities follow from Proposition 2.84 2(b) since the result of the intersection is a past set (resp. future set). The sets $\uparrow \! I^{-}(p)$, $\downarrow \! I^{+}(p)$ are particularly interesting since they are constructed from the chronological relation. Let $p\le q$, and let $r\in I^-(p)$ then $r\in I^-(q)$ so $I^+(r)\supset \uparrow \! I^-(q)$, which implies $\uparrow \! I^-(p)\supset \uparrow \! I^-(q)$. Summarizing

$$\begin{aligned} p\le q\quad \Rightarrow \quad \uparrow \! I^-(p)\supset \uparrow \! I^-(q) \text { and } \downarrow \! I^+(p) \subset \downarrow \! I^+(q). \end{aligned}$$

(4.3)

In order to avoid ambiguities, we might denote $A={\bar{J}}$. Notice that $A^+(p)\ne \overline{J^+(p)}$, consistently with the notation for abstract relations introduced in Sect. 1.10. For the following result see Minguzzi (2008a) (see also Sect. 4.3.7)

Proposition 4.5

We have the identities:

$$\begin{aligned} \uparrow \! I^{-}(p)=\text {Int} \,D_p^{+}(p)=\text {Int} A^{+}(p),&\qquad \overline{D_p^{+}(p)}=A^{+}(p)=\overline{\uparrow \! I^{-}(p)}, \\ \downarrow \! I^{+}(p)=\text {Int} \,D_f^{-}(p)=\text {Int} A^{-}(p),&\qquad \overline{D_f^{-}(p)}=A^{-}(p)=\overline{\downarrow \! I^{+}(p)}. \end{aligned}$$

Proof

The characterization $D_p=\{(p,q):\forall r \in I^{-}(p), r \ll q \}$ implies

$$\begin{aligned} D^{+}_p(p)=\{q \in M:\forall r \in I^{-}(p), r \ll q \}=\bigcap _{r\in I^-(p)} I^+(r), \end{aligned}$$

(4.4)

and hence $\uparrow \! I^{-}(p)=\text {Int} \,D_p^{+}(p)$.

The inclusion $D_p^{+}(p)\subset A^+(p)$ follows from the first characterization in Eq. (4.2). Since $A^+$ is closed, $\overline{D_p^{+}(p)}\subset \overline{A^+(p)}=A^+(p)$. For the other direction, let $q\in A^+(p)$, that is $(p,q)\in {\bar{J}}$ and let $r \in I^+(q)$, then $q\in I^-(r)$ and by the openness of I, $p\in \overline{I^-(r)}$, that is $(p,r)\in D_p$. By taking the limit $r\rightarrow q$, we get $q\in \overline{D_p^{+}(p)}$.

Moreover, $D_p$ is transitive and $I\subset D_p$, thus if $q\in D^+_p(p)$ and $r\in I^+(q)$, we have $r\in D^+_p(p)$. As a consequence, $I^+(q)\subset D^+_p(p)$ hence $I^+(q)\subset \text {Int} D^+_p(p)$ and finally $q\in \overline{I^+(q)}\subset \overline{\text {Int} D_p^+(p)}$, which proves $D_p^+(p)\subset \overline{\text {Int} D_p^+(p)}$ hence $\overline{D_p^+(p)}= \overline{\text {Int} D^+_p(p)}=\overline{\uparrow \! I^{-}(p)}$.

If $q\in \text {Int} A^+(p)$ then we can find $r \ll q$ sufficiently close to q that $(p,r)\in {\bar{J}}$, hence $p\in \overline{J^-(q)}$. By the arbitrariness of q, $\text {Int} A^+(p)\subset D^+_p(p)$, hence $\text {Int} A^+(p)\subset \text {Int} D^+_p(p)=\uparrow \! I^{-}(p)$. The other inclusion follows from $D^+_p(p)\subset A^+(p)$. $\square$

Definition 4.6

The spacetime (M, g) is future reflecting if any of the following equivalent properties holds true. For every $p,q\in M$

• (i) $(p,q)\in {\bar{J}} \Rightarrow q\in \overline{J^+(p)}$,    (equivalently $D_f= {\bar{J}}$),

• (ii) $p\in \overline{J^{-}(q)} \Rightarrow q\in \overline{J^+(p)}$,    (equivalently $D_p \subset D_f$, equivalently $D=D_p$),

• (iii) $p\in \dot{J}^{-}(q) \Rightarrow q\in \dot{J}^+(p)$ ,

• (iv) $I^-(p) \subset I^-(q) \Rightarrow I^+(q)\subset I^+(p)$ ,

• (v) $\uparrow \! I^-(p)=I^+(p)$,

• (vi) $p\mapsto I^+(p)$ is outer continuous,

• (vii) the volume function $t^+(p)=-\mu (I^+(p))$ is continuous.

In (vii), $\mu$ is a probability measure as in Proposition 4.4. Due to Theorem 2.27 in (i), (ii) and (iii) we can replace the causal relation with the chronological relation. There is another characterization that we shall prove after the introduction of the K relation, namely (viii) $K^+(p)= \overline{J^+(p)}$, see Proposition 4.108.

Remark 4.7

Of course there is an analogous definition of past reflecting spacetime in which the last three right arrows are replaced by left arrows and $D_p \subset D_f$ is replaced by $D_p \supset D_f$. Point (i) is replaced by “$(p,q)\in {\bar{J}} \Rightarrow p\in \overline{J^-(q)}$, (equivalently $D_p= {\bar{J}}$)”, point (v) is replaced by ‘$\downarrow I^+(p)=I^-(p)$’, and (vi) by ‘$p\mapsto I^-(p)$ is outer continuous’.

Reflectivity was introduced by Kronheimer and Penrose (1967) through condition (iv). They actually imposed causality and our terminology of future and past is inverted with respect to theirs, but consistent with Vyas and Akolia (1986), Minguzzi and Sánchez (2008) and the subsequent literature (the terminological choice by Kronheimer and Penrose seems less natural in view of characterization (vi), but it is more natural in view of other results, cf. Remark 4.14). This concept was further elaborated by Hawking and Sachs (1974) (in the non-time oriented version, see our Definition 4.9) who proved characterizations (ii), (v), (vi), see also Clarke and Joshi (1988) who gave (iii). The relational formulation in (i)–(ii) was introduced in Minguzzi (2008a, e) and will help us to clarify the relative strength of the levels in the causal ladder.

The above properties could be used to define future reflectivity at a single point, e.g. through (v). Ishikawa (1979) and Vyas and Akolia (1986) studied the set where such a property fails.

Proof of the equivalence

We compare most properties with (ii).

(ii) $\Rightarrow$ (i). Let $(p,q)\in {\bar{J}}$ and let $r\in I^+(q)$, hence $q\in I^-(r)$ and $p\in \overline{J^-(r)}$, which implies $r\in \overline{J^+(p)}$. Since the set $\overline{J^+(p)}$ is closed and r can be chosen arbitrarily close to q, we conclude $q\in \overline{J^+(p)}$.

(i) $\Rightarrow$ (ii). $p\in \overline{J^{-}(q)} \Rightarrow (p,q)\in \bar{J} \Rightarrow q\in \overline{J^+(p)}$.

(ii) $\Rightarrow$ (iii). $p\in \dot{J}^{-}(q) \Rightarrow p\in \overline{J^{-}(q)}\Rightarrow q\in \overline{J^+(p)}$, but by assumption $p \notin \text {Int} J^-(q)=I^{-}(q)$, thus $q \notin I^+(p)=\text {Int} J^+(p)$, hence $q \in \dot{J}^+(p)$.

(iii) $\Rightarrow$ (ii). $p\in \overline{J^{-}(q)}$ $\Rightarrow$ “$p\in \dot{J}^-(q)$ or $(p,q)\in I$” $\Rightarrow$ “$q\in \dot{J}^+(p)$ or $(p,q)\in I$” $\Rightarrow$ $q\in \overline{J^+(p)}$.

(ii) $\Rightarrow$ (iv). Suppose $I^-(p) \subset I^-(q)$, as $p\in \overline{I^-(p)}$ we have $p\in \overline{I^-(p)} \subset \overline{J^-(q)}$ $\Rightarrow$ $q\in \overline{J^+(p)}$, thus every $r\in I^+(q)$ is such that $q\in I^{-}(r)$ and hence the open neighborhood of q, $I^-(r)$, contains some point of $J^+(p)$, thus $r\in I^+(p)$, which by the arbitrariness of r implies $I^+(q)\subset I^+(p)$.

(iv) $\Rightarrow$ (ii). Let $p\in \overline{J^{-}(q)}$ and let $r\in I^-(p)$, then the neighborhood of p, $I^+(r)$, contains some point of $J^-(q)$, which implies $r\in I^-(q)$, hence $I^-(p)\subset I^-(q)$, due to arbitrariness of r. By the assumption $I^+(q)\subset I^+(p)$, thus $q\in \overline{I^+(q)}\subset \overline{I^+(p)}$.

(ii) $\Rightarrow$ (v). For every $r\in I^-(p)$, $I^+(r)\supset I^+(p)$, thus $\uparrow I^-(p)\supset I^+(p)$, so we have only to prove the other inclusion. Let $q\in \uparrow I^-(p)$, then there is a neighborhood $O\ni q$, $O\subset \uparrow I^-(p)$. Let $r\in I^-(q,O)$, then for every $x\in I^-(p)$, we have $r\in I^+(x)$, i.e.  $x\in I^-(r)$, and letting $x \rightarrow p$, we get $p\in \overline{I^-(r)}$, so using (ii) $r\in \overline{I^+(p)}$, which implies by the openness of I, $q\in I^+(p)$.

(v) $\Rightarrow$ (iv). Suppose $I^-(p) \subset I^-(q)$ then, due to the definition of common future, $\uparrow I^-(q) \subset \uparrow I^-(p)$, and using (v), $I^+(q) \subset I^+(p)$.

(ii) $\Rightarrow$ (vi). Let $K\subset M\backslash \overline{I^+(p)}$. For every $q\in K$ we can find $r=r(q) \in I^+(q)\cap [M\backslash \overline{I^+(p)}]$ such that $\overline{I^-(r)}\cap I^+(p)=\emptyset$, for if not for every $r\in I^+(q)$ we have $r\in I^+(p)$, which taking $r\rightarrow q$ implies $q\in \overline{I^+(p)}$, a contradiction. Notice that $p\notin \overline{I^-(r)}$ otherwise by future reflectivity $r\in \overline{I^+(p)}$, a contradiction. As $I^-(r(q))$ is a neighborhood for q, we can find $r_1,\ldots ,r_k$ such that $\{I^-(r_i)\}$ is a finite covering of K. Now, $U=M\backslash \cup _i \overline{I^-(r_i)}$ is an open future set containing p. Since $I^+(U)$ does not intersect the open set $\cup _i I^-(r_i)$ neither does $\overline{I^+(U)}$, thus $M\backslash \overline{I^+(U)}\supset \cup _i I^-(r_i)\supset K$, so U is the desired neighborhood of p.

(vi) $\Rightarrow$ (ii). Let $p\in \overline{I^-(q)}$ and suppose by contradiction that $q\notin \overline{I^+(p)}$. As $\{q\}$ is a compact set we can find a neighborhood $U\ni p$, such that $q \notin \overline{I^+(p')}$, for every $p'\in U$. But as $p\in \overline{I^-(q)}$, there is a sequence $p_k\in I^-(q)$, $p_k\rightarrow p$ which gives a contradiction as for sufficiently large k, $p_k\in U$.

(vi) $\Rightarrow$ (vii). The function $t^+$ is upper semi-continuous by Proposition 4.4. Suppose that $p \mapsto I^+(p)$ is outer continuous, and let $\epsilon >0$. By the regularity of the measure we can find a compact set $K \subset M\backslash \overline{I^+(p)}$ such that $\mu (M\backslash [\overline{I^+(p)}\cup K])<\epsilon$, and by outer continuity there is a neighborhood $U\ni p$ such that for every $q\in U$, $K\subset M\backslash \overline{I^+(q)}$, then $\mu (I^+(q))\le \mu (M\backslash K)=\mu (M\backslash [\overline{I^+(p)}\cup K])+\mu (\overline{I^+(p)})$. Now observe that $\mu (\partial I^+(p))=0$ because $\partial I^+(p)$ being an achronal boundary is a Lipschitz graph and hence has zero measure. Thus $\mu (I^+(q))\le \mu (I^+(p))+\epsilon$.

(vii) $\Rightarrow$ (vi). If $p \mapsto I^+(p)$ is not outer continuous there is a compact set $K\subset M\backslash \overline{I^+(p)}$ and a sequence $q_n\rightarrow p$ such that $\overline{I^+(q_n)}\cap K\ne \emptyset$. Let $p_n$ be a sequence converging to p with the property $p_n\ll p_{n+1}\ll p$, for every n. Then for every n there is some m(n) such that $q_m\gg p_n$, thus $\overline{I^+(p_n)}\cap K\ne \emptyset$. Moreover, these non-empty sets get smaller with n so the family $\{\overline{I^+(p_n)}\cap K\}$ satisfies the finite intersection property, and hence, by compactness of K, $\cap _n [\overline{I^+(p_n)}\cap K]\ne \emptyset$. We can find r in this intersection and $s\gg r$ sufficiently close to r that $s\notin \overline{I^+(p)}$, thus $I^+(s)\backslash \overline{I^+(p)}$ is a non-empty open set contained in $I^+(p_n)$ for every n, which does not intersect $I^+(p)$. By denoting with $\epsilon >0$ its measure we get that $\mu (I^+(p_n))\ge \mu (I^+(p_n)\backslash \overline{I^+(p)})\cup \mu (I^+(p))\ge \mu (I^+(p))+\epsilon$, in contradiction with the upper semi-continuity of $-t^+$. $\square$

Example 4.8

A simple example of future reflecting but non-past reflecting spacetime is obtained by removing a past timelike ray from Minkowski $1+1$ spacetime.

The previous result shows that the properties in the next definition are equivalent.

Definition 4.9

The spacetime (M, g) is reflecting if it is both future and past reflecting. Equivalently, it satisfies any of the following equivalent properties. For every $p,q\in M$

• (a) $p\in \overline{J^{-}(q)} \Leftrightarrow q\in \overline{J^+(p)}$,    (equivalently $D_p = D_f$),

• (b) $p\in \dot{J}^{-}(q) \Leftrightarrow q\in \dot{J}^+(p)$ ,

• (c) $I^-(p) \subset I^-(q) \Leftrightarrow I^+(q)\subset I^+(p)$ ,

• (d) $\downarrow I^+(p)=I^-(p)$ and $\uparrow I^-(p)=I^+(p)$,

• (e) the maps $p\mapsto I^+(p)$ and $p\mapsto I^-(p)$ are outer continuous,

• (f) $D={\bar{J}}$,

• (g) the volume functions $t^+$ and $t^-$ are continuous,

in which case $D=D_f=D_p ={\bar{J}}$.

The following result is due to Clarke and Joshi (1988) and justifies interest in the reflecting property. It will imply that stationary complete spacetimes which are distinguishing are causally continuous, which ultimately implies the contraction of the causal ladder into a smaller ladder. A similar result holds for spacetimes admitting a parallel null vector. In that case strong causality is identified with stable causality (Minguzzi 2012a).

Theorem 4.10

If the spacetime admits a complete timelike Killing field then it is reflecting.

The proof really shows that completeness to the past implies past reflectivity, and dually.

Proof

Let $x\mapsto \phi _t(x)$ be the flow of the timelike Killing field. We prove $q\in \overline{J^{+}(p)} \Rightarrow p\in \overline{J^{-}(q)}$, the other direction being similar. We can find a sequence $q_k=\phi _{\epsilon _k}(q)$ with $\epsilon _k\rightarrow 0$, so that $q\in I^{-}(q_k)$, and by the openness of I, $q_k\in J^+(p)$. As a consequence, defining $p_k=\phi _{-\epsilon _k}(p)$, we have by translational invariance $p_k\in J^-(q)$, and since $p_k\rightarrow p$, $p\in \overline{J^-(q)}$. $\square$

Definition 4.11

A causal diamond is a set of the form $J^+(p)\cap J^-(q)$ with $p,q\in M$.

The property of being closed for the causal relation can be expressed in some equivalent ways, see also Minguzzi and Sánchez (2008).

Theorem 4.12

The following properties are equivalent:

• (i) J is closed in the topology of $M\times M$,

• (ii) $J^+(p)$ and $J^-(p)$ are closed for every $p\in M$,

• (iii) $J^+(K)$ and $J^-(K)$ are closed for every compact subset $K\subset M$,

• (iv) the causal diamonds are closed.

The equivalence between (i) and (ii) admits an analogous open version that we shall not use in this work, see Minguzzi (2008a, Theorem 2.2).

Proof

(i) $\Rightarrow$ (iii). This implication is well known from the theory of closed ordered spaces (Nachbin 1965). Since J is closed if $(p,q)\notin J$, there are open sets $U\ni p$, $V\ni q$, such that $(U\times V)\cap J=\emptyset$. Let $q\notin J^+(K)$, then for every $p\in K$ we can find $U_p\ni p$ and $V_p\ni q$, such that $(U_p\times V_p)\cap J=\emptyset$. Let $\{U_{p_i}\}$ be a finite covering for K and $V=\cap _i V_{p_i}$, then no point in V intersects $J^+(K)$, thus $J^+(K)$ is closed.

(iii)$\Rightarrow$ (ii) is clear.

(ii) $\Rightarrow$ (i). Let $(p_k,q_k)\rightarrow (p,q)$, $(p_k,q_k)\in J$, and let $r \in I^+(q)$, so that for sufficiently large k, $q_k\in I^-(r)$. We deduce $p_k\in J^-(r)$ and so using (ii), $p\in J^-(r)$, hence $r\in J^+(p)$ so letting $r\rightarrow q$ and using again (ii), $q\in J^+(p)$, which proves that J is closed.

(ii)$\Rightarrow$ (iv) is clear.

(iv) $\Rightarrow$ (ii). Let $q \in \overline{J^+(p)}$, then there are $q_k\in J^+(p)$ such that $q_k\rightarrow q$. Let $r \in I^+(q)$, then $D=J^+(p)\cap J^-(r)$ is a closed set (by assumption) which by the openness of $I^-(r)$ contains $q_k$ for sufficiently large k, thus $q\in D\subset J^+(p)$. Thus $J^+(p)$ is closed for every p. An analogous argument shows that $J^-(p)$ is closed for every p. $\square$

In Minguzzi (2009e) we introduced the transverse ladder, a useful structure that might be used to clarify the central position of stable causality.

Theorem 4.13

(Transverse ladder) Compactness of causal diamonds $\Rightarrow$ The causal relation is closed $\Rightarrow$ Reflectivity $\Rightarrow$ Transitivity of ${\bar{J}}$.

Proof

Compactness of causal diamonds $\Rightarrow$ The causal relation is closed. This result follows immediately from the previous theorem.

The causal relation is closed $\Rightarrow$ Reflectivity. It is clear that $J={\bar{J}}$ implies $D_p=D_f=J={\bar{J}}$, which implies reflectivity.

Reflectivity $\Rightarrow$ Transitivity of ${\bar{J}}$. Under reflectivity $D_p=D_f={\bar{J}}$, but $D_f$ and $D_p$ are transitive by Proposition 4.1, thus ${\bar{J}}$ is transitive. $\square$

Remark 4.14

The characterization in Definition 4.6(ii) of future reflectivity has this consequence: the causal relation is past closed (i.e. $J^-(p)$ is closed for every $p\in M$) implies future reflectivity. Moreover, future reflectivity implies $D_f={\bar{J}}$ hence the transitivity of ${\bar{J}}$. We conclude that the transverse ladder could be conjugated in oriented versions (although each version mixes past and future).

Geodesic completeness and other fairly reasonable energy and genericity conditions imply that lightlike geodesics develop conjugate points and so cannot be maximizing. Let us study the consequences of the absence of lightlike lines for causality. We prefer to use this concept as it is conformally invariant. We shall explore later on the connection with the mentioned more physically motivated conditions. The following result appeared in Minguzzi (2009c).

Theorem 4.15

If (M, g) does not admit lightlike lines then $\bar{J}$ is transitive.

The fact that $\bar{J}$ is both closed and transitive shall have a number of useful consequences, for in this case one can apply Nachbin’s theory of closed ordered spaces (Nachbin 1965). For instance, under chronology it implies the existence of a semi-time function (Theorem 4.101), while under strong causality it implies the existence of a time function (Proposition 4.105).

Proof

Let us consider two pairs $(p,q) \in {\bar{J}}$ and $(q,r) \in {\bar{J}}$ and two sequences of causal curves $\sigma _n$ of endpoints $(p_n, q_n) \rightarrow (p,q)$, and $\gamma _n$ of endpoints $(q'_n,r_n) \rightarrow (q,r)$. We apply the limit curve theorem to both sequences, and consider first the case in which the limit curve, in both cases, does not connect the limit points. By the limit curve theorem, $\sigma _n$ has a limit curve $\sigma$ which is a past inextendible continuous causal curve ending at q. Analogously $\gamma _n$ has a limit curve $\gamma$ which is a future inextendible continuous causal curve starting from q. The inextendible curve $\gamma \circ \sigma$ cannot be a lightlike line, thus there are points $p'\in \sigma \backslash \{q\}$, $r' \in \gamma \backslash \{q\}$ such that $(p',r')\in I$ and (pass to a subsequence) points $p'_n \in \sigma _n$, $p'_n \rightarrow p'$ and $r'_n \in \gamma _n$, $r'_n \rightarrow r'$. Since I is open, for sufficiently large n, $(p'_n,r'_n) \in I$ and $(p_n,r_n) \in I$, and finally $(p,r) \in \bar{I}={\bar{J}}$.

If both limit curves join the limit points then clearly $(p,r) \in J\subset {\bar{J}}$. If, say, $\sigma$ joins p to q but $\gamma$ does not join q to r, take $p'_n\in I^{-}(p)$, $p'_n \rightarrow p$, so that $p'_n\ll q$ and for large m, $p'_n\ll q'_m\le r_m$, thus in the limit $(p,r) \in {\bar{J}}$. The remaining case is analogous. Thus ${\bar{J}}$ is transitive. $\square$

Every lightlike line becomes a lightlike ray if its domain is suitably restricted. Thus the absence of future (or past) lightlike rays implies the absence of lightlike lines. We have also that under chronology the absence of future lightlike rays implies global hyperbolicity and the fact that the only TIP is M, see Minguzzi (2009a, c).

4.2 The lower levels

In this section we study the lower levels of the causal ladder. We shall prove that every level implies that below it, and we shall provide examples which clarify that they are actually different. Since the causality properties are conformally invariant, and so depend only on the distribution of light cones, these examples will often be introduced through qualitative pictures in which past cones are depicted in black.

The worst causal circumstance is that in which through every event there passes a closed timelike curve. These spacetimes are called totally vicious because the spacetimes that admit some closed timelike curve are called vicious (Carter 1968) or non-chronological. They are called non-trivially vicious if the causal pathology cannot be removed by passing to a covering.

Before we introduce the ladder, let us mention that many of the levels below stable causality are characterized by the antisymmetry of some relation R, a property known as R-causality. The formulation in terms of an antisymmetry property is often convenient, for if $A\subset B$, then B-causality implies A-causality, as the relative strength of the antisymmetry conditions is reflected in the relative inclusion of the relations.

Other properties have been used to characterize the causality levels in a unified way beside antisymmetry. Rácz (1987) observed that many causality conditions can be restated as injectivity conditions for the set-valued maps $p \mapsto R^\pm (p)$. The two properties are in fact connected, due to the following result (Minguzzi 2008a). We denote by P(M) the family of subsets of M, see also Sect. 1.10 for the meaning of $R^+$ and $R^-$.

Theorem 4.16

The generic relation R satisfies

• (a) If $R^+:M \rightarrow P(M)$ or $R^{-}:M \rightarrow P(M)$ are injective and R is transitive, then R is antisymmetric.

• (b) If R is antisymmetric and reflexive, then both maps $R^{+}:M \rightarrow P(M)$ and $R^{-}:M \rightarrow P(M)$ are injective.

• (c) If R is transitive and reflexive, then the injectivity of the map $R^{+}:M \rightarrow P(M)$ is equivalent to the injectivity of the map $R^{-}:M \rightarrow P(M)$. Moreover, the injectivity is equivalent to the antisymmetry.

Proof

Proof of (a). Assume $p \rightarrow R^{+}(p)$ is injective and that R is transitive. Take $p,q \in M$ such that $(p,q)\in R$ and $(q,p) \in R$. Let $r \in R^{+}(p)$, since R is transitive $r\in R^{+}(q)$, thus $R^{+}(p) \subset R^{+}(q)$. The other inclusion is analogous, thus $R^{+}(p)=R^{+}(q)$ and by injectivity $p=q$.

Proof of (b). Assume R is antisymmetric and reflexive and take $p,q \in M$ such that $R^{+}(p)=R^{+}(q)$. Then, because of reflexivity $p \in R^{+}(p)=R^{+}(q)$ and analogously $q \in R^{+}(p)$, thus by antisymmetry $p=q$.

Proof of (c). It is a trivial consequence of (a) and (b). $\square$

This theorem shows that under the assumption of transitivity and reflexivity the injectivity is equivalent to the antisymmetry and hence R-causality can be expressed in terms of the injectivity of the point based maps $p\mapsto R^{+}(p)$. For instance, weak distinction is equivalent to the injectivity of the map $p\mapsto D^\pm (p)$. In what follows the injectivity characterization will be mentioned only in those cases in which it is not a trivial consequence of the previous theorem.

Another unifying approach is that by Vyas and Joshi (1983), Dieckmann (1988), Joshi (1989, 1993), see also Hounnonkpe (2018), who expressed many causality properties by means of the volume function, a concept first introduced by Geroch in his proof of the topological splitting theorem for globally hyperbolic spacetimes (Hawking 1968; Geroch 1970).

Definition 4.17

A volume function is a function of the form $p\mapsto \mp \mu (R^{\pm }(p))$, where R is some causal relation of interest and $\mu$ is a probability measure absolutely continuous with respect to the Lebesgue measures of the coordinate charts.

In most cases one takes $R=I$, in which case these functions are semi-continuous cf. Proposition 4.4, and actually continuous under reflectivity Definition 4.9. We shall see that they are strictly increasing over causal curves under distinction, Theorem 4.58.

4.2.1 Non-totally vicious spacetimes

We recall (Definition 2.76) that the chronology violating set $\mathcal {C}$ is the open set of points through which there passes a closed timelike curve. In other words,

$$\begin{aligned} \mathcal {C}=\{p\in M:p\ll p\}. \end{aligned}$$

As observed by Carter, the relation $p\sim q$ iff $p\ll q\ll p$ is an equivalence relation and so $\mathcal {C}$ is really the union of open equivalence classes (Hawking and Ellis 1973, Proposition 6.4.1). If $p\in \mathcal {C}$ we denote by [p] the class which contains p (Fig. 8).

Fig. 8

The lower portion of the causal ladder of spacetimes. An arrow between two properties $\mathcal {P}_1 \Rightarrow \mathcal {P}_2$ means that the former implies the latter and that there are examples of spacetimes in which the latter holds and the former does not hold

According to Definition 1.6 our spacetimes are non-compact unless otherwise specified. The following result and Theorem 4.29 are the only ones in which we do not assume non-compactness. A proof of the next result, due to Carter (1971) can also be found in Senovilla (1998).

Proposition 4.18

On a compact spacetime $\mathcal {C}\ne \emptyset$.

Proof

The family $\{I^+(p):p \in M\}$ is really a covering of M since for every $q\in M$, we can find $p\ll q$ in a neighborhood of q. Thus there is a finite subcovering $\{I^+(p_i), i=1,\ldots , k\}$. Since every $p_i$ stays in the chronological future of some $p_{j(i)}$, it is possible to construct a closed timelike curve by going backward while connecting points. $\square$

Definition 4.19

A non-totally vicious spacetime is a spacetime for which $\mathcal {C}\ne M$.

Proposition 4.20

In a totally vicious spacetime for every $p\in M$, we have $[p]=M$. Moreover, if on a spacetime there is some p such that $[p]=M$ then the spacetime is totally vicious.

Proof

Since $M=\mathcal {C}$, M is the disjoint union of open equivalence classes. Connectedness of M implies that there is just one class. For the latter claim of the proposition, if $[p]=M$ then $M=\mathcal {C}$, thus M is totally vicious. $\square$

Notice that in a non-totally vicious spacetime for every $p\in \mathcal {C}$, we have $[p]\ne M$. Thus for every $p\in \mathcal {C}$ either $I^+(p)\ne M$ or $I^-(p)\ne M$. Moreover, if in a spacetime there is a point $p\in M$, such that $I^+(p)\ne M$ or $I^-(p)\ne M$ then the spacetime is non-totally vicious.

The following classical result can be found in Kriele (1989, Proposition 2), see also the proof of Minguzzi (2009c, Theorem 12).

Theorem 4.21

Through every point $p\in \partial \mathcal {C}$ there passes a future or a past lightlike ray entirely contained in $\partial \mathcal {C}$.

Proof

Let $p_n \rightarrow p$, with $p_n\in \mathcal {C}$, and let $\sigma _n$ be closed timelike curves with starting and ending point $p_n$. Since p admits a causal neighborhood (cf. Theorem 2.11) the curve $\sigma _n$ do not contract to p, so the application of the limit curve theorem gives two possibilities. Case (a), there is a closed causal curve $\eta$ passing through p. The curve $\eta$ cannot enter $\mathcal {C}$ for if $q\in \eta \cap \mathcal {C}$, $p\le q\ll q\le p$, thus $p\ll p$, a contradiction since $p\in \partial C$. Moreover, the curve $\eta$ is achronal, for if there are $x\ll y$, $x,y\in \eta$, by the closedness of $\eta$, $x\ll x$, i.e. $x\in \mathcal {C}$ in contradiction with $\eta \cap \mathcal {C}=\emptyset$. Thus $\eta$ is a lightlike line. Case (b), there are a future inextendible causal curve $\sigma$ starting from p and a past inextendible causal curve $\gamma$ ending at p, such that for every $q\in \sigma$ and $r\in \gamma$, $(q,r)\in {\bar{J}}$. It follows that either $\sigma \backslash \{p\}\cap I^+(p)=\emptyset$ or $\gamma \backslash \{p\}\cap I^-(p)=\emptyset$, for otherwise having chosen $q\gg p$ and $r\ll p$ as above, we have $p\ll p$, a contradiction. In the former case $\sigma$ is achronal, for if $q',q\in \sigma$, $q'\ll q$, then $p\ll q$, a contradiction. Analogously, in the latter case $\gamma$ is achornal hence a lightlike ray. $\square$

Fig. 9

The simplest totally vicious spacetime

Not all spacetimes are non-totally vicious as the following examples show.

Example 4.22

An example of totally vicious spacetime is $S^1\times \mathbb {R}$ of coordinates $(\theta ,x)$ and metric $g=-\mathrm{d}\theta ^2+\mathrm{d}x^2$. It can be obtained by identifying the spacelike lines $t=0$ and $t=0$ in $1+1$ Minkowski spacetime, see Fig. 9. This spacetime satisfies the vacuum Einstein equations.

Example 4.23

Gödel (1949) found the following totally vicious spacetime: $M=\mathbb {R}^4$ and

$$\begin{aligned} g= \frac{1}{2\omega ^2} [ -(dt + e^x dz)^2 + dx^2 + dy^2 + \tfrac{1}{2} e^{2x} dz^2], \end{aligned}$$

which is actually a solution of Einstein equations with cosmological constant $\varLambda =-\omega ^2$ and a stress-energy tensor of dust type.

4.2.2 Chronology

A relation $R\subset M\times M$ is irreflexive if $(p,p)\notin R$ for every $p\in M$. For the chronological relation this condition reads: for every $p\in M$, $p\not \!\ll p$

Definition 4.24

A spacetime is chronological if the following equivalent conditions hold true:

• (i) there are no closed timelike curves,

• (ii) $\mathcal {C}=\emptyset$,

• (iii) the chronological relation I is irreflexive: $p\not \ll p$,

• (iv) the chronological relation I is antisymmetric (same for $\varDelta \cup I$ which is a preorder),

• (v) $p\notin \,\uparrow \! I^-(p)$.

Proof of the equivalence

The simple proof of the equivalence between the first three properties is left to the reader. As for (iv) it is sufficient to note that in absence of closed timelike curves (iv) holds because the assumption ‘$(p,q)\in I$ and $(q,p)\in I$’ in the implication defining antisymmetry is false. If instead there are closed timelike curves, picking two points over it one sees that (iv) does not hold.

Let us prove the last characterization (due to Joshi 1993, Proposition 4.7). If $p\notin \uparrow \! I^-(p)$ then since $I^+(p)\subset \uparrow \! I^-(p)$, we must have $p\notin I^+(p)$, hence chronology due to the arbitrariness of p.

Conversely, under chronology we cannot have $p \in \uparrow \! I^-(p)$, for this set is open hence there would be $r\ll p$, $r\in \uparrow \! I^-(p)$, but since $r\in I^-(p)$ there would be a timelike curve from r to r, a contradiction. $\square$

The following obvious fact provides the first step in the causal ladder

Proposition 4.25

Every chronological spacetime is non-totally vicious.

The following result is due to Clarke and Joshi (1988).

Proposition 4.26

A reflecting non-totally vicious spacetime is chronological.

Proof

Suppose not, and let $p\in \mathcal {C}$, then by a previous observation $I^+(p) \ne M$ or $I^-(p)\ne M$. Without loss of generality let us consider the former possibility. Let $q\in \partial I^+(p)$, by reflectivity $p\in \partial I^-(q)$. Since $p\ll p$, $I^+(p)$ is an open neighborhood of p, thus there is $s\in I^+(p)\cap I^-(q)$, which implies $q\in I^+(p)$, a contradiction. $\square$

The next corollary, which follows from Theorem 4.10, can be found, in a somewhat different form, in a paper by Clarke and de Felice (1982), see also Vyas (2008).

Corollary 4.27

A non-totally vicious spacetime admitting a complete timelike Killing field is chronological.

Fig. 10

An example of non-totally vicious non-chronological spacetime. The middle closed lightlike curve runs at the boundary of the chronology violating set

Not all non-totally vicious spacetimes are chronological.

Example 4.28

The Kerr and Taub-NUT spacetimes provide vacuum solutions of Einstein equations which are non-totally vicious and non-chronological. The Misner spacetime is also non-totally vicious and non-chronological (Hawking and Ellis 1973). A simple causal structure with the same property is displayed in Fig. 10. It is obtained from a manifold $\mathbb {R}\times S^1$ endowed with the metric

$$\begin{aligned} g=-\alpha \otimes \beta , \qquad \alpha = -\sin f(t) \mathrm{d}\theta +\cos f(t) \mathrm{d}t, \quad \beta = \cos f(t) \mathrm{d}\theta +\sin f(t) \mathrm{d}t, \end{aligned}$$

with $f(t)\in (0,\pi /2]$ for $t>0$ and $f(t)\in [-\pi /2,0)$ for $t<0$, for instance $f= \arctan t$. A last example of non-chronological non-totally vicious spacetime is given by Fig. 1.

We give a simple proof of the following result which passes through Clarke and Joshi’s Theorem 4.10. For another proof see Sánchez (2006) and Minguzzi and Sánchez (2008).

Theorem 4.29

Any compact spacetime which admits a timelike conformal Killing vector field K is totally vicious, i.e. $\mathcal {C}=M$.

Proof

If K is timelike $g(K,K)\ne 0$, thus K is Killing and normalized for $g'=\frac{1}{-g(K,K)} g$. Standard ODE theory tells us that K is necessarily complete due to the compactness of M, thus by Theorem 4.10 $(M,g')$ is reflecting. Since M is compact $(M,g')$ is non-chronological thus, by Proposition 4.26, it is totally vicious. $\square$

4.2.3 Causality

We recall that a relation R is antisymmetric if $(p,q)\in R$ and $(q,p)\in R$ $\Rightarrow q=p$. A reflexive, transitive and antisymmetric relation is a (partial) order. A (partial) order is a total order if any two points are comparable ‘$(p,q)\in R$ or $(q,p)\in R$’.

Definition 4.30

A spacetime is causal if the following equivalent conditions hold true:

• (i) there are no closed causal curves,

• (ii) the causal relation J is antisymmetric (that is, a partial order),

• (iii) the set-valued map $p\mapsto J^+(p)$ is injective.

Of course (iii) has an analogous past version. Since every timelike curve is causal, we have

Proposition 4.31

Every causal spacetime is chronological.

Chronological spacetimes need not be causal, see Fig. 11.

Fig. 11

An example of chronological non-causal spacetime of topology $\mathbb {R}\times S^1$. The middle closed lightlike curve is expected from Proposition 4.32

Proposition 4.32

A chronological but non-causal spacetime contains a closed inextendible achronal lightlike geodesic (hence a lightlike line), $\gamma :\mathbb {R}\rightarrow M$ necessarily such that for some $a,b\in \mathbb {R}$, $a<b$, $\gamma (a)=\gamma (b)$, ${\dot{\gamma }}(a)\propto {\dot{\gamma }}(b)$.

Proof

Since (M, g) is non-causal there is a closed causal curve $\gamma$ such that for some values a, b, $a<b$, in its domain $\gamma (a)=\gamma (b)$. There cannot be any two points $p,q\in \gamma$ such that $p\ll q$, otherwise $p\ll q\le p\Rightarrow p\ll p$ in contradiction with chronology. Thus $\gamma$ is achronal and hence a geodesic up to parametrization. Once parametrized it cannot develop a corner anywhere for otherwise there would be $p,q\in \gamma$ such that $p\ll q$, hence ${\dot{\gamma }}(a)\propto {\dot{\gamma }}(b)$. $\square$

With the notation of Sect. 1.13 we have (Minguzzi and Sánchez 2008)

Theorem 4.33

In a causal spacetime $\rightarrow ^{(\le )}=\rightarrow$ and $\ll ^{(\le )}=\ll$.

Proof

It is sufficient to prove the former identity.

The implication $p\rightarrow q \Rightarrow p \rightarrow ^{(\le )}q$, follows from Theorem 2.26.

Let $p \rightarrow ^{(\le )} q$ then clearly $p\le q$. By contradiction, suppose that $p\ll q$ and let $p',q'$ be such that $p\ll p'\ll q'\ll q$. Let $D=J^+(p')\cap J^-(q')$ then there is an order homeomorphism $t:D\rightarrow [0,1]$, but then $t^{-1}([0,1])$ would be a curve connecting just p to q, not the whole D. $\square$

4.2.4 Interlude: abstract approaches to causality

Kronheimer and Penrose (1967) proposed to axiomatize causality theory on the basis of a few properties satisfied by the chronological and causal relations in causal spacetimes.

Definition 4.34

A KP-causal space is a triple (M, J, I) where (M, J) is a partial order, $I\subset J$ is irreflexive, and I is a (two-sided) J-ideal in the sense that $I\circ J\cup J\circ I\subset I$.

In this setting one also defines the relation $\mathcal {E}=J\backslash I$ (in fact, axiom (VII) in Kronheimer and Penrose 1967) can be regarded as a definition for $\mathcal {E}$).

Proposition 4.35

Let (M, g) be a spacetime and let I be the chronological relation and J the causal relation. Then the triple (M, J, I) is a KP-causal space if and only if (M, g) is causal.

Proof

This follows immediately from Theorem 2.24 and from the fact that causality implies chronology. $\square$

Kronheimer and Penrose’s work introduced many causality concepts that are explored in this review and that are really of interest, still some parts of their paper appear as too involved possibly due to their very abstract point of view.

A very interesting and related approach is that advocated by Martin and Panangaden (2006, 2011) and Ebrahimi (2015). It uses elements from theoretical computer science and domain theory which have been much more explored by mathematicians. In both the KP and MP abstract approaches no topological assumption is made on I or J, for the topology is recovered from the order. Other important logical structures useful for quantum physics and connected to the spacetime manifold are explored in Cegła and Jadczyk (1977) and Casini (2002).

I proposed a different approach towards the axiomatization of causality (Minguzzi 2019). In my view we could work with just one closed partial order, which in the Lorentzian setting should be identified with the K or $J_S$ relation, to be introduced later on. In this framework many important results on time functions follow from Nachbin’s theory of closed ordered spaces (Nachbin 1965). Also this approach clarifies that there is really no need to recover topology from order, or the other way around, because both are unified by, and descend from, a more general and elegant structure, that of quasi-uniformity.

Harris (1998) had also proposed an axiomatization based on just one relation, his choice being the chronological relation. He was motivated by Geroch, Kronheimer and Penrose’s boundary construction (Geroch et al. 1972).

4.3 The non-imprisoning levels

The levels of this section do not remove the causal pathologies connected to almost closed causal curves (and variations) but at least are non-totally imprisoning, a property which is particularly useful when it comes to applications of the limit curve theorem.

4.3.1 Non-total imprisonment

We recall the following definition (Remark 2.54) attributed by Carter to Misner (Carter 1971).

Definition 4.36

A spacetime is non-totally imprisoning or simply non-imprisoning if no future inextendible causal curve is contained in a compact set.

The definition formulated with the past adjective would have given the same property since, by Lemma 2.74, the imprisonment of a future inextendible or of a past inextendible causal curve implies that of an inextendible continuous causal curve (Beem 1976a).

Proposition 4.37

Every non-imprisoning spacetime is causal.

Proof

Every closed causal curve can be made inextendible while keeping its compact image by winding over the image. $\square$

Fig. 12

Carter’s example of causal totally imprisoning spacetime of topology $\mathbb {R}\times T^2$. One of the identification involves a translation of an irrational number $\epsilon$

Example 4.38

A classical example of causal non-imprisoning spacetime is Carter’s. The causal structure is depicted in Fig. 12. The topology is $\mathbb {R}\times S^1\times S^1$. The coordinates are $t,\theta ,\psi$, $t\in \mathbb {R}$, $\theta ,\psi \in [0,1]$ and we have the identifications $(t,\theta ,0)\sim (t,\theta ,0)$, $(t,0,\psi )\sim (t,1,\psi +\epsilon )$ where $\epsilon$ is an irrational number. The metric can be chosen to be

$$\begin{aligned} g=-\alpha \otimes \beta +\mathrm{d}\psi ^2, \quad \alpha = -\sin f(t) \mathrm{d}\theta +\cos f(t) \mathrm{d}t, \quad \beta = \cos f(t) \mathrm{d}\theta +\sin f(t) \mathrm{d}t, \end{aligned}$$

with $f(t)\in (0,\pi /2]$ for $t\ne 0$ and $f(0)=0$. For instance $f= \arctan t^2$. Notice that the lightlike curves running at $t=0$ are really geodesics, in fact this surface is the past Cauchy Horizon $H^-(S)$ for the partial Cauchy surface $S=t^{-1}(1)$, so that Theorem 3.24 applies.

We recall the following characterization which follows from Lemma 2.17, Theorem 2.55 and Lemma 2.75 (see also Sämann 2016, Lemma 2.7).

Theorem 4.39

Let h be an auxiliary Riemannian metric. A spacetime is non-totally imprisoning if and only if for every compact set K we can find a constant $c(K)>0$ such that the h-arc length of any continuous causal curve contained in K is bounded by c.

Here h does not need to be complete because it can be extended outside K to a complete Riemannian metric, so that Lemma 2.17 applies.

Beem and Ehrlich (1987), Beem (1994) and Beem et al. (1996, Definition 11.17) introduced the following concepts

Definition 4.40

The spacetime (M, g) is causally (null) geodesically disprisoning provided no causal (resp. null) inextendible geodesic is future or past totally imprisoned in a compact set.

In most cases these properties are not new, in fact we have

Proposition 4.41

For a chronological spacetime the notions (a) non-totally imprisoning, (b) causally geodesically disprisoning, and (c) null geodesically disprisoning, are equivalent.

Proof

It is clear that (a) $\Rightarrow$ (b) $\Rightarrow$ (c). Assume (c), if (a) does not hold by Theorem 2.77 we can find a lightlike line imprisoned in compact set, a contradiction. $\square$

We recall that $g<g'$ means that the causal cones of g are contained in the timelike cones of $g'$. A spacetime (M, g) is stably causal if there is $g'>g$ which is causal. We have the following characterization of non-total imprisonment (Beem 1976a)

Theorem 4.42

A spacetime is non-totally imprisoning if and only if every open relatively compact subset $O\subset M$ is stably causal once regarded as a spacetime $(O,g\vert _O)$ with the induced metric.

Proof

$\Rightarrow$. Assume non-total imprisonment and suppose, by contradiction, that there is $O\subset M$ relatively compact, such that $(O,g\vert _O)$ is not stably causal. Let $g_n\rightarrow g$, $g<g_{n+1}<g_n$, be a sequence of metrics defined just over O save for $g_1$ which is defined in a compact neighborhood of ${\bar{O}}$, then for every such metric $g_n$ we can find a closed $g_n$-causal curve $\sigma _n\subset O$. Due to the compactness of ${\bar{O}}$ there is an accumulation point $p\in {\bar{O}}$ for the sequence $\sigma _n$. The curves cannot contract to p, for p admits a $g_1$-causal neighborhood (Theorem 2.11), hence $g_n$-causal for $n\ge 1$. By the limit curve theorem on (M, g) and by the causality of (M, g) we find an inextendible continuous causal curve $\sigma$ passing through p and contained in ${\bar{O}}$, a contradiction with non-total imprisonment.

$\Leftarrow$. By contradiction, suppose that there is a future inextendible continuous causal curve imprisoned in a compact set K and let O be a relatively compact open neighborhood of K. By Theorem 2.75 we can find an inextedible continuous causal curve $\alpha \subset K$ such that $\varOmega _f(\alpha )={\bar{\alpha }}$. Let $p,q\in \alpha$ with $p<q$, then since the curve accumulates on itself at p, $p\in \overline{J_g^+(q)}$. Let $g'>g$ on O, then $p\in I^-_{g'}(q)$ and $p\in \overline{J_{g'}^+(q)}$, which implies $q\ll _{g'} q$, thus as $g'$ is arbitrary, $(O,g\vert _O)$ is not stably causal. $\square$

A spacetime is causally geodesically complete if every inextendible causal geodesic is complete, that is, the affine parameter has domain $\mathbb {R}$. It is useful to recall that under the conformal change $g'=\varOmega ^2 g$, the proper time of timelike curves, and hence the affine parameter of timelike geodesics, changes as follows $\mathrm{d}\lambda '=\varOmega \mathrm{d}\lambda$. For lightlike geodesics the parameter change is instead $\mathrm{d}\lambda ' =\varOmega ^2 \mathrm{d}\lambda$, see Wald (1984b, Appendix D).

If a future incomplete lightlike geodesic is future imprisoned in a compact set K, then through a conformal change of metric there is no chance to attain completeness of the causal curve (that would still be a lightlike geodesic up to parametrization), for the conformal factor would be bounded over the compact set K. In fact Misner constructed a spacetime that contains such an imprisoned incomplete lightlike geodesic. Clarke (1971) showed that strongly causal spacetimes could be made lightlike geodesically complete through a conformal change of metric and Seifert (1971) showed that under stable causality it could also be made causally geodesically complete. From the causal point of view the optimal result in this direction was obtained by Beem with the following theorem (Beem et al. 1996; Ehrlich and Easley 2004) that implies the results by Clarke and Seifert.

Theorem 4.43

In every non-totally imprisoning spacetime (M, g) it is possible to find a positive function $\varOmega$ such that $(M,\varOmega ^2 g)$ is causally geodesically complete.

4.3.2 Weak distinction

In Sect. 4.1 we studied the reflecting property and introduced the transitive relations $D_p$, $D_f$ and

$$\begin{aligned} D=D_p\cap D_f&=\{(p,q): p\in \overline{J^-(q)} \text { and } q \in \overline{J^+(p)}\}\\&=\{(p,q): I^+(p)\supset I^+(q) \text { and } I^-(p)\subset I^-(q)\}. \end{aligned}$$

All contain J and are contained in ${\bar{J}}$.

Let $p \in M$, a neighborhood U of p is said to future distinguish p if there is no future directed continuous causal curve $\gamma :[0,1]\rightarrow M$ that starts from p, $\gamma (0)=p$, escapes U and reenters it, in other words $\gamma ^{-1}(U)$ is connected. A similar definition is given with past replacing future.

Theorem 4.44

The following properties are equivalent:

• (i) the set valued map $p \mapsto I^+(p)$ is injective (i.e. $I^+(p)=I^+(q) \Rightarrow p=q$),

• (ii) $D_f$ is antisymmetric,

• (ii’) $(q,p)\in J$ and $q\in \overline{J^+(p)} \Rightarrow p=q$,

• (iii) every event admits arbitrarily small future distinguishing neighborhoods (i.e. for every $V\ni p$ we can find an open neighborhood $U\ni p$, $U\subset V$, such that every continuous causal curve with starting point p and ending point in U is entirely contained in U),

• (iv) For every $p\in M$ and for every neighborhood $V\ni p$, we can find an open neighborhood $U\subset V$, $p\in U$, such that $J^+(p,U)=J^+(p)\cap U$,

• (v) The volume function $t^+(p)= -\mu (I^+(p))$ is strictly increasing over causal curves,

• (v’) There is an upper semi-continuous function which is strictly increasing over causal curves.

Of course there is an analogous past version, for instance (v) reads: The volume function $t^-(p)=\mu (I^-(p))$ is strictly increasing over causal curves, while $(v')$ reads: There is a lower semi-continuous function which is strictly increasing over causal curves. Characterization $(v')$ has been recently given by Hounnonkpe (2018).

Remark 4.45

The neighborhood U in (iii) or (iv) can be chosen to be any element of the basis $\{V_k\}$ of Theorem 1.35 for sufficiently large k. In fact let $V'=V_1\cap V$, then the theorem tells us that there is $U'\subset V'$ with property (iii) (or (iv)). For sufficiently large k, $V_k\subset U'$ and $V_k$ is causally convex in $V_1$, so every causal curve which starts from p and leaves $V_k$ to reenter it, will have to leave $V_1$ and hence $U'$. In case (iii) this is impossible. In case (iv) there is another causal curve with the same endpoints (in $V_k$) contained in $U'\subset V_1$ and hence in $V_k$. Thus, in both cases, $U=V_k$ has the property of the theorem.

Proof

$(i)\Rightarrow (ii)$. If $D_f$ is not antisymmetric we can find $p,q\in M$, $p\ne q$, such that $q\in \overline{J^+(p)}$ and $p\in \overline{J^+(q)}$. Let $r\in I^+(p)$ then $p\in I^-(r)$ and since it is open, $q\in I^-(r)$. From the arbitrariness of r, $I^+(p)\subset I^+(q)$. The other inclusion is analogous.

Not $(iii) \Rightarrow$ not $(ii')$ and not (iv). Suppose that the property (iii) does not hold, hence there is $V\ni p$, such that taking a basis $\{V_k\}$ as in Theorem 1.35 with $V_1\subset W\subset V$, and W convex normal, we have for every k the existence of a continuous causal curve $\gamma _k$ starting from p that escapes $V_k$ and reenters it. Since $V_k$ is causally convex in $V_s$, for $s\le k$, it escapes and reenters $V_s$ too, thus there is a last reentrance point $r_{ks}\in \partial V_s$, $r_{ks}\le r_{kk}$. For fixed s, we find that there is $r_s\in \partial V_s$ such that (passing to a subsequence if necessary) $r_{ks}\rightarrow r_s$ for $k\rightarrow \infty$, thus $r_s\in \overline{J^+(p)}$. Since $(r_{ks}, r_{kk}) \in J_W$ by Theorem 2.11, $(r_s,p)\in J_W\subset J$. Thus $(r_s,p)\in J$ and $(p,r_s)\in D_f$ while $r_s\ne p$, that is, not $(ii')$. Moreover, suppose that (iv) does hold then there is ${\tilde{U}}\subset W$, $p\in {\tilde{U}}$, such that $J^+(p,{\tilde{U}})=J^+(p)\cap {\tilde{U}}$. However, pick s so large that $r_s\in {\bar{V}}_s\subset {\tilde{U}}$. We know that $r_s\in \overline{J^+(p)\cap {\tilde{U}}}$, thus $r_s\in \overline{J^+(p,{\tilde{U}})}\subset \overline{J^+(p,W)}$ hence $r_s\in J^+(p,W)$ (by Theorem 2.11), which is impossible because W is causal. The contradiction proves “not (iv)”.

$(iii) \Rightarrow (iv)$. Trivial. $(ii) \Rightarrow (ii')$. Follows from $J\subset D_f$.

Not $(i) \Rightarrow$ not (iii). Let $p\ne q$ be such that $I^+(p)=I^+(q)$ and let V be a neighborhood of p such that $q\notin {\overline{V}}$. Let $U\subset V$, $p\in U$, and let $r\in I^+(p,U)$, then $r\in I^+(q)$, thus if W is a neighborhood of q which does not intersect V, we can find ${\bar{r}}\in I^-(r)\cap I^+(q,W)$. Thus $p\ll {\bar{r}} \ll r$ and the timelike curve that connects these points starts from p, and escapes and reenters U.

$(i) \Rightarrow (v)$. Let $p<q$ then $I^+(p)\supset I^+(q)$ and these sets actually differ due to (i). Thus there is some $r\in I^+(p)\backslash I^+(q)$, since $I^+(p)$ is open we can find $r'\ll r$, $r'\in I^+(p)$ and necessarily $r'\notin \overline{I^+(q)}$ (otherwise $r\in I^+(q)$, a contradiction). Thus $I^+(r')\backslash \overline{I^+(q)}$ is a non-empty open set contained in $I^+(p)$ but not in $I^+(q)$, which implies that the volume function does indeed strictly increase over causal curves.

$(v) \Rightarrow (ii')$. Suppose that $(q,p)\in J$ and $q\in \overline{J^+(p)}$. As a consequence $I^+(p)=I^+(q)$ and $-\mu (I^+(p))=-\mu (I^+(q))$, but $q \le p$ and the volume function is bound to increase if $q<p$, we conclude that $q=p$.

$(v) \Rightarrow (v')$ is clear. $(v') \Rightarrow (ii')$. Let t be the upper semi-continuous function of the assumption and let $(q,p)\in J$ and $q\in \overline{J^+(p)}$. If $q=p$ we have finished, otherwise $t(q)<t(p)$ and given $q_n\in J^+(p)\backslash \{p\}$, $q_n\rightarrow q$, $t(q)\ge \limsup t(q_n)\ge \limsup t(p)=t(p)$. The contradiction proves that the latter case does not apply, hence $p=q$. $\square$

Definition 4.46

A spacetime satisfying the previous equivalent conditions is called future distinguishing (resp. past distinguishing).

This definition is due to Kronheimer and Penrose (1967, p. 486) who also gave the following definition through property (i). We studied weak distinction quite in detail in Minguzzi (2008e) where we proved the equivalence with (ii) and (iii).

Definition 4.47

A spacetime is weakly distinguishing if the following equivalent properties hold true

• (i) ‘$I^-(p)=I^-(q)$ and $I^+(p)=I^+(q)$’ $\Rightarrow p=q$,

• (ii) $p\mapsto I^-(p)\cup I^+(p)$ is injective,

• (iii) D is antisymmetric.

Proof of the equivalence

$(i) \Rightarrow (iii)$. If D is not antisymmetric we can find $p,q\in M$, $p\ne q$, such that $(p,q)\in D$, i.e. $q\in \overline{J^+(p)}$ and $p\in \overline{J^-(q)}$, and $(q,p)\in D$, i.e. $p\in \overline{J^+(q)}$ and $q\in \overline{J^-(p)}$, which implies ‘$(p,q)\in D_f$ and $(q,p)\in D_f$’ (and hence by the previous proof $I^+(p)=I^+(q)$) and ‘$(p,q)\in D_p$ and $(q,p)\in D_p$’ (and hence by the previous proof $I^-(p)=I^-(q)$).

$(iii) \Rightarrow (i)$. If $p\ne q$ are such that (for any choice of sign) $I^\pm (p)=I^\pm (q)$, then $p\in \overline{I^\pm (p)}= \overline{I^\pm (q)}$, and similarly $q\in \overline{I^\pm (p)}$, thus $(p,q)\in D$ and $(q,p)\in D$.

$(ii) \Rightarrow (i)$ is clear. $(i) \Rightarrow (ii)$. Any two distinct points on a closed timelike curve have the same chronological past and future, thus (i) implies chronology. Suppose $I^-(p)\cup I^+(p)=I^-(q)\cup I^+(q)$, if $I^+(q)\cap I^-(p)\ne \emptyset$, then $q\ll p$, which implies $p\in I^+(q)\cup I^-(q)=I^-(p)\cup I^+(p)$, thus $p\ll p$, a contradiction. Thus $I^+(q)\cap I^-(p)=\emptyset$, which implies $I^+(q)\subset I^+(p)$, and reversing the roles of p and q, $I^+(p)\subset I^+(q)$, which gives $I^+(p)=I^+(q)$. The proof of the equality for the minus case is analogous, hence from (i) $p=q$, which proves (ii). $\square$

From the relational point of view weak distinction is better behaved than the posterior distinction property (Hawking and Sachs 1974) to be treated in a next section. In fact it is easily expressible as an antisymmetry condition (see also Theorem 4.49). As previously mentioned, in general it is particularly convenient to rephrase a causality condition as an antisymmetry property for some relation, as antisymmetry is inherited through the inclusion of relations. As an example, future or past distinction imply weak distinction because $D\subset D_p,D_f$ (Fig. 13).

Fig. 13

On the left: a non-totally imprisoning, reflecting, non-weakly distinguishing spacetime. On the right: a weakly distinguishing spacetime which is neither future nor past distinguishing. The causal relation $D^{+}$ is antisymmetric while $D^{+}_p$ and $D^{+}_f$ are not. Image reproduced with permission from Minguzzi (2008e), copyright by IOP

The non-imprisoning conditions have been among the last levels to be placed into the causal ladder (Minguzzi 2008d). Thanks to our study of imprisoned curves we can easily prove (Minguzzi 2008d) (notice that old references assume strong causality Hawking 1966b; Carter 1971; Hawking and Ellis 1973; Senovilla 1998; Minguzzi and Sánchez 2008)

Theorem 4.48

Every weakly distinguishing spacetime is non-totally imprisoning.

Actually, we introduced an intermediate step called feeble distinction (Minguzzi 2008e). Hounnonkpe (2018) has recently shown that it is equivalent to the property of the volume function $t^++t^-$ being strictly increasing over causal curves.

Proof

If there were an imprisoned curve by Theorem 2.75 we could find two distinct points with the same chronological past and chronological future. $\square$

In the context of KP-causal spaces given the chronological relation, the best causal relation that one can place on M is D, see Minguzzi (2008e) and Kronheimer and Penrose (1967).

Theorem 4.49

The largest relation (not necessarily transitive, reflexive or antisymmetric) R for which I is an R-ideal, that is $R\circ I\cup I\circ R\subset I$, is $R=D$. The triple (M, D, I) is a KP-causal space iff the spacetime is weakly distinguishing.

Proof

We prove first the latter result. The inclusion $D_p\circ I\subset I$ follows from the first characterization in Eq. (4.2) and from the openness of I. Similarly, $I\circ D_f\subset I$, thus $D\circ I\cup I\circ D\subset I$, and as D is reflexive and transitive, (M, D, I) is a KP-causal space iff D is antisymmetric, namely under weak distinction.

Assume there is $R \supset D_f$, $R\ne D_f$, such that $I\circ R \subset I$. Take $(p,q) \in R\backslash D_f$ then for every r such that $(q,r) \in I$ we have $(p,r) \in I$, i.e. $I^+(q)\subset I^+(p)$, which reads $(p,q) \in D_f$, a contradiction. Analogously, $D_p$ is the largest set which satisfies $R\circ I \subset I$. Notice that we did not assume reflexivity or transitivity of R.

If $D=D_f\cap D_p$ is not the largest set which satisfies $D\circ I\cup I\circ D\subset I$ then there is $(p,q) \notin D$, such that $(p,q) \circ I \subset I$ and $I \circ (p,q) \subset I$. The pair (p, q) can’t belong to both $D_p$ and $D_f$, so assume without loss of generality $(p,q)\notin D_p$, then $R=D_p \cup (p,q)$ is larger than $D_p$ and satisfies $R \circ I\subset I$, a contradiction. $\square$

4.3.3 Moderate distinction

Definition 4.50

A spacetime for which every point admits arbitrarily small neighborhoods that are future or past distinguishing is called moderately distinguishing.

Proposition 4.51

Future or past distinguishing spacetimes are moderately distinguishing. Moderately distinguishing spacetimes are weakly distinguishing.

Proof

The first statement is clear. Let us prove the second statement. By contradiction, suppose that (M, g) is not weakly distinguishing, then there are $p\ne q$ such that $I^+(p)=I^+(q)$ and $I^-(p)=I^-(p)$. Point p admits a neighborhood U whose closure does not contain q and which is future or past distinguishing. Let us assume the former possibility, the latter being analogous. From $I^+(p)=I^+(q)$, arguing as in the proof of ‘Not $(i) \Rightarrow$ not (iii)’ of Theorem 4.44 we obtain a contradiction. $\square$

Fig. 14

Figure adapted from Minguzzi (2008e). Points p and q are the only ones with the same chronological past and future. The removed sets are such that some causal curves starting from p pass the filters while having the abscissa in their closure, but if the starting point is moved to the right (say r) then the future causal curves hit the filter if they stay to close to the abscissa, and dually if we move the point to the left

Example 4.52

A weakly distinguishing spacetime need not be moderately distinguishing. Consider Fig. 14 with the point q removed. The spacetime is weakly distinguishing but point p does not admit arbitrarily small neighborhoods that are future or past distinguishing.

A moderately distinguishing spacetime need not be future or past distinguishing. Again Fig. 14 with the points p and q removed provides an example.

Definition 4.53

A bijective map $f:M\rightarrow M'$ between two spacetimes (M, g) and $(M',g')$ is a conformal isometry if it is a $C^1$ diffeomorphism with $f^*g'=\varOmega ^2 g$ for some positive function $\varOmega$.

Definition 4.54

A bijective map $f:M\rightarrow M'$ between two spacetimes (M, g) and $(M',g')$ is called causal if it preserves the causal relation, that is $p\le q \Leftrightarrow f(p)\le f(q)$ (equivalently, $f\times f (J)= J'$) An analogous definition is given in the chronological case, with J replaced by I, and in the horismos case, with J replaced by $\mathcal {E}=J\backslash I$.

Theorem 4.55

• (a) Let (M, g) and $(M,g')$ be two moderately distinguishing spacetimes over the same manifold. If $J=J'$ or $I=I'$ or $\mathcal {E}=\mathcal {E}'$, then g and $g'$ are conformally related.

• (b) Let (M, g) and $(M',g')$ be two moderately distinguishing spacetimes and let $f:M\rightarrow M'$ be a $C^{2,1}$ diffeomorphism which is chronological, causal or horismotical, then f is a conformal isometry.

Moreover, if $J=J'$ or $I=I'$ then the assumption on the moderate distinction of the target spacetime can be dropped.

The argument really requires that the metrics be $C^{1,1}$ and f be $C^{2,1}$, for it uses the exponential map (Minguzzi 2015b; Kunzinger et al. 2014a). So far our assumption on the metric has been $C^2$, so sufficient, but in (b) we have to be careful of the regularity of f too.

Remark 4.56

As a consequence, in a moderately distinguishing spacetime the knowledge of any among I, J or $\mathcal {E}$ fixes the other two as well as the conformal class of the metric.

Proof

It is sufficient to prove (b), in fact (b) follows by applying (a) to the pair g, $f^*g'$, because f maps $f^*g'$- timelike (causal) curves into $g'$-timelike (resp. causal) curves and conversely.

We start from the last statement. If $(M,g')$ were not moderately distinguishing we could find $p\in M$ and $V\ni p$ such that for every $U\subset V$, $p\in U$, U is neither future nor past distinguishing for p, that is there is a future $g'$-timelike curve that starts from p reaches some point q outside U and ends at some point $r\in U$, and similarly in the past case. That is $p\ll _{g'} q\ll _{g'} r$, thus $p\le _{g} q\le _{g} r$ provided I or J is preserved, which gives a contradiction with the moderate distinction of (M, g) at p.

Let $p\in M$ and suppose without loss of generality that p admits arbitrarily small future distinguishing neighborhoods, then we can find one, say U, contained in a convex normal neighborhood. Due to the property of U, $J^+(p,U)=J^+(p)\cap U$. For every sufficiently small open neighborhood $W\subset T_pM$ of the zero vector we have

$$\begin{aligned} \{\exp _p^{-1}[ J^+(p)\cap U]\}\cap W =\{\exp _p^{-1} J^+(p,U)\}\cap W=C_p\cap W \end{aligned}$$

where $C_p$ is the cone of future directed causal vectors. Thus the causal cone can be recovered from J, hence the two metrics have the same cones and so are conformally related. The proof in the chronological and horismos cases are analogous because $I^+(p)\cap U=I^+(p,U)$, $E^+(p)\cap U=E^+(p,U)$, so in the right-hand side of the previous equation in display we would have the timelike cone or the lightlike cone. $\square$

Remark 4.57

In the definition of causal map we have imposed the condition that $f:M\rightarrow M'$ preserves the causal relation jointly with the inverse $f^{-1}$. García-Parrado and Senovilla in a series of papers have explored an equivalence notion between spacetimes termed isocausality in which the map from $M'$ to M preserving the causal relation need not be $f^{-1}$, see García-Parrado and Senovilla (2003, 2005), García-Parrado and Sánchez (2005) and Minguzzi and Sánchez (2008). Two isocausal spacetimes do not need to be conformally related but still share many causality property (though not all of them; causal simplicity and causal continuity are not preserved under isocausality).

4.3.4 Distinction

Let $p \in M$, a neighborhood U of p is said to distinguish p if no continuous causal curve $\gamma :\mathbb {R} \rightarrow M$ that passes through p, $\gamma (0)=p$, can escape U to reenter it, in other words $\gamma ^{-1}(U)$ is connected.

Theorem 4.58

The following properties are equivalent:

• (i) (M, g) is both future and past distinguishing,

• (ii) ‘$I^-(p)=I^-(q)$ or $I^+(p)=I^+(q)$’ $\Rightarrow p=q$,

• (iii) Every point admits arbitrarily small distinguishing neighborhoods,

• (iv) Every point $p\in M$ admits arbitrarily small open neighborhoods U such that $J^\pm (p,U)=J^\pm (p)\cap U$ for both sign choices,

• (v) The volume functions $t^+$ and $t^-$ are strictly increasing over causal curves,

• (v’) There are upper and lower semi-continuous functions which are strictly increasing over causal curves.

As in Remark 4.45 the neighborhood U in (iii) or (iv) can be chosen to be an element of the topological basis $\{V_k\}$ of Theorem 1.35.

Proof

$(i) \Rightarrow (ii)$. Suppose $I^-(p)=I^-(q)$ then by past distinction $p=q$, if instead $I^+(p)=I^+(q)$ by future distinction $p=q$, thus (ii).

$(ii) \Rightarrow (i)$ Let us prove future distinction. If $I^+(p)=I^+(q)$ then ‘$I^-(p)=I^-(q)$ or $I^+(p)=I^+(q)$’ is true, thus $p=q$, namely future distinction holds. The proof of past distinction is analogous.

$(i)\Rightarrow (iii)$ and (iv). Immediate from Theorem 4.44 and Remark 4.45.

$(iii)\Rightarrow (i)$. Every distinguishing neighborhood is future distinguishing, thus future distinction holds. Similarly, past distinction holds.

$(iii)\Rightarrow (iv)$ is clear. $(iv)\Rightarrow (i)$. Clear, because it implies characterization (iv) of Theorem 4.44, hence future distinction. Similarly, it implies past distinction.

$(i)\Leftrightarrow (v) \Leftrightarrow (v')$. Trivial from Theorem 4.44. $\square$

Hawking and Ellis (1973) and Hawking and Sachs (1974) introduced the following definition through property (ii).

Definition 4.59

A spacetime is distinguishing if it is satisfies the equivalent properties of Theorem 4.58.

The main advantage of distinction over weak distinction is related to its nice characterization in terms of causal curves, see characterization (iii) in the previous theorem.

It is natural to ask if the differentiability conditions on f in Theorem 4.55 can be weakened. In that respect the following result by Hawking is very important (notice that the spacetime dimension must be at least 3).

Theorem 4.60

(Hawking 2014, Lemma 19) If (M, g) and $(M',g')$ are $n+1$ dimensional $C^r$ manifolds ($n \ge 2$, $r \ge 3$) with $C^{r-1}$ Lorentz metrics such that the strong causality assumption holds on M, and if f is a bijection $f:M\rightarrow M'$ such that f and $f^{-1}$ preserve the causal relationships I and J, then f is a $C^r$ diffeomorphism.

The previous result was further elaborated as follows

Theorem 4.61

(Hawking et al. 1976, Theorem 5) A homeomorphism $f:M \rightarrow M'$, from (M, g) to $(M,g')$ which takes future directed null geodesics to future directed null geodesics is a $C^\infty$ diffeomorphism and hence a conformal isometry.

Malament was able to drop the continuity condition. Following Hawking, King and McCarthy he works with isochronal curves, that is, maps $\gamma :I\rightarrow M$ such that $\gamma (t)\ll \gamma (t')$ iff $t<t'$ (isochronal curves might be $C^1$ and null at some point, e.g. $(\tanh t,t)$ in $1+1$ Minkowski spacetime).

Theorem 4.62

(Malament 1977, Theorem 1) Suppose (M, g) and $(M',g')$ are spacetimes and $f:M \rightarrow M'$ is a bijection where both f and $f^{-1}$ preserve isochronal curves. Then f is a homeomorphism. (In fact they also preserve future directed null geodesics so, by Hawking’s theorem, f must also be a smooth conformal isometry.)

Theorem 4.63

(Malament 1977, Theorem 2; Malament 2012, Proposition 2.2.4) Suppose (M, g) and $(M',g')$ are distinguishing spacetimes and $f:M \rightarrow M'$ is a chronological bijection. Then f is a homeomorphism. (By Hawking’s theorem f must also be a smooth conformal isometry.)

Fig. 15

A future distinguishing spacetime which is not distinguishing. This is really Malament’s example (Malament 1977, 2012): the upper portions of the spacetime can be switched so giving a chronological bijection $f:M\rightarrow M$ which is not a homeomorphism

Moreover, Malament provides a simple example (see Fig. 15) which shows that the assumptions in Theorem 4.63 are optimal: distinction cannot be weakened to future or past distinction. Vyas and Akolia (1984) studied the preservation of causal properties under chronological bijections and concluded that in Malament’s second theorem it is sufficient to assume that (M, g) is distinguishing.

Levichev observed that a similar theorem holds for causal bijections

Theorem 4.64

(Levichev 1987) Suppose (M, g) and $(M',g')$ are distinguishing spacetimes and $f:M \rightarrow M'$ is a causal bijection. Then f is a smooth conformal isometry.

We observed in Remark 4.56 that under moderate distinction I determines J and conversely, so that the previous theorem can be recovered from Malament’s. Similarly, we deduce (see also Minguzzi 2009d)

Theorem 4.65

Suppose (M, g) and $(M',g')$ are distinguishing spacetimes and $f:M \rightarrow M'$ is a horismotical bijection. Then f is a smooth conformal isometry.

Kronheimer and Penrose proved the following result under a strong causality assumption. We improved it to distinction (Minguzzi 2009d).

Theorem 4.66

In a distinguishing spacetime the causal relation J is the smallest transitive relation containing the horismos relation $\mathcal {E}$, i.e $J=\varDelta \cup \mathcal {E}\cup \mathcal {E}^2 \cup \ldots$ or, with the notation of Sect. 1.13

$$\begin{aligned} \le ^{(\rightarrow )}=\le , \qquad \ll ^{(\rightarrow )}=\ll . \end{aligned}$$

Example 4.67

The previous theorem is optimal in the sense that distinction cannot be weakened to future or past distinction. Consider the spacetime of Fig. 15, let p be a point below the middle circle and let q be a point on it. Then $p\le q$ but no sequence of achronal lightlike segments can connect the two points, indeed the last segment cannot be achronal.

The previous theorems prove that most of the spacetime structure can be recovered from the causal order, in fact the spacetime dimension can be recovered as well (Parrikar and Surya 2011; Stoica 2016) (related references are Janardhan and Saraykar 2013; Dribus 2017). These results suggest to regard the spacetime as an abstract partial order and finally, getting rid of the manifold structure, as an oriented graph. Indeed, this is one of the ideas of Causal Set Theory (Bombelli et al. 1987; Sorkin 1991; Dowker et al. 2003; Johnston 2008).

4.3.5 Non-partial imprisonment

According to Carter (1971) the following definition is due to Misner.

Definition 4.68

An inextendible continuous causal curve $\gamma :\mathbb {R} \rightarrow M$ is partially imprisoned is a compact set K, if $\gamma ^{-1}(K)$ is non-compact. A spacetime is non-partially imprisoning if there are no imprisoned continuous causal curves.

It is also possible to give past and future versions of these definitions by replacing non-compact with unbounded from below and unbounded from above, respectively .

As with non-total imprisonment, non-partial imprisonment can be placed into the causal ladder (Minguzzi 2008d).

Theorem 4.69

Every non-partially imprisoning spacetime is distinguishing.

Proof

Assume that (M, g) does not have future partially imprisoned curves; we are going to show that it is past distinguishing. Suppose not then there are $p \ne q$ such that $I^{-}(p)=I^{-}(q)$. Let $U\ni p$ be an open relatively compact set such that $q \notin \bar{U}$, and let $V\ni q$ be an open relatively compact set such that $p \notin \bar{V}$, $\bar{U}\cap \bar{V}=\emptyset$. Take $p_1 \in I^{-}(p)\cap \partial {U}$, then there is a timelike curve $\sigma _1^q$ which connects $p_1$ to q. Let $q_1 \in \sigma _1^q \cap \partial {V} \subset I^{-}(q)$, and parametrize $\sigma _1^q$ so that $p_1=\sigma ^q_1(0)$ and $q_1=\sigma ^q_1(1)$. There is a timelike curve $\sigma _1^p$ which connects $q_1$ to p. Let $p_2 \in \sigma _1^p \cap \partial {U}\subset I^{-}(p)$, and parametrize $\sigma _1^p$ so that $q_1=\sigma ^p_1(1)$ and $p_2=\sigma ^p_1(2)$. Continue in this way and obtain sequences $p_n \in \partial {U}$, $q_n \in \partial {V}$, $\sigma _n^p$, $\sigma _n^q$. The timelike curve

$$\begin{aligned} \sigma = \cdots \circ \sigma _2^p\vert _{[3,4]} \circ \sigma _2^q\vert _{[2,3]} \circ \sigma _1^p\vert _{[1,2]} \circ \sigma _1^q\vert _{[0,1]} \end{aligned}$$

is future inextendible and is partially future imprisoned in both $\bar{U}$ and $\bar{V}$. The contradiction proves that (M, g) is past distinguishing (Fig. 16). $\square$

Fig. 16

Figure adapted from Minguzzi (2008d)

A partial imprisoning spacetime which is distinguishing. The gray set $\varGamma$ has been removed. It is made of all the points which can be connected to q with a causal curve that intersects $\theta =0$ at most at the endpoints. The cones are tangent to $t=0$

Example 4.70

Consider the spacetime $N=\mathbb {R} \times S^1 \times \mathbb {R}$ of coordinates $(t,\theta ,y)$, $\theta \in [0,2\pi )$, and metric

$$\begin{aligned} g=-\mathrm{d}t\otimes \mathrm{d}\theta - \mathrm{d}\theta \otimes \mathrm{d}t+t^2 \mathrm{d}\theta ^2+(\mathrm{d}y+y \mathrm{d}\theta )^2 \end{aligned}$$

Call $\varGamma$ the set of events on the surface $\theta =0$ which can be connected to $q=(0,0,0)$ through a causal curve which intersects the surface $\theta =0$ only at the endpoints, and let $M=N\backslash \varGamma$. The spacetime (M, g) is distinguishing (due to the removal of $\varGamma$) but the lightlike curve $\gamma =(t(\lambda ), \theta (\lambda ),y(\lambda ))$ with $t(\lambda )=0$, $\theta (\lambda )=\lambda$, $y=-\exp (-\lambda )$ is partially imprisoned in the compact set $[-1,1]\times [\pi /2,\pi ]\times [-1,1]$. More details can be fund in Minguzzi (2008d) (where there is a typo in the metric though).

4.3.6 Strong causality

A chronological diamond is a set of the form $I^+(p)\cap I^-(q)$, for $p,q\in M$. For the following result see also Penrose (1972, Proposition 4.21).

Lemma 4.71

The chronological diamonds form a basis for some topology.

Proof

Let $r\in \bigcap _{i=1}^k [I^+(p_i)\cap I^-(q_i)]$ for some $p_i,q_i$, $i=1,\ldots k$, and let $p\ll r$ be so close to r that, due to the openness of I, $p \gg p_i$ for every i. Similarly, let $q\gg r$ be so close to r that $q \ll q_i$ for every i. Then $r\in I^+(p)\cap I^-(q)\subset \bigcap _{i=1}^k I^+(p_i)\cap I^-(q_i)$. $\square$

Definition 4.72

On a spacetime (M, g) the Alexandrov topology $\mathcal {A}$ or interval topology is the coarsest (smallest) topology for which the chronological futures and pasts $I^+(p)$, $I^-(p)$, of events are open, in other words the one for which the chronological diamonds form a basis for the topology.

Clearly the manifold topology is finer than $\mathcal {A}$ since the elements of the basis of $\mathcal {A}$ are open in the manifold topology.

Remark 4.73

In the above definition the cited author is Alexandr D. Alexandrov. In the literature there is another topology under the same name due to Pavel S. Alexandrov.

We recall a definition that we gave already, cf. Definitions 1.32 and 1.34.

Definition 4.74

A spacetime it strongly causal if every event admits arbitrarily small causally convex neighborhoods.

In other words, for every $p\in M$ and neighborhood $V\ni p$, we can find a neighborhood $U\subset V$, $p\in U$, such that U is causally convex. By Theorem 1.35 U can be chosen of the form $V_k$, described by that theorem.

Theorem 4.75

The following properties are equivalent:

• (i) (M, g) is strongly causal,

• (ii) $\mathcal {A}$ coincides with the manifold topology,

• (iii) $\mathcal {A}$ is Hausdorff,

• (iv) Every point admits arbitrarily small open neighborhoods U such that $J_U=J\cap (U\times U)$,

• (v) $(p,q)\in J$ and $(q,p)\in {\bar{J}} \Rightarrow p=q$,

Again the neighborhood U in (iii) or (iv) can be chosen to be an element of the topological basis $\{V_k\}$ of Theorem 1.35.

The equivalence of the first four properties is classical, see Hawking (2014), Kronheimer and Penrose (1967) and Penrose (1972). Characterization (v) was given by the author in Minguzzi (2008a).

Proof

$(i) \Rightarrow (ii)$. Let $r\in M$ and let $O\ni r$ be open. There is a causally convex neighborhood $V\subset O$, $r\in V$, thus taking $p\in I^-(r,V)$, $q \in I^+(r,V)$, we have $r\in I^+(p)\cap I^-(q)\subset V\subset O$.

$(ii) \Rightarrow (iii)$ . Trivial. $(i) \Rightarrow (iv)$ . Trivial.

Not $(v) \Rightarrow$ not (iii). Let $(p,q)\in J$, $(q,p)\in {\bar{J}}$ and $p\ne q$. Let $r\ll q$ and $s\gg q$, then $p\in I^-(s)$ and $p\in \overline{I^+(r)}$, thus $p\in \overline{I^+(r)\cap I^-(s)}$ and any chronological diamond which contains p necessarily contains points of $I^+(r)\cap I^-(s)$, that is, $\mathcal {A}$ does not separate p and q.

Not $(i) \Rightarrow$ not (iv) and not (v). Suppose that the property (i) does not hold, hence there is $V\ni p$, such that taking a basis $\{V_k\}$ as in Theorem 1.35 with $V_1\subset W\subset V$, and W convex normal, we have for every k the existence of a continuous causal curve $\gamma _k$ starting from p that escapes $V_k$ and reenters it. Since $V_k$ is causally convex in $V_s$, for $s\le k$, it escapes and reenters $V_s$ too, thus there is a first escaping point $q_{ks}\in \partial V_s$, $q_{kk}\le q_{ks}$, and a last reentrance point $r_{ks}\in \partial V_s$, $r_{ks}\le r_{kk}$. For fixed s, we find that there are $q_s,r_s\in \partial V_s$ such that (passing to subsequences if necessary) $q_{ks}\rightarrow q_s$, $r_{ks}\rightarrow r_s$ for $k\rightarrow \infty$, thus $(p,r_s)\in {\bar{J}}$ due to $q_{kk}\le r_{ks}$ (notice also that $(q_s,r_s)\in {\bar{J}}$ due to $q_{ks}\le r_{ks}$). Since $(r_{ks}, r_{kk}) \in J_W$, by Theorem 2.11 $(r_s,p)\in J_W\subset J$ (notice also that $(q_{kk}, q_{ks}) \in J_W$, by Theorem 2.11 $(p,q_s)\in J_W\subset J$). Thus $(r_s,p)\in J$ and $(p,r_s)\in {\bar{J}}$ while $r_s\ne p$, that is, not (v). Moreover, suppose that (iv) does hold then there is ${\tilde{U}}\subset W$, $p\in {\tilde{U}}$, such that $J_{{\tilde{U}}}=J\cap {\tilde{U}}\times {\tilde{U}}$. However, pick s so large that $q_s,r_s\in {\bar{V}}_s\subset {\tilde{U}}$. We know that $(q_s,r_s)\in \overline{J\cap {\tilde{U}}\times {\tilde{U}}}$, thus $(q_s,r_s)\in \overline{J_{{\tilde{U}}}}\subset \overline{J_W}$ hence $(q_s,r_s)\in J_W$ (by Theorem 2.11), which is impossible because W is causal. The contradiction proves “not (iv)”. $\square$

Remark 4.76

In Hawking (1966b), Kronheimer and Penrose (1967) and Penrose (1972) another more involved characterization is given, namely

$$\begin{aligned} (p,q)\in J\text { and} \!\! \bigcap _{r\in I^-(q)}\!\!\! I^+(r) \supset I^+(p) \,\, \Rightarrow \, p=q, \end{aligned}$$

or equivalently

$$\begin{aligned} (p,q)\in J\text { and } \uparrow \! I^-(q) \supset I^+(p) \,\, \Rightarrow \, p=q. \end{aligned}$$

(4.5)

However, due to formula (4.4), $\bigcap _{r\in I^-(q)} I^+(r)=D^+_p(q)$, by Proposition 4.5 $\overline{D^+_p(q)}=A^+(q)$, and by Proposition 2.84 2(a), this statement can be rewritten as (v).

The following Lemma adapts an argument introduced by Rácz (1987).

Lemma 4.77

Let (M, g) be chronological. Suppose that strong causality fails at $p\in M$ and let $\sigma$ be the lightlike line passing though p over which strong causality fails of Theorem 2.69. Then we have also: for every $a,b\in \sigma$, $\uparrow \! I^-(a)=$ $\uparrow \! I^-(b)$ (and dually).

Proof

Let $a,b\in \sigma$, we know that $(a,b)\in {\bar{J}}$. Let $r \in I^+(b)$ then $a\in \overline{J^-(r)}$, which implies $r\in \cap _{s\in I^-(a)} I^+(s)$, that is, since $I^+(b)$ is open, $I^+(b)\subset \uparrow \! I^-(a)$. Since $b\in \sigma$ is arbitrary, $I^+(\sigma ) \subset \uparrow \! I^-(a)$ for every $a\in \sigma$. Now we want to show that $\uparrow \! I^-(b)\subset \uparrow \! I^-(a)$ for every $a,b\in \sigma$ (for exchanging the roles of a and b we get the desired result). If $a \le b$ this follows from Eq. (4.3) so we can assume that a follows b over $\sigma$, hence $b<a$. Let $r\in \uparrow \! I^-(b)\backslash I^+(\sigma )$ (if $r\in I^+(\sigma )$ we have finished because $I^+(\sigma ) \subset \uparrow \! I^-(a)$). Since $\uparrow \! I^-(b)$ is open we can find $r'\ll r$, $r'\in \uparrow \! I^-(b)$. Let $b_n\ll b$, $b_n\rightarrow b$, let $\gamma _n$ be causal curves connecting $b_n$ to $r'$, there is a limit causal curve $\gamma$ starting from b. If $\gamma$ connects b to $r'$ then $r'\in J^+(b)$, which implies $r\in I^+(\sigma )$, a contradiction. Thus $\gamma$ is future inextendible. If $\gamma$ is not achronal then it enters $I^+(b)\subset I^+(\sigma )$, thus some $\gamma _n$ intersects $I^+(\sigma )$ and hence $r\in I^+(\sigma )$, again a contradiction. The same happens if $\gamma$ is a lightlike ray but not tangent to $\sigma$ at b. We conclude that $\gamma$ is half $\sigma$ and hence $a\in \gamma$. Let $q\in I^-(a)$, $I^+(q)$ intersects some $\gamma _n$ hence $r'\in \bigcap _{q\in I^-(a)} I^+(q)$ and finally $r\in \uparrow \!I^-(a)$. $\square$

We arrive at the characterization proved by Rácz (1987).

Theorem 4.78

A spacetime is strongly causal iff the map $p \mapsto \uparrow \!I^-(p)$ (or $p \mapsto \downarrow \!I^+(p)$) is injective.

Proof

$\Leftarrow$. The result follows from Lemma 4.77 provided (M, g) is chronological. Suppose there is a closed timelike curve $\gamma$ and let $p\in \gamma$. Since $p\ll p$, any $q \in D^+_p(p)$, namely any $q\in M$ such that $p\in \overline{J^-(q)}$ really belongs to $I^+(p)$. By Proposition 4.5, $\uparrow I^-(p)=I^+(p)$, hence for every $p,q\in \gamma$, $\uparrow I^-(p)=\uparrow I^-(q)$. The contradiction with injectivity proves that (M, g) is chronological, hence the desired result.

$\Rightarrow$. Suppose $\uparrow \!I^-(p)=\uparrow \!I^-(q)$ and $p\ne q$, then $I^+(q)\subset \uparrow \!I^-(q)=\uparrow \!I^-(p)$. Let $p_n\ll p$ and $q_n\gg q$ be two sequences $p_n\rightarrow p$, $q_n\rightarrow q$. There is a causal curve $\gamma _n$ connecting $p_n$ to $q_n$, thus in the limit we find a limit curve $\gamma$ ending at q (and possibly starting at p). Let $r\in \gamma \backslash \{q\}$, as r is an accumulation point of $\gamma _n$, for every $s\in I^+(r)$ we have that $p_n\in I^-(s)$, hence $s\in \uparrow \!I^-(p)$ and $I^+(r) \subset \uparrow \!I^-(p)=\uparrow \!I^-(q)$, since $r<q$ we get a contradiction with property (4.5). $\square$

The following result is due to Podoksenov (1992).

Theorem 4.79

A spacetime is strongly causal iff it is stably causal under local perturbations of the metric, that is, every point $p\in M$ admits a neighborhood $U\ni p$ such that there exists a causal metric $g'$ with $g'> g$ in U, $g'=g$ in $M\backslash U$.

Proof

$\Rightarrow$. Let $p\in M$, by Eq. (1.7) we can find a basis $\{V_k\}$ for the topology at p which consists of causally convex neighborhood built as chronological diamonds for a wider flat metric $g^+$. Let $g'$ be such that $g<g'<g^+$ on a compact neighborhood $U\subset V_1$ of p and such that $g'\vert _{M\backslash U}=g$. No closed $g'$-causal curve can form in $V_1$ since $g^+$ is flat, but any closed $g'$-causal curve intersects necessarily $V_1$ (for $g'=g$ outside U where causality holds) so contradicting its causal convexity.

$\Leftarrow$. Suppose that strong causality fails at p. By Theorem 2.69 we can find a causal curve $\sigma$ such that for every $a,b\in \sigma$, $(a,b)\in {\bar{J}}$. Let U be any open neighborhood of p and let $a,b\in U\cap \sigma$ be such that $b<_U p<_U a$, then whatever the choice of $g'$, $b\ll _{g'} p\ll _{g'} a$ so by the openness of $I_{g'}$ there is a closed $g'$-causal curve. $\square$

The following result is due to Hawking Hawking (1966b), Carter (1971) and Hawking and Ellis (1973).

Proposition 4.80

Strong causality implies non-partial imprisonment.

Proof

Any compact set K is covered by a finite number of relatively compact causally convex sets of the type of Theorem 1.35. A future inextendible causal curve cannot be future totally imprisoned in any of them due to property (d) of Theorem 1.35. Thus, it escapes each of them not to reenter them (so it leaves definitely a neighborhood of K). The past case is done analogously. $\square$

Fig. 17

A non-partial imprisoning spacetime which is not strongly causal. The point p does not admit arbitrarily small causally convex neighborhoods

Example 4.81

Figure 17 provides an example of non-partially imprisoning spacetime which is not strongly causal. It is obtained from Minkowski $1+1$ spacetime in its standard coordinate by identifying $t=0$ with $t=1$ and by removing two spacelike half-geodesics. The dotted line is tilted at $45^\circ$.

One can say that strong causality holds at $p\in M$ if p admits arbitrarily small causally convex neighborhoods. The following result might be useful.

Proposition 4.82

The set of points at which strong causality holds is open (that is, the strong causality violating set is closed).

Proof

Let $V_1$ be the strongly causal and causally convex neighborhood of p constructed in Theorem 1.35. Let $q\in V_1$, since $(V_1,g)$ is strongly causal (recall that it is a chronological diamond of a flat metric), if U is a neighborhood of q we can find a neighborhood $V\subset V_1\cap U$, which is causally convex in $V_1$ and hence in M. Thus every point of $V_1$ admits arbitrarily small causally convex neighborhoods, namely strong causality holds true at every point of $V_1$. $\square$

4.3.7 The A-causality subladder

We have already introduced the notation $A={\bar{J}}$, and explained that the antisymmetry of a reflexive relation R is also called R-causality. Thus

Definition 4.83

A spacetime is A-causal if A is antisymmetric.

An equivalent concept was introduced by Woodhouse (1973) though he defined A as follows

$$\begin{aligned} (p,q)\in A \text { iff } \uparrow \! I^-(p)\supset I^+(q). \end{aligned}$$

Works exploring this causal relation include Akolia et al. (1981), Rácz (1987) and Choudhury and Mondal (2013). The equivalence with the simpler definition of A as closure of the causal relation follows from our Proposition 4.5, and from Proposition 2.84 2(a), and was first recognized by Akolia et al. (1981), see also Minguzzi (2008a).

Woodhouse referred to $A^+(p)$ as the almost causal future of p, so Akolia et al. (1981) referred to Woodhouse’s causality condition as almost-causality. We do not follow this terminology since it suggests that A-causality is a weaker condition than causality, while it is stronger. Also as a causality condition it is not that close to causality given the many levels of the causal ladder between the two properties. Rácz (1987) calls it W-causality.

From Theorem 4.75, characterization (v), it is immediate that

Proposition 4.84

A-causal spacetimes are strongly causal.

Fig. 18

A strongly causal spacetime which is not A-causal

It is quite clear, and soon understood by Carter (1971) and Penrose (1972) that it is possible to construct a hierarchy of causality conditions. Since the construction by Carter is quite involved, we follow the presentation by Penrose, see also Rácz (1987).

Definition 4.85

We say that (M, g) is k-th order strongly causal if the condition $(p_1,p_2)\in A$, $(p_2,p_3)\in A$, $\ldots$ $(p_k,p_1)\in A$ implies that all points of the sequence coincide.

So A-causality correspond to second-order strong causality. By construction, $k+1$-th order strong causality implies k-th order strong causality. For $k=2s$ the condition is really equivalent to $A^s$-causality. So a coarser ladder is that given by the $A^s$-causality properties. All these properties are really different: examples are constructed as in Fig. 18 by selecting the height appropriately and by removing the right number of spacelike half lines in a zig-zag fashion (Penrose 1972, Fig. 25).

The important point to observe here is that there really seems to be no ending to the sequence of ascending causality conditions. For instance, we could consider the smallest transitive relation containing A

$$\begin{aligned} A^\infty :=\varDelta \cup A\cup A^2\cup \ldots \end{aligned}$$

and impose the $A^\infty$-causality condition (i.e. impose the antisymmetry of this relation). But one could still be unsatisfied because $A^\infty$ is not closed, a property which would be very useful in a number of limit arguments. Unfortunately, the stronger condition of $\overline{A^\infty }$-causality is not fully satisfying because $\overline{A^\infty }$ is not transitive. One could continue in this way by taking closures and transitivizations without ever reaching a satisfactory causal relation and a satisfactory causality condition, cf. Table 1. We might say that through this approach the problem of almost closed causal curves (and their concatenations) is not going to be solved.

Table 1 The causal ladder below stable causality and, for each level, the corresponding causal relation whose antisymmetry determines the causality condition

There are really two ways out here, namely K-causality and stable causality. The latter really predates the former but it is more natural to introduce K-causality first. Before we do that, we have to mention another causality condition.

4.3.8 Compact stable causality

With Beem’s Theorem 4.42 we learned that a non-totally imprisoning spacetime is characterized by the property that every relatively compact open subset is really a stably causal spacetime in its own. Observe that in this result one disregards what happens outside the subset.

With Podoksenov’s Theorem 4.79 we learned that a strongly causal spacetime is characterized by being causally stable under local enlargements of the light cones. In this result one really looks at the causal curves over the whole manifold.

So it is natural to ask a stronger condition than the previous ones: what sort of causality condition is that for which for any relatively compact subset it is possible to enlarge the cones over the subset without spoiling causality on M? This is a new causality condition introduced in Minguzzi (2009c).

Definition 4.86

A spacetime (M, g) is compactly stably causal if, for every relatively compact open set B, there is a metric $g_B \ge g$ such that $g_B > g$ on B, $g_B = g$ on $M\backslash B$ and $(M, g_B)$ is causal.

The family of metrics that satisfy the condition of the definition will also be denoted $\{g\}_B$, so $g_B$ is a representative.

The remarkable fact is that it can be neatly placed into the causal ladder.

Theorem 4.87

$\overline{A^\infty }$-causality $\Rightarrow$ compact stable causality $\Rightarrow$ $A^\infty$-causality, and these causality properties differ.

Unfortunately, compact stable causality is a somewhat technical notion, for this reason I do not give the proofs here, the interested reader is referred to Minguzzi (2009c) and Minguzzi and Rinaldelli (2009).

Another result worth mentioning is the following (Minguzzi and Rinaldelli 2009).

Theorem 4.88

Compact stable causality is equivalent to the antisymmetry of the relation

$$\begin{aligned} J_{CS}=\bigcup _B \bigcap _{g'\in \{g\}_B} J_{g'} \end{aligned}$$

where B runs over the relatively compact open subsets of M.

4.4 Stable and K-causality

Given two metrics g, $g'$, over M, denote as usual $g' >g$ if every causal vector for g is timelike for $g'$, and $g'\ge g$ if every causal vector for g is causal for $g'$. In presence of different metrics, the sets $I_{g}, J_{g} \subset M\times M$, are the chronological and causal sets of (M, g).

Hawking (1968) solved the problem of almost closed causal curves by introducing the following property

Definition 4.89

A spacetime (M, g) is stably causal if there is $g'>g$ such that $(M,g')$ is causal.

In fact he showed that this property guarantees the existence of time functions. No almost closed causal curve can really exist in presence of a time function for the function increases strictly over causal curves (see also Remark 4.92).

Hawking’s time function is constructed as follows. Let $g'>g$ and consider the family of Lorentzian metrics $g_a=(1-\frac{a}{3}) g +\frac{a}{3} g'$, then Hawking’s time function is

$$\begin{aligned} t^H(p)=\int _1^2 \mu (I^-_{g_a}(p)) \mathrm{d}a, \end{aligned}$$

where $\mu$ is a probability measure absolutely continuous with respect to the Lebsegue measure of the coordinate charts. A proof that $t^H$ is a time function can be found in Hawking and Ellis (1973) and Minguzzi (2019). Notice that the argument is a volume function. In general the volume functions are not continuous (unless we are in a causally continuous spacetime, Sect. 4.5.2). The average cures this problem.

The Geroch interval topology is the topology on the space Con(M) of conformal classes of Lorentzian metrics over M and it is generated by the basis $\{g:\underline{g}<g<\overline{g}\}$, where $\underline{g}, g, \overline{g}$ are representatives of the conformal classes. The topology so obtained in Con(M) is equivalent to the quotient of the $C^0$ topology on the space Lor(M) of Lorentzian metrics over M, thus stable causality is the stability of causality in the $C^0$ topology for the (conformal classes of) Lorentzian metrics. For more on this topology see Lerner (1973), Aguirre-Dabán and Gutiérrez-López (1989) and Beem et al. (1996).

Stable causality is best understood with the introduction of the Seifert relation. Unfortunately, the paper by Seifert (1971) (but also others by this author, e.g. Seifert 1977) is rather obscure, has gaps, and, as commented elsewhere, really proves less than it claims. I rather recommend Minguzzi (2008b).

Definition 4.90

The Seifert or stable relation is

$$\begin{aligned} J_S =\bigcap _{g'>g} J_{g'}. \end{aligned}$$

(4.6)

Lemma 4.91

If $\hat{g}<\check{g}$ then $\bar{J}_{\hat{g}} \subset \varDelta \cup I_{\check{g}}$.

Proof

Let $(p,q) \in \bar{J}_{\hat{g}}\backslash \varDelta$, let $\sigma _n$ be a sequence of $\hat{g}$-causal curves of endpoints $p_n$, $q_n$ in $(M,\hat{g})$. By the limit curve theorem there are a future directed $\hat{g}$-causal curve $\sigma ^p$ starting from p, and a past directed $\hat{g}$-causal curve $\sigma ^q$ ending at q, such that for every $p' \in \sigma ^p\backslash \{p\}$, $q' \in \sigma ^q\backslash \{q\}$ we have $(p,p')\in J_{\hat{g}}$, $(p',q') \in \bar{J}_{\hat{g}}$ and $(q',q)\in J_{\hat{g}}$ or, in terms of the causal relations of $\check{g}$, $(p,p')\in I_{\check{g}}$, $(p',q') \in \bar{J}_{\check{g}}$ and $(q',q)\in I_{\check{g}}$, which implies, by the openness of $I_{\check{g}}$, that $(p,q) \in I_{\check{g}}$. $\square$

Remark 4.92

With reference to the proof, if $(p,q)\in \bar{J}_{\hat{g}}\backslash \varDelta$ we can find $p' \in \sigma ^p\backslash \{p\}$, $q' \in \sigma ^q\backslash \{q\}$ with $(p,p')\in J_{\hat{g}}$, $(p',q') \in \bar{J}_{\hat{g}}$ and $(q',q)\in J_{\hat{g}}$ as in the proof. If there is a time function t, then $t(p)<t(p')$, $t(q')<t(q)$, and by continuity, $t(p')\le t(q')$, thus $t(p)<t(q)$. We conclude that if there is a time function there cannot be closed chains of ${\bar{J}}$-related events.

Lemma 4.93

Some equivalent expressions for $J_{S}$ are

$$\begin{aligned} J_{S} = \bigcap _{g'>g} \bar{J}_{g'}=\varDelta \cup \bigcap _{g'>g} {I}_{g'}. \end{aligned}$$

(4.7)

Proof

We have only to show that $\bigcap _{g'>g} \bar{J}_{g'} \subset \varDelta \bigcap _{g'>g} I_{g'}$ the other inclusions being obvious. Let $\bar{g}>g$ , taking $\tilde{g}$ such that $g<\tilde{g}<\bar{g}$, by Lemma 4.91 we have $\bar{J}_{\tilde{g}} \subset \varDelta \cup I_{\bar{g}}$, thus $\bigcap _{g'>g} \bar{J}_{g'} \subset \varDelta \cup I_{\bar{g}}$, since $\bar{g}>g$ is arbitrary we get the desired result. $\square$

Theorem 4.94

The Seifert relation $J_S$ is closed, transitive and contains J.

Proof

From the definition it is clear that $J_S$ is transitive and contains J. Closure follows from the alternative expression of Lemma 4.93. $\square$

The following results are among the most important results of causality theory. Unfortunately the proofs are rather long, so we omit them. Recently I wrote a review with self contained proofs of all the results of this section. The interested reader might want to check it out (Minguzzi 2019).

We start with the next result (attributed to Seifert though there is no correct proof in his work). Again I recommend Minguzzi (2008b) (compare Hawking and Sachs 1974).

Theorem 4.95

Stable causality is equivalent to the antisymmetry of $J_S$.

The following object is connected to the failure of stable causality.

Definition 4.96

The stable recurrent set $vJ_S$ is the set of all $p\in M$ such that for every $g'>g$ there is a closed $g'$-causal curve passing through p.

In fact we have the following result which is worth mentioning (Minguzzi 2008b, Lemma 4.3; Bernard and Suhr 2018a).

Theorem 4.97

The stable recurrent set is closed and consists of those $p\in M$ for which there exists $q\ne p$ such that $(p,q)\in J_S$ and $(q,p)\in J_S$.

Hence the spacetime is stably causal iff the stable recurrent set vanishes.

Since $J_S$ is closed and transitive one is led to consider the following definition due to Sorkin and Woolgar (1996).

Definition 4.98

The K relation is the smallest closed and transitive relation which contains J.

Thus $K\subset J_S$ and since stable causality is equivalent to $J_S$-causality, stable causality implies K-causality. It is clear that

$$\begin{aligned} J\subset {\bar{J}}=A\subset A^\infty \subset \overline{A^\infty } \subset \cdots \subset K \end{aligned}$$

since all the relations but K have been constructed from J taking closures or through transitivization. As a result, K-causality as stable causality implies all the causality levels introduced so far. In Minguzzi (2009c) I described how to modify an example of Minguzzi (2008a) to get an $\overline{A^\infty }$-causal but non-K-causal spacetime.

K-causality and the K relation were studied in Sorkin and Woolgar (1996), Dowker et al. (2000), Minguzzi (2008a, b, 2009e, 2019), Janardhan and Saraykar (2008, 2013), Ebrahimi (2015), Bernard and Suhr (2018b), Miller (2018) and Sorkin et al. (2019).

The following problem was formulated by Low (Sorkin and Woolgar 1996).

Is K-causality equivalent to stable causality? Is $K=J_S$?

It turns out that Seifert (1971) had stated the last identity, but once again his proof of a few lines did not really work. In fact the two relations might differ in causal spacetimes, see Fig. 19.

Fig. 19

In this spacetime $K\ne J_S$, in fact $K=J$ but $J_S=M\times M$, because for every $g'>g$, $J_{g'}=M\times M$. It can be made causal, though totally imprisoning, by considering a section $S^1\times S^1$ instead of $S^1$ and using the same trick used for Carter’s example (Fig. 12). In such a case $K={\bar{J}}$ but still $J_S=M\times M$

Much of the difficulty with this problem is connected to the fact that the K relation is characterized through abstract properties, not by means of causal curves.

After some attempts (Minguzzi 2008b), in 2008 I finally solved the problem (Minguzzi 2009e, 2010). Recently, I have given a cleaner version of the proof valid under low regularity conditions (Minguzzi 2019), and subsequently yet another low regularity proof inspired by Conley theory on dynamical systems has been obtained by Bernard and Suhr (2018b).

Theorem 4.99

K-causality coincides with stable causality and under this condition $K=J_S$.

This result is extremely powerful, for instance the proof that causal continuity implies stable causality is just a few lines thanks to it. Also with it we shall prove an important singularity theorem (Sect. 6.6.1).

We arrive at an important result which clarifies the connection between stable causality and the existence of a time function (this result was also claimed by Seifert but his proof is regarded as incorrect though it contained some good ideas).

The first reference credited for a proof of the equivalences $(i){-}(iii)$ in the $C^2$ case is Bernal and Sánchez (2004, 2005), while the proof of the last statement was given by the author in Minguzzi (2009e, 2010). In any case, many other proofs are now available (Fathi and Siconolfi 2012; Chruściel et al. 2016; Bernard and Suhr 2018a, b; Minguzzi 2019), I recommend my last review (Minguzzi 2019) since it proves all the equivalences by using rather elementary arguments based on volume functions (the properties of convex neighborhoods and exponential map are not used).

Theorem 4.100

The following properties are equivalent:

• (i) Stable causality,

• (ii) Existence of a time function,

• (iii) Existence of a smooth temporal function,

Moreover, in this case $J_S=K=T_1=T_2$ where

$$\begin{aligned} T_1&=\{(p,q):t(p)\le t(q), \text { for every time function } t \}, \\ T_2&=\{(p,q):t(p)\le t(q), \text { for every (smooth) temporal function } t \}. \end{aligned}$$

It is remarkable that in stably causal spacetimes the Seifert order can be recovered from the set of time functions. This fact suggests that the Seifert order is actually more fundamental than the causal order. One could ask whether the manifold topology could also be recovered from the set of time functions. Again the answer is affirmative and it is due to the fact that stably causal spacetimes are quasi-uniformizable (Minguzzi 2013). This property implies that they can be Nachbin-compactified, so that the Seifert closed order extends to a closed order in the compactified space. This is the spacetime compactification for stably causal spacetime that I proposed in Minguzzi (2013).

A result similar to Theorem 4.100 holds under quite weak causality conditions provided time functions are replaced by semi-time functions (Minguzzi 2010) (recall that reflectivity implies the transitivity of ${\bar{J}}$).

Theorem 4.101

Let (M, g) be a chronological spacetime for which ${\bar{J}}$ is transitive, then there is a semi-time function t which is also a continuous utility for $K={\bar{J}}$, namely it satisfies:

• (a) $(p,q)\in {\bar{J}} \Rightarrow t(p)\le t(q)$, and

• (b) $(p,q)\in {\bar{J}}$ and $(q,p)\notin {\bar{J}} \Rightarrow t(p)< t(q)$.

Moreover, the set of these utilities and hence that of semi-time functions can be used to recover ${\bar{J}}$, namely

$$\begin{aligned} {\bar{J}}&=\{(p,q):t(p)\le t(q), \text { for every semi-time function } t \}. \end{aligned}$$

We end the section mentioning two causality properties which are preserved under enlargements of the cones (Minguzzi 2019).

Theorem 4.102

(One-sided stability of the absence of lightlike lines) Suppose that (M, g) does not have lightlike lines. There is ${\tilde{g}}>g$, such that for every $g'$, $g<g'<{\tilde{g}}$, $(M,g')$ does not have lightlike lines.

An analogous result holds for the absence of past/future rays.

We recall that by Theorem 2.108 under non-total imprisonment for a non-empty compact set S, $E^+(S)$ is non-empty and $E^+(S)=\overline{E^+(S)}$, moreover, S is future trapped if $E^+(S)$ is compact or equivalently, there are no future lightlike rays starting from S entirely contained in $E^+(S)$.

Theorem 4.103

(Stability of compact trapped sets) Let (M, g) be non-totally imprisoning. Let S be a non-empty compact set such that $\overline{E^+(S)}$ is compact. There is a Geroch interval $({\underline{g}}, {\overline{g}})\ni g$, such that for every ${\hat{g}} \in ({\underline{g}}, {\overline{g}})$, $\overline{{\hat{E}}^+(S)}$ is compact.

If (M, g) is stably causal we can take ${\overline{g}}$ stably causal and also for every ${\hat{g}} \in ({\underline{g}}, {\overline{g}})$, we have that ${{\hat{E}}^+(S)}$ is compact hence S is future trapped in $(M,{\hat{g}})$.

Proof

Suppose not, let us consider sequences ${\underline{g}}_k< g<{\overline{g}}_k$, ${\underline{g}}_{k}<{\underline{g}}_{k+1}$, ${\overline{g}}_{k+1}<{\overline{g}}_k$, ${\underline{g}}_k,{\overline{g}}_k\rightarrow g$. Then we can find ${\hat{g}}_k\in ({\underline{g}}_k,{\overline{g}}_k)$ admitting a ${\hat{g}}_k$-causal curve $\sigma _k$ starting from S and entirely contained in ${\hat{E}}_k^+(S)$, such that the endpoints $q_k$ go to infinity. Thus there is a limit future inextendible continuous g-causal curve $\sigma$ starting from S. Since S is trapped we can find $p\in S$ and $r\in \sigma \backslash S$ such that there is a g-timelike curve $\gamma$ from p to r. However, due to the compact domain of $\gamma$ there is $g'<g$ such that $\gamma$ is $g'$-timelike, thus there are open sets $U\ni p$, $r\ni V$, such that $U\times V\subset I'$. But for sufficiently large k, $g'<{\underline{g}}_k$, thus $U\times V\subset I'\subset I_k$, and (passing to a subsequence if necessary) there are points $p_k,r_k\in \sigma _k$, $p_k\in S$, $p_k\rightarrow p$, $r_k\rightarrow r$, such that for sufficiently large k, $p_k\in U$, $r_k\in V$, which contradicts the inclusion of $\sigma _k$ in ${\hat{E}}_k^+(S)$.

If (M, g) is stably causal we can take ${\overline{g}}$ stably causal, thus all the metrics in $({\underline{g}}, {\overline{g}})$ are non-totally imprisoning so for them the compactness of $E^+(S)$ is equivalent to the compactness of $\overline{E^+(S)}$ by Theorem 2.108. $\square$

4.5 The higher levels

Once the lower levels of the causal ladder have been discussed, the higher levels, whose purpose is that of limiting the nasty influence of infinity on spacetime, are easly placed by taking advantage of the transverse ladder, see Fig. 20.

Fig. 20

The upper levels of the causal ladder and how they are obtained from some of the lower levels by applying the properties of the transverse ladder

4.5.1 Causal easiness

This property is not among the classical ones but its introduction is convenient for otherwise some theorems would be expressed in an unnecessarily weak form Minguzzi (2009e) (notice that two implications end at this level in Fig. 20)

Definition 4.104

A spacetime is causally easy if it is strongly causal and ${\bar{J}}$ is transitive.

Proposition 4.105

Causally easy spacetimes are stably causal.

If in the definition of causally easy the strong causality condition were weakened to distinction this result would not hold (Minguzzi 2009e).

A spacetime can be stably causal without being causally easy: the spacetime of Fig. 17 without the identification.

Proof

As a first step we prove A-causality. Assume that the spacetime is strongly causal and $\bar{J}$ is transitive, and assume that the spacetime is not A-causal, then there are events p, q, $p \ne q$, such that $(p,q) \in {A}$ and $(q,p) \in A$. Let $\sigma _n$ be a sequence of causal curves of endpoints $(p_n,q_n) \rightarrow (p,q)$. By the limit curve theorem there is a limit causal curve $\sigma ^q$ ending at q (past inextendible or such that it connects p to q) and if $r \in \sigma ^q\backslash \{q\}$ then $(p,r) \in \bar{J}$. Since $\bar{J}$ is transitive $(q,r) \in \bar{J}$ while clearly $(r,q) \in J$, thus by Theorem 4.75(v) the spacetime is not strongly causal, a contradiction. Since ${\bar{J}}$ is transitive, $K={\bar{J}}$, and by A-causality K is antisymmetric, thus the spacetime is K-causal hence stably causal. $\square$

We arrive at an important result which shall be read as a singularity theorem (Minguzzi 2009c).

Theorem 4.106

Chronological spacetimes without lightlike lines are causally easy (hence stably causal).

Proof

Strong causality follows from Theorem 2.69 while Theorem 4.15 proves that ${\bar{J}}$ is transitive. $\square$

Proposition 4.107

A spacetime which is future distinguishing and future reflecting is causally easy.

Proof

Future distinction reads: $D_f$ is antisymmetric. By future reflectivity $D_f={\bar{J}}$, thus ${\bar{J}}$ is transitive hence $K=D_f={\bar{J}}$, in particular ${\bar{J}}$ is transitive and the spacetime is K-causal hence strongly causal. $\square$

4.5.2 Causal continuity

We begin the section with a promised characterization of reflectivity in terms of the K relation (Hawking and Sachs 1974; Dowker et al. 2000; Minguzzi 2008a).

Proposition 4.108

A spacetime is future reflecting iff $K=D_f$ (i.e. $K^+(p)=\overline{J^+(p)}$ for every $p\in M$).

Under future distinction the same statement holds with $J_S$ replacing K.

Without the future distinction condition the second statement is false, a counterexample is given by the spacetime of Fig. 19.

Proof

Since $D_f\subset {\bar{J}}\subset K$, if $D_f=K$ then $D_f={\bar{J}}$, which is one of the characterizations of future reflectivity, see Definition 4.6.

Under reflectivity $D_f={\bar{J}}$, which implies that $D_f$ is not only transitive but also closed, thus by the definition of K, ${\bar{J}}\subset K\subset D_f$, which implies $K=D_f$.

Suppose that (M, g) is future distinguishing. If $J_S=D_f$ then $D_f$ is closed, thus from $J\subset D_f$ we get taking closure, ${\bar{J}}\subset D_f$ and hence ${\bar{J}}=D_f$.

If ${\bar{J}}=D_f$ then $D_f$ is closed and transitive, thus $K=D_f$, but future distinction coincides with the antisymmetry of $D_f$ and hence K, thus, as the spacetime is K-causal, $J_S=K=D_f$. $\square$

Definition 4.109

A spacetime is causally continuous if it is weakly distinguishing and reflecting.

The traditional definition due to Hawking and Sachs (1974) uses distinction in place of weak distinction. The possibility of improving the definition by weakening one condition was observed in Budic and Sachs (1974) and Minguzzi (2008e). In fact it can be weakened further to feeble distinction (Minguzzi 2008e).

Theorem 4.110

Causally continuous spacetimes are causally easy.

Thus the definition of causally continuous spacetime could indeed be: reflecting and distinguishing spacetime. A spacetime can be causally easy without being causally continuous ($1+1$ Minkowski spacetime with a timelike geodesic segment removed).

Proof

By reflectivity (Definition 4.9) $D={\bar{J}}$, since the former is transitive and the latter closed, $K=D={\bar{J}}$, in particular ${\bar{J}}$ is transitive. By weak distinction D is antisymmetric, hence (M, g) is K-causal, which implies strong causality. $\square$

We recall that according to an equivalence proved with Definition 4.6: future reflectivity iff the volume function $t^+(p)=-\mu (I^+(p))$ is continuous (and dually).

Theorem 4.111

• (a) The condition “future distinction and future reflectivity” is equivalent to the volume function $t^+(p)=-\mu (I^+(p))$ being a time function.

• (b) Causal continuity is equivalent to both $t^+(p)= -\mu (I^+(p))$ and $t^-(p)=\mu (I^-(p))$ being time functions.

A non-causally continuous spacetime satisfying the condition in (a) is given by $1+1$ Minkowski spacetime minus a past lightlike ray.

Proof

(a). Future reflectivity is equivalent to the continuity of $t^+$, while future distinction is equivalent to the fact that $t^+$ strictly increases over causal curves (Theorem 4.44).

(b). Immediate because causal continuity is equivalent to “future distinction and future reflectivity” plus “past distinction and past reflectivity”. $\square$

4.5.3 Causal simplicity (and absence of Cauchy holes)

Definition 4.112

A spacetime which is causal and such that J is closed is called causally simple.

The second condition has many equivalent formulations, see Theorem 4.12. The traditional definition (Hawking and Ellis 1973) demanded strong causality in place of causality. The improved definition appeared in Bernal and Sánchez (2007) and Minguzzi and Sánchez (2008).

Proposition 4.113

Causally simple spacetimes are causally continuous.

Causally continuous spacetimes need not be causally simple, e.g. Minkowski $1+1$ spacetime minus a point. As another example, plane wave gravitational metrics are known to be causally continuous but not causally simple (Penrose 1965b; Ehrlich and Emch 1992a). In general, generalized plane waves might have interesting causal pathologies (Hubeny and Rangamani 2003; Hubeny et al. 2005; Flores and Sánchez 2003, 2006; Minguzzi 2012a).

Proof

Recall that $J\subset D_f\cup D_p\subset {\bar{J}}$, thus ${\bar{J}}=J=D_f=D_p$, and by causality $D_f$ and $D_p$ are antisymmetric which is the distinction property. Moreover, with the transverse ladder we proved that the closure property of J implies reflectivity. $\square$

A spacetime might admit a partial Cauchy hypersurface whose Cauchy development is smaller than what is potentially possible. In such a case there is a breakdown of predictability as if portions of spacetimes had been removed from the manifold.

Geroch (1977b) had first tried to formalize this concept of Cauchy hole. Krasnikov (2009) showed that Geroch’s definition was untenable, for according to it even Minkowski spacetime is holed. It turns out that the concept is technical and quite sensitive to the details of the definition. Manchak (2009) worked with a correction of the concept which had been suggested by Geroch himself, but still there are technical problems with the new version, for the region $t<0$ of Minkowski spacetime becomes holed in his formulation. Clarke (1976) gives another definition and credits J. Earman and N. Woodhouse (Earman refers to the hole-free condition as the determinism maximal propertyEarman 1995, Sect. 3.8). However, Manchak points out that Clarke’s definition runs into the same problems of Geroch’s.

I proposed the following definition (Minguzzi 2012b) that does not run into the previously mentioned problems. Subsequently Manchak (2014) changed his definition and adopted a version that seems more closely related to this one.

Definition 4.114

A spacetime (M, g) has a future Cauchy hole (or simply a future hole) if there is a partial Cauchy hypersurface S and an isometry $\varphi : \tilde{D}(S) \rightarrow N$, on a spacetime $(N,\sigma )$, such that $\varphi (S)$ is acausal and $\varphi (H^+(S))\cap D^{+}(\varphi (S))\ne \emptyset$. The definition of past Cauchy hole is given dually. A spacetime is Cauchy holed if it has a future or a past hole. A spacetime is (future/past) hole-free if it has no (future/past) hole.

Likely the hole-free condition should be regarded as a property to be added to the very definition of spacetime. It is unlikely that it could be derived from other physically reasonable conditons, for the removal of just one point would preserve those physical conditions while spoiling hole-freeness. In a sense hole-freeness guarantees that nobody has tampered with the spacetime manifold, hence that all the events are at their place.

Clarke (1993) suggested that global hyperbolicity implies hole-freeness, but as mentioned there were problems with his definition and also with the proof.

Causal simplicity is not particularly robust under removal of points from spacetime, for the closure property of J would be spoiled. So one could suspect a relationship between hole-freeness and causal simplicity. In fact we proved (Minguzzi 2012b).

Theorem 4.115

Every inextendible and causally simple spacetime is hole-free.

The theorem is optimal in the sense that causal simplicity cannot be weakened to causal continuity: let M be Minkowski 3 + 1 spacetime with the origin o removed. The spacetime metric is multiplied by a conformal factor different from unity in $I^+(o)$ in such a way that the timelike geodesic $t > 0$, $x = y = z = 0$, becomes geodesically complete in the past direction. This spacetime is causally continuous, inextendible, but holed.

More information on holed spacetime is given by the following theorem (Minguzzi 2012b).

Theorem 4.116

Every inextendible future holed spacetime admits a future lightlike incomplete geodesic and a future timelike incomplete geodesic. These geodesics are contained in D(S) and the Riemann tensor, and its covariant derivatives of any order, evaluated on a parallely transported base over them have a finite limit.

Thus the causally geodesically complete inextendible spacetimes are hole-free.

It would be interesting to know if hole-freeness promotes some causality conditions. At present we have only partial results (Minguzzi 2012b).

4.5.4 Global hyperbolicity

Definition 4.117

A spacetime is globally hyperbolic if the following equivalent conditions hold

• (a) Non-total imprisonment and for every $p,q\in M$, $\overline{J^{+}(p)\cap J^-(q)}$ is compact.

• (b) Causality and for every $p,q\in M$, $J^{+}(p)\cap J^-(q)$ is compact.

• (c) Stable causality and for every $p,q\in M$, $J_S^{+}(p)\cap J_S^-(q)$ is compact.

Moreover, in this case $J=J_S$ and for every compact set K, $J^+(K)\cap J^-(K)$ is compact.

Proof

(Proof of equivalence) (a) $\Rightarrow$ (b). Let $r_n \in J^{+}(p)\cap J^-(q)$ with $r_n\rightarrow r$. By the limit curve theorem there are causal curves connecting p to r and r to q, for otherwise there would be future or past inextendible curves entirely contained in a compact set, in contradiction with non-total imprisonment.

(b) $\Rightarrow$ (c). The causal diamonds are compact hence closed, thus by Theorem 4.12 J is closed and (M, g) is causally simple hence stably causal. Moreover, J is transitive and by stable causality and Theorem 4.99 $J_S=K=J$.

(c) $\Rightarrow$ (a). Clearly $J^{+}(p)\cap J^-(q)\subset J_S^{+}(p)\cap J_S^-(q)$, thus the relative compactness of the latter set implies the relative compactness of the former.

As for the last statement, the identity $J=J_S$ follows from the just given proof, while $J^+(K)\cap J^-(K)$ is relatively compact by (a) (notice that there are points $p_1, \ldots p_k$ such that $K\subset \cup _k I^+(p_k)$, and a similar dual property) and closed by Theorem 4.12. $\square$

The traditional definition within causality theory is: strong causality and compactess of the causal diamonds (Hawking and Ellis 1973). The improved version (b) appeared in Bernal and Sánchez (2007). The version (a) appeared in Minguzzi (2009a). It has several advantages over the others because it does not require that the causal diamonds be closed. Notice that (a) makes it obvious that by narrowing the cones one does not spoil global hyperbolicity, a fact not at all obvious from the other formulations. In fact this is also the version used to prove the stability of global hyperbolicity, cf. Theorem 4.121. The last characterization (c) is interesting because its shows that global hyperbolicity is expressible through the Seifert relation.

Proposition 4.118

Globally hyperbolic spacetime are causally simple.

Proof

The compactess of the causal diamonds implies that they are closed which implies that J is closed (Theorem 4.12). $\square$

The causally simple spacetimes need not be globally hyperbolic, consider for instance $1+1$ Minkowski spacetime minus a point. A more interesting example is the following gravitational wave spacetime $M=\mathbb {R}^2\times \mathbb {R}^2\backslash \{(0,0)\}$ (here $\mu >0$ is a constant)

$$\begin{aligned} g=\mu (\mathrm{d}r^2+r^2\mathrm{d}\theta ^2)-2 \mathrm{d}t\mathrm{d}y+2 \mu M \log r \, \mathrm{d}t^2 , \end{aligned}$$

(4.8)

which we showed to be causally simple non-globally hyperbolic and to satisfy the vacuum Einstein equations (Minguzzi 2012a).

The following topological splitting theorem is due to Geroch (1970) and Hawking and Ellis (1973) who proved it using volume functions.

Theorem 4.119

A spacetime (M, g) is globally hyperbolic iff it admits a Cauchy hypersurface ${\tilde{S}}$, i.e. $D({\tilde{S}})=M$. All Cauchy hypersurfaces are homeomorphic. If (M, g) is globally hyperbolic there is a homeomorphism $\varphi :M\rightarrow \mathbb {R}\times {S}$, such that $t:=\pi _1\circ \varphi$ is a time function, the level sets $S_a=t^{-1}(a)$, $a \in \mathbb {R}$, are Cauchy hypersurfaces ($\varphi$ can be chosen so that ${\tilde{S}}=S_0$), and the curves $t\mapsto \varphi ^{-1}(t,s)$, $s\in S$, are timelike.

The following important result was proved by Bernal and Sánchez (2003, 2005, 2007). The steepness part appeared in Müller and Sánchez (2011), see also Minguzzi (2016b). A previous incorrect proof was given in Seifert (1977) and cited by Hawking and Ellis (1973). Only more recently some of Seifert’s ideas have been used in a correct proof by Chruściel et al. (2016). There are also other proofs (Fathi and Siconolfi 2012; Müller 2013; Bernard and Suhr 2018a; Minguzzi 2019), some of which are more refined, hold under much weaker differentiability conditions and for general cone structures.

In the theorem the smoothness assumption can be replaced by a lower degree of differentiability, see the mentioned references for details.

Theorem 4.120

Every smooth globally hyperbolic spacetime admits a smooth Cauchy temporal function, which furthermore can be chosen steep. As a consequence, M is smoothly isometric to a product manifold $\mathbb {R}\times S$, endowed with coordinates (t, x) and metric $-\beta \mathrm{d}t^2+h_t$, where t is a smooth Cauchy temporal steep function whose level sets are Cauchy hypersurfaces smoothly diffeomorphic to S. The function $\beta$ is smooth with values in [0, 1], while $g_t$ are time-dependent Riemannian metrics over S. Finally, the fibers of constant x are smooth timelike curves.

As observed in Chernov and Nemirovski (2013), if furthermore M is contractible then it is diffeomorphic to the Euclidean space.

The first correct proof of the following stability result was given by Benavides Navarro and Minguzzi (2011). Geroch (1970) in his seminal paper gave a proof that turned out to be incorrect, see Benavides Navarro and Minguzzi (2011) (arXiv version) for a discussion. The simplest proof can be found in Minguzzi (2019), but there are others (Fathi and Siconolfi 2012; Chruściel and Grant 2012; Sämann 2016; Aké et al. 2018).

Theorem 4.121

Global hyperbolicity is stable in the interval topology, namely there is $g'>g$ such that $(M,g')$ is globally hyperbolic.

The following related result is also interesting (Minguzzi 2019; Aké et al. 2018)

Theorem 4.122

Cauchy temporal functions are stable, namely if $t:M\rightarrow \mathbb {R}$ is Cauchy temporal for (M, g), then it is Cauchy temporal for $(M,g')$ for some $g'>g$.

Globally hyperbolic spacetimes are causally geodesically connected (Avez 1963; Seifert 1967).

Theorem 4.123

(Avez–Seifert) Let (M, g) be globally hyperbolic and let $(p,q)\in J\backslash \varDelta$, then there is a causal geodesic $\sigma$ connecting p to q such that $d(p,q)=l(\sigma )$. In particular, d is finite.

Proof

Let $\sigma _k$ be a sequence of causal curves connecting p to q, such that $l(\sigma _k)\rightarrow d(p,q)$. The sequence must necessarily converge h-uniformly to a continuous causal curve $\sigma$ (pass to a subsequence if necessary), for the other option of the limit curve theorem would imply the existence of a future inextendible continuous causal curve imprisoned in the compact set $J^+(p)\cap J^-(q)$, in contradiction with non-total imprisonment. By the upper semi-continuity of the Lorentzian distance (Theorem 2.41)

$$\begin{aligned} d(p,q)=\limsup l(\sigma _k) \le l(\sigma ), \end{aligned}$$

thus d is finite and $d(p,q)=l(\sigma )$. $\square$

The previous result follows also from Theorem 3.48 which implies, see also Beem et al. (1996, Lemma 4.5),

Theorem 4.124

On a globally hyperbolic spacetime d is finite and continuous.

Proof

The globally hyperbolic spacetime admits a Cauchy hypersurface S hence acausal, $D(S)=M$, $H(S)=\emptyset$. The result follows from Theorem 3.48. $\square$

Under non-total imprisonment the finiteness of d on the conformal class characterizes global hyperbolicity (Beem et al. 1996; Minguzzi 2009a, Lemma 2.1). For more results characterizing causality condition through the Lorentzian distance, see Minguzzi (2009a).

5 Lorentzian distance and causality

In this section we collect, for the reader convenience, some results on the relationship between Lorentzian distance and causality conditions. Most results will be presented without proof, the reader is referred to the original works (Beem et al. 1996; Minguzzi 2007, 2009a). A recent contribution is Rennie and Whale (2019).

The simplest result relating a property of d with causality is the following.

Proposition 5.1

If d is finite then (M, g) is chronological.

Proof

If through p passes a closed timelike curve $\gamma$, then by considering curves that wind over $\gamma$ we find that $d(p,p)=\infty$. $\square$

By the equivalence $(p,q)\in I\Leftrightarrow d(p,q)>0$ it is clear that any causality condition that can be expressed through the chronological relation can also be expressed through the Lorentzian distance. Fortunately, there are results that are not mere translations of known set theoretical ones.

We recall that the conformal class of g, denoted [g] or ${\varvec{g}}$, is the family of metrics on M that are conformal to g. The Lorentzian distance is not conformally invariant, though some sets derived from it are, e.g., the loci $d>0$ and $d=0$ (vanishing distance set). A natural way to get a conformally invariant concept out of the Lorentzian distance consists in making use of quantifiers in connection with the conformal class, for instance “there is a metric in the conformal class for which the Lorentzian distance is continuous”.

Let us start with two results connected with the properties of the transverse ladder.

The following result appeared in Beem and Ehrlich (1977) (Beem et al. 1996, Theorem 4.24) and Minguzzi (2007, Theorem 3.3).

Proposition 5.2

If there is a metric in the conformal class for which the Lorentzian distance is continuous wherever it vanishes, then (M, g) is reflecting.

Proof

If (M, g) were not reflecting then it would be non-past or non-future reflecting. We can assume the first possibility as the other case can be treated similarly. Thus there is a pair (x, z) and an event y such that $I^{+}(x) \supset I^{+}(z)$ but $y \in I^{-}(x)$ while $y \notin I^{-}(z)$. In particular, $d(y,z)=0$. Since $I^{+}(z)\subset I^{+}(x)$, $z \in \bar{I}^{+}(x)$. Let $z_n \rightarrow z$, $z_{n} \in I^{+}(x)$, then

$$\begin{aligned} d(y,z_n)\ge d(y,x)+d(x,z_{n})>d(y,x)>0, \end{aligned}$$

thus there is a discontinuity at (y, z), where $d(y,z)=0$, a contradiction. $\square$

The following result is proved in Minguzzi (2009b, Lemma 2.1).

Proposition 5.3

Let a spacetime be non-totally imprisoning. If for every metric choice in the conformal class the Lorentzian distance is finite or continuous wherever it vanishes, then J is closed.

As for the connection with causal continuity we have the following result from Minguzzi (2009b, Theorem 2.4). In one direction strong causality can be weakened to distinction.

Theorem 5.4

A strongly causal spacetime is causally continuous if and only if there is a metric in the conformal class for which the Lorentzian distance is continuous wherever it vanishes.

Causal simplicity can be characterized through the following result taken from Minguzzi (2009b, Theorem 2.2).

Theorem 5.5

A non-totally imprisoning spacetime is causally simple if and only if for every metric choice in the conformal class the Lorentzian distance is continuous wherever it vanishes.

As for global hyperbolicity, the following result proved in Theorem 4.124 is classical (Beem et al. 1996, Lemma 4.5).

On a globally hyperbolic spacetime d is finite and continuous for every metric choice in the conformal class.

We have also the following characterization in terms of the finiteness of the Lorentzian distance due to Beem and Ehrlich (1979b, Theorem 3.5) (Beem et al. 1996, Theorem 4.30).

Theorem 5.6

A strongly causal spacetime is globally hyperbolic if and only if for every metric choice in the conformal class the Lorentzian distance is finite.

In general, the following result is quite useful when considering the effect of conformal transformations on the Lorentzian distance function (Minguzzi 2009a, Lemma 2.3).

Lemma 5.7

Let $x\in M$ and let $B_n(x)$ be the open ball centered at x and of radius n with respect to a complete Riemannian metric. If the spacetime is strongly causal, then there is a representative g of the conformal class such that

$$\begin{aligned} \mathrm {diam}(M,g):=\sup _{p,q\in M} d(p,q) \end{aligned}$$

is finite and for every $\epsilon >0$ there is a $n \in \mathbb {N}$ such that if $\gamma : I \rightarrow M$ is any $C^1$ causal curve,

$$\begin{aligned} \int _{I\cap \gamma ^{-1}(M\backslash \bar{B}_n) } \!\!\!\!\!\!\! \sqrt{-g(\dot{\gamma },\dot{\gamma })} \, \mathrm{d}t <\epsilon \end{aligned}$$

that is, its many connected pieces contained in the open set $M\backslash \bar{B}_n$ have a total Lorentzian length smaller than $\epsilon$.

Thus, in a strongly causal spacetime the conformal factor can be chosen in such a way that d is bounded.

Finally, we have a characterization in terms of the continuity of d proved in Minguzzi (2009b, Theorem 3.6).

Theorem 5.8

A non-totally imprisoning spacetime is globally hyperbolic if and only if for every metric choice in the conformal class the Lorentzian distance is continuous.

5.1 The distance formula

With Theorem 4.100 we learned that in a stably causal spacetime the Seifert relation can be recovered from the set of time or temporal functions. We also mentioned that one can recover the spacetime topology as well. One might want to recover the Lorentzian distance in a similar fashion. This is indeed possible (Minguzzi 2019) but one has first to correct the definition of Lorentzian distance.

Definition 5.9

The stable distance $d_S$ is

$$\begin{aligned} d_S(p,q)=\inf _{g'\succ g} d'(p,q), \end{aligned}$$

(5.1)

where $g'\succ g$ here means not only that the causal cone of g is contained in the timelike cone of $g'$, but also that $g(v,v)=-1\Rightarrow g'(v,v)<-1$.

The stable distance is obtained, so to say, by enlarging the indicatrices, not just the causal cones. This modification is analogous to that which brings J to $J_S$ (under global hyperbolicity $J_S=J$ and $d_S=d$).

The Lorentzian distance can be shown to be stably finite, i.e. finite for some $g'\succ g$, if and only if $d_S$ is finite (Minguzzi 2019, Theorem 2.61). The stably causal spacetimes admitting a stably finite Lorentzian distance are called stable spacetimes and are really coincident with the Lorentzian submanifolds of Minkowski spacetime (Minguzzi 2019, Theorem 4.13). Moreover, the distinguishing spacetimes for which d is continuous satisfy $d=d_S$, so if they have finite Lorentzian distance (e.g. the globally hyperbolic spacetimes) they are stable (Minguzzi 2019, Theorem 4.8, Corollary 4.1). The stably causal spacetimes are conformal to stable spacetimes (Minguzzi 2019, Theorem 2.62).

Let $\mathscr {S}$ denote the family of steep functions (see Definition 1.24), we have that the spacetime is stable iff $\mathscr {S}$ is non-empty and in this case (Minguzzi 2019, Theorem 4.6)

$$\begin{aligned} d_S(p,q)=\mathrm {inf} \big \{[f(q)-f(p)]^+:f \in \mathscr {S}\big \}. \end{aligned}$$

(5.2)

where $c^+=\max \{0, c\}$.

A more general result holds true for stably causal spacetimes, in which the representing continuous J-isotone functions could attain an infinite value, the steepness condition holding only where the functions are finite (Minguzzi 2019, Theorem 4.11). The distance formula should clarify that $d_S$ is likely the best distance on a stably causal spacetime. We shall find another result that supports this idea in Theorem 5.17.

A special case of the previous result is given by the following theorem (Minguzzi 2019, Theorem 4.9).

Theorem 5.10

Let (M, g) be a distinguishing spacetime and let $\mathscr {S}$ be the family of steep temporal functions. The distance formula

$$\begin{aligned} d(p,q)=\mathrm {inf} \big \{[f(q)-f(p)]^+:f \in \mathscr {S}\big \}, \end{aligned}$$

(5.3)

holds true if and only if the Lorentzian distance is finite and continuous, in which case $d=d_S$.

This is the Lorentzian version of Connes’ distance formula first conjectured by Parfionov and Zapatrin (2000). Rennie and Whale (2019) in a recent preprint state that the distinguishing condition can be dropped provided the representing functions are not demanded to be $C^1$.

5.2 The product spacetime $M\times \mathbb {R}$

Let us consider the direct product spacetime ${\tilde{M}}=M\times \mathbb {R}$ endowed with the metric ${\tilde{g}}=g+\mathrm{d}z^2$, where $z=x^{n+1}$ is the extra-coordinate. Notice that the $\mathbb {R}$-fibers are spacelike, and that the projection of causal curves (timelike) is causal (resp. timelike).

I refer to the idea of studying the metric properties of (M, g) by means of the causality properties of $({\tilde{M}}, {\tilde{g}})$ as the product trick. In fact, the properties of the Lorentzian distance d on (M, g) are connected with the causality properties of $({\tilde{M}}, {\tilde{g}})$. We mention some results in this direction which are particular cases of more general results on warped product spacetimes (Minguzzi 2007).

To start with, we recall the following simple result (Beem et al. 1996, Proposition 3.61-3.68) Walschap (1995) Minguzzi (2007).

Theorem 5.11

The spacetime $({\tilde{M}},{\tilde{g}})$ is chronological (resp. non-totally vicious, causal, non-totally imprisoning, future distinguishing, strongly causal, stably causal, globally hyperbolic, geodesically connected) iff (M, g) has the same property.

The causality properties on $({\tilde{M}},{\tilde{g}})$ not mentioned in this result are precisely those connected with the continuity properties of the Lorentzian distance.

Given a topological space X, the upper semi-continuous envelope $h:X\rightarrow \mathbb {R}\cup \{+\infty \}$ of a function $f:X\rightarrow \mathbb {R}\cup \{+\infty \}$, is the function given by

$$\begin{aligned} h(x)=\inf _{U\ni x} \sup _{y\in U} f(y)=\limsup _{y \rightarrow x} f(y), \end{aligned}$$

where U is any neighborhood of x. It is actually the smallest upper semi-continuous function that bounds f from above, $f\le h$.

Let ${\bar{d}}$ be the upper semi-continuous envelope of d. It is supported on $\overline{J}$. Moreover, for $x,y\in M$, let $d_f(x, \cdot )$ be the upper semi-continuous envelope of $d(x,\cdot )$, and let $d_p(\cdot , y)$ be the upper semi-continuous envelope of $d(\cdot , y)$. They are supported in $D_f$ and $D_p$, respectively. Recall also the definition of stable distance $d_S$ from Eq. (5.1). The distance $d_S$ is known to be upper semi-continuous, supported on $J_S$ and to satisfy the reverse triangle inequality for $J_S$-related events (Minguzzi 2019, Theorem 2.60).

Definition 5.12

The K-distance $d_K:M\rightarrow [0,+\infty ]$ is the smallest upper semi-continuous function supported on K that bounds d from above and which satisfies the reverse triangle inequality for K-related events.

It exists because the function on $M\times M$ that equals $+\infty$ on K and zero elsewhere has the required properties. From the definitions we deduce

$$\begin{aligned} d\le \text {min}( d_f, d_p) \le \text {max}( d_f, d_p) \le {\bar{d}}\le d_K \le d_S, \end{aligned}$$

which is analogous to the inclusion $J\subset D_f\cap D_p\subset D_f\cup D_p \subset \overline{J}\subset K \subset J_S$.

Theorem 5.13

If d is continuous then ${\overline{J}}$ is transitive and $d={\bar{d}}=d_K$.

It is worth to recall that under transitivity of ${\overline{J}}$, the antisymmetry of $\overline{J}$ (namely A-causality) is equivalent to strong causality.

Proof

The continuity condition reads $d={\bar{d}}$. From Proposition 5.2 (M, g) is reflecting hence, by the transverse ladder, $\overline{J}$ is transitive. Let (x, y) and (y, z) be two pairs of $\overline{J}$-related events. We have $(x,z)\in {\overline{J}}$. If both pairs belong to I, then d satisfies the reverse triangle inequality over the triple x, y, z because d does. If neither (x, y) nor (y, z) belongs to I, then $d=0$ over them so d satisfies the reverse triangle inequality over the triple. If $(x,y)\in I$, and $(y,z)\in \overline{J}\backslash I$, let $\gamma _n$ be a sequence of timelike curves connecting x to y, such that $\lim _n \ell (\gamma _n)\rightarrow d(x,y)$. Let $\beta _k$ be a sequence of causal curves of endpoints $y_k\rightarrow y$, $z_k\rightarrow z$. The curves $\gamma _n$ can be modified in a neighborhood of y so as to be joined with $y_{k(n)}$, so as to get new causal curves $\alpha _n$ that reach $z_{k(n)}$. These curves $\alpha _n$ can be chosen in such a way that $\ell (\alpha _n) \rightarrow d(x,y)$, because they can be chosen to differ from $\gamma _n$ just in an arbitrarily small neighborhood of y. As a result ${\bar{d}}(x,z)\ge d(x,y)$, which, due to $d(y,z)=0$, is the reverse triangle inequality for ${\bar{d}}=d$. The case $(x,y)\in \overline{J}\backslash I$, $(y,z)\in I$ is similar to the previous one. We conclude that $d={\bar{d}}$ satisfies the reverse triangle inequality for ${\overline{J}}$-related events. $\square$

Let ${\tilde{I}}$ and ${\tilde{J}}$ be the chronological and causal relations on $({\tilde{M}},{\tilde{g}})$, and let ${\tilde{d}}$ be the Lorentzian distance on $({\tilde{M}},{\tilde{g}})$. We have the following identities that clarify that the continuity of d is related to some causality properties of $({\tilde{M}},{\tilde{g}})$ (Minguzzi 2007).

Theorem 5.14

The following identities hold true:

$$\begin{aligned} {\tilde{I}}&=\left\{ ((x_1,z_1), (x_2,z_2)):(x_1,x_2)\in I {\mathrm { and }} \vert z_2-z_1 \vert < d(x_1,x_2) \right\} ,\\ {\tilde{J}}&\subset \left\{ ((x_1,z_1), (x_2,z_2)):(x_1,x_2)\in J {\mathrm { and }} \vert z_2-z_1 \vert \le d(x_1,x_2) \right\} , \\ {{\tilde{D}}}&=\left\{ ((x_1,z_1), (x_2,z_2)):(x_1,x_2)\in D {\mathrm { and }} \vert z_2-z_1 \vert \le \mathrm {min}(d_f,d_p)(x_1,x_2) \right\} ,\\ {{\tilde{D}}}_f&=\left\{ ((x_1,z_1), (x_2,z_2)):(x_1,x_2)\in D_f {\mathrm { and }} \vert z_2-z_1 \vert \le d_f(x_1,x_2) \right\} ,\\ {{\tilde{D}}}_p&=\left\{ ((x_1,z_1), (x_2,z_2)):(x_1,x_2)\in D_p {\mathrm { and }} \vert z_2-z_1 \vert \le d_p(x_1,x_2) \right\} , \\ \overline{{\tilde{J}}}&=\left\{ ((x_1,z_1), (x_2,z_2)):(x_1,x_2)\in \overline{J} {\mathrm { and }} \vert z_2-z_1 \vert \le {\bar{d}}(x_1,x_2) \right\} ,\\ {\tilde{K}}&= \left\{ ((x_1,z_1), (x_2,z_2)):(x_1,x_2)\in K {\mathrm { and }} \vert z_2-z_1 \vert \le d_K(x_1,x_2) \right\} ,\\ {\tilde{J}}_S&= \left\{ ((x_1,z_1), (x_2,z_2)):(x_1,x_2)\in J_S {\mathrm { and }} \vert z_2-z_1 \vert \le d_S(x_1,x_2) \right\} ,\\ {\tilde{d}}^{\, 2}&((x_1,z_1), (x_2,z_2))=\max \left\{ 0, { d^2(x_1,x_2)-(z_2-z_1)^2}\right\} . \end{aligned}$$

The third identity follows from the fourth and the fifth. The eighth identity is not proved in the mentioned reference but follows easily from the first identity and Eq. (4.7). The seventh identity follows from the following result.

Theorem 5.15

Let R be a reflexive relation on M, and $r:M\times M\rightarrow [0,+\infty ]$ a function supported on R. The reflexive relation on ${\tilde{M}}$

$$\begin{aligned} {\tilde{R}}= \left\{ ((x_1,z_1), (x_2,z_2)):(x_1,x_2)\in R \mathrm { and } \vert z_2-z_1 \vert \le r(x_1,x_2) \right\} , \end{aligned}$$

(5.4)

is transitive iff R is transitive and r satisfies the reverse triangle inequality for R-related events. It is closed iff R is closed and r is upper semi-continuous. The relation ${\tilde{R}}$ is closed (resp. transitive) iff so is the reflexive relation

$$\begin{aligned} {\tilde{R}}^\downarrow =\left\{ ((x_1,z_1), (x_2,z_2)):(x_1,x_2)\in R \mathrm { and } z_2-z_1 \le r(x_1,x_2) \right\} . \end{aligned}$$

(5.5)

Suppose that ${\tilde{R}}$ is transitive. For every $x\in M$ we can only have $r(x,x)=0$ or $r(x,x)=\infty$. In the latter case ${\tilde{R}}$ and ${\tilde{R}}^\downarrow$ are not antisymmetric. In the former case, the antisymmetry of any among R, ${\tilde{R}}$, ${\tilde{R}}^\downarrow$ implies that of the other two.

Proof

Let $(x^k_1,z^k_1)\rightarrow (x_1,z_1)$, $(x^k_2,z^k_2)\rightarrow (x_2,z_2)$, with $((x^k_1,z^k_1), (x^k_2,z^k_2))\in {\tilde{R}}$, namely $(x^k_1,x^k_2)\in R$ and $\vert z^k_2-z^k_1 \vert \le r(x^k_1,x^k_2)$. Then $(x_1,x_2)\in {\bar{R}}$ and $\vert z_2-z_1\vert \le \limsup _k r(x^k_1,x^k_2)$. Thus if R is closed and r is upper semi-continuous then $((x_1,z_1), (x_2,z_2)) \in {\tilde{R}}$, namely ${\tilde{R}}$ is closed.

Conversely, suppose that ${\tilde{R}}$ is closed and consider a sequence such that $R\ni (x^k_1,x^k_2)\rightarrow (x_1,x_2)$. Let $z_2=(\limsup r)(x_1,x_2)$, and pass to a subsequence denoted in the same way such that $z^k_2:=r(x^k_1,x^k_2) \rightarrow z_2$. Moreover, let $z^k_1=z_1=0$, and consider the sequence $((x^k_1,0),(x^k_2, z^k_2))$ converging to $((x_1,0),(x_2,z_2))$. We conclude that $(x_1,x_2)\in R$ and $(\limsup r)(x_1,x_2) \le r(x_1,x_2)$, namely R is closed and r is upper semi-continuous.

The statement that if R is transitive and r satisfies the reverse triangle inequality for R-related events then ${\tilde{R}}$ is transitive, follows from the inequalities

$$\begin{aligned} \vert z_3-z_1 \vert \le \vert z_2-z_1 \vert + \vert z_3-z_2\vert \le r(x_1,x_2)+r(x_2,x_3)\le r(x_1,x_3), \end{aligned}$$

where $(x_1,x_2)\in R$ and $(x_2,x_3)\in R$. For the converse, let $(x_1,x_2)\in R$, $(x_2,x_3)\in R$, and let $z_1=0$, $z_2=r(x_1,x_2)$, $z_3=r(x_1,x_2)+r(x_2,x_3)$, then $((x_1,z_1),(x_2,z_2))\in {\tilde{R}}$, $((x_2,z_2),(x_3,z_3))\in {\tilde{R}}$, thus by transitivity of ${\tilde{R}}$, $(x_1,x_3)\in R$ and $r(x_1,x_2)+r(x_2,x_3)=\vert z_3- z_1 \vert \le r(x_1,x_3)$. The proofs for ${\tilde{R}}^\downarrow$ are similar.

By reflexivity $(x,x)\in R$, thus by transitivity of ${\tilde{R}}$, $r(x,,x)+r(x,x)\le r(x,x)$, which has the only solutions $r(x,x)=0$ and $r(x,x)=+\infty$. Under the condition $r(x,x)=0$, no two distinct points P, Q in the fiber of $x\in M$ can be such that $(P,Q)\in {\tilde{R}}$ and $(Q,P)\in {\tilde{R}}$, from which the other statements follow. $\square$

Theorem 5.16

The distance $d_f$ satisfies the reverse triangle inequality over $D_f$-related events. A similar statement for $d_p$ holds true.

The distance $\mathrm {min}(d_f,d_p)$ satisfies the reverse triangle inequality over D-related events.

Proof

By Proposition 4.1 the relation ${\tilde{D}}_f$ is transitive, hence the first claim follows from Theorem 5.15. The last claim follows from the transitivity of ${\tilde{D}}$. $\square$

The following result, which generalizes Theorem 4.99, clarifies that in stably causal spacetimes the natural distance is $d_S$ much in the same way as $J_S$ is the natural causality relation.

Theorem 5.17

In a stably causal spacetime $d_K=d_S$ (and $K=J_S$).

Proof

The stable causality of (M, g) implies the stable causality of $({\tilde{M}}, {\tilde{g}})$, and by Theorem 4.99 the identity ${\tilde{K}}={\tilde{J}}_S$, which implies $d_K=d_S$ and $K=J_S$. $\square$

Corollary 5.18

If d is continuous in a distinguishing (and hence causally continuous) spacetime then $d=d_S$, namely all distances become identical to the usual one.

Notice that the assumption is satisfied in a globally hyperbolic spacetime.

Proof

By Proposition 5.2 the spacetime is causally continuous. The condition of continuity for d reads $d={\bar{d}}$, but by Theorem 5.13 it also implies that $d=d_K$, and hence, by stable causality, $d=d_S$. $\square$

Proposition 5.19

Chronology (strong causality, K-causality or stable causality) implies that $d\vert _{\varDelta }=0$ (resp. ${\bar{d}}\vert _{\varDelta }=0$, $d_K\vert _{\varDelta }=d_S\vert _{\varDelta }=0$).

Proof

The statement under chronology is clear. In a strongly causal spacetime, by Theorem 2.35, ${\bar{d}}=d$ in a neighborhood of $\varDelta$, in particular ${\bar{d}}\vert _{\varDelta }=0$. We recall that stable causality is equivalent to K-causality. In a stably causal spacetime there cannot be $p\in M$ such that $d_S(p,p)>0$ otherwise, by definition of $d_S$, the stable recurrent set would be non-empty (as it would include p) and hence by Theorem 4.97 stable causality would be violated, which is a contradiction. $\square$

By using the identities of Theorem 5.14 we arrive at the following result.

Theorem 5.20

On the spacetime $({\tilde{M}},{\tilde{g}})$ the closure of the causal relation $\overline{{\tilde{J}}}$ is transitive, iff (a) on (M, g) the relation $\overline{J}$ is transitive, and (b) ${\bar{d}}$ satisfies the reverse triangle inequality over $\overline{J}$-related events (hence $d_K={\bar{d}}$).

The next result generalizes Theorem 4.15.

Theorem 5.21

If (M, g) does not have lightlike lines then (a) and (b) of the previous theorem hold true, namely $\overline{J}=K$ and ${\bar{d}}=d_K$.

Proof

We proceed as in the proof of Theorem 4.15 where this time the sequences $\sigma _n$ and $\gamma _n$ are chosen to be limit maximizing. Let us consider two pairs $(p,q) \in {\bar{J}}$ and $(q,r) \in {\bar{J}}$ and two sequences of causal curves $\sigma _n$ of endpoints $(p_n, q_n) \rightarrow (p,q)$, and $\gamma _n$ of endpoints $(q'_n,r_n) \rightarrow (q,r)$. We apply the limit curve theorem to both sequences, and consider the case in which the limit curve, in both cases, does not connect the limit points. The other cases are indeed simpler and can be treated similarly.

By the limit curve theorem, $\sigma _n$ has a limit curve $\sigma$ which is a past inextendible continuous causal curve ending at q. Analogously $\gamma _n$ has a limit curve $\gamma$ which is a future inextendible continuous causal curve starting from q. The inextendible curve $\gamma \circ \sigma$ cannot be a lightlike line, thus there are points $p'\in \sigma \backslash \{q\}$, $r' \in \gamma \backslash \{q\}$ such that $(p',r')\in I$ and (pass to a subsequence) points $p'_n \in \sigma _n$, $p'_n \rightarrow p'$ and $r'_n \in \gamma _n$, $r'_n \rightarrow r'$. Since I is open, for sufficiently large n, $(p'_n,r'_n) \in I$ thus $(p_n,r_n) \in I$, and finally $(p,r) \in \bar{I}={\bar{J}}$.

However, for every $\epsilon >0$ we can take n so large that by the upper semi-continuity of the length functional, and with obvious meaning of the notation, $\ell (\sigma _n \vert _{p'_n\rightarrow q_n})\le \ell (\sigma \vert _{p'\rightarrow q})+\epsilon$, and similarly $\ell (\gamma _n \vert _{q'_n\rightarrow r'_n})\le \ell (\gamma \vert _{q\rightarrow r'})+\epsilon$. The causal curve $(\gamma \circ \sigma )\vert _{p'\rightarrow r'}$ can be replaced by a longer timelike curve, which can be shortened of at most $2 \epsilon$ to joint $p'_n$ and $r'_n$. As a result we find a causal curve $\eta _n$ connecting $p_n$ to $r_n$ of length

$$\begin{aligned} \ell (\eta _n)&\ge \ell (\sigma _n \vert _{p_n \rightarrow p'_n})+ \ell (\gamma \circ \sigma \vert _{p_n'\rightarrow r'_n})+ \ell (\gamma _n \vert _{r_n'\rightarrow r_n}) -2 \epsilon \\&\ge \ell (\sigma _n \vert _{p_n \rightarrow p'_n})+\ell ( \sigma _n \vert _{p_n'\rightarrow q_n})+\ell (\gamma \vert _{q_n'\rightarrow r'_n}) +\ell (\gamma _n \vert _{r_n'\rightarrow r_n}) -4 \epsilon \\&\ge \ell (\sigma _n)+\ell (\gamma _n)-4 \epsilon . \end{aligned}$$

By using the fact that $\sigma _n$ and $\gamma _n$ are limit maximizing and by using the arbitrariness of $\epsilon$ we get that ${\bar{d}}$ does indeed satisfy the reverse triangle inequality. $\square$

Corollary 5.22

Suppose that a chronological spacetime (M, g) does not have lightlike lines and has finite ${\bar{d}}$, then it is stable and hence embeddable in a Minkowski spacetime of sufficiently large dimension.

Theorem 5.23

The spacetime $({\tilde{M}},{\tilde{g}})$ is future reflecting iff (a) (M, g) is future reflecting and (b) for every $(x,y)\in D_f(={\bar{J}} \text { by future reflectivity})$ we have $d_f(x,y)={\bar{d}}(x,y)$ (or equivalently, for every $(x,y)\in D_p$, $d_p(x,y)\le d_f(x,y)$).

The spacetime $({\tilde{M}},{\tilde{g}})$ is reflecting iff (a) (M, g) is reflecting and (b) for every $(x,y)\in D_f(=D_p \text { by reflectivity})$ we have $d_f(x,y)=d_p(x,y)$ (or equivalently, for every $(x,y)\in D$, $\mathrm {min}(d_f,d_p)(x,y)= {\bar{d}}(x,y)$).

Theorem 5.24

The spacetime $({\tilde{M}},{\tilde{g}})$ is causally easy iff (M, g) is causally easy and ${\bar{d}}$ satisfies the reverse triangle inequality over $\overline{J}$-related events.

Theorem 5.25

The spacetime $({\tilde{M}},{\tilde{g}})$ is causally continuous iff (a) (M, g) is causally continuous and (b) for every $(x,y)\in D_f(=D_p \text { by reflectivity})$ we have $d_f(x,y)= d_p(x,y)$ (or equivalently, for every $(x,y)\in D$, $\mathrm {min}(d_f,d_p)(x,y)$ $= {\bar{d}}(x,y)$).

Theorem 5.26

The spacetime $({\tilde{M}},{\tilde{g}})$ is causally simple if and only if (a) (M, g) is causally simple, (b) d is continuous, and (c) every pair of distinct causally related events $(p,q)\in J$ on (M, g) for which $d(p,q)<\infty$ is connected by a maximizing causal geodesic.

It can also be shown that none of the conditions (a), (b), (c) follows from the other two.

The following general result can be used to obtain interesting versions of the distance formula. The idea is to specialize it to the cases $(R,r) \rightarrow (\overline{J},{\bar{d}})$, $(K,d_K)$ or $(J_S,d_S)$. The assumption $r\vert _{\varDelta }=0$ is then weaker than stable causality, cf. Proposition 5.19.

Theorem 5.27

Let R be a closed, reflexive and transitive relation (closed preorder), and let $r:M\times M\rightarrow [0,\infty ]$ be an upper semi-continuous function supported on R which satisfies the reverse triangle inequality over R-related points, cf. Theorem 5.15. Suppose that $r\vert _{\varDelta }=0$.

Let $\mathcal {R}$ be the family of continuous functions $f:M\rightarrow [-\infty , +\infty ]$ which satisfy, for every $(p,q)\in R$

$$\begin{aligned} r(p,q)\le f(q)-f(p), \end{aligned}$$

with the convention $\infty -\infty =\infty$ (in particular they are R-isotone), and with the strict inequality if additionally $r(p,q)<\infty$ and $(q,p)\notin R$. Then

$$\begin{aligned} r(p,q)=\inf \{[f(q)-f(p)]^+:f\in \mathcal {R}\}. \end{aligned}$$

Proof

The proof is similar to that of Minguzzi (2019, Theorem 4.11). The inequality $\le$ is clear. Let us consider the converse. Suppose that $(p,q)\notin R$, by the definition of ${\tilde{R}}^\downarrow$ the points $P=(p,0)$, $Q=(q,0)$ are such that $(P,Q)\notin {\tilde{R}}^\downarrow$. By the representation of closed preorders by continuous utility functions (Auslander-Levin theorem, cf. Minguzzi 2010, 2019 and references therein) there is a ${\tilde{R}}^\downarrow$ utility function F on ${\tilde{M}}$, such that $F(Q)<F(P)$. Notice that F is strictly decreasing over each fiber as the fiber parameter grows, in fact ${\tilde{R}}^\downarrow$ restricted to a fiber gives the opposite of the canonical order on $\mathbb {R}$ (here the equality $r\vert _{\varDelta }=0$ is used). Let $a\in \mathbb {R}$ be such that $F(Q)<a<F(P)$. Given $x\in M$ let $f(x)=+\infty$ if the fiber of x is in the region $F>a$, let $f(x)=-\infty$ if the fiber of x is in the region $F<a$. Otherwise, let f(x) be that number such that $(x,f(x)\in F^{-1}(a)$. There is only one such number because F is monotone over each fiber. It is easy to check that $f\in \mathcal {R}$ and $f(q)<0<f(p)$, which proves that the right-hand side vanishes and so $\ge$ is proved in this case.

Suppose $(p,q)\in R$. It is sufficient to prove that if $r(p,q)<\infty$ for every $\epsilon >0$ we can find $f\in \mathcal {R}$ finite on p and q such that $f(q)-f(p)<r(p,q)+\epsilon$. Let $P=(p,0)$ and $Q=(q,r(p,q)+\epsilon )$, then $(P,Q)\notin {\tilde{R}}^\downarrow$ thus there is F continuous ${\tilde{R}}^\downarrow$-utility function on ${\tilde{M}}$ such that $F(P)>F(Q)$. Notice that $Q'=(Q,r(p,q))$ is such that $(P,Q')\in {\tilde{R}}^\downarrow$ thus $F(P)\le F(Q')$. Let $a:=F(P)$ so that $F(Q)<a=F(P)$, and let us define f as done previously, so that $f\in \mathcal {R}$. Then $f(p)=0$ and $r(p,q)\le f(q)< r(p,q)+\epsilon$, which implies $f(q)-f(p)<r(p,q)+\epsilon$. $\square$

Corollary 5.28

Let (M, g) be a chronological spacetime with continuous Lorentzian distance. Let $\mathcal {R}$ be the family of continuous functions $f:M\rightarrow [-\infty , +\infty ]$, such that $d(p,q)\le f(q)-f(p)$ for $(p,q)\in \overline{J}$, with the convention $\infty -\infty =\infty$, and with the strict inequality if additionally $d(p,q)<\infty$ and $(q,p)\notin \overline{J}$. Then

$$\begin{aligned} d(p,q)=\inf \{[f(q)-f(p)]^+:f\in \mathcal {R}\}. \end{aligned}$$

Of course, this result implies that $\mathcal {R}$ is non-empty, so it can be read as an existence result.

Under strong causality, the spacetime is actually causally easy, hence stably causal. The functions belonging to $\mathcal {R}$ are then sort of extended rushing times. However, under stable causality Theorem 4.11 of Minguzzi (2019) provides a more detailed result.

Proof

In a chronological spacetime $d\vert _{\varDelta }=0$. By Theorem 5.13${\overline{J}}$ is transitive and $d={\bar{d}}=d_K$. Thus the previous theorem for $R= \overline{J}$, $r=d$ proves the claim. $\square$

6 The geometry of geodesic congruences

We recall that the Einstein equations are

$$\begin{aligned} R_{ab}-\frac{1}{2} g_{ab} R=8\pi T_{ab}, \end{aligned}$$

where $R_{ab}$ is the Ricci tensor, $R=g^{ab} R_{ab}$ is the curvature scalar, and $T_{ab}$ is the stress-energy tensor. These equations are non-conformally invariant, for this reason in this section we shall have to consider a few physically relevant non-conformally invariant properties.

Definition 6.1

A spacetime is causally (null, timelike, spacelike) geodesically complete if every causal (resp. null, timelike, spacelike) inextendible geodesic is complete in the sense that its affine parameter has domain $\mathbb {R}$.

Of course, this definition admits future and past versions.

Definition 6.2

A pregeodesic or unparametrized geodesic $t'\mapsto x(t')$ is a solution to the equation

$$\begin{aligned} \nabla _{x'} x'=\kappa (t') x' \end{aligned}$$

for some function $\kappa$ (a prime denotes differentiation with respect to $t'$).

It changes to a geodesic provided the parameter is chosen to be

$$\begin{aligned} t(t')=a+b\int ^{t'} \!e^{\int ^r\! \kappa (s) \,\mathrm{d}s}\mathrm{d}r, \end{aligned}$$

where a and $b>0$ are constants dependent also on the chosen domains of the integrals.

It is well known that conformally related spacetimes share the same unparametrized null geodesics (Wald 1984b, Appendix D). Let ${\bar{g}}=\varOmega ^2 g$, then $t \mapsto x(t)$ is a lightlike geodesic for g, namely $\nabla _{\dot{x}} \dot{x}=0$ iff reparametrized with ${\bar{t}}(t)$, such that

$$\begin{aligned} \frac{\mathrm{d}{\bar{t}}}{\mathrm{d}t} =\varOmega ^2(x(t)), \end{aligned}$$

it is a lightlike geodesic for $(M,{\bar{g}})$.

The notion of null completeness is not conformally invariant unless $\log \varOmega$ is bounded from below and above over the curve (thus the notion of completeness for imprisoned lightlike geodesics is indeed conformally invariant).

The notions of null, timelike, spacelike geodesic completeness are mutually independent (Beem 1976b; Ehrlich and Easley 2004). The stability of completeness and incompleteness was studied by Beem and Ehrlich (Lerner 1973; Beem and Ehrlich 1987; Beem et al. 1996; Beem 1997).

A spacetime is generically said to be singular if it is causally geodesically incomplete.

6.1 Conjugate and focal points

The exponential map associates to $v\in T_p M$ the point $\exp _p v:=x(1)$ of the unique geodesic $t\mapsto x(t)$ having initial condition $x(0)=p$, $\dot{x}(0)=v$. It is known to establish a local diffeomorphism from a neighborhood of $0\in T_p M$ to a neighborhood of $p\in M$, see Whitehead (1932, 1933, 1935).

The 1-time flow map $(p,v) \rightarrow (x(1),\dot{x}(1))$, and hence the previously mentioned diffeomorphism, has the same regularity as the connection coefficients (as can be easily seen by rewriting the geodesic equation as a first order ODE on TM and by using standard results from ODE theory, Hartman 2002). We say that p has conjugate point $q=\exp _p v$ if $(\exp _p)_*:T_v T_p M\rightarrow T_q M$ is not injective.

Let H be a spacelike hypersurface (the notation H is unusual but will allow us to join two cases), let v denote a timelike vector orthogonal to H. The map $(p,v)\mapsto \exp _p v$, where $p\in H$, can be show to provide a local diffeomorphism from a neighborhood of the zero section of the normal bundle $NH\rightarrow H$ to a neighborhood of H, again of the same regularity as the connection (Minguzzi 2015b). We say that H has focal point $q=\exp _p v$, if the map $\exp _*: T_{(p,v)}NH \rightarrow T_qM$ is not injective.

A similar definition holds for a spacelike codimension 2 surface S. At every point $p\in S$, we have two null vectors orthogonal to S. Locally we have two lightlike normal bundles depending on the selected lightlike normals. If S is 2-sided (e.g. it is orientable and a neighborhood of S is orientable as a spacetime) they form two distinct lightlike normal bundles. In any case let NS denote one such bundle. The definition of focal point is analogous to the previous one, but here the local diffeomorphism is between a neighborhood of the zero section of NS and the neighborhood of a lightlike hypersurface passing though S.

All these concepts can be formulated in terms of Jacobi fields. Let us denote for shortness $R_u(X):=R(X,u)u$, that is

$$\begin{aligned} R_u(X):=\nabla _X \nabla _uu-\nabla _u \nabla _X u-\nabla _{[X,u]} u. \end{aligned}$$

(6.1)

The trace of the endomorphism $X\mapsto R_u (X)$ is the Ricci tensor contracted twice with u and will also be denoted Ric(u). We have

Proposition 6.3

Let x(t, s) be a geodesic variation, namely $x_s:=x(\cdot , s)$ is a geodesic for each $s\in (-\epsilon ,\epsilon )$. Then defining $J=\partial /\partial s\vert _{s=0}$ we have

$$\begin{aligned} \nabla _{\dot{x}}\,\,\nabla _{\dot{x}} J+ R_{\dot{x}} (J)=0. \end{aligned}$$

(6.2)

Proof

Immediate from $\nabla _J \dot{x}-\nabla _{\dot{x}} J=[ J,\dot{x}]=0$ and Eq. (6.1) using $D_{\dot{x}}\dot{x}=0$. $\square$

The Jacobi field J(t) represents the result of the pushforward of the exponential map as we move over the geodesic. In the conjugate point case we have to consider the initial conditions

$$\begin{aligned} J(0)&=0, \\ \nabla _{\dot{x}} J(0)&=\mathrm {given}\,\mathrm {vector}\,\mathrm {orthogonal}\,\mathrm {to}\, \dot{x}, \end{aligned}$$

while in the focusing case we have to consider the initial condition

$$\begin{aligned} J(0)&={\mathrm {given}\,\mathrm {vector}\,\mathrm {orthogonal}\,\mathrm {to}} \dot{x},\\ \nabla _{\dot{x}} J(0)&=\nabla _J \dot{x}. \end{aligned}$$

The presence of a conjugate or focal point is signaled by the vanishing of J for $t=1$.

Observe that if J satisfies Eq. (6.2), then for every constants a, b, $J+(a+bt)\dot{x}$ satisfies the same equation, thus this arbitrariness can be used to adjust the $\dot{x}$ component of the variational field at two distinct points. For any Jacobi field $g(J,\dot{x})=c t+d$ for some constants c, d, so with the given initial conditions $c=d=0$ (provided $g(\dot{x}, \dot{x})$ is a constant), which implies $0=g(J,\dot{x})=g(\nabla _{\dot{x}}J,\dot{x})$ for every t. We shall only be interested in Jacobi fields with this property.

For any two Jacobi fields $J, J'$ the quantity $g(J,\nabla _{\dot{x}} J')-g(\nabla _{\dot{x}} J, J')$ is independent of t.

If $q=x(1)$ is not a conjugate point of $p=x(0)$ then for any chosen $J(0)\in T_pM$ and $J(1)\in T_qM$ orthogonal to $\dot{x}$ we can find a Jacobi field J with these boundary conditions (see also Beem et al. 1996, Lemma 12.11). For consider the Jacobi field with initial condition ${\tilde{J}}(0)=J(0)$, $\nabla _{\dot{x}} {\tilde{J}}=0$. It has final value ${\tilde{J}}(1)$ and since p and q are not conjugate there is a Jacobi field with some initial condition ${\check{J}}(0)=0$, $\nabla _{\dot{x}} {\check{J}}=X$ whose end value is ${\check{J}}(1)=J(1)-{\tilde{J}}(1)$, thus $J={\tilde{J}}+{\check{J}}$ is the desired Jacobi field.

Conjugate points for a congruence of timelike geodesics issued from $p\in M$ are really special instances of focal points. In fact by the Gauss lemma the congruence will develop a focal point for the hypersurface $S=\exp _p (\epsilon \mathcal {I}_p)$, where $\epsilon >0$ is a small constant and $\mathcal {I}_p \subset T_pM$ is the indicatrix (observer space) at p. Similar considerations hold for null congruences (Remark 6.17). Due to this observation it is not restrictive to consider just the implications of focal points for causality.

Let $V\subset TM$ be the subbundle of vectors orthogonal to $\dot{x}$. It is sometimes convenient to work with the linear map $A:V_{x(0)} \rightarrow V_{x(t)}$ which sends the initial condition (which we have seen to be given by a vector orthogonal to $\dot{x}$) to the Jacobi field J(t) determined by that initial condition. In other words, let $\{e_i\}$ be a basis of $V_{x(0)}$ and $J_i(t)\in V_{x(t)}$ the Jacobi field with initial condition $e_i$, then $A(t)= J_i(t)\otimes e^i$ and

$$\begin{aligned} \nabla _{\dot{x}}\,\,\nabla _{\dot{x}} A+ R_{\dot{x}} A=0. \end{aligned}$$

In the conjugate point case the initial condition is $A(0)=0$, $\nabla _{\dot{x}}A=Id$, while in the focusing case $A(0)=Id$, $\nabla _{\dot{x}}A(0)=b A(0)$ where $X \mapsto b(X):=\nabla _X \dot{x}$ is an endomorphism of V called shape operator.

The linear map A can be really represented with a matrix $A= a^k_{ i} e_k \otimes e^i$, $J_i=a^k_{ i} e_k$, provided we extend the basis $\{e_i\}$ all over x, e.g. through parallel transport. In this case lack of injectivity is signaled by the vanishing of the determinant $\det a^k_{ i}$.

Setting $b=(\nabla _{\dot{x}} A) A^{-1}$ wherever A is invertible, we have, multiplying the previous equation by $A^{-1}$

$$\begin{aligned} \nabla _{\dot{x}} b+b^2+R_{\dot{x}}=0. \end{aligned}$$

Unfortunately, in the null case, namely for $g(\dot{x},\dot{x})=0$, since $(a+b t) \dot{x}$ is a Jacobi field one can show that A(t) isn’t really invertible. We shall have to separate the analysis in timelike and null cases.

The following treatment of the Raychaudhuri equation is adapted from Minguzzi (2015c), but it seems quite standard, see Kupeli (1987) and the publications by Galloway, most notably Galloway (2000). Other useful references are Hawking and Ellis (1973), Tipler (1978b), Beem et al. (1996) and Tong (2009).

6.2 The Raychaudhuri equation: timelike case

Let H be a $C^2$ spacelike hypersurface and let u be a $C^1$ future directed timelike, normalized, geodesic vector field orthogonal to it

$$\begin{aligned} \nabla _u u=0, \quad g(u,u)=-1, \quad \text {ker} g(u,\cdot )\vert _H=TH. \end{aligned}$$

It is interesting to observe that H has a natural metric induced by g. Since u is timelike for g we have that $(H,g\vert _H)$ is a Riemannian manifold.

The flow of u propagates the hypersurface H into a foliation $H_s$, $H=H_0$, $u=\frac{d}{d s}$, at least in a neighborhood of $H_0$ before the development of focal points. Similarly, the flow propagates a vector field X tangent to $H_0$ into a vector field, denoted in the same way, tangent to the foliation and such that $L_u X=[u,X]=0$. As a consequence, the foliation remains orthogonal to u because, for every vector field X tangent to the foliation, we have $\partial _u g(u,X)=0$ as it follows immediately from

$$\begin{aligned} \partial _u g(u,X)=&g(\nabla _u u, X)+g(u,\nabla _u X)=g(u,\nabla _X u)=\partial _X g(u,u)/2=0. \end{aligned}$$

In the domain of the field u we consider the vector bundle V which consists of vectors ${X}\in TM$ orthogonal to u: $g(u,{X})=0$. Clearly, this bundle has n-dimensional fibers. We introduce a positive definite (space) metric on V

$$\begin{aligned} h({X},{Y}):=g({X},{Y}), \end{aligned}$$

an endomorphism (Weingarten map) (which coincides with the shape operator or second fundamental form of $H_s$ where the foliation exists)

$$\begin{aligned} b:V_p \rightarrow V_p,\quad {X}\mapsto b({X}):= \nabla _{{X}} u , \end{aligned}$$

a second endomorphism

$$\begin{aligned} \bar{R}:V_p \rightarrow V_p, \quad \bar{R}({X}):=R_u( X), \end{aligned}$$

and a third endomorphism which is the trace free part of $\bar{R}$

$$\begin{aligned} \bar{Q}:V_p \rightarrow V_p,\quad \bar{Q}({X}):=\bar{R}-\tfrac{1}{n} \,\text {tr} \bar{R} \,Id . \end{aligned}$$

The definition of b is well posed because $g(u,\nabla _X u)=0$, while $\bar{R}$ is well posed due to $g(u,R_u(X)=0$, which follows from the symmetries of the Riemann tensor.

The endomorphisms $b, \bar{R}, \bar{Q}$ are all self-adjoint with respect to h. The self-adjointness of $\bar{R}$ (and hence of $\bar{Q}$) follows from the identity

$$\begin{aligned} g(X, R_u(Y))=g(Y, R_u(X)), \end{aligned}$$

due to the symmetries of the Riemann tensor. In order to show that b is self-adjoint, let $X,Y \in V_p$ and let extend them to two commuting vector fields tangent to the foliation and denoted in the same way. We have $[X,Y]=0$ hence

$$\begin{aligned} h({X},b({Y}))&=g(X,\nabla _Y u)=-g(\nabla _Y X, u)=-g(\nabla _X Y, u)=g(Y,\nabla _X u)\\&=h({Y},b({X})). \end{aligned}$$

Let us prove

$$\begin{aligned} \text {tr} \bar{R}&=\text {tr} R_u=Ric(u), \end{aligned}$$

(6.3)

Indeed let $\{u,e_1,$ $\ldots , e_{n}\}$ be an orthonormal basis of $T_pM$ such that $\{e_i\}$ is a basis of $V_p$. Observe that $h( e_i, e_j)=g(e_i,e_j)=\delta _{ij}$. Thus using $R_u(u)=0$,

$$\begin{aligned} \text {tr} \bar{R}&=\sum _i h( e_i,\bar{R}( e_i))=\sum _i g(e_i, R_u(e_i))= \sum _i g(e_i, R_u(e_i))-g(u,R_u(u))\\ {}&=\text {tr} {R}_u. \end{aligned}$$

Both endomorphisms $\bar{R}$ and $\bar{Q}$ depend on u at the considered point p but not on the whole geodesic congruence.

Definition 6.4

We define the properties:

• Timelike convergence condition: at every p and for every timelike vector u, $Ric(u)\ge 0$,

• Timelike genericity condition: every inextendible complete timelike geodesic admits some point p at which the tangent vector u satisfies $\bar{R}(p,u)\ne 0$, i.e. the endomorphism ${\bar{R}}$ is non-trivial.

This last condition can also be written in terms of the curvature $R_u$, see Beem et al. (1996, Proposition 2.7)

$$\begin{aligned} u_{[a} R_{u\, b] [c}\, u_{d]}\ne 0, \text { or equivalently } R_u \ne 0. \end{aligned}$$

The first formulation allows one to join the timelike genericity condition and the null genericity condition (see below) into a causal genericity condition.

Let $P:TM\rightarrow V$ be the projection with kernel $\text {Span} (u)$. The derivative ${\nabla _{u}}$, induces a derivative $X':=P( {\nabla _{u}} X)$ on sections of V, and hence, as usual, a derivative on endomorphisms as follows $E'(X):=(E(X))'-E(X')$. It can be observed that if $[u,X]=0$ then $X'={\nabla _{u}} X$ indeed $g(u,{\nabla _{u}} X)=0$.

Proposition 6.5

The Weingarten map satisfies the Riccati equation

$$\begin{aligned} b'=-\bar{R}-b^2, \end{aligned}$$

(6.4)

Proof

Let $X\in V_p$ and extend it in a neighborhood of p so as to remain tangent to the foliation and in such a way that $[X,u]=0$. Using Eq. (6.1)

$$\begin{aligned} R_u(X)=-\nabla _u \nabla _X u=-\nabla _u\nabla _u X. \end{aligned}$$

Thus

$$\begin{aligned} b'( X)&=P({\nabla _{u}} b(X))-b({\nabla _{u}} X)=P({\nabla _{u}} {\nabla _X u})-b({{ \nabla _{X}} u})\\&= P(\nabla _{u} \nabla _{u} X)-b(b({X}))=-R_u(X)-b^2({X}), \end{aligned}$$

which concludes the proof. $\square$

It can also be observed that $h'=0$ because for X, Y vector fields orthogonal to u, extended so that $[X,u]=[Y,u]=0$, we have

$$\begin{aligned} h'(X,Y):=&\, (h(X,Y))'-h(X',Y)-h(X,Y')\\=&\, \partial _u g(X,Y)-g(\nabla _u X, Y)-g(X,\nabla _u Y)=0. \end{aligned}$$

Let us define

$$\begin{aligned} \theta :=\text {tr} \,b, \ {\bar{\sigma }}:\quad =b-\frac{1}{n}\, \theta \, {Id}, \end{aligned}$$

so that $\bar{\sigma }$ is the trace-free part of b. They are called expansion and shear, respectively. Let us denote for short $\sigma ^2:=\text {tr} \bar{\sigma }^2$. A trivial consequence of this definition is $\sigma ^2\ge 0$ with equality if and only if $\bar{\sigma }=0$.

Taking the trace and the trace-free parts of (6.4) we obtain

$$\begin{aligned} \theta '&=-{\text {Ric}}(n)-\sigma ^2-\frac{1}{n} \, \theta ^2, \qquad ({\text {Raychaudhuri}}) \end{aligned}$$

(6.5)

$$\begin{aligned} \bar{\sigma }'&= -\bar{Q}-\left( \bar{\sigma }^2-\frac{1}{n} \, {\text {tr}} \bar{\sigma }^2 \, {Id}\right) -\frac{2}{n}\, \theta \, \bar{\sigma }, \end{aligned}$$

(6.6)

the term in parenthesis is the trace-free part of $\bar{\sigma }^2$.

Let H be a $C^2$ spacelike hypersurface and let u be the $C^1$ future directed timelike normal. We say that the congruence is converging if $\theta :=\text {tr}( {X}\mapsto \nabla _{{X}} u)$ is negative, diverging if it is positive. This is really a property of the hypersurface H as it is mediated by the shape operator.

Proposition 6.6

Suppose that the timelike convergence condition holds true. Let $s \mapsto \gamma (s)$ be a geodesic of the timelike congruence and suppose that $\theta _1=\theta (s_1)<0$, then $\theta$ diverges to $-\infty$ within the domain $[s_1, s_1+n/(-\theta _1)]$ provided the affine parameter extends sufficiently far.

Notice that this result (Hawking and Ellis 1973, Proposition 4.4.1) establishes a property of a timelike congruence which, in our assumptions, starts orthogonally to a $C^2$ spacelike hypersurface H. Although H evolves regularly in the beginning, it cannot really be defined at such large affine parameters, for if it were the shape operator would be well defined and hence $\theta$ would be finite. This loss of regularity is connected to the development of focal points, see Theorem 6.16.

Proof

By the Raychaudhuri equation $\theta '\le -\frac{1}{n} \, \theta ^2$, thus multiplying by $-n/\theta ^2$ and integrating in the interval $[s_1,s]$, we get $\frac{n}{\theta (s)}- \frac{n}{\theta _1}\ge s-s_1$, that is $\theta (s)\le \frac{n}{s-[s_1+n/(-\theta _1)]}$. $\square$

This section will be useful in the proof of Hawking’s (1967) singularity theorem or of Hawking and Penrose’s (1970) singularity theorem.

6.3 The Raychaudhuri equation: null case

A $C^1$ hypersurface is null if its tangent spaces are orthogonal to null vectors (equivalently, the induced metric is degenerate). A hypersurface H is ruled by lightlike geodesics if every point $p\in H$ belongs to the interior of a lightlike geodesic segment contained in H. Notice that a timelike hyperplane in Minkowski spacetime is ruled by lightlike geodesics but it is not achronal. The “if” direction of the following result can be found in Kupeli (1987). The “only if” direction is more of a folklore result, which still is quite important. In fact, the definition of $C^0$ null hypersurface is based on the following characterization for the $C^2$ case (Galloway 2000).

Theorem 6.7

Every $C^2$ hypersurface H is null if and only if it is locally achronal and ruled by lightlike geodesics.

Proof

Suppose that H is null. Let $p\in H$, and let n be the lightlike vector such that $T_pH=\mathrm {ker} g(n,\cdot )$. Since H is $C^1$, we can choose n at every point so as to be a $C^1$ vector field over H (e.g. normalize it with respect to a Riemannian metric). Let $v\in T_pH$, $v\ne n$. We can extend v to a local vector field over H and tangent to H which commutes with n. Since $v\in TH$, we have $g(n,v)=0$, thus

$$\begin{aligned} 0&=\nabla _n g(n,v)=g(\nabla _n n,v)+g(n,\nabla _nv)=g(\nabla _n n,v)+g(n,\nabla _v n)\\&=g(\nabla _n n,v)+\frac{1}{2} \nabla _v g(n,n)=g(\nabla _n n,v). \end{aligned}$$

From the arbitrariness of $v\in T_p H$ it follows $\nabla _n n=\kappa n$ for some continuous function $\kappa$. Thus the integral curve of n is really a lightlike pregeodesic.

Let us prove achronality. Let p in H, there is a local function $f:C\rightarrow \mathbb {R}$, where C is a neighborhood of p, such that $H\cap C=f^{-1}(0)$, $\mathrm{d}f\ne 0$ on $H\cap C$ (for instance, f can be constructed using a flow transverse to H and ODE theory). In fact C can be redefined to be a convex neighborhood of p. Notice that over H, $\text {ker}\,\mathrm{d}f=TH$, thus $\mathrm{d}f=a g(n,\cdot )$ where $a\ne 0$ is some function. Without loss of generality we can assume $a<0$ (otherwise redefine the sign of f). No timelike curve x(t) can cross from region $f\ge 0$ to region $f<0$, for at the last point in H we would have $(f\circ x)\,\dot{} \le 0$ while $-g(n,v)>0$ for every timelike vector v. As a consequence $H=\partial I^+(H, C)$ hence H is a local achronal boundary.

For the converse, by the $C^1$ assumption $TH=\mathrm {ker}g(w,\cdot )$ for some vector field w over H. Here w cannot be spacelike at some point otherwise TH would be timelike at some point and hence H would be chronal. Moreover, w cannot be timelike because for every null vector $g(w,n)<0$, thus the hypersurface could not be ruled by lightlike geodesics. The only conclusion is that w is lightlike. $\square$

Let H be a $C^2$ null hypersurface and let n be a $C^1$ lightlike vector field tangent to H so that its integral curves are lightlike pregeodesics running over H. As we have shown in the previous proof

$$\begin{aligned} \nabla _n n=\kappa n , \end{aligned}$$

(6.7)

where $\kappa$ is a continuous function over H. The tangent space at a point $p\in H$ is $T_pH=\ker g(n,\cdot )$.

Remark 6.8

Any $C^2$ null hypersurface H (with boundary) can be enlarged to a hypersurface $H'$ by extending the null generators in the future direction. The question is whether it remains null. The answer is affirmative provided it remains $C^2$.

Indeed, let $X\in T_pH'$, at some extended point $p\in H'$. There is a geodesic variation made of hypersurface generators whose Jacobi field J, $[J,n]=0$, is such that $J(p)=X$. Then

$$\begin{aligned} \nabla _n g(n,J)-\kappa g(n,J)=g(n,\nabla _n J)=g(n,\nabla _Jn)=\nabla _J g(n,n)/2=0, \end{aligned}$$

which shows that the null condition $g(n,J)=0$ will be propagated from H to $H'$.

On the $C^2$ null hypersurface we consider the vector bundle $V=TH/\!\!\sim$ obtained regarding as equivalent any two vectors $X, Y\in T_pH$ such that $Y-X\propto n$. Clearly, this bundle has $n-1$-dimensional fibers. Let us denote with an overline $\bar{X}$ the equivalence class of $\sim$ containing X. At each $p\in H$, we introduce a positive definite metric

$$\begin{aligned} h(\bar{X},\bar{Y}):=g(X,Y), \end{aligned}$$

an endomorphism (shape operator, null Weingarten map)

$$\begin{aligned} b:V_p \rightarrow V_p,\qquad \bar{X}\mapsto b(\bar{X}):= \nabla _{\bar{X}} n:=\overline{\nabla _X n}, \end{aligned}$$

a second endomorphism

$$\begin{aligned} \bar{R}:V_p \rightarrow V_p, \qquad \bar{R}(\bar{X}):=\overline{R_n(X)}, \end{aligned}$$

and a third endomorphism which is the trace free part of $\bar{R}$

$$\begin{aligned} \bar{C}:V_p \rightarrow V_p,\qquad \bar{C}(\bar{X}):=\bar{R}-\tfrac{1}{n-1} \,\text {tr} \bar{R} \,Id . \end{aligned}$$

The definition of b is well posed because, as $\nabla _X$ is linear in X and $\nabla _n n\propto n$ we have $\nabla _{X+a n} n=\nabla _X n+k n$, for some k. Moreover, $g(n,\nabla _X n)=\frac{1}{2}\nabla _X g(n,n)=0$, which means that $\nabla _Xn\in TH$. The definition of $\bar{R}$ is well posed since $R_n(n)=0$ and $g(n,R_n(X))=0$, which implies that for every $X\in T_pM$, $R_n(X) \in T_pH$.

The endomorphisms $b, \bar{R}, \bar{C}$ are all self-adjoint with respect to h. In order to show that b is self-adjoint, let $X,Y \in T_pH$ and let us extend them to two commuting vector fields tangent to H and denoted in the same way. We have

$$\begin{aligned} h(\bar{X},b(\bar{Y}))&=g(X,\nabla _Y n)=-g(\nabla _YX, n)=-g(\nabla _XY, n)=g(Y,\nabla _X n)\\&=h(\bar{Y},b(\bar{X})). \end{aligned}$$

The self-adjointness of $\bar{R}$ follows from the symmetries of the Riemann tensor, while that of $\bar{C}$ follows from that of $\bar{R}$.

Let us prove

$$\begin{aligned} \text {tr} \bar{R}&=\text {tr} R_n=Ric(n). \end{aligned}$$

(6.8)

Let $\{n,m,e_1,$ $\ldots , e_{n-1}\}$ be a basis of $T_pM$ such that m is lightlike, $g(m,n)=-1$, and $\{e_i\}$ is a basis of the spacelike codimension 2 subspace orthogonal to both n and m. Observe that $h({\bar{e}}_i, {\bar{e}}_j)=g(e_i,e_j)=\delta _{ij}$. Thus

$$\begin{aligned} \text {tr} \bar{R}&=\sum _i h({\bar{e}}_i,\bar{R}({\bar{e}}_i))=\sum _i g(e_i, R_n(e_i))\\&= \sum _i g(e_i, R_n(e_i))-g(m,R_n(n))-g(n, R_n(m))=\text {tr} {R}_n. \end{aligned}$$

The Weyl curvature is

$$\begin{aligned} C^m_{ \, n c d}= \Big \{R^{m b}_{ c d}-\frac{4}{n-1}\, \delta ^{[m}_{[c} R^{s b]}_{ \, s d]}+\frac{2 R^{s r}_{ s r}}{n (n-1)}\, \delta ^{[m}_{[c} \delta ^{b]}_{d]}\Big \}g_{b n}. \end{aligned}$$

Given $v\in T_pM$, we define the endomorphism of $T_pM$, $X\mapsto C_v(X)$ of components

$$\begin{aligned} (C_v)^m_{ \, c}=C^m_{ \, n c d} v^n v^d. \end{aligned}$$

It is easily checked to be traceless and such that $C_v(v)=0$. Furthermore, if v is lightlike and $g(v,X)=0$ then

$$\begin{aligned} C_v(X)= T_v(X)+ \text { terms Proposition to } v, \quad T_v(X):= \left[ R_v- \frac{\text {tr} R_v}{n-1} \,\text {Id}\right] (X).\nonumber \\ \end{aligned}$$

(6.9)

Proposition 6.9

We have the equality $\bar{C}({\bar{X}})=\overline{C_n(X)}$.

Proof

Indeed,

$$\begin{aligned} \overline{C_n(X)}&=\overline{T_n(X)}=\overline{R_n(X)}- \frac{1}{n-1}(\text {tr} \bar{R}) {\bar{X}}=\left[ \bar{R}-\frac{1}{n-1} \,\text {tr} \bar{R} \,Id\right] ({\bar{X}})=\bar{C}({\bar{X}}). \end{aligned}$$

$\square$

Both endomorphisms $\bar{R}$ and $\bar{C}$ depend on n at the considered point p but not on the whole geodesic congruence tangent to H.

Definition 6.10

We define the properties:

• Null convergence condition: for every lightlike vector n, $Ric(n)\ge 0$,

• Null genericity condition: every inextendible complete lightlike geodesic admits some point p at which the tangent vector n satisfies $\bar{R}(p,n)\ne 0$, i.e. the endomorphism ${\bar{R}}$ is non-trivial (if at p, $Ric(n)=0$, this is equivalent to a non-trivial ${\bar{C}}$).

This last condition can also be written in terms of the contracted curvature $R_n$, see Beem et al. (1996, Proposition 2.7)

$$\begin{aligned} n_{[a} R_{n\, b] [c}\, n_{d]}\ne 0 . \end{aligned}$$

By definition the causal convergence condition holds if the null and timelike versions hold, and similarly for the causal genericity condition.

The derivative ${\nabla _{n}}$, induces a derivative $\bar{X}':=\overline{{\nabla _{n}} X}$ on sections of V (well defined as independent of the representative X), and hence, as usual, a derivative on endomorphisms as follows $E'(\bar{X}):=(E(\bar{X}))'-E(\bar{X}')$.

Proposition 6.11

Along a generator of H the null Weingarten map satisfies the Riccati equation

$$\begin{aligned} b'=-\bar{R}-b^2+ \kappa \, b, \end{aligned}$$

(6.10)

The proof is taken from Galloway (2000).

Proof

Let $X\in T_pH$ and extend it in a neighborhood of p so as to remain tangent to H and in such a way that $[X,n]=0$. We have

$$\begin{aligned} R_n(X)=\nabla _X \nabla _nn-\nabla _n \nabla _X n=\kappa \nabla _X n+(\partial _X\kappa )n-\nabla _n\nabla _nX. \end{aligned}$$

Thus

$$\begin{aligned} b'({\bar{X}})&=\overline{\nabla _{n} b({\bar{X}})}-b(\overline{{\nabla _{n}} X})=\overline{\nabla _{n} \overline{\nabla _X n}}-b(\overline{{ \nabla _{X}} n})= \overline{\nabla _{n} \nabla _X n}-b(b(\bar{X}))\\&=\overline{\nabla _{n} \nabla _n X}-b^2(\bar{X})=-\overline{R_n(X)}+\kappa \overline{\nabla _X n}-b^2(\bar{X}), \end{aligned}$$

which concludes the proof. $\square$

It can also be observed that $h'=0$; indeed

$$\begin{aligned} h'(\bar{X},\bar{Y}):=&(h(\bar{X},\bar{Y}))'-h(\bar{X}',\bar{Y})-h(\bar{X},\bar{Y}') \end{aligned}$$

(6.11)

$$\begin{aligned} =&\nabla _n g(X,Y)-g(\nabla _n X,Y)-g(X,\nabla _n Y)=0. \end{aligned}$$

(6.12)

Let us define the expansion $\theta :=\text {tr} \,b$ and the shear

$$\begin{aligned} {\bar{\sigma }}:=b-\frac{1}{n-1}\, \theta \, {Id}, \end{aligned}$$

so that $\bar{\sigma }$ is the trace-free part of b. Let us denote for short $\sigma ^2:=\text {tr} \bar{\sigma }^2$. A trivial consequence of this definition is $\sigma ^2\ge 0$ with equality if and only if $\bar{\sigma }=0$.

Taking the trace and the trace-free parts of (6.10) we obtain

$$\begin{aligned} \theta '&=-\text {Ric}(n)-\sigma ^2-\frac{1}{n-1} \, \theta ^2+\kappa \, \theta , \qquad (\text {Raychaudhuri}) \end{aligned}$$

(6.13)

$$\begin{aligned} \bar{\sigma }'&= -\bar{C}-\left( \bar{\sigma }^2-\frac{1}{n-1} \, \text {tr} \bar{\sigma }^2 \, {Id}\right) -\frac{2}{n-1}\, \theta \, \bar{\sigma }+\kappa \,\bar{\sigma }. \end{aligned}$$

(6.14)

The term in parenthesis is the trace-free part of $\bar{\sigma }^2$ and vanishes in the physical four dimensional spacetime case ($n=3$).

Remark 6.12

In most circumstances it is possible to choose the lightlike vector field n to be geodesic, so that $\kappa =0$. This is not the case for null generators accumulating on themselves, as it happens in compact Cauchy horizons.

The proof of the next result is identical to that of Proposition 6.6, so it is omitted.

Proposition 6.13

Suppose that the null convergence condition holds true and that $\kappa =0$, cf. Eq. (6.7). Let $s \mapsto \gamma (s)$ be a geodesic of the null congruence and suppose that $\theta _1=\theta (s_1)<0$, then $\theta$ diverges to $-\infty$ within the domain $[s_1, s_1+(n-1)/(-\theta _1)]$ provided the affine parameter extends sufficiently far.

Notice that this result establishes a property of a null congruence which, in our assumptions, starts orthogonally to a $C^2$ null hypersurface H. Although in the beginning H evolves regularly, it cannot really be defined at too large affine parameters, for if it were the shape operator would be well defined and hence $\theta$ would be finite. This loss of regularity is connected to the development of focal points, see Theorem 6.16.

Let S be a codimension 2, oriented, $C^2$ spacelike compact manifold without boundary. Let $p\in S$, since $T_p S$ does not intersect the future causal cone (save for the origin), by the convexity of this cone there are exactly two hyperplanes $B_p^{\pm }\subset T_pM$ containing $T_pS$ and tangent to the cone. These hyperplanes determine two future lightlike vectors $n^{\pm }$ up to a proportionality constant: $B_p^{\pm }=\ker g(n^\pm , \cdot )$. Let us denote in the same way a $C^1$ choice of vector field $n^\pm$ over S. It exists by orientability provided the spacetime is orientable in a neighborhood of S. Its exponential map generates, at least locally, a $C^2$ locally achronal null hypersurface $H^{\pm }$. The expansion is defined as above $\theta ^\pm =\text {tr}(X\mapsto \overline{D_X n^\pm })$.

Definition 6.14

The manifold S is future trapped or a trapped surface if $\theta ^+,\theta ^- < 0$; future weakly trapped if $\theta ^+,\theta ^- \le 0$; future marginally trapped if weakly trapped and either $\theta ^+$ or $\theta ^-$ is negative. Outer trapped if $\theta ^+ < 0$ and inner trapped if $\theta ^- < 0$.

Notice that in our terminology trapped surfaces are closed (i.e. compact, without boundary).

Remark 6.15

The term trapped surface is not very satisfactory. The main point of singularity theorems is to show that trapped surfaces are not trapped (sets) after all! (Because, null geodesic completeness does not hold.) The name focusing/converging surfaces could have been more appropriate (O’Neill 1983).

This section will be useful in the proof of Penrose (1965a, b) singularity theorem, Gannon’s (1975), and some others.

6.4 Relationships between second fundamental forms

The cases of Definition 6.14 can be introduced in a slightly different way by using the Gauss’s equation for S rather than the Weingarten equation. Namely, let us consider two vectors fields X, Y on the spacelike codimension 2 manifold S, then

$$\begin{aligned} \nabla _XY= \nabla ^S_X Y-B(X,Y), \end{aligned}$$

(6.15)

where $\nabla ^S$ is a connection on S (which turns out to be metric with respect to the induced metric $g_S$, Kobayashi and Nomizu 1969) and $B:TS\times TS\rightarrow TS^\perp$ is a symmetric map called shape tensor or second fundamental form (O’Neill 1983; Senovilla 2011). The average ${\bar{H}}\mapsto TS^\perp$

$$\begin{aligned} H=\text {tr} (g_S^{-1} B) \end{aligned}$$

is the mean curvature vector.⁶

In our case let $n^+$ and $n^-$ be two lightlike fields orthogonal to S and such that

$$\begin{aligned} g(n^+,n^-)=-k, \end{aligned}$$

for some constant $k>0$. Let $b^\pm (X):=\nabla _X n^\pm +f^\pm (X) n^\pm$ be the associated shape operators. Notice that their image is orthogonal to $n^\pm$. They are really representatives of the endomorphisms we considered previously since we are not taking quotients here. The arbitrary linear functions $f^\pm$ can be chosen so that $\text {Im} b^\pm \subset \text {ker} g(\cdot , n^\mp )$, and hence $\text {Im} b^\pm \subset TS$. We have that

$$\begin{aligned} B(X,Y)=\alpha ^+(X,Y)\,n^++\alpha ^-(X,Y)\, n^-, \end{aligned}$$

for some functions $\alpha ^\pm :TS\times TS\rightarrow \mathbb {R}$, so extending Y to a vector field orthogonal to $n^+$,

$$\begin{aligned} -k\alpha ^-(X,Y)&=g(B(X,Y),n^+)=\nabla _X g(Y,n^+)-g(\nabla _XY,n^+)=g(Y,\nabla _Xn^+)\\&=g(Y,b^+(X)). \end{aligned}$$

Moreover, observe that $\text {tr} (g_S^{-1} \alpha ^-)=-\frac{1}{k}\text {tr} \,b^+=-\frac{1}{k}\theta ^+$ (the first equation is obtained using the above representative, but the result does not depend on the representative if the second trace is understood in the quotient space). We conclude that the shape tensor reads

$$\begin{aligned} B(X,Y)=-\frac{1}{k}\,g(Y,b^-(X))\,n^+-\frac{1}{k} \,g(Y,b^+(X))\, n^-, \end{aligned}$$

(6.16)

so we can write

$$\begin{aligned} g(B(X,Y), n^\pm )=g(Y, b^\pm (X)), \end{aligned}$$

(6.17)

while the mean curvature vector reads

$$\begin{aligned} H=-\frac{1}{k}\, \theta ^-\,n^+-\frac{1}{k}\, \theta ^+\, n^-, \end{aligned}$$

(6.18)

and hence

$$\begin{aligned} \theta ^\pm = g(H,n^\pm ). \end{aligned}$$

(6.19)

As a consequence, H is future directed timelike iff S is a future trapped set, future directed causal or zero iff S is weakly trapped set, future directed null iff S is a marginally trapped set.

Let the codimension 2 surface S be a submanifold of a hypersurface N. Let u be the unit, future directed, timelike vector normal to N, $g(u,u)=-1$. Let $\nu$ be a vector field normal to S and u, and let $n^\pm =u\pm \nu$, so that $k=2$.

The Gauss and Weingarten equations for N read

$$\begin{aligned} \nabla _X Y&=\nabla ^N_X Y+g_N(Y,K(X)) u, \ \nabla _X u&= K(X), \end{aligned}$$

where X, Y are vector fields over N, $g_N$ is the metric induced by g on N, $\nabla ^N_X$ is the Levi-Civita connection on $(N,g_N)$ and $K:TN\rightarrow TN$ is the ($g_N$-symmetric) second fundamental form of N. If X, Y are restricted to be vector fields over S extended to N, then the first equation gives using Eq. (6.15)

$$\begin{aligned} \nabla ^N_X Y=\nabla ^S_X Y- B(X,Y)-g_N(Y,K(X)) u=\nabla ^S_X Y-g_S(Y,R(X))\nu . \end{aligned}$$

In the last equation we have used the fact that the two covariant derivatives are orthogonal to u and so the introduced $g_S$-symmetric function $R:TS\rightarrow TS$ is the second fundamental form for S on N (thus $\nabla ^N_X \nu =R(X)$). Using Eq. (6.16) we get that for $X,Y\in TS$

$$\begin{aligned} g_N(Y,K(X))&=\frac{1}{2} [g(Y,b^+(X))+ g(Y,b^-(X))],\ R(X)&=\frac{1}{2} [b^+(X)-b^-(X)]. \end{aligned}$$

Contracting the latter equation we get $\theta ^+-\theta ^-=2 {\bar{R}}$, where ${\bar{R}}$ is the mean curvature of S in N. Doing the same on the former equation we get $\text {tr}_S K=\theta ^++\theta ^-$, where we stress that $\text {tr}_S K=\text {tr} K-g_N(\nu ,K(\nu ))$, is just a partial trace. So we obtain

$$\begin{aligned} \theta ^\pm =\text {tr}_S K\pm {\bar{R}}, \end{aligned}$$

(6.20)

see, for instance, Galloway (1983a), Andersson et al. (2011) and Galloway and Ling (2018). Special cases of this formula appeared very early in the study of singularities, see Hawking (1965). A spacetime expands in all directions if N can be found such that $g_N K$ is positive definite. In this case any minimal surface S on N would have $\theta ^\pm =\text {tr}_S K>0$, namely it would be past trapped (Galloway 1983a; Galloway and Ling 2018). From here, under reasonable energy conditions, Penrose’s theorem guarantees the existence of a geodesic singularities, see Sect. 6.6.2.

6.5 Completeness implies focusing which spoils maximization

In this section we prove that geodesic completeness can be used to infer the existence of focal points in certain hypersurface-orthogonal congruences, and that the presence of focal points spoils certain Lorentzian length maximization properties.

The following proposition is stated so as to hold in both the null and timelike cases. The proof of the chronality statement (a) is more topological and in the end much simpler than that given in textbooks.

The traditional textbook proofs Hawking and Ellis (1973, Proposition 4.5.12), O’Neill (1983, Proposition 10.48) and Kriele (1999, Lemma 4.6.15) for the null case of (a) are somewhat incomplete since the compactness argument there used does not prove that the geodesic variation is causal near the endpoints. The proof given by Beem et al. seems to be fine in this respect (Beem et al. 1996, Theorem 10.72). A cleaner proof can also pass through the more general Causality Lemma given by Galloway (1996). Here this lemma is included in (b) which also shows that the weak null convexity condition in Galloway (1996) is not required. The timelike case is shown to be a corollary of the null case by using a product trick.

Theorem 6.16

Let us consider a null (resp. timelike and normalized) geodesic congruence $\varGamma (t,\tau )$, $\varGamma (0,\tau )=\tau$, orthogonal to a local codimension one hypersurface H, where the starting point $\tau \in T$ belongs to a manifold T transverse to the congruence (coincident with H in the timelike case, included in H and of dimension $n-1$ in the null case). Let $\gamma (t)=\varGamma (t,p)$ be a geodesic belonging to the congruence, $p=\gamma (0)\in T$.

The first focal point $q=\gamma (t_q)$, $t_q>0$, of the congruence on $\gamma$ is actually the first point where $\theta \rightarrow -\infty$.

Assume that this focal point exists.

• (a) Let $r= \gamma (t_r)$, $t_r>t_q$. There is a $C^1$ curve $\xi :(-1,1)\rightarrow T$, $s\mapsto \xi (s)$, $\xi (0)=p$, such that for $s\ne 0$, and sufficiently small $\vert s\vert$, that $\varGamma (0,\xi (s))$ can be connected to r by a timelike curve whose Lorentzian length is larger than the Lorentzian length $l(\gamma \vert _{[0,t_r]})$ of the geodesic between p and r.

• (b) Let $T'$ be a spacelike manifold orthogonal to $\gamma$ at q (of codimension two in the null case, and one in the timelike case). Let $U_q$ be a compact neighborhood of q. There is a $C^1$ curve $\xi :(-1,1)\rightarrow T$, $s\mapsto \xi (s)$, $\xi (0)=p$, such that for $s\ne 0$, and sufficiently small $\vert s\vert$, we have that $\varGamma (0,\xi (s))$ can be connected to $U_q\cap T'$ with a timelike curve of Lorentzian length larger than the Lorentzian length $l(\gamma \vert _{[0,t_q]})$ of the geodesic between p and q (see Figs. 21, 22).

Concerning the existence of focal points, let us assume that the null (resp. timelike) convergence condition holds. We have:

• (c) If $\theta (p)<0$ then the geodesic congruence necessarily develops a focal point $q=\gamma (t_q)$, provided $\gamma$ extends to sufficiently large affine parameters.

• (d) If there is a compact manifold $T\subset H$ transverse to the congruence and such that $\theta <0$ on it then every geodesic crossing T develops a focal point in the future within a certain bounded affine parameter provided the affine parameters extend sufficiently far.

Fig. 21

A figure that illustrates the statement and the proof of points (a)–(b) of Theorem 6.16 in the null case. Here $H'$ is a null hypersurface generated by the spacelike manifold $T'$. Its shape operator is bounded in a neighborhood of q. For case (a) $H'$ can be taken to be the image of the past lightlike cone at r. The main idea is that the null hypersurface H generated by the lightlike congruence $\varGamma$ is well defined till the first focal point q. At some point b before q along $\gamma$, due to $\theta \rightarrow -\infty$, H attains a so large shape operator that moving in some congruence-transverse directions (the dotted line passing through b) it enters the past of $I^-(H')=I^-(T')$ (notice that H and $H'$ are tangent along $\gamma$ near b). As a consequence, for some point in T (more precisely for any point in the image of a curve $\xi :I\rightarrow T$ minus p, which unfortunately in this figure gets identified with T) there is a timelike curve connecting the point to $T'$

Fig. 22

A figure that illustrates the statement and proof of points (a)–(b) of Theorem 6.16 in the timelike case. Here $T'$ is any spacelike hypersurface passing through the focal point q. We can find a curve $\xi :I\rightarrow H=T$ passing through p such that any point of the curve but p can be connected to $T'$ by a timelike curve of length larger than the length of $\gamma$ between p and q. Case (a) can be regarded as a consequence of (b) where $T'$ is the exponential map, in a convex neighborhood of q, of a rescaled past indicatrix at r. This result can be deduced as follows. For sufficiently small t the spacelike hypersurface $T'(t)=\{x:d(x,T')=t_q-t\}$ is well defined and orthogonal to $\gamma$. The congruence-orthogonal hypersurface $H_t$ (dotted line), $H_0=H$, has a divergent shape operator due to $\theta (t)\rightarrow -\infty$ for $t\rightarrow t_q$. For some t sufficiently close to $t_q$, $T'(t)$ and $H_t$ intersect tangentially at b, but $H_t$ bends so much that when moving from b in the direction determined by $\xi$, it enters the chronological past of $T'(t)$. The gap between the hypersurfaces in dotted and solid lines expresses the statement of the theorem

Observe that H is transverse to the congruence in the timelike case, and contains the congruence in a neighborhood of p in the null case (it is a null hypersurface). The statement does not claim that the focal point is inside H, for we assume that in H the congruence is determined by a $C^1$ vector field (thus H has edge in the null case).

Remark 6.17

One might ask whether the theorem applies to congruences of half-geodesics issued by a single point p. The answer is affirmative. In the null case it is sufficient to consider a convex neighborhood C of p and take as H the exponential map (on C) of the future light cone at p minus the zero vector. In the timelike case it is sufficient to recall Gauss’ lemma, and having chosen a convex neighborhood C of p, define H as the image under the exponential map (on C) of the subset of $T_pM$ which consists of future directed timelike unit vectors. Then the conjugate point q for p becomes a focal point for H and the theorem applies giving the usual results for conjugate points.

Remark 6.18

Tipler (1978a, b) showed that in this type of results the convergence (positive energy) condition can be given a weaker averaged form. Among the works that have explored this generalization we mention Borde (1987), Roman (1988) and Fewster and Galloway (2011).

Proof

In the null case we denote by n the geodesic field tangent to the congruence, $\nabla _nn=0$, while we use u in the timelike normalized case. Let us first prove that at the first focal point $q=\gamma (t_q)$ we have $\theta \rightarrow -\infty$. Indeed, let $\{e_i\}$ be a basis at $V_p$ and let us transport it over $\gamma$ through the condition $e'_i=0$. The Jacobi equation provides a linear map from $V_p$ to $V_q$ whose Jacobian is $J^j_i(t_q)$ where $J_i:=J^j_i(t) e_j$ is the value at $\gamma (t)$ of the Jacobi field $J_i$ whose initial condition is $J_i(0)=e_i$, $J_i'(0)=\nabla _{e_i} n$ (in the timelike case replace n with u in this and the following formulas). Observe that $J_i$ is such that $[J_i, n]=0$ at $t=0$, thus at every later instants because by (6.1) and (6.2) we have the linear differential equation in $[J_i,n]$, $\nabla _n [J_i,n]+\nabla _{[J_i,n]} n=0$.

Observe also that $J^j_i(0)=\delta ^j_i$; thus by continuity $\det J^j_i > 0$ at least before the first focal point. As q is a focal point this linear map is not injective, that is $\det J^j_i(t_q)=0$, which implies $\ln \det J^j_i(t) \rightarrow -\infty$ for $t\rightarrow t_q$, and hence $\frac{\mathrm{d}}{\mathrm{d}t} \ln \det J^j_i(t_k)\rightarrow -\infty$ for some sequence $t_k\rightarrow t_q$. Using Jacobi’s formula for the derivative of a determinant we get

$$\begin{aligned} \frac{\mathrm{d}}{\mathrm{d}t} \ln \det J^j_i(t_k)&= (J^{-1})^i_j \frac{\mathrm{d}}{\mathrm{d}t} J^j_i(t_k)= \text {tr} (J\mapsto \nabla _{n} J)(t_k)= \text {tr} (J\mapsto \nabla _{J} n)(t_k)\\&= \theta (t_k), \end{aligned}$$

thus $\theta \rightarrow -\infty$ at the first focal point.

Conversely, let us consider the first point q where $\theta \rightarrow -\infty$. Let T be a k-dimensional ($k=n$ in the timelike case and $k=n-1$ in the null case) manifold $T\subset H$, $p\in T$, transverse to the congruence and determined by the restriction of the vector field (u in the timelike case, n in the null case) on T. There must be a focal point on $\gamma$ at q or before q for otherwise the exponential map from T would provide a well defined local diffeomorphism in a neighborhood of every vector $t \dot{\gamma }(0)$, $t\in [0,b]$, $\exp _p(b \dot{\gamma }(0))=q$, which would imply that the vector field (u in the timelike case, n in the null case) is well defined and $C^1$ in a neighborhood of $\gamma$, and so its divergence $\theta$ would be well defined and finite at q, a contradiction. Thus the focal point can only be q, in fact since $\theta \rightarrow -\infty$ at the focal points, q would not be the first point where the expansion diverges.

Let us prove (c). Let us consider the Raychaudhuri equation evaluated on the half-geodesic $t\rightarrow \gamma (t)$ with initial point $p=\gamma (0)$. The Raychaudhuri equation gives the inequality $\frac{d \theta }{d t}\le -\frac{1}{k} \,\theta ^2$. As $\theta (t) \le k/[t-k/(-\theta (p))]$ we have $\theta \rightarrow -\infty$ at some $0<t_q<k/(-\theta (p))$ provided the affine parameter extends sufficiently far.

Statement (d) is clear given the compactness of T.

Let us prove (a) in the null case. Let C be a convex neighborhood of q, and let us consider three points in sequence $b<_C q<_C r$ over $\gamma \cap C$. The geodesic congruence at b forms a $C^2$ hypersurface H in a neighborhood of b because there is no focal point in the segment $\gamma \vert _{[0,t_b]}$. Similarly, the exponential map of the past light cone at r provides a $C^2$ hypersurface $H'$ containing the segment $\gamma \vert _{[t_b,t_q]}$. By construction they are tangent but when regarded as local graphs they might have different second order Taylor expansion at b. Below we are going to compare the second derivatives in some directions.

Observe that the second derivative of the graphing function of $H'$ is bounded on a compact neighborhood of q, however for what concerns H, $\theta (t) \rightarrow -\infty$ for $t\rightarrow t_q$, which proves that the Weingarten map of H is not bounded there. Since $\theta =tr(X\rightarrow \overline{\nabla _X n})$, there is some large negative eigenvalue of this map, namely a h-normalized vector $e^{(k)}$ such that $\nabla _{e^{(k)}} n=\lambda _k e^{(k)}+s_k n$, $\lambda _k \rightarrow -\infty$ as $t_k\rightarrow t_q$, thus $g(e^{(k)}, \nabla _{e^{(k)}} n)=h(e^{(k)}, \overline{\nabla _{e^{(k)}} n})=\lambda _k\rightarrow -\infty$. Let us extend each $e^{(k)}$ in a neighborhood of $\gamma (t_k)$ so as to remain in TH. We have

$$\begin{aligned} g(n,\nabla _{e^{(k)}}e^{(k)})=-g(e^{(k)}, \nabla _{e^{(k)}} n)\rightarrow +\infty . \end{aligned}$$

This equation clarifies that H, at least in some directions, bends so much below the exponential map of the tangent plane $\ker g(n,\cdot )(b)$ that for b sufficiently close to q it bends more than $H'$ and hence enters the chronological past of r. Let J be the Jacobi field at p which evolves into $e^{k}$ for sufficiently large k. Any $C^1$ curve $\xi$ with tangent J has the property of the theorem.

In the null case the statement (b) involving $T'$ is similar, we just need to use the past lightlike congruence issued from $T'$ and containing $\gamma$, in place of the exponential map of the past light cone at r, to generate a local null hypersurface $H'$ whose edge includes $T'$. Observe that $H'$ has bounded second fundamental form near q and is tangent to H at b. From here the argument is exactly the same as before.

The timelike cases for (a) and (b) are in fact corollaries of the null case. It is sufficient to apply the null case to the spacetime $M^\times =M\times \mathbb {R}$ endowed with the Lorentzian metric $g^\times =g+\mathrm{d}z^2$, and lift the timelike normalized congruence to a lightlike congruence as follows (alternatively, one can project to M the objects of the next construction, so getting the argument outlined in Fig. 22). Given the set H on M, and the timelike geodesics $\varGamma (t,p)$ starting from H we consider the set $H \times \{0\}$, and the lightlike geodesics starting from it (light lifts) $(\varGamma (t,p),t)$. We denote by $\tilde{H}$ the hypersurface spanned by these geodesics in a neighborhood of $H\times \{0\}$. The vector field $n=(u,1)$ is tangent to $\tilde{H}$ where u is the normalized timelike field on M which generates the timelike congruence. The vector field n is also normal to $H\times \{0\}$, thus $\tilde{H}$ is a $C^2$ null hypersurface which is the local exponential map of a lightlike bundle normal to $H\times \{0\}$. This null hypersurface has the form ${\tilde{H}}=\cup _t (H_t, t)$ where $H_t$ is the evolved congruence-orthogonal hypersurface in M (Sect. 6.2). The null hypersurface ${\tilde{H}}$ can be further enlarged extending the generators as long as it remains $C^2$ (Remark 6.8). The Killing vector field $k=(0,1)$ generates an isometry of $(M^\times ,g^\times )$, ($g^\times$ is independent of z). As a consequence, over the light lift geodesics g(n, k) is constant, thus k cannot become tangent to ${\tilde{H}}$ since it is transverse to it over $H\times \{0\}$. In conclusion, ${\tilde{H}}$ remains transverse to k before the development of focal points. The projection establishes a correspondence between first focal points, in fact the Jacobi fields of ${\tilde{H}}$ coincide with those of H in all components but the last one which is zero.

The light lift can be defined for any timelike curve starting at H, by imposing the extra-coordinate to be the proper time of the lifted curve. Let us consider (a) for the timelike congruence case. The points (p, 0), $(q,t_q)$, $(r,t_r)$, $t_r>t_q>0$, all belong to the lightlike geodesic $(\gamma (t),t)$, with $\gamma (t)= \varGamma (t,p)$. The result (a) for the null case implies that there is a timelike curve $(\sigma (\tau ), f(\tau ))$ from $(\xi (s),0)$ to $(\gamma (t_r),t_r)$, where the (timelike) projection $\sigma$ has been parametrized with respect to proper time. This timelike condition reads $1=-g({\dot{\sigma }},{\dot{\sigma }})(t)>(\dot{f})^2$, which taking the square root, integrating, and using $\int \vert \dot{f}\vert \mathrm{d}\tau \ge \int \dot{f} \mathrm{d}\tau =t_r$, gives that the Lorentzian length of $\sigma$ is larger than the Lorentzian length of $\gamma \vert _{[0,t_r]}$, which proves (a) for the timelike case. The proof of (b) is similar, one has to consider the set $T'\times \{t_q\}$ and the local null hypersurface $\tilde{H}'$ generated by the exponential map in the past direction of the local lightlike normal bundle to $T'\times \{t_q\}$ which includes $(-{\dot{\gamma }}(t_q),1)$. The local null hypersurface $\tilde{H}'$ has edge which includes $T'\times \{t_q\}$. On the light lift of $\gamma$ just before $(\gamma (t_q),t_q)$, the hypersurface ${\tilde{H}}$ bends so much that it enters $I^-(T'\times \{t_q\})$, thus for any sufficiently small s, $(\xi (s),0)$ can be connected to $T'\times \{t_q\}$ by a timelike curve. The comparison of the projected Lorentzian lengths is as before.

It can be observed that the timelike convergence condition for M coincides with the null convergence condition for $M^\times$, thus (c) and (d) in the timelike case could also be regarded as corollaries of the null case. $\square$

The previous result shows that the presence of a conjugate or focal point over a lightlike geodesic spoils achronality. Under global hyperbolicity one can show the converse, namely that achronality is spoiled only due to the presence of intermediate conjugate/focal points or of intermediate points reached by other lightlike geodesics starting from the initial point/surface, see Beem and Ehrlich (1979b, Theorem 5.3), Beem et al. (1996, Theorem 9.15), Minguzzi and Sánchez (2006, Corollary 2.1) and Akers et al. (2018) for precise statements.

The following important result on the existence of conjugate points does not follow from the previous theorem. The proof can be found in Hawking (1966a), Hawking and Ellis (1973, Proposition 4.4.2,5), Ehrlich and Kim (1994), Beem et al. (1996) and Tong (2009).

Theorem 6.19

Let $\gamma$ be a complete timelike geodesic and suppose that the timelike convergence and genericity conditions hold. Then $\gamma$ admits a pair of conjugate points and hence is not maximazing. A similar statement holds with “null” replacing “timelike”.

Corollary 6.20

A timelike geodesically complete spacetime such that (a) the timelike convergence condition holds and (b) the timelike genericity condition holds, does not have timelike lines.

A lightlike geodesically complete spacetime such that (a) the null convergence condition holds and (b) the null genericity condition holds, does not have lightlike lines.

It can be recalled here that some stronger energy conditions imply the absence of future or past lightlike rays (Tipler 1977; Joshi 1981; Borde 1987), a condition which under chronology implies global hyperbolicity (Minguzzi 2009a, c).

6.6 Some singularity theorems

Most singularity theorems are composed of the following three steps:

• 1. A non-causal (namely non-conformally invariant) statement assuming some form of geodesic completeness, plus some genericity and positive energy condition and implying the existence of conjugate points in geodesics or focal points for certain (hyper)surfaces S with special convergence properties, e.g. Theorems 6.19 and 6.24. This step typically makes use of the Raychaudhuri equation.

• 2. A non-causal (namely non-conformally invariant) statement to the effect that the presence of conjugate or focal points spoils some Lorentzian length maximization property (achronal property in the null case), see Sect. 6.5, Theorem 6.16.

• 3. A causal statement to the effect that under some causality conditions and in presence of some special set (trapped set, Cauchy hypersurface) the spacetime must actually have a causal line or a causal S-ray.

The first two results go in contradiction with the last one, so from here one infers geodesic incompleteness. For instance, in Penrose’s theorem one first observes that the lightlike geodesics issued normally to the trapped surface S necessarily develop focal points (point 1). The lightlike geodesics enter the chronological future of S, namely there are no lightlike S-rays (point 2). However, (point 3) if the spacetime admits a non-compact Cauchy hypersurface, then there must exist a lightlike S-ray.

Point 1 requires the genericity condition only if lightlike lines rather than S-rays are involved in point 3. So singularity theorems roughly separate themeselves into two groups: those that use the genericity condition and those that do not, or equivalently, those that prove the existence of a causal line in point 3, and those that prove the existence of an S-ray in point 3.

Another important observation is the following: the first two steps basically coincide for all the singularity theorems. For instance, Penrose’s and Gannon’s singularity theorem, but also the topological censorship theorem, use the same versions of 1 and 2. Similarly, Hawking and Penrose ’s and Borde’s singularity theorems use the same versions of 1 and 2. They really differ just for the causality statement in 3. For this reason, it might be convenient to identify the singularity theorem with what we call its causality core statement, namely part 3.

In a sense the first two steps hide the causality content of the singularity theorem. Of course, they are important since the physical content of the theorem is better appreciated by passing to the non-conformally invariant formulation, for only in this way one can make contact with the positive energy condition or with the geodesic completeness condition, which are, of course, non-conformally invariant.

Having so dissected the singularity theorems it becomes easy to structure their generalizations.

Most of causality theory can be generalized to $C^{1,1}$ metrics, since under this regularity convex neighborhoods do exist (Minguzzi 2015b; Kunzinger et al. 2014a, b). It is natural to ask if the singularity theorems can be generalized to this regularity. The answer is positive and the available results are even stronger if one focuses on the causality core, that is on point 3.

In fact much of causality theory can be generalized even further i.e. to $C^0$ or even upper semi-continuous light cone distributions (Chruściel and Grant 2012; Fathi and Siconolfi 2012; Sbierski 2018; Sämann 2016; Bernard and Suhr 2018a; Minguzzi 2019; Graf and Ling 2018). In the end the causality core of singularity theorems can be proved under very weak regularity conditions ranging from upper semi-continuity to Lipschitzness of the light cone distribution or metric. Moreover, it can also be generalized to anisotropic (i.e. Lorentz–Finsler) theories (Minguzzi 2019). This fact should not be too surprising since the type of arguments entering point 3 are quite topological in nature.

As already mentioned, points 1 and 2 are also quite robust. They admit generalizations to Lorentz–Finsler theory (Minguzzi 2015c; Aazami and Javaloyes 2016) and to $C^{1,1}$ differentiability assuptions on the metric (Kunzinger et al. 2014a, b, 2015a, b; Graf et al. 2018). Other generalizations are possible, for instance Case (2010) showed that the singularity theorems are generalizable to metric measure theories. Of course, in his work he generalized just point 1, in fact the geodesics of the spacetime and its causal structure are not affected by the weight, so points 2 and 3 do not require any modification.

6.6.1 Singularities and existence of time

The first singularity theorem that we consider is rather primitive and is the most recent of our list. It was proved by the author in Minguzzi (2009c) and is presented first because it simplifies the proofs of the other singularity theorems. The proof of this first theorem is rather easy because it takes advantage of much preliminary work on the equivalence between stable causality and K-causality (Minguzzi 2009e, 2019). By Theorem 4.106 we know that: chronological spacetimes without lightlike lines are stably causal. So, joining with Corollary 6.20 and Theorem 4.100 we get

Theorem 6.21

A spacetime which is chronological and satisfies the null convergence and the null genericity conditions is null geodesically incomplete or admits a time function.

The theorem establishes that under fairly weak conditions if time does not exist the spacetime is singular. Stated in another way, under some weak requirements chronology gets promoted to stable causality.

Remark 6.22

Starting from the landmark paper on singularities by Hawking and Penrose (1970), the null or timelike genericity conditions have been presented as physically reasonable, mathematically sound requirements (Hawking and Ellis 1973, p. 101), see also Beem and Parker (1990), Beem and Harris (1993a, b) and Beem et al. (1996) for in depth discussions of these conditions. In my opinion the genericity conditions are not weak and are possibly quite unreasonable, unless non-total imprisonment is assumed. In fact it is not unreasonable that a geodesic could have some special alignment property with the curvature if its image is relatively compact (e.g. the generators of some compact Cauchy horizon). I do agree that the genericity property is instead quite reasonable for non-imprisoned geodesics, as they explore, so to say, far away regions of spacetime. Even with this caveat the previous theorem is still useful and quite strong, it is sufficient to replace chronology with non-total imprisonment.

We have already mentioned that the analogous condition of absence of lightlike rays, or the more physical energy and genericity conditions that imply it, have much stronger implications as they promote chronology to global hyperbolicity (Minguzzi 2009c). In general it might be difficult to motivate those physical conditions (Tipler 1977; Joshi 1981; Borde 1987).

6.6.2 Penrose’s theorem and Gannon’s theorem

We recall that a future trapped set is a non-empty set S such that $E^{+}(S)$ is non-empty and compact. Under chronology a non-empty compact set S is a future trapped set if $E^+(S)$ is compact, see Theorem 2.100.

The following result improves the original theorem by Penrose (1965a). Indeed, in the original version it is tacitly assumed that $E^{+}(S)$ is non-empty, which would follow if S were required to be achronal. However, thanks to the compactness of S we don’t need to assume that S is achronal nor that $E^+(S)$ is non-empty.

Theorem 6.23

(Penrose 1965a, b, conformally invariant formulation) Let (M, g) be a globally hyperbolic spacetime with a non-compact Cauchy hypersurface then there is no non-empty compact set S which is a future trapped set (equivalently, such that $\overline{E^{+}(S)}$ is compact, see Theorem 2.108). Moreover, any non-empty compact set S admits a future lightlike ray starting from S and entirely contained in $E^{+}(S)$.

Proof

By Theorem 2.108 a non-empty compact set S such that $E^{+}(S)$ is relatively compact is indeed trapped. By Theorem 2.100 the set $A=S\cap E^{+}(S)$ is non-empty, compact, achronal and such that $E^{+}(A)=E^{+}(S)$, hence A is trapped.

Since the spacetime is globally hyperbolic it is causally simple, thus by Proposition 2.143, $E^{+}(A)=\dot{I}^{+}(A)$ and $\text {edge}(E^{+}(A))=\emptyset$. By Theorems 2.87 and 2.147 $E^+(A)$ is a locally Lipschitz topological hypersurface. Let V be a global timelike vector field and let C be a Cauchy hypersurface to the past of S. The flow of V can be used to project $E^+(A)$ to the Cauchy hypersurface C, then the projected set must have boundary in C, since C is non-compact while the projection is compact. There is some point $q\in E^+(A)$ that projects to such boundary, but in a neighborhood of q any integral line of V enters $I^+(q)\subset I^+(E^+(A))$, namely crosses $E^+(A)$, thus q cannot really project to a boundary point of the projection, a contradiction which proves that a compact trapped set does not exist. The last statement is a consequence of Theorem 2.112. $\square$

A trapped surface need not be achronal (for the definition of trapped surface see Definition 6.14). Even in the simply connected $2+1$ Minkowski spacetime (multiplied by a suitable factor strongly decreasing with t) it is possible to find trapped surfaces which are not achronal (imagine a closed spacelike curve rounding twice the axis t so that the curve does not intersect itself and at some point it lies in its chronological future).

The following theorem relates the non-conformal but physically significant part of the original Penrose’s theorem (null convergence condition, trapped surface, null completeness) to the conformal one (araying set, trapped set).

Theorem 6.24

Let (M, g) be future null geodesically complete and such that the null convergence condition holds. Every future trapped surface is a future null araying set (so it is a trapped set provided it does not intersect the chronology violating set, cf. Theorem 2.116).

Proof

Assume S is a trapped surface that admits a future lightlike S-ray, hence contained in $E^{+}(S)$. This ray must start perpendicularly to S otherwise it would be entirely contained (but for possibly the starting point) in $I^{+}(S)$. Thus this ray belongs to one of the two congruences of converging lightlike geodesics issued from S. By the Raychaudhuri equation and null geodesic completeness, and due to Proposition 6.13 and Theorem 6.16, this geodesic reaches a focal point (to the surface S) and by Theorem 6.16 it enters $I^{+}(S)$, a contradiction. $\square$

As a corollary we obtain Penrose’s theorem in its original formulation.

Theorem 6.25

(Penrose 1965a, b) Let (M, g) be a globally hyperbolic spacetime which admits a non-compact Cauchy hypersurface and satisfies the null convergence condition. If it admits a trapped surface then it is future null geodesically incomplete.

Proof

If it were null geodesically complete the trapped surface would be a trapped set by Theorems 2.116 and 6.24, a fact which goes in contradiction with Theorem 6.23. $\square$

Remark 6.26

In order to get a trapped set one does not really need to consider the ingoing congruence of lightlike geodesics. For instance, if S is the closure of a relatively compact open subset of a spacelike hypersurface and $\partial S$ is $C^2$ and has the outgoing congruence of orthogonal lightlike geodesics which is converging, $\theta ^+<0$, then S is a future trapped set under null completeness and the null convergence condition. One says that $\partial S$ is an outer trapped surface. These trapped objects are quite natural in view of the notion of trapped zone or region, see Theorem 2.121.

Bardeen gave an example of null geodesically complete spacetime which satisfies all the assumptions of Penrose’s theorem but global hyperbolicity (Hawking and Ellis 1973; Borde 1994). His result suggested that global hyperbolicity could be indeed a necessary condition. Nevertheless, Borde (1994) observed that in Penrose’s proof what seems essential is the topological condition on the non-compactness of the Cauchy hypersurface rather than global hyperbolicity itself. Therefore, one could hope for a weakening of the causality condition. We are going to prove that this is indeed the case by weakening global hyperbolicity to a causality condition weaker than causal continuity.

Proposition 6.27

Let (M, g) be a non-totally imprisoning spacetime. For every compact connected locally achronal topological hypersurface we can find a spacelike hypersurface homeomorphic to it (if the former is achronal the latter can be found achronal).

Notice that the converse is obvious since spacelike hypersurfaces are locally achronal.

Proof

Let S be the compact locally achronal topological hypersurface. Let ${\tilde{S}}$ be one copy of S in Geroch’s covering $M_G$, so that ${\tilde{S}}$ is homeomorphic to S and achronal (cf. Sect. 2.15). Let $N\subset M_G$ be the spacetime obtained cutting out all the other copies and taking the connected portion including ${\tilde{S}}$. We have that ${\tilde{S}}$ is still achronal in N. By Theorem 3.52 $\mathrm {Int}D_N({\tilde{S}})\ne \emptyset$, and by Theorem 3.45 this set with the induced metric is globally hyperbolic. By Theorem 4.120 it admits a Cauchy temporal function t, thus the level sets are spacelike and Cauchy. Since ${\tilde{S}}$ is compact, t is bounded over it so we can find a constant a, such that the level set ${\tilde{S}}'=t^{-1}(a)$ does not intersect ${\tilde{S}}$. Being Cauchy it is homeomorphic to ${\tilde{S}}$ (Theorem 4.119). By Theorem 3.50 it is edgeless as a subset of $M_G$. Moreover, it is achronal in $M_G$ for if there is a timelike curve $\sigma$ connecting $p\in {\tilde{S}}'$ to $q\in {\tilde{S}}'$ either it already intersects ${\tilde{S}}$ twice or using the fact that ${\tilde{S}}$ is Cauchy in $\mathrm {Int}D_N({\tilde{S}})$ it can be continued to intersect ${\tilde{S}}$ twice, which gives a contradiction with the achronality of ${\tilde{S}}$. Thus by Theorem 2.147 ${\tilde{S}}'$ is a topological hypersurface. Let $S'$ be its projection to M. We have only to show that ${\tilde{S}}'$ and $S'$ are homeomorphic. For this to be the case we have to check that no two distinct points ${\tilde{p}}_1$, ${\tilde{p}}_2$ of ${\tilde{S}}'$ project to the same point p. If not a curve in ${\tilde{S}}'$ connecting ${\tilde{p}}_1$ to ${\tilde{p}}_2$ would intersect a copy of S on $M_G$, which is impossible since by construction ${\tilde{S}}'$ does not intersect the counterimage of S.

The proof in the achronal case is simpler since the covering is not needed. Let S be the compact achronal topological hypersurface. By Theorem 3.52 $\mathrm {Int}D(S)$ $\ne \emptyset$, and by Theorem 3.45 this set with the induced metric is globally hyperbolic. By Theorem 4.120 it admits a Cauchy temporal function, thus the level sets are spacelike and Cauchy. Let $S'$ be one such level set. Being Cauchy it is homeomorphic to S (Theorem 4.119). By Theorem 3.50 it is edgeless as a subset of M. Moreover, it is achronal in M for if there is a timelike curve $\sigma$ connecting $p\in S'$ to $q\in S'$ either it already intersects S twice or using the fact that S is Cauchy in $\mathrm {Int}D(S)$ it can be continued to intersect S twice, which gives a contradiction with the achronality of S. Thus $S'$ is an achronal spacelike hypersurface homeomorphic to S. $\square$

Definition 6.28

We say that a spacetime is (spatially) open if it does not contain compact locally achronal topological hypersurfaces. We say that a spacetime is (spatially) achronally open if it does not contain achronal compact topological hypersurfaces.

Bardeen spacetime is not open in this sense. Clearly open spacetimes are achronally open.

Proposition 6.29

Every spacetime admitting a non-compact Cauchy hypersurface (hence globally hyperbolic) is open.

Proof

The argument is as in Penrose’s theorem and makes use of the flow of a global timelike vector field v to project any spacelike hypersurface S to the Cauchy surface C. As S is spacelike such a projection is open, but C is connected, thus S and C are homeomorphic, hence S is non-compact. $\square$

The main point is to infer the absence of edge without using causal simplicity.

Theorem 6.30

Let (M, g) be past reflecting. If S is a compact and achronal future null araying set then $\dot{I}^+(S)=E^+(S)$ and hence $\text {edge}({E^{+}(S)})=\emptyset$.

Proof

Suppose not then there is $q\in \dot{I}^+(S)\backslash E^+(S)$. Let $\sigma _n$ be a sequence of timelike curves starting from S end ending at $q_n$ with $q_n\rightarrow q$. By achronality $S\subset \dot{I}^+(S)$. Due to the compactness of S, the limit curve theorem tells us that there are either a continuous causal curve connecting $r\in S$ to q, which is impossible since it would entail $q\in J^+(S)$ and hence $q\in E^+(S)$, a contradiction, or there are $r\in S$, a future inextendible continuous causal curve $\sigma ^r$, and a past inextendible continuous causal curve $\sigma ^q$ to which some subsequence of $\sigma _n$, here denoted in the same way, converges in suitable parametrizations. Since S is a future null araying set, $\sigma ^r$ cannot be a future null S-ray, hence it enters $I^+(S)$. Let $b\in \sigma ^r$, such that $U\ni b$ is an open neighborhood contained in $I^+(S)$. Let $p\in I^-(b,U)$, then for sufficiently large n, $\sigma _n$ enters $I^+(p,U)$, thus $q\in \overline{I^+(p)}$ and by past reflectivity $p\in \overline{I^-(q)}$, thus as $p\in I^+(S)$, $q\in I^+(S)$, a contradiction. $\square$

We have the next improvement of Penrose’s theorem in which global hyperbolicity is weakened while retaining a global topological condition on the space sections.

Theorem 6.31

Let (M, g) be past reflecting. If (M, g) is achronally open, it does not admit compact future null araying sets that do not intersect the strong causality violating set.

The typical causal structure of an evaporating black hole is past reflecting but not future reflecting, see e.g. the conformal diagram in Hiscock (1981) and Brown and Lindesay (2008). Under these conditions the singularity cannot be regarded as a consequence of Penrose’s theorem since global hyperbolicity does not hold. However, one can use this theorem to infer that trapped surfaces still lead to a singularity.

Proof

By contradiction, let S be such an araying set. By. Theorem 2.114 it can be assumed to be achronal. By Theorem 6.30$\mathrm {edge}(E^+(S))=\emptyset$, thus by Theorem 2.147 $E^+(S)$ is a locally Lipschitz topological hypersurface. By Theorem 2.116 S is a future trapped set, so $E^+(S)$ is compact, thus (M, g) is not achronally open, a contradiction. $\square$

Corollary 6.32

Let (M, g) be strongly causal and past reflecting. If (M, g) is achronally open, it does not admit compact or achronal future trapped sets.

Proof

Suppose that (M, g) admits an achronal or compact future trapped set. By Proposition 2.111 it admits an achronal and compact trapped set S. By Theorem 2.116 it admits a compact and achronal null araying set, a contradiction with Theorem 6.31. $\square$

Of course the non-conformally invariant formulation is

Theorem 6.33

Let (M, g) be a past reflecting spacetime which is achronally open and satisfies the null convergence condition. Suppose that it admits a future trapped surface S that does not intersect the strong causality violating set, then it is future null geodesically incomplete.

Proof

Suppose not. By Theorem 6.24 S is a future null araying set, a contradiction with Theorem 6.31. $\square$

We are now going to present Gannon’s theorem (Gannon 1975) (see also Lee 1976). He works on the interior of the Cauchy development of a partial Cauchy hypersurface N. We do not lose generality by assuming directly global hyperbolicity.

Lemma 6.34

Let N be a $C^1$ spacelike Cauchy hypersurface and let S be a connected 2-sided $C^1$ codimension one submanifold of N. Assume that (a) N is simply connected, or (b) $S=\partial _N V$ where V is an open subset of N. Then the generators of $E^+(S)$ which have initial tangents on different sides of S do not intersect.

Proof

If not there would be a closed curve $\sigma :[0,1]\rightarrow E^+(S)$ of the form $\gamma \circ \eta$. Here $\eta$ is made of two lightlike geodesics (the second with past orientation), it starts at $p\in S$ and ends at $q\in S$, while $\gamma \subset S$ connects q to p (it could be just a point if $p=q$). The flow of a timelike vector field would project it to a closed curve ${\tilde{\sigma }}:[0,1]\rightarrow N$, that intersects S just in $\gamma$ because $I^+(S)\cap E^+(S)=\emptyset$. Notice that ${\tilde{\sigma }}$ escapes S on one side and reenters it on the other side, so by pushing the curve to one side of S we can deform it to a curve ${\check{\sigma }}$ in such a way that it intersects S at just one point and transversally.

Under (a) the loop ${\check{\sigma }}$ is not trivial since under homotopies the number of intersections with S changes by even numbers, a contradiction with the simple connectedness of N. Under (b), since $S=\partial _N V$ the curve ${\check{\sigma }}$ being closed would have to intersect S at least twice (the compact set ${{\check{\sigma }}}^{-1}(N\backslash V)$ has at least two boundary points), a contradiction. $\square$

Let $E^+_+(S)$ be the union of the achronal generators starting from one side of S and let $E^+_-(S)$ be the union of the generators starting from the other side, then $E^+_+(S)\cap E^+_-(S)\subset S$. Notice that since $E^+(S)=\dot{I}^+(S)$, they are both locally Lipschitz topological manifolds with boundary S.

We recall that inner trapped surfaces are compact by definition.

Theorem 6.35

(Gannon 1975) Let (M, g) be a globally hyperbolic spacetime which satisfies the null convergence condition. Let N be a $C^1$ spacelike Cauchy hypersurface and let $V\subset N$ be an open non-simply connected set such that (i) $S=\partial _N V$ is a connected, simply connected, inner trapped surface, and (ii) $N\backslash {\bar{V}}$ is homeomorphic to $S\times R_+$. Then (M, g) is null incomplete.

Typically one applies the theorem in asymptotically flat spacetimes. Here S is chosen to be a sphere sufficiently close to infinity to become inner trapped. So, the theorem implies that asymptotically flat spacetimes with non-simply connected Cauchy surfaces develop singularities. The role of non-trivial topologies in the formation of singularities has been explored in several papers, we mention Gannon (1976), Galloway (1983a), Friedman et al. (1993), Costa e Silva (2010) and Galloway and Ling (2018).

Proof

Suppose not and let us consider the universal covering $\pi :{\tilde{M}}\rightarrow M$ endowed with the lifted metric. Then $({\tilde{M}},g)$ is still globally hyperbolic (a Cauchy hypersurface is ${\tilde{N}}=\pi ^{-1}(N)$), satisfies the null convergence condition and it is null complete. The connected components of $\pi ^{-1}(S)$ are homeomorphic to S because S is simply connected. Let ${\tilde{S}}$ be one such component, then the assumptions of Lemma 6.34-(a) are met in ${\tilde{M}}$. By the Raychaudhuri equation and null geodesic completeness, any complete lightlike geodesics issued inwardly and orthogonally from ${\tilde{S}}$ reaches a focal point to ${\tilde{S}}$ (due to Proposition 6.13 and Theorem 6.16) and hence by Theorem 6.16 it enters $I^{+}({\tilde{S}})$. This result means that no lightlike ${\tilde{S}}$-ray is issued inwardly, so denoting by ${\tilde{E}}^+_-({\tilde{S}})$ the boundary of $I^+({\tilde{S}})$ generated by the inwardly directed geodesics issued from ${\tilde{S}}$, by the same arguments used in the proofs of Theorems 2.108 and 2.112, ${\tilde{E}}^+_-({\tilde{S}})$ is a compact topological hypersurface with boundary ${\tilde{S}}$. However, let $q\in {\tilde{E}}^+_-({\tilde{S}}) \cap \pi ^{-1}(V)$, which exists because the projected generators are still lightlike geodesics directed inwardly and hence enter V. Since V is not simply connected we can find a curve starting from q and reaching some point $p\in {\tilde{S}}'$ without crossing ${\tilde{S}}$, where ${\tilde{S}}'$ is a component of $\pi ^{-1}(S)$ different from ${\tilde{S}}$, and then from here to infinity along a fiber of the cylinder ${\tilde{S}}'\times R_+$. By compactness of ${\tilde{E}}^+_-({\tilde{S}})$ the curve is going to escape this set at a point not belonging to ${\tilde{S}}$, a contradiction. $\square$

6.6.3 Hawking and Penrose’s theorem and Borde’s theorem

We have seen that Penrose’s theorem explores the consequences of the existence of a trapped set S. There the main idea is to show that $\text {edge}(E^+(S))$ is empty a fact which, under suitable causality conditions, would contradict the non-compactness of the spacelike sections of spacetime. In Hawking and Penrose’s theorem (Hawking and Penrose 1970) the causality conditions are relaxed and one is no more trying to prove $\text {edge}(E^+(S))=\emptyset$, rather the idea is to show that $E^+(S)$ causally disconnects the spacetime. By Theorem 2.68 this property implies the existence of causal lines and hence causal geodesic incompleteness whenever suitable positive energy and genericity conditions are assumed.

The important role of causal disconnection in Hawking and Penrose’s theorem was stressed by Beem et al. (1996) (see also Beem and Ehrlich 1977; Ehrlich and Easley 2004).

The following result is stated without a detailed proof in Hawking and Penrose (1970, Proof of Lemma 2.12)

Lemma 6.36

Let S be a closed and achronal set. We have

$$\begin{aligned} \tilde{D}^{+}(\dot{I}^{+}(S))&= \tilde{D}^{+}(\overline{E^{+}(S)})\cup [\dot{I}^{+}(S)\backslash \overline{E^{+}(S)}] \end{aligned}$$

(6.21)

$$\begin{aligned} H^{+}(\dot{I}^{+}(S))&=H^{+}(\overline{E^{+}(S)}) \cup [\dot{I}^{+}(S)\backslash \overline{E^{+}(S)}] \end{aligned}$$

(6.22)

$$\begin{aligned} \text {Int}\, {D}^{+}(\dot{I}^{+}(S))&= \text {Int}\, {D}^{+}(\overline{E^{+}(S)}). \end{aligned}$$

(6.23)

Proof

If $q \in \dot{I}^{+}(S)\backslash E^{+}(S)$ then by Theorem 2.56 there is a past inextendible lightlike geodesic $\sigma$ contained in $\dot{I}^{+}(S)\backslash E^{+}(S)$ ending at q. Since $\dot{I}^{+}(S)$ is achronal $\sigma$ does not intersect $I^{-}(\dot{I}^{+}(S))$. By Proposition 3.27 q is not in $D^{+}(\dot{I}^{+}(S))\backslash H^{+}(\dot{I}^{+}(S))$, that is $\dot{I}^{+}(S)\backslash E^{+}(S)\cap D^{+}(\dot{I}^{+}(S))\backslash H^{+}(\dot{I}^{+}(S))=\emptyset$. But $\dot{I}^{+}(S)\backslash E^{+}(S)\subset D^{+}(\dot{I}^{+}(S))$, thus $\dot{I}^{+}(S)\backslash E^{+}(S)\subset H^{+}(\dot{I}^{+}(S))\subset \tilde{D}^{+}(\dot{I}^{+}(S))$. Since $\overline{E^{+}(S)} \subset \dot{I}^{+}(S)$, $\tilde{D}^+(\overline{E^{+}(S)})\subset \tilde{D}^{+}(\dot{I}^{+}(S))$, thus one direction in Eq. (6.21) is proved.

Consider a point $r \in \tilde{D}^{+}(\dot{I}^{+}(S))$, the past inextendible timelike curves ending at r can all intersect $\overline{E^{+}(S)}$ in which case $r \in \tilde{D}^{+}(\overline{E^{+}(S)})$ or there is one which intersects $\dot{I}^{+}(S)\backslash \overline{E^{+}(S)} \subset \dot{I}^{+}(S)\backslash E^{+}(S)\subset H^{+}(\dot{I}^{+}(S))$, which is impossible if the intersection point is different from r because we would have $I^{-}(\tilde{D}^{+}(\dot{I}^{+}(S)))\cap H^{+}(\dot{I}^{+}(S)) \ne \emptyset$, a contradiction. We conclude $\tilde{D}^{+}(\dot{I}^{+}(S))\subset \tilde{D}^{+}(\overline{E^{+}(S)})\cup [\dot{I}^{+}(S)\backslash \overline{E^{+}(S)}]$, which concludes the proof of Eq. (6.21).

Note that $I^{-}(\dot{I}^{+}(S)\backslash \overline{E^{+}(S)})$ can not intersect $\dot{I}^{+}(S)\backslash \overline{E^{+}(S)}$ because $\dot{I}^{+}(S)$ is achronal. Also $I^{-}(\dot{I}^{+}(S)\backslash \overline{E^{+}(S)})$ cannot intersect $\tilde{D}^{+}(\overline{E^{+}(S)})$ otherwise, as $\overline{E^{+}(S)} \subset \dot{I}^{+}(S)$ there would be a timelike curve from $\dot{I}^{+}(S)$ to itself, again in contradiction with its achronality. Thus

$$\begin{aligned}&\{\tilde{D}^{+}(\overline{E^{+}(S)})\cup [\dot{I}^{+}(S)\backslash \overline{E^{+}(S)}]\}\backslash \{I^{-}(\tilde{D}^{+}(\overline{E^{+}(S)})\cup [\dot{I}^{+}(S)\backslash \overline{E^{+}(S)}])\}\\&\quad =\{ \tilde{D}^{+}(\overline{E^{+}(S)})\cup [\dot{I}^{+}(S)\backslash \overline{E^{+}(S)}]\}\backslash \{I^{-}(\tilde{D}^{+}(\overline{E^{+}(S)}))\}\\&\quad =H^{+}(\overline{E^{+}(S)}) \cup [\dot{I}^{+}(S)\backslash \overline{E^{+}(S)}]. \end{aligned}$$

In the last step we have used the fact that $I^{+}(\dot{I}^{+}(S)\backslash \overline{E^{+}(S)})\cap \tilde{D}^{+}(\overline{E^{+}(S)})=\emptyset$. Indeed a timelike curve from $\dot{I}^{+}(S)\backslash \overline{E^{+}(S)}$ to $\tilde{D}^{+}(\overline{E^{+}(S)})$, would imply, once made timelike past inextedible, that it intersects $\overline{E^{+}(S)}$, however this is impossible since it already has a point in $\dot{I}^{+}(S)\backslash \overline{E^{+}(S)}$ and $\dot{I}^{+}(S)$ is achronal. In conclusion, using Eq. (6.21)

$$\begin{aligned} H^{+}(\dot{I}^{+}(S))=H^{+}(\overline{E^{+}(S)}) \cup [\dot{I}^{+}(S)\backslash \overline{E^{+}(S)}]. \end{aligned}$$

From the previous equation

$$\begin{aligned}{}[H^{+}(\dot{I}^{+}(S))\cup \dot{I}^{+}(S)]= [H^{+}(\overline{E^{+}(S)}) \cup \overline{E^{+}(S)}]\cup [\dot{I}^{+}(S)\backslash \overline{E^{+}(S)}] \end{aligned}$$

and from Eq. (3.2) of Propositions 3.16 and 3.10,

$$\begin{aligned} \text {Int} {D}^{+}(\dot{I}^{+}(S))= \text {Int} {D}^{+}(\overline{E^{+}(S)}). \end{aligned}$$

$\square$

Lemma 6.37

If S is a closed and achronal set then $H^{+}(\overline{E^{+}(S)})$ is either (i) empty, (ii) non-compact or (iii) compact and there is $r \in H^{+}(\overline{E^{+}(S)})$ and a past inextendible timelike curve $\eta$ contained in $I^{+}(S)\cap \tilde{D}^{+}(\overline{E^{+}(S)})^{C}$ which is partially imprisoned in any compact neighborhood of r.

Proof

Assume $H^{+}(\overline{E^{+}(S)})$ is compact and non-empty. Let K be a compact neighborhood of $H^{+}(\overline{E^{+}(S)})$. Cover $H^{+}(\overline{E^{+}(S)})$ with a finite number of globally hyperbolic open neighborhoods $U_i, i=1\ldots n$ whose closures are respectively contained in globally hyperbolic open neighborhoods $V_i, i=1\ldots n$, i.e. $\bar{U}_i \subset V_i$, which in turn are contained in K. Take a point $p_1\in H^{+}(\overline{E^{+}(S)})$, we have $p_1 \in U_{i_1}$ for some $0\le i_1\le n$. Let $q_1 \in I^{+}(p_1)\cap U_{i_1}$. Clearly $q_1 \notin \tilde{D}^{+}(\overline{E^{+}(S)})$ otherwise $p_1\in I^{-}(\tilde{D}^{+}(\overline{E^{+}(S)}))$, a contradiction. Moreover, $q_1 \notin \dot{I}^{+}(S)\backslash \overline{E^{+}(S)}$ otherwise $\dot{I}^{+}(S)$ would not be achronal. As a consequence, by Lemma 6.36, $q_1 \notin \tilde{D}^{+}(\dot{I}^{+}(S))$.

As $H^{+}(\overline{E^{+}(S)})\subset \overline{E^{+}(S)}\cup I^{+}(\overline{E^{+}(S)})\subset \overline{I^{+}(S)}$ we have $q_1\in I^{+}(S)$. Since $q_1 \notin \tilde{D}^{+}(\dot{I}^{+}(S))$ there is a past inextendible timelike curve $\gamma _1$ that does not intersect $\dot{I}^{+}(S)$ (and hence $\tilde{D}^{+}(\dot{I}^{+}(S))$), and thus it is entirely contained in $I^{+}(S)$. This curve cannot be totally imprisoned in $\bar{U}_{i_1}$ due to the global hyperbolicity of $V_{i_1}$. Thus there is a point $q_1'\in \gamma _1\cap I^{+}(S)\cap U_{i_1}^{C}\cap \tilde{D}^{+}(\dot{I}^{+}(S))^{C}$. The timelike curve $\mu _1$ joining S to $q_1'$ leaves the closed set $\tilde{D}^{+}(\overline{E^{+}(S)})\subset \tilde{D}^{+}(\dot{I}^{+}(S))$ at a last point $p_2 \in \dot{\tilde{D}}^{+}(\overline{E^{+}(S)})=H^{+}(\overline{E^{+}(S)})\cup \overline{E^{+}(S)}$. We cannot have $p_2 \in \overline{E^{+}(S)}\backslash H^{+}(\overline{E^{+}(S)})$, indeed by Corollary 3.20 every causal curve issued from $p_2$ would be contained for a non-degenerate segment in $\tilde{D}^{+}(\overline{E^{+}(S)})$. Thus $p_2 \in H^{+}(\overline{E^{+}(S)})$, and there is some $i_2$ such that $p_2 \in U_{i_2}$ (here we do not claim that $i_2\ne i_1$, the important fact is that $q_1'\notin U_{i_1}$). Following $\mu _1$ after $p_2$ we can find a point $q_2 \in I^{+}(p_2)\cap U_{i_2}$ before $q_1'$. Repeating the arguments given above and continuing in this way we get a timelike curve $\eta$ which joins (past direction) $q_1$ to $q_1'$ (along $\gamma _1$), $q_1'$ to $q_2$ (along $\mu _1$), $q_2$ to $q_2'$ (along $\gamma _2$), and so on with $q_n \in U_{i_n}$ and $q'_n\notin U_{i_n}$. As a consequence, as the sets $U_i$ are finite in number, there is some $U_s$ such that $\eta$ is partially imprisoned in $\bar{U}_s$ and hence in K, which implies $\varOmega _p(\eta )\cap K\ne \emptyset$.

Consider the family of compact sets $\{\varOmega _p(\eta )\cap K\}$ where K runs over the compact neighborhoods of $H^{+}(\overline{E^{+}(S)})$. The family has the finite intersection property so it has non-empty intersection, namely $\varOmega _p(\eta )\cap H^{+}(\overline{E^{+}(S)}) \ne \emptyset$. The point r is chosen in this set. $\square$

The following result is Hawking and Ellis (1973, Lemma 8.2.1).

Lemma 6.38

If S is a closed and achronal set and if the strong causality condition holds on $\overline{J^{+}(S)}$ then $H^{+}(\overline{E^{+}(S)})$ is non-compact or empty.

Proof

Assume $H^{+}(\overline{E^{+}(S)})$ is compact and non-empty. Note that $H^{+}(\overline{E^{+}(S)})\subset \overline{J^{+}(S)}$, thus strong causality holds at $H^{+}(\overline{E^{+}(S)})$. We conclude that strong causality holds at the point r of Lemma 6.37, which is a contradiction as r admits an arbitrarily small causally convex compact neighborhood while $\eta$ is partially imprisoned in it. $\square$

Corollary 6.39

Let S be a closed and achronal set. If $\overline{E^{+}(S)}$ is compact and if the strong causality condition holds on $\overline{J^{+}(S)}$ then there is a future inextendible timelike curve issued from S and contained in $D^{+}(\overline{E^{+}(S)})$.

For an illustration of this result see Fig. 6.

Proof

By time orientability we can find a $C^1$ complete future directed timelike field $x\mapsto v(x)$ (completeness can be obtained multiplying by a function, see Godbillon 1969, Proposition 1.13, Ch. 5).

If $H^{+}(\overline{E^{+}(S)})$ is empty the claim is trivial, just follow an integral line starting from S. If not the integral lines of the field ending at $H^{+}(\overline{E^{+}(S)})$ must intersect $\overline{E^{+}(S)}$ as $H^{+}(\overline{E^{+}(S)})\subset \tilde{D}^{+}(\overline{E^{+}(S)})$. Thus we have a continuous map from $H^{+}(\overline{E^{+}(S)})$ to $\overline{E^{+}(S)}$ which would be an homeomorphism if surjective (the sets are given the induced topology). However, this is impossible because the former is non-compact while the latter is compact. Thus there is a future inextendible timelike integral curve issued from $\overline{E^{+}(S)}$ which does not intersect $H^{+}(\overline{E^{+}(S)})$ though it enters $\text {Int} D^{+}(\overline{E^{+}(S)})$ (Corollary 3.20). By achronality it cannot intersect $\overline{E^{+}(S)}$, thus it is contained in $D^{+}(\overline{E^{+}(S)})$. $\square$

We arrive at a convenient causal reformulation of Hawking and Penrose’s theorem.

Theorem 6.40

(Hawking and Penrose, conf. inv. version I) The following conditions cannot all hold on the spacetime (M, g)

• (i) (M, g) is chronological,

• (ii) (M, g) has no lightlike line and it is causally connected,

• (iii) there is an achronal or compact trapped set S.

Proof

Assume they all hold true. Since the spacetime is chronological and has no lightlike line it is strongly causal (actually stably causal, Theorem 4.106). Let us prove that S can be assumed to be closed and achronal. Assume that S is compact. By Proposition 2.100 the set $A=S\backslash I^{+}(S)$ is non-empty, compact and achronal, and moreover, $E^{+}(A)=E^{+}(S)$ is compact, thus A is a closed achronal trapped set. Thus assume S is achronal and let us prove that is can be assumed closed and achronal. Indeed, if it is not closed then $\bar{S}$ is closed and achronal, moreover by Lemma 2.104, $E^{+}(\bar{S})=E^{+}(S)$ is compact.

Thus let S be closed and achronal, we have $S \subset E^{+}(S)$, and hence $E^{+}(S)\ne \emptyset$. By Corollary 6.39 there is a future inextendible timelike curve issued from S and contained in $D^{+}(E^{+}(S))$. Extend it to the past so as to obtain an inextendible timelike curve $\gamma :\mathbb {R} \rightarrow M$. This curve intersects $E^{+}(S)$ only once because of the achronality of this set. Let $p_n=\gamma (t_n)$ with $t_n \rightarrow -\infty$, and let $q_n=\gamma (t'_n)$ with $t'_n \rightarrow +\infty$. Strong causality implies non-partial imprisonment, thus these sequences escape every compact set. We have for all n, $q_n \in D^{+}(\overline{E^{+}(S)})\cap I^{+}(S)$ and $p_n\in I^{-}(E^{+}(S))$. No point $p_n$ belongs to $I^+(S)$ because $E^+(S)$ has empty intersection with $I^+(S)$. Let us prove that the compact set $E^{+}(S)$ causally disconnects (M, g). We have only to show that every causal curve $\sigma _n$ connecting $p_n$ to $q_n$ intersects $E^{+}(S)$. Continue $\sigma _n$ below $p_n$ along $\gamma$ to obtain a past inextendible curve. Since $q_n \in \tilde{D}^{+}(\overline{E^{+}(S)})$, this curve intersects $E^{+}(S)$ and the intersection point cannot be before $p_n$ otherwise, as it has to enter $I^{+}(S)$ it would intersect $\dot{I}^{+}(S)$ twice contrary to the achronality of this set. Thus the intersection point is in $\sigma _n$ as required. $\square$

Remark 6.41

(iii) can be changed to (iii$'$): there is a closed achronal or compact set such that $\overline{E^{+}(S)}$ is compact. Indeed, as shown in the proof, points (i) and (ii) imply strong causality, thus Theorem 2.108 proves the claim for compact S. If S is closed and achronal, then as $S\subset E^+(S)\subset \overline{E^+(S)}$, S is compact and we are back to the previous case. Note that while the compactness of $E^{+}(S)$ is relaxed, one demands that S be closed. It is not possible to weaken the assumptions in both ways. Indeed, a spacetime which satisfies (i) and (ii) is strongly causal and it is therefore always possible to find a small achronal spacelike disk without edge S. For this set $\overline{E^{+}(S)}=\bar{S}$ is compact, thus (iii) could be altogether removed from the statement of the theorem, which is clearly not the case.

When we convert the statement into non-conformally invariant properties we find the same difficulty met in Remark 6.22. The null genericity condition has to be used over lightlike geodesics to promote chronology up to non-total imprisonment (and eventually strong causality) and so the property has to be assumed over totally imprisoned lightlike geodesics. We have argued that such an assumption is not physically reasonable. Therefore, it is better to assume non-total imprisonment from the start, for this assumption allows us to take advantage of Proposition 2.67. Thus a physically reasonable and mathematically more elegant variation is

Theorem 6.42

(Hawking and Penrose, conf. inv. version II) Non-totally imprisoning causally connected spacetimes do not admit achronal or compact trapped sets.

This formulation can be easily compared with the improved Penrose’s theorem 6.32. Essentially, we are changing the topological assumption from achronally open to causally connected while weakening the causality assumption from strongly causal and past reflecting (globally hyperbolic in the original formulation) to non-totally imprisoning.

By Theorem 4.106 a chronological spacetime without lightlike lines is stably causal hence non-totally imprisoning, and by Theorem 2.68 a non-totally imprisoning spacetime which does not have causal lines is causally connected, thus from version 6.42 we obtain the next interesting formulation

Theorem 6.43

(Hawking and Penrose, conf. inv. version III) Chronological spacetimes without causal lines do not admit achronal or compact trapped sets.

This version is very similar in the assumptions to our Theorem 4.106 and it is also the easiest to relate to non-conformally invariant properties, for the causal convergence condition and the causal genericity conditions together with causal geodesic completeness imply the absence of causal lines (Theorem 6.20).

We give Hawking and Penrose’s theorem in its original non-conformally invariant formulation.

Theorem 6.44

(Hawking and Penrose 1970) Let (M, g) be a chronological spacetime which satisfies the causal convergence condition and the causal genericity condition. Suppose that there exist one of the following

• (i) a compact achronal set without edge,

• (ii) a trapped surface,

• (iii) a point p such that on every past (or every future) null geodesic from p the divergence $\theta$ of the null geodesics from p becomes negative (i.e. the null geodesics start to reconverge),

then (M, g) is causally geodesically incomplete.

Proof

We have just to show that under the causal convergence and genericity conditions and causal geodesic completeness instances $(i)-(iii)$ imply the formation of a trapped set. For case (i) this follows from Corollary 2.145. For case (ii) it follows from Theorem 6.24. As for (iii), let us show that $S=\{p\}$ is itself a trapped set. To start with $\{p\}$ is future null araying set, for if there were a lightlike ray $\gamma$ starting from p, then by Theorem 6.16 $\gamma$ would not have points conjugate to p. However, the regular null hypersurface defined in a neighborhood of $\gamma$ by the exponential of the null cone at p, and generated by the ligthlike geodesics issued from p, would have negative expansion. By the Raychaudhuri equation (6.13), the null convergence condition and null geodesic completeness it would develop a focal point (Proposition 6.13 and Theorem 6.16) and hence a point conjugate to p, a contradiction. By Theorem 2.116 the future null araying set $\{p\}$ is actually a trapped set. $\square$

Remark 6.45

We have mentioned that, physically speaking, the genericity condition is not reasonable unless non-total imprisonment is assumed. Another drawback of Hawking and Penrose’s theorem is that it cannot be used as a replacement for Penrose’s, in fact it only infers the existence of a singularity, but it does not tell us if this singularity is in the future or in the past. This difficulty is due to the fact that the proof passes through the notion of line rather than through that of future ray. Evidence for a past singularity is better provided by Hawking’s theorem, to be discussed in the next section, and then, if we agree that the Universe admits a past singularity, Hawking and Penrose’s theorem does not add any information, contrary to Penrose’s.

If the set S is an acausal compact spacelike hypersurface, the proof can be considerably simplified. We give the following simple result which is a conformally invariant reformulation of Borde’s Theorem (Borde 1985)

Theorem 6.46

(Borde 1985) Let S be an acausal compact spacelike hypersurface, and suppose that (M, g) is chronological or S is such that no past lightlike ray has future endpoint at S, then (M, g) does admit causal lines.

This theorem is related to a previous theorem by Geroch (1966) who, however, assumed global hyperbolicity. The compactness assumption was subsequently weakened by Galloway (1986b), see also the following section.

Proof

Suppose not. Since S is a hypersurface it has no edge, so $H^{\pm }(S)$ have no edge. Notice that these Cauchy horizons cannot be compact otherwise the generators would be imprisoned in a compact set, and so there would be a limit lightlike line on the horizon. Let v be a global timelike vector field. As in Penrose’s theorem, if the integral lines of v that start from S reach $H^{\pm }(S)$ then the horizons are homeomorphic to S, and hence compact, which is impossible. Thus there is a future intextendible timelike curve $\mu \subset D^+(S)$ starting from S, and a past inextendible timelike curve $\gamma \subset D^-(S)$ ending at S. The tangents to $\mu$ and $\gamma$ are proportional to v. These curves cannot be partially imprisoned in a compact set, otherwise they would accumulate on a point $q\in \overline{D^\pm (S)}$, and hence on a timelike curve generated by v. From here it is easy to show that chronology would be violated in $\text {Int}(D^\pm (S))$, which is impossible.

Suppose chronology, then non-total imprisonment holds (Theorem 2.69), and so $\mu$ can be continued in the past direction escaping, at least temporarily, every compact set. From here it is immediate that S causally disconnects the spacetime, it is sufficient to take the sequence of points $p_n,q_n$, in the definition of disconnected spacetime, over $\mu$. Thus there is a causal line intersecting S, cf. Theorem 2.68, a contradiction.

Suppose there is no past lightlike ray with endpoint at S. Suppose there is $p\in \dot{J}^+(\gamma )\cap S$. By Theorem 2.56 through p there passes a past lightlike ray entirely contained in $\dot{I}^+(\gamma )$, which is impossible. Thus $S\subset I^+(\gamma )$ and hence $\mu \subset I^+(\gamma )$, so the points $p_n,q_n$, in the definition of disconnected spacetime can be taken over $\mu$ and $\gamma$ and can in fact be connected by a maximizing causal geodesic. Since S is compact the sequence accumulates on a inextendible maximizing causal curve (Theorem 2.59), hence a causal line. $\square$

One expects that the spacetime could contain a complete timelike line if the timelike genericity condition fails, and hence only under very special conditions. In fact the Lorentzian splitting theorem, the Lorentzian analogue of the Cheeger–Gromoll splitting theorem of Riemannian geometry, states (Beem et al. 1996)

Theorem 6.47

Let (M, g) be a spacetime of dimension $n>2$ which satisfies the following conditions:

• 1. (M, g) is either globally hyperbolic or timelike geodesically complete,

• 2. (M, g) satisfies the timelike convergence condition,

• 3. (M, g) contains a complete timelike line.

Then (M, g) splits isometrically as a product $(\mathbb {R}\times V, -\,\mathrm{d}t^2 \oplus h)$ where (V, h) is a complete Riemannian manifold.

This type of rigidity theorems could be used to relax the genericity conditions in Hawking and Penrose’s theorem.

6.6.4 Hawking’s theorem

We are going to prove Hawking (1966a, b) singularity theorem, see also O’Neill (1983). In its first version Hawking’s theorem included a global hyperbolicity assumption which was removed in Hawking (1967) and Hawking and Ellis (1973). Our proof stresses the roles of the causally trapped and causal araying properties, but save for that it is really similar to the original one.

First, let us present a new formulation which in our opinion best expresses the geometrical content of Hawking’s singularity theorem.

Theorem 6.48

On spacetime there is no compact partial Cauchy hypersurface S which is future causally trapped.

By Theorem 2.127 and acausality future causally trapped can be replaced by future causal araying. Notice that in Theorem 2.65 we already proved this result under non-total imprisonment.

Proof

Suppose there is such a set. Theorem 3.48 implies $D^+(S)\subset C^+(S)$, so by the compactness (hence closure) of $C^+(S)$, $\overline{D^+(S)}\subset C^+(S)$ and $H^+(S)$ is compact. By Eq. (3.6) $H^+(S)\cap S=\emptyset$. Moreover, $H^+(S)$ is non-empty, in fact suppose not and consider a future inextendible timelike curve starting from S. By Corollary 3.20 it enters $\text {Int} D^+(S)$. Since it cannot escape $D^+(S)$ it remains imprisoned in $C^+(S)$ and hence accumulates on a lightlike line contained in $\text {Int} D^+(S)$ (by the acausality of S) that accumulates on itself (Theorem 2.75), namely for every $p\in \gamma$, $p\in \varOmega _f(\gamma )$, in contradiction with the strong causality of this set (Proposition 3.44). Thus $H^+(S)\ne \emptyset$ and since the function $d(S,\cdot )$ is lower semi-continuous and positive on it (for every $q\in H^+(S)$ we can find a timelike curve connecting S to q), it has a positive minimum at some $q\in H^+(S)$. Let $\eta ^q$ be the S-maximizing curve connecting S to q. If r is a point before q on the lightlike generator passing through q, then we can reach q from S by first reaching r from the maximizing segment $\eta ^r$ connecting S to r and then by moving over the generator. Since $l(\eta ^r)=d(S,r)\ge d(S,q)=l(\eta ^q)$, this connecting curve is at least as long as $\eta ^q$ and being timelike for a segment and lightlike on another segment it can be deformed to give a timelike curve connecting S to q longer that $\eta ^q$ (Theorem 2.22), a contradiction. $\square$

Let us give the singularity theorem in its original version. Remarkably, it does not depend on causality conditions on (M, g), not even on an acausality condition on S, in fact the latter condition can be removed by passing to a covering.

Theorem 6.49

(Hawking 1966a, b, 1967) Let (M, g) be such that

• (1) the timelike convergence condition holds on M (i.e. $\mathrm {Ric} (v)\ge 0$ for all timelike vectors v),

• (2) M contains a $C^2$ compact spacelike hypersurface S (hence without edge),

• (3) S is contracting, i.e. the expansion scalar $\theta$ (i.e. the mean curvature of S, see Sect. 6.2) is negative.

Then M is future timelike geodesically incomplete.

The observed local expansion of the Universe (Hubble law), and the observed space homogeneity of the Universe (cosmological principle) support the validity of the time dual assumptions and hence the conclusion that the Universe is past timelike geodesically incomplete provided it has a compact spacelike section.

Proof

If S is not acausal one can pass to the covering spacetime $M_G$ which contains an acausal homeomorphic copy of S (Theorem 2.98). Since the other assumptions lift to the covering spacetime, and timelike geodesic incompleteness projects to the base, we can assume that S is acausal.

Suppose that (M, g) is causally complete. The conditions (1)–(3) imply, by the Raychaudhuri equation (6.5) that S is a future causal araying set (Theorem 6.16), in fact all S-maximizing curves are timelike by Proposition 2.21. However, this set cannot exist by Theorem 6.48. $\square$

Hawking’s theorem has the limitation of requiring a compact spacelike hypersurface, and hence of being applicable on just a cosmological, rather than astrophysical, context. We can obtain a more versatile theorem by using Theorem 2.65, namely

Theorem 6.50

A non-totally imprisoning spacetime does not admit compact future causal araying sets.

This result suggests to give the following definition

Definition 6.51

A future causally trapped hypersurface S is a spacelike $C^2$ submanifold, possibly with $C^2$ edge, such that $\text {edge}(S)$ is an outer trapped surface, and the mean curvature of $S\backslash \text {edge}(S)$ is negative.

For what follows it will be irrelevant if the tangent hyperplane to S becomes null at the edge.

In other words the timelike and null congruences emitted from S and its edge are converging in the future. A spacelike compact hypersurface (without edge), as appearing in Hawking’s theorem, is a special case with $\text {edge}(S)=\emptyset$. Also a trapped surface might be seen as a special degenerate case in which $S\backslash \text {edge}(S)=\emptyset$, namely as the limit of a strip whose width goes to zero.

The following result leads to predictions similar to Penrose (1965a, b) in an astrophysical context ($\text {edge} (S)\ne \emptyset$) and similar to Hawking (1966a, 1966a) in a cosmological context ($\text {edge} (S)= \emptyset$).

Theorem 6.52

Let (M, g) be a non-totally imprisoning spacetime such that

• (1) the causal convergence condition holds on M (i.e. $\mathrm {Ric} (v)\ge 0$ for all causal vectors v),

• (2) M contains a $C^2$ compact future causally trapped hypersurface S.

Then M is future causally geodesically incomplete.

Proof

It is immediate from Theorem 6.50 using already presented arguments on the focusing of causal geodesics. $\square$

A strategy to remove the compactness assumption in Hawking’s theorem was proposed by Galloway (1986b). He defines a spacelike slice as a closed set S which admits an open neighborhood U such that S is acausal and edgeless in U. He defines a spacelike slice S to be future causally complete if for every $p\in J^+(S)$, $\overline{J^-(p)}\cap S$ is compact. For example, the slices $t = \text {const}. \ne 0$ in the spacetime obtained by removing the origin from Minkowski spacetime are causally complete, although they are neither Cauchy nor compact. The slice $t = 0$ in the previous example and the hyperboloid $t = -\sqrt{1 + \sum _i x_i^2}$ in Minkowski spacetime (where $(t, x_1 \ldots , x_n)$ are canonical coordinates) are examples of slices which are not causally complete.

Galloway (1986b) shows that assumption (2) of Hawking’s Theorem 6.49 can be weakened to: S is a $C^2$ future causally complete spacelike slice. This result is based on the following lemma which is interesting in its own right.

Lemma 6.53

Let S be an acausal spacelike hypersurface, and let $p\in H^+(S)$ be such that $\overline{J^-(p)}\cap S$ is compact, then there exists a future inextendible timelike S-ray $\gamma \subset D^+(S)\cap I^-(p)$.

Notice that in Galloway’s result S is still without edge so his singularity result applies mostly to cosmological frameworks. It is not meant as an improvement of Penrose’s. One should also take into account that the condition of future causal completeness is not localized to S but rather depends on the future development of spacetime. It might be difficult to justify such assumptions on physical grounds.

7 Conclusions and outlook

The mathematical reader coming from analysis might likely look at the spacetime manifold as the outcome of an initial value problem, where the dynamical equations are deduced from Einstein’s and the initial condition and constraints are placed over a 3-manifold S, to be a posteriori interpreted as a Cauchy hypersuface. Unfortunately, from this perspective the spacetime would be identified with the Cauchy development D(S), hence it would be globally hyperbolic.

Under the assumption of global hyperbolicity the results of causality theory simplify considerably and become rather elementary, if not uninteresting. Even if one believes that the spacetime is globally hyperbolic (strong cosmic censorship) causality theory should be used to consider the alternatives and to prove that it is indeed so. Also the mathematician can use causality theory as a tool to obtain global differential geometric results under much weaker conditions than global hyperbolicity.

To the physically minded reader causality theory has a more important role. Physical considerations suggest that the spacetime could be non-globally hyperbolic after all. The black hole evaporation process is a rather robust prediction of general relativity coupled with quantum field theory on a curved background. The spacetime of an evaporating black hole can hardly be represented by a globally hyperbolic manifold, in fact there are indications that even if the singularity were not naked, causal continuity would be violated (Kodama 1979; Wald 1984a; Lesourd 2019). As a consequence, Einstein’s equations alone cannot determine the evolution of the spacetime manifold.

This fact does not mean that the spacetime is not described by a Lorentzian manifold or that causality theory loses its value. It is rather the initial value approach that shows its limitation. Causality theory preserves its predictive power since, as we have previously emphasized, it only relies on energy inequalities that are derived from Einstein’s equations and that are expected to hold even in a quantum field theoretical setting. After all causality theory has something to say whenever the propagation of information is limited by a distribution of cones over M.

The smooth description of matter to be found in theories such as continuum mechanics is known to be just an approximation, an emergent description, hiding the more fundamental atomic description of matter. Similarly, many physicists believe the concept of smooth manifold might prove to be inadequate to describe the spacetime continuum. Still physicists would be less prepared to abandon any notion of causality. For instance, theories exist (e.g. Causal Set Theory) in which the spacetime continuum is replaced by an oriented graph, where the orientation plays the role of causality.

The study of causality theory in a classical Lorentzian setting might help to identify the causality concepts that are indeed of more fundamental importance, and that could be preserved at a more fundamental scale. In this review we have explored and organized many causality concepts that have been introduced in the last decades. Our study reveals, for instance, that the Seifert relation $J_S$ is more natural than all the other relations. One could expect that parents to this causality relation should be found in a more accurate and fundamental spacetime theory. Of course, this is just the author’s opinion, other researchers might well disagree. Similarly, the stable distance might play a fundamental role, e.g. in a unification approach à la Connes.

In order to identify similar fundamental concepts one can weaken the differentiability assumptions of mathematical relativity and look for concepts that better help to structure the development of the theory. This recent program, pursed by a number of young researchers, is under development and involves elements from the mathematics of partially ordered spaces, cone structures, length spaces, Alexandrov geometry, metric measure spaces, and optimal transport (Minguzzi 2015b; Kunzinger et al. 2014a, b, 2015a, b; Graf et al. 2018; Graf and Ling 2018; Fathi and Siconolfi 2012; Fathi 2015; Chruściel and Grant 2012; Sbierski 2018; Galloway et al. 2018; Galloway and Ling 2017; Sämann 2016; Kunzinger and Sämann 2018; McCann 2018; Bernard and Suhr 2018a; Mondino and Suhr 2018). It can also be the case that at the more fundamental level the light cones are no longer round (Lorentzian). Here causality theory can also be developed leading to the theory of rough Lorentz–Finsler spaces (Minguzzi 2015b, c, 2019).