Abstract
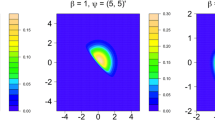
The characteristics of a feature vector in the transform domain of a perturbation model differ significantly from those of its corresponding feature vector in the input domain. These differences—caused by the perturbation techniques used for the transformation of feature patterns—degrade the performance of machine learning techniques in the transform domain. In this paper, we proposed a semi-parametric perturbation model that transforms the input feature patterns to a set of elliptical patterns and studied the performance degradation issues associated with random forest classification technique using both the input and transform domain features. Compared with the linear transformation such as principal component analysis (PCA), the proposed method requires less statistical assumptions and is highly suitable for the applications such as data privacy and security due to the difficulty of inverting the elliptical patterns from the transform domain to the input domain. In addition, we adopted a flexible block-wise dimensionality reduction step in the proposed method to accommodate the possible high-dimensional data in modern applications. We evaluated the empirical performance of the proposed method on a network intrusion data set and a biological data set, and compared the results with PCA in terms of classification performance and data privacy protection (measured by the blind source separation attack and signal interference ratio). Both results confirmed the superior performance of the proposed elliptical transformation.


Similar content being viewed by others
References
Aghion, P., Bloom, N., Blundell, R., Griffith, R., Howitt, P.: Competition and innovation: an inverted-u relationship. Q. J. Econ. 120(2), 701–728 (2005)
Boscolo, R., Pan, H., Roychowdhury, V.P.: Independent component analysis based on nonparametric density estimation. IEEE Trans. Neural Netw. 15(1), 55–65 (2004)
Breiman, L.: Bagging predictors. Mach. Learn. 24(2), 123–140 (1996)
Breiman, L.: Random forests. Mach. Learn. 45(1), 5–32 (2001)
Bruce, P., Bruce, A.: Practical Statistics for Data Scientists: 50 Essential Concepts. O’Reilly Media, Inc., Sebastopol (2017)
Caiafa, C.F., Proto, A.N.: A non-gaussianity measure for blind source separation. In: Proceedings of SPARS05 (2005)
Chaudhary, A., Kolhe, S., Kamal, R.: A hybrid ensemble for classification in multiclass datasets: an application to oilseed disease dataset. Comput. Electron. Agric. 124, 65–72 (2016)
Chaudhuri, K., Monteleoni, C., Sarwate, A.D.: Differentially private empirical risk minimization. J. Mach. Learn. Res. 12(Mar), 1069–1109 (2011)
Du, K.L., Swamy, M.: Principal component analysis. In: Neural Networks and Statistical Learning, pp. 355–405. Springer, London (2014)
Fan, J., Li, R.: Variable selection via nonconcave penalized likelihood and its oracle properties. J. Am. Stat. Assoc. 96, 1348–1360 (2001)
Fienberg, S.E., Steele, R.J.: Disclosure limitation using perturbation and related methods for categorical data. J. Off. Stat. 14(4), 485–502 (1998)
Gaber, M.M., Zaslavsky, A., Krishnaswamy, S.: Mining data streams: a review. SIGMOD Rec. 34(2), 18–26 (2005). https://doi.org/10.1145/1083784.1083789
Geiger, B.C.: Information loss in deterministic systems. Ph. D. Thesis, Graz University of Technology, Graz, Austria (2014)
Hung, C.C., Liu, H.C., Lin, C.C., Lee, B.O.: Development and validation of the simulation-based learning evaluation scale. Nurse Educ. Today 40, 72–77 (2016)
Jeyakumar, V., Li, G., Suthaharan, S.: Support vector machine classifiers with uncertain knowledge sets via robust optimization. Optimization 63(7), 1099–1116 (2014)
Jin, S., Yeung, D.S., Wang, X.: Network intrusion detection in covariance feature space. Pattern Recogn. 40(8), 2185–2197 (2007
Jolliffe, I.T., Cadima, J.: Principal component analysis: a review and recent developments. Philos. Trans. R. Soc. A 374(2065), 20150202 (2016)
Jones, D.G., Beston, B.R., Murphy, K.M.: Novel application of principal component analysis to understanding visual cortical development. BMC Neurosci. 8(S2), P188 (2007)
Lasko, T.A., Vinterbo, S.A.: Spectral anonymization of data. IEEE Trans. Knowl. Data Eng. 22(3), 437–446 (2010)
Lee, S., Habeck, C., Razlighi, Q., Salthouse, T., Stern, Y.: Selective association between cortical thickness and reference abilities in normal aging. NeuroImage 142, 293–300 (2016)
Lichman, M.: UCI machine learning repository (2013). http://archive.ics.uci.edu/ml. Accessed 1 Nov 2017
Little, R.J.: Statistical analysis of masked data. J. Off. Stat. 9(2), 407–426 (1993)
Liu, K., Giannella, C., Kargupta, H.: A survey of attack techniques on privacy-preserving data perturbation methods. In: Aggarwal, C.C., Yu, P.S. (eds.) Privacy-Preserving Data Mining, pp. 359–381. Springer, US (2008)
Muralidhar, K., Sarathy, R.: A theoretical basis for perturbation methods. Stat. Comput. 13(4), 329–335 (2003)
Murthy, S.K.: Automatic construction of decision trees from data: a multi-disciplinary survey. Data Min. Knowl. Discov. 2(4), 345–389 (1998)
Oliveira, S.R., Zaïane, O.R.: Achieving privacy preservation when sharing data for clustering. In: Jonker, W., Petković, M. (eds.) Workshop on Secure Data Management, pp. 67–82. Springer, Berlin Heidelberg (2004)
Qian, Y., Xie, H.: Drive more effective data-based innovations: enhancing the utility of secure databases. Manag. Sci. 61(3), 520–541 (2015)
Rubens, N., Elahi, M., Sugiyama, M., Kaplan, D.: Recommender systems handbook. In: Ricci, F., Rokach, L., Shapira B. (eds.) Active Learning in Recommender Systems, pp. 809–846. Springer, Boston (2016)
Sørensen, M., De Lathauwer, L.: Blind signal separation via tensor decomposition with Vandermonde factor: canonical polyadic decomposition. IEEE Trans. Signal Process. 61(22), 5507–5519 (2013)
Suthaharan, S.: Machine Learning Models and Algorithms for Big Data Classification: Thinking with Examples for Effective Learning, vol. 36. Springer, New York (2015)
Suthaharan, S.: Support vector machine. In: Machine Learning Models and Algorithms for Big Data Classification, pp. 207–235. Springer, US (2016)
Suthaharan, S., Panchagnula, T.: Relevance feature selection with data cleaning for intrusion detection system. In: Southeastcon, 2012 Proceedings of IEEE, pp. 1–6. IEEE (2012)
Thrun, S., Pratt, L.: Learning to Learn. Springer, New York (2012)
Whitworth, J., Suthaharan, S.: Security problems and challenges in a machine learning-based hybrid big data processing network systems. ACM SIGMETRICS Perform. Eval. Rev. 41(4), 82–85 (2014)
Zarzoso, V., Nandi, A.: Blind source separation. In: Nandi, A. (ed.) Blind Estimation Using Higher-Order Statistics, pp. 167–252. Springer, US (1999)
Zumel, N., Mount, J., Porzak, J.: Practical data science with R, 1st edn. Manning, Shelter Island (2014)
Acknowledgements
This research of the first author was partially supported by the Department of Statistics, University of California at Irvine, and by the University of North Carolina at Greensboro. This material was based upon work partially supported by the National Science Foundation under Grant DMS-1638521 to the Statistical and Applied Mathematical Sciences Institute. Any opinions, findings, and conclusions or recommendations expressed in this material are those of the author(s) and do not necessarily reflect the views of the National Science Foundation. Shen’s research is partially supported by Simons Foundation Award 512620. The authors thank the Editor, the Associate Editor, and the referees for their valuable comments.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Suthaharan, S., Shen, W. Elliptical modeling and pattern analysis for perturbation models and classification. Int J Data Sci Anal 7, 103–113 (2019). https://doi.org/10.1007/s41060-018-0117-y
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s41060-018-0117-y