Describing environmental phenomena variation using entropy theory

Abstract

We propose a novel approach for calculating an air temperature entropy of environment over a region using concepts from statistical mechanics. The proposed method is intended for use in analysing spatially distributed environmental data. Spatially distributed environmental time-series temperature data from an atmospheric model have been used to illustrate this approach. Our results show that entropy reveals the underlying structure of a data distribution for which a standard statistical analysis may be insufficient.

1 Introduction

Entropy has been a subject of study within the research community since its inception in the 1850s by Rudolf Clausius [1], who coined the term entropy when he was analysing the Carnot cycle process. The concept of entropy from classical thermodynamics was further developed by Boltzmann [2] who, in the 1870s, introduced a probabilistic definition based on microstates of a system. Since then there has been further development of the concept by Planck [3] and Gibbs [4], ultimately leading to the development of statistical mechanics. The entropy measure signifies changes in the microstates of a system and the distribution of entities therein. Entropy has been used in various areas of research, such as thermodynamics, cosmology (i.e. entropy of black holes [5]), information theory (i.e. Shannon entropy [6]) and in environmental science [7,8,9,10].

The statistical mechanics formalism explains the macroscopic thermodynamic behaviour of a bulk system by treating the system as an assembly of microscopic interactions. This enables the aggregate behaviour of large numbers of molecules to be predicted using statistical concepts, such as entropy. Shipley et al. [7] adopted a similar approach to predict the ways in which biodiversity varies within ecological communities, based on the particular traits of the plant species within these communities. They regarded individual species-to-species interactions as random events and so were able to predict aggregate behaviour leading to various biodiversity outcomes using statistical mechanics concepts. Such techniques become necessary, and feasible, when the number of species interactions is very large, as is the case in most plant-based communities. Ruddell and Kumar [9] adopted an information-theoretical statistical method called “transfer entropy” for measuring the information flow between ecohydrological variables using time-series data. Considering that ecohydrological systems are too complex for specific variable-to-variable interactions to be represented individually, these authors used statistical concepts, including entropy, to study the aggregate behaviour of these systems. We have extended the application of the concept of entropy by applying it to environmental air temperature data coming from microsensors and observe correlation with environmental phenomena, such as high wind speed, heavy rainfall.

In any application, many particles (or entities) are required in order to estimate entropy. An ideal system would contain a large number of tiny sensors distributed within an environmental sensing domain providing real-time spatio-temporal distributed environmental data. Over recent years technology has evolved rapidly, with enormous advances in electronics enabling the development of miniature sensing devices [11] to collect environmental data—thereby creating the opportunity to utilize these devices in the environmental research, and for many environmental applications, a large number of these sensors are needed.

Environmental parameters, for example temperature, are measured over time at a weather station providing data for that location. Although this way of collecting data provides information on the distribution of temperature over time, it does not necessarily provide a good knowledge of its distribution over space. A spatial distribution of the data could help us to understand variation in a specific environmental variable over a given region. Therefore, our primary motivation is to understand more fundamental aspects of the environment using temporal and spatially distributed data. In particular, we wish to understand and calculate air temperature Shannon entropy of the environment and infer its meaning.

A statistical analysis provides an overall picture of a distribution. The mean value provides a central expected value, and the standard deviation indicates how widely a series of data is distributed from its mean value. Nevertheless, analysing the data distribution, for example exploring the different states in the distribution that contain all of the data, requires the use of statistical mechanics. The formalism to calculate entropy using statistical mechanics provides an internal picture of the data distribution at different states, $\eta _i$ in Eq. (1), upon which an entropy is calculated.

In this paper, we present a methodology, using statistical mechanics which deals with a system of many particles, to calculate an air temperature Shannon entropy of the environment from a spatio-temporal distributed temperature data set. In presenting the results, we show how the data are distributed in two different systems, one with high and one with low Shannon entropy. As large numbers of microsensors are not available yet, we use output from an atmospheric model (the South Esk Hydrological model [12]) to develop the methodology.

Therefore, the major theoretical contribution in terms of statistics emerging from this work is the possibility to parameterize the degree of order of any distribution (not only a normal distribution, which is already well described by mean and standard deviation). While these classical metrics of central tendency and dispersion of data represent a number of natural phenomena effectively, it is still not enough to depict the degree of order of any given assembly of data. Data Science could benefit from this approach as it employs the entire formalism from statistical mechanics, which is considered to be one of the most elegant and powerful theoretical frameworks to describe large numbers of particles in a given system. Entropy describes the degree of (dis)order of a system, and many other thermodynamic states (e.g. enthalpy, internal energy) and constants (e.g. heat capacitance) could provide additional insights into large data assets and constitute a powerful tool in data science. The novelty of our contribution is that we use the concept of entropy to reveal the structure of a data distribution, in circumstances where standard statistical methods are insufficient.

2 Entropy in statistical mechanics and information systems

The Boltzmann equation for entropy is written as $S=k \ln {\mathcal {M}}$, where k is the Boltzmann constant and $\mathcal {M}$ is the number of microstates [13, 14]. $\mathcal {M}$ is defined by

$$\begin{aligned} {\mathcal {M}}&= \frac{N!}{(\eta _{a}!)(\eta _{b}!)(\eta _{c}!)\cdots }\nonumber \\&=\frac{N!}{\prod _{i} \eta _{i}!}, \end{aligned}$$

(1)

where N is the total number of particles of the systems and $\eta _i$ is the number of particles at energy state i. The number of particles $\eta _i$ at an energy state i corresponds to the Boltzmann distribution law

$$\begin{aligned} \eta _i = \eta _0 e^{-\beta \epsilon _i}, \end{aligned}$$

(2)

where $\epsilon _i$ is the energy of the state i ($\epsilon _0< \epsilon _1<\cdots <\epsilon _n$) and $N=\sum _i\eta _i$. Using Eq. (1) and Stirling’s approximation ($\ln N! = N\ln N-N$), the entropy S can be written as

$$\begin{aligned} S=k\ln {\mathcal {M}} = k\left( N\ln N - \sum _i \eta _i \ln \eta _i\right) . \end{aligned}$$

(3)

The inclusion of the Boltzmann constant k produces an exact coincidence between the statistical entropy and the classical thermodynamic entropy, i.e. $kd\ln {\mathcal {M}}= \frac{dE}{T}$, where $\beta =\frac{1}{kT}$  [13].

As our environmental system does not consider individual atoms or molecules (in a physical system a gas constant and the Avogadro constant lead to the value of the Boltzmann constant), we may set $k=1$ for simplicity and hence, we obtain

$$\begin{aligned} S=N\ln N - \sum _i \eta _i \ln \eta _i. \end{aligned}$$

(4)

If we define the probability of particles being in the ith state as $p_i=\frac{\eta _i}{N}$, then the statistical entropy S can be presented in terms of Shannon’s information entropy ($-\sum _i p_i\ln p_i$)

$$\begin{aligned} \ln {\mathcal {M}}= & {} N\ln (N)-\sum _i\eta _i\ln \eta _i \nonumber \\ \frac{\ln {\mathcal {M}}}{N}= & {} -\sum _i p_i\ln p_i. \end{aligned}$$

(5)

Redefining $S \equiv \frac{\ln {\mathcal {M}}}{N}$ provides the Shannon entropy $S= -\sum _i p_i\ln p_i$. The Shannon entropy tells us about the disorderedness of the temperature distribution in the given environment. We perform our calculations for the Shannon entropy S. As for the discrete energy levels discussed above, the temperature scale of our environmental system is made discrete by considering level width constrained by the precision limit of a temperature measuring sensor, as discussed in the next section.

3 Data sets

3.1 Atmospheric modelling data set

This first data set was used extensively to develop and test the proposed methodology for the research that is the CSIRO 9-level atmospheric general circulation model [12, 15, 16]. The model was applied to a region covering the South Esk catchment [12] of Tasmania, Australia, extending from 42.0 to $41.0^{\circ }\mathrm{S}$ latitude and 147.0 to $148.5^{\circ }\mathrm{E}$ longitude. Each degree of latitude and longitude is divided into 100 units providing a grid size of $101\times 151$ grid cells. This means that the data set contains 15,251 data points per unit time (hourly). In each run of the model, the data are generated on an hourly basis starting at 00:00 A.M. at night and finishing after 3 days at 00:00 A.M. at night providing a total of 73 time slices per run. The data used in this work extended from January to December 2013. The minimum temperature value of our whole data set is $-7.42\,^{\circ }\mathrm{C}$, and maximum value is $33.76\,^{\circ }\mathrm{C}$. The data are freely available in [17].

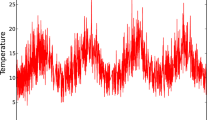
In Fig. 1, the average temperature for the South Esk region is presented, together with the standard deviation $\sigma$, on an hourly basis. A set of values for the uncertainty of temperature sensors are considered to be from 0.10 to $1.0\,^{\circ }\mathrm{C}$ with a step size of $0.10\,^{\circ }\mathrm{C}$. The quantization of the temperature readings, based on the uncertainty related to equipment accuracy, is considered to be an analogous concept to the size of the energy gaps in quantum systems, for the purpose of the entropy calculations.

3.2 Hydrodynamic modelling data set

This second data set was used to demonstrate the robustness of the proposed methodology. In this case, the data have been generated by the CSIRO Sparse Hydrodynamic Ocean Code (SHOC) model applied to the south-east coastal region of Tasmania, Australia, extending from approximately $42.6^{\circ }\hbox {S}$ to approximately $43.6^{\circ }\hbox {S}$ latitude and from approximately $147^{\circ }\hbox {E}$ to approximately $148.0^{\circ }\hbox {E}$ longitude. The model has a grid size of $132 \times 233$ grid cells and 10 depth layers and so contains 307,560 data points per unit time (hour). The data have been generated hourly, from 01 October 2015 to 30 October 2016, providing a total of 720 time slices per run. This data set is accessible online via the CSIRO Data Access Portal (http://data.csiro.au) [18].

Fig. 1

Hourly average temperature for each time slice over spatially distributed temperature data from the South Esk Hydrological model for the entire region of South Esk Catchment of Tasmania

Fig. 2

The structure of the temperature distributions at different levels for high entropy (top) and low entropy (bottom). The harmonic oscillator potential-type function is adopted to represent the data at different levels, where the level width for the figure corresponds to $\triangle T = 0.20\,^{\circ }{\hbox {C}}$. In the inset, the distribution of temperature over the South Esk Catchment area is presented using a colour scale to represent the temperature

4 From uncertainties to states

To calculate an air temperature Shannon entropy from our environmental data set, we need to divide the data set into discrete subsets representing the different states i referred to the Eqs. (1) and (2). An approach to do this is to consider the data distribution for each time slice at intervals of $\triangle T= 0.10,\,0.20,\ldots ,1.0\,^{\circ }\mathrm{C}$, which are assumed to be the different precisions of the instrument or sensor measuring the temperature. Considering different widths for the discretization provides us with an opportunity to test how the discretization affects the Shannon entropy.

The environmental data set currently of interest is the data from the South Esk Hydrological model from the year 2013. The temperature frequencies are calculated for each time slice, and a sample of frequency distributions is shown in Fig. 2. Each bin with a width of $\triangle T$ is considered analogous to the concept of a state in quantum systems, with the number of entities in a state corresponding to a count of frequency in that state or bin. However, as evident, the distributions of particle-equivalent quantities over states are nonuniform. Nevertheless, from the distributions of a “number of particles-equivalent” quantity residing in each state, the number of microstates may be calculated. It is noted that the number of temperature values in each state is analogous to the number of particles in a quantum mechanical system.

Below we describe the process of creating equivalent states and calculating entropy:

• Consider the data distribution for each time slice at intervals of $\triangle T= 0.10,0.20,\ldots ,1.0\,^{\circ }\mathrm{C}$;

• The temperature frequencies are calculated for each time slice;

• Each bin with a width of $\triangle T$ is considered to be equivalent to a state with the frequency corresponding to the number of particles in that state;

• Count the “number of particles-equivalent” quantity residing in each state;

• Calculate the number of microstates and entropy using Eqs. 1 and 4, respectively.

The top part of Fig. 2 corresponds to a state with high entropy, while the bottom represents a low entropy state. The harmonic oscillator potential function is adopted just to represent the distributions of data in different states. The gaps ($\triangle T$) are presented in the harmonic oscillator shapes, where the discrete levels are shown by the horizontal lines and the particles are occupied in the levels. A significant difference in the data distributions in high and low entropy cases is evident, where the data in the high entropy case are more sparse than that in the low entropy case.

5 Results

In Fig. 3, the air temperature entropy has been presented for the South Esk Hydrological model data over 1 year. A large variation is evident as is observed in the temperature data shown in Fig. 1. The maximum entropy change appears to be $\sim$30%. This entropy variation may have some correlation with other environmental parameters, such as relative humidity, wind speed. In particular, the relative humidity changes by 40% in this time period. Overall the entropy variations are smaller in the winter (June–August) than in the other seasons of the year. It is noted that there are some time-series data missing in the South Esk Hydrological model resulting in the presence of gaps in the entropy calculations in Fig. 3. In Fig. 4, the correlation of entropy with the standard deviation of temperature is presented for $\triangle T=0.10\,^{\circ }\mathrm{C}$. A significant correlation of entropy with standard deviation is observed as would be expected (the correlation coefficient = 0.90). The width of the entropy fluctuation may be due to the bin-edge effect, and therefore for a better estimation of entropy change with $\sigma$ we perform a theoretical fit to the entropy. The variation of entropy with $\sigma$ is fitted with a function $F(\sigma )=a+b\times \log (\sigma )$, and the fit is presented with a red solid line. The entropy change is more sensitive at small temperature variation, i.e. the rate of entropy change is higher for small $\sigma$ values ($\sigma <3.0$) and the sensitivity decreases for higher values of $\sigma$. While the standard deviation is useful to understand the spread of the distributions around mean, the entropy may be more useful to understand the system’s change of internal structure over time. In Fig. 5, the fits with $F(\sigma )$ for different values of $\triangle T$ are presented and the fit parameters are given in Table 1. The parameter a presents the value of $F(\sigma )$ at $\sigma =1$, and b governs the curvature of the function $F(\sigma )$.

Fig. 3

Calculated Shannon entropy plotted against time of the year for $\triangle T=0.10\,^{\circ }\mathrm{C}$. The entropy is calculated on an hourly basis over the entire South Esk Catchment area

Fig. 4

Calculated entropy plotted against the standard deviation of temperature, with a correlation coefficient $r= 0.90$. The solid line presents the fit to the data with a fit function $F(\sigma ) = a + b\times \log (\sigma )$

If a set of data points $D_i, i=1,\ldots , n$ are discrete in ${\mathbb {R}}^{n}$, or a continuous set of values can be discretized as m discrete states, then the entropy is bounded to be $0\le S \le N\log {m}$ (see also [9]). A fine banding of the states or a large value of m can capture more accurate entropy variations of the microstates, and only sensors with higher precisions can provide data for this variation to be manifested. In Table 1 and Fig. 6, the value of parameter b is 0.45% for $\triangle T$ values from 0.10 to $0.40\,^{\circ }$C and 2.5% for $\triangle T$ values up to $1.0\,^{\circ }$C indicating the importance of fine banding or fine $\triangle T$ values. Our observation is also consistent with the investigation in Ref. [9] in observing that mutual information and transfer entropy plateaus appear at finer banding.

Fig. 5

Fits to the entropy variation with standard deviation of temperature are shown for the various $\triangle T$ values considered in the analysis. The fit parameters are given in Table 1

In Table 1 and Fig. 6, the value of parameter b is only $0.23\%$ when we consider $\triangle T$ values from 0.10 to $0.30\,^{\circ } \mathrm{C}$, and it is $2\%$ for $\triangle T$ values up to $1.0\,^{\circ } \mathrm{C}$ indicating the importance of finer banding or finer $\triangle T$ values. The overall consistency of the parameters within 2% suggests the methodology is robust in extracting qualitative features of the underlying systems.

Table 1 Fit parameters a and b of the fit equation $F(\sigma ) = a + b\times \log (\sigma )$ for the $\triangle T$ values considered in the analysis

In Fig. 7, average temperature and entropy are presented for the four seasons. The day-to-day hourly results are averaged over a season, i.e. mean entropy at 1:00 A.M., 2:00 $\hbox {A.M.}, \ldots$, over the season, and standard deviations are calculated and presented using a 24-h clock. A sinusoidal variation in temperature over 24 h is expected with the maximum values being reached during the day. On the other hand, the pattern of hourly entropy changes and their variations differs significantly for the various seasons, in contrast to the temperature changes, where the pattern is similar for all four seasons.

Fig. 6

Fit parameter b plotted against $\triangle T$ ($^{\circ }{C}$). A decrease in the parameter b with increasing $\triangle T$ is evident. An overall variation of only $2\%$ of parameter b signifies the stability of the rate of entropy variation with $\sigma$

In Fig. 8, coefficients of variation of entropy are presented on an hourly basis for the four seasons. A significant dispersion of entropy is evident over a 24-h time period, where the dispersions are high in summer and lower in winter. Also, the four seasons entropy dispersions are quite different at midnight, where the four curves exhibit a spread in coefficient of variation over a factor of four. However, all four curves converge in the afternoon indicating that the environmental system is more stable during the afternoon period. The results for all the $\triangle T$ values are consistent and qualitatively very similar. In Fig. 8, it is evident that the variations in dispersion are very similar for $\triangle T=0.10$, 0.50 and $1.0\,^{\circ }\mathrm{C}$.

Fig. 7

The seasonal average hourly temperature variation is presented in the left column, while the seasonal average hourly entropy variation is shown in the right column for $\triangle T=0.20\,^{\circ }\mathrm{C}$

Fig. 8

An hourly calculated coefficient of variation of entropy plotted for the four seasons, for $\triangle T=0.10^{\circ }\mathrm{C}$ (top), $0.50^{\circ }\mathrm{C}$ (middle) and $1.0^{\circ }\mathrm{C}$ (bottom)

6 Discussion

Figure 2 (bottom) presents a normal temperature data distribution which appears in our calculation as a low entropy phenomenon. On the other hand the top figure shows a completely different temperature distribution corresponding to a high entropy phenomenon. These phenomena exist for all the $\triangle T$ values considered in the analysis. This presents an interesting phenomenon in which at low entropy the system converges to a particular distribution, such as normal in this case, which is in accord with the physical principle that at absolute zero temperature (ideally), the system collapses to a single state with zero variance providing an entropy of zero.

Another observation from Fig. 2 is that since the low entropy phenomenon appears to be a normal-type distribution, it provides an explicit mean and variance and the low entropy manifestation is simple as expected. On the other hand, the high entropy phenomenon is quite complex as the distribution is more sparse and the distribution may correspond to a superposition of several normal distributions. In this case a deconvolution can provide means and variances corresponding to each of the normal distributions for a high entropy phenomenon. The Shannon entropy, therefore, exhibits a more straightforward visual connection between the data characteristics and the entropy.

The change in average entropy appears to be more stable (Fig. 3), over the year considered in this analysis than the variation in temperature (Fig. 1) where the average temperature decreases significantly in the winter season than summer. This indicates that, in addition to the temperature variation, other environmental parameters might also be playing a crucial role in entropy change, compensating for some effects of temperature, thus keeping the average entropy more consistent over time. The entropy changes at some times are sharper than at adjacent times, and these changes are fluctuating on a day-to-day basis, with a larger value of entropy occurring during the daytime (Fig. 7).

It is also interesting to observe reduced entropy variations in the winter season (May–August 2013) which illustrates the crucial role that temperature plays in entropy variation, as would be expected. In addition to the effect of temperature on entropy, therefore, it will be interesting to observe how other environmental parameters, such as relative humidity, wind speed and solar radiation, affect the entropy variation.

Since the difference between maximum and minimum temperatures in summer is larger, the number of populated microstates changes significantly in this season and as a result the fluctuations of entropy increase as well as the errors (Fig. 7). Also, as the season progresses towards winter, the entropy fluctuations settle down with reduced standard deviation. The time for the smallest value of entropy during the day changes from season to season. In summer the smallest value appears at around 6:00 A.M., and in autumn, it is at 11:00 A.M., in winter at 12:00 P.M. and in spring at 8:00 A.M. The smallest values correspond to the lowest number of microstates at these times which in turn correspond to large numbers of particles clustering at particular states.

In Fig. 9, the results of temperature distributions at two different date times are presented. The distributions provide the same mean temperature ($\mu _T$) and standard deviation ($\sigma _T$), but the entropies are different. This is an interesting result in that, while the mean value and standard deviation are unable to indicate the structure of the data, the entropy can be used to extract and understand the underlying structure of the data distribution. Our results show that an entropy difference of 0.18 is sufficient to manifest two completely different data distributions.

Fig. 9

Results of temperature distributions with the same mean temperatures ($\mu _T$) and standard deviation ($\sigma _T$), but different entropy (S) values. The top figure corresponds to a distribution with the value of entropy equal to 4.20, whereas the bottom figure corresponds to an entropy value of 4.38

Fig. 10

Frequency distribution of hourly percentile change of entropy. A change of greater than ±4% is considered to be significant

Fig. 11

Results of salinity distributions with the same mean and standard deviation (top row) and temperature distributions with the same mean and standard deviation (bottom row), but different entropy (S) values

We also applied the proposed methodology to a data set from another domain (Sect. 3.2) for the purpose of demonstrating the robustness of the methodology. In this case, the data set consisted of water and salinity data derived from a hydrodynamic model of a coastal ocean region off the south-east coast of Tasmania and the results of this analysis are presented in Fig. 11.

Both the salinity and temperature distributions exhibited similar features to those exhibited by air temperature data (Fig. 9). While the mean and standard deviation of the two distributions were the same, the entropy values were different, providing potential insights into the differences between two distributions. The entropy value is also highly sensitive to the shape of the distribution. For example, in the case of salinity, an entropy value change of just 6% corresponds to a significant change in the distribution. These analyses demonstrate the robustness of the formalism and methodology that we have developed.

7 Interpretation

The most interesting result is the change of entropy as a $\log$ function of the standard deviation of temperature $\sigma$ (Fig. 5), i.e. the rate of change of entropy becomes smaller with respect to $\sigma$ at large $\triangle T$ values. The value of entropy corresponds to the distribution of energy (heat energy, wind energy, solar radiation, relative humidity) in the environmental system and will be greater than unity if there is a variation of energy fluctuation in the system. If the value of entropy is unity, then that implies that the environmental energy is in a perfectly stable state; in other words, no energy fluctuations exist and the energy values are the same everywhere.

As our system is based on temperature, any entropy value greater than unity means there is an inhomogeneous distribution of energy in the system and thereby in the distribution of different temperature values in the region of interest. A higher variation of energy leads to a higher distribution of entities, for example temperature, subsequently providing a higher entropy value. This higher variation of energy can be considered analogous to an information signal transfer with higher bandwidth, as represented by the concept of Shannon entropy used in the analysis of communication systems. In Fig. 10, a frequency distribution of the hourly percentile change of entropy is presented. This frequency distribution is quite interesting in that it exhibits a feature similar to the Gaussian distribution, where the tail of the distribution presents a larger percentile change in the entropy. Considering $\triangle S/h > \pm 4.0$ to be a large change in the entropy, we attempted to look for any natural events, such as higher wind speed and higher rainfall that may have occurred within the South Esk Catchment area over the time period of interest (January–December 2013) and that may correspond to such higher values in the change of entropy.

The entropy change values of greater than ±4.0% constitute $\sim$1.0% of total number of values in Fig. 10. We attempted to find any wind speed events within the top $\sim$2.0% of the wind speed data values over the same time period that could be matched up with these entropy change values. We also considered a time window of 7 h for any events to be matched up. Based on the above criteria, we found two wind speed events that matched up with high entropy change values over a 7-h time window. Although these observations were interesting, the probability of correctly predicting a significant wind speed event using the entropy change data was found to be very small. We also looked at rainfall data over the same time period, but were unable to find any significant rainfall events within that data. This might be because some other environmental parameters, such as precipitation, solar radiation, atmospheric pressure and their entropic pictures, need to be calculated, and then, combining these effects with air temperature entropy may lead to a better prediction of natural events.

In addition to classical statistical measures such as mean, median, mode, minimum and maximum, standard deviation or amplitudes, we offer a new measure that can explain structures of measured quantities, such as temperature, in a region. For the purpose of presenting the methodology a model output is required such as the South Esk Hydrological model, as an example. When a large number of sensors are available, such as in swarm sensing research, the results of Shannon entropy should be very useful for describing and characterizing a given environmental phenomenon.

Apart from environmental analysis, from the data science perspective the methodology can be applied in situations where:

• a high density of data is available (such as for the analysis of social media data),

• the structure of a data distribution is to be better understood and quantified,

• the means and standard deviations of such distributions are very similar or equal and are unable to provide insights into the structure of the data distributions.

8 Conclusions

Statistical mechanics has been applied to calculate an air temperature Shannon entropy of the environment, and results of the entropy have been presented. In presenting the entropy, time-series temperature data obtained from the South Esk Hydrological model have been used. The temperature scale has been discretized by setting the width of the states, $\triangle T$ values, at $\{0.10,0.20,\ldots ,1.0\,^{\circ }\mathrm{C}\}$, and a “number of particle-equivalent” quantity have been estimated (i.e. the frequency of temperature readings which fall within each particular temperature state). The number of microstates was then calculated, and from this, the entropy was determined.

While mean and standard deviation are useful statistical quantities for a normal distribution, they are insufficient to provide insights into the structure of the distribution if it is not normal. The entropy, on the other hand, captures the structure and underlying science of the distributed system and may be a useful way to express new characteristics of non-normal distributions. Therefore, as well as using statistical mechanical theory, this paper has also shown how the underlying dynamics of data distribution can be correlated with changes of entropy.

The estimated entropy values fluctuated significantly over the time period considered in this work. However, the average of the entropy was more stable than the average temperature. Therefore, the fluctuating behaviour of the calculated entropy seems to have some relationship with other environmental parameters, such as relative humidity, wind speed, atmospheric pressure, precipitation and solar radiation, and this will be the subject of future investigations.

The variation of average entropy over all four seasons has been presented. While the hourly average entropy changes fluctuated more widely with increased errors in summer, more consistency in the entropy changes was observed in winter.

Dispersion of the entropy values has also been presented on an hourly basis for all four seasons. The dispersion of entropy is more significant at midnight for all four seasons, but they converge in the afternoon. The presented results are also consistent for different $\triangle T$ values. By analysing data from miniaturized sensors when they are available and calculating entropy we can understand the dispersion of a quantity of interest in the environment.

The methodology developed in this paper can be applied to any spatially and temporally distributed environmental data including other environmental factors, such as wind speed, relative humidity and rainfall, which will be the subject of future investigations. The robustness of the approach has been demonstrated by applying it to two different domains: air temperature data provided by an atmospheric model (Fig. 9) and water salinity and water temperature data obtained from a hydrodynamic model (Fig. 11). The approach could also be applied to the analysis of social media data with high density. Since the methodology uses the concepts of particles in states (bins), the greater the density of data in the bins, the more consistent the results will be and the smaller the variations in entropy. The future work will also include using time-series methods, such as ARIMA, to provide predictions of entropy changes.