Weakening faithfulness: some heuristic causal discovery algorithms

Abstract

We examine the performance of some standard causal discovery algorithms, both constraint-based and score-based, from the perspective of how robust they are against (almost) failures of the Causal Faithfulness Assumption. For this purpose, we make only the so-called Triangle-Faithfulness assumption, which is a fairly weak consequence of the Faithfulness assumption, and otherwise allows unfaithful distributions. In particular, we allow violations of Adjacency-Faithfulness and Orientation-Faithfulness. We show that the (conservative) PC algorithm, a representative constraint-based method, can be made more robust against unfaithfulness by incorporating elements of the GES algorithm, a representative score-based method; similarly, the GES algorithm can be made less error-prone by incorporating elements of the conservative PC algorithm. As our simulations demonstrate, the increased robustness seems to matter even when faithfulness is not exactly violated, for with only finite sample, distributions that are not exactly unfaithful may be sufficiently close to being unfaithful to make trouble.

1 Introduction

Although it is usually more reliable to infer causal relations from experimental data than from observational data, the problem of causal discovery from observational data has been drawing increasingly more attention, thanks on the one hand to the practical difficulties in carrying out well-designed experiments and on the other hand to the relative ease of obtaining large volumes of data from various records and measurements. A widely adopted framework is to use graphs to represent causal structures and to relate causal graphs to probability distributions via various assumptions. Two well-known assumptions are known as the Causal Markov Assumption and the Causal Faithfulness Assumption [15]. The Causal Markov Assumption states that the joint distribution of a set of variables satisfies the Markov property of the true causal graph over them, or in other words, satisfies the conditional independence relations that are implied by the causal graph according to its Markov property. The Causal Faithfulness Assumption states the converse that the conditional independence relations satisfied by the joint distribution are all implied by the causal graph.

While the Causal Markov Assumption—when applied to causally sufficient systems where no common direct cause of two variables in the system is left out—is backed by substantial metaphysical principles relating causality and probability, such as Reichenbach’s principle of common cause [11], the Causal Faithfulness Assumption is usually taken to be a sort of Occam’s razor or methodological preference of simplicity [19]. As a result, the Causal Faithfulness Assumption is more dubious than the Causal Markov Assumption. Moreover, even if the Causal Faithfulness Assumption is not exactly violated, the distribution may be sufficiently close to being unfaithful to the causal graph in that a (conditional) dependence may be sufficiently weak to be almost indistinguishable from independence in finite samples (with a moderate sample size). The point that such “almost violations” of faithfulness pose serious challenges to causal discovery was already made in the relatively early days of the graphical modeling approach to causal discovery [7]. Recently, it was also established that the standard defense for the Causal Faithfulness Assumption that violations thereof are unlikely does not justify assuming away “almost unfaithfulness,” especially when the number of variables is large [17].

For these reasons, it is worth investigating, for those causal discovery methods that adopt the Causal Faithfulness Assumption, the extent to which the methods rely on the assumption, as well as the possibility of relaxing the assumption and adjusting the methods accordingly. The existing investigations of this sort have focused on the constraint-based approach to causal discovery [10, 14, 20]. In this paper, we follow this line of inquiry and bring the score-based approach to bear on the problem. In particular, we argue that the (conservative) PC algorithm, a representative constraint-based method, can be made more robust against unfaithfulness by incorporating elements of the GES algorithm, a representative score-based method, and that the GES algorithm can be made less error-prone by incorporating elements of the conservative PC algorithm.

The rest of the paper is organized as follows. We review the basic framework and notations in Sect. 2 and survey a number of consequences of the faithfulness assumption that may serve as weaker substitutes for the faithfulness assumption in Sect. 3. Then, in Sect. 4, we examine the behavior of PC and that of GES against certain kinds of unfaithfulness and motivate some natural hybrid algorithms. We test these hybrid algorithms through simulations in Sect. 5, which suggest, among other things, that the proposed algorithms are less error-prone than PC and GES at realistic sample sizes, even though the Faithfulness Assumption is not exactly violated. We conclude with discussions of some open problems in Sect. 6.

2 Preliminaries

We will use the following graph terminology. A (mixed) graph is a pair $({\mathbf {V}},{\mathbf {E}})$, where ${\mathbf {V}}$ is a set of vertices (each representing a distinct random variable),¹ and ${\mathbf {E}}$ is a set of edges between vertices such that between each pair of vertices there is at most one edge. For the purpose of this paper we need only two kinds of edges: directed ($\rightarrow$) and undirected ($-\!\!\!-$). Given a graph ${\mathcal {G}}({\mathbf {V}}, {\mathbf {E}})$ and any $X, Y\in {\mathbf {V}}$, if there is an edge between X and Y of any kind, X and Y are said to be adjacent. If the edge is directed, e.g., $X\rightarrow Y$, X is called a parent of Y and Y a child of X; if the edge is undirected, i.e., $X-\!\!\!-Y$, then X and Y are called neighbors of each other. A path in ${\mathcal {G}}$ is a sequence of distinct vertices $(V_1, \ldots , V_n)$ such that for $1\le i\le n-1$, $V_i$ and $V_{i+1}$ are adjacent in ${\mathcal {G}}$. A path between $V_1$ and $V_n$ is called a directed path from $V_1$ to $V_n$ if the edge between $V_i$ and $V_{i+1}$ is $V_i\rightarrow V_{i+1}$ for $1\le i\le n-1$. A vertex X is called an ancestor of a vertex Y and Y a descendant of X in ${\mathcal {G}}$ if $X=Y$ or there is a directed path from X to Y in ${\mathcal {G}}$.

An (ordered) triple of vertices (X, Y, Z) in ${\mathcal {G}}$ is called an unshielded triple if X, Y are adjacent and Y, Z are adjacent, but X, Z are not adjacent. It is called a shielded triple or triangle if in addition to X, Y and Y, Z, X and Z are also adjacent. An unshielded or shielded triple (X, Y, Z) is called a collider if the edge between X and Y and the edge between Z and Y are both directed at Y, i.e., $X\rightarrow Y\leftarrow Z$. Otherwise, it is called a non-collider.

A graph with only directed edges is called a directed graph, and a directed acyclic graph (DAG) is a directed graph in which no two distinct vertices are ancestors of each other. We assume that we are working with a set of variables ${\mathbf {V}}$, the underlying causal structure of which can be represented by a DAG over ${\mathbf {V}}$. A DAG entails a set of conditional independence statements according to its (local or global) Markov property. One statement of the (global) Markov property uses the notion of d-separation [8]. Given a path $(V_1,\ldots ,V_n)$ in a DAG, $V_i$ ($1<i<n$) is said to be a collider (non-collider) on the path if the triple $(V_{i-1}, V_i, V_{i+1})$ is a collider (non-collider). Given a set of vertices ${\mathbf {Z}}$, a path is blocked by ${\mathbf {Z}}$ if some non-collider on the path is in ${\mathbf {Z}}$ or some collider on the path has no descendant in ${\mathbf {Z}}$. For any $X, Y\notin {\mathbf {Z}}$, X and Y are said to be d-separated by ${\mathbf {Z}}$ if every path between X and Y is blocked by ${\mathbf {Z}}$. For any ${\mathbf {X}}, {\mathbf {Y}}, {\mathbf {Z}}$ that are pairwise disjoint, ${\mathbf {X}}$ and ${\mathbf {Y}}$ are d-separated by ${\mathbf {Z}}$ if every vertex in ${\mathbf {X}}$ and every vertex in ${\mathbf {Y}}$ are d-separated by ${\mathbf {Z}}$. According to the (global) Markov property, a DAG entails that ${\mathbf {X}}$ and ${\mathbf {Y}}$ are independent conditional on ${\mathbf {Z}}$ if and only if ${\mathbf {X}}$ and ${\mathbf {Y}}$ are d-separated by ${\mathbf {Z}}$.

Two DAGs are said to be Markov equivalent if they entail the exact same conditional independence statements. A well-known characterization is that two DAGs are Markov equivalent if and only if they have the same adjacencies (or skeleton, the undirected graph resulting from ignoring the direction of edges in a DAG) and the same unshielded colliders [18]. A Markov equivalence class of DAGs, ${\mathcal {M}}$, can be represented by a graph called a pattern (a.k.a an essential graph or complete partially directed acyclic graph); the pattern has the same adjacencies as every DAG in ${\mathcal {M}}$ such that for every X and Y that are adjacent, the pattern contains $X\rightarrow Y$ if $X\rightarrow Y$ appears in every DAG in ${\mathcal {M}}$, and contains $X-\!\!\!-Y$ if $X\rightarrow Y$ appears in some DAGs in ${\mathcal {M}}$ and $X\leftarrow Y$ appears in others.

In this paper we assume that all variables in the given set ${\mathbf {V}}$ are observed, or in other words, the set of observed variables is causally sufficient so that we need not introduce latent variables to properly model the system. Under this simplifying assumption, the problem we are concerned with is that of inferring information about the causal DAG over ${\mathbf {V}}$ from i.i.d. data sampled from a joint distribution P over ${\mathbf {V}}$. All methods we know of make the following assumption:

Causal Markov Assumption: The joint distribution P over ${\mathbf {V}}$ is Markov to the true causal DAG ${\mathcal {G}}$ over ${\mathbf {V}}$ in the sense that every conditional independence statement entailed by ${\mathcal {G}}$ is satisfied by P.

And many methods also make the following assumption:²

Causal Faithfulness Assumption: The joint distribution P over ${\mathbf {V}}$ is faithful to the true causal DAG ${\mathcal {G}}$ over ${\mathbf {V}}$ in the sense that every conditional independence statement satisfied by P is entailed by ${\mathcal {G}}$.

Under these two assumptions, the pattern of the true causal DAG is in principle determinable by the distribution, and many causal discovery algorithms aim to recover the pattern from data. In what follows, we will often omit the qualifier “causal” and refer to the assumptions simply as “Markov” and “Faithfulness,” respectively.

3 Weaker notions of faithfulness

As stated in Sect. 1, our work here follows a line of inquiry that seeks to adjust some standard causal discovery procedures to make them more robust against violations of Faithfulness. From this line of work a number of weaker notions of Faithfulness have emerged. Ramsey et al. [10] highlighted two consequences of the Faithfulness assumption (recall that we use ${\mathcal {G}}$ to denote the true causal DAG over ${\mathbf {V}}$, and P the true joint distribution of ${\mathbf {V}}$ from which samples are drawn):

Adjacency-Faithfulness: For every $X, Y\in {\mathbf {V}}$, if X and Y are adjacent in ${\mathcal {G}}$, then they are not conditionally independent given any subset of ${\mathbf {V}}\backslash \{X, Y\}$.

Orientation-Faithfulness: For every $X, Y, Z\in {\mathbf {V}}$ such that (X, Y, Z) is an unshielded triple in ${\mathcal {G}}$:

• (i) If (X, Y, Z) is a collider (i.e., $X\rightarrow Y\leftarrow Z$) in ${\mathcal {G}}$, then X and Z are not conditionally independent given any subset of ${\mathbf {V}}\backslash \{X, Z\}$ that includes Y.

• (ii) Otherwise, X and Z are not conditionally independent given any subset of ${\mathbf {V}}\backslash \{X, Z\}$ that excludes Y.

These consequences of the faithfulness assumption are singled out because they are what standard constraint-based search procedures such as the PC algorithm exploit, in the stage of inferring adjacencies and in the stage of inferring orientations, respectively. Ramsey et al. [10] showed that under the Markov and Adjacency-Faithfulness assumptions, Orientation-Faithfulness can be tested and hence need not be assumed. This consideration leads to a variation of the PC algorithm known as the Conservative PC (CPC) algorithm. We will return to these algorithms in Sect. 4.

A still weaker consequence of the Faithfulness assumption than Adjacency-Faithfulness is the following, first introduced by [20]:

Triangle-Faithfulness: For every $X, Y, Z\in {\mathbf {V}}$ such that (X, Y, Z) is a triangle in ${\mathcal {G}}$:

• (i) If (X, Y, Z) is a (shielded) collider in ${\mathcal {G}}$, then X and Z are not conditionally independent given any subset of ${\mathbf {V}}\backslash \{X, Z\}$ that includes Y.

• (ii) Otherwise, X and Z are not conditionally independent given any subset of ${\mathbf {V}}\backslash \{X, Z\}$ that excludes Y.

Clearly Triangle-Faithfulness is strictly weaker than Adjacency-Faithfulness (for the former is only about adjacent variables in a triangle). Triangle-Faithfulness is of special interest when combined with another very weak consequence of Faithfulness:

SGS-minimality: No proper subgraph of ${\mathcal {G}}$ satisfies the Markov assumption with P.

Where a proper subgraph of ${\mathcal {G}}$ is a DAG over ${\mathbf {V}}$ with a proper subset of the edges in ${\mathcal {G}}$. This is known as the Causal Minimality Condition in the literature [15]. To distinguish it from another minimality condition that is relevant to our discussion, we follow [19] to refer to it as SGS-minimality (Spirtes, Glymour and Scheines’s minimality condition). Zhang and Spirtes [21] showed that it is in general very safe to assume the SGS-minimality condition.

An interesting result is that if one assumes Markov, SGS-minimality, and Triangle-Faithfulness, then the rest of the Faithfulness assumption, including in particular Adjacency-Faithfulness as well as Orientation-Faithfulness, can in principle be tested [14, 20].

In fact, the assumption needed to make the Faithfulness assumption testable is even weaker than Triangle-Faithfulness (plus SGS-minimality). It will be referred to as P-minimality (Pearl’s minimality condition, [9]):

P-minimality: No proper independence-submodel of ${\mathcal {G}}$ satisfies the Markov assumption with P.

Where a proper independence-submodel of ${\mathcal {G}}$ is a DAG over ${\mathbf {V}}$ that entails a proper superset of the conditional independence statements entailed by ${\mathcal {G}}$. In other words, the P-minimality assumption states that, for every DAG that entails all the conditional independence statements entailed by ${\mathcal {G}}$ plus some additional ones, P does not satisfy some of the additional ones entailed by the DAG.

Zhang [19] showed that P-minimality is weaker than Triangle-Faithfulness plus SGS-minimality, and if one assumes Markov and P-minimality, the Faithfulness assumption can in principle be tested. However, the Markov and P-minimality assumptions together are so weak that in general the adjacencies of the causal DAG over ${\mathbf {V}}$ are not uniquely determined by the distribution of ${\mathbf {V}}$. That is, there are cases where two DAGs over ${\mathbf {V}}$ have different adjacencies but both satisfy the Markov and P-minimality assumptions with a given distribution of ${\mathbf {V}}$. Here is an example that will prove relevant to our later discussion of the GES algorithm.

Example 1

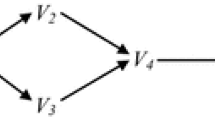
Suppose ${\mathbf {V}} = \{V_1, V_2, V_3, V_4\}$, and the true causal structure is represented by the DAG in Fig. 1a. Suppose that the parameterization is such that the causal influence along the path $V_1\rightarrow V_2\rightarrow V_4$ and that along the path $V_1\rightarrow V_3\rightarrow V_4$ balance out. As a result, in addition to the conditional independence relations entailed by the graph, the distribution satisfies one (and only one) extra independence: , which is a violation of Orientation-Faithfulness. Under such a circumstance, the DAG in Fig. 1b also satisfies the Markov and P-minimality assumptions with the distribution. (It is Markov because it entails only that , which is satisfied by the given distribution. It is P-minimal because every DAG that entails and some more conditional independence statements entails one that is not satisfied by the given distribution).

Fig. 1

An illustration of a violation of Orientation-Faithfulness. a The true causal DAG that generates an unfaithful distribution due to balancing out of the two paths from $V_1$ to $V_4$. b A DAG that satisfies the Markov and P-minimality assumptions with the supposed distribution

So the Markov and P-minimality assumptions together are not strong enough to entail that adjacencies are uniquely determined by a distribution. We do not know whether the Markov, SGS-minimality and Triangle-Faithfulness assumptions together are sufficiently strong to entail that adjacencies are uniquely determined by a distribution. In Example  1, obviously, the distribution is not Triangle-Faithful to the DAG in Fig. 1b, for according to the distribution, which violates Triangle-Faithfulness with respect to the triangle $(V_2, V_4, V_3)$. Indeed, in this example, given the Markov and Triangle-Faithfulness assumptions the distribution entails that the adjacencies in the true causal DAG must be the same as those in Fig. 1a.

We conjecture that at least for linear models, adjacencies are in general uniquely determined by the true distribution under the Markov, SGS-minimality and Triangle-Faithfulness assumptions. If this is true, then Triangle-Faithfulness (plus SGS-minimality) is at once much weaker than (Adjacency-)Faithfulness [20], and sufficiently strong to not only allow the Faithfulness assumption to be testable but also have the true causal skeleton (i.e., the adjacencies) be determined by data in the large sample limit. It is therefore worth investigating methods of causal discovery under this much weaker notion of faithfulness. As we already mentioned, this investigation is potentially useful even if the Faithfulness assumption is rarely exactly violated, for methods that do not rely on strong notions of faithfulness will probably be less error-prone at realistic sample sizes than those that do.

4 PC and GES against unfaithfulness and some more Robust algorithms

We are yet to work out a feasible method that is provably correct given only the Triangle-Faithfulness assumption, but an examination of standard causal discovery algorithms with respect to violations of Faithfulness suggests some simple variations that, though not exactly correct given only the Triangle-Faithfulness assumption, are better heuristic methods than the original. In this section, we focus on two well-known algorithms, PC [15] and GES [1, 7].

4.1 PC and violations of faithfulness

As a representative constraint-based procedure, the PC algorithm has two stages, a stage of inferring the skeleton or adjacencies (lines 1–6 in Algorithm 1), and a stage of inferring the orientations of as many edges in the skeleton as possible (lines 7–8 in Algorithm 1). The basic idea of the first stage is simple: For every pair of variables X and Y, search for a set of variables given which X and Y are conditionally independent, and infer them to be adjacent if and only if no such set is found. The justification for this step clearly relies on the Adjacency-Faithfulness assumption. In the second stage, the key step is to infer unshielded colliders and non-colliders; for this purpose, the PC algorithm uses a simple rule: For every unshielded triple (X, Y, Z), infer that it is a collider if and only if the set found in the first stage that renders X and Z conditionally independent does not include Y. The justification for this step is clearly related to the Orientation-Faithfulness assumption.

As a result, the PC algorithm is very sensitive to a failure of Adjacency-Faithfulness or that of Orientation-Faithfulness. For a violation of Orientation-Faithfulness, Example  1 provides a simple illustration. In that example, if we feed an oracle of conditional independence derived from the distribution (or constructed based on statistical tests on a sufficiently large sample from the distribution) to the PC algorithm, the algorithm will output the triple $(V_1, V_2, V_4)$ as an unshielded collider, and similarly for the triple $(V_1, V_3, V_4)$.

Ramsey et al. [10] showed that such unreliability of PC in the presence of violations of Orientation-Faithfulness can be remedied in principle, by using a more cautious or conservative step of inferring the orientation of unshielded triples. The idea is that given the correct skeleton, whether Orientation-Faithfulness is true for an unshielded triple is testable, by checking more statements of conditional independence. The adjusted algorithm is named CPC (Conservative PC). We will discuss the conservative orientation step and its variations in more details in Sect. 4.3. For the moment, suffice it to say that it is a principled way to guard against violations of Orientation-Faithfulness.

What about failures of Adjacency-Faithfulness? Here is a simplest example (that does not violate Triangle-Faithfulness):

Example 2

Suppose ${\mathbf {V}} = \{V_1, V_2, V_3, V_4\}$, and the true causal structure is represented by the DAG in Fig. 2a. Suppose that the parameterization is such that the causal influence along the edge $V_1\rightarrow V_4$ and that along the path $V_1\rightarrow V_2\rightarrow V_3\rightarrow V_4$ balance out. As a result, in addition to the conditional independence relations entailed by the graph, the distribution satisfies one (and only one) extra independence: , which is a violation of Adjacency-Faithfulness. (Notice that Triangle-Faithfulness trivially holds, as there is no triangle in the graph).

Fig. 2

An illustration of a violation of Adjacency-Faithfulness. a The true causal DAG that generates an unfaithful distribution due to balancing out of the two paths from $V_1$ to $V_4$. b The output of the PC algorithm given an input of an oracle of conditional independence associated with the supposed distribution. c The pattern that represents the Markov equivalence class of the true causal DAG

In this example, the PC algorithm, given an input of an oracle of conditional independence from the distribution, would output the pattern in Fig. 2b, while the true pattern is depicted in Fig. 2c. That is, the PC algorithm would miss the edge between $V_1$ and $V_4$, due to the extra, unfaithful independence (and consequently miss the collider).

Before we discuss how to mitigate this problem, it is worth noting that although an edge is missing from the skeleton returned by PC, the edges present in the PC skeleton are all correct. This is no accident. Spirtes and Zhang [14] observed that even if the Adjacency-Faithfulness fails, the SGS algorithm, a predecessor of PC, is provably asymptotically correct in this aspect: The adjacencies in the output are true, though non-adjacencies may be false. This is because the SGS algorithm searches through all subsets of ${\mathbf {V}}\backslash \{X, Y\}$ to look for a set that renders X and Y conditionally independent; if no such set is found, then the Markov assumption alone entails that X and Y are adjacent. Only the inference of non-adjacencies relies on the assumption of Adjacency-Faithfulness.

This argument does not straightforwardly apply to PC, as PC does not necessarily look at every subset. Still, no example is known to show that the PC algorithm, when supplied with a perfect oracle of conditional independence that does not respect Adjacency-Faithfulness, not only makes mistakes on non-adjacencies, but also may err about adjacencies. We suspect that there is no such example, but we are currently unable to find a proof. In any case, it is probably safe to think that in most cases, PC is asymptotically correct in its inference of adjacencies (as opposed to its inference of non-adjacencies), even if Adjacency-Faithfulness is violated.

Regarding the issue with the inferred non-adjacencies, Spirtes and Zhang [14] suggested a way to confirm some non-adjacencies as opposed to others by testing some forms of Markov condition in the output of (conservative) PC, which was elaborated and implemented by [4]. A limitation of this approach is that it only seeks to confirm some non-adjacencies, without attempting to fill in the missing edges. A natural, alternative idea is to search for a best way to add edges back to the PC/CPC output. For this purpose, the algorithm known as Greedy Equivalence Search (GES) may play a role.

4.2 GES and violations of faithfulness

The GES algorithm [1, 7] is a score-and-search procedure over the space of patterns that represent Markov equivalence classes of DAGs. It searches for a pattern that maximizes a certain score, usually a Bayesian score or a penalized likelihood such as BIC (which is used in our simulations on Gaussian models). The algorithm traverses though the space in a moderately “greedy” fashion, in two phases. In the first, forward phase (lines 1–9), the algorithm starts with some pattern, usually the empty one (i.e., without any edge), and tries adding edges, one in each step,³ to improve the score until a (local) optimum is reached. It then enters the second, backward phase (lines 10–17), which differs from the first phase only in that instead of adding edges it moves through patterns by deleting edges, one in each step. The basic search procedure is summarized in Algorithm 2, where $G_{ini}$ denotes the pattern the algorithm starts with, $G^+(G)$ denotes the set of patterns $G'$ such that some DAG represented by $G'$ has exactly one more edge than some DAG represented by G, and $G^-(G)$ denotes the set of patterns $G'$ such that some DAG represented by $G'$ has exactly one fewer edge than some DAG represented by G.

For our present purpose, it is worth highlighting that in the forward phase of the algorithm, every time the search moves from a current pattern to a new one, the DAGs represented by the current pattern are proper independence-submodels of the DAGs represented by the new one. Likewise, in the backward phase of the algorithm, every time the search moves from a current pattern to a new one, the DAGs represented by the new pattern are proper independence-submodels of the DAGs represented by the current one. A score is said to be consistent if in the large sample limit, (1) any DAG (or its pattern) that is Markov to the underlying distribution has a higher score than any DAG (or its pattern) that is not Markov to the underlying distribution, (2) if two DAGs are both Markov to the underlying distribution and one is a proper independence-submodel of the other, then the former has a higher score than the latter. For linear Gaussian models and multinomial models, for example, the Bayesian scores and BIC are all consistent [1].

It follows from the consistency of the scoring and the way GES moves in the search space that asymptotically the output of the algorithm satisfies the Markov and P-minimality conditions with the underlying distribution. Therefore, if the Faithfulness assumption holds, the GES algorithm is asymptotically correct, for given Faithfulness, the pattern of the true causal DAG is the unique pattern that satisfies the Markov and P-minimality conditions. What if the Faithfulness assumption does not hold? For the kind of unfaithfulness described in Example 2, the GES algorithm remains valid, for despite the unfaithfulness, the pattern in Fig. 2c remains the only pattern that satisfies the Markov and P-minimality conditions with the unfaithful distribution. We suspect that this is generally the case for violations of Adjacency-Faithfulness (that do not violate Triangle-Faithfulness).

In contrast, failures of Orientation-Faithfulness can easily lead GES astray. Take Example 1 for instance. As we already pointed out, in that case there are more than one pattern that satisfy the Markov and P-minimality conditions with the underlying distribution. As a result, there is little guarantee that the GES algorithm would end up with the true causal pattern, even in the large sample limit. For example, if we parameterize the graph in Fig. 1a as a linear structural equation model with Gaussian error terms and make the two pathways cancel as required by the example, then the GES algorithm will frequently return the pattern for the DAG in Fig. 1b, even at big sample sizes. Section 5.1 reports some simulation results to illustrate this point.

These considerations suggest that GES is probably more unreliable under failures of Orientation-Faithfulness than it is under failures of Adjacency-Faithfulness. This motivates us to consider combining GES with a CPC-like orientation step, to which we now turn.

4.3 Some heuristic hybrid algorithms

As already mentioned, the CPC algorithm [10] modifies PC’s rule of inferring unshielded colliders or non-colliders into a more cautious or conservative step. For an unshielded triple (X, Y, Z) in a skeleton, the CPC algorithm does not just consider one conditioning set that renders X and Z conditionally independent, but will check, roughly speaking, all subsets of the set of variables that are adjacent to X and of the set of variables that are adjacent to Z. If all sets that render X and Z conditionally independent exclude Y, then (X, Y, Z) is judged to be a collider. If all sets that render X and Z conditionally independent include Y, then (X, Y, Z) is judged to be a non-collider. If, however, some such sets exclude Y while the other such sets include Y, then (X, Y, Z) is marked to be an ambiguous triple (i.e., the judgment is suspended regarding whether the triple is a collider or a non-collider), for the result indicates that Orientation-Faithfulness fails.

A more recent variation on the theme [2] uses a majority rule decision procedure as follows. As in CPC, this procedure first finds, for any unshielded triple (X, Y, Z) in a skeleton, all subsets of variables adjacent to X or of variables adjacent to Z that render X and Z conditionally independent. Then the triple is marked according to a majority rule: If Y is excluded from a majority of such sets, then the triple is marked as a collider; if Y is included in a majority of such sets, then the triple is marked as a non-collider; if, however, Y is excluded from (or included in) exactly half of such sets, then the triple is marked as ambiguous.

In our experiments, we found that the original CPC orientation is often too cautious to be sufficiently informative; it marks too many triples as ambiguous. On the other hand, the majority rule orientation rarely suspends judgment and so does not effectively serve the purpose of guarding against (almost) failures of Orientation-Faithfulness. We thus generalize them into a ratio rule with a parameter $0\le \alpha \le 0.5$. Given a skeleton and an unshielded triple (X, Y, Z) therein, let O(X, Y, Z) be the number of sets that render X and Z conditionally independent and exclude Y, and let I(X, Y, Z) be the number of sets that render X and Z conditionally independent and include Y. The $\alpha$-conservative orientation rule states that

• (i) if $I(X, Y, Z)/(O(X, Y, Z)+I(X, Y, Z)) \le \alpha$, then mark (X, Y, Z) as a collider;

• (ii) if $I(X, Y, Z)/(O(X, Y, Z)+I(X, Y, Z)) \ge 1-\alpha$, then mark (X, Y, Z) as a non-collider;

• (iii) otherwise, mark (X, Y, Z) as ambiguous.

Obviously, the greater $\alpha$ is, the less conservative the rule becomes (i.e., the less frequently the rule suspends judgment). The original CPC orientation rule is just an $\alpha$-conservative rule with $\alpha =0$, and the majority rule is just an $\alpha$-conservative rule with $\alpha =0.5$. They thus represent two extremes in this family of conservative orientation rules. The optimal value of $\alpha$ probably depends on several factors, including dimension, sample size, and, especially, how important avoiding errors is relative to gaining information. Obviously, for example, if it is of utmost importance to avoid errors and informativeness is categorically only secondary, then the extreme choice of $\alpha =0$, as in CPC, is advisable. Most of the time, however, the goal is to strike a best balance between avoiding misinformation and seeking information. Given a well-defined scoring metric of the goodness of balance, an optimal value of $\alpha$ is then a value that maximizes the expectation of the score. We are yet to work out a sophisticated analysis of this issue and a practical method for tuning this parameter.⁴ In the simulations reported in the next section, $\alpha$ is set to 0.4, as this value appears to achieve the best result on the measure we use, compared to the other values we tried in a small-scale experiment.

Our previous examinations of PC and GES suggest the following three heuristic algorithms that are expected to be more robust against unfaithfulness:

• PC+GES: Run PC first and feed the output pattern to GES (and prohibit GES to take away any adjacency in the PC output).⁵

• GES+c: Run GES first, take the skeleton of the output and apply the $\alpha$-conservative rule followed by Meek’s orientation rules.⁶

• PC+GES+c: Run PC+GES, take the skeleton of the output and apply the $\alpha$-conservative rule followed by Meek’s orientation rules.

Specifically, PC+GES is expected to mitigate PC’s vulnerability to failures of Adjacency-Faithfulness, and GES+c is expected to mitigate GES’s vulnerability to failures of Orientation-Faithfulness (likewise for PC+GES vs PC+GES+c). In the next section we report simulation results on linear Gaussian models that provide some evidence.

5 Simulations

We report two sets of simulation results. One is on the two toy examples mentioned previously, in which we try exact violations of Orientation-Faithfulness and of Adjacency-Faithfulness, respectively. The results not only serve to support our earlier claims about the aforementioned algorithms, but also show that two other state-of-the-art algorithms, the Max-Min Hill Climbing (MMHC) algorithm [16] and the PC-stable algorithm [2], would stumble over one or both of the examples.

The other is from much more comprehensive experiments that follow a fairly standard setup, in which the probability of having exact violations of faithfulness is zero. These results indicate that the proposed algorithms are less error-prone at realistic sample sizes even when Faithfulness is not exactly violated. All experiments reported below are done on linear Gaussian models.

5.1 Toy examples with exact faithfulness violations

We first present some results on the two toy examples, in which it is easy to create exact violations of faithfulness. Recall that Example 1 in Sect. 3 involves a violation of Orientation-Faithfulness, in which the true causal structure is represented by the DAG in Fig. 1a, and the two causal pathways, $V_1\rightarrow V_2\rightarrow V_4$ and $V_1\rightarrow V_3\rightarrow V_4$, are supposed to exactly cancel so that $V_1$ and $V_4$ are independent according to the true distribution. In our experiment, we randomly draw edge coefficients for the following three edges in Fig. 1a, $V_1\rightarrow V_2$, $V_2\rightarrow V_4$ and $V_1\rightarrow V_3$, uniformly from $[-1,-0.1]\cup [0.1, 1]$, and then set the coefficient associated with $V_3\rightarrow V_4$ as $-\beta _{12}\beta _{24}/\beta _{13}$, where $\beta _{12}, \beta _{24}, \beta _{13}$ denote the edge coefficients for $V_1\rightarrow V_2$, $V_2\rightarrow V_4$, $V_1\rightarrow V_3$, respectively. The variance of each error term in the model is drawn uniformly from [0.5, 1]. (Means are all set to 0.) We generate 100 linear structural equation models this way and draw from each model 50 i.i.d samples of size 5000. We use a big sample size for this experiment, for the errors we aim to reveal are not a matter of sample size.

On the $100 \times 50$ datasets we run various algorithms. We use significance level of 0.01 in tests of conditional independence and use BIC in the GES algorithm. For this simulation, the value of $\alpha$ in the conservative orientation does not seem to matter; all values of $\alpha$ give essentially the same results.

As expected, PC and GES very frequently judge the triple $V_1\rightarrow V_2\rightarrow V_4$ and the triple $V_1\rightarrow V_3\rightarrow V_4$ to be colliders. In particular, as we predicted in Sect. 4.2, GES frequently—about 65% of the time—outputs the pattern for the DAG in Fig. 1b.

Just as CPC (and PC-stable, which uses the majority rule for orientation and is reasonably robust against simple violations of Orientation-Faithfulness like this one) can to a good extent avoid such errors of PC, GES+c helps to decrease such orientation errors of GES. In this simple example, GES+c in most cases mark the triple $V_1\rightarrow V_2\rightarrow V_4$ and the triple $V_1\rightarrow V_3\rightarrow V_4$ as ambiguous. Table 1 lists the average arrow precisions of the relevant algorithms in this case, where arrow precision is the percentage of true directed edges (i.e., directed edges that also appear in the true pattern) among all the directed edges in the estimated graph. (Since arrow precision is used here to measure how well mistaken inferences to arrows are avoided, we take arrow precision to be 1 when the estimated graph contains no directed edges.) Thanks to the conservative orientation, GES+c improves the arrow precision of GES (i.e., avoids some mistaken arrows in the GES output), as CPC does to PC.

On this example, the MMHC algorithm, which has been shown to be empirically more accurate than PC and GES [16], also mistakes the triple $V_1\rightarrow V_2\rightarrow V_4$ and the triple $V_1\rightarrow V_3\rightarrow V_4$ as colliders in almost half of the cases (about 45% of the time). This drags down its average arrow precision as listed in Table 1.

Table 1 Arrow precisions in the experiment on Example 1

Example 2 in Sect. 4.1 is intended to illustrate a simple violation of Adjacency-Faithfulness: The true causal structure is taken to be the DAG in Fig. 2a, but the true distribution is such that $V_1$ and $V_4$ are independent (despite their adjacency). Again, we generate exact violations by randomly selecting three edge coefficients (associated with $V_1\rightarrow V_2$, $V_2\rightarrow V_3$, and $V_3\rightarrow V_4$, respectively), and setting the fourth (associated with $V_1\rightarrow V_4$) to exactly balance the two directed paths from $V_1$ to $V_4$ in Fig. 2a. The setting is otherwise the same as in the previous example.

In 99% of the $100 \times 50$ trials, the PC algorithm misses the adjacency between $V_1$ and $V_4$. The PC-stable algorithm, which uses an order-independent search of adjacencies and is usually more accurate than PC, does not help with this case. As we predicted, PC+GES is able to pick up the edge most of the time. Indeed, GES by itself outputs the true pattern most of the time (68% of the trials), which is consistent with our analysis in Sect. 4.2. MMHC, on the other hand, almost always misses the edge between $V_1$ and $V_4$, and outputs the pattern in Fig. 2b most of the time.

Table 2 summarizes the average true adjacency rates and false adjacency rates of these algorithms, where true adjacency rate is the number of true adjacencies in the estimated graph divided by the number of edges in the true graph, and false adjacency rate is the number of false adjacencies in the estimated graph divided by the number of non-adjacencies in the true graph.

Table 2 True adjacency rates and false adjacency rates in the experiment on Example 2

Ideally, we would like to run a more systematic experiment using perhaps random graphs and more complex faithfulness violations. Unfortunately, we have not yet thought of a way to automatically generate exact violations of Adjacency-Faithfulness (without being violations of Triangle-Faithfulness) and/or of Orientation-Faithfulness on a random graph. Still, the above toy simulations well illustrate the main points we made earlier.

5.2 Systematic simulations without exact faithfulness violations

We now report systematic simulations on random models generated in the usual way. These models do not give us exact faithfulness violations, but an important motivation to design algorithms that are more reliable under exact faithfulness violations is the thought that such theoretical benefits may also show up when Faithfulness is not exactly violated. The simulations were performed on linear Gaussian models, with 2 levels of sparsity and 4 different dimensions, with 10, 20, 30, 40 variables, respectively. For the sparse case, each DAG has at most the same number of edges as the number of variables, while for the dense case, each DAG has at most twice as many edges as the number of nodes. In both settings, the maximum degree was set at 10. In both sparse and dense settings, for each dimension, 100 DAGs were randomly generated, and from each DAG, a linear structural equation model was constructed by drawing edge coefficients uniformly from $[-1,-0.1]\cup [0.1, 1]$, and variances of error terms from [0.5, 1]. From each model, 50 i.i.d samples of size 200, 500, 1000 and 5000, respectively, were generated.

Fig. 3

True adjacency rates in all settings. The reported rate for each setting is the mean value of the 100 (models) $\times$ 50 (datasets) runs for each setting

Fig. 4

False adjacency rates in all settings. The reported rate for each setting is the mean value of the 100 (models) $\times$ 50 (datasets) runs for each setting

Again, we use significance level of 0.01 in tests of conditional independence and use BIC in the GES algorithm. For the conservative orientation, we tried a number of values of $\alpha$ in a small-scale experiment, all of which gave qualitatively similar results, but $\alpha =0.4$ seemed to strike the best balance between being cautious and being informative (as measured by the F1 score we describe below). This finding is not necessarily generalizable,⁷ but provides some indication that $\alpha =0.4$ works reasonably well in our setting. So we use $\alpha =0.4$ in the present simulation.

For the estimation of skeleton or adjacencies, we compared the performance of PC, GES and PC+GES, by measuring their respective true adjacency rates and false adjacency rates, as defined in Sect. 5.1. Figure 3 shows the comparison of the average true adjacency rates of GES, PC and PC+GES, and Fig. 4 shows the comparison of their average false adjacency rates. The measurements were plotted against sample size and dimension for dense and sparse settings, respectively. As expected, the PC algorithm in general has very low rates of false adjacencies. This has partly to do with the low significance level we use in the conditional independence tests, but we think also has to do with the fact that even in the presence of (almost) violations of Adjacency-Faithfulness, the correctness of the adjacencies (as opposed to non-adjacencies) produced by the PC algorithm are not much affected. However, as is also evident from the results, the PC algorithm also has much lower true adjacency rates, implying that its non-adjacencies are much more problematic. Again, we think that this has a lot to do with the fact that non-adjacencies are very sensitive to (almost) failures of Adjacency-Faithfulness. It is clear that running GES⁸ helps PC to pick up a lot of missing edges.

Fig. 5

Arrow precisions in all settings. The reported precision for each setting is the mean value of the 100 (models) $\times$ 50 (datasets) runs for each setting

Fig. 6

A box plot of arrow precisions for sample size = 1000

Fig. 7

F1 measures of orientation accuracies in all settings. The reported score for each setting is the mean value of the 100 (models) $\times$ 50 (datasets) runs for each setting

Fig. 8

F1 scores of MMHC, in comparison with those of GES+c and PC+GES+c

For orientations, we first compare GES+c vs GES, and PC+GES vs PC+GES+c in terms of their arrow precisions as defined in Sect. 5.1, which suggest how good they are at avoiding false arrows. Figure 5 shows the average arrow precisions of the 4 algorithms in various settings. It is clear that GES+c significantly increases the arrow precision of GES in all settings, and likewise for PC+GES+c vs PC+GES. Figure 6 also presents a boxplot of the AP values for a fixed sample size (n = 1000), with similar implications.

However, arrow precision on its own does not mean much, as an extremely conservative orientation rule can achieve maximum precision or avoid all errors by always suspending judgment. So we also compare the standard F1 measure that combines arrow precision and arrow recall, where arrow recall is the number of true directed edges in the estimate graph (i.e., directed edges that also appear in the true pattern) divided by the number of directed edges in the true pattern,⁹ and $\text {F}1 = 2(\text {Precision}\times \text {Recall})/(\text {Precision} + \text {Recall})$, with the standard stipulation that $\text {F}1=0$ if $\text {Precision}=\text {Recall}=0$. Figure 7 shows the F1 scores of the 4 algorithms in all settings. On this measure, GES+c clearly outperforms GES, except for the two settings with the lowest dimension, in which the two stay very close. So our conservative orientation rule does not improve precision by simply sacrificing informativeness. For PC+GES, the conservative orientation rule also improves the F1 score in sparse settings, while for dense settings, PC+GES and PC+GES+c have quite comparable F1 scores.

We suspect that the observed improvements are connected to the fact that the proposed algorithms are designed to better handle faithfulness violations, but we realize that it is premature to claim a definite connection. After all, other hybrid algorithms [3, 16] such as MMHC achieve better performance, without being designed to deal with exact violations of faithfulness as illustrated by the simple simulations in Sect. 5.1.¹⁰ Indeed, as shown in Fig. 8, the F1 scores of MMHC are fairly comparable to those of GES+c and PC+GES+c. Still, it is interesting to see that certain modifications motivated by theoretical concerns with unfaithfulness turn out to improve performance even when faithfulness is not exactly violated, and this seems to make it at least reasonable to hypothesize a connection.

6 Conclusion

We examined two representative causal discovery algorithms that normally assume the Faithfulness assumption, from the perspective of how robust they are against unfaithfulness. One of them is the GES algorithm, and it is the first time that a score-based method is brought to bear on a line of inquiry that has thus far been confined to the constrain-based approach. Although our discussion was not yet fully rigorous or general, it yielded some insights that motivated a couple of simple hybrid algorithms, which proved to be worthy candidates in our simulation studies.

A component in our hybrid algorithms is a conservative orientation rule indexed by a parameter $\alpha$ that generalizes the conservative rule in the CPC algorithm and the majority rule in the PC-stable algorithm. An open question is how to choose the value of this parameter in a systematic and sophisticated way (which, as we indicated in Sect. 4.3, will probably be formulated as an optimization problem, with an objective function that measures the expected extent to which the outcome is well balanced between accuracy and informativeness). At this point, we can only report that in our simulations, $\alpha =0.4$ appears to be a good choice. We hope to work out more convincing recommendations in future work.

As we argued in Sect. 3, there seem to be excellent reasons to explore feasible methods of causal discovery that are provably correct given only the Triangle-Faithfulness assumption. In this regard, all the algorithms we considered in this paper are heuristic methods; none of them is provably correct given only the Triangle-Faithfulness assumption. It is clear that the CPC orientation rule is provably correct given a correct skeleton, but it is unclear how to efficiently find the true skeleton given only the Triangle-Faithfulness assumption, nor indeed is it clear that the skeleton is in principle determinable (unless our conjecture is proved to be true). These questions are both theoretically interesting and potentially beneficial to practice and are in our view worth studying further.