Identifiability and transportability in dynamic causal networks

Abstract

In this paper, we propose a causal analog to the purely observational dynamic Bayesian networks, which we call dynamic causal networks. We provide a sound and complete algorithm for the identification of causal effects in dynamic causal networks, namely for computing the effect of an intervention or experiment given a dynamic causal network and probability distributions of passive observations of its variables, whenever possible. We note the existence of two types of hidden confounder variables that affect in substantially different ways the identification procedures, a distinction with no analog in either dynamic Bayesian networks or standard causal graphs. We further propose a procedure for the transportability of causal effects in dynamic causal network settings, where the result of causal experiments in a source domain may be used for the identification of causal effects in a target domain.

1 Introduction

Bayesian networks (BN) are a canonical formalism for representing probability distributions over sets of variables and reasoning about them. A useful extension for modeling phenomena with recurrent temporal behavior is the dynamic Bayesian networks (DBN). While regular BN is directed acyclic graphs, DBN may contain cycles, with some edges indicating dependence of a variable at time $t+1$ on another variable at time t. The cyclic graph in fact compactly represents an infinite acyclic graph formed by infinitely many replicas of the cyclic net, with some of the edges linking nodes in the same replica, and others linking nodes in consecutive replicas.

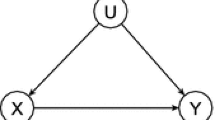
BN and DBN model conditional (in)dependences, so they are restricted to observational, noninterventional data or, equivalently, model association, not causality. Pearl’s causal graphical models and do-calculus [20] are a leading approach to modeling causal relations. They are formally similar to BN, as they are directed acyclic graphs with variables as nodes, but edges represent causality. A new notion is that of a hidden confounder, an unobserved variable X that causally influences two variables Y and Z so that the association between Y and Z may erroneously be taken for causal influence. Hidden confounders are unnecessary in BNs since the association between Y and Z represents their correlation, with no causality implied. Causal graphical models allow to consider the effect of interventions or experiments, that is externally forcing the values of some variables regardless of the variables that causally affect them, and studying the results.

The do-calculus is an algebraic framework for reasoning about such experiments: an expression $\Pr (Y|do(X))$ indicates the probability distribution of a set of variables Y upon performing an experiment on another set X. In some cases, the effect of such an experiment can be obtained given a causal network and some observational distribution only; this is convenient as some experiments may be impossible, expensive, or unethical to perform. When $\Pr (Y|do(X))$, for a given causal network, can be rewritten as an expression containing only observational probabilities, without a do operator, we say that it is identifiable. Huang and Valtorta [13] and Shpitser and Pearl [25] showed that a do-expression is identifiable if and only if it can be rewritten in this way with a finite number of applications of the three rules of do-calculus, and Shpitser and Pearl [25] proposed the ID algorithm which performs this transformation if at all possible, or else returns fail indicating non-identifiability.

In this paper, we use a causal analog of DBNs to model phenomena where a finite set of variables evolves over time, with some variables causally influencing others at the same time t but also others at time $t+1$. The infinite DAG representing these causal relations can be folded, when regular enough, into a directed graph, with some edges indicating intra-replica causal effects and other indicating effect on variables in the next replica. Central to this representation is of course the intuitive fact that causal relations are directed toward the future, and never toward the past.

Existing work on causal models usually focuses on two main areas: the discovery of causal models from data and causal reasoning given an already known causal model. Regarding the discovery of causal models from data in dynamic systems, Iwasaki and Simon [14] and Dash and Druzdzel [7] propose an algorithm to establish an ordering of the variables corresponding to the temporal order of propagation of causal effects. Methods for the discovery of cyclic causal graphs from data have been proposed using independent component analysis [15] and using local d-separation criteria [17]. Existing algorithms for causal discovery from static data have been extended to the dynamic setting by Chicharro and Panzeri [2] and Moneta and Spirtes [18]. Dahlhaus and Eichler [3], White et al. [33] and White and Lu [34] discuss the discovery of causal graphs from time series by including granger causality concepts into their causal models.

Dynamic causal systems are often modeled with sets of differential equations. However, Dash [4] and Dash and Druzdzel [5, 6] show the caveats of the discovery of causal models based on differential equations which pass through equilibrium states, and how causal reasoning based on the models discovered in such way may fail. Voortman et al. [32] propose an algorithm for the discovery of causal relations based on differential equations while ensuring those caveats due to system equilibrium states are taken into account. Timescale and sampling rate at which we observe a dynamic system play a crucial role in how well the obtained data may represent the causal relations in the system. Aalen et al. [1] discuss the difficulties of representing a dynamic system with a DAG built from discrete observations, and Gong et al. [12] argue that under some conditions the discovery of temporal causal relations is feasible from data sampled at lower rate than the system dynamics.

Our paper does not address the discovery of dynamic causal networks from data. Instead, we focus on causal reasoning: given the formal description of a dynamic causal network and a set of assumptions, our paper proposes algorithms that evaluate the modified trajectory of the system over time, after an experiment or intervention. We assume that the observation timescale is sufficiently small compared to the system dynamics, and that causal models include the non-equilibrium causal relations and not only those under equilibrium states. We assume that a stable set of causal dependencies exist which generate the system evolution along time. Our proposed algorithms take such models (and under these assumptions) as an input and predict the system evolution upon intervention on the system.

Regarding reasoning from a given dynamic causal model, one existing line of research is based on time series and granger causality concepts [9–11]. The authors in [24] use multivariate time series for identification of causal effects in traffic flow models. The work [16] discusses intervention in dynamic systems in equilibrium, for several types of time-discreet and time-continuous generating processes with feedback. Didelez [8] uses local independence graphs to represent time-continuous dynamic systems and identify the effect of interventions by re-weighting involved processes.

Existing work on causality does not thoroughly address causal reasoning in dynamic systems using do-calculus. The works [9–11] discuss back-door and front-door criteria in time series but do not extend to the full power of do-calculus as a complete logic for causal identification. One of the advantages of do-calculus is its nonparametric approach so that it leaves the type of functional relation between variables undefined. Our paper extends the use of do-calculus to time series, while requiring less restrictions than existing parametric causal analysis. Parametric approaches may require to differentiate the intervention impacts depending on the system state, non-equilibrium or equilibrium, while our nonparametric approach is generic across system states. Our paper shows the generic methods and explicit formulas revealed by the application of do-calculus to the dynamic setting. These methods and formulas simplify the identification of time-evolving effects and reduce the complexity of causal identification algorithms.

Required work is to precisely define the notion and semantics of do-calculus and hidden confounders in the dynamic setting and investigate whether and how existing do-calculus algorithms for identifiability of causal effects can be applied to the dynamic case.

As a running example (more for motivation than for its accurate modeling of reality), let us consider two roads joining the same two cities, where drivers choose every day to use one or the other road. The average travel delay between the two cities at any given day depends on the traffic distribution among the two roads. Drivers choose between a road or another depending on recent experience, in particular how congested a road was last time they used it. Figure 1 indicates these relations: the weather (w) has an effect on traffic conditions on a given day ($tr1,\,tr2$) which affects the travel delay on that same day (d). Driver experience influences the road choice next day, impacting tr1 and tr2. To simplify, we assume that drivers have short memory, being influenced by the conditions on the previous day only. This infinite network can be folded into a finite representation as shown in Fig. 2, where $+1$ indicates an edge linking two consecutive replicas of the DAG. Additionally, if one assumes the weather to be an unobserved variable then it becomes a hidden confounder as it causally affects two observed variables, as shown in Fig. 3. We call the hidden confounders with causal effect over variables in the same time slice static hidden confounders, and hidden confounders with causal effect over variables at different time slices dynamic hidden confounders. Our models allow for causal identification with both types of hidden confounders, as will be discussed in Sect. 4.

Fig. 1

Dynamic causal network. The weather w has an effect on traffic flows $tr1,\,tr2$, which in turn have an impact on the average travel delay d. Based on the travel delay, car drivers may choose a different road next time, having a causal effect on the traffic flows

This setting enables the resolution of causal effect identification problems where causal relations are recurrent over time. These problems are not solvable in the context of classic DBNs, as causal interventions are not defined in such models. For this we use causal networks and do-calculus. However, time dependencies cannot be modeled with static causal networks. As we want to predict the trajectory of the system over time after an intervention, we must use a dynamic causal network. Using our example, in order to reduce travel delay traffic controllers could consider actions such as limiting the number of vehicles admitted to one of the two roads. We would like to predict the effect of such action on the travel delay a few days later, e.g., $\Pr (d_{t+\alpha }|do(tr1_t))$.

Fig. 2

Compact representation of the dynamic causal network in Fig. 1 where $+1$ indicates an edge linking a variable in $G_t$ with a variable in $G_{t+1}$

Fig. 3

Dynamic causal network where tr1 and tr2 have a common unobserved cause, a hidden confounder. Since both variables are in the same time slice, we call it a static hidden confounder

Our contributions in this paper are:

• We introduce dynamic causal networks (DCN) as an analog of dynamic Bayesian networks for causal reasoning in domains that evolve over time. We show how to transfer the machinery of Pearl’s do-calculus [20] to DCN.

• We extend causal identification algorithms [25–27] to the identifiability of causal effects in DCN settings. Given the expression $P(Y_{t+\alpha }|do(X_t))$, the algorithms either compute an equivalent do-free formula or conclude that such a formula does not exist. In the first case, the new formula provides the distribution of variables Y at time $t+\alpha$ given that a certain experiment was performed on variables X at time t. For clarity, we present first an algorithm that is sound but not complete (Sect. 4), then give a complete one that is more involved to describe and justify (Sect. 5).

• Hidden confounder variables are central to the formalism of do-calculus. We observe a subtle difference between two types of hidden confounder variables in DCN (which we call static and dynamic). This distinction is genuinely new to DCN, as it appears neither in DBN nor in standard causal graphs, yet the presence or absence of hidden dynamic confounders has crucial impacts on the post-intervention evolution of the system over time and on the computational cost of the algorithms.

• Finally, we extend from standard Causal Graphs to DCN the results by Pearl and Bareinboim [22] on transportability, namely on whether causal effects obtained from experiments in one domain can be transferred to another domain with similar causal structure. This opens up the way to studying relational knowledge transfer learning [19] of causal information in domains with a time component.

2 Previous definitions and results

In this section, we review the definitions and basic results on the three existing notions that are the basis of our work: DBN, causal networks, and do-calculus. New definitions introduced in this paper are left for Sect. 3.

All formalisms in this paper model joint probability distributions over a set of variables. For static models (regular BN and causal networks), the set of variables is fixed. For dynamic models (DBN and DCN), there is a finite set of “metavariables,” meaning variables that evolve over time. For a metavariable X and an integer $t,\,X_t$ is the variable denoting the value of X at time t.

Let V be the set of metavariables for a dynamic model. We say that a probability distribution P is time-invariant if $P(V_{t+1}| V_t)$ is the same for every t. Note that this does not mean that $P(V_t) = P(V_{t+1})$ for every t, but rather that the laws governing the evolution of the variable do not change over time. For example, planets do change their positions around the Sun, but the Kepler–Newton laws that govern their movement do not change over time. Even if we performed an intervention (say, pushing the Earth away from the Sun for a while), these laws would immediately kick in again when we stopped pushing. The system would not be time-invariant if, e.g., the gravitational constant changed over time.

2.1 Dynamic Bayesian networks

Dynamic Bayesian networks (DBN) are graphical models that generalize Bayesian networks (BN) in order to model time-evolving phenomena. We rephrase them as follows.

Definition 1

A DBN is a directed graph D over a set of nodes that represent time-evolving metavariables. Some of the arcs in the graph have no label, and others are labeled “$+1$.” It is required that the subgraph G formed by the nodes and the unlabeled edges must be acyclic, therefore forming a directed acyclic graph (DAG). Unlabeled arcs denote dependence relations between metavariables within the same time step, and arcs labeled “$+1$” denote dependence between a variable at one time and another variable at the next time step.

Definition 2

A DBN with graph G represents an infinite Bayesian network $\hat{G}$ as follows. Timestamps t are the integer numbers; $\hat{G}$ will thus be a biinfinite graph. For each metavariable X in G and each time step t, there is a variable $X_t$ in $\hat{G}$. The set of variables indexed by the same t is denoted $G_t$ and called “the slice at time t.” There is an edge from $X_t$ to $Y_t$ iff there is an unlabeled edge from X to Y in G, and there is an edge from $X_t$ to $Y_{t+1}$ iff there is an edge labeled “$+1$” from X to Y in G. Note that $\hat{G}$ is acyclic.

The set of metavariables in G is denoted V(G), or simply V when G is clear from the context. Similarly $V_t(G)$ or $V_t$ denote the variables in the tth slice of G.

In this paper, we will also use transition matrices to model probability distributions. Rows and columns are indexed by tuples assigning values to each variable, and the (v, w) entry of the matrix represents the probability $P(V_{t+1} = w|V_t = v)$. Let $T_t$ denote this transition matrix. Then we have, in matrix notation, $P(V_{t+1})=T_t\,P(V_t)$ and, more in general, $P(V_{t+\alpha }) = (\prod _{i=t}^{t+\alpha -1}T_i) \, P(V_t)$. In the case of time-invariant distributions, all $T_t$ matrices are the same matrix T, so $P(V_{t+\alpha }) = T^{\alpha } P(V_t)$.

2.2 Causality and do-calculus

The notation used in our paper is based on causal models and do-calculus [20, 21].

Definition 3

(Causal model) A causal model over a set of variables V is a tuple $M=\langle V,U,F,P(U) \rangle$, where U is a set of random variables that are determined outside the model (“exogenous” or “unobserved” variables) but that can influence the rest of the model, $V=\{ V_1,V_2,\ldots V_n\}$ is a set of n variables that are determined by the model (“endogenous” or “observed” variables), F is a set of n functions such that $V_{k} = f_k(pa(V_{k}),U_{k}, \theta _k),\,pa(V_{k})$ are the parents of $V_{k}$ in $M,\,\theta _k$ are a set of constant parameters and P(U) is a joint probability distribution over the variables in U.

In a causal model, the value of each variable $V_k$ is assigned by a function $f_k$ which is determined by constant parameters $\theta _k$, a subset of V called the “parents” of $V_k$ ($pa(V_{k}$)), and a subset of U ($U_k$).

A causal model has an associated graphical representation (also called the “induced graph of the causal model”) in which each observed variable $V_k$ corresponds to a vertex; there is one edge pointing to $V_k$ from each of its parents, i.e., from the set of vertex ${pa(V_{k})}$, and there is a doubly-pointed edge between the vertex influenced by a common unobserved variable in U (see Fig. 3). In this paper, we call the unobserved variables in U “hidden confounders.”

Causal graphs encode the causal relations between variables in a model. The primary purpose of causal graphs is to help estimate the joint probability of some of the variables in the model upon controlling some other variables by forcing them to specific values; this is called an action, experiment, or intervention. Graphically this is represented by removing all the incoming edges (which represent the causes) of the variables in the graph that we control in the experiment. Mathematically, the do() operator represents this experiment on the variables. Given a causal graph where X and Y are sets of variables, the expression P(Y|do(X)) is the joint probability of Y upon doing an experiment on the controlled set X.

A causal relation represented by P(Y|do(X)) is said to be identifiable if it can be uniquely computed from an observed, non-interventional, distribution of the variables in the model. In many real-world scenarios it is impossible, impractical, unethical or too expensive to perform an experiment, thus the interest in evaluating its effects without actually having to perform the experiment.

The three rules of do-calculus [20] allow us to transform expressions with do() operators into other equivalent expressions, based on the causal relations present in the causal graph.

For any disjoint sets of variables $X,\,Y,\,Z$ and W:

• 1. $P(Y|Z,W,do(X))=P(Y|W,do(X))$ if $(Y\perp Z|X,W)_{G_{\overline{X}}}$

• 2. $P(Y|W,do(X),do(Z))=P(Y|Z,W,do(X))$ if $(Y\perp Z|X,W)_{G_{\overline{X}\underline{Z}}}$

• 3. $P(Y|W,do(X),do(Z))=P(Y|W,do(X))$ if $(Y\perp Z|X,W)_{G_{\overline{X}\overline{Z(W)}}}$

$G_{\overline{X}}$ is the graph G where all edges incoming to X are removed. $G_{\underline{Z}}$ is the graph G where all edges outgoing from Z are removed. Z(W) is the set of Z-nodes that are not ancestors of any W-nodes in $G_{\overline{X}}$.

Do-calculus was proven to be complete [13, 25] in the sense that if an expression cannot be converted into a do-free one by iterative application of the three do-calculus rules, then it is not identifiable.

2.3 The ID algorithm

The ID algorithm [25], and earlier versions by Tian and Pearl [29] and Tian [28] implement an iterative application of do-calculus rules to transform a causal expression P(Y|do(X)) into an equivalent expression without any do() terms in semi-Markovian causal graphs (with hidden confounders). This enables the identification of interventional distributions from non-interventional data in such graphs.

The ID algorithm is sound and complete [25] in the sense that if a do-free equivalent expression exists it will be found by the algorithm, and if it does not exist the algorithm will exit and provide an error.

The algorithm specifications are as follows. Inputs: a causal graph G, variable sets X and Y, and a probability distribution P over the observed variables in G; Output: an expression for P(Y|do(X)) without any do() terms, or fail.

Remark

In our algorithms of Sects. 4 and 5, we may invoke the ID algorithm with a slightly more complex input: P(Y|Z, do(X)) (note the “extra” Z to the right of the conditioning bar). In this case, we can solve the identification problem for the more complex expression with two calls to the ID algorithm using the following identity (definition of conditional probability):

$$\begin{aligned} P(Y|Z,do(X)) = \frac{P(Y,Z|do(X))}{P(Z|do(X))} \end{aligned}$$

Therefore, the expression P(Y|Z, do(X)) is identifiable if and only if both P(Y, Z|do(X)) and P(Z|do(X)) are [25].

Another algorithm for the identification of causal effects is given in [26].

The algorithms we propose in this paper show how to apply existing causal identification algorithms to the dynamic setting. In this paper, we will refer as “ID algorithm” any existing (non-dynamic) causal identification algorithm.

3 Dynamic causal networks and do-calculus

In this section, we introduce the main definitions of this paper and state several lemmas based on the application of do-calculus rules to DCNs.

In the Definition 3 of causal model, the functions $f_k$ are left unspecified and can take any suitable form that best describes the causal dependencies between variables in the model. In natural phenomenon, some variables may be time independent while others may evolve over time. However, rarely does Pearl specifically treat the case of dynamic variables.

The definition of dynamic causal network is an extension of Pearl’s causal model in Definition 3, by specifying that the variables are sampled over time, as in [30].

Definition 4

(Dynamic causal network) A dynamic causal network D is a causal model in which the set F of functions is such that $V_{k,t} = f_k(pa(V_{k,t}),U_{k,t-\alpha }, \theta _k)$; where $V_{k,t}$ is the variable associated with the time sampling t of the observed process $V_k$; $U_{k,t-\alpha }$ is the variable associated with the time sampling $t-\alpha$ of the unobserved process $U_k$; t and $\alpha$ are discreet values of time.

Note that $pa(V_{k,t})$ may include variables in any time sampling previous to t up to and including t, depending on the delays of the direct causal dependencies between processes in comparison with the sampling rate. $U_{k,t-\alpha }$ may be generated by a noise process or by a hidden confounder. In the case of noise, we assume that all noise processes $U_{k}$ are independent of each other and that their influence to the observed variables happens without delay, so that $\alpha =0$. In the case of hidden confounders, we assume $\alpha \ge 0$ as causes precede their effects.

To represent hidden confounders in DCN, we extend to the dynamic context the framework developed in [23] on causal model equivalence and latent structure projections. Let’s consider the projection algorithm [31], which takes a causal model with unobserved variables and finds an equivalent model (with the same set of causal dependencies), called a “dependency-equivalent projection,” but with no links between unobserved variables and where every unobserved variable is a parent of exactly two observed variables.

The projection algorithm in DCN works as follows. For each pair $(V_{m},V_{n})$ of observed processes, if there is a directed path from $V_{m,t}$ to $V_{n,t+\alpha }$ through unobserved processes then we assign a directed edge from $V_{m,t}$ to $V_{n,t+\alpha }$; however, if there is a divergent path between them through unobserved processes then we assign a bidirected edge, representing a hidden confounder.

In this paper, we represent all DCN by their dependency-equivalent projection. Also we assume the sampling rate to be adjusted to the dynamics of the observed processes. However, both the directed edges and the bidirected edges representing hidden confounders may be crossing several time steps depending on the delay of the causal dependencies in comparison with the sampling rate. We now introduce the concept of static and dynamic hidden confounder.

Definition 5

(Static hidden confounder) Let D be a DCN. Let $\beta$ be the maximal number of time steps crossed by any of the directed edges in D. Let $\alpha$ be the maximal number of time steps crossed by a bidirected edge representing a hidden confounder. If $\alpha \le \beta$ then the hidden confounder is called “static.”

Definition 6

(Dynamic hidden confounder) Let $D,\,\beta$ and $\alpha$ be as in Definition 5. If $\alpha >\beta$ then the hidden confounder is called “dynamic.” More specifically, if $\beta <\alpha \le 2\beta$ we call it “first-order” dynamic hidden confounder; if $\alpha >2\beta$ we call it “higher-order” dynamic hidden confounder.

In this paper, we consider three case scenarios in regards to DCN and their time invariance properties. If a DCN D contains only static hidden confounders, we can construct a first-order Markov process in discrete time, by taking $\beta$ (per Definition 5) consecutive time samples of the observed processes $V_k$ in D. This does not mean the DCN generating functions $f_k$ in Definition 4 are time-invariant, but that a first-order Markov chain can be built over the observed variables when marginalizing the static confounders over $\beta$ time samples.

In a second scenario, we consider DCN with first-order dynamic hidden confounders. We can still construct a first-order Markov process in discrete time, by taking $\beta$ consecutive time samples. However, we will see in later sections how the effect of interventions on this type of DCN has a different impact than on DCN with static hidden confounders.

Finally, we consider DCN with higher-order dynamic hidden confounders, in which case we may construct a first-order Markov process in discrete time by taking a multiple of $\beta$ consecutive time samples.

As we will see in later sections, the difference between these three types of DCN is crucial in the context of identifiability. Dynamic hidden confounders cause a time-invariant transition matrix to become dynamic after an intervention, e.g., the post-intervention transition matrix will change over time. However, if we perform an intervention on a DCN with static hidden confounders, the network will return to its previous time-invariant behavior after a transient period. These differences have a great impact on the complexity of the causal identification algorithms that we present.

Considering that causes precede their effects, the associated graphical representation of a DCN is a DAG. All DCN can be represented as a biinfinite DAG with vertices $V_{k,t}$; edges from $pa(V_{k,t})$ to $V_{k,t}$; and hidden confounders (bi-directed edges). DCN with static hidden confounders and DCN with first-order dynamic hidden confounders can be compactly represented as $\beta$ time samples (a multiple of $\beta$ time samples for higher-order dynamic hidden confounders) of the observed processes $V_{k,t}$; their corresponding edges and hidden confounders; and some of the directed and bi-directed edges marked with a “$+$1” label representing the dependencies with the next time slice of the DCN.

Definition 7

(Dynamic causal network identification) Let D be a DCN, and $t,\,t+\alpha$ be two time slices of D. Let X be a subset of $V_{t}$ and Y be a subset of $V_{t+\alpha }$. The DCN identification problem consists of computing the probability distribution P(Y|do(X)) from the observed probability distributions in D, i.e., computing an expression for the distribution containing no do() operators.

In this paper, we always assume that X and Y are disjoint and we only consider the case in which all intervened variables X are in the same time sample. It is not difficult to extend our algorithms to the general case.

The following lemma is based on the application of do-calculus to DCN. Intuitively, future actions have no impact on the past.

Lemma 1

(Future actions) Let D be a DCN. Take any sets $X \subseteq V_{t}$ and $Y \subseteq V_{t-\alpha }$, with $\alpha >0$. Then for any set Z the following equalities hold:

• 1. $P(Y|do(X),do(Z))=P(Y|do(Z))$

• 2. $P(Y|do(X))=P(Y)$

• 3. $P(Y|Z,do(X))=P(Y|Z)$ whenever $Z \subseteq V_{t-\beta }$ with $\beta > 0$.

Proof

The first equality derives from rule 3 and the proof in [25] that interventions on variables which are not ancestors of Y in D have no effect on Y. The second is the special case $Z=\emptyset$. We can transform the third expression using the equivalence

$$\begin{aligned} P(Y|Z,do(X))= P(Y,Z|do(X))/P(Z|do(X)); \end{aligned}$$

since Y and Z precede X in D, by rule 3 $P(Y,Z|do(X)) = P(Y,Z)$ and $P(Z|do(X)) = P(Z)$, and then the above equals $P(Y,Z)/P(Z) = P(Y|Z)$. $\square$

In words, traffic control mechanisms applied next week have no causal effect on the traffic flow this week.

The following lemma limits the size of the graph to be used for the identification of DCNs.

Lemma 2

Let D be a DCN with biinfinite graph $\hat{G}$. Let $t_x,\,t_y$ be two time points in $\hat{G}$. Let $G_{xy}$ be subgraph of $\hat{G}$ consisting of all time slices in between (and including$) G_{t_x}$ and $G_{t_y}$. Let $G_{lx}$ be graph consisting of all time slices in between (and including) $G_{t_x}$ and the left-most time slice connected to $G_{t_x}$ by a path of dynamic hidden confounders. Let $G_{{d}x}$ be the graph consisting of all time slices that are in $G_{lx}$ or $G_{xy}$. Let $G_{dx-}$ be the graph consisting of the time slice preceding $G_{{d}x}$. Let $G_\mathrm{id}$ be the graph consisting of all time slices in $G_{dx-}$ and $G_{{d}x}$. If P(Y|do(X)) is identifiable in $\hat{G}$ then it is identifiable in $G_\mathrm{id}$ and the identification provides the same result on both graphs.

Proof

Let $G_{\mathrm{past}}$ be the graph consisting of all time slices preceding $G_\mathrm{id}$, and $G_\mathrm{future}$ be the graph consisting of all time slices succeeding $G_\mathrm{id}$ in $\hat{G}$. By application of do-calculus rule 3, non-ancestors of Y can be ignored from $\hat{G}$ for the identification of P(Y|do(X)) [25], so $G_\mathrm{future}$ can be discarded. We will now show that identifying P(Y|do(X)) in the graph including all time slices of $G_{\mathrm{past}}$ and $G_\mathrm{id}$ is equal to identifying P(Y|do(X)) in $G_\mathrm{id}$.

By C-component factorization [25, 27], the set V of variables in a causal graph G can be partitioned into disjoint groups called C-components by assigning two variables to the same C-component if and only if they are connected by a path consisting entirely of hidden confounder edges, and

$$\begin{aligned} P(Y|do(X))=\sum _{V{\setminus } (Y\cup X)}\prod _{i} P(S_i|do(V{\setminus } S_i)) \end{aligned}$$

where $S_i$ are the C-components of $G_{An(Y)}{\setminus } X$ expressed as $C(G_{An(Y)}{\setminus } X)=\{S_1,\ldots ,S_k\}$ and $G_{An(Y)}$ is the subgraph of G including only the variables that are ancestors of Y. If and only if every C-component factor $P(S_i|do(V{\setminus } S_i))$ is identifiable then P(Y|do(X)) is identifiable.

C-component factorization can be applied to DCN. Let $V_{G_{\mathrm{past}}},\,V_{G_{dx-}}$ and $V_{G_{{d}x}}$ be the set of variables in $G_{\mathrm{past}},\,G_{dx-}$ and $G_{{d}x}$, respectively. Then $(V_{G_{\mathrm{past}}}\cup V_{G_{dx-}}) \cap (Y\cup X)=\emptyset$ and it follows that $V{\setminus } (Y\cup X)=V_{G_{\mathrm{past}}}\cup V_{G_{dx-}} \cup (V_{G_{{d}x}}{\setminus } (Y\cup X))$.

If $S_i \in C(G_{An(S_i)})$ the C-component factor $P(S_i|do(V{\setminus } S_i))$ is computed as [25]:

$$\begin{aligned} P(S_i|do(V{\setminus } S_i))=\prod _{\left\{ j|v_j\in S_i\right\} } P(v_j|v_{\pi }^{(j-1)}) \end{aligned}$$

Therefore there is a $P(v_j|v_{\pi }^{(j-1)})$ factor for each variable $v_j$ in the C-component, where $v_{\pi }^{(j-1)}$ is the set of all variables preceding $v_j$ in some topological ordering $\pi$ in G. stop Let $v_j$ be any variable $v_j \in V_{G_{\mathrm{past}}}\cup V_{G_{dx-}}$. There are no hidden confounder edge paths connecting $v_j$ to X, and so $v_j \in S_i \in C(G_{An(S_i)})$. Therefore the C-component factors $Q_{V_{G_{\mathrm{past}}}\cup V_{G_{dx-}}}$ of $V_{G_{\mathrm{past}}}\cup V_{G_{{d}x-}}$ can be computed as (chain rule of probability):

$$\begin{aligned}&Q_{V_{G_{\mathrm{past}}}\cup V_{G_{dx-}}}=\prod _{\{j|v_j\in V_{G_{\mathrm{past}}}\cup V_{G_{dx-}}\}} P(v_j|v_{\pi }^{(j-1)})\\&\quad =P(V_{G_{\mathrm{past}}}\cup V_{G_{dx-}}) \end{aligned}$$

We will now look into the C-component factors of $V_{G_{{d}x}}$. As the DCN is a first-order Markov process, the C-component factors of $V_{G_{{d}x}}$ can be computed as [25]:

$$\begin{aligned}&Q_{V_{G_{{d}x}}}=\prod _{i}\sum _{S_i{\setminus } Y} \prod _{\{j|v_j\in S_i\}} P\left( v_j|v_{\pi }^{(j-1)}\right) \\&\quad =\prod _{i}\sum _{S_i{\setminus } Y} \prod _{\{j|v_j\in S_i\}} P\left( v_j|v_{\pi }^{(j-1)}\cap (V_{G_{dx-}}\cup V_{G_{{d}x}})\right) \end{aligned}$$

So these factors have no dependency on $V_{G_{\mathrm{past}}}$, and therefore, P(Y|do(X)) can be marginalized over $V_{G_{\mathrm{past}}}$ and simplified as:

$$\begin{aligned}&P(Y|do(X))=\sum _{V{\setminus } (Y\cup X)}\prod _{i} P\left( S_i|do(V{\setminus } S_i)\right) \\&\quad =\sum _{V_{G_{\mathrm{past}}}\cup V_{G_{dx-}} \cup (V_{G_{{d}x}}{\setminus } (Y\cup X))}Q_{V_{G_{\mathrm{past}}}\cup V_{G_{dx-}}}Q_{V_{G_{{d}x}}}\\&\quad =\sum _{V_{G_{dx-}} \cup (V_{G_{{d}x}}{\setminus } (Y\cup X))}P(V_{G_{dx-}})Q_{V_{G_{{d}x}}} \end{aligned}$$

We can now replace $V_{G_{dx-}} \cup V_{G_{{d}x}}$ by $V_{G_\mathrm{id}}$ and define $S'_i$ as the C-component factors of $V_{G_\mathrm{id}}$ which leads to

$$\begin{aligned} P(Y|do(X))=\sum _{V_{G_\mathrm{id}}{\setminus } (Y\cup X)}\prod _{i} P\left( S'_i|do(V{\setminus } S'_i)\right) \end{aligned}$$

Therefore the identification of P(Y|do(X)) can be computed in the limited graph $G_\mathrm{id}$. Note that if a DCN contains no dynamic hidden confounders, then $G_\mathrm{id}$ consists of $G_{xy}$ and the time slice preceding it. In a DCN with dynamic hidden confounders, $G_\mathrm{id}$ may require additional time slices into the past, depending on the reach of hidden dynamic confounder paths. Note that $G_\mathrm{id}$ may include infinite time slices to the past, if hidden dynamic confounders connect with each other cyclically in successive time slices. However, in this paper we will consider only finite dynamic confounding. $\square$

This result is crucial to reduce the complexity of identification algorithms in dynamic settings. In order to describe the evolution of a dynamic system over time, after an intervention, we can run a causal identification algorithm over a limited number of time slices of the DCN, instead of the entire DCN.

4 Identifiability in dynamic causal networks

In this section, we analyze the identifiability of causal effects in the DCN setting. We first study DCNs with static hidden confounders and propose a method for identification of causal effects in DCNs using transition matrices. Then we extend the analysis and identification method to DCNs with dynamic hidden confounders. As discussed in Sect. 3, both the DCNs with static hidden confounders and with dynamic hidden confounders can be represented as a Markov chain. For graphical and notational simplicity, we represent these DCN graphically as recurrent time slices as opposed to the shorter time samples, on the basis that one time slice contains as many time samples as the maximal delay of any directed edge among the processes. Also for notational simplicity, we assume the transition matrix from one time slice to the next to be time-invariant; however, removing this restriction would not make any of the lemmas, theorems or algorithms invalid, as they are the result of graphical nonparametric reasoning.

Consider a DCN under the above assumptions, and let T be its time-invariant transition matrix from any time slice $V_{t}$ to $V_{t+1}$. We assume that there is some time $t_0$ such that the distribution $P(V_{t_0})$ is known. Fix now $t_x > t_0$ and a set $X \subseteq V_{t_x}$. We will now see how performing an intervention on X affects the distributions in D.

We begin by stating a series of lemmas that apply to DCNs in general.

Lemma 3

Let t be such that $t_0 \le t < t_x$, with $X \subseteq V_{t_x}$. Then $P(V_{t}|do(X)) = T^{t-t_0} P(V_{t_0})$. Namely, transition probabilities are not affected by an intervention in the future.

Proof

By Lemma 1, (2), $P(V_{t}|do(X))= P(V_{t})$ for all such t. By definition of T, this equals $T\,P(V_{t-1})$. Then induct on t with $P(V_{t_0}) = T^0 P(V_{t_0})$ as base. $\square$

Lemma 4

Assume that an expression $P(V_{t+\alpha }|V_{t},do(X))$ is identifiable for some $\alpha >0$. Let A be the matrix whose entries $A_{ij}$ correspond to the probabilities $P(V_{t+\alpha } = v_j|V_t = v_i, do(X))$. Then $P(V_{t+\alpha }|do(X)) = A\,P(V_t|do(X))$.

Proof

Case by case evaluation of A’s entries. $\square$

4.1 DCNs with static hidden confounders

DCNs with static hidden confounders contain hidden confounders that impact sets of variables within one time slice only, and contain no hidden confounders between variables at different time slices (see Fig. 3).

The following three lemmas are based on the application of do-calculus to DCNs with static hidden confounders. Intuitively, conditioning on the variables that cause time-dependent effects d-separates entire parts (future from past) of the DCN (Lemmas 5, 6, 7).

Lemma 5

(Past observations and actions) Let D be a DCN with static hidden confounders. Take any set X. Let $C \subseteq V_{t}$ be the set of variables in $G_t$ that are direct causes of variables in $G_{t+1}$. Let $Y \subseteq V_{t+\alpha }$ and $Z \subseteq V_{t-\beta }$, with $\alpha > 0$ and $\beta > 0$ (positive natural numbers). The following distributions are identical:

• 1. P(Y | do(X), Z, C)

• 2. P(Y | do(X), do(Z), C)

• 3. P(Y | do(X), C)

Proof

By the graphical structure of a DCN with static hidden confounders, conditioning on C d-separates Y from Z. The three rules of do-calculus apply, and (1) equals (3) by rule 1, (1) equals (2) by rule 2, and also (2) equals (3) by rule 3. $\square$

In our example, we want to predict the traffic flow Y in two days caused by traffic control mechanisms applied tomorrow X, and conditioned on the traffic delay today C. Any traffic controls Z applied before today are irrelevant, because their impact is already accounted for in C.

Lemma 6

(Future observations) Let $D,\,X$ and C be as in Lemma 5. Let $Y \subseteq V_{t-\alpha }$ and $Z \subseteq V_{t+\beta }$, with $\alpha > 0$ and $\beta > 0$, then:

$$\begin{aligned} P(Y|do(X),Z,C)=P(Y|do(X),C) \end{aligned}$$

Proof

By the graphical structure of a DCN with static hidden confounders, conditioning on C d-separates Y from Z and the expression is valid by rule 1 of do-calculus. $\square$

In our example, observing the travel delay today makes observing the future traffic flow irrelevant to evaluate yesterday’s traffic flow.

Lemma 7

If $t > t_x$ then $P(V_{t+1}|do(X)) = TP(V_{t}|do(X))$. Namely, transition probabilities are not affected by intervention more than one time unit in the past.

Proof

$P(V_{t+1}|do(X)) = T'\,P(V_{t}|do(X))$ where the elements of $T'$ are $P(V_{t+1}|V_t, do(X))$. As $V_{t}$ includes all variables in $G_{t}$ that are direct causes of variables in $G_{t+1}$, conditioning on $V_{t}$ d-separates X from $V_{t+1}$. By Lemma 5 we exchange the action do(X) by the observation X and so $P(V_{t+1}|V_t, do(X)) = P(V_{t+1}|V_t, X)$.

Moreover $V_t$ d-separates X from $V_{t+1}$, so they are statistically independent given $V_t$. Therefore

$$\begin{aligned} P(V_{t+1}|V_t, do(X)) = P(V_{t+1}|V_t, X) = P(V_{t+1}|V_t) \end{aligned}$$

which are the elements of matrix T as required. $\square$

Theorem 1

Let D be a DCN with static hidden confounders, and transition matrix T. Let $X\subseteq V_{t_x}$ and $Y\subseteq V_{t_y}$ for two time points $t_x < t_y$.

If the expression $P(V_{t_x+1}|V_{t_x-1}, do(X))$ is identifiable and its values represented in a transition matrix A, then P(Y|do(X)) is identifiable and

$$\begin{aligned} P(Y|do(X))=\sum _{V_{t_y}{\setminus } Y} T^{t_y-(t_x+1)}AT^{t_x-1-t_0}P(V_{t_0}). \end{aligned}$$

Proof

Applying Lemma 3, we obtain that

$$\begin{aligned} P(V_{t_x-1}|do(X)) = T^{t_x-1-t_0}P(V_{t_0}). \end{aligned}$$

We assumed that $P(V_{t_x+1}|V_{t_x-1}, do(X))$ is identifiable, and therefore Lemma 4 guarantees that

$$\begin{aligned} P(V_{t_x+1}|do(X)) = A\,P(V_{t_x-1}|do(X)) = A\,T^{t_x-1-t_0}P(V_{t_0}). \end{aligned}$$

Finally, $P(V_{t_y}|do(X)) = T^{(t_y-(t_x+1))} P(V_{t_x+1}|do(X))$ by repeatedly applying Lemma 7. P(Y|do(X)) is obtained by marginalizing variables in $V_{t_y}{\setminus } Y$ in the resulting expression $T^{t_y-(t_x+1)}AT^{t_x-1-t_0}P(V_{t_0})$. $\square$

As a consequence of Theorem 1, causal identification of D reduces to the problem of identifying the expression $P(V_{t_x+1}|V_{t_x-1},do(X))$. The ID algorithm can be used to check whether this expression is identifiable and, if it is, compute its joint probability from observed data.

Note that Theorem 1 holds without the assumption of transition matrix time- invariance by replacing powers of T with products of matrices $T_t$.

4.1.1 DCN-ID algorithm for DCNs with static hidden confounders

The DCN-ID algorithm for DCNs with static hidden confounders is given in Fig. 4. Its soundness is immediate from Theorem 1, the soundness of the ID algorithm [25], and Lemma 2.

Theorem 2

(Soundness) Whenever DCN-ID returns a distribution for P(Y|do(X)), it is correct. $\square$

Observe that line 2 of the algorithm calls ID with a graph of size 4|G|. By the remark of Sect. 2.3, this means two calls but notice that in this case we can spare the call for the “denominator” $P(V_{t_x-1}|do(X))$ because Lemma 1 guarantees $P(V_{t_x-1}|do(X)) = P(V_{t_x-1})$. Computing transition matrix A on line 3 has complexity $O((4k)^{(b+2)})$, where k is the number of variables in one time slice and b the number of bits encoding each variable. The formula on line 4 is the multiplication of $P(V_{t_0})$ by $n=(t_y-t_0)$ matrices, which has complexity $O(n\cdot b^2)$. To solve the same problem with the ID algorithm would require running it on the entire graph of size n|G| and evaluating the resulting joint probability with complexity $O((n\cdot k)^{(b+2)})$ compared to $O((4k)^{(b+2)}+n\cdot b^2)$ with DCN-ID.

If the problem we want to solve is evaluating the trajectory of the system over time

$$\begin{aligned} \left( P(V_{t_x+1}),P(V_{t_x+2}),P(V_{t_x+3}),\ldots P(V_{t_x+n})\right) \end{aligned}$$

after an intervention at time slice $t_x$, with ID we would need to run ID n times and evaluate the n outputs with overall complexity $O((k)^{(b+2)}+(2k)^{(b+2)}+(3k)^{(b+2)}+\cdots +(n\cdot k)^{(b+2)})$. Doing the same with DCN-ID requires running ID one time to identify $P(V_{t_x+1})$, evaluating the output and applying successive transition matrix multiplications to obtain the joint probability of the time slices thereafter, with resulting complexity $O((4k)^{(b+2)}+n\cdot b^2)$.

Fig. 4

DCN-ID algorithm for DCNs with static hidden confounders

4.2 DCNs with dynamic hidden confounders

We now discuss the case of DCNs with dynamic hidden confounders, that is, with hidden confounders that influence variables in consecutive time slices.

The presence of dynamic hidden confounders d-connects time slices, and we will see in the following lemmas how this may be an obstacle for the identifiability of the DCN.

If dynamic hidden confounders are present, Lemma 7 does no longer hold, since d-separation is no longer guaranteed. As a consequence, we cannot guarantee the DCN will recover its “natural” (non-interventional) transition probabilities from one cycle to the next after the intervention is performed.

Our statement of the identifiability theorem for DCNs with dynamic hidden confounders is weaker and includes in its assumptions those conditions that can no longer be guaranteed.

Theorem 3

Let D be a DCN with dynamic hidden confounders. Let T be its transition matrix under no interventions. We further assume that:

• 1. $P(V_{t_x+1}|V_{t_x-1}, do(X))$ is identifiable and its values represented in a transition matrix A

• 2. For all $t > t_x+1,\,P(V_{t}|V_{t-1}, do(X))$ is identifiable and its values represented in a transition matrix $M_t$

Then P(Y|do(X)) is identifiable and computed by

$$\begin{aligned} P(Y|do(X))=\sum _{V_{t_y}{\setminus } Y} \left[ \prod \limits _{t=t_x+2}^{t_y} M_t\right] \,A\,T^{t_x-1-t_0}P(V_{t_0}). \end{aligned}$$

Proof

Similar to the proof of Theorem 1. By Lemma 3, we can compute the distribution up to time $t_x-1$ as

$$\begin{aligned} P(V_{t_x-1}|do(X)) = T^{t_x-1-t_0}P(V_{t_0}). \end{aligned}$$

Using the first assumption in the statement of the theorem, by Lemma 4 we obtain

$$\begin{aligned} P(V_{t_x+1}|do(X)) = A\,T^{t_x-1-t_0}P(V_{t_0}). \end{aligned}$$

Then we compute the final $P(V_{t_y}|do(X))$ using the matrices $M_t$ from the statement of the theorem that allows us to compute probabilities for subsequent time slices. Namely,

$$\begin{aligned} P(V_{t_x+2}|do(X))&= M_{t_x+2}\,A\,T^{t_x-1-t_0}P(V_{t_0}), \\ P(V_{t_x+3}|do(X))&= M_{t_x+3}\,M_{t_x+2}\,A\,T^{t_x-1-t_0}P(V_{t_0}), \end{aligned}$$

and so on until we find

$$\begin{aligned} P(V_{t_y}|do(X)) = \left[ \prod \limits _{t=t_x+2}^{t_y} M_t\right] \,A\,T^{t_x-1-t_0}P(V_{t_0}). \end{aligned}$$

Finally, the do-free expression of P(Y|do(X)) is obtained by marginalization over variables of $V_{t_y}$ not in Y. $\square$

Again, note that Theorem 3 holds without the assumption of transition matrix time invariance by replacing powers of T with products of matrices $T_t$.

4.2.1 DCN-ID algorithm for DCNs with dynamic hidden confounders

The DCN-ID algorithm for DCNs with dynamic hidden confounders is given in Fig. 5.

Fig. 5

DCN-ID algorithm for DCNs with dynamic hidden confounders

Its soundness is immediate from Theorem 3, the soundness of the ID algorithm [25], and Lemma 2.

Theorem 4

(Soundness) Whenever DCN-ID returns a distribution for P(Y|do(X)), it is correct. $\square$

Notice that this algorithm is more expensive than the DCN-ID algorithm for DCNs with static hidden confounders. In particular, it requires $(t_y - t_x)$ calls to the ID algorithm with increasingly larger chunks of the DCN. To identify a single future effect P(Y|do(X)), it may be simpler to invoke Lemma 2 and do a unique call to the ID algorithm for the expression P(Y|do(X)) restricted to the causal graph $G_{\mathrm{id}}$. However, to predict the trajectory of the system over time after an intervention, the DCN-ID algorithm for dynamic hidden confounders directly identifies the post-intervention transition matrix and its evolution. A system characterized by a time-invariant transition matrix before the intervention may be characterized by a time-dependent transition matrix, given by the DCN-ID algorithm, after the intervention. This dynamic view offers opportunities for the analysis of the time evolution of the system, and conditions for convergence to a steady state.

To give an intuitive example of a DCN with dynamic hidden confounders, let’s consider three roads in which the traffic conditions are linked by hidden confounders from tr1 to tr2 the following day, and from tr2 to tr3 the day after. After applying control mechanisms to tr1, the traffic transition matrix to the next day is different than the transition matrix several days later, because it is not possible to d-separate the future from the controlling action by just conditioning on a given day. As a consequence, the identification algorithm must calculate every successive transition matrix in the future.

5 Complete DCN identifiability

In this section, we show that the identification algorithms as formulated in previous sections are not complete, and we develop complete algorithms for complete identification of DCNs. To prove completeness, we use previous results [25]. It is shown there that the absence of a structure called “hedge” in the graph is a sufficient and necessary condition for identifiability. We first define some graphical structures that lead to the definition of hedge, in the context of DCNs.

Definition 8

(C-component) Let D be a DCN. Any maximal subset of variables of D connected by bidirected edges (representing hidden confounders) is called a C-component.

Definition 9

(C-forest) Let D be a DCN and C one of its C-components. If all variables in C have at most one child, then C is called a C-forest. The set R of variables in C that have no descendants is called the C-forest root, and the C-forest is called R-rooted.

Definition 10

(Hedge) Let X and Y be sets of variables in D. Let F and $F'$ be two R-rooted C-forests such that $F'\subseteq F,\,F\cap X \ne \emptyset ,\,F'\cap X = \emptyset ,\,R\subset An(Y)_{D_{\bar{X}}}$. Then F and $F'$ form a Hedge for P(Y|do(X)) in D.

Notice that $An(Y)_{D_{\bar{X}}}$ refers to those variables that are ancestors of Y in the causal network D where incoming edges to X have been removed. We may drop the subscript as in An(Y) in which case we are referring to the ancestors of Y in the unmodified network D (in which case, the network we refer to should be clear from the context). Moreover we overload the definition of the ancestor function and we use An(Z, V) to refer to the ancestors of the union of sets Z and V, that is, $An(Z,V) = An(Z \cup V)$.

The presence of a hedge prevents the identifiability of causal graphs [25]. Also any non-identifiable graph necessarily contains a hedge. These results applied to DCNs lead to the following lemma.

Lemma 8

(DCN complete identification) Let D be a DCN with hidden confounders. Let X and Y be sets of variables in D. P(Y|do(X)) is identifiable iif there is no hedge in D for P(Y|do(X)).

We can show that the algorithms presented in the previous section, in some cases, introduce hedges in the sub-networks they analyze, even if no hedges existed in the original expanded network.

Lemma 9

The DCN-ID algorithms for DCNs with static hidden confounders (Sect. 4.1) and dynamic hidden confounders (Sect. 4.2) are not complete.

Proof

Let D be an DCN. Let X be such that D contains two R-rooted C-forests F and $F',\,F'\subseteq F,\,F\cap X \ne 0,\,F'\cap X = 0$. Let Y be such that $R\not \subset An(Y)_{D_{\bar{X}}}$. The condition for Y implies that D does not contain a hedge and is therefore identifiable by Lemma 8. Let the set of variables at time slice $t_x+1$ of $D,\,V_{t_x+1}$, be such that $R\subset An(V_{t_x+1})_{D_{\bar{X}}}$. By Definition 10, D contains a hedge for $P(V_{t_x+1}|V_{t_x-1},do(X))$. The identification of P(Y|do(X)) requires DCN-ID to identify $P(V_{t_x+1}|V_{t_x-1},do(X))$ which fails. $\square$

The proof of Lemma 9 provides the framework to build a complete algorithm for identification of DCNs.

Fig. 6

Identifiable dynamic causal network which the DCN-ID algorithm fails to identify. F and $F'$ are R-rooted C-forests, but since R is not an ancestor of Y there is no hedge for P(Y|do(X)). However R is an ancestor of $V_{t_x+1}$ and DCN-ID fails when finding the hedge for $P(V_{t_x+1}|V_{t_x-1}, do(X))$

Figure 6 shows an identifiable DCN that DCN-ID fails to identify.

5.1 Complete DCN identification algorithm with static hidden confounders

The DCN-ID algorithm can be modified so that no hedges are introduced if none existed in the original network. This is done at the cost of more complicated notation, because the fragments of network to be analyzed do no longer correspond to natural time slices. More delicate surgery is needed.

Lemma 10

Let D be a DCN with static hidden confounders. Let $X\subseteq V_{t_x}$ and $Y\subseteq V_{t_y}$ for two time slices $t_x < t_y$. If there is a hedge H for P(Y|do(X)) in D then $H\subseteq V_{t_x}$.

Proof

By definition of hedge, F and $F'$ are connected by hidden confounders to X. As D has only static hidden confounders $F,\,F'$ and X must be within $t_x$. $\square$

Lemma 11

Let D be a DCN with static hidden confounders. Let $X\subseteq V_{t_x}$ and $Y\subseteq V_{t_y}$ for two time slices $t_x < t_y$. Then P(Y|do(X)) is identifiable if and only if the expression $P(V_{t_x+1}\cap An(Y)|V_{t_x-1}, do(X))$ is identifiable.

Proof

(if) By Lemma 8, if

$$\begin{aligned}&P(V_{t_x+1}\cap An(Y)|V_{t_x-1},do(X)) \\&\quad =\frac{P(V_{t_x+1}\cap An(Y),V_{t_x-1}|do(X))}{P(V_{t_x-1})} \end{aligned}$$

is identifiable then there is no hedge for this expression in D. By Lemma 10 if D has static hidden confounders, a hedge must be within time slice $t_x$. If time slice $t_x$ does not contain two R-rooted C-forests F and $F'$ such that $F'\subseteq F,\,F\cap X \ne 0,\,F'\cap X = 0$, then there is no hedge for any set Y so there is no hedge for the expression P(Y|do(X)) which makes it identifiable. Now let’s assume time slice $t_x$ contains two R-rooted C-forests F and $F'$ such that $F'\subseteq F,\,F\cap X \ne 0,\,F'\cap X = 0$, then $R\not \subset An(V_{t_x+1}\cap An(Y),V_{t_x-1})_{D_{\bar{X}}}$. As R is in time slice $t_x$, this implies $R\not \subset An(Y)_{D_{\bar{X}}}$ and so there is no hedge for the expression P(Y|do(X)) which makes it identifiable.

(only if) By Lemma 8, if P(Y|do(X)) is identifiable then there is no hedge for P(Y|do(X)) in D. By Lemma 10 if D has static hidden confounders, a hedge must be within time slice $t_x$. If time slice $t_x$ does not contain two R-rooted C-forests F and $F'$ such that $F'\subseteq F,\,F\cap X \ne 0,\,F'\cap X = 0$, then there is no hedge for any set Y so there is no hedge for the expression

$$\begin{aligned}&P(V_{t_x+1}\cap An(Y)|V_{t_x-1},do(X)) \\&\quad =\frac{P(V_{t_x+1}\cap An(Y),V_{t_x-1}|do(X))}{P(V_{t_x-1})} \end{aligned}$$

which makes it identifiable. Now let’s assume time slice $t_x$ contains two R-rooted C-forests F and $F'$ such that $F'\subseteq F,\,F\cap X \ne 0,\,F'\cap X = 0$, then $R\not \subset An(Y)_{D_{\bar{X}}}$ (if $R\subset An(Y)_{D_{\bar{X}}} D$ would contain a hedge by definition). As R is in time slice $t_x,\,R\not \subset An(Y)_{D_{\bar{X}}}$ implies $R\not \subset An(V_{t_x+1}\cap An(Y))_{D_{\bar{X}}}$ and $R\not \subset An(V_{t_x+1}\cap An(Y),V_{t_x-1})_{D_{\bar{X}}}$ so there is no hedge for $P(V_{t_x+1}\cap An(Y)|V_{t_x-1}, do(X))$ which makes this expression identifiable. $\square$

Lemma 12

Assume that an expression $P(V'_{t+\alpha }|V_{t},do(X))$ is identifiable for some $\alpha >0$ and $V'_{t+\alpha }\subseteq V_{t+\alpha }$. Let A be the matrix whose entries $A_{ij}$ correspond to the probabilities $P(V'_{t+\alpha } = v_j|V_t = v_i, do(X))$. Then $P(V'_{t+\alpha }|do(X)) = A\,P(V_t|do(X))$.

Proof

Case by case evaluation of A’s entries. $\square$

Lemma 13

Let D be a DCN with static hidden confounders. Let $X\subseteq V_{t_x}$ and $Y\subseteq V_{t_y}$ for two time slices $t_x < t_y$. Then $P(Y|do(X))=\left[ \prod \nolimits _{t=t_x+2}^{t_y} M_t\right] P(V_{t_x+1}\cap An(Y)|do(X))$ where $M_t$ is the matrix whose entries correspond to the probabilities $P(V_{t}\cap An(Y) = v_j|V_{t-1}\cap An(Y) = v_i)$.

Proof

For the identification of P(Y|do(X)), we can restrict our attention to the subset of variables in D that are ancestors of Y. Then we repeatedly apply Lemma 7 on this subset from $t=t_x+2$ to $t=t_y$ until we find $P(V_{t_y}\cap An(Y)|do(X))=P(Y|do(X))$. $\square$

Theorem 5

Let D be a DCN with static hidden confounders and transition matrix T. Let $X\subseteq V_{t_x}$ and $Y\subseteq V_{t_y}$ for two time slices $t_x < t_y$. If P(Y|do(X)) is identifiable then $P(Y|do(X))=\left[ \prod \limits _{t=t_x+2}^{t_y} M_t\right] AT^{t_x-1-t_0}P(V_{t_0})$ where A is the matrix whose entries $A_{ij}$ correspond to $P(V_{t_x+1}\cap An(Y)|V_{t_x-1}, do(X))$ and $M_t$ is the matrix whose entries correspond to the probabilities $P(V_{t}\cap An(Y) = v_j|V_{t-1}\cap An(Y) = v_i)$.

Proof

Applying Lemma 3, we obtain that

$$\begin{aligned} P(V_{t_x-1}|do(X)) = T^{t_x-1-t_0}P(V_{t_0}). \end{aligned}$$

By Lemma 11 $P(V_{t_x+1}\cap An(Y)|V_{t_x-1}, do(X))$ is identifiable. Lemma 12 guarantees that $P(V_{t_x+1}\cap An(Y)|do(X)) = A\,P(V_{t_x-1}|do(X)) = A\,T^{t_x-1-t_0}P(V_{t_0})$. Then we apply Lemma 13 and obtain the resulting expression

$$\begin{aligned} P(Y|do(X))=\left[ \prod \limits _{t=t_x+2}^{t_y} M_t\right] AT^{t_x-1-t_0}P(V_{t_0}). \end{aligned}$$

$\square$

The cDCN-ID algorithm for identification of DCNs with static hidden confounders is given in Fig. 7.

Theorem 6

(Soundness and completeness) The cDCN-ID algorithm for DCNs with static hidden confounders is sound and complete.

Fig. 7

cDCN algorithm for DCNs with static hidden confounders

Proof

The completeness derives from Lemma 11 and the soundness from Theorem 5. $\square$

5.2 Complete DCN identification algorithm with dynamic hidden confounders

We now discuss the complete identification of DCNs with dynamic hidden confounders. First we introduce the concept of dynamic time span from which we derive two lemmas.

Definition 11

(Dynamic time span) Let D be a DCN with dynamic hidden confounders and $X\subseteq V_{t_x}$. Let $t_m$ be the maximal time slice d-connected by confounders to X; $t_m-t_x$ is called the dynamic time span of X in D.

Note that the dynamic time span of X in D can be in some cases infinite, the simplest case being when X is connected by a hidden confounder to itself at $V_{t_x+1}$. In this paper, we consider finite dynamic time spans only. We will label the dynamic time span of X as $t_{{d}x}$.

Lemma 14

Let D be a DCN with dynamic hidden confounders. Let $X,\,Y$ be sets of variables in D. Let $t_{{d}x}$ be the dynamic time span of X in D. If there is a hedge for P(Y|do(X)) in D, then the hedge does not include variables at $t>t_x+t_{{d}x}$.

Proof

By definition of hedge, F and $F'$ are connected by hidden confounders to X. The maximal time point connected by hidden confounders to X is $t_x+t_{{d}x}$. $\square$

Lemma 15

Let D be a DCN with dynamic hidden confounders. Let $X\subseteq V_{t_x}$ and $Y\subseteq V_{t_y}$ for two time slices $t_x, t_y$. Let $t_{{d}x}$ be the dynamic time span of X in D and $t_x + t_{{d}x} < t_y$. P(Y|do(X)) is identifiable if and only if $P(V_{t_x+t_{{d}x}+1}\cap An(Y)|V_{t_x-1}, do(X))$ is identifiable.

Proof

Similarly to the proof of Lemma 11, but replacing “static” by “dynamic,” $V_{t_x+1}$ by $V_{t_x+t_{{d}x}+1}$, Lemma 10 by Lemma 14, and “time slice $t_x$” by “time slices $t_x$ to $t_x+t_{{d}x}$.”

$\square$

Theorem 7

Let D be a DCN with dynamic hidden confounders and T be its transition matrix under no interventions. Let $X\subseteq V_{t_x}$ and $Y\subseteq V_{t_y}$ for two time slices $t_x, t_y$. Let $t_{{d}x}$ be the dynamic time span of X in D and $t_x + t_{{d}x} < t_y$. If P(Y|do(X)) is identifiable then:

• 1. $P(V_{t_x+t_{{d}x}+1}\cap An(Y)|V_{t_x-1}, do(X))$ is identifiable by matrix A

• 2. For $t > t_x+t_{{d}x}+1,\,P(V_{t}\cap An(Y)|V_{t-1}\cap An(Y), do(X))$ is identifiable by matrix $M_t$

• 3. $P(Y|do(X))=\left[ \prod \nolimits _{t=t_x+t_{{d}x}+2}^{t_y} M_t\right] \,A\,T^{t_x-1-t_0}P(V_{t_0})$

Proof

We obtain the first statement from Lemma 15 and Lemma 12. Then if $t > t_x+t_{{d}x}+1$, then the set $(V_{t}\cap An(Y),V_{t-1}\cap An(Y))$ has the same ancestors than Y within time slices $t_x$ to $t_x+t_{{d}x}+1$, so if P(Y|do(X)) is identifiable then $P(V_{t}\cap An(Y)|V_{t-1}\cap An(Y), do(X))$ is identifiable, which proves the second statement. Finally, we obtain the third statement similarly to the proof of Theorem 3 but using statements 1 and 2 as proved instead of assumed. $\square$

Fig. 8

cDCN algorithm for DCNs with dynamic hidden confounders

The cDCN-ID algorithm for DCNs with dynamic hidden confounders is given in Fig. 8.

Theorem 8

(Soundness and completeness) The cDCN-ID algorithm for DCNs with dynamic hidden confounders is sound and complete.

Proof

The completeness derives from the first and second statements of Theorem 7. The soundness derives from the third statement of Theorem 7. $\square$

6 Transportability in DCN

Pearl and Bareinboim [22] introduced the sID algorithm, based on do-calculus, to identify a transport formula between two domains, where the effect in a target domain can be estimated from experimental results in a source domain and some observations on the target domain, thus avoiding the need to perform an experiment on the target domain.

Let us consider a country with a number of alternative roads linking city pairs in different provinces. Suppose that the alternative roads are all consistent with the same causal model (such as the one in Fig. 3, for example) but have different traffic patterns (proportion of cars/trucks, toll prices, traffic light durations...). Traffic authorities in one of the provinces may have experimented with policies and observed the impact on, say, traffic delay. This information may be usable to predict the average travel delay in another province for a given traffic policy. The source domain (province where the impact of traffic policy has already been monitored) and target domain (new province) share the same causal relations among variables, represented by a single DCN (see Fig. 9).

Fig. 9

DCN with selection variables s and $s'$, representing the differences in the distribution of variables tr1 and tr1 in two domains $M_1$ and $M_2$ (two provinces in the same country). This model can be used to evaluate the causal impacts of traffic policy in the target domain $M_2$ based on the impacts observed in the source domain $M_1$

The target domain may have specific distributions of the toll price and traffic signs, which are accounted for in the model by adding a set of selection variables to the DCN, pointing at variables whose distribution differs among the two domains. If the DCN with the selection variables is identifiable for the traffic delay upon increasing the toll price, then the DCN identification algorithm provides a transport formula which combines experimental probabilities from the source domain and observed distributions from the target domain. Thus the traffic authorities in the new province can evaluate the impacts before effectively changing traffic policies. This amounts to relational knowledge transfer learning between the two domains [19].

Consider a DCN with static hidden confounders only. We have demonstrated already that for identification of the effects of an intervention at time $t_x$ we can restrict our attention to four time slices of the DCN, $t_x-2,\,t_x-1,\,t_x$, and $t_x+1$. Let $M_1$ and $M_2$ be two domains based on this same DCN, though the distributions of some variables in $M_1$ and $M_2$ may differ. Then we have

$$\begin{aligned} P_{M_2}(Y|do(X))=T_{M_2}^{t_y-(t_x+1)}A_{M_2}T_{M_2}^{t_x-1-t_0}P(V_{t_0}), \end{aligned}$$

where the entry ij of matrix $A_{M_2}$ corresponds to the transition probability $P_{M_2}(V_{t_x+1}=v_i|V_{t_x-1}=v_j, do(X))$.

By applying the identification algorithm sID, with selection variables, to the elements of matrix A, we then obtain a transport formula, which combines experimental distributions in $M_1$ with observational distributions in $M_2$. The algorithm for transportability of causal effects with static hidden confounders is given in Fig. 10.

Fig. 10

DCN-sID algorithm for the transportability in DCNs with static hidden confounders

For brevity, we omit the algorithm extension to dynamic hidden confounders, and the completeness results, which follow the same caveats already explained in the previous sections.

7 Experiments

In this section, we provide some numerical examples of causal effect identifiability in DCN, using the algorithms proposed in this paper.

In our first example, the DCN in Fig. 3 represents how the traffic between two cities evolves. There are two roads and drivers choose every day to use one or the other road. Traffic conditions on either road on a given day ($tr1,\,tr2$) affect the travel delay between the cities on that same day (d). Driver experience influences the road choice next day, impacting tr1 and tr2. For simplicity, we assume variables $tr1,\,tr2$ and d to be binary. Let’s assume that from Monday to Friday the joint distribution of the variables follow transition matrix $T_1$ while on Saturday and Sunday they follow transition matrix $T_2$. These transition matrices indicate the traffic distribution change from the previous day to the current day. This system is a DCN with static hidden confounders, and has a Markov chain representation as in Fig. 3.

$$\begin{aligned} T_1= & {} \left( \begin{matrix} 0.0&{}\quad 0.4&{}\quad 0.0&{}\quad 0.3&{}\quad 0.0&{}\quad 0.2&{}\quad 0.0&{}\quad 0.1 \\ 0.0&{}\quad 0.4&{}\quad 0.0&{}\quad 0.3&{}\quad 0.0&{}\quad 0.2&{}\quad 0.0&{}\quad 0.1 \\ 0.0&{}\quad 0.4&{}\quad 0.0&{}\quad 0.3&{}\quad 0.0&{}\quad 0.2&{}\quad 0.0&{}\quad 0.1 \\ 0.0&{}\quad 0.4&{}\quad 0.0&{}\quad 0.3&{}\quad 0.0&{}\quad 0.2&{}\quad 0.0&{}\quad 0.1 \\ 0.2&{}\quad 0.0&{}\quad 0.0&{}\quad 0.1&{}\quad 0.4&{}\quad 0.0&{}\quad 0.0&{}\quad 0.3 \\ 0.2&{}\quad 0.0&{}\quad 0.0&{}\quad 0.1&{}\quad 0.4&{}\quad 0.0&{}\quad 0.0&{}\quad 0.3 \\ 0.2&{}\quad 0.0&{}\quad 0.0&{}\quad 0.1&{}\quad 0.4&{}\quad 0.0&{}\quad 0.0&{}\quad 0.3 \\ 0.2&{}\quad 0.0&{}\quad 0.0&{}\quad 0.1&{}\quad 0.4&{}\quad 0.0&{}\quad 0.0&{}\quad 0.3 \\ \end{matrix} \right) \\ T_2= & {} \left( \begin{matrix} 0.1&{}\quad 0.0&{}\quad 0.3&{}\quad 0.1&{}\quad 0.2&{}\quad 0.2&{}\quad 0.0&{}\quad 0.1 \\ 0.1&{}\quad 0.0&{}\quad 0.3&{}\quad 0.1&{}\quad 0.2&{}\quad 0.2&{}\quad 0.0&{}\quad 0.1 \\ 0.1&{}\quad 0.0&{}\quad 0.3&{}\quad 0.1&{}\quad 0.2&{}\quad 0.2&{}\quad 0.0&{}\quad 0.1 \\ 0.1&{}\quad 0.0&{}\quad 0.3&{}\quad 0.1&{}\quad 0.2&{}\quad 0.2&{}\quad 0.0&{}\quad 0.1 \\ 0.0&{}\quad 0.2&{}\quad 0.1&{}\quad 0.0&{}\quad 0.1&{}\quad 0.3&{}\quad 0.3&{}\quad 0.0 \\ 0.0&{}\quad 0.2&{}\quad 0.1&{}\quad 0.0&{}\quad 0.1&{}\quad 0.3&{}\quad 0.3&{}\quad 0.0 \\ 0.0&{}\quad 0.2&{}\quad 0.1&{}\quad 0.0&{}\quad 0.1&{}\quad 0.3&{}\quad 0.3&{}\quad 0.0 \\ 0.0&{}\quad 0.2&{}\quad 0.1&{}\quad 0.0&{}\quad 0.1&{}\quad 0.3&{}\quad 0.3&{}\quad 0.0 \\ \end{matrix} \right) \end{aligned}$$

The average travel delay d during a two week period is shown in Fig. 11.

Fig. 11

Average travel delay of the DCN without intervention

Now let’s perform an intervention by altering the traffic on the first road tr1 and evaluate the subsequent evolution of the average travel delay d. We use the algorithm for DCNs with static hidden confounders. We trigger line 1 of the DCN-ID algorithm in Fig. 7 and build a graph consisting of four time slices $G'=(G_{t_x-2},G_{t_x-1},G_{t_x},G_{t_x+1})$ as shown in Fig. 12.

Fig. 12

Causal graph $G'$ consisting of four time slices of the DCN, from $t_x-2$ to $t_x+1$

The ancestors of any future delay at $t=t_y$ are all the variables in the DCN up to $t_y$, so in line 2 we run the standard ID algorithm for $\alpha =P(v_{10},v_{11},v_{12}|v_4,v_5,v_6, do(v_7))$ on $G'$, which returns the expression $\alpha$:

$$\begin{aligned} \sum _{v_1,v_2,v_3,v_8,v_9}\frac{P(v_1,v_2,...v_{12})\sum _{v_7,v9}P(v_7,v_8,v_9|v_4,v_5,v_6)}{P(v_4,v_5,v_6)\sum _{v_9}P(v_7,v_8,v_9|v_4,v_5,v_6)} \end{aligned}$$

Using this expression, line 3 of the algorithm computes the elements of matrix A. If we perform the intervention on a Thursday, the matrices A for $v_7=0$ and $v_7=1$ can be evaluated from $T_1$.

$$\begin{aligned} A_{v_7=0}= & {} \left( \begin{matrix} 0.0&{}\quad 0.4&{}\quad 0.0&{}\quad 0.3&{}\quad 0.0&{}\quad 0.2&{}\quad 0.0&{}\quad 0.1 \\ 0.0&{}\quad 0.4&{}\quad 0.0&{}\quad 0.3&{}\quad 0.0&{}\quad 0.2&{}\quad 0.0&{}\quad 0.1 \\ 0.0&{}\quad 0.4&{}\quad 0.0&{}\quad 0.3&{}\quad 0.0&{}\quad 0.2&{}\quad 0.0&{}\quad 0.1 \\ 0.0&{}\quad 0.4&{}\quad 0.0&{}\quad 0.3&{}\quad 0.0&{}\quad 0.2&{}\quad 0.0&{}\quad 0.1 \\ 0.0&{}\quad 0.4&{}\quad 0.0&{}\quad 0.3&{}\quad 0.0&{}\quad 0.2&{}\quad 0.0&{}\quad 0.1 \\ 0.0&{}\quad 0.4&{}\quad 0.0&{}\quad 0.3&{}\quad 0.0&{}\quad 0.2&{}\quad 0.0&{}\quad 0.1 \\ 0.0&{}\quad 0.4&{}\quad 0.0&{}\quad 0.3&{}\quad 0.0&{}\quad 0.2&{}\quad 0.0&{}\quad 0.1 \\ 0.0&{}\quad 0.4&{}\quad 0.0&{}\quad 0.3&{}\quad 0.0&{}\quad 0.2&{}\quad 0.0&{}\quad 0.1 \\ \end{matrix} \right) \\ A_{v_7=1}= & {} \left( \begin{matrix} 0.2&{}\quad 0.0&{}\quad 0.0&{}\quad 0.1&{}\quad 0.4&{}\quad 0.0&{}\quad 0.0&{}\quad 0.3 \\ 0.2&{}\quad 0.0&{}\quad 0.0&{}\quad 0.1&{}\quad 0.4&{}\quad 0.0&{}\quad 0.0&{}\quad 0.3 \\ 0.2&{}\quad 0.0&{}\quad 0.0&{}\quad 0.1&{}\quad 0.4&{}\quad 0.0&{}\quad 0.0&{}\quad 0.3 \\ 0.2&{}\quad 0.0&{}\quad 0.0&{}\quad 0.1&{}\quad 0.4&{}\quad 0.0&{}\quad 0.0&{}\quad 0.3 \\ 0.2&{}\quad 0.0&{}\quad 0.0&{}\quad 0.1&{}\quad 0.4&{}\quad 0.0&{}\quad 0.0&{}\quad 0.3 \\ 0.2&{}\quad 0.0&{}\quad 0.0&{}\quad 0.1&{}\quad 0.4&{}\quad 0.0&{}\quad 0.0&{}\quad 0.3 \\ 0.2&{}\quad 0.0&{}\quad 0.0&{}\quad 0.1&{}\quad 0.4&{}\quad 0.0&{}\quad 0.0&{}\quad 0.3 \\ 0.2&{}\quad 0.0&{}\quad 0.0&{}\quad 0.1&{}\quad 0.4&{}\quad 0.0&{}\quad 0.0&{}\quad 0.3 \\ \end{matrix} \right) \end{aligned}$$

In line 4, we find that transition matrices $M_t$ are the same than for the DCN without intervention. Figure 13 shows the average travel delay without intervention, and with intervention on the traffic conditions of the first road.

Fig. 13

Average travel delay of the DCN without intervention, and with interventions $tr1=0$ and $tr1=1$ on the first Thursday

In a second numerical example, we consider that the system is characterized by a unique transition matrix T and the delay d tends to a steady state. We measure d without intervention and with intervention on tr1 at $t=15$. The system’s transition matrix T is shown below:

$$\begin{aligned} T= & {} \left( \begin{matrix} 0.02&{}\quad 0&{}\quad 0.03&{}\quad 0&{}\quad 0.26&{}\quad 0.13&{}\quad 0.34&{}\quad 0.22 \\ 0.02&{}\quad 0&{}\quad 0.03&{}\quad 0&{}\quad 0.26&{}\quad 0.13&{}\quad 0.34&{}\quad 0.22 \\ 0.02&{}\quad 0&{}\quad 0.03&{}\quad 0&{}\quad 0.26&{}\quad 0.13&{}\quad 0.34&{}\quad 0.22 \\ 0.02&{}\quad 0&{}\quad 0.03&{}\quad 0&{}\quad 0.26&{}\quad 0.13&{}\quad 0.34&{}\quad 0.22 \\ 0.34&{}\quad 0.1&{}\quad 0.24&{}\quad 0.21&{}\quad 0&{}\quad 0.02&{}\quad 0.09&{}\quad 0 \\ 0.34&{}\quad 0.1&{}\quad 0.24&{}\quad 0.21&{}\quad 0&{}\quad 0.02&{}\quad 0.09&{}\quad 0 \\ 0.34&{}\quad 0.1&{}\quad 0.24&{}\quad 0.21&{}\quad 0&{}\quad 0.02&{}\quad 0.09&{}\quad 0 \\ 0.34&{}\quad 0.1&{}\quad 0.24&{}\quad 0.21&{}\quad 0&{}\quad 0.02&{}\quad 0.09&{}\quad 0 \\ \end{matrix} \right) \end{aligned}$$

Figure 14 shows the evolution of d with no intervention and with intervention.

Fig. 14

Average d of the DCN without intervention and with intervention on tr1 at $t=15$

As shown in the examples, the DCN-ID algorithm calls ID only once with a graph of size 4|G| and evaluates the elements of matrix A with complexity $O((4k)^{(b+2)}$, where $k=3$ is the number of variables per slice and $b=1$ is the number of bits used to encode the variables. The rest is the computation of transition matrix multiplications, which can be done with complexity $O(n.b^2)$, with $n=40-15$ in example 2. To obtain the same result with the ID algorithm by brute force, we would require processing n times the identifiability of a graph of size 40|G|, with overall complexity $O((k)^{(b+2)}+(2k)^{(b+2)}+(3k)^{(b+2)}+\cdots +(n.k)^{(b+2)})$.

8 Conclusions and future work

This paper introduces dynamic causal networks and their analysis with do-calculus, so far studied thoroughly only in static causal graphs. We extend the ID algorithm to the identification of DCNs and remark the difference between static versus dynamic hidden confounders. We also provide an algorithm for the transportability of causal effects from one domain to another with the same dynamic causal structure.

For future work, note that in the present paper we have assumed all intervened variables to be in the same time slice; removing this restriction may have some moderate interest. We also want to extend the introduction of causal analysis to a number of dynamic settings, including Hidden Markov Models, and study properties of DCNs in terms of Markov chains (conditions for ergodicity, for example). Finally, evaluating the distribution returned by ID is in general unfeasible (exponential in the number of variables and domain size); identifying tractable sub-cases or feasible heuristics is a general question in the area.