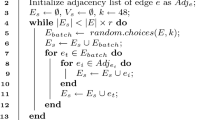Discovering Hierarchical Subgraphs of K-Core-Truss

Abstract

Discovering dense subgraphs in a graph is a fundamental graph mining task, which has a wide range of applications in social networks, biology and visualization to name a few. Even the problem of computing most cohesive subgraphs is NP-hard (like clique, quasi-clique, k-densest subgraph), there exists a polynomial time algorithm for computing the k-core and k-truss. In this paper, we propose a novel dense subgraph model, ${\mathsf {k}}$-${\mathsf {core}}$-${\mathsf {truss}}$, which leverages on a new type of important edges based on the basis of k-core and k-truss. We investigate the structural properties of the ${\mathsf {k}}$-${\mathsf {core}}$-${\mathsf {truss}}$ model. Compared to k-core and k-truss, ${\mathsf {k}}$-${\mathsf {core}}$-${\mathsf {truss}}$ can significantly discover the interesting and important structural information out the scope of k-core and k-truss. We study two useful problems of ${\mathsf {k}}$-${\mathsf {core}}$-${\mathsf {truss}}$ decomposition and ${\mathsf {k}}$-${\mathsf {core}}$-${\mathsf {truss}}$ search. In particular, we develop a k-core-truss decomposition algorithm to find all ${\mathsf {k}}$-${\mathsf {core}}$-${\mathsf {truss}}$ in a graph G by iteratively removing edges with the smallest ${\mathsf {degree}}$-${\mathsf {support}}$. In addition, we offer a ${\mathsf {k}}$-${\mathsf {core}}$-${\mathsf {truss}}$ search algorithm to identifying a particular ${\mathsf {k}}$-${\mathsf {core}}$-${\mathsf {truss}}$ containing a given query node such that the core number k is the largest. Extensive experiments on several web-scale real-world datasets show the effectiveness and efficiency of ${\mathsf {k}}$-${\mathsf {core}}$-${\mathsf {truss}}$ model and proposed algorithms.

1 Introduction

Graph model is widely used to represent connection relationships between entities in a wide variety of domains such as social and web networks, biology, communication networks, and so on [1]. In the analysis of massive graphs, it is important to discover various dense subgraphs for efficient and effective analysis of a network, due to the large size of the network [2]. Identifying cohesive subgraphs is a fundamental graph-theoretic problem, which lies in the heart of many graph mining applications, ranging from community mining in social networks [3,4,5,6,7], to real-time story identification in streaming news [8, 9], detecting regulatory motifs in DNA [10], graph visualization [11], and distance oracle indexing [12, 13].

In the literature, numerous definitions of dense subgraphs have been proposed. A classic definition is k-clique that is a complete graph of k vertices with $\frac{k(k-1)}{2}$ edges [14, 15]. However, the definition of k-clique is usually too rigid for real applications. Thus, several more relaxed forms of dense subgraphs are proposed, such as k-plex [16], n-clan [17], n-club [17], and quasi-clique [18]. Unfortunately, the problems of computing all these dense subgraphs are NP-hard. Another interesting problem of dense subgraph mining is to find the densest subgraph of a given graph [19]. It is known that this problem can be solved optimally in polynomial time complexity using parametric flow [20]. But, if one wants to find a large densest subgraph containing at least k nodes, the problem becomes NP-hard [21].

Thereto, the definitions of k-core [22, 23] and k-truss [2, 3] have been recently proposed for a good balance of cohesive structure and efficient computations. A k-core of a graph G is the largest subgraph of G such that every vertex has at least k neighbors in this subgraph. A k-truss of a graph G is the largest subgraph of G such that each edge is contained in at least $k-2$ triangles in this subgraph. Graph decomposition of finding all k-cores and all k-truss both can be done in polynomial time. On one hand, k-core and k-truss both are hierarchical subgraphs that represent the cores of a network at different levels of granularity, with regard to number k. In this sense, k-core and k-truss are similar. On the other hand, basis elements of constructing k-core and k-truss are different. k-core is defined on the important vertices having degree at least k, whereas k-truss is defined on the important edges that are involved in several stable and strong triangle relationships. Thus, let us reconsider the importance of an relationship between two endpoints. Intuitively, if two vertices have more common neighbors, their relationship is stronger, which is overlooked in k-core model; Meanwhile, vertices tends to be more important if they have a higher degree in graphs. Thus, if two vertices with high degrees, their relationship is also regarded as a strong connection. Such these important relationships are neglected in k-truss model.

Fig. 1

An example of graph $H_1$ with ${\mathsf {k}}$-${\mathsf {core}}$-${\mathsf {truss}}$, k-core, and k-truss, where $k=3$ and parameter $\alpha\, {=}\,1$

In this paper, we study a novel dense subgraph, ${\mathsf {k}}$-${\mathsf {core}}$-${\mathsf {truss}}$, which are based on a new concept of important edges. Specifically, given a parameter $\alpha >0$, the importance of an edge $e=(u,v)$ in a graph G is defined as the maximum one between the value equaling to $\alpha$ times minimum degree of v and u, and the number of triangles containing e plus 2. Then, the ${\mathsf {k}}$-${\mathsf {core}}$-${\mathsf {truss}}$ of a graph G is the largest subgraph of G that every edge has the importance value at least k in this subgraph. For instance, consider the graph $H_1$ in Fig. 1. This whole graph is a 3-core-truss for $\alpha =1$. It is because that for every edge e, e is contained in at least one triangle, or its two endpoints have degree at least 3. In addition, the whole graph of 3-core-truss contains two overlapping subgraphs of 3-core and 3-truss. By the definition of 3-core, it is obvious that the vertex $v_5$ with the degree of 2 does not belong to 3-core. Meanwhile, the edge $e=(v_{12}, v_{13})$ is not contained in any triangle, indicating that it does not belong to 3-truss. In light of the above, mining and querying ${\mathsf {k}}$-${\mathsf {core}}$-${\mathsf {truss}}$ in graphs is a pressing need, which is not simply dominated by the k-core and k-truss.

To summarize, we make the following contributions:

• We give a novel dense subgraph, ${\mathsf {k}}$-${\mathsf {core}}$-${\mathsf {truss}}$, and motivate two problems of ${\mathsf {k}}$-${\mathsf {core}}$-${\mathsf {truss}}$ decomposition and ${\mathsf {k}}$-${\mathsf {core}}$-${\mathsf {truss}}$ search. We also formally formulate the problems (Sect. 2).

• We analyze the structural properties of ${\mathsf {k}}$-${\mathsf {core}}$-${\mathsf {truss}}$, and show that the ${\mathsf {k}}$-${\mathsf {core}}$-${\mathsf {truss}}$ can generalize the basic notions of k-core and k-truss with the proper parameters. In addition, we also give a proof of the inequality between the core-truss number and the maximum one of core number and truss number (Sect. 3).

• We develop a ${\mathsf {k}}$-${\mathsf {core}}$-${\mathsf {truss}}$ decomposition algorithm to find all ${\mathsf {k}}$-${\mathsf {core}}$-${\mathsf {truss}}$ in a graph G by iteratively removes edges with the smallest ${\mathsf {degree}}$-${\mathsf {support}}$. For the application of community search, we also design a ${\mathsf {k}}$-${\mathsf {core}}$-${\mathsf {truss}}$ search algorithm for identifying a particular ${\mathsf {k}}$-${\mathsf {core}}$-${\mathsf {truss}}$ containing a given query node with the highest k. In addition, we analyze the time and space complexity of proposed algorithms (Sect. 4).

• We conduct extensive experiments on five web-scale real-world datasets, and show that our ${\mathsf {k}}$-${\mathsf {core}}$-${\mathsf {truss}}$ algorithms can efficiently and effectively find cohesive substructures over real-world networks, which can significantly discover the interesting and important relationships out the scope of k-core and k-truss (Sect. 5).

In addition, we review the related work in Sect. 6, and conclude this paper in Sect. 7.

2 Problem Statement

Consider an undirected graph $G=(V, E)$ where V and E denote the node set and edge set, respectively. We denote the number of nodes by $n = |V|$ and the number of edges in G by $m = |E|$. The set of neighbors of a vertex v is denoted by N(v), i.e., $N(v) =\{u\in V: (v, u)\in E\}$. We use $d_{max}$ to represent the maximum vertex degree in graph G.

Table 1 Important Notations and Descriptions

Given a graph $H=(V_H, E_H)$, H is a subgraph of G iff $V_H \subseteq V$ and $E_H = \{(u, v)|u, v \in V_H, (u, v) \in E\}$. For a vertex $v\in V(H)$, the set of neighbors of vertex v is denoted by $N_{H}(v)=\{u\in V_H: (v, u)\in E_H\}$. Thus, the degree of v in H is defined as $\deg _{H}(v) =|N_{H}(v)|$. A triangle is a cycle of length 3 in graph. Let v, u, w be the three vertices on the cycle, then we use $\triangle _{uvw}$ to represent this triangle. For an edge $e(u,v)\in E(H)$, the support of an edge e, is defined as the number of triangles containing e, denoted by $\sup _{H}(e) = |\{\triangle _{uvw}: (u,w), (v,w)\in E_H\}|$. In this paper, w.l.o.g, we assume that the graph G we consider is connected, which implies $m\ge n-1$. The important definitions and descriptions in this paper are shown in Table  1. In the following, we define the ${\mathsf {degree}}$ for an edge based on the definition of vertex degree.

Definition 1

(Degree of an Edge) Given a subgraph $H\subseteq G$, the ${\mathsf {degree}}$ of an edge $e(u, v)\in E_H$ is denoted by $\deg _{H}(e)=\min \{\deg _H(v), \deg _H(u)\}$.

Example 1

Consider the graph G in Fig. 2. The vertex $v_5$ has 3 neighbors as $N(v_5)=\{v_3,v_8,v_9\}$, and the degree of vertex $v_5$ in graph G is $\deg _{G}(v_5) =3$. The graph $H_1$ in Fig. 2 is a subgraph of G. For a vertex $v_5 \in V_{H_1}$, the degree of vertex $v_5$ in $H_1$ is 2, i.e., $\deg _{H_1}(v_5) =2$. For an edge $e=(v_5, v_8)$ in $H_1$, the degree of an edge e is $\deg _{H}(e)=\min \{\deg _H(v_5), \deg _H(v_8)\} = 2$ by the definition  1, as $\deg _{H_1}(v_8) =6$ holds.

Based on the definitions of degree and support for an edge, we give a new definition of ${\mathsf {degree}}$-${\mathsf {support}}$ as follow.

Definition 2

(Degree-Support) For a subgraph $H\subseteq G$ and a given number $\alpha \ge 0$, the ${\mathsf {degree}}$-${\mathsf {support}}$ of an edge $e(u, v)\in E_H$ is denoted by ${{\mathsf {degsup}}} _H(e) =$ $\max$ $\{\sup _H(e)+2,$ $\alpha \cdot \deg _H(e)\}$.

The ${\mathsf {degree}}$-${\mathsf {support}}$ of an edge e(u, v), ${{\mathsf {degsup}}} _H(e)$, represents the strength of the connection between vertices v and u in graph topology. The underlying principles of ${{\mathsf {degsup}}} _H(e)$ contain twofold. On the one hand, a triangle indicates two vertices have a common neighbor, which shows a strong and stable connection among three vertices. Intuitively, if two vertices have more common neighbors with a larger $\sup _H(e)$, their relationship is stronger. On the other hand, if one vertex has a higher degree with more connections, the vertex tends to be more important in this graph. Thus, two endpoints of an edge both have high degree, their relationship is also regarded as a strong connection. Due to different measurements of support and degree, we invoke a parameter $\alpha$ to adjust the relative weight of degree, w.r.t. the support. The larger $\alpha$ is, the more important the degree is. Unless otherwise specified, we assume $\alpha =1$ throughout this whole paper.

Example 2

In Fig. 2, there are several triangles such as $\triangle _{v_5,v_8,v_9}$, $\triangle _{v_6,v_8,v_9}$, $\triangle _{v_7,v_8,v_9}$, and so on. For each one of these triangles, two vertices have a common neighbor. For an edge $e=(v_5, v_8)$ in $H_1$, the edge support of e is $sup_{H_1}(e)=1$. For $\alpha =1$ and $\deg _{H_1}(e) = 2$, the ${\mathsf {degree}}$-${\mathsf {support}}$ of edge e is ${{\mathsf {degsup}}} _{H_1}(e) =$ $\max$ $\{\sup _{H_1}(e)+2,$ $\alpha \cdot \deg _{H_1}(e)\}=3$. Then, if we adjust the parameter $\alpha$ to a higher value as $\alpha =2$, ${{\mathsf {degsup}}} _{H_1}(e) =$ $\max$ $\{\sup _{H_1}(e)+2,$ $2 \cdot \deg _{H_1}(e)\}=4$.

On the basis of the definition of ${\mathsf {degree}}$-${\mathsf {support}}$, we define the ${\mathsf {k}}$-${\mathsf {core}}$-${\mathsf {truss}}$ in a graph G as follows.

Definition 3

(K-Core-Truss) Given a subgraph $H\subseteq G$, a parameter $\alpha \ge 0$ and an integer $k\ge 2$, a ${\mathsf {k}}$-${\mathsf {core}}$-${\mathsf {truss}}$ H is the maximal subgraph of G, in which each edge e satisfies ${{\mathsf {degsup}}} _H(e)\ge k$. Let $CT_{k}$ represents the ${\mathsf {k}}$-${\mathsf {core}}$-${\mathsf {truss}}$ of G for a specific k.

By definition, the 2-core-truss is simply G itself, i.e., $CT_2 = G$. We discuss several natural structural properties for ${\mathsf {k}}$-${\mathsf {core}}$-${\mathsf {truss}}$ in Sect. 3 and provide several rational principle for designing our dense subgraph model.

Base on the definition of ${\mathsf {k}}$-${\mathsf {core}}$-${\mathsf {truss}}$, we can make a definition of core-truss number as follows.

Definition 4

(Core-Truss Number) For an edge e in graph $G=(V, E)$, the core-truss number of e, denote by ct(e) = $max\{k : e\in E_{CT_k}\}$.

For an given edge e with $ct(e)=k$, we have $e\in E_{CT_k}$, but $e\notin E_{CT_{k+1}}$. We use $k_{max}$ to represent the maximum core-truss number of any edge in G, i.e., $k_{max}= \max \{ct(e): e\in E\}$. We use the following example to illustrate the concept of ${\mathsf {k}}$-${\mathsf {core}}$-${\mathsf {truss}}$ and core-truss number.

Fig. 2

A running example of graph G. The parameter $\alpha\, {=}\,1$

Example 3

Consider an undirected graph G shown in Fig. 2. The graph G has 23 nodes named from $v_1$ to $v_{23}$. Assume that the parameter $\alpha$ is set to 1. We can see that every vertex has degree at least 2. Thus, for each edge $e\in E$, the ${\mathsf {degree}}$-${\mathsf {support}}$ of e as ${{\mathsf {degsup}}} _G(e)\ge 2$ holds. By the definition 3, the entire graph G is 2-core-truss, i.e., G =$CT_2$. In addition, the edge $(v_3, v_4)$ is not contained in any triangle, and the degree of $(v_3, v_4)$ has $\deg ((v_3, v_4))=2$. Thus, the edge $(v_3, v_4)$ does not belong to 3-core-truss, indicating the core-truss number $ct((v_3, v_4))=2$. The 3-core-truss of G is depicted in light green color in Fig. 2, which is consisted of three connected components $H_1$, $H_2$, and $H_3$. Moreover, we can see that the subgraph $H_2$ of G is 4-core-truss as $CT_4$, because $H_2$ is a 4-clique and every edge e of $H_2$ is contained in 2 triangles with ${{\mathsf {degsup}}} _{H_2}(e) \ge \sup _{H_2}(e) = 2+2=4$.

In this paper, we study two different but related problems of ${\mathsf {k}}$-${\mathsf {core}}$-${\mathsf {truss}}$ decomposition and ${\mathsf {k}}$-${\mathsf {core}}$-${\mathsf {truss}}$ search in a graph.

The first problem is ${\mathsf {k}}$-${\mathsf {core}}$-${\mathsf {truss}}$ decomposition. The problem is to find all ${\mathsf {k}}$-${\mathsf {core}}$-${\mathsf {truss}}$ $CT_{k}$ for $2\le k \le k_{max}$ in graph G. As a cohesive subgraph of ${\mathsf {k}}$-${\mathsf {core}}$-${\mathsf {truss}}$, ${\mathsf {k}}$-${\mathsf {core}}$-${\mathsf {truss}}$ decomposition identifies various cohesive subgraphs for efficient and effective analysis of a complex network. The problem is formulated as follows.

Problem 1

Given a graph $G=(V, E)$, a parameter $\alpha$ , the problem of ${\mathsf {k}}$-${\mathsf {core}}$-${\mathsf {truss}}$ decomposition is to find all ${\mathsf {k}}$-${\mathsf {core}}$-${\mathsf {truss}}$ $CT_{k}$ in G for $2\le k \le k_{max}$.

Example 4

Take the graph G in Fig. 2 with number $\alpha =1$ as an example. The problem of ${\mathsf {k}}$-${\mathsf {core}}$-${\mathsf {truss}}$ is to find all possible ${\mathsf {k}}$-${\mathsf {core}}$-${\mathsf {truss}}$ $CT_{k}$ of G. Specifically, the $CT_{2}$ is the whole graph G; the $CT_{3}$ is the subgraph of G that are composed of three components $H_1$, $H_2$, $H_3$; the $CT_{4}$ is exactly the subgraph $H_2$. There exists no 5-core-truss in G.

Fig. 3

The $CT_3$ contains node 8

The second problem to study is ${\mathsf {k}}$-${\mathsf {core}}$-${\mathsf {truss}}$ search. For a given query node, the problem is to find a particular ${\mathsf {k}}$-${\mathsf {core}}$-${\mathsf {truss}}$ containing this query node. ${\mathsf {k}}$-${\mathsf {core}}$-${\mathsf {truss}}$ search can benefit the recent attractive and important task of community search, that is to find ${\mathsf {k}}$-${\mathsf {core}}$-${\mathsf {truss}}$-based communities. The problem formulation is shown below.

Problem 2

Given a graph $G=(V, E)$, a parameter $\alpha$ and a query node q, the problem of ${\mathsf {k}}$-${\mathsf {core}}$-${\mathsf {truss}}$ search is to find a connected maximal ${\mathsf {k}}$-${\mathsf {core}}$-${\mathsf {truss}}$ with the highest k such that it contains node q.

Example 5

Continue with the above example using graph G in Fig. 2 with number $\alpha =1$ to illustrate Problem 2. Given a query node $q=v_8$, the problem of ${\mathsf {k}}$-${\mathsf {core}}$-${\mathsf {truss}}$ search is to find a maximal connected ${\mathsf {k}}$-${\mathsf {core}}$-${\mathsf {truss}}$ containing $v_8$ such that the core-truss number k is largest. We can observe that the connected 3-core-truss of $H_1$ contains $v_8$ with the highest value $k=3$, since there exists no such $CT_4$ containing $v_8$ in this example. As a result, $H_1$ is the answer of ${\mathsf {k}}$-${\mathsf {core}}$-${\mathsf {truss}}$ search for this query.

3 Properties of ${\mathsf {k}}$-${\mathsf {core}}$-${\mathsf {truss}}$

In this section, we study properties of ${\mathsf {k}}$-${\mathsf {core}}$-${\mathsf {truss}}$. A ${\mathsf {k}}$-${\mathsf {core}}$-${\mathsf {truss}}$ has several good structural properties, such as hierarchic structure and a generalization of k-core and k-truss. In addition, we study the core-truss number and analyze its useful relationships with k-core and k-truss, which help designing efficient algorithms for ${\mathsf {k}}$-${\mathsf {core}}$-${\mathsf {truss}}$ decomposition.

Generalization of k-core[24] and k-truss[25]. Our new dense subgraph model of ${\mathsf {k}}$-${\mathsf {core}}$-${\mathsf {truss}}$ is a generalization of k-core and k-truss. Let’s recall the formal definitions of k-core and k-truss. A k-core, denoted by $C_k$, is the largest subgraph of G, in which every vertex v has degree of at least k in $C_k$, i.e., $\deg _{C_k}(v)\ge k$ [24]. In addition, for every edge e(v, u) in a k-core $C_k$, the degree of e is $\deg _{C_k}(e) = \min \{\deg _{C_k}(v), \deg _{C_k}(u)\} \ge k$. Thus, a k-core $C_k$ is a subgraph of ${\mathsf {k}}$-${\mathsf {core}}$-${\mathsf {truss}}$ $CT_k$ for $\alpha =1$. On the other hand, a k-truss $T_k$ is the largest subgraph of G that every edge e is contained in at least $k-2$ triangles in $T_k$, i.e., $\sup _{T_k}(e)\ge k-2$ [25]. Thus, a k-truss $T_k$ is also a subgraph of ${\mathsf {k}}$-${\mathsf {core}}$-${\mathsf {truss}}$ $CT_k$ for any parameter $\alpha \ge 0$. Overall, the typical dense subgraph concepts of k-core and k-truss are special cases of ${\mathsf {k}}$-${{\mathsf {core}}}$-${\mathsf {truss}}$. In other words, ${\mathsf {k}}$-${\mathsf {core}}$-${\mathsf {truss}}$ is a mix model of k-core and k-truss models, which inherits good properties of both k-core and k-truss. For example, consider the graph G in Fig. 1. For $\alpha =1$, the entire graph is a 3-core-truss, which includes two overlapping subgraphs of 3-core and 3-truss.

Now, consider the variants of our ${\mathsf {k}}$-${\mathsf {core}}$-${\mathsf {truss}}$ with the parameter $\alpha$. The parameter $\alpha$ can make the graph size of ${\mathsf {k}}$-${\mathsf {core}}$-${\mathsf {truss}}$ flexible by changing its value. If more nodes need to be contained in the subgraph, we can increase the value of $\alpha$. On the contrary, we can reduce it for finding the subgraphs whose vertices are more closely related for only the edges with higher $\deg _{H}(e)$ will be contained in the $CT_k$ with the same k. Moreover, ${\mathsf {k}}$-${\mathsf {core}}$-${\mathsf {truss}}$ with suitable settings of parameter $\alpha$ can be equivalent to the definition of k-core or k-truss. Assume that $\alpha =0$, our ${\mathsf {k}}$-${\mathsf {core}}$-${\mathsf {truss}}$ is equivalent to k-truss. On the other hand, if $\alpha =\frac{k}{k-1}$, our ${\mathsf {k}}$-${\mathsf {core}}$-${\mathsf {truss}}$ is equivalent to $(k-1)$-core. The conclusions are shown in the following lemma.

We first prove the equivalence of ${\mathsf {k}}$-${\mathsf {core}}$-${\mathsf {truss}}$ and k-truss for $\alpha =0$ as follows.

Lemma 1

For $\alpha =0$, a ${\mathsf {k}}$-${\mathsf {core}}$-${\mathsf {truss}}$ is equivalent to a k-truss, i.e., $CT_k = T_k$.

Proof

Consider a given $2\le k\le k_{max}$. According to the Definitions  2 and $\alpha = 0$, for an edge in G, ${{\mathsf {degsup}}} _H(e) =$ $\max$ $\{\sup _H(e)+2,$ $0\cdot \deg _H(e)\}=\sup _H(e)+2$. Now, we establish $CT_k = T_k$ by proving $E_{CT_k} = E_{T_k}$.

$(\Rightarrow )$::

Suppose an edge $e\in E_{CT_k}$. Since ${{\mathsf {degsup}}} _H(e) \ge k$ by Definition 3, we have ${{\mathsf {degsup}}} _H(e) =\sup _H(e)+2 \ge k$, i.e., $\sup _H(e) \ge k-2$. Thus, $e\in E_{T_k}$ and $E_{CT_k} \subseteq E_{T_k}$ hold.

$(\Leftarrow )$::

For an edge $e\in E_{T_k}$, we have $\sup _H(e) \ge k-2$ by the definition of k-truss and ${{\mathsf {degsup}}} _H(e) =\sup _H(e)+2 \ge k$. Thus, $e\in E_{CT_k}$ and $E_{T_k} \subseteq E_{CT_k}$ hold.

$\square$

In the following, we show one useful lemma on ${\mathsf {k}}$-${\mathsf {core}}$-${\mathsf {truss}}$ and k-core.

Lemma 2

For $\alpha >0$, a ${\mathsf {k}}$-${\mathsf {core}}$-${\mathsf {truss}}$ is a $min\{k/\alpha ,k-1\}$-core.

Proof

Assume that a given $2\le k\le k_{max}$ and $\alpha >0$. According to the Definitions  2 and  3, for an edge in G, ${{\mathsf {degsup}}} _H(e) =$ $\max$ $\{\sup _H(e)+2,$ $\alpha \cdot \deg _H(e)\} \ge k$. Suppose that an edge $e\in E_{CT_k}$. Since ${{\mathsf {degsup}}} _H(e) \ge k$ , we have $\sup _H(e)+2 \ge k$ or $\deg _H(e) \ge k/\alpha$. If $\sup _H(e) \ge k-2$, then $e\in E_{T_k}$ holds. Obviously, $e\in E_{T_k} \in E_{C_{k-1}}$ [25]; Otherwise, $\deg _H(e) \ge k/\alpha$, we have $e\in E_{C_{k/\alpha }}$. As a result, $E_{CT_k} \subseteq E_{C_{min\{k/\alpha ,k-1\}}}$ holds. $\square$

Based on the lemma, we can prove the equivalence of ${\mathsf {k}}$-${\mathsf {core}}$-${\mathsf {truss}}$ and $(k-1)$-core for $\alpha =\frac{k}{k-1}$ in the following.

Lemma 3

For $\alpha =\frac{k}{k-1}$, a ${\mathsf {k}}$-${\mathsf {core}}$-${\mathsf {truss}}$ is equivalent to a $(k-1)$-core i.e., $CT_k= C_k$.

Proof

Consider a given $2\le k\le k_{max}$. According to the Definitions  2, 3 and $\alpha = \frac{k}{k-1}$, for an edge in G, ${{\mathsf {degsup}}} _H(e) =$ $\max$ $\{\sup _H(e)+2,$ $\frac{k}{k-1}\cdot \deg _H(e)\}\ge k$. Now, we establish $CT_k = C_{k-1}$ by proving $E_{CT_k} = E_{C_{k-1}}$.

$(\Rightarrow )$::

Based on the Lemma 2 and $\alpha =\frac{k}{k-1} >0$ , $E_{CT_k} \subseteq E_{C_{k-1}}$ holds.

$(\Leftarrow )$::

For an edge $e\in E_{C_{k-1}}$, we have $\deg _H(e)\ge k-1$ by the definition of k-core and ${{\mathsf {degsup}}} _H(e) \ge \frac{k}{k-1}\cdot \deg _H(e)=k$. Thus, $e\in E_{CT_k}$ and $E_{C_{k-1}} \subseteq E_{CT_k}$ hold.

$\square$

For each vertex u and edge e in a graph G, there exists a k-core (a k-truss) with the largest value k containing the vertex u (the edge e). In the following, we recall the definitions of core number and truss number, respectively, in k-core and k-truss.

Definition 5

For a node u in graph $G=(V, E)$, the core number of u denote by core(u) = $max\{k : u\in V_{C_k}\}$. Similarly, the core number of an edge $e=(u,v)\in E$ is represented by $\delta (e)$ = $max\{k : e\in E_{C_k}\}$=$min\{core(u),core(v)\}$. In any case, we have $\delta (e)\le \deg _H(e)$.

Definition 6

For an edge e in graph $G=(V, E)$, the truss number of e (or trussness of e) is denoted by $\tau (e)$ = $max\{k : e\in E_{T_k}\}$.

For an edge e, its core number $\delta (e)$, truss number $\tau (e)$, and core-truss number ct(e), respectively, shows each of the possible largest k of k-core, k-truss, and k-core-truss containing e. Based on the definitions of $\delta (e)$ and $\tau (e)$, we have an important lemma on ct(e) as follows.

Lemma 4

For an edge $e=(u,v)$ in graph G, the core-truss number $ct(e)\ge$ $max\{\tau ({ e}), \alpha \cdot \delta ({ e})\}$.

Proof

Consider a given $2\le k\le k_{max}$. According to the Definitions  2, 3 and  4, for an edge e in G,$\tau (e)=k_1$($T_{k_1}$, subgraph $H_1\subseteq G$),$\delta (e)=k_2$($C_{k_2}$, subgraph $H_2\subseteq G$).Since $T_{k_1}$ is a $CT_{k_1}$,$C_{k_2}$ is a $CT_{k_2}$,we have ${{\mathsf {degsup}}} _{H_1}(e) =$ $\max$ $\{\sup _{H_1}(e)+2,$ $\alpha \cdot \deg _{H_1}(e)\}\ge k_1$ for $\sup _{H_1}(e)+2 \ge \tau (e)$ and ${{\mathsf {degsup}}} _{H_2}(e) =$ $\max$ $\{\sup _{H_2}(e)+2,$ $\alpha \cdot \deg _{H_2}(e)\}\ge \alpha \cdot k_2$ for $\deg _{H_2}(e) \ge delta(e)$. Thus ct(e) = $max\{k : e\in E_{CT_k}\}$= ${{\mathsf {degsup}}} _{H_{max}}(e) \ge {{\mathsf {degsup}}} _{H_1}(e)$ or ${{\mathsf {degsup}}} _{H_2}(e)$,$ct(e)\ge$ $max\{\tau (e), \alpha \cdot \delta (e)\}$ hold $\square$

Fig. 4

An example of $ct(e)>$ $max\{\tau (e), \alpha \cdot \delta (e)\}$ on subgraph $H_3$ of G

Example 6

In Fig. 4, we use the subgraph $H_3$ of G in Fig. 2 and number $\alpha =1$. Consider the edge $e=(v_{20},v_{23})$ in red color in Fig. 4. The core number of $v_{20}$ and $v_{23}$ both are 2, since there exists no 3-core in $H_3$. Thus, the core number of $e=(v_{20}, v_{23})$ is 2, as $\delta (e)$=$min\{core(v_{20}),core(v_{23})\}=\min \{2,2\}=2$. In addition, there exists no triangle containing e, thus the truss number of e is $\tau (e)=2$. On the other hand, the whole graph $H_3$ is 3-core-truss. The edge $e=(v_{20},v_{23})\in$ $E_{CT_3}$ and $e \not \in$ $E_{CT_4}$. Overall, we have $ct(e)=3 > 2= \max \{\delta (e), \alpha \cdot \tau (e)\}$.

Hierarchic structure. The ${\mathsf {k}}$-${\mathsf {core}}$-${\mathsf {truss}}$ has hierarchical structure, that is, k-core-truss is always contained in the $(k-1)$-core-truss, which displays the cores of a community at different levels of granularity. The hierarchic structure of ${\mathsf {k}}$-${\mathsf {core}}$-${\mathsf {truss}}$ is described in the following lemma.

Lemma 5

A $(k+1)$-core-truss is contained in a ${\mathsf {k}}$-${\mathsf {core}}$-${\mathsf {truss}}$, i.e., $CT_k\supseteq CT_{k+1}$.

Proof

Consider a given $2\le k\le k_{max}$. According to the Definitions  2, 3, for an edge in G, ${{\mathsf {degsup}}} _H(e) =$ $\max$ $\{\sup _H(e)+2,$ $\alpha \cdot \deg _H(e)\}$. Now, we establish $CT_k\supseteq CT_{k+1}$ by proving $E_{CT_k} \supseteq E_{CT_{k+1}}$.

Suppose an edge $e\in E_{CT_{k+1}}$. Since ${{\mathsf {degsup}}} _H(e) \ge k+1$, then ${{\mathsf {degsup}}} _H(e) > k$. Therefore, $e\in E_{CT_k}$ and $E_{CT_k} \supseteq E_{CT_{k+1}}$ hold. $\square$

4 K-Core-Truss Algorithms

In this section, we focus on developing efficient algorithms for Problem 1 and Problem 2. Specifically, we first propose a ${\mathsf {k}}$-${\mathsf {core}}$-${\mathsf {truss}}$ decomposition method for solving Problem 1, which intuitively follows the definition of ${\mathsf {k}}$-${\mathsf {core}}$-${\mathsf {truss}}$. In addition, to solve Problem 2, we design a query search algorithm to find a ${\mathsf {k}}$-${\mathsf {core}}$-${\mathsf {truss}}$ with the largest k such that this ${\mathsf {k}}$-${\mathsf {core}}$-${\mathsf {truss}}$ contains the input query node. Moreover, we analyze the complexity of two proposed algorithms. Finally, we use running examples to introduce how these two algorithms detailed work on graph in Fig. 2.

4.1 K-Core-Truss Decomposition Algorithms

Here, we introduce a basic algorithm for ${\mathsf {k}}$-${\mathsf {core}}$-${\mathsf {truss}}$ decomposition that is to find ${\mathsf {k}}$-${\mathsf {core}}$-${\mathsf {truss}}$ for all possible k. Similar with the core decomposition [24] and truss decomposition [3], the core idea of our algorithm is to start from $k=2$ and then iteratively find ${\mathsf {k}}$-${\mathsf {core}}$-${\mathsf {truss}}$ with the increasing k by one each time. To find a ${\mathsf {k}}$-${\mathsf {core}}$-${\mathsf {truss}}$, the algorithm iteratively removes edges violating the constraint of ${\mathsf {k}}$-${\mathsf {core}}$-${\mathsf {truss}}$.

The outline of our basic algorithm is represented in Algorithm 1. The algorithm starts with an initialization by computing the degree and the support of every edge in graph G (line 1 to 6). Let H represent the graph G in the following decomposition process. After initialization, for each k starting from $k=2$, the algorithm iteratively deletes every edge $e=(u,v)$ with the ${\mathsf {degree}}$-${\mathsf {support}}$ no greater than k, because e cannot be in the (k+1)-core-truss by definition. Let the core-truss number of e as k, i.e., $ct(e)=k$ (line 15). Obviously, the deletion of $e=(u,v)$ will, respectively, decrease the degree of u and v by one (line 8 to 9). Moreover, the deletion of e may also lead to the invalidation of all triangles consisting of e, i.e., $\forall \triangle _{uvw}$ where $w\in W = N_H(u) \cap N_H(v)$, the triangle $\triangle _{uvw}$ is no longer valid any more after the deletion of $e=(u,v)$ (line 16). The $\sup _H(e)$ and $\deg _H(e)$ are needed to recompute(line 10 to 14). This process is repeated iteratively until all the remaining edges in G have ${\mathsf {degree}}$-${\mathsf {support}}$ at least $k+1$, which is the $(k+1)$-core-truss. If there still exists some edges not yet deleted in G, we increase the k by one and continue repeating the above process, i.e., Steps 7-17(line 18 to 19). The algorithm returns the core-truss numbers of all edges in G as shown in Fig. 5 (line 20).

Fig. 5

The ct(e) in graph G where $\alpha =1$

To prove the exactness of our basic algorithm, we have a lemma as follows.

Lemma 6

For an edge $e=(u,v)$ in $k_1$-core-truss $CT_{k_1}$ of G, e will not be deleted by Algorithm  1 for the loop $k=k_1-1$.

Proof

Since e is in $k_{1}-core-truss$ $CT_{k_1}$, ${{\mathsf {degsup}}} _H(e) =$ $\max$ $\{\sup _H(e)+2,$ $\alpha \cdot \deg _H(e)\}\ge k_1$ holds, indicating $\sup _H(e)\ge k_1$ or $\deg _H(e)\ge \frac{k_1}{\alpha }$. In the iteration $k=k_1-1$, e does not satisfy one constraint, either $\deg _{H}(e)\le k /\alpha$ or $\sup _{H}(e)\le k-2$. As a result, e will not be deleted in line 16. $\square$

In the following, we use an example to simulate the process of ${\mathsf {k}}$-${\mathsf {core}}$-${\mathsf {truss}}$ decomposition.

Example 7

Consider an graph $G=(V, E)$ shown in Fig. 2 and $\alpha {=}1$. We apply Algorithm 1 on G for ${\mathsf {k}}$-${\mathsf {core}}$-${\mathsf {truss}}$ decomposition. From line 2 to 6, we get all $deg_H(e)$ and $sup_H(e)$ of 35 edges in G, e.g., $deg_H(v_1,v_4)=sup_H(v_1,v_4)=2$, $deg_H(v_1,v_{14})=3,sup_H(v_1,v_{14})=2$, $deg_H(v_8,v_9)=6,sup_H(v_8,v_9)=3$, $deg_H(v_5,v_8)=3,sup_H(v_5,v_8)=1$. Now, we start from $k=2$ to find all edges with the core-truss of k.

Case $k=2$::

Since $(v_1,v_2)$,$(v_1,v_4)$, $(v_1,v_{14})$, $(v_2,v_3)$, $(v_2,v_{18})$ , $(v_3,v_4)$, $(v_3,v_5)$ are satisfied $\deg _{H}(e)\le k/\alpha \wedge sup_{H}(e)\le k-2$ directly or indirectly , e.g.,$(v_1,v_{14})$ is not satisfied the conditions for $deg_H(v_1,v_{14})=3$ at first, but when $(v_1,v_4)$ is deleted, which will update $deg_H(v_1,v_{14})$ to 2. All these seven edges will be deleted and assigned with the core-truss number of 2. In addition, the algorithm updates the $deg_H(e)$ or $sup_H(e)$ for the remaining 28 edges, i.e., $deg_H(v_5,v_8)=2$. The remaining graph of $CT_3$ consists of three component: $H_1$, $H_2$, and $H_3$.

Case $k=3$: all:

edges except $(v_{14},v_{15})$, $(v_{14},v_{16})$, $(v_{14},v_{17})$, $(v_{15},v_{16})$, $(v_{15},v_{17})$, $(v_{16},v_{17})$ are satisfied $\deg _{H}(e)\le k/\alpha \wedge sup_{H}(e)\le k-2$, which are deleted from graph. We assign the core-truss number of 3 to each deleted edge.

Case $k=4$::

all remaining edges will be deleted in this loop. We assign the core-truss number of 4 to each deleted edge, and terminated the algorithm.

Finally, the core-truss numbers of all edges in G are shown in Fig. 5.

We analyze the time and space complexity of Algorithm 1 in the following theorem.

Theorem 1

Algorithm 1 takes $O(m^{1.5})$ time using $O(n+m)$ space, where $n=|V|$ and $m=|E|$.

Proof

In the Algorithm 1, the most time-consuming step is to compute $\sup (e)$ for every $e\in E$. This step takes $O(m^{1.5})$ time complexity [2]. Similarly, updating the support of all edges (in lines 11–12) also consume $O(m^{1.5})$ time. The removal of all edges and the computation and updating the degree of all edges take O(m) time in total. As a consequence, the total time cost of Algorithm 1 is $O(m^{1.5})$.

In addition, we analyze the space cost of Algorithm 1. Clearly, Algorithm 1 needs to store the graph G using $O(n+m)$ space. For each edge $e\in E$, it also use O(m) space to store the edge degree $\deg _{H}(e)$, support $\sup _{H}(e)$, and core-truss number ct(e). Thus, the space complexity of Algorithm 1 is $O(m+n)$ in total. $\square$

4.2 Querying ${\mathsf {k}}$-${\mathsf {core}}$-${\mathsf {truss}}$

In this section, we investigate Problem 2, that is, given a query node q, to find a connected maximal ${\mathsf {k}}$-${\mathsf {core}}$-${\mathsf {truss}}$ containing q with the largest k. We develop a ${\mathsf {k}}$-${\mathsf {core}}$-${\mathsf {truss}}$ search algorithm in Algorithm 2 to solve Problem 2 as follows.

We first outline the framework of Algorithm 2, which consists of the following two main stages. The first stage is to identify the largest k such that there exists a ${\mathsf {k}}$-${\mathsf {core}}$-${\mathsf {truss}}$ containing node q. We apply the ${\mathsf {k}}$-${\mathsf {core}}$-${\mathsf {truss}}$ decomposition method in Algorithm 1 to compute the maximum core-truss number of an edge containing q, denoted by the largest k as $K_{max} = \max _{u\in N(q)} ct((q, u))$. In the second stage, we start from the query node q and expand the answer graph in BFS (breadth-first search) manner, which collect all adjacent edges having the core-truss number at least $K_{max}$ into the answer. Specifically, for each vertex u in the neighborhood of q as $u\in N(q)$, if edge (q, u) is unvisited and $ct(q, u)= K_{max}$, we add the edge $e=(q,u)$ into an empty search queue Q and mark it as visited (line 22 to 25). Then, we process the BFS search from the nonempty queue Q. We iteratively pick an edge (u, v) from Q, and then add all adjacent edges of nodes u and v with the core-truss number no less than $K_{max}$ into Q (line 26 to 33).

In the following, we show a running example for Algorithm 2.

Example 8

Consider the graph shown in Fig. 2 and the parameter $\alpha=1$. We test query node $q=v_8$, and run Algorithm 2 for finding the ${\mathsf {k}}$-${\mathsf {core}}$-${\mathsf {truss}}$ with the largest k such that it contains $v_8$.

Identifying $K_{max}$: We apply Algorithm 1 to compute the core-truss numbers of all edges in G. The results are shown in Fig. 5. We calculate the maximum core-truss number $K_{max} = \max _{u\in N(v_8)} ct((v_8, u)) = 3$, since $ct(v_8,v_5)=ct(v_8,v_6)=ct(v_8,v_7)=ct(v_8,v_9)=ct(v_8,v_{11})=ct(v_8,v_{13})=3$.

Graph Expansion in BFS manner: Then it starts from $v_8$ by expanding the graph in the BFS manner. The answer graph includes all edges that are connected to $v_8$ with $ct(e)\ge 3$. The subgraph $H_1$ is the 3-core-truss. For, since the edge $(v_3,v_5)$ with $ct(v_3,v_5)=2$ is not in 3-core-truss, all edges of $H_2$ with $ct(e)\ge 3$ are disconnected to q. The final result of connected 3-core-truss containing $v_8$ is $H_1$ in Fig. 3.

We analyze the time and space complexity of Algorithm 2 as follows.

Theorem 2

The time complexity of Algorithm 2 is $O(m^{1.5})$. The space complexity of Algorithm 2 is $O(n+m)$.

Proof

In the Algorithm 2, the most time-consuming step is the same as Algorithm 1(line 1 to 19), whose time complexity is $O(m^{1.5})$. Then, the algorithm takes $O(m+n)$ time to compute $K_{max}$ (line 20 to 21) and perform BFS process (line 22 to 33) in worst case. Also, we can easily derive that the space complexity of Algorithm 2 is $O(m+n)$ as Algorithm 1. $\square$

5 Performance Studies

In this section, we conduct extensive experiments to evaluate the efficiency and quality of proposed algorithms. Our experiments include 3 parts. The first experiment tests the runtime of three different graph decompositions: k-core decomposition, k-truss decomposition and ${\mathsf {k}}$-${\mathsf {core}}$-${\mathsf {truss}}$ decomposition. The second experiment shows the query processing time for three different models: k-core, k-truss, and ${\mathsf {k}}$-${\mathsf {core}}$-${\mathsf {truss}}$. The running time results are averaged in 1000 tested queries. In the third experiment, we use case studies on real DBLP networks to evaluate the effective of ${\mathsf {k}}$-${\mathsf {core}}$-${\mathsf {truss}}$ model.

Table 2 Datasets

Fig. 6

Running time in three graph decompositions: k-core decompositions, k-truss decompositions and ${\mathsf {k}}$-${\mathsf {core}}$-${\mathsf {truss}}$ decompositions

Fig. 7

Running time in query processing of finding k-core, k-truss and ${\mathsf {k}}$-${\mathsf {core}}$-${\mathsf {truss}}$ for a given node

All algorithms are implemented in C++. All experiments are conducted on a computer with 3.20 GHz Intel Core(TM) i5-6500 CPU and 8 GB memory running Windows 7 professional (64-bit). In all experiments, both graph storage and query processing are conducted in main memory.

Table 3 Running time of graph decomposition and query processing in three different models: k-core,k-truss and k-core-truss (in seconds)

5.1 Datasets

We use five web-scale real-world graphs in our experiments. All of the datasets except DBLP are downloaded from (http://snap.stanford.edu). Among the five graphs, Gowalla is a location-based online social network. NotreDame is a web graph. wiki-Talk is a communication network. LiveJournal1 is a social network. DBLP is a co-author network from the computer science bibliography website (http://dblp.uni-trier.de/). Here, each node corresponds to an author, and an edge represents the co-authorship relationship of two authors. The statistical details of all dataset are listed in Table  2, in terms of vertex size, edge size, average clustering coefficient, and the total number of triangles.

In the following two experiments, we evaluate the efficiency of proposed graph decomposition and query processing algorithms. All detailed values of running times are reported in Table  3.

5.2 Performance Evaluation of k-core, k-truss and ${\mathsf {k}}$-${\mathsf {core}}$-${\mathsf {truss}}$ Decompositions

We first compare the time consumption of graph decompositions on five datasets: Gowalla, NotreDame, wiki-Talk, and LiveJournal1. Figure 6 reports all results. It shows that k-core decomposition is the most effective among all three methods. In addition, the time consumptions of ${\mathsf {k}}$-${\mathsf {core}}$-${\mathsf {truss}}$ decomposition take much more than the k-core decomposition, but achieves the same order of the running time consumed by k-truss decomposition in all datasets. It is can be easily explained by the time complexity of all three method. The k-core decomposition is equivalent to compute the $\delta (e)$ values of every edge e in graph G[26], which takes O(m) time complexity. The k-truss decomposition is equivalent to compute the $\tau (e)$ values of every edge e in graph G[25], which takes $O(m^{1.5})$ time complexity. In addition, ${\mathsf {k}}$-${\mathsf {core}}$-${\mathsf {truss}}$ also takes $O(m^{1.5})$ time complexity.

5.3 Efficiency Evaluation of Querying Processing for Finding k-core, k-truss and ${\mathsf {k}}$-${\mathsf {core}}$-${\mathsf {truss}}$

In this experiment, we compare the performance of querying processing for finding k-core, k-truss and ${\mathsf {k}}$-${\mathsf {core}}$-${\mathsf {truss}}$ on all datasets. For a given query node, three methods, respectively, find the k-core, k-truss, and ${\mathsf {k}}$-${\mathsf {core}}$-${\mathsf {truss}}$ with the largest value k containing this query node. For each dataset, we generate 1000 sample of queries by randomly select one vertex in graph. The average query time is reported in Fig. 7. As we can see that, the query processing of finding k-truss is the most efficient among all three methods, due to the smallest size of k-truss. In addition, the query processing of finding ${\mathsf {k}}$-${\mathsf {core}}$-${\mathsf {truss}}$ achieve nearly the same time as finding k-core, which shows a good efficiency performance of our query processing algorithm.

Fig. 8

Query node “Homare Murakami” in different models. a (9-core with 21 nodes,105 edges). b (9-truss with 10 nodes,45 edges). c (9-core-truss 24 nodes,126 edges)

Fig. 9

Query node “Antoni Broquetas” in different models a (6-core with 15 nodes,82 edges). b (6-truss with 17 nodes,90 edges). c (6-core-truss 17 nodes,92 edges)

Fig. 10

Query node “Andreas Pfitzmann” in different models. a (8-core with 19 nodes,83 edges). b (8-truss with 11 nodes,50 edges). c (8-core-truss 21 nodes,97 edges)

Fig. 11

The case study on 9-core-truss of “Homare Murakami”

5.4 Case Study on DBLP Network

In this section, we use a real-world DBLP network to test the effectiveness of our new model ${\mathsf {k}}$-${\mathsf {core}}$-${\mathsf {truss}}$. In this DBLP network, each node represents an author, and an edge is added between two authors if they have co-authored at least three times. The parameter $\alpha$ is set as 1. For a given author in DBLP and number k, we apply Algorithm 2 to find the connected ${\mathsf {k}}$-${\mathsf {core}}$-${\mathsf {truss}}$ containing this query author. For comparison, we also report the connected subgraphs of k-core and k-truss, which both contain this query author with the same input k.

First, we use the query $Q=$“Homare Murakami” and number $k=9$ to test our ${\mathsf {k}}$-${\mathsf {core}}$-${\mathsf {truss}}$ for finding cohesive groups. In this example, we can see the superiority of ${\mathsf {k}}$-${\mathsf {core}}$-${\mathsf {truss}}$ against k-core and k-truss models. Figure 8a shows the results of k-core model, which has 21 nodes, 105 edges and the average-degree of 10. Every vertex has 9 neighbors in 9-core. In addition, k-truss containing Q is represented in Fig. 8b. It has 10 nodes, 45 edges and the average-degree of 9. Every edge is contained in $7 (= 9-2)$ triangles, indicating every vertex also has degree at least 8. We show the result of ${\mathsf {k}}$-${\mathsf {core}}$-${\mathsf {truss}}$ in Fig. 8c, which contains 24 nodes and 126 edges. The average-degree of ${\mathsf {k}}$-${\mathsf {core}}$-${\mathsf {truss}}$ is 10.5, which is higher than the k-core and k-truss results. It is because ${\mathsf {k}}$-${\mathsf {core}}$-${\mathsf {truss}}$ discover more important edges than k-core and k-truss. To clearly show the difference of our ${\mathsf {k}}$-${\mathsf {core}}$-${\mathsf {truss}}$ with the results of k-core and k-truss, we scale up Fig. 8c to Fig. 11, where the nodes and edges in red color present in ${\mathsf {k}}$-${\mathsf {core}}$-${\mathsf {truss}}$ but not in k-core and k-truss. As we can see,${\mathsf {k}}$-${\mathsf {core}}$-${\mathsf {truss}}$ include 3 red nodes, which are authors “Jongsik Lim”, “Mohammadali Khosravifard”, and “I Gusti Bagus”. They have consistently densely connected with “Jongsik Lim” and “Homare Murakami”. There are 3 authors “Jongsik Lim”,“Mohammadali Khosravifard” and “I Gusti Bagus” missing in the 9-core and 9-truss (Fig. 8-a, b) comparing to 9-core-truss. They have not directly co-authored with “Homare Murakami”, however, cooperated with others who co-authored directly with “Homare Murakami”, i.e., “Jongsik Lim” and “Homare Murakami” have a same co-author named “Atsushi Igarashi”, these three authors are all engaged in the research of communications, which make it sense that they are in the same clique. ${\mathsf {k}}$-${\mathsf {core}}$-${\mathsf {truss}}$ represents a larger and stronger connected research community than k-core and k-truss. One more interesting case study is to query the author $Q=$ “Jee-Hyub Kim” using the parameter $k=27$. We find a 27-core-truss (114 nodes, 2662 edges), a 27-core(105 nodes, 2464 edges) and a 27-truss (28 nodes, 378 edges). The visualization of discovered subgraphs is omitted, due to the complex network structures.

In summary, the case studies on DBLP network shows that our ${\mathsf {k}}$-${\mathsf {core}}$-${\mathsf {truss}}$ model indeed include more nodes and edges and discover a more dense substructure, than k-core and k-truss. This additional structural information helps a deep and comprehensive understanding of complex networks.

6 Related Work

In this paper, we firstly propose a novel model of dense subgraph called k-core-truss. Our work is closely related with k-core and k-truss, which are extensively studied in the literature.

Considering k-core, in [24], Seidman first introduced the concept of k-core to measure the group cohesion in a network. The cohesion of k-core increases as k increases. Recently, the k-core decomposition in graphs has been used in many applications. From an algorithmic perspective, Batagelj and Zaversnik proposed an $O(n+m)$ algorithm for k-core decomposition in general graphs [26]. Their algorithm recursively deletes the node with the lowest degree and uses the bin-sort algorithm to maintain the order of the nodes. However, this algorithm has to randomly access the graph, thus it could be inefficient for the disk-resident graphs. To overcome this issue, Cheng et al. [22] proposed an efficient k-core decomposition algorithm for disk-resident graphs. Their algorithm works in a top-to-down manner to calculate k-core. To make the k-core decomposition more scalable, Montresor et al. [27] proposed a distributed algorithm for k-core decomposition by exploiting the locality property of k-core. All the mentioned algorithms focus on k-core decomposition in static graph except for [28]. For the dynamic graph, in [28], Miorandi and Pellegrini applied the $O(n+m)$ algorithm [26] to recompute the core numbers of the nodes when the graph is updated, which is inefficient in large graphs. In k-core maintenance, [29] propose a new efficient algorithm to maintain the core number for every node in a dynamic graph, which is the one base of our Pruned CTupdate Algorithm.

The concept of truss was firstly introduced by Cohen [25] in 2008, when social networks developed fast and corresponding research prevailed. Compared with other cohesive subgraph models, k-truss has its own advantage. The truss decomposition has been studied in [25, 2]. Cohen proposed the first truss decomposition algorithm [25], which is later outperformed by an improved in-memory algorithm proposed by Wang and Cheng [2]. Wang and Cheng proposed an out-of-memory algorithm for truss decomposition and a top-t k-truss evaluation algorithm [2]. Recently, Zhao and Tung [30] studied the truss decomposition problem and consider that the networked data is stored in a graph database. They also studied how to visualize the graph. Different from all the above works, [31] do not consider finding the trusses from scratch. They aim to maintain the trusses in face of frequent updates. [3] and [31] investigated the problem of updating k-truss in dynamic graphs. Rui Zhou [31] proposed algorithms on maintaining trusses on edge deletions and insertions, which is another base of our Pruned CTupdate Algorithm. Huang et al. [32] studied truss decomposition in uncertain graphs.

In order to mine transient stories and their correlations implicit in social streams, Lee et. al. proposed a new model of cohesive subgraph named (k, d)-core [9], in which every node has at least k neighbors and two end nodes of every edge have at least d common neighbors. In other words, each edge in subgraph is included by a k-core and a $(d+2)$-truss at the same time. The constraints of (k, d)-core are much stricter than ${\mathsf {k}}$-${\mathsf {core}}$-${\mathsf {truss}}$. To provide structural relations among cliques, Sariyuce et al. [1] defines the nucleus decomposition of a graph, which represented the graph as a forest of nuclei. Each nucleus is a subgraph where smaller cliques are present in many larger cliques. With the right parameters, the nucleus decomposition generalizes the classic notions of k-cores and k-truss decompositions. Both (k, d)-core and nucleus are different from our ${\mathsf {k}}$-${\mathsf {core}}$-${\mathsf {truss}}$ model in terms of structural constraints.

7 Conclusion

In this paper, we propose a novel dense subgraph of ${\mathsf {k}}$-${\mathsf {core}}$-${\mathsf {truss}}$ that combines the nice structural properties of k-core and the k-truss. We study two useful problems of ${\mathsf {k}}$-${\mathsf {core}}$-${\mathsf {truss}}$ decomposition and ${\mathsf {k}}$-${\mathsf {core}}$-${\mathsf {truss}}$ search. We develop a k-core-truss decomposition algorithm to find all ${\mathsf {k}}$-${\mathsf {core}}$-${\mathsf {truss}}$ in a graph G by iteratively removing edges with the smallest ${\mathsf {degree}}$-${\mathsf {support}}$. In addition, we offer a ${\mathsf {k}}$-${\mathsf {core}}$-${\mathsf {truss}}$ search algorithm to identifying a particular ${\mathsf {k}}$-${\mathsf {core}}$-${\mathsf {truss}}$ containing a given query node such that the core number k is the largest. Extensive experiments on five web-scale real-world datasets, and show that our ${\mathsf {k}}$-${\mathsf {core}}$-${\mathsf {truss}}$ algorithms can efficiently and effectively find cohesive substructures over real-world networks, which can significantly discover the interesting and important relationships out the scope of k-core and k-truss.

Our work takes an important first step toward enriching dense subgraph models in the network analysis. It opens up several interesting directions for further research. One of intuitive open problem is to study ${\mathsf {k}}$-${\mathsf {core}}$-${\mathsf {truss}}$ decomposition and search in the environment of stream or dynamic graphs, that is, the nodes/edges are frequently inserted/deleted.