Abstract
Parallel mechanisms are finding wide applications in manufacturing. The design methodology of parallel mechanisms is generally considered as a complex procedure. Many times they are custom designed to suit a specific task. In this work, a generalized analytical approach to forward, inverse kinematics and workspace analysis of three-degrees-of-freedom 3RPS (revolute–prismatic–spherical) and 3RPS-R (revolute–prismatic–spherical–revolute) parallel manipulator is presented. Methodology for obtaining various position and orientation of the moving platform for the provided actuation by varying the distance between the base platform and the moving platform has been discussed in detail. The actuation is given to the prismatic joint of the manipulator, which results in a variation of limb lengths, thereby altering the position and orientation of the moving platform. Sylvester dialytic elimination method is used to solve the nonlinear polynomial expressions originally obtained from the loop–closure equations. Various numerical solutions have been obtained for a different combination of limb lengths and by changing the height of the manipulator. The workspace obtained is not evenly distributed, and hence, an additional degree of freedom (DOF) of base rotation has been suggested. With the addition of one DOF, the volume of workspace obtained is enhanced without any discontinuities which would enable the manipulator to generate circular trajectories. The methodology presented in this work is general and will be suitable for similar geometries by altering the loop closure equations suitably.











Similar content being viewed by others
Notes
References
Babu SR et al (2013) Design for optimal performance of 3-RPS parallel manipulator using evolutionary algorithms. Trans Can Soc Mech Eng 37(2):135–160
Epsteen S (1903) Analog of Sylvester’s dialytic method of elimination. Am Math Mon 10(3):63–64
Fang Y, Huang Z (1997) Kinematics of a three-degree-of-freedom in-parallel actuated manipulator mechanism. Mech Mach Theory 32(7):789–796
Fang H, Fang Y, Zhang K (2013) Kinematics and workspace analysis of a novel 3-DOF parallel manipulator with virtual symmetric plane. Proc Inst Mech Eng C J Mech Eng Sci 227(3):620–629
Gallardo J, Orozco H, Rico JM (2008) Kinematics of 3-RPS parallel manipulators by means of screw theory. Int J Adv Manuf Technol 365:598–605
Gallardo-Alvarado J (2013) Mobility analysis and kinematics of the semi-general 2 (3-RPS) series-parallel manipulator. Robot Comput Integr Manuf 29(6):463–472
Gallardo-Alvarado J, García-Murillo MA (2013) A parallel manipulator inspired by the original Stewart platform. Proc Inst Mech Eng C J Mech Eng Sci 227(4):831–844
Geng M, Zhao T, Wang C, Chen Y, Li E (2014) Forward kinematics analysis of parallel mechanisms with restricted workspace. Proc Inst Mech Eng C J Mech Eng Sci 229(14):1–12
Ghosal A (2006) Robotics: fundamental concepts and analysis. Oxford University Press, New Delhi
Hao Z, Qiyi W, Qunming L, Bo Z (1996) December. The kinematics and workspace analyses of a parallel manipulator for manufacturing. In: Proceedings of The IEEE international conference on industrial technology, pp 647–650
Hunt KH (1983) Structural kinematics of in-parallel-actuated robot-arms. ASME J Mech Transm Autom Des 105(4):705–712
Ibrahim O, Khalil W (2007) Kinematic and dynamic modeling of the 3-RPS parallel manipulator. In: 12th IFToMM world congress, Besançon
Kosinska A, Galicki M, Kedzior K (2003) Design of parameters of parallel manipulators for a specified workspace. Robotica 21(05):575–579
Kumar V (1992) Characterization of workspaces of parallel manipulators. Trans ASME J Mech Des 114:368
Lee KM, Shah DK (1988) Kinematic analysis of a three-degrees-of-freedom in-parallel actuated manipulator. IEEE J Robot Autom 4(3):354–360
Li Y, Xu Q (2007) Kinematic analysis of a 3-PRS parallel manipulator. Robot Comput Integr Manuf 23(4):395–408
Li Q, Chen Z, Chen Q, Wu C, Hu X (2011) Parasitic motion comparison of 3-PRS parallel mechanism with different limb arrangements. Robot Comput Integr Manuf 27(2):389–396
Liu D, Che R, Li Z, Luo X (2003) Research on the theory and the virtual prototype of 3-DOF parallel-link coordinate-measuring machine. IEEE Trans Instrum Meas 52(1):119–125
Merlet JP (1994) Parallel manipulators: state of the art and perspectives. Adv Robot 8:589–596
Merlet JP (2006) Parallel robots. Springer, Berlin
Özdemir M (2016) Singularity robust balancing of parallel manipulators following inconsistent trajectories. Robotica 34(9):1–12
Patel YD, George PM (2012) Parallel manipulators applications—a survey. Mod Mech Eng 2(1):57–64
Patel Y, George P (2014) Constraint and inverse kinematic analysis of 3-RPS parallel manipulator. In: 5th International & 26th all India manufacturing technology, design and research conference
Rao NM (2010) Synthesis of a spatial 3-RPS parallel manipulator based on physical constraints. Sadhana 35(6):739–746
Rao NM (2011) Synthesis of a spatial 3-RPS parallel manipulator based on physical constraints using hybrid GA simplex method. Int J Adv Manuf Technol 52(5–8):777–787
Rao NM, Rao KM (2009) Dimensional synthesis of a spatial 3-RPS parallel manipulator for a prescribed range of motion of spherical joints. Mech Mach Theory 44(2):477–486
Rao PS, Rao NM (2013) Position analysis of spatial 3-RPS parallel manipulator. Int J Mech Eng Robit Res 2(2):79–90
Rogers DF, Adams JA (1989) Mathematical elements for computer graphics. McGraw-Hill, New York
Schadlbauer J, Walter DR, Husty ML (2014) The 3-RPS parallel manipulator from an algebraic viewpoint. Mech Mach Theory 75:161–176
Tsai LW (1999) Robot analysis: the mechanics of serial and parallel manipulators. Wiley, New York
Wang QY, Zou H, Zhao MY, Li QM, Zheng HW (1997) Design and kinematics of a parallel manipulator for manufacturing. CIRP Ann Manuf Technol 46(1):297–300
Yuan WH, Tsai MS (2014) A novel approach for forward dynamic analysis of 3-PRS parallel manipulator with consideration of friction effect. Robot Comput Integr Manuf 30(3):315–325
Zhang J, Yu H, Gao F, Zhao X (2011) Key issues in studying parallel manipulators. In: IEEE international conference on advanced mechatronic systems (ICAMechS), pp 234–244
Zhao JS, Feng ZJ, Wang LP, Dong JX (2006) The free mobility of a parallel manipulator. Robotica 24(05):635–641
Zhao JS, Lu W, Chu F, Feng ZJ (2009) The kinematics and statics of manipulators. Proc Inst Mech Eng C J Mech Eng Sci 223(9):2155–2166
Author information
Authors and Affiliations
Corresponding author
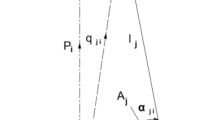
Appendix
Appendix
Rights and permissions
About this article
Cite this article
Desai, R., Muthuswamy, S. A Forward, Inverse Kinematics and Workspace Analysis of 3RPS and 3RPS-R Parallel Manipulators. Iran J Sci Technol Trans Mech Eng 45, 115–131 (2021). https://doi.org/10.1007/s40997-020-00346-9
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40997-020-00346-9