Abstract
The paper contains an intelligible construction of the ring W(A) of Witt vectors over an arbitrary commutative ring A.
Similar content being viewed by others
I will describe a functor \(A\mapsto W(A)\) from the category of commutative rings to itself. The ring W(A) of ‘Witt vectors’ over A has many applications (to algebraic geometry, local rings, etc.), but I won’t discuss those. Convention: rings have 1’s that are respected by ring homomorphisms. By A I will always denote a commutative ring.
The literature on the functor W is in a somewhat unsatisfactory state: nobody seems to have any interest in Witt vectors beyond applying them for a purpose, and they are often treated in appendices to papers devoted to something else; also, the construction usually depends on a set of implicit or unintelligible formulae. Apparently, anybody who wishes to understand Witt vectors needs to construct them personally. That is what is now happening to myself.
One may compare the construction of W(A) to the construction of the polynomial ring A[X]: the ring operations in the latter are also defined by formulae, but those are both explicit and intelligible. In addition, A[X] can be thought of in a conceptual way: it is an A-algebra that represents the forgetful functor from the category of A-algebras to the category of sets. It is quite possible that W(A) also represents some functor, and that this helps in constructing W; but I never saw a satisfactory treatment along these lines. For W(A), the arrows run in the opposite direction: A is a W(A)-algebra rather than the other way around, and if W(A) represents a functor then most likely it is a contravariant one.
If the only available way to construct W is by implicit formulae, then one is doomed to using those formulae whenever one wishes to prove any result about Witt vectors. The theory as found in the literature is indeed formula-ridden.
My treatment depends also on a formula (see (ii) below), but it is both explicit and intelligible. One may be hopeful that my approach will pass the test of allowing a smooth development of the entire theory of Witt vectors. For example, one can use it to construct an important morphism  that turns each W(A) into a ‘lambda-ring’.
that turns each W(A) into a ‘lambda-ring’.
I start by defining a ring \(\Lambda (A)\) that is isomorphic to W(A), the only difference being notational. Let A[[T]] be the ring of power series in one indeterminate T over A. Let the A-algebra homomorphism \(A[[T]]\rightarrow A\) map T to 0, and hence any power series to its constant coefficient. It induces a homomorphism \(A[[T]]^*\!\rightarrow A^*\) on the unit groups, and I define

This is a multiplicative group, and \(\Lambda \) is a functor from the category of commutative rings to the category of abelian groups. The multiplication on \(\Lambda (A)\) will serve as the “addition” in a new ring structure to be defined on \(\Lambda (A)\).
There is a unique system of maps

one for each commutative ring A, such that:
-
(i)
\(*\) is left and right distributive with respect to \(\times \);
-
(ii)
for all A and all \(a,b \in A\), one has
$$\begin{aligned} (1-aT)^{-1}\! * (1-bT)^{-1} = (1-abT)^{-1}; \end{aligned}$$and
-
(iii)
\(*_A\) is functorial in A; that is, for each homomorphism \(f:A\rightarrow B\) of commutative rings, the diagram

commutes.
For each A, the map \(*_A\) is T-adically continuous and makes \(\Lambda (A)\) into a commutative ring with addition \(\times \), multiplication \(*\) and unit element \((1-T)^{-1}\).
Finally, \(\Lambda \) is a functor from the category of commutative rings to itself.
The elements occurring in (ii) are sums of geometric progressions:

Thus, on elements of this form, the operation \(*\) is given by coefficientwise multiplication, the “Hadamard product”.
The unit element \((1-T)^{-1}\) has all coefficients equal to 1. One finds also other normalizations in the literature, leading to unit element \(1-T\) (invert all elements of \(\Lambda (A)\)) or \(1+T\) (substitute \(-T\) for T). My convention keeps the formulae simple, and leads for zeta functions of varieties X, Y over a finite field k to the pleasing formula  .
.
I now first prove existence of the operations \(*_A\). For each \(n\geqslant 0\), put

(by the map \(T \mapsto 0\)), so that one has \(\Lambda (A)=\varprojlim {}_{n} \,\Lambda _n(A)\). Define
to be the subgroup of \(\Lambda _n(A)\) generated by  . The strategy is to first make each \(M_n(A)\) into a ring, next extend the ring structure to \(\Lambda _n(A)\) (this will require varying A), and finally pass to \(\Lambda (A)\) by taking the projective limit.
. The strategy is to first make each \(M_n(A)\) into a ring, next extend the ring structure to \(\Lambda _n(A)\) (this will require varying A), and finally pass to \(\Lambda (A)\) by taking the projective limit.
For each commutative ring A and non-negative integer n, the abelian group \(M_n(A)\) has a unique composition \(*_A\) satisfying property (ii) and making \(M_n(A)\) into a commutative ring; also, \(M_n\) is a functor from the category of commutative rings to itself, and the natural maps \(M_{n+1} \rightarrow M_n\) are morphisms of functors.
FormalPara ExampleThe map \(A\rightarrow M_1(A)\) sending a to \(1+aT\,(\mathrm{mod}\, T^2)\) is bijective, and the ring structure on \(M_1(A)\) makes it into an isomorphism of rings.
FormalPara ProofFor \(a \in A\), the A-algebra endomorphism
induces an element \(\varphi _a\) of the endomorphism ring \(\mathrm{End}\,\Lambda _n(A)\) of \(\Lambda _n(A)\). Clearly one has \(\varphi _a\varphi _b=\varphi _{ab}\) for \(a,b\in A\). Hence, if \(E \subset \mathrm{End}\,\Lambda _n(A)\) denotes the additive subgroup generated by  , then E is a commutative subring of \(\mathrm{End}\,\Lambda _n(A)\). The natural action of E on \(\Lambda _n(A)\) makes \(\Lambda _n(A)\) into an E-module, and I write the action exponentially.
, then E is a commutative subring of \(\mathrm{End}\,\Lambda _n(A)\). The natural action of E on \(\Lambda _n(A)\) makes \(\Lambda _n(A)\) into an E-module, and I write the action exponentially.
The map
is an E-module homomorphism that sends \(\varphi _a\) to \((1-aT)^{-1}\). The image of this E-module homomorphism is \(M_n(A)\), since it is generated by the images of generators. The kernel is a left ideal I of E, and one obtains a group isomorphism
Since E is commutative, I is a two-sided ideal of E, so E / I has a ring structure. One can now transport the ring structure from E / I to \(M_n(A)\). All assertions in the lemma are then straightforward to verify. \(\square \)
Next I pass from \(M_n(A)\) to \(\Lambda _n(A)\). It would be convenient if every monic polynomial over A were a product of linear factors, since then one had identities like
showing that \(\Lambda _n(A)=M_n(A)\). This is true, for example, if A is an algebraically closed field. Also for \(A=\mathbb R\) one can show that \(\Lambda _n(A)=M_n(A)\). In general one must vary the ring.
For each A, there is an A-algebra \(\overline{A}\) such that
-
(i)
for all n, one has \(\Lambda _n(\overline{A})=M_n(\overline{A})\);
-
(ii)
as an A-module, \(\overline{A}\) has a basis containing the unit element.
From (ii) one sees that \(\overline{A}\) is free as an A-module, and that the map from A to \(\overline{A}\) is injective.
The lemma is much stronger than what I need. It would be enough to show that for each n and for each finite subset \(F\subset \Lambda _n(A)\) there exists a faithfully flat A-algebra \(A_{F,n}\) with \(F\subset M_n(A_{F,n})\).
Let

and put

Every  has the linear factor
has the linear factor  in \(A'[X]\), where
in \(A'[X]\), where  denotes the image of
denotes the image of  in \(A'\). Also, the collection of elements
in \(A'\). Also, the collection of elements  with \(0 \leqslant i(f)< \deg f\) for all f and \(i(f)=0\) for almost all f, is a basis for \(A'\) as an A-module, so \(A\subset A'\). Repeating the construction, write \(A''\!=(A')'\), and inductively \(A^{(n)}\!=(A^{(n-1)})'\) (where \(A^{(0)}\!=A\)). It is now routine to verify that the A-algebra
with \(0 \leqslant i(f)< \deg f\) for all f and \(i(f)=0\) for almost all f, is a basis for \(A'\) as an A-module, so \(A\subset A'\). Repeating the construction, write \(A''\!=(A')'\), and inductively \(A^{(n)}\!=(A^{(n-1)})'\) (where \(A^{(0)}\!=A\)). It is now routine to verify that the A-algebra
has the properties stated in the lemma. \(\square \)
There are many ways of making other rings that do the job just as well, but the following lemma shows that there is no reason to care about this at all.
Let \(A \subset B\) be commutative rings, \(n \geqslant 0\), and let \(u,v \in \Lambda _n(A)\) be such that \(u,v \in M_n(B)\). Then  and
and  lie in \(\Lambda _n(A)\) and are equal.
lie in \(\Lambda _n(A)\) and are equal.
If \(B \subset C\), then  since \(*\) is functorial. Choose
since \(*\) is functorial. Choose  . Since one can write
. Since one can write  with \(e_0=1\), one has \(C= \bigoplus _{i \in I} B e_i\). From this one sees that there are inclusions \(B,\overline{A} \subset C\), and that inside C one has \(B \cap \overline{A} = A\) (elements of B can only at \(e_0\) have a non-zero coefficient).
with \(e_0=1\), one has \(C= \bigoplus _{i \in I} B e_i\). From this one sees that there are inclusions \(B,\overline{A} \subset C\), and that inside C one has \(B \cap \overline{A} = A\) (elements of B can only at \(e_0\) have a non-zero coefficient).
Therefore one has  , and this element lies in \(\Lambda _n(B) \cap \Lambda _n(\overline{A}) = \Lambda _n(A)\). \(\square \)
, and this element lies in \(\Lambda _n(B) \cap \Lambda _n(\overline{A}) = \Lambda _n(A)\). \(\square \)
Since a ring B as in the lemma exists for every n, u, v (take for example \(B=\overline{A}\)), one concludes that \(\Lambda _n(A)\) is a subring of \(\Lambda _n(\overline{A})\) for every n. This gives a ring structure on \(\Lambda _n(A)\). It is functorial in A; that is, if \(f:A\rightarrow B\) is a homomorphism of commutative rings, then the map \(\Lambda _n(A) \rightarrow \Lambda _n(B)\) induced by f is a ring homomorphism. To prove this, let \(u,v\in \Lambda _n(A)\). Then u, v are in \(M_n(\overline{A})\), so the images \(\tilde{u}\) and \(\tilde{v}\) of u and v in \(\Lambda _n(B)\) are in  . Applying Lemma 3 to the inclusion
. Applying Lemma 3 to the inclusion  in the role of \(A\subset B\), one sees that the product
in the role of \(A\subset B\), one sees that the product  can be computed in
can be computed in  ; since \(M_n\) is a functor one concludes that this product equals the image of
; since \(M_n\) is a functor one concludes that this product equals the image of  in \(\Lambda _n(B)\), as required.
in \(\Lambda _n(B)\), as required.
Each \(\Lambda _n\) is a functor from the category of commutative rings to itself, and the natural maps \(\Lambda _{n+1}\!\rightarrow \Lambda _n\) are morphisms of functors. Thus \(\Lambda (A)=\varprojlim {}_n\, \Lambda _n(A)\) now gets a ring structure. This proves the existence part of the theorem, and also shows the additional properties of \(*_A\). The only thing left to prove is uniqueness.
Let I and J be sets, and let
be a map, one for each commutative ring A, functorial in A. Then each \(\vartheta _A\) is continuous (where A has the discrete topology and \(A^I\) and \(A^J\) the product topologies); more precisely, for each \(j \in J\) there is a finite subset  such that for all A there exists a commutative diagram
such that for all A there exists a commutative diagram

the vertical maps being the obvious projections.
FormalPara ProofThe functor \(-^I\) (taking \(A \mapsto A^I\)) from the category of commutative rings to the category of sets is isomorphic to the functor  (taking A to the set of ring homomorphisms
(taking A to the set of ring homomorphisms  ). By Yoneda’s lemma, the system of maps \(\vartheta _A\) corresponds to a ring homomorphism
). By Yoneda’s lemma, the system of maps \(\vartheta _A\) corresponds to a ring homomorphism  . Lemma 4 now comes down to the statement that for every \(j\in J\) there is a finite subset
. Lemma 4 now comes down to the statement that for every \(j\in J\) there is a finite subset  such that the image of
such that the image of  is in the subring
is in the subring  of
of  , and this is clear. \(\square \)
, and this is clear. \(\square \)
To prove the uniqueness statement in the theorem, suppose that  satisfies conditions (i), (ii), and (iii). Applying the lemma to \(\vartheta _A=\#_A\), with \(J=\mathbb Z_{>0}\) and I equal to the disjoint union of two copies of \(\mathbb Z_{>0}\), one sees that \(\#_A\) is T-adically continuous. Let \(M(A)\subset \Lambda (A)\) be the subgroup generated by
satisfies conditions (i), (ii), and (iii). Applying the lemma to \(\vartheta _A=\#_A\), with \(J=\mathbb Z_{>0}\) and I equal to the disjoint union of two copies of \(\mathbb Z_{>0}\), one sees that \(\#_A\) is T-adically continuous. Let \(M(A)\subset \Lambda (A)\) be the subgroup generated by  . Then \(\#\) and \(*\) agree on
. Then \(\#\) and \(*\) agree on  by (ii) and (i), and since \(\Lambda (A)\) is Hausdorff, they also agree on
by (ii) and (i), and since \(\Lambda (A)\) is Hausdorff, they also agree on  ; here \(\overline{M(A)}\) denotes the closure of M(A) in \(\Lambda (A)\), which equals \(\varprojlim {}_n\,M_n(A)\). Applying this result to \(\overline{A}\) one sees that \(\#=*\) on \(\Lambda (\overline{A})\) and hence on the subring \(\Lambda (A)\). This completes the proof of the theorem.
; here \(\overline{M(A)}\) denotes the closure of M(A) in \(\Lambda (A)\), which equals \(\varprojlim {}_n\,M_n(A)\). Applying this result to \(\overline{A}\) one sees that \(\#=*\) on \(\Lambda (\overline{A})\) and hence on the subring \(\Lambda (A)\). This completes the proof of the theorem.
By way of exercises I list some identities in \(\Lambda (A)\).
-
(1)
For all \(a\in A\) and \(u\in \Lambda (A)\) one has
 ; i.e. $$\begin{aligned} \biggl (\,\sum _{i=0}^{\infty } \,a^i T^i\biggr )*\biggl (\,\sum _{i=0}^{\infty }\, b_i T^i\biggr )=\sum _{i=0}^{\infty } \,a^i b_i T^i \end{aligned}$$
; i.e. $$\begin{aligned} \biggl (\,\sum _{i=0}^{\infty } \,a^i T^i\biggr )*\biggl (\,\sum _{i=0}^{\infty }\, b_i T^i\biggr )=\sum _{i=0}^{\infty } \,a^i b_i T^i \end{aligned}$$(the Hadamard product!). From this one can deduce that the ideal I occurring in the proof of Lemma 1 is 0.
-
(2)
For \(a_1,a_2,b_1,b_2\in A\) one has
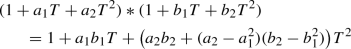
in \(\Lambda _2(A)\). Also, one has \(\Lambda _2(A)=M_2(A)\).
-
(3)
Let m, n be positive integers, and put \(l=\mathrm{lcm}(m,n)\),
 . Then for \(a,b \in A\), one has $$\begin{aligned} (1-aT^m)^{-1}\!*(1-bT^n)^{-1}\! = \bigl (1-a^{l/m}b^{l/n}T^{l}\bigr )^{-g}\!. \end{aligned}$$
. Then for \(a,b \in A\), one has $$\begin{aligned} (1-aT^m)^{-1}\!*(1-bT^n)^{-1}\! = \bigl (1-a^{l/m}b^{l/n}T^{l}\bigr )^{-g}\!. \end{aligned}$$Equivalently: if two collections of \(\alpha \)’s and \(\beta \)’s satisfy

then one has
$$\begin{aligned} {\prod }_{\,\alpha ,\beta }(X-\alpha \beta )=\bigl (X^{l}-a^{l/m}b^{l/n}\bigr )^g\!. \end{aligned}$$This is particularly easy to see if A is a field of characteristic 0.
-
(4)
For relatively prime positive integers m, n one has

This is best understood through an interpretation of \(\Lambda (\mathbb Z)\) as a Burnside ring. Taking \(m=14\), \(n=15\) one concludes that \(\Lambda (A)\) is not a domain for any A.
To conclude, I exhibit the relationship between the given construction of Witt vectors and the standard one.
Define the maps \(\gamma _n:\Lambda (A) \rightarrow A\) by

where \(u'\) is the formal derivative of u with respect to T.
Each \(\gamma _n\) is a ring homomorphism, functorial in A. The ring structure on the set \(\Lambda (A)\) is characterized by being functorial in A and all \(\gamma _n\) being ring homomorphisms.
FormalPara ProofIt is well-known that the logarithmic derivative  transforms multiplication into addition. For \(u=(1-aT)^{-1}\) one has
transforms multiplication into addition. For \(u=(1-aT)^{-1}\) one has
so
This is multiplicative in a, so on elements of the form \((1-aT)^{-1}\) each \(\gamma _n\) transforms \(*\) into multiplication. Using functoriality and continuity one concludes that it gives a ring homomorphism. As for the last statement, with Yoneda’s lemma one reduces the proof to the case of polynomial rings over \(\mathbb Z\), and one uses that for those rings the map  is injective; the details are left to the reader. \(\square \)
is injective; the details are left to the reader. \(\square \)
For each commutative ring A, the maps

for \(n=0,1,2,\dots \) as well as the map

are bijective.
The proof is routine.
I can now relate the standard definition of W(A) to the construction given.
The Witt ring W(A) is the set \(\prod _{\,m \geqslant 1}A\) with ring structure  ,
,  , where \(\varphi \) is as in Lemma 5.
, where \(\varphi \) is as in Lemma 5.
Here is a diagram in the category of commutative rings that is important in the theory of Witt vectors:

The top horizontal map is \(\varphi \). The right vertical map sends u to  ; by the proposition, it is a ring homomorphism if
; by the proposition, it is a ring homomorphism if  has the usual addition and Hadamard multiplication. The bottom horizontal map sends \((a_n)_{n \geqslant 1}\) to
has the usual addition and Hadamard multiplication. The bottom horizontal map sends \((a_n)_{n \geqslant 1}\) to  ; it is a ring isomorphism if
; it is a ring isomorphism if  has componentwise ring operations. The left vertical map is defined by the commutativity of the diagram. By a straightforward computation, it sends \((a_n)_{n=1}^{\infty }\) to \((a^{(n)})_{n=1}^{\infty }\), where the “ghost components” \(a^{(n)}\) are given by
has componentwise ring operations. The left vertical map is defined by the commutativity of the diagram. By a straightforward computation, it sends \((a_n)_{n=1}^{\infty }\) to \((a^{(n)})_{n=1}^{\infty }\), where the “ghost components” \(a^{(n)}\) are given by

By the proposition, the ring structure on W(A) is characterized by functoriality and by the ghost components being ring homomorphisms \(W(A)\rightarrow A\). This is often taken as the definition of W(A).
March 4, 2002
Author information
Authors and Affiliations
Corresponding author
Additional information
Editor’s note. This paper is published here exactly as it had appeared (as a preprint) in 2002 and therefore may be viewed also as a historical document. The abstract, MSC codes and keywords were provided by the editor.
Based on notes made by John Voight (jvoight@math.berkeley.edu) from two lectures on February 27 and March 1, 2002, in the Number Theory Seminar, University of California, Berkeley.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Lenstra, H.W. Construction of the ring of Witt vectors. European Journal of Mathematics 5, 1234–1241 (2019). https://doi.org/10.1007/s40879-018-0294-1
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40879-018-0294-1




 ; i.e.
; i.e. 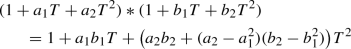
 . Then for
. Then for 
