Abstract
In 1981 William L. Edge discovered and studied a pencil \(\mathscr {C}\) of highly symmetric genus 6 projective curves with remarkable properties. Edge’s work was based on an 1895 paper of Anders Wiman. Both papers were written in the satisfying style of 19th century algebraic geometry. In this paper and its sequel Geometry of the Wiman–Edge pencil, II: hyperbolic, conformal and modular aspects (in preparation), we consider \(\mathscr {C}\) from a more modern, conceptual perspective, whereby explicit equations are reincarnated as geometric objects.
Similar content being viewed by others
1 Introduction
The purpose of this paper is to explore what we call the Wiman–Edge pencil \(\mathscr {C}\), a pencil of highly symmetric genus 6 projective curves with remarkable properties. The smooth members of \(\mathscr {C}\) can be characterized (see Theorem 3.3) as those smooth genus 6 curves admitting a nontrivial action of alternating group \(\mathfrak {A}_5\). This mathematical gem was discovered in 1981 by William L. Edge [10, 11], who based his work on a discovery in 1895 by Anders Wiman of a non-hyperelliptic curve \(C_0\) of genus 6 (now called the Wiman curve) with automorphism group isomorphic to the symmetric group \(\mathfrak {S}_5\). The results of both Wiman and Edge are in the satisfying style of 19th century mathematics, with results in terms of explicit equations.
In this paper and its sequel [12], we consider \(\mathscr {C}\) from a more modern, conceptual perspective, whereby explicit equations are reincarnated as geometric objects. In particular we will view \(\mathscr {C}\) through a variety of lenses: from algebraic geometry to representation theory to hyperbolic and conformal geometry. We will address both modular and arithmetic aspects of \(\mathscr {C}\), partly through Hodge theory. Given the richness and variety of structures supported by \(\mathscr {C}\), we can say in hindsight that the Wiman–Edge pencil deserved such a treatment, and indeed it seems odd that this had not happened previously.
In the introduction of his Lectures on the Icosahedron [18], Felix Klein writes: “A special difficulty, which presented itself in the execution of my plan, lay in the great variety of mathematical methods entering in the theory of the Icosahedron.” We believe that this is still very much true today, in ways Klein probably never anticipated. This, by the way, is followed by the sentence: “On this account it seemed advisable to take granted no specific knowledge in any direction, but rather to introduce, where necessary, such explanations \(\ldots \)” While we are writing only about one aspect of Klein’s book, in this paper we have tried to take Klein’s advice seriously.
1.1 The Wiman–Edge pencil
As mentioned above, the story starts with Wiman [24], who, while classifying algebraic curves of genus \(g = 4,5\) and 6 whose automorphisms group contains a simple group, discovered a curve \(C_0\) of genus 6 with automorphism group isomorphic to the symmetric group \(\mathfrak {S}_5\). On the last page of his paper, Wiman gives the equation of a 4-nodal plane sextic birationally isomorphic to W:

He reproduces this equation on p. 208 of his later paper [25], related to the classification of finite subgroups of the plane Cremona group. Wiman states there that the group of birational automorphisms of \(C_0\) is generated by a group of projective transformations isomorphic to the symmetric group \(\mathfrak {S}_4\) together with the standard quadratic birational involution with fundamental points at its three singular points.
Wiman erroneously claims that his curve is the unique non-hyperelliptic curve of genus 6 whose automorphism group contains a non-cyclic simple group, the alternating group \(\mathfrak {A}_5\) in his case. This mistake was corrected almost a hundred years later by Edge [10, 11], who placed W inside a pencil
of 4-nodal plane sextics each of whose members admits a group of automorphisms isomorphic to \(\mathfrak {A}_5\). In projective coordinates different from the one chosen by Wiman, the pencil is generated by the curves defined by the homogeneous equations:

and

where the Wiman curve W corresponds to the parameters  .
.
Edge showed that it is more natural to view the pencil as a pencil \(\mathscr {C}\) of curves on a quintic del Pezzo surface S obtained by blowing up the four base points of the pencil. In this picture, the lift \(C_0\) to S of Wiman’s curve W is, as Edge discovered, “a uniquely special canonical curve of genus 6” on S. That is, the standard action of \(\mathfrak {S}_5\) on the quintic del Pezzo surface S permutes the 1-parameter family of smooth genus 6 curves on S but leaves invariant a unique such curve, namely the Wiman sextic \(C_0\).
The action of \(\mathfrak {S}_5\) on S induces an action of \(\mathfrak {S}_5\) on \(\mathscr {C}\), whereby the subgroup \(\mathfrak {A}_5\) leaves each member of the pencil \(\mathscr {C}\) invariant, and acts faithfully on each curve by automorphisms. In addition to \(C_0\), the pencil \(\mathscr {C}\) has precisely one other \(\mathfrak {S}_5\)-fixed member, a reducible curve that is a union of 10 lines intersecting in the pattern of the Petersen graph (see Fig. 2), with the \(\mathfrak {S}_5\)-action on this union inducing the standard \(\mathfrak {S}_5\)-action on the Petersen graph. The other four singular members of \(\mathscr {C}\) come in pairs, the curves in each pair being switched by any odd permutation. A schematic of \(\mathscr {C}\), and the \(\mathfrak {S}_5\)-action on it, is given (with explanation) in Fig. 1.
A schematic of the Wiman–Edge pencil \(\mathscr {C}\), consisting of genus 6 projective curves containing the alternating group \(\mathfrak {A}_5\) in their automorphism group. The generic curve  has
has  , while there is a unique smooth member
, while there is a unique smooth member  , the Wiman sextic, with more symmetry:
, the Wiman sextic, with more symmetry:  . There are five singular members of \(\mathscr {C}\): two irreducible curves, 6-noded rational curves \(C_{\mathrm{ir}}\) and \(C'_{\mathrm{ir}}\); two curves \(C_\mathrm{c}\) and \(C'_\mathrm{c}\), each consisting of five conics whose intersection graph is the complete graph on five vertices; and a union \(C_\infty \) of 10 lines whose intersection graph is the Petersen graph. The group \(\mathfrak {S}_5\) acts on \(\mathscr {C}\) with \(\mathfrak {A}_5\) leaving each member of \(\mathscr {C}\) invariant. This action has two \(\mathfrak {S}_5\)-invariant members, \(C_0\) and \(C_\infty \), while any odd permutation switches \(C_{\mathrm{ir}}\) with \(C'_{\mathrm{ir}}\) and \(C_\mathrm{c}\) with \(C'_\mathrm{c}\)
. There are five singular members of \(\mathscr {C}\): two irreducible curves, 6-noded rational curves \(C_{\mathrm{ir}}\) and \(C'_{\mathrm{ir}}\); two curves \(C_\mathrm{c}\) and \(C'_\mathrm{c}\), each consisting of five conics whose intersection graph is the complete graph on five vertices; and a union \(C_\infty \) of 10 lines whose intersection graph is the Petersen graph. The group \(\mathfrak {S}_5\) acts on \(\mathscr {C}\) with \(\mathfrak {A}_5\) leaving each member of \(\mathscr {C}\) invariant. This action has two \(\mathfrak {S}_5\)-invariant members, \(C_0\) and \(C_\infty \), while any odd permutation switches \(C_{\mathrm{ir}}\) with \(C'_{\mathrm{ir}}\) and \(C_\mathrm{c}\) with \(C'_\mathrm{c}\)
Since Edge’s discovery, the pencil \(\mathscr {C}\), which we propose to call the Wiman–Edge pencil, has appeared in several modern research papers. For example, its nonsingular members have been identified with the quotient of one of the two 1-parameter families of lines on a nonsingular member of the Dwork pencil of Calabi–Yau quintic threefolds:

by the group of order 125 of obvious symmetries of the Dwork pencil (see [3, 27]; we elaborate a bit on the connection in the present paper).The Wiman–Edge occupies a prominent place in the monograph [4] on birational geometry of algebraic varieties with \(\mathfrak {A}_5\)-symmetry. It also appears in a recent posting by Cheltsov–Kuznetsov–Shramov [5].
1.2 This paper
The purpose of the present paper is two-fold. First, we reprove all previously known facts about the Wiman–Edge pencil that can be found in Edge’s papers. Instead of computations based on the pencil’s equation (used also in a later paper [14] whose authors it seems were not aware of Edges’s work), our proofs rely on the representation theory of the symmetry group of the pencil, and also on the moduli-theoretical interpretation of the quintic del Pezzo surface. Although our approach is not new, and has been used also in [4] or [16], respectively, we would like to believe that our methods are more conceptual and geometric.
The other goal of the paper is to answer some natural questions that arise while one gets familiar with the pencil. Thus we give a purely geometric proof of the uniqueness of the Wiman–Edge pencil as an \(\mathfrak {A}_5\)-invariant family of stable curves of genus 6, and in particular, the uniqueness of the Wiman curve W as a non-hyperelliptic curve of genus 6 with the group of automorphisms isomorphic to \(\mathfrak {S}_5\). In fact, we give two different proofs of this result: an algebraic geometrical one given in Theorem 3.3 below, and a second one in the sequel [12] that is essentially group-theoretical and topological.
Secondly, we give a lot of attention to the problem only barely mentioned by Edge and later addressed in the paper [20]: describe an \(\mathfrak {A}_5\)-equivariant projection of the Wiman–Edge pencil to a Klein plane realizing an irreducible 2-dimensional projective representation of \(\mathfrak {A}_5\). It reveals a natural relation between the Wiman–Edge pencil and the symmetry of the icosahedron along the lines of Klein’s book [18]. In particular, we relate the singular members of the pencil with some attributes of the geometry of the Clebsch diagonal cubic surface as well with some rational plane curves of degree 6 and 10 invariant with respect to a projective group of automorphisms isomorphic to \(\mathfrak {A}_5\) which were discovered by Roy Winger [26].
In the sequel [12] we will discuss some other aspects of the Wiman paper related to hyperbolic geometry, the moduli space of curves and Shimura curves.
1.3 Section-by-section outline of this paper
Section 2 collects a number of mostly known facts regarding quintic del Pezzo surfaces, but with emphasis on naturality, so that it is straightforward to keep track of how the automorphism group of such a surface acts on the vector spaces associated to it. We also recall the incarnation of such a surface as the Deligne–Knudsen–Mumford compactification \(\overline{\mathscr {M}}_{0,5}\) and mention how some its features can be recognized in either description. Perhaps new is Lemma 2.1 and its use to obtain Proposition 2.3.
Section 3 introduces the principal object of this paper, the Wiman–Edge pencil \(\mathscr {C}\). Our main result here is that its smooth fibres define the universal family of genus 6 curves endowed with a faithful \(\mathfrak {A}_5\)-action. We also determine the singular fibers of \(\mathscr {C}\). Each of these turns out to be a stable curve. Indeed, the whole pencil consists of all the stable genus 6 curves endowed with a faithful \(\mathfrak {A}_5\)-action that can be smoothed as an \(\mathfrak {A}_5\)-curve. We further prepare for the next two sections by describing \(\mathfrak {S}_5\)-orbits in \(\overline{\mathscr {M}}_{0,5}\), thus recovering a list due to Coble. This simplifies considerably when we restrict to the \(\mathfrak {A}_5\)-action and this what we will only need here.
The following two sections concern the projection to a Klein plane. These are \(\mathfrak {A}_5\)-equivariant projections as mentioned above. Section 4 concentrates on the global properties of this projection, and proves among other things that the ramification curve of such a projection is in fact a singular member of the Wiman–Edge pencil. It is perhaps worthwhile to point out that we prove this using the Thom–Boardman formula for cusp singularities. This is the only instance we are aware of where such a formula for a second order Thom–Boardman symbol is used to prove an algebro-geometric property. We also show that the image of the Wiman–Edge pencil in a Klein plane under the projection is no longer a pencil, but a curve of degree 5 with two singular points.
As its title makes clear, Sect. 5 focusses on the images in the Klein plane of special members of the Wiman–Edge pencil. We thus find ourselves suddenly staring at a gallery of planar representations of degree 10 of genus 6 curves with \(\mathfrak {A}_5\)-action, probably all known to our predecessors in the early 20th century if not earlier. Among them stand out (what we have called) the Klein decimic and the Winger decimic. Less exciting perhaps at first is the case of a conic with multiplicity 5; but this turns out to be the image of a member of the Wiman–Edge pencil which together with its \(\mathfrak {S}_5\)-conjugate is characterized by possessing a pencil of even theta characteristics.
In the final section, Sect. 6, we look at the \(\mathfrak {S}_5\)-orbit space of \(\overline{\mathscr {M}}_{0,5}\) (which is just the Hilbert–Mumford compactification of the space of binary quintics given up to projective equivalence) and make the connection with the associated invariant theory.
1.4 Conventions
Throughout this paper the base field is \(\mathbb {C}\) and S stands for a quintic del Pezzo surface (the definition is recalled in Sect. 2). The canonical line bundle \(\Omega _M^n\) of a complex n-manifold M will be often denoted by \(\omega _M\). As this is also the dualizing sheaf for M, we use the same notation if M is possibly singular, but has such a sheaf (we only use this for curves with nodes).
For a vector space V, let \(\mathbb {P}(V)\) denote the projective space of 1-dimensional subspaces of V and \(\check{\mathbb {P}} (V)=\mathbb {P}(V^\vee )\) denotes the projective space of hyperplanes of V. We write  for dth symmetric power of the vector space V. For a space or variety X we denote by
for dth symmetric power of the vector space V. For a space or variety X we denote by  the quotient of \(X^d\) by the permutation group \(\mathfrak {S}_d\).
the quotient of \(X^d\) by the permutation group \(\mathfrak {S}_d\).
2 Del Pezzo surfaces of degree 5
2.1 A brief review
Here we recall some known facts about quintic del Pezzo surfaces, i.e., del Pezzo surfaces of degree 5, that one can find in many sources (such as [8]). By definition a del Pezzo surface is a smooth projective algebraic surface S with ample anticanonical bundle \(\omega _S^{-1}\). For such a surface S, the first Chern class map  is an isomorphism. Denoting by
is an isomorphism. Denoting by  the canonical class of S, i.e., the first Chern class of \(\omega _S\) (and hence minus the first Chern class of the tangent bundle of S), the self-intersection number \(d = (-K_S)^2 = K_S^2\) is called the degree of S. With the exception of surfaces isomorphic to
the canonical class of S, i.e., the first Chern class of \(\omega _S\) (and hence minus the first Chern class of the tangent bundle of S), the self-intersection number \(d = (-K_S)^2 = K_S^2\) is called the degree of S. With the exception of surfaces isomorphic to  (which are del Pezzo surfaces of degree 8), a del Pezzo surface of degree d admits a birational morphism \(\pi :S\rightarrow \mathbb {P}^2\) whose inverse is the blow-up of \(9-d\) distinct points (so we always have \(d\leqslant 9\)) satisfying some genericity conditions. But beware that when \(d\leqslant 6\), there is more that one way to contract curves in S that produce a copy of \(\mathbb {P}^2\).
(which are del Pezzo surfaces of degree 8), a del Pezzo surface of degree d admits a birational morphism \(\pi :S\rightarrow \mathbb {P}^2\) whose inverse is the blow-up of \(9-d\) distinct points (so we always have \(d\leqslant 9\)) satisfying some genericity conditions. But beware that when \(d\leqslant 6\), there is more that one way to contract curves in S that produce a copy of \(\mathbb {P}^2\).
When \(d=5\) (which we assume from now on), these genericity conditions amount to having no three (of the four) points lie on a line so that we can adapt our coordinates on \(\mathbb {P}^2\) such that the points in question, after having them numbered \((p_1,p_2,p_3, p_4)\), are the vertices of the coordinate system:

This shows that any two quintic del Pezzo surfaces are isomorphic and also proves that the automorphism group of S contains the permutation group \(\mathfrak {S}_4\). The complete linear system  defined by nonzero sections of the dual of the canonical line bundle of S is then the strict transform of the linear system in \(\mathbb {P}^2\) of plane cubic curves passing through these points in the sense that a general member is the strict transform of such a cubic. This is a linear system of dimension \(9-4=5\) and gives an embedding in a 5-dimensional projective space
defined by nonzero sections of the dual of the canonical line bundle of S is then the strict transform of the linear system in \(\mathbb {P}^2\) of plane cubic curves passing through these points in the sense that a general member is the strict transform of such a cubic. This is a linear system of dimension \(9-4=5\) and gives an embedding in a 5-dimensional projective space

with image a surface of degree 5. We call S, thus embedded in a projective space, an anticanonical model of S.
The automorphism group of S is, however, bigger than \(\mathfrak {S}_4\): the embedding  extends to an isomorphism
extends to an isomorphism

given by assigning to the transposition (45) the lift of the Cremona transformation

which indeed lifts to an involution of S (see [8, Theorem 8.5.8]).
The image of a nonsingular rational curve on S with self-intersection number \(-1\) (in other words, an exceptional curve of the first kind) is a line on the anticanonical model, and any such line is so obtained. Any line on the quintic del Pezzo surface S is either the strict transform of a line through \(p_i\) and  , \(1\leqslant i<j\leqslant 4\), or the preimage of \(p_i\), \(i=1,\dots , 4\), so that there are \(\left( {\begin{array}{c}4\\ 2\end{array}}\right) +4=10\) lines on S.
, \(1\leqslant i<j\leqslant 4\), or the preimage of \(p_i\), \(i=1,\dots , 4\), so that there are \(\left( {\begin{array}{c}4\\ 2\end{array}}\right) +4=10\) lines on S.
The strict transform \(\mathscr {P}_i\) of the pencil of lines through \(p_i\) makes a pencil \(\mathscr {P}_i\) of rational curves on S whose members are pairwise disjoint: they are the fibers of a morphism from S to a projective line. The strict transform of the conics through \(p_1,\dots , p_4\) makes up a pencil \(\mathscr {P}_5\) with the same property. The intersection number of a member of \(\mathscr {P}_i\) with \(-K_S\) is equal to the intersection number of a cubic with a line in \(\mathbb {P}^2\) minus 1 if \(i\ne 5\), resp. cubic with a conic minus 4 if \(i = 5\), hence is equal to 2. This is therefore also a conic in the anticanonical model, and that is why we refer to \(\mathscr {P}_i\) as a pencil of conics and call the corresponding morphism from S to a projective line a conic bundle.
Every pencil of conics has exactly three singular fibers; these are unions of two different lines. For example, the pencil \(\mathscr {P}_i, i\ne 5\), has singular members equal to the pre-images on S of the lines  joining the point \(p_i\) with the point
joining the point \(p_i\) with the point  . The singular members of pencil \(\mathscr {P}_5\) are proper transforms of the pairs of lines
. The singular members of pencil \(\mathscr {P}_5\) are proper transforms of the pairs of lines  with all indices distinct.
with all indices distinct.
It follows that each of 10 lines on S is realized as an irreducible component of exactly three different pencils of conics. This allows one to label it with a 2-element subset of  , being the complement of the corresponding 3-element subset. We thus obtain a bijection between the set of 10 lines and the collection of 2-element subsets of
, being the complement of the corresponding 3-element subset. We thus obtain a bijection between the set of 10 lines and the collection of 2-element subsets of  , with two lines intersecting if and only if the associated 2-element subsets are disjoint, or equivalently, when the two lines constitute a singular member of one of the five pencils of conics. Thus the intersection graph \(\mathscr {G}\) of the set lines, i.e., the graph whose vertex set is the set of lines and in which two vertices are connected by an edge if and only if the associated lines intersect, is the Petersen graph (Fig. 2). We see here
, with two lines intersecting if and only if the associated 2-element subsets are disjoint, or equivalently, when the two lines constitute a singular member of one of the five pencils of conics. Thus the intersection graph \(\mathscr {G}\) of the set lines, i.e., the graph whose vertex set is the set of lines and in which two vertices are connected by an edge if and only if the associated lines intersect, is the Petersen graph (Fig. 2). We see here  also represented as the automorphism group of \(\mathscr {G}\).
also represented as the automorphism group of \(\mathscr {G}\).
The Petersen graph \(\mathscr {G}\). This is the graph with vertices corresponding to 2-element subsets of  , with two vertices
, with two vertices  and
and  connected by an edge precisely when
connected by an edge precisely when  . The graph \(\mathscr {G}\) is the intersection graph of the 10 lines on the quintic del Pezzo surface, with a vertex for each line and an edge connecting vertices corresponding to lines with nontrivial intersection
. The graph \(\mathscr {G}\) is the intersection graph of the 10 lines on the quintic del Pezzo surface, with a vertex for each line and an edge connecting vertices corresponding to lines with nontrivial intersection
The edges of the Petersen graph represent reducible conics on S, and there are indeed  of them. The three reducible conics of a conic bundle are then represented by three disjoint edges whose indices are three 2-element subsets of a subset of
of them. The three reducible conics of a conic bundle are then represented by three disjoint edges whose indices are three 2-element subsets of a subset of  of cardinality 4. If we regard the missing item as a label for the conic pencil, we see that
of cardinality 4. If we regard the missing item as a label for the conic pencil, we see that  is realized as the full permutation group of the set of conic pencils.
is realized as the full permutation group of the set of conic pencils.
2.2 The modular incarnation
A quintic del Pezzo surface has the—for us very useful—incarnation as the Deligne–Mumford moduli space of stable 5-pointed rational curves, \(\overline{\mathscr {M}}_{0,5}\), see [17]. In the present case, this is also the Hilbert–Mumford (or GIT) compactification of \(\mathscr {M}_{0,5}\), which means that a point of \(\overline{\mathscr {M}}_{0,5}\) is uniquely represented up to automorphism by a smooth rational curve C and a 5-tuple \((x_1,\dots , x_5)\in C^5\) for which the divisor  has all its multiplicities \(\leqslant 2\). One of the advantages of either model is that the \(\mathfrak {S}_5\)-action is evident. The 10 lines appear as the irreducible components of the boundary
has all its multiplicities \(\leqslant 2\). One of the advantages of either model is that the \(\mathfrak {S}_5\)-action is evident. The 10 lines appear as the irreducible components of the boundary  of the compactification: these are the loci defined by
of the compactification: these are the loci defined by  , where
, where  is a 2-element subset of
is a 2-element subset of  . We thus recover the bijection between the set of 10 lines and the collection of 2-element subsets of
. We thus recover the bijection between the set of 10 lines and the collection of 2-element subsets of  .
.
The conic bundles also have a modular interpretation, namely as forgetful maps: if a point of \(\overline{\mathscr {M}}_{0,5}\) is represented by a Deligne–Mumford stable curve \((C; x_1, \dots , x_5)\), then forgetting \(x_i\), \(i=1,\dots , 5\), followed by contraction unstable components (and renumbering the points by  in an order preserving manner) yields an element of \(\overline{\mathscr {M}}_{0,4}\). There is a similar definition in case a point of \(\overline{\mathscr {M}}_{0,5}\) is represented in a Hilbert–Mumford stable manner, but beware that a Hilbert–Mumford stable representative of \(\overline{\mathscr {M}}_{0,4}\) is given uniquely up to isomorphism by a 4-tuple \((x_1, \dots , x_4)\in C^4\) for which the divisor
in an order preserving manner) yields an element of \(\overline{\mathscr {M}}_{0,4}\). There is a similar definition in case a point of \(\overline{\mathscr {M}}_{0,5}\) is represented in a Hilbert–Mumford stable manner, but beware that a Hilbert–Mumford stable representative of \(\overline{\mathscr {M}}_{0,4}\) is given uniquely up to isomorphism by a 4-tuple \((x_1, \dots , x_4)\in C^4\) for which the divisor  is either reduced or twice a reduced divisor; if for example \(x_1=x_2\), then we also require that \(x_3=x_4\) (but \(x_2\not = x_3\)). The moduli space \(\overline{\mathscr {M}}_{0,4}\) is a smooth rational curve and
is either reduced or twice a reduced divisor; if for example \(x_1=x_2\), then we also require that \(x_3=x_4\) (but \(x_2\not = x_3\)). The moduli space \(\overline{\mathscr {M}}_{0,4}\) is a smooth rational curve and  consists of three points indexed by the three ways we can partition
consists of three points indexed by the three ways we can partition  into two 2-element subsets. The resulting morphism \(f_i:\overline{\mathscr {M}}_{0,5}\rightarrow \overline{\mathscr {M}}_{0,4}\) represents \(\mathscr {P}_i\) and over the three points of
into two 2-element subsets. The resulting morphism \(f_i:\overline{\mathscr {M}}_{0,5}\rightarrow \overline{\mathscr {M}}_{0,4}\) represents \(\mathscr {P}_i\) and over the three points of  lie the three singular fibres.
lie the three singular fibres.
Let us focus for a moment on \(\mathscr {P}_5\), in other words, on \(f_5:\overline{\mathscr {M}}_{0,5}\rightarrow \overline{\mathscr {M}}_{0,4}\). Each \(x_i\), \(i=1, \dots , 4\), then defines a section \(\overline{\mathscr {M}}_{0,4}\rightarrow \overline{\mathscr {M}}_{0,5}\) of \(f_5\), and \(f_5\) endowed with these four sections can be understood as the “universal stable 4-pointed rational curve”. Note that the images of these sections are irreducible components of  and hence lines in the anticanonical model. They are indexed by the unordered pairs
and hence lines in the anticanonical model. They are indexed by the unordered pairs  , \(i=1,\dots , 4\). The singular fibers of \(f_5\) are those over the 3-element set
, \(i=1,\dots , 4\). The singular fibers of \(f_5\) are those over the 3-element set  ; each such fiber is a union of two intersection lines, so that in this way all 10 lines are accounted for.
; each such fiber is a union of two intersection lines, so that in this way all 10 lines are accounted for.
The \(\mathfrak {S}_5\)-stabilizer of the conic bundle defined by \(f_5\) is clearly \(\mathfrak {S}_4\). Let us take a closer look at how \(\mathfrak {S}_4\) acts on \(f_5\). First observe that every smooth fiber of \(f_5\) (i.e., a strict transform of a smooth conic) meets every fiber of every \(f_i\), \(i\not =5\), with multiplicity one. We also note that \(\mathfrak {S}_4\) acts on the 3-element set  as its full permutation group, the kernel being the Klein Vierergruppe. So the Vierergruppe acts trivially on \(\overline{\mathscr {M}}_{0,4}\), but its action on the universal pointed rational curve \(\overline{\mathscr {M}}_{0,5}\) is of course faithful. The homomorphism \(\mathfrak {S}_4\rightarrow \mathfrak {S}_3\) can also be understood as follows. If we are given a smooth rational curve C endowed and a 4-element subset \(X\subset C\), then the double cover \(\widetilde{C}\) of C ramified at X is a smooth genus 1 curve. If we enumerate the points of X by
as its full permutation group, the kernel being the Klein Vierergruppe. So the Vierergruppe acts trivially on \(\overline{\mathscr {M}}_{0,4}\), but its action on the universal pointed rational curve \(\overline{\mathscr {M}}_{0,5}\) is of course faithful. The homomorphism \(\mathfrak {S}_4\rightarrow \mathfrak {S}_3\) can also be understood as follows. If we are given a smooth rational curve C endowed and a 4-element subset \(X\subset C\), then the double cover \(\widetilde{C}\) of C ramified at X is a smooth genus 1 curve. If we enumerate the points of X by  , then we can choose \(x_1\) as origin, so that \((\widetilde{C}, x_1)\) becomes an elliptic curve. This then makes
, then we can choose \(x_1\) as origin, so that \((\widetilde{C}, x_1)\) becomes an elliptic curve. This then makes  the set of elements of \((\widetilde{C},x_1)\) of order 2. Thus \(\mathscr {M}_{0,4}\) can be regarded as the moduli space of elliptic curves endowed with a principal level 2 structure. This also suggests that we should think of X as an affine plane over \(\mathbb {F}_2\); for this interpretation the three boundary points of \(\overline{\mathscr {M}}_{0,4}\) are cusps, and correspond to the three directions in this plane. We now can think of \(\mathfrak {S}_4\) as the affine group of X, the Vierergruppe as its translation subgroup, and the quotient \(\mathfrak {S}_3\) as the projective linear group
the set of elements of \((\widetilde{C},x_1)\) of order 2. Thus \(\mathscr {M}_{0,4}\) can be regarded as the moduli space of elliptic curves endowed with a principal level 2 structure. This also suggests that we should think of X as an affine plane over \(\mathbb {F}_2\); for this interpretation the three boundary points of \(\overline{\mathscr {M}}_{0,4}\) are cusps, and correspond to the three directions in this plane. We now can think of \(\mathfrak {S}_4\) as the affine group of X, the Vierergruppe as its translation subgroup, and the quotient \(\mathfrak {S}_3\) as the projective linear group  .
.
Choose an affine coordinate z for the base of \(\overline{\mathscr {M}}_{0,4}\) such that  is the root set of
is the root set of  . Then the full permutation group of
. Then the full permutation group of  is the group of Möbius transformations consisting of the rotations \(z\mapsto \zeta z\) and the involutions \(z\mapsto \zeta /z\), with
is the group of Möbius transformations consisting of the rotations \(z\mapsto \zeta z\) and the involutions \(z\mapsto \zeta /z\), with  . From this we see that this action has three irregular orbits: two 3-element orbits: besides the root set of
. From this we see that this action has three irregular orbits: two 3-element orbits: besides the root set of  which is
which is  , the root set of \(z^3=-1\), and one 2-element orbit:
, the root set of \(z^3=-1\), and one 2-element orbit:  . The root set of
. The root set of  is represented by \(\mathbb {P}^1\) with an enumeration of the 4th roots of unity in \(\mathbb {C}\subset \mathbb {P}^1\), and the third orbit is given by
is represented by \(\mathbb {P}^1\) with an enumeration of the 4th roots of unity in \(\mathbb {C}\subset \mathbb {P}^1\), and the third orbit is given by  .
.
We will be more concerned with the last orbit that gives rise to two special conics in the pencil. So every conic bundle has two special conics as fibers and \(\mathfrak {S}_5\) permutes these 10 special conics transitively. Two distinct special conics intersect unless they are in the same pencil. The two points \(0,\infty \) have the same \(\mathfrak {S}_3\)-stabilizer in \(\mathbb {P}^1\) of order 3. In the action of \(\mathfrak {S}_4\) on the total space of the pencil, the two special conics are fixed by the subgroup \(\mathfrak {A}_4\). It follows from the preceding that these two fibers define the locus represented by \((x_1, \dots , x_5)\in C^5\) (with C a smooth rational curve) for which there exists an affine coordinate z on C such that  is the union of \(\{\infty \}\) and the root set of
is the union of \(\{\infty \}\) and the root set of  . Our discussion also shows that the subgroup \(\mathfrak {A}_5\) has two orbits in that set, with each orbit having exactly one special conic in each conic bundle.
. Our discussion also shows that the subgroup \(\mathfrak {A}_5\) has two orbits in that set, with each orbit having exactly one special conic in each conic bundle.
2.3 Representation spaces of \(\mathfrak {S}_5\)
In what follows we make repeated use of the representation theory of \(\mathfrak {S}_5\) and \(\mathfrak {A}_5\), and so let us agree on its notation. In Tables 1 and 2, the columns are the conjugacy classes of the group, indicated by the choice of a representative. We partially followed Fulton–Harris [13] for the notation of the types of the irreducible representations of \(\mathfrak {S}_5\). Here \(\mathbf {1}\) denotes the trivial representation, \(\text {sgn}\) denotes the sign representation, V denotes the Coxeter representation, that is, the standard 4-dimensional irreducible representation of \(\mathfrak {S}_5\) and E stands for  . Note that each of these representations is real and hence admits a nondegenerate \(\mathfrak {S}_5\)-invariant quadratic form, making it self-dual.
. Note that each of these representations is real and hence admits a nondegenerate \(\mathfrak {S}_5\)-invariant quadratic form, making it self-dual.
Our labeling of the irreducible representations of \(\mathfrak {A}_5\) overlaps with that of \(\mathfrak {S}_5\), and this is deliberately so: the \(\mathfrak {S}_5\)-representations V and  become isomorphic when restricted to \(\mathfrak {A}_5\), but remain irreducible and that is why we still denote them by V. The same applies to W and
become isomorphic when restricted to \(\mathfrak {A}_5\), but remain irreducible and that is why we still denote them by V. The same applies to W and  (and of course to \(\mathbf {1}\) and \(\text {sgn}\)). On the other hand, the restriction to \(\mathfrak {A}_5\) of \(\mathfrak {S}_5\)-representation
(and of course to \(\mathbf {1}\) and \(\text {sgn}\)). On the other hand, the restriction to \(\mathfrak {A}_5\) of \(\mathfrak {S}_5\)-representation  is no longer irreducible, but is isomorphic as an \(\mathfrak {A}_5\)-representation
is no longer irreducible, but is isomorphic as an \(\mathfrak {A}_5\)-representation  (cf. Table 2). The representations I and \(I'\) differ by the outer automorphism of \(\mathfrak {A}_5\) induced by conjugation with an element of
(cf. Table 2). The representations I and \(I'\) differ by the outer automorphism of \(\mathfrak {A}_5\) induced by conjugation with an element of  . Both I and \(I'\) are realized as the group of isometries of Euclidean 3-space that preserve an icosahedron. In particular, they are real (and hence orthogonal).
. Both I and \(I'\) are realized as the group of isometries of Euclidean 3-space that preserve an icosahedron. In particular, they are real (and hence orthogonal).
We will often use the fact that the natural map  (given by conjugation) is an isomorphism of groups. So the outer automorphism group of \(\mathfrak {A}_5\) is of order 2 and representable by conjugation with an odd permutation.
(given by conjugation) is an isomorphism of groups. So the outer automorphism group of \(\mathfrak {A}_5\) is of order 2 and representable by conjugation with an odd permutation.
The isomorphism  depends of course on the model of S as a blow-up \(\mathbb {P}^2\), but since
depends of course on the model of S as a blow-up \(\mathbb {P}^2\), but since  permutes these models transitively, this isomorphism is unique up to an inner automorphism. This implies that the characters of
permutes these models transitively, this isomorphism is unique up to an inner automorphism. This implies that the characters of  , or equivalently, the isomorphism types of the finite dimensional irreducible representations of this group, are naturally identified with those of \(\mathfrak {S}_5\).
, or equivalently, the isomorphism types of the finite dimensional irreducible representations of this group, are naturally identified with those of \(\mathfrak {S}_5\).
Via this action of \(\mathfrak {S}_5\) on S, all linear spaces naturally associated to S can be made into linear representations of \(\mathfrak {S}_5\). For example, \(H^2(S; \mathbb {C})\) contains the trivial representation, spanned by the anticanonical class \(c_1(S)=-K_S\). The intersection pairing gives an integral, symmetric bilinear form on \(H^2(S;\mathbb {Z})\). The orthogonal complement of \(K_S\) in \(H^2(S; \mathbb {Z})\), denoted here by \(H^2_0(S; \mathbb {Z})\), contains (and is spanned by) a root system of type \(A_4\), the roots being the elements of self-intersection \(-2\). A root basis is

where \(e_0\) is the class of a preimage of a line in \(\mathbb {P}^2\) and \(e_i\) is the class of the line over \(p_i\). This identifies \(H^2_0(S; \mathbb {C})\) as an \(\mathfrak {S}_5\)-representation with the Coxeter representation V. The (classes of) lines themselves in \(H^2(S; \mathbb {Z})\) make up an \(\mathfrak {S}_5\)-orbit. In the language of root systems, it is the orbit of a fundamental weight; for the given root basis this weight is represented by the orthogonal projection of \(e_4\) in \(H^2_0(S; \mathbb {Q})\). Thus \(H^2_0(S; \mathbb {C})\) is isomorphic to V as an \(\mathfrak {S}_5\)-representation.
Another example is \(H^0(S,\omega _S^{-1})\), a 6-dimensional representation of \(\mathfrak {S}_5\). Using the explicit action of \(\mathfrak {S}_5\) on S and hence on the space of cubic polynomials representing elements of \(H^0(S,\omega _S^{-1})\), we find that it has the same character as  . This is why we shall write \(E_S\) for \(H^0(S,\omega _S^{-1})\), so that
. This is why we shall write \(E_S\) for \(H^0(S,\omega _S^{-1})\), so that  and
and  .
.
2.4 The Plücker embedding
We here show how S can be obtained in an intrinsic manner as a linear section of the Grassmannian of lines in projective 4-space. The naturality will make this automatically  -equivariant. Let \(C_\infty \) denote the union of the 10 lines on S. It is clear that \(C_\infty \) is a normal crossing divisor in S (under the modular interpretation of \(S\cong \overline{\mathscr {M}}_{0,5}\) it is the Deligne–Mumford boundary).
-equivariant. Let \(C_\infty \) denote the union of the 10 lines on S. It is clear that \(C_\infty \) is a normal crossing divisor in S (under the modular interpretation of \(S\cong \overline{\mathscr {M}}_{0,5}\) it is the Deligne–Mumford boundary).
Lemma 2.1
The sheaf of logarithmic differentials  is globally generated. The action of \(\mathfrak {S}_5\) on S makes the space of global sections
is globally generated. The action of \(\mathfrak {S}_5\) on S makes the space of global sections

an irreducible 5-dimensional \(\mathfrak {S}_5\)-representation isomorphic to W.
Proof
Denote by \(\mathscr {L}\) the 10-element set of lines on S and consider the residue exact sequence

where \(i_L:L\hookrightarrow S\) is the inclusion. All homomorphisms here are natural and the exact sequence of cohomology gives an exact sequence of \(\mathfrak {S}_5\)-representations:

The \(\mathfrak {S}_5\)-representation \(\mathbb {C}^{\mathscr {L}}\) is the permutation representation on the vertices of the Petersen graph. Its character is that of  , as one can see by looking at pairs of complementary pentagons inside of the Petersen graph. We also note that \(H^1(S;\Omega _S^1)\cong H^2(S;\mathbb {C})\) is as a representation isomorphic to
, as one can see by looking at pairs of complementary pentagons inside of the Petersen graph. We also note that \(H^1(S;\Omega _S^1)\cong H^2(S;\mathbb {C})\) is as a representation isomorphic to  . The blow-up model makes it obvious that \(H^2(S;\mathbb {C})\) is generated by the classes of lines, so that the homomorphism \(\phi \) is surjective, and we obtain an isomorphism of representations
. The blow-up model makes it obvious that \(H^2(S;\mathbb {C})\) is generated by the classes of lines, so that the homomorphism \(\phi \) is surjective, and we obtain an isomorphism of representations

It remains to show that \(W_S\) generates  . For this, we use the description of S as the blow-up of \(\mathbb {P}^2\) in the vertices of its coordinate simplex. In terms of the coordinates
. For this, we use the description of S as the blow-up of \(\mathbb {P}^2\) in the vertices of its coordinate simplex. In terms of the coordinates  , the logarithmic forms \(dt_1/t_1-dt_0/t_0\) and \(dt_2/t_2-dt_0/t_0\) generate the sheaf of differentials on \(\mathbb {P}^2\) outside the coordinate simplex and so they define elements \(\zeta _1\) and \(\zeta _2\) of \(W_S\) which generate
, the logarithmic forms \(dt_1/t_1-dt_0/t_0\) and \(dt_2/t_2-dt_0/t_0\) generate the sheaf of differentials on \(\mathbb {P}^2\) outside the coordinate simplex and so they define elements \(\zeta _1\) and \(\zeta _2\) of \(W_S\) which generate  . Since
. Since  is transitive on the vertices of the Petersen graph, it remains to prove generation along just one line, say the strict transform of
is transitive on the vertices of the Petersen graph, it remains to prove generation along just one line, say the strict transform of  . A straightforward computation shows that \(\zeta _1\) and \(\zeta _2\) take care of this, except at the point at infinity (where
. A straightforward computation shows that \(\zeta _1\) and \(\zeta _2\) take care of this, except at the point at infinity (where  ), but the origin is included. Since
), but the origin is included. Since  is also transitive on the edges of the Petersen graph, this finishes the proof. \(\square \)
is also transitive on the edges of the Petersen graph, this finishes the proof. \(\square \)
Remark 2.2
A local computation shows right away that  . Since \(C_\infty \) is a divisor of \(\omega _S^{-2}\), the latter is isomorphic to \(\omega _S^{-1}\), so that
. Since \(C_\infty \) is a divisor of \(\omega _S^{-2}\), the latter is isomorphic to \(\omega _S^{-1}\), so that  . The residue exact sequence allows one to compute
. The residue exact sequence allows one to compute  also we have
also we have

As is well-known, \(c_2(S)\) is the cohomology class in top degree whose value on the fundamental class is the Euler characteristic of S, which is 7 (since S is the blow-up of four points in \(\mathbb {P}^2\)). Using the identities  and
and  , together with the fact that the Petersen graph has 15 edges, we then find that
, together with the fact that the Petersen graph has 15 edges, we then find that  .
.
Since  is globally generated, for every \(x\in S\) the evaluation map
is globally generated, for every \(x\in S\) the evaluation map  is onto. So
is onto. So  is of dimension 3 and the annihilator of this kernel in \(W_S^\vee \) is of dimension 2. We thus obtain a morphism
is of dimension 3 and the annihilator of this kernel in \(W_S^\vee \) is of dimension 2. We thus obtain a morphism

Under this map, the pull-back of the dual of the tautological subbundle on the Grassmannian becomes isomorphic to  .
.
Proposition 2.3
The morphism f is a closed, \(\mathfrak {S}_5\)-equivariant embedding. Its composition with the Plücker embedding

is the anticanonical embedding into the subspace  , where \(E_S\) is identified with a direct summand of the representation
, where \(E_S\) is identified with a direct summand of the representation

In particular, the anticanonical model of S is \(\mathfrak {S}_5\)-equivariantly isomorphic to the intersection of  with the subspace \(\mathbb {P}(E)\) in its Plücker embedding.
with the subspace \(\mathbb {P}(E)\) in its Plücker embedding.
Proof
A locally free sheaf \(\mathscr {E}\) of rank r on a compact variety X that is globally generated determines a morphism  whose composite with the Plücker embedding
whose composite with the Plücker embedding  is given by the invertible sheaf \(\det \mathscr {E}\). Applying this to our situation, we find that the composite of f with the Plücker embedding is given by the complete linear system \(|-K_S|\). We know that it defines a closed embedding, from this the first claim follows.
is given by the invertible sheaf \(\det \mathscr {E}\). Applying this to our situation, we find that the composite of f with the Plücker embedding is given by the complete linear system \(|-K_S|\). We know that it defines a closed embedding, from this the first claim follows.
To see the second claim, we compute the character of the representation of \(\mathfrak {S}_5\) in  by means of the formula \(\chi _{{\scriptscriptstyle \bigwedge ^2}W}(g) = (\chi _W(g)^2-\chi _W(g^2))/2\). The standard character theory gives us the decomposition (1). \(\square \)
by means of the formula \(\chi _{{\scriptscriptstyle \bigwedge ^2}W}(g) = (\chi _W(g)^2-\chi _W(g^2))/2\). The standard character theory gives us the decomposition (1). \(\square \)
Remark 2.4
The linear map  of \(\mathfrak {S}_5\)-representations found above defines an equivariant linear embedding
of \(\mathfrak {S}_5\)-representations found above defines an equivariant linear embedding

whose geometry is discussed in [8, Example 10.2.20]. We note that this gives rise to a rational map

obtained as the composite of the Veronese map  and the projectivization of the linear map
and the projectivization of the linear map

It is clear that \(\widetilde{F}\) is given by a 4-dimensional linear system of quadrics. Its indeterminacy locus is where F(v) has rank \(\leqslant 2\) instead of 4 (as one might expect) and consists of five points in general position (so these are the vertices of a coordinate simplex of the 4-dimensional  ) and \(\widetilde{F}\) is then given by the linear system of quadrics through these. The \(\mathfrak {S}_5\)-equivariant map \(\widetilde{F}\) appears in modular setting which we shall now recall (and which is discussed for example in [8, Section 9.4.4]).
) and \(\widetilde{F}\) is then given by the linear system of quadrics through these. The \(\mathfrak {S}_5\)-equivariant map \(\widetilde{F}\) appears in modular setting which we shall now recall (and which is discussed for example in [8, Section 9.4.4]).
The moduli space \(\overline{\mathscr {M}}_{0,6}\) of stable 6-pointed genus zero curves is isomorphic to the blow-up of \(\mathbb {P}^3\) at the five vertices of its coordinate simplex followed by the blow-up of the proper transforms of the lines of this simplex (see [17]). There is a natural map from \(\overline{\mathscr {M}}_{0,6}\) to the Hilbert–Mumford compactification of \(\mathscr {M}_{0,6}\). The latter appears as the image an \(\overline{\mathscr {M}}_{0,6}\) in a 4-dimensional projective space via the linear system of quadrics in \(\mathbb {P}^3\) through the five coordinate vertices so that this reproduces a copy of our map \(\Phi \) above. The image of this map is a cubic hypersurface, called the Segre cubic \(\mathscr {S}_3\).
The Segre cubic has 10 nodal points, each of which is the image of an exceptional divisor over a line of the coordinate simplex. Observe that the modular interpretation of the morphism \(\overline{\mathscr {M}}_{0,6}\rightarrow \mathscr {S}_3\) makes evident an action of \(\mathfrak {S}_6\), although in the above model, only its restriction to the subgroup \(\mathfrak {S}_5\) is manifest. The ambient 4-dimensional projective space of the Segre cubic \(\mathscr {S}_3\) is the projectivization of an irreducible 5-dimensional representation of \(\mathfrak {S}_6\) corresponding to the partition (3, 3) (see [8, p. 470]). \(\square \)
2.5 The anticanonical model
Some of what follows can be found in Shepherd-Barron [23]; see also Mukai [19].
We have just seen that an anticanonical model of S is obtained as linear section of a Grassmannian \(G_1(W_S^\vee )\) for its Plücker embedding. It is well-known that the Plücker equations define the image of  as the intersection of five quadrics: these are given by the map
as the intersection of five quadrics: these are given by the map

or rather by its dual  . The latter is a nonzero map of \(\mathfrak {S}_5\)-representations. As we mentioned, the irreducible representation W is self-dual, and the character table of \(\mathfrak {S}_5\) shows that the \((-1)\)-eigenspace of the transposition \((12)\in \mathfrak {S}_5\) in W has dimension 2. Hence
. The latter is a nonzero map of \(\mathfrak {S}_5\)-representations. As we mentioned, the irreducible representation W is self-dual, and the character table of \(\mathfrak {S}_5\) shows that the \((-1)\)-eigenspace of the transposition \((12)\in \mathfrak {S}_5\) in W has dimension 2. Hence  is the trivial representation and
is the trivial representation and  can as an \(\mathfrak {S}_5\)-representation be identified with the irreducible representation \(W_S\). Thus we have obtained an \(\mathfrak {S}_5\)-equivariant embedding
can as an \(\mathfrak {S}_5\)-representation be identified with the irreducible representation \(W_S\). Thus we have obtained an \(\mathfrak {S}_5\)-equivariant embedding

(unique up to scalars) and this realizes \(\mathbb {P}(W_S)\) as the linear system of (Plücker) quadrics in  that define \(G_1(W_S^\vee )\). By restriction to \(E_S^\vee \), we can also understand \(W_S\) as defining the linear system of quadrics in
that define \(G_1(W_S^\vee )\). By restriction to \(E_S^\vee \), we can also understand \(W_S\) as defining the linear system of quadrics in  that has
that has  as its base locus. When thus interpreted, we will write \(I_S(2)\) for \(W_S\).
as its base locus. When thus interpreted, we will write \(I_S(2)\) for \(W_S\).
The character of  can be computed by means of the formula
can be computed by means of the formula  . We then find that
. We then find that

We have already singled out the subrepresentation \(I_S(2)\) as a copy of W and so the remaining summands in (2) will add up to a representation that embeds in \(H^0(S,\omega _S^{-2})\). An application of Riemann–Roch or the explicit discussion below shows that this is in fact an isomorphism, so that we have an exact sequence of \(\mathfrak {S}_5\)-representations
and an \(\mathfrak {S}_5\)-equivariant isomorphism

The summands \(\mathbf {1}\) and \(\text {sgn}\) in  are explained by restricting the representation \(E_S\) to \(\mathfrak {A}_5\): then \(E_S\) decomposes into two irreducible \(\mathfrak {A}_5\)-representations:
are explained by restricting the representation \(E_S\) to \(\mathfrak {A}_5\): then \(E_S\) decomposes into two irreducible \(\mathfrak {A}_5\)-representations:  , each of which is orthogonal. This means that \((\) and
, each of which is orthogonal. This means that \((\) and  are of dimension 1. If Q is a generator of
are of dimension 1. If Q is a generator of  , then its image \(Q'\) under an element of
, then its image \(Q'\) under an element of  is a generator of
is a generator of  . So
. So  is \(\mathfrak {S}_5\)-invariant (it spans the \(\mathbf {1}\)-summand) and
is \(\mathfrak {S}_5\)-invariant (it spans the \(\mathbf {1}\)-summand) and  transforms according to the sign character (it spans the \(\text {sgn}\)-summand). The above discussion shows that their images in \(H^0(S, \omega _S^{-2})\) remain independent.
transforms according to the sign character (it spans the \(\text {sgn}\)-summand). The above discussion shows that their images in \(H^0(S, \omega _S^{-2})\) remain independent.
Corollary 2.5
The image of \(Q-Q'\) in \(H^0(S, \omega _S^{-2})\), which spans a copy of the sign representation, has divisor \(C_\infty \).
Proof
As is well-known, ‘taking the residue at infinity’ identifies the space of rational 3-forms on \(\mathbb {C}^3\) that are invariant under scalar multiplication (i.e., are homogeneous of degree zero) with the space of rational 2-forms on \(\mathbb {P}^2\). Thus

can be understood as a rational section of \(\omega _{\mathbb {P}^2}^{2}\) whose divisor is minus the sum of the six coordinate lines. It follows that \(\pi ^*\alpha \) can be regarded as a generating section of \(\omega _S^{2}(C_\infty )\). Hence its inverse \(\pi ^*\alpha ^{-1}\) becomes a generating section of \(\omega _S^{-2}(-C_\infty )\), making \(H^0(S, \omega _S^{-2}(-C_\infty ))\) an \(\mathfrak {S}_5\)-invariant subspace of \(H^0(S, \omega _S^{-2})\). Exchanging \(t_1\) and \(t_2\) clearly takes \(\alpha \) to  and so the span \(H^0(S, \omega _S^{-2}(-C_\infty ))\) of \(\pi ^*\alpha ^{-1}\) is a copy of the sign representation in \(H^0(S, \omega _S^{-2})\). It follows that \(\pi ^*\alpha ^{-1}\) must be proportional to the image of \(Q-Q'\) in \(H^0(S, \omega _S^{-2})\), so that the divisor of \(Q-Q'\) is \(C_\infty \). \(\square \)
and so the span \(H^0(S, \omega _S^{-2}(-C_\infty ))\) of \(\pi ^*\alpha ^{-1}\) is a copy of the sign representation in \(H^0(S, \omega _S^{-2})\). It follows that \(\pi ^*\alpha ^{-1}\) must be proportional to the image of \(Q-Q'\) in \(H^0(S, \omega _S^{-2})\), so that the divisor of \(Q-Q'\) is \(C_\infty \). \(\square \)
Remark 2.6
We can make the canonical embedding and \(I_2(S)\) explicit in terms of the blow-up model of S. Let us first observe that the Petersen graph has twelve 5-cycles (pentagons). The stabilizer subgroup of a 5-cycle is the dihedral subgroup \(D_{10}\) of \(\mathfrak {S}_5\) of order 10. For example, the cycle formed by the vertices (12), (23), (34), (45), (15) is stabilized by the subgroup generated by permutations (12345) and (25)(34). A geometric interpretation of a 5-cycle is a hyperplane section of S which consists of a pentagon of lines. Note that they come in pairs with respect to taking the complementary subgraph. A pentagon of lines, viewed as reduced divisor on S, is a member of the anticanonical system of S. For our description of S as a blown-up \(\mathbb {P}^2\) these must be transforms of triangles in \(\mathbb {P}^2\). The list of these triangles is as follows:

A direct check gives that the left-hand column can be linearly expressed in terms of the right-hand column (and vice versa), as follows:
But beware that in order to get actual of sections of \(\omega _S^{-1}\), we need to multiply these elements with  : the resulting 3-vector fields are then invariant under scalar multiplication and have a residue at infinity that can be understood as an element of \(H^0(S, \omega _S^{-1})\). Note that \((f_0,\ldots ,f_5)\) is a basis of the linear space \(H^0(S,\omega _S^{-1})\), and so these basic elements can serve as the coordinates of an anticanonical embedding \(S\hookrightarrow \mathbb {P}^5\). Since
: the resulting 3-vector fields are then invariant under scalar multiplication and have a residue at infinity that can be understood as an element of \(H^0(S, \omega _S^{-1})\). Note that \((f_0,\ldots ,f_5)\) is a basis of the linear space \(H^0(S,\omega _S^{-1})\), and so these basic elements can serve as the coordinates of an anticanonical embedding \(S\hookrightarrow \mathbb {P}^5\). Since  , we see that S is contained in the intersection of quadrics defined by equations
, we see that S is contained in the intersection of quadrics defined by equations  , where \(x_i' \) is the linear form in \(x_0, \dots , x_5\) that expresses \(f'_i\) in terms of the \(f_0, \dots , f_5\). The five linear independent quadratic forms \(x_ix_i'-x_0x_0' \), \(i = 1,\ldots ,5\), then give us the defining equations for S in \(\mathbb {P}^5\). We easily check that the quadratic form
, where \(x_i' \) is the linear form in \(x_0, \dots , x_5\) that expresses \(f'_i\) in terms of the \(f_0, \dots , f_5\). The five linear independent quadratic forms \(x_ix_i'-x_0x_0' \), \(i = 1,\ldots ,5\), then give us the defining equations for S in \(\mathbb {P}^5\). We easily check that the quadratic form  corresponding to the sum of pentagons of lines spans the \(\text {sgn}\) summand. It cuts out on S the union \(C_\infty \) of lines on S. The linear space spanned by quadratic forms
corresponding to the sum of pentagons of lines spans the \(\text {sgn}\) summand. It cuts out on S the union \(C_\infty \) of lines on S. The linear space spanned by quadratic forms  decomposes as the direct sum
decomposes as the direct sum  . As we have already observed, the space of quadrics \(V(x_ix_i'-x_6x_6')\) span the kernel \(I_S(2)\) of
. As we have already observed, the space of quadrics \(V(x_ix_i'-x_6x_6')\) span the kernel \(I_S(2)\) of  .
.
It is a priori clear that \(\mathfrak {S}_5\) permutes the pentagons of lines listed above, but we see that it in fact preserves the 12-element set and the preceding discussion makes explicit how.
3 The Wiman–Edge pencil and its modular interpretation
3.1 The Wiman–Edge pencil and its base locus
We found in Sect. 2.5 that there are exactly two \(\mathfrak {S}_5\)-invariant quadrics on  , one defined by \(Q+Q'\) and spanning the \(\mathbf {1}\)-summand, the other by \(Q-Q'\) and spanning the \(\text {sgn}\)-summand and (by Corollary 2.5) cutting out on S the 10-line union \({C_\infty }\). The trivial summand spanned by \(Q+Q'\) cuts out a curve that we shall call the Wiman curve and denote by \({C_0}\). We shall find it to be smooth of genus 6. We observe that the plane spanned by Q and \(Q'\) is the fixed point set of \(\mathfrak {A}_5\) in
, one defined by \(Q+Q'\) and spanning the \(\mathbf {1}\)-summand, the other by \(Q-Q'\) and spanning the \(\text {sgn}\)-summand and (by Corollary 2.5) cutting out on S the 10-line union \({C_\infty }\). The trivial summand spanned by \(Q+Q'\) cuts out a curve that we shall call the Wiman curve and denote by \({C_0}\). We shall find it to be smooth of genus 6. We observe that the plane spanned by Q and \(Q'\) is the fixed point set of \(\mathfrak {A}_5\) in  and hence defines a pencil \(\mathscr {C}\) of curves on S whose members come with a (faithful) \(\mathfrak {A}_5\)-action. This pencil is of course spanned by \(C_0\) and \(C_\infty \) and these are the only members that are in fact \(\mathfrak {S}_5\)-invariant. We refer to \(\mathscr {C}\) as the Wiman–Edge pencil; we sometimes also use this term for its image in \(\mathbb {P}^2\) under the natural map \(\pi :S\rightarrow \mathbb {P}^2\).
and hence defines a pencil \(\mathscr {C}\) of curves on S whose members come with a (faithful) \(\mathfrak {A}_5\)-action. This pencil is of course spanned by \(C_0\) and \(C_\infty \) and these are the only members that are in fact \(\mathfrak {S}_5\)-invariant. We refer to \(\mathscr {C}\) as the Wiman–Edge pencil; we sometimes also use this term for its image in \(\mathbb {P}^2\) under the natural map \(\pi :S\rightarrow \mathbb {P}^2\).
Lemma 3.1
(Base locus) The base locus  of \(\mathscr {C}\) is the unique 20-element \(\mathfrak {S}_5\)-orbit in \(C_\infty \). The curves \(C_0\) and \(C_\infty \) intersect transversally so that each member of the Wiman–Edge pencil is smooth at \(\Delta \).
of \(\mathscr {C}\) is the unique 20-element \(\mathfrak {S}_5\)-orbit in \(C_\infty \). The curves \(C_0\) and \(C_\infty \) intersect transversally so that each member of the Wiman–Edge pencil is smooth at \(\Delta \).
Proof
Since this  is \(\mathfrak {S}_5\)-invariant, it suffices to determine how a line L on S meets \(C_0\). We first note that the intersection number
is \(\mathfrak {S}_5\)-invariant, it suffices to determine how a line L on S meets \(C_0\). We first note that the intersection number  (taken on S) is
(taken on S) is  . When we regard L as an irreducible component of \(C_\infty \), or rather, as defining a vertex of the Petersen graph, then we see that the other lines meet L in three distinct points and that the \(\mathfrak {S}_5\)-stabilizer of L acts on L as the full permutation group of these three points. So if we choose an affine coordinate z on L such that the three points in question are the third roots of 1, then we find that the \(\mathfrak {S}_5\)-stabilizer of L acts on L with three irregular orbits: two of size 3 (the roots of \(z^3-1\) and the roots of \(z^3+1\)) and one of size 2 (
. When we regard L as an irreducible component of \(C_\infty \), or rather, as defining a vertex of the Petersen graph, then we see that the other lines meet L in three distinct points and that the \(\mathfrak {S}_5\)-stabilizer of L acts on L as the full permutation group of these three points. So if we choose an affine coordinate z on L such that the three points in question are the third roots of 1, then we find that the \(\mathfrak {S}_5\)-stabilizer of L acts on L with three irregular orbits: two of size 3 (the roots of \(z^3-1\) and the roots of \(z^3+1\)) and one of size 2 ( ). It follows that the \(C_0\) meets L in the size 2 orbit. In particular, the intersection of \(C_0\) with \(C_\infty \) is transversal and contained in the smooth part of \(C_\infty \). \(\square \)
). It follows that the \(C_0\) meets L in the size 2 orbit. In particular, the intersection of \(C_0\) with \(C_\infty \) is transversal and contained in the smooth part of \(C_\infty \). \(\square \)
3.2 Genus 6 curves with \(\mathfrak {A}_5\)-symmetry
Any reduced \(C\in \mathscr {C}\), being a member of \(|-2K_S|\), has its normal sheaf in S isomorphic to  . By the adjunction formula, its dualizing sheaf \(\omega _C\) is therefore isomorphic to
. By the adjunction formula, its dualizing sheaf \(\omega _C\) is therefore isomorphic to

In particular

It follows that C has arithmetic genus 6, that the natural map \(E_S\rightarrow H^0(C, \omega _C)\) is an \(\mathfrak {A}_5\)-equivariant isomorphism and that C is canonically embedded in \(\mathbb {P}_S\). Our goal is to give the Wiman–Edge pencil a modular interpretation.
Proposition 3.2
(\(\mathfrak {A}_5\) and \(\mathfrak {S}_5\) orbit spaces) Let C be a smooth projective curve genus 6 endowed with a faithful action of \(\mathfrak {A}_5\). Then \(\mathfrak {A}_5\backslash C\) is of genus zero and \(\mathfrak {A}_5\) has four irregular orbits with isotropy orders 3, 2, 2 and 2.
If the \(\mathfrak {A}_5\)-action extends to a faithful \(\mathfrak {S}_5\)-action, then \(\mathfrak {S}_5\backslash C\) is of genus zero and \(\mathfrak {S}_5\) has three irregular orbits with isotropy orders 6, 4 and 2. The union of these irregular \(\mathfrak {S}_5\)-orbits is also the union of the irregular \(\mathfrak {A}_5\)-orbits: the \(\mathfrak {S}_5\)-orbit with isotropy order 6, resp. 4, is an \(\mathfrak {A}_5\)-orbit with isotropy order 3, resp. 2, and the \(\mathfrak {S}_5\)-orbit with isotropy order 2 decomposes into two \(\mathfrak {A}_5\)-orbits with the same isotropy groups. (In other words, the double cover \(\mathfrak {A}_5\backslash C\rightarrow \mathfrak {S}_5\backslash C\) only ramifies over the points of ramification of order 6 and 4.) Such a curve exists.
See also [4, Theorem 5.1.5].
Proof
The stabilizer of a point of a smooth curve under a faithful finite group action is cyclic. So when \(G=\mathfrak {S}_5\), the stabilizer of a point of C is a cyclic group of order \(i\leqslant 6\), but when \(G=\mathfrak {A}_5\), it cannot be of order 4 or 6. Let for \(i>1\), \(k_i\) be the number of G-orbits of size |G| / i. By the Hurwitz formula we have

where \(g'\) is the genus of the quotient.
For \(G=\mathfrak {S}_5\) we have \(|G| =120\) and so this shows right away that  . It follows that
. It follows that

It is then immediate that \(k_5=0\) and \(k_6\leqslant 1\). We find that the only solutions for  are (1, 0, 1, 1) and (0, 2, 1, 0). The latter possibility clearly does not occur because it would imply that an element of order 6 acts without fixed points, contradicting the Hurwitz equality
are (1, 0, 1, 1) and (0, 2, 1, 0). The latter possibility clearly does not occur because it would imply that an element of order 6 acts without fixed points, contradicting the Hurwitz equality  .
.
For \(G=\mathfrak {A}_5\), we have \(|G| =60\) and hence we then also have  . The formula now becomes
. The formula now becomes  , which has as only solution
, which has as only solution  .
.
The assertion concerning the map \(\mathfrak {A}_5\backslash C\rightarrow \mathfrak {S}_5\backslash C\) formally follows from the above computations.
The last assertion will follow from the Riemann existence theorem, once we find a regular \(\mathfrak {S}_5\)-covering of  with the simple loops yielding monodromies \(\alpha ,\beta ,\gamma \in \mathfrak {S}_5\) of order 6, 4, 2 respectively, which generate \(\mathfrak {S}_5\) and for which \(\alpha \beta \gamma =1\). This can be arranged: take \(\alpha =(123)(45)\) and \(\beta =(1245)\) and \(\gamma =(14)(23)\). \(\square \)
with the simple loops yielding monodromies \(\alpha ,\beta ,\gamma \in \mathfrak {S}_5\) of order 6, 4, 2 respectively, which generate \(\mathfrak {S}_5\) and for which \(\alpha \beta \gamma =1\). This can be arranged: take \(\alpha =(123)(45)\) and \(\beta =(1245)\) and \(\gamma =(14)(23)\). \(\square \)
We next show that any smooth projective curve genus 6 endowed with a faithful action of \(\mathfrak {A}_5\) appears in the Wiman–Edge pencil. For this we shall invoke a theorem of Mukai [19], which states that a canonical smooth projective curve C of genus 6 lies on a quintic del Pezzo surface if and only if it is neither bielliptic (i.e., it does not double cover a genus 1 curve), nor trigonal (it does not triple cover a genus zero curve), nor isomorphic to a plane quintic.
Theorem 3.3
Every smooth projective curve of genus 6 endowed with a faithful \(\mathfrak {A}_5\)-action is \(\mathfrak {A}_5\)-equivariantly isomorphic to a member of the Wiman–Edge pencil. This member is unique up to the natural action of the involution \(\mathfrak {S}_5/\mathfrak {A}_5\).
Proof
Let C be such a curve. We first show that C is not hyperelliptic, so that we have a canonical model. If it were, then it is so in a unique manner so that the set of its 14 Weierstraß points is in invariant with respect to \(\mathfrak {A}_5\). But we found in Proposition 3.2 that \(\mathfrak {A}_5\) has in C one irregular orbit of size 20, three of size 30, and no others, and thus such an invariant subset cannot exist.
From now on we assume that C is canonical. We first show that it is neither trigonal, nor bielliptic, nor isomorphic to a plane quintic.
C is trigonal: This means that C admits a base point free pencil of degree 3. This pencil is then unique [2, p. 209] so that the \(\mathfrak {A}_5\)-action on C permutes the fibers. Consider the associated morphism \(C\rightarrow \mathbb {P}^1\). The Riemann–Hurwitz formula then tells us that the ramification divisor of this morphism on C has degree 16. It must be \(\mathfrak {A}_5\)-invariant. But our list of orbit sizes precludes this possibility and so such a divisor cannot exist.
C is isomorphic to a plane quintic: It is then so in a unique manner [2, p. 209] and hence the \(\mathfrak {A}_5\)-action on C will extend as a projective representation to the ambient \(\mathbb {P}^2\).
The resulting projective representation cannot be reducible, for then \(\mathfrak {A}_5\) has a fixed point, \(p\in \mathbb {P}^2\) say, and the action of \(\mathfrak {A}_5\) on the tangent space  will be faithful. But as Table 2 shows, \(\mathfrak {A}_5\) has no faithful representation. So the projective representation is irreducible and hence the projectivization of copy of I or \(I'\). Either representation is orthogonal and so the ambient projective plane contains an \(\mathfrak {A}_5\)-invariant conic. The quintic defines on this conic an effective divisor of degree 10. Since \(\mathfrak {A}_5\) acts on the conic (a Riemann sphere) as the group of motions of a regular icosahedron, no \(\mathfrak {A}_5\)-orbit on this conic has fewer than 12 points and so such a divisor cannot exist.
will be faithful. But as Table 2 shows, \(\mathfrak {A}_5\) has no faithful representation. So the projective representation is irreducible and hence the projectivization of copy of I or \(I'\). Either representation is orthogonal and so the ambient projective plane contains an \(\mathfrak {A}_5\)-invariant conic. The quintic defines on this conic an effective divisor of degree 10. Since \(\mathfrak {A}_5\) acts on the conic (a Riemann sphere) as the group of motions of a regular icosahedron, no \(\mathfrak {A}_5\)-orbit on this conic has fewer than 12 points and so such a divisor cannot exist.
C is bielliptic: This means that C comes with an involution \(\iota \) whose orbit space is of genus 1. Let  be the subgroup generated by \(\mathfrak {A}_5\) and \(\iota \). By a theorem of Hurwitz,
be the subgroup generated by \(\mathfrak {A}_5\) and \(\iota \). By a theorem of Hurwitz,  and so
and so  can be 1, 2, 4 or 6.
can be 1, 2, 4 or 6.
Let us first deal with the index 6 case. For this we note that the G-action (by left translations) on \(G/\mathfrak {A}_5\) has a kernel contained in \(\mathfrak {A}_5\). This kernel is a normal subgroup and contained in \(\mathfrak {A}_5\). Since \(\mathfrak {A}_5\) is simple, this kernel is either trivial or all of \(\mathfrak {A}_5\). It cannot be all of \(\mathfrak {A}_5\), because \(G/\mathfrak {A}_5\) is then cyclic of order 6 and hence cannot be generated by the image of \(\iota \). It follows that G acts faithfully on \(G/\mathfrak {A}_5\) so that we get an embedding of G in \(\mathfrak {S}_6\). Its image is then a subgroup of index 2 and so this image must be \(\mathfrak {A}_6\): \(G\cong \mathfrak {A}_6\). We now invoke the Hurwitz formula to this group action: the stabilizer of a point is cyclic of order \(\leqslant 6\) and so if for a divisor i of |G|, \(k_i\) is the number of G-orbits in C of size |G| / i, then

where \(g'\) is the genus of the quotient. This implies that  and then this comes down to
and then this comes down to

It is clear that \(k_5\) must be zero. Since the left-hand side is odd, we must have \(k_4=1\), and we then find that no solution exists.
If the index \(\leqslant 4\), then the argument above gives a map \(G\rightarrow \mathfrak {S}_4\). Its kernel is contained in \(\mathfrak {A}_5\), but cannot be trivial for reasons of cardinality. It follows that the kernel equals \(\mathfrak {A}_5\), so that \(\mathfrak {A}_5\) is normal in G. Since the image of \(\iota \) generates \(G/\mathfrak {A}_5\), it then follows that the index is 1 or 2.
In the last case, G is either isomorphic to  or to \(\mathfrak {S}_5\), depending on whether or not conjugation by \(\iota \) induces in \(\mathfrak {A}_5\) an inner automorphism. In the first case, the action of \(\mathfrak {A}_5\) descends to a faithful action on the elliptic curve. This would make \(\mathfrak {A}_5\) an extension of finite cyclic group by an abelian group, which is evidently not the case. It follows that \(G\subset \mathfrak {S}_5\) and that \(\iota \) is conjugate to (12) or to (12)(34).
or to \(\mathfrak {S}_5\), depending on whether or not conjugation by \(\iota \) induces in \(\mathfrak {A}_5\) an inner automorphism. In the first case, the action of \(\mathfrak {A}_5\) descends to a faithful action on the elliptic curve. This would make \(\mathfrak {A}_5\) an extension of finite cyclic group by an abelian group, which is evidently not the case. It follows that \(G\subset \mathfrak {S}_5\) and that \(\iota \) is conjugate to (12) or to (12)(34).
Denote by \(\chi \) the character of the \(\mathfrak {S}_5\)-representation \(H^0(C, \Omega _C)\). Since the quotient of C by \(\iota \) has genus 1, we have  . If \(\iota \) is conjugate to (12), then we then read off from Table 1 that \(\chi \) is the character of
. If \(\iota \) is conjugate to (12), then we then read off from Table 1 that \(\chi \) is the character of  or
or  . Its restriction to \(\mathfrak {A}_5\) is then the trivial character resp.
. Its restriction to \(\mathfrak {A}_5\) is then the trivial character resp.  . But this contradicts the fact that the \(\mathfrak {A}_5\)-orbit space of C has genus zero. If \(\iota \) is conjugate to (12)(34), then we then read off from Table 2 that the \(\mathfrak {A}_5\)-representation \(H^0(C, \Omega _C)\) takes on \(\iota \) a value \(\geqslant -2\), which contradicts the fact that this value equals
. But this contradicts the fact that the \(\mathfrak {A}_5\)-orbit space of C has genus zero. If \(\iota \) is conjugate to (12)(34), then we then read off from Table 2 that the \(\mathfrak {A}_5\)-representation \(H^0(C, \Omega _C)\) takes on \(\iota \) a value \(\geqslant -2\), which contradicts the fact that this value equals  .
.
According to Mukai [19], it now follows that C lies on a weak quintic del Pezzo surface \(S_C\) in  . It may have singular points, and in fact quadric sections of a weak del Pezzo quintic form a divisor D in the moduli space \({\mathscr {M}}_6\). However, we claim that C must lie on a smooth del Pezzo surface.
. It may have singular points, and in fact quadric sections of a weak del Pezzo quintic form a divisor D in the moduli space \({\mathscr {M}}_6\). However, we claim that C must lie on a smooth del Pezzo surface.
To prove this claim, first note that if C lies on a singular surface then it has fewer than five \(g_4^1\)’s, where by a \(g_4^1\) we mean a linear series of degree 4 and dimension 1. In the plane model this is because three points are collinear or two points coincide. The five \(g_4^1\)’s are defined by four pencils through nodes of the sextic and the pencil of conics through four nodes. In the singular case, when, we choose three collinear points, there is no pencil of conics. The divisor D in \({\mathscr {M}}_6\) mentioned above is characterized by the fact that it has at most four \(g_4^1\)’s. Now, \(\mathfrak {A}_5\) acts on these \(g_4^1\)’s, and hence leaves them all invariant. Thus it preserves a map \(C\rightarrow \mathbb {P}^1\) of degree 4. This is impossible since there are no invariant subset of ramification points. This proves the claim.
It is also known [23] that \(S_C\) is unique. This uniqueness property implies that the faithful \(\mathfrak {A}_5\)-action on C, which extends naturally to  , will leave \(S_C\) invariant. A choice of an \(\mathfrak {A}_5\)-equivariant isomorphism \(h:S_C\xrightarrow {\scriptscriptstyle \cong \;} S\) will then identify C in an \(\mathfrak {A}_5\)-equivariant manner with a member of the Wiman–Edge pencil. Any two \(\mathfrak {A}_5\)-equivariant isomorphisms \(h, h':S_C\xrightarrow {\scriptscriptstyle \cong \;} S\) differ by an automorphism of S, so by an element \(g\in \mathfrak {S}_5\). But the \(\mathfrak {A}_5\)-equivariance then amounts to g centralizing \(\mathfrak {A}_5\). This can happen only when g is the identity. So h is unique. \(\square \)
, will leave \(S_C\) invariant. A choice of an \(\mathfrak {A}_5\)-equivariant isomorphism \(h:S_C\xrightarrow {\scriptscriptstyle \cong \;} S\) will then identify C in an \(\mathfrak {A}_5\)-equivariant manner with a member of the Wiman–Edge pencil. Any two \(\mathfrak {A}_5\)-equivariant isomorphisms \(h, h':S_C\xrightarrow {\scriptscriptstyle \cong \;} S\) differ by an automorphism of S, so by an element \(g\in \mathfrak {S}_5\). But the \(\mathfrak {A}_5\)-equivariance then amounts to g centralizing \(\mathfrak {A}_5\). This can happen only when g is the identity. So h is unique. \(\square \)
Let \(\mathscr {B}\) denote the base of the Wiman–Edge pencil (a copy of \(\mathbb {P}^1\)) so that we have projective flat morphism \(\mathscr {C}\rightarrow \mathscr {B}\). Recall that \(\mathfrak {S}_5\) acts on the family in such a manner that the action on \(\mathscr {C}\rightarrow \mathscr {B}\) is through an involution \(\iota \) which has two fixed points. We denote by  the locus over which this morphism is smooth. So the restriction over \(\mathscr {B}^\circ \) is a family of smooth projective genus 6 curves endowed with a faithful \(\mathfrak {A}_5\)-action. It has the following modular interpretation.
the locus over which this morphism is smooth. So the restriction over \(\mathscr {B}^\circ \) is a family of smooth projective genus 6 curves endowed with a faithful \(\mathfrak {A}_5\)-action. It has the following modular interpretation.
Theorem 3.4
(Universal property) The smooth part of the Wiman–Edge pencil, \(\mathscr {C}_{\mathscr {B}^\circ }\rightarrow \mathscr {B}^\circ \), is universal in the sense that every family  of smooth projective genus 6 curves endowed with a fiberwise faithful \(\mathfrak {A}_5\)-action fits in a unique \(\mathfrak {A}_5\)-equivariant fiber square
of smooth projective genus 6 curves endowed with a fiberwise faithful \(\mathfrak {A}_5\)-action fits in a unique \(\mathfrak {A}_5\)-equivariant fiber square

Moreover, the natural morphism  factors through an injection
factors through an injection  .
.
Proof
Theorem 3.3 (and its proof) has an obvious extension to families of genus 6-curves with \(\mathfrak {A}_5\)-action. This yields the first assertion. If  are such that \(C_t\) and \(C_{t'}\) are isomorphic as projective curves, then as we have seen, an isomorphism
are such that \(C_t\) and \(C_{t'}\) are isomorphic as projective curves, then as we have seen, an isomorphism  is induced by an element of \(\mathfrak {S}_5\) and so
is induced by an element of \(\mathfrak {S}_5\) and so  . \(\square \)
. \(\square \)
We will find in Sect. 3.3 that the singular members of the Wiman–Edge pencil are all stable. We found already one such curve, namely the union of the 10 lines, and so this element will map in \(\mathscr {M}_6\) to the boundary.
From now on we identify the base of Wiman–Edge pencil with \(\mathscr {B}\).
Corollary 3.5
The Wiman curve \(C_0\) is smooth and is \(\mathfrak {S}_5\)-isomorphic to the curve found in Proposition 3.2. It defines the unique \(\iota \)-fixed point of \(\mathscr {B}^\circ \).
Proof
By Theorem 3.4, there is a unique member of the Wiman–Edge pencil whose base point maps the unique point of \(\mathscr {B}^\circ \) which supports a smooth genus 6 curve with \(\mathfrak {S}_5\)-action. The Wiman–Edge pencil has two members with \(\mathfrak {S}_5\)-action, one is the union of the 10 lines and the other is the Wiman curve. So it must be the Wiman curve. \(\square \)
Corollary 3.6
Let C be a smooth projective curve genus 6 endowed with a faithful action of \(\mathfrak {A}_5\). If the resulting map  is not surjective, then it extends to an isomorphism
is not surjective, then it extends to an isomorphism  , and \(C=C_0\) is the Wiman curve. The \(\mathfrak {A}_5\)-representation, resp. \(\mathfrak {S}_5\)-representation, \(H^0(C, \omega _C)\) is equivalent to
, and \(C=C_0\) is the Wiman curve. The \(\mathfrak {A}_5\)-representation, resp. \(\mathfrak {S}_5\)-representation, \(H^0(C, \omega _C)\) is equivalent to  , resp. E, and \(H^1(C; \mathbb {C})\) is equivalent to
, resp. E, and \(H^1(C; \mathbb {C})\) is equivalent to  , resp. \(E^{ \oplus 2}\).
, resp. \(E^{ \oplus 2}\).
Proof
Since the \(\mathfrak {A}_5\)-curve C is represented by a member of the Wiman–Edge pencil, we can assume it is a member of that pencil. Since C is canonically embedded, an automorphism of C extends naturally of the ambient projective space and hence also to S (as it is the unique quintic del Pezzo surface containing C). This implies that  . This inclusion is an equality precisely when C is the Wiman curve.
. This inclusion is an equality precisely when C is the Wiman curve.
As for the last assertion, we know that the representation space \(H^0(C, \omega _C)\) is as asserted, since it is a member of the Wiman curve. The representations  , resp. E, are self-dual, and since \(H^1(C, \mathbb {C})\) contains \(H^0(C, \omega _C)\) as an invariant subspace with quotient the (Serre-)dual of \(H^0(C, \omega _C)\), the last assertion follows also. \(\square \)
, resp. E, are self-dual, and since \(H^1(C, \mathbb {C})\) contains \(H^0(C, \omega _C)\) as an invariant subspace with quotient the (Serre-)dual of \(H^0(C, \omega _C)\), the last assertion follows also. \(\square \)
Remark 3.7
If an \(\mathfrak {A}_5\)-curve C represents a point \(z\in \mathscr {B}^\circ \), then \(\mathfrak {A}_5\) acts nontrivially (and hence faithfully) on \(H^0(C,\omega _C^{2})\) and hence also on its Serre dual \(H^1(C,\omega _C^{-1})\). Since \(\mathfrak {A}_5\) is not a complex reflection group, a theorem of Chevalley implies that the orbit space \(\mathfrak {A}_5\backslash H^1(C,\omega _C^{-1})\) must be singular at the image of the origin. The local deformation theory of curves tells us that when \(\mathfrak {A}_5\) is the full automorphism group of C, the germ of this orbit space at the origin is isomorphic to the germ of \(\mathscr {M}_6\) at the image of z. Hence \(\mathscr {B}^\circ \) maps to the singular locus of \(\mathscr {M}_6\). (This is a special case of a theorem of Rauch–Popp–Oort which states that any curve of genus \(g\geqslant 4\) with nontrivial group of automorphisms defines a singular point of \(\mathscr {M}_g\).)
3.3 Singular members of the Wiman–Edge pencil
The singular members of the Wiman–Edge pencil were found by Edge [11]. A modern proof of his result can be found in [4, Theorem 6.2.9]. Here we obtain them in a different manner as part of a slightly stronger result that we obtain with a minimum of computation.
Let us begin with an a priori characterization of the reducible genus 5 curves with \(\mathfrak {A}_5\)-action that occur in the Wiman–Edge pencil.
Lemma 3.8
There are precisely two reducible members \(C_\mathrm{c}\) and \(C'_\mathrm{c}\) of \(\mathscr {C}\) distinct from \(C_\infty \); each is is a stable union of five special conics whose intersection graph is \(\mathfrak {A}_5\)-equivariantly isomorphic to the full graph on a 5-element set. Any element of  exchanges \(C_\mathrm{c}\) and \(C'_\mathrm{c}\).
exchanges \(C_\mathrm{c}\) and \(C'_\mathrm{c}\).
Proof
Let C be such a member of \(\mathscr {C}\) and let Y be an irreducible component of C. Then Y cannot be a line and so its degree  in the anticanonial model must be \(\geqslant 2\). Since \(\mathfrak {A}_5\) has no subgroup of index \(< 5\), the number r of irreducible components in the \(\mathfrak {A}_5\)-orbit of Y, must be \(\geqslant 5\). But we also must have
in the anticanonial model must be \(\geqslant 2\). Since \(\mathfrak {A}_5\) has no subgroup of index \(< 5\), the number r of irreducible components in the \(\mathfrak {A}_5\)-orbit of Y, must be \(\geqslant 5\). But we also must have  , and so the only possibility is that \((d, r)=(2,5)\).
, and so the only possibility is that \((d, r)=(2,5)\).
An irreducible, degree 2 curve in a projective space is necessarily a smooth conic. Its \(\mathfrak {A}_5\)-stabilizer has index 5 in \(\mathfrak {A}_5\), and so must be \(\mathfrak {S}_5\)-conjugate to \(\mathfrak {A}_4\). This implies that Y is a special conic. The five irreducible components of its \(\mathfrak {A}_5\)-orbit lie in distinct conic bundles \(\mathscr {P}_i\), and we number them accordingly \(Y_1, \dots , Y_5\). For \(1\leqslant i<j\leqslant 5\), any smooth member of \(\mathscr {P}_i\) meets any smooth member of  with multiplicity one, and so this is in particular true for \(Y_i\) and
with multiplicity one, and so this is in particular true for \(Y_i\) and  . Hence the set of singular points of C is covered in an \(\mathfrak {A}_5\)-equivariant manner by the set of 2-element subsets of
. Hence the set of singular points of C is covered in an \(\mathfrak {A}_5\)-equivariant manner by the set of 2-element subsets of  . The action of \(\mathfrak {A}_5\) on this last set is transitive, and so either the singular set of C is a singleton \(\{p\}\) (a point common to all the irreducible components) or the intersections
. The action of \(\mathfrak {A}_5\) on this last set is transitive, and so either the singular set of C is a singleton \(\{p\}\) (a point common to all the irreducible components) or the intersections  , \(1\leqslant i<j\leqslant 5\), are pairwise distinct. The first case is easily excluded, for p must then be a fixed point of the \(\mathfrak {A}_5\)-action and there is no such point. So C is as described by the lemma.
, \(1\leqslant i<j\leqslant 5\), are pairwise distinct. The first case is easily excluded, for p must then be a fixed point of the \(\mathfrak {A}_5\)-action and there is no such point. So C is as described by the lemma.
The sum of the classes of the five conic bundles is \(\mathfrak {S}_5\)-invariant and hence proportional to \(-K_S\). The intersection product with \(-K_S\) is \(5.2=10\) and hence this class is equal to \(-2K_S\), in other words, the class of the Wiman–Edge pencil. Since an \(\mathfrak {A}_5\)-orbit of a special conic takes precisely one member from every conic bundle, its follows that the sum of such an orbit indeed gives a member of \(\mathscr {C}\). There two such orbits and so we get two such members. \(\square \)
There are precisely two faithful projective representations of \(\mathfrak {A}_5\) on \(\mathbb {P}^1\) up to equivalence, and they only differ by precomposition with an automorphism of \(\mathfrak {A}_5\) that is not inner. We will refer to theses two representations as the Schwarzian representations of \(\mathfrak {A}_5\). Both appear as the symmetry groups of a regular icosahedron drawn on the Riemann sphere. This action has three irregular orbits, corresponding to the vertices, the barycenters of the faces and the midpoints of the edges, and so are resp. 12, 20 and 30 in size. Their points come in (antipodal) pairs and the \(\mathfrak {A}_5\)-action preserves these pairs. We give a fuller discussion in Sect. 4.1.
Lemma 3.9
There exists an irreducible stable curve C of genus 6 with six nodes endowed with a faithful \(\mathfrak {A}_5\)-action. Such a C is unique up to an automorphism of \(\mathfrak {A}_5\).
Proof
Let C be such a curve with six nodes and denote by \(D\subset C\) its singular set. Then the normalization of \(\widetilde{C}\rightarrow C\) is of genus zero: \(\widetilde{C}\cong \mathbb {P}^1\). If \(\widetilde{D}\subset \widetilde{C}\) denotes the preimage of D, then \(\widetilde{D}\) consists of 12 points that come in six pairs. The \(\mathfrak {A}_5\)-action on \(\widetilde{C}\) lifts to \(\widetilde{C}\) and will preserve \(\widetilde{D}\) and its decomposition into six pairs. From the above remarks it follows that \(\mathfrak {A}_5\) acts on \(\widetilde{C}\) as the symmetry group of an icosahedron drawn on \(\widetilde{C}\) which has \(\widetilde{D}\) as vertex set and such that antipodal pairs are the fibers of \(\widetilde{C}\rightarrow C\). This shows both existence and uniqueness up to an automorphism of \(\mathfrak {A}_5\). \(\square \)
Proposition 3.10
An irreducible singular member of the Wiman–Edge pencil is necessarily as in Lemma 3.9: a stable curve with six nodes and of geometric genus zero. It appears in the Wiman–Edge pencil together with its outer transform.
Proof
We have already encountered the singular members \(C_\infty \) and \(C_\mathrm{c},C_\mathrm{c}'\). A well-known formula (see, for example, [15, p. 509–510]) applied to the Wiman pencil gives

where  stands for the Euler–Poincaré characteristic, C denotes a general fiber and \(C_t\) denotes a fiber over a point \(t\in \mathscr {B}\). The left-hand side equals
stands for the Euler–Poincaré characteristic, C denotes a general fiber and \(C_t\) denotes a fiber over a point \(t\in \mathscr {B}\). The left-hand side equals  . The reducible fibers \(C_\infty ,C_\mathrm{c},C'_\mathrm{c}\) contribute to the right hand side
. The reducible fibers \(C_\infty ,C_\mathrm{c},C'_\mathrm{c}\) contribute to the right hand side  , so that there is 12 left as the contribution coming the irreducible fibers.
, so that there is 12 left as the contribution coming the irreducible fibers.
It is known that \(e(C_t)-e(C)\) is equal to the sum of the Milnor numbers of singular points of \(C_t\). We know that \(\mathfrak {A}_5\) leaves invariant each fiber, but that no fiber other than \(C_\infty \) (which is reducible) or the Wiman curve \(C_0\) (which is smooth) is \(\mathfrak {S}_5\)-invariant. In other words, the irreducible fibers come in pairs. Since \(\mathfrak {A}_5\) cannot fix a point on S (because it has no a nontrivial linear representations of dimension 2 and hence cannot act nontrivially on the tangent space at this point), and a proper subgroup of \(\mathfrak {A}_5\) has index \(\geqslant 5\), the irreducible fibers come as a single pair, with each member having exactly six singular points, all of Milnor number 1, that is, having six ordinary double points. Hence the normalization of such a fiber is a rational curve as in Lemma 3.9 \(\square \)
We sum up with the following.
Corollary 3.11
(Classification of singular members of \(\mathscr {C}\)) Each singular member of the Wiman–Edge pencil \(\mathscr {C}\) is a stable curve of genus 6 with \(\mathfrak {A}_5\)-action. The set of these curves is a union of three sets:
-
(lines)
\({C_\infty }\), a union of 10 lines with intersection graph the Petersen graph.
-
(conics)
a pair \(C_\mathrm{c},C'_\mathrm{c}\), each of which is a union of five conics whose intersection graph is the complete graph on five vertices.
-
(irred)
a pair \(C_{\mathrm{ir}},C_{\mathrm{ir}}'\) of irreducible rational curves, each with six nodes.
The action of \(\mathfrak {S}_5\) on \(\mathscr {C}\) leaves \({C_\infty }\) invariant; the induced action on the set of 10 lines of \({C_\infty }\) induces an action on the corresponding intersection graph that is isomorphic to the \(\mathfrak {S}_5\)-action on the Petersen graph. The action of any odd permutation of \(\mathfrak {S}_5\) on \(\mathscr {C}\) interchanges \(C_\mathrm{c}\) and \(C'_\mathrm{c}\), and also interchanges \(C_{\mathrm{ir}}\) and \(C_{\mathrm{ir}}'\) .
Remark 3.12
Our discussion in Sect. 2.1 shows that  , when regarded as a curve on \(\overline{\mathscr {M}}_{0,5}\), meets \(\mathscr {M}_{0,5}\) in the locus parameterizing 5-pointed rational curves \((C; x_1, \dots , x_5)\) with the property that there exists an affine coordinate z for C such that
, when regarded as a curve on \(\overline{\mathscr {M}}_{0,5}\), meets \(\mathscr {M}_{0,5}\) in the locus parameterizing 5-pointed rational curves \((C; x_1, \dots , x_5)\) with the property that there exists an affine coordinate z for C such that  contains the union of \(\{0\}\) and the roots of
contains the union of \(\{0\}\) and the roots of  . So we can characterize the Wiman–Edge pencil on \(\overline{\mathscr {M}}_{0,5}\) as the pencil which contains in
. So we can characterize the Wiman–Edge pencil on \(\overline{\mathscr {M}}_{0,5}\) as the pencil which contains in  and these two loci. It is desirable to have a modular interpretation of this pencil.
and these two loci. It is desirable to have a modular interpretation of this pencil.
3.4 Connection with the Dwork pencil
Since the singular members of the Wiman–Edge pencil also play a special role in the work of Candelas et al. [3], this is perhaps a good place to make the connection with that paper. Let \(p=(p_1, \dots ,p_5)\) be distinct points of \(\mathbb {P}^1\). As Zagier [27] points out, there exist linear forms \(\ell _i\) on \(\mathbb {C}^2\) defining \(p_i\), such that

for some \(\psi \in \mathbb {C}\) with the 5-tuple  being unique up to a common scalar (so that \(\psi ^5\) only depends on \(p_1, \dots ,p_5\)). In other words,
being unique up to a common scalar (so that \(\psi ^5\) only depends on \(p_1, \dots ,p_5\)). In other words,

maps to a line on a member of the Dwork pencil, that is, the pencil of quintic 3-folds  defined by
defined by  , such that the coordinate hyperplane \(z_i=0\) defines \(p_i\).
, such that the coordinate hyperplane \(z_i=0\) defines \(p_i\).
This construction is essentially  -equivariant and has some symmetries, perhaps the most obvious ones being its \(\mathfrak {S}_5\)-symmetry. But we also have acting the group \(T[5]\cong \mu _5{}^4\) of order 5 elements in the diagonal torus T of
-equivariant and has some symmetries, perhaps the most obvious ones being its \(\mathfrak {S}_5\)-symmetry. But we also have acting the group \(T[5]\cong \mu _5{}^4\) of order 5 elements in the diagonal torus T of  . Together with \(\mathfrak {S}_5\) this gives a faithful action of the subgroup
. Together with \(\mathfrak {S}_5\) this gives a faithful action of the subgroup  on the total space of the pencil. It acts on the parameter \(\psi \) through a character
on the total space of the pencil. It acts on the parameter \(\psi \) through a character  , the latter being given as a nontrivial \(\mathfrak {S}_5\)-invariant character \(\chi :T[5]\rightarrow \mu _5\). So
, the latter being given as a nontrivial \(\mathfrak {S}_5\)-invariant character \(\chi :T[5]\rightarrow \mu _5\). So  is as a group isomorphic to \(\mu _5{}^3\) and every \(X_\psi \) is stabilized by
is as a group isomorphic to \(\mu _5{}^3\) and every \(X_\psi \) is stabilized by  . A good way to express this is that we have thus obtained the following:
. A good way to express this is that we have thus obtained the following:
-
(i)
an unramified T[5]-covering \(\mathscr {T}_{0,5}\rightarrow \mathscr {M}_{0,5}\) endowed with an action
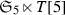 which extends the T[5]-action and is compatible with the \(\mathfrak {S}_5\)-action on \(\mathscr {M}_{0,5}\),
which extends the T[5]-action and is compatible with the \(\mathfrak {S}_5\)-action on \(\mathscr {M}_{0,5}\), -
(ii)
a regular function \(\psi :\mathscr {T}_{0,5}\rightarrow \mathbb {C}\), equivariant with respect to the above character (so that \(\psi ^5\) is defined as an \(\mathfrak {S}_5\)-invariant function on \(\mathscr {M}_{0,5}\)),
-
(iii)
an
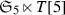 -equivariant lift of \(\psi \) from \(\mathscr {T}_{0,5}\) to the Fano variety
-equivariant lift of \(\psi \) from \(\mathscr {T}_{0,5}\) to the Fano variety  of lines on the Dwork pencil.
of lines on the Dwork pencil.
The main results of [3] can then be summed up as follows:
A fiber of \(\mathscr {M}_{0,5}\xrightarrow {\scriptscriptstyle \psi ^5}\mathbb {C}\) is the sum of a member of the Wiman pencil plus its transform under an odd permutation and for a suitable parametrization of the pencil base \(\mathscr {B}\) by a parameter \(\phi \) such that \(C_0\), resp. \(C_\infty \), is defined by \(\phi =0\), resp. \(\phi =\infty \), and we have  . Moreover, the morphisms above with their symmetry extend (uniquely) over the blow-up \(\mathscr {C}\rightarrow \overline{\mathscr {M}}_{0,5}\) of \(\overline{\mathscr {M}}_{0,5}\) in \(\Delta \) (recall that this is simply the total space of the Wiman–Edge pencil \(\phi :\mathscr {C}\rightarrow \mathbb {P}^1\)): we have a T[5]-cover \(\pi :\widetilde{\mathscr {C}}\rightarrow \mathscr {C}\) with a compatible
. Moreover, the morphisms above with their symmetry extend (uniquely) over the blow-up \(\mathscr {C}\rightarrow \overline{\mathscr {M}}_{0,5}\) of \(\overline{\mathscr {M}}_{0,5}\) in \(\Delta \) (recall that this is simply the total space of the Wiman–Edge pencil \(\phi :\mathscr {C}\rightarrow \mathbb {P}^1\)): we have a T[5]-cover \(\pi :\widetilde{\mathscr {C}}\rightarrow \mathscr {C}\) with a compatible  -action and an equivariant extension of the Fano map to \(\widetilde{\mathscr {C}}\) which makes the Dwork pencil and the symmetrized Wiman–Edge pencil fit in the following commutative diagram:
-action and an equivariant extension of the Fano map to \(\widetilde{\mathscr {C}}\) which makes the Dwork pencil and the symmetrized Wiman–Edge pencil fit in the following commutative diagram:

Here the slant map is the structural map and the bottom map is given by  . For \(\psi \not =0, \infty \), \(\widetilde{C}_\psi \) parametrizes all the nonisolated points of
. For \(\psi \not =0, \infty \), \(\widetilde{C}_\psi \) parametrizes all the nonisolated points of  ; for
; for  it consists of two irreducible curves, each of which is an unramified
it consists of two irreducible curves, each of which is an unramified  (of arithmetic genus 626), but for
(of arithmetic genus 626), but for  , there is only one irreducible curve (which covers the Wiman curve).
, there is only one irreducible curve (which covers the Wiman curve).
The singular members of the Wiman–Edge pencil are accounted for as follows: the Fermat quintic (\(\psi =0\)) yields the sum of 10 lines with multiplicity 2 (\(2C_\infty \)), the sum of the five coordinate hyperplanes (\(\psi =\infty \)) yields \(C_\mathrm{c}+C'_\mathrm{c}\), and if \(\psi \) is a 5th root of unity, we get \(C_\mathrm{ir}+C'_\mathrm{ir}\).
3.5 Plane model of the Wiman–Edge pencil
Let \(\pi :S\rightarrow \mathbb {P}^2\) be the blowing-down morphism. The Wiman–Edge pencil is the proper inverse transform of a pencil of curves of degree 6 with points of multiplicity \(\geqslant 2\) at the fundamental points invariant with respect to the Cremona group G of transformations isomorphic to \(\mathfrak {A}_4\). Following Edge, we choose the fundamental points of \(\pi ^{-1}\) to be the points

The group generated by projective transformations that permute the coordinates and their sign changes is isomorphic to \(\mathfrak {S}_4\), where the sign changes are even permutations of order 2. Together with the additional symmetry defined by the Cremona involution T with the first reference points, we obtain a subgroup of Cremona transformations isomorphic to \(\mathfrak {S}_5\). The subgroup \(\mathfrak {A}_5\) is generated by cyclic permutations, sign changes and the transformation T.
Let \(F = 0\) be the equation of a curve from the Wiman–Edge pencil. The condition that F is invariant with respect the sign changes shows that F must be a combination of monomials \(x^ay^bz^c\) with a, b, c even. This allows us to write
The additional conditions that  will guarantee that the fundamental points are singular points. The Cremona involution T is given by
will guarantee that the fundamental points are singular points. The Cremona involution T is given by

The invariance of F with respect to T gives (a, b, c) is a linear combination of (2, 1, 1) and \((0,1,-1,0)\). This gives the equation of the Wiman–Edge pencil

We check that the Wiman curve B is the member of the pencil with  . Computing the partial derivatives, we find that the curve is indeed smooth confirming Corollary 5.10 (Fig. 3).
. Computing the partial derivatives, we find that the curve is indeed smooth confirming Corollary 5.10 (Fig. 3).
The base locus of the pencil should be a subscheme of length  . The four reference points contribute 16 to this number, the rest is the image of 20 base points of the Wiman–Edge pencil on S in the plane. It easy to find them. Each line through two fundamental points intersects \(C_0\) at two nonsingular points, this gives us 12 points:
. The four reference points contribute 16 to this number, the rest is the image of 20 base points of the Wiman–Edge pencil on S in the plane. It easy to find them. Each line through two fundamental points intersects \(C_0\) at two nonsingular points, this gives us 12 points:

The remaining eight points are on the exceptional curves where they represent the directions of the tangent lines to the branches of singular points of B. The equations of the four pairs of these tangent lines are

where \(\epsilon = ({-1+\sqrt{-3}})/{2}\) is a primitive root of 1. One checks that each tangent line passing through \(p_i\) together with three of the lines  form a harmonic 4-tuple of lines in the pencil of lines through \(p_i\) (Footnote 1).
form a harmonic 4-tuple of lines in the pencil of lines through \(p_i\) (Footnote 1).
Choose one of the branch tangents, say \(x+\epsilon y+\epsilon ^2 z = 0\). It intersects the Wiman sextic B at two nonsingular points  and
and  . We see that each double point of W is a biflecnode, i.e., the branch tangents at singular point intersect the curve at this point with multiplicity 4 instead of expected 3.
. We see that each double point of W is a biflecnode, i.e., the branch tangents at singular point intersect the curve at this point with multiplicity 4 instead of expected 3.
The singular irreducible members \(C_{\mathrm{ir}}\), resp. \(C_{\mathrm{ir}}'\), are proper transforms of the members of the pencil corresponding to the parameters  , resp.
, resp.  . The singular points of \(C_{\mathrm{ir}}\) besides the fundamental points are
. The singular points of \(C_{\mathrm{ir}}\) besides the fundamental points are

where \(\lambda = ({1+\sqrt{5}})/{2}\),  . The six singular points of \(C_{\mathrm{ir}}'\) are obtained from these points by replacing \(\lambda \) with \(\lambda '\).
. The six singular points of \(C_{\mathrm{ir}}'\) are obtained from these points by replacing \(\lambda \) with \(\lambda '\).
The reducible members \(C_\mathrm{c}\) and \(C_\mathrm{c}'\) of the Wiman–Edge pencil are proper transforms of the members of the pencil of plane curves

where \(\epsilon \ne 1\),  . As shown already by Edge, they correspond to parameters
. As shown already by Edge, they correspond to parameters  . We leave these computations to the reader, they are straightforward.
. We leave these computations to the reader, they are straightforward.
3.6 Irregular orbits in S
Recall that if a group acts on a set, an orbit is called regular if the stabilizer of one (and hence any) of its points is trivial; otherwise it is called an irregular orbit. For what follows it will helpful to have a catalogue of irregular an \(\mathfrak {S}_5\)-orbits and \(\mathfrak {A}_5\)-orbits in S. Here we can observe that an \(\mathfrak {S}_5\)-orbit is an \(\mathfrak {A}_5\)-orbit if and only if its \(\mathfrak {S}_5\)-stabilizer is not contained in \(\mathfrak {A}_5\) (otherwise it splits into two \(\mathfrak {A}_5\)-orbits). So a determination of the irregular \(\mathfrak {S}_5\)-orbits determines one of the irregular \(\mathfrak {A}_5\)-orbits. The \(\mathfrak {S}_5\)-equivariant incarnation of S as the moduli space of stable, 5-pointed genus zero curves makes this determination (which is in fact due to Coble) rather straightforward, as we will now explain.
A point of \(\overline{\mathscr {M}}_{0,5}\) is the same thing as a stable map  (where ‘stable’ means here that every fiber has at most two elements), given up to a composition with a Möbius transformation. The \(\mathfrak {S}_5\)-stabilizer of a stable map x consists of the set of \(\sigma \in \mathfrak {S}_5\) for which there exists a
(where ‘stable’ means here that every fiber has at most two elements), given up to a composition with a Möbius transformation. The \(\mathfrak {S}_5\)-stabilizer of a stable map x consists of the set of \(\sigma \in \mathfrak {S}_5\) for which there exists a  with the property that
with the property that  . Since x is stable, its image has at least three distinct points, and so \(\rho (\sigma )\) will be unique. It follows that \(\rho \) will be a group homomorphism. Its image will be a finite subgroup of
. Since x is stable, its image has at least three distinct points, and so \(\rho (\sigma )\) will be unique. It follows that \(\rho \) will be a group homomorphism. Its image will be a finite subgroup of  with the property that it has in \(\mathbb {P}^1\) an orbit of size \(\leqslant 5\).
with the property that it has in \(\mathbb {P}^1\) an orbit of size \(\leqslant 5\).
Klein determined the finite subgroups of  up to conjugacy: they are the cyclic groups, represented by the group \(\mu _n\) of nth roots of unity acting in \(\mathbb {C}\subset \mathbb {P}^1\) as scalar multiplication; the dihedral groups, represented by the semidirect product of \(\mu _n\) and the order 2 group generated by the inversion \(z\mapsto z^{-1}\); and the tetrahedral, octahedral and icosahedral groups, which are isomorphic to \(\mathfrak {A}_4,\mathfrak {S}_4,\mathfrak {A}_5\) respectively. The octahedral and icosahedral groups have no orbit of size \(\leqslant 5\) in \(\mathbb {P}^1\), and hence cannot occur here. The tetrahedral group has one such orbit: it is of size 4 (the vertices of a tetrahedron), but since we want a degree 5 divisor, it then must have a fixed point, and this is clearly not the case.
up to conjugacy: they are the cyclic groups, represented by the group \(\mu _n\) of nth roots of unity acting in \(\mathbb {C}\subset \mathbb {P}^1\) as scalar multiplication; the dihedral groups, represented by the semidirect product of \(\mu _n\) and the order 2 group generated by the inversion \(z\mapsto z^{-1}\); and the tetrahedral, octahedral and icosahedral groups, which are isomorphic to \(\mathfrak {A}_4,\mathfrak {S}_4,\mathfrak {A}_5\) respectively. The octahedral and icosahedral groups have no orbit of size \(\leqslant 5\) in \(\mathbb {P}^1\), and hence cannot occur here. The tetrahedral group has one such orbit: it is of size 4 (the vertices of a tetrahedron), but since we want a degree 5 divisor, it then must have a fixed point, and this is clearly not the case.
It remains to go through the dihedral and cyclic cases. We denote by \(\mathfrak {C}_{n}\) a cyclic group of order n and by \(\mathfrak {D}_{2n}\) the dihedral group of order 2n isomorphic to  (Footnote 2). The conjugacy classes of the nontrival cyclic subgroups of \(\mathfrak {A}_5\) are represented by \(\langle (12)(34)\rangle \cong \mathfrak {C}_2\) and \(\langle (123)\rangle \cong \mathfrak {C}_3\), and for \(\mathfrak {S}_5\) we have the two additional classes represented by \(\langle (12)\rangle \cong \mathfrak {C}_2\) and \(\langle (12)(345)\rangle \cong \mathfrak {C}_6\). Likewise, there are three conjugacy classes of dihedral subgroups in \(\mathfrak {A}_5\) represented by
(Footnote 2). The conjugacy classes of the nontrival cyclic subgroups of \(\mathfrak {A}_5\) are represented by \(\langle (12)(34)\rangle \cong \mathfrak {C}_2\) and \(\langle (123)\rangle \cong \mathfrak {C}_3\), and for \(\mathfrak {S}_5\) we have the two additional classes represented by \(\langle (12)\rangle \cong \mathfrak {C}_2\) and \(\langle (12)(345)\rangle \cong \mathfrak {C}_6\). Likewise, there are three conjugacy classes of dihedral subgroups in \(\mathfrak {A}_5\) represented by

and additional three conjugacy classes in \(\mathfrak {S}_5\):

To distinguish the conjugacy classes of dihedral subgroups of order 4 or 6 we denote them by \(\mathfrak {D}_{4}^{\mathrm{ev}}, \mathfrak {S}_3^{\mathrm{ev}}\), resp. \(\mathfrak {D}_{4}^{\mathrm{odd}}, \mathfrak {S}_3^{\mathrm{odd}}\) if they are contained in \(\mathfrak {A}_5\), resp. in \(\mathfrak {S}_5\), but not in \(\mathfrak {A}_5\). A similar convention applies to \(\mathfrak {C}_2\): we have  and
and  .
.
We then end up with the following list, due to Arthur Coble [7, pp. 400–401].
Theorem 3.13
(The irregular orbits of \(\mathfrak {S}_5\) acting on S) The set of irregular orbits of \(\mathfrak {S}_5\) acting on S is one of the following sets, named by the conjugacy class of a stabilizer subgroup:
-
 :
: -
For example, \(\langle (12)\rangle \) is the stabilizer of \((0,0,\infty , 1,z)\) when z is generic. An orbit of this type has size 60. It is a regular \(\mathfrak {A}_5\)-orbit.
-
 :
: -
For example, \(\langle (12)(34)\rangle \) is the stabilizer of
 when z is generic. An orbit of this type has size 60 and decomposes into two \(\mathfrak {A}_5\)-orbits of size 30.
when z is generic. An orbit of this type has size 60 and decomposes into two \(\mathfrak {A}_5\)-orbits of size 30. -
 :
: -
For example, \(\langle (1234)\rangle \) is the stabilizer of \((1,\sqrt{-1}, -1,-\sqrt{-1},\infty )\). This is an \(\mathfrak {S}_5\)-orbit of size 30. It is also an \(\mathfrak {A}_5\)-orbit of type
 (take \(z=\sqrt{-1}\)).
(take \(z=\sqrt{-1}\)). - \(\mathfrak {D}_4^{\mathrm{odd}}\) :
-
For example \(\langle (12),(34)\rangle \) is the stabilizer of \((0,0, 1 , -1,\infty )\). This is an \(\mathfrak {S}_5\)-orbit of size 30, which is also an \(\mathfrak {A}_5\)-orbit of type
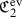 (let \(z\rightarrow 0\)).
(let \(z\rightarrow 0\)). - \(\mathfrak {S}_3^{\mathrm{ev}}\) :
-
For example \(\langle (23)(45),(123)\rangle \) is the stabilizer of \((1, \zeta _3, \zeta _3^2, 0,\infty )\). This is an \(\mathfrak {S}_5\)-orbit of size 20 which splits into two \(\mathfrak {A}_5\)-orbits of size 10.
- \(\mathfrak {D}_8\) :
-
For example, \(\langle (12),(1324)\rangle \) is the stabilizer of \((0, 0,\infty ,\infty , 1)\). This is the unique \(\mathfrak {S}_5\)-orbit of size 15. It is also an \(\mathfrak {A}_5\)-orbit of type \(\mathfrak {D}_4^{\mathrm{ev}}\).
- \(\mathfrak {C}_6\) :
-
For example, \(\langle (12)(345)\rangle \) is the stabilizer of \((\infty , \infty , 1, \zeta _3, \zeta _3^2)\). This is a single orbit of size 20 which is also an \(\mathfrak {A}_5\)-orbit of type \(\mathfrak {C}_3\).
- \(\mathfrak {D}_{10}\) :
-
For example, \(\langle (25)(34),(12345)\rangle \) is the stabilizer of \((1, \zeta _5, \zeta _5^2, \zeta _5^3, \zeta _5^4)\). The associated orbit is of size 12 and splits into two \(\mathfrak {A}_5\)-orbits of size 6.
In particular, the irregular \(\mathfrak {A}_5\)-orbits are of type  are parametrized by a punctured rational curve.
are parametrized by a punctured rational curve.
Remark 3.14
It is clear from Theorem 3.13 that we have a curve of irregular \(\mathfrak {A}_5\)-orbits of size 30. However the locus of such points in S has 15 irreducible components. This is because the preimage of an \(\mathfrak {A}_5\)-orbit under the map  is generically of the form
is generically of the form  . An example of the closure such an irreducible component is the preimage of the line defined in \(\mathbb {P}^2\) by \(t_2=t_0+t_1\) under the blow-up of the vertices of the coordinate vertex (it is pointwise fixed under an even linear permutation of these vertices). Since this line does not pass through any of the four vertices, this also shows that its preimage in S is a rational normal curve of degree 3. We thus obtain an \(\mathfrak {S}_5\)-invariant curve on S of degree 45 (defined by a section of \(\omega _S^{-9}\)) with 15 irreducible components. A priori this section is \(\mathfrak {A}_5\)-invariant, but as Clebsch [6] showed, it is in fact \(\mathfrak {S}_5\)-invariant (see also Remark 6.6).
. An example of the closure such an irreducible component is the preimage of the line defined in \(\mathbb {P}^2\) by \(t_2=t_0+t_1\) under the blow-up of the vertices of the coordinate vertex (it is pointwise fixed under an even linear permutation of these vertices). Since this line does not pass through any of the four vertices, this also shows that its preimage in S is a rational normal curve of degree 3. We thus obtain an \(\mathfrak {S}_5\)-invariant curve on S of degree 45 (defined by a section of \(\omega _S^{-9}\)) with 15 irreducible components. A priori this section is \(\mathfrak {A}_5\)-invariant, but as Clebsch [6] showed, it is in fact \(\mathfrak {S}_5\)-invariant (see also Remark 6.6).
Since we have already determined the size of some orbits in the anticanonical model, we can now interpret the orbits thus found. We do this only insofar it concerns \(\mathfrak {A}_5\)-orbits, because that is all we need. Note that this is not a closed subset. Here is what remains, but stated in terms of the Wiman–Edge pencil:
Corollary 3.15
The irregular \(\mathfrak {A}_5\)-orbits in \(S\cong \overline{\mathscr {M}}_{0,5}\) of size 30 are parametrized by punctured rational curve and the others (named by the conjugacy class of a stabilizer subgroup) are as follows:
- \(\mathfrak {C}_3\) :
-
This 20-element orbit is the base point locus \(\Delta \) of \(\mathscr {C}\).
- \(\mathfrak {D}_4^{\mathrm{ev}}\) :
-
This 15-element orbit is the singular locus of \(C_\infty \).
- \(\mathfrak {S}^{\mathrm{ev}}_3\) :
-
This consists of two 10-element orbits in
 equal to
equal to  and
and  .
. - \(\mathfrak {D}_{10}\) :
-
This consists of two 6-element orbits, namely the singular loci of the two irreducible members of the Wiman–Edge pencil,
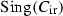 and
and  .
.
The orbit pairs of type \(\mathfrak {S}^{\mathrm{ev}}_3\) and \(\mathfrak {D}_{10}\) are swapped by an a conjugacy with an element of  (which induces a nontrivial outer automorphism of \(\mathfrak {A}_5\)).
(which induces a nontrivial outer automorphism of \(\mathfrak {A}_5\)).
Proof
Theorem 3.13 yields a complete list of the irregular \(\mathfrak {A}_5\)-orbits in terms of \(\overline{\mathscr {M}}_{0,5}\) of size smaller than 30. We have already encountered some of these orbits as they appear in this corollary. All that is then left to do is to compare cardinalities. \(\square \)
4 Projection to a Klein plane
4.1 The Klein plane
The two representations I and \(I'\) of \(\mathfrak {A}_5\) are the complexification of two real representations that realize \(\mathfrak {A}_5\) as the group of motions of a regular icosahedron. They differ only in the way we have identified this group of motions with \(\mathfrak {A}_5\). The full group of isometries of the regular icosahedron (including reflections) is a direct product  , and is in fact a Coxeter group of type \(H_3\), a property that will be quite helpful to us when we need to deal with the \(\mathfrak {A}_5\)-invariants in the symmetric algebra of I. Both \(\mathfrak {A}_5\)-actions give rise to \(\mathfrak {A}_5\)-actions on the unit sphere in Euclidean 3-space. Via the isomorphism
, and is in fact a Coxeter group of type \(H_3\), a property that will be quite helpful to us when we need to deal with the \(\mathfrak {A}_5\)-invariants in the symmetric algebra of I. Both \(\mathfrak {A}_5\)-actions give rise to \(\mathfrak {A}_5\)-actions on the unit sphere in Euclidean 3-space. Via the isomorphism  , they can also be considered as actions of \(\mathfrak {A}_5\) on the Riemann sphere \(\mathbb {P}^1\). These projective representations are what we have called the Schwarzian representations and are the only two nontrivial projective representations of \(\mathfrak {A}_5\) on \(\mathbb {P}^1\) up to isomorphism.
, they can also be considered as actions of \(\mathfrak {A}_5\) on the Riemann sphere \(\mathbb {P}^1\). These projective representations are what we have called the Schwarzian representations and are the only two nontrivial projective representations of \(\mathfrak {A}_5\) on \(\mathbb {P}^1\) up to isomorphism.
We observed above that a Schwarzian representation has three irregular orbits of sizes 12, 20 and 30, corresponding respectively to the vertices, the barycenters and the midpoints of the edges of a spherical icosahedron. The antipodal map, when considered as an involution \(\mathbb {P}^1\), is antiholomorphic: it comes from assigning to a line in \(\mathbb {C}^2\) its orthogonal complement. We can think of this as defining an \(\mathfrak {A}_5\)-invariant real structure on \(\mathbb {P}^1\) without real points. In particular, the involution is not in the image of \(\mathfrak {A}_5\). Yet it preserves the \(\mathfrak {A}_5\)-orbits, so that each orbit decomposes into pairs. The preimages of  under the degree 2 isogeny
under the degree 2 isogeny  define two representations of degree 2 of an extension \(\widetilde{\mathfrak {A}}_5\) of \(\mathfrak {A}_5\) by a central subgroup of order 2, called binary icosahedral group. As above, these two representations of \(\widetilde{\mathfrak {A}}_5\) differ by an outer automorphism. If we take the symmetric square of such a representation, then the kernel \(\{ \pm 1\}\) of this isogeny acts trivially and hence factors through a linear representation of \(\mathfrak {A}_5\) of degree 3. This is an icosahedral representation of type I or \(I'\).
define two representations of degree 2 of an extension \(\widetilde{\mathfrak {A}}_5\) of \(\mathfrak {A}_5\) by a central subgroup of order 2, called binary icosahedral group. As above, these two representations of \(\widetilde{\mathfrak {A}}_5\) differ by an outer automorphism. If we take the symmetric square of such a representation, then the kernel \(\{ \pm 1\}\) of this isogeny acts trivially and hence factors through a linear representation of \(\mathfrak {A}_5\) of degree 3. This is an icosahedral representation of type I or \(I'\).
We can phrase this solely in terms of a given Schwarzian representation of \(\mathfrak {A}_5\) on a projective line K. For then the projective plane P underlying the associated icosahedral representation is the one of effective degree 2 divisors on K (the symmetric square of K) and K embeds \(\mathfrak {A}_5\)-equivariantly in P as the locus defined by points with multiplicity 2. This is of course the image of K under the Veronese embedding and makes K appear as a conic.
We will identify K with its image in P, and following Klein [18] we refer to this image as the fundamental conic. It is also defined by a non-degenerate \(\mathfrak {A}_5\)-invariant quadratic form on the icosahedral representation (which we know is self-dual). We call P a Klein plane. So an  can be understood as a 2-element subset of K. The latter spans a line in P and this is simply the polar that the conic K associates to x (when \(x\in K\), this will be the tangent line of X at x).
can be understood as a 2-element subset of K. The latter spans a line in P and this is simply the polar that the conic K associates to x (when \(x\in K\), this will be the tangent line of X at x).
Following Winger, we can now identify all the irregular \(\mathfrak {A}_5\)-orbits in P. As we have seen, K has exactly three irregular \(\mathfrak {A}_5\)-orbits having sizes 30, 20 and 12, each of which being invariant under an antipodal map. This antipodal invariance implies that the antipodal pairs in the above orbits span a collection of resp. 15, 10 and 6 lines in P, each of which makes up an \(\mathfrak {A}_5\)-orbit. When we regard these pairs as effective divisors of degree 2, they also yield \(\mathfrak {A}_5\)-orbits in  of the same size (K parameterizes the nonreduced divisors). The bijection between lines and points is induced by polarity with respect to K. This yields all the irregular orbits in the Klein plane:
of the same size (K parameterizes the nonreduced divisors). The bijection between lines and points is induced by polarity with respect to K. This yields all the irregular orbits in the Klein plane:
Lemma 4.1
(Winger [26, Section 1]) There are unique irregular \(\mathfrak {A}_5\)-orbits in P having size 12, 20 (both in K), 6, 10 or 15 (all three in  ). The remaining irregular orbits in P have size 30 and are parametrized by a punctured rational curve. Further, the points with stabilizer a fixed \(\tau \in \mathfrak {A}_5\) of order 2 is open and dense in the image of the map \(K\rightarrow P\) given by \(z\in K\mapsto (z) +(\tau (z))\).
). The remaining irregular orbits in P have size 30 and are parametrized by a punctured rational curve. Further, the points with stabilizer a fixed \(\tau \in \mathfrak {A}_5\) of order 2 is open and dense in the image of the map \(K\rightarrow P\) given by \(z\in K\mapsto (z) +(\tau (z))\).
Proof
We can think of a point of K as a point on the icosahedron in Euclidean 3-space. An element of  is represented by an effective degree 2 divisor on K which has the same \(\mathfrak {A}_5\)-stabilizer. If we identify K with its \(\mathfrak {A}_5\)-action as a spherical icosahedron in Euclidean 3-space with its group of motions, then such a divisor spans an affine line in Euclidean 3-space with the same stabilizer. When the line passes through the origin, we get the three orbits of sizes 30, 20 and 12, otherwise the stabilizer is of order 2. \(\square \)
is represented by an effective degree 2 divisor on K which has the same \(\mathfrak {A}_5\)-stabilizer. If we identify K with its \(\mathfrak {A}_5\)-action as a spherical icosahedron in Euclidean 3-space with its group of motions, then such a divisor spans an affine line in Euclidean 3-space with the same stabilizer. When the line passes through the origin, we get the three orbits of sizes 30, 20 and 12, otherwise the stabilizer is of order 2. \(\square \)
We call a member of the 6-element \(\mathfrak {A}_5\)-orbit in  , a fundamental point and denote this orbit by F. We call the polar line of such a point a fundamental line.
, a fundamental point and denote this orbit by F. We call the polar line of such a point a fundamental line.
4.2 Two projections
The irreducible \(\mathfrak {S}_5\)-representation \(E_S\) splits into two 3-dimensional irreducible \(\mathfrak {A}_5\)-representations \(I_S\) and \(I'_S\). The two summands give a pair of disjoint planes  and
and  in
in  , to which we shall refer as Klein planes. We abbreviate them by P resp. \(P'\), and denote by \(K\subset P\) and
, to which we shall refer as Klein planes. We abbreviate them by P resp. \(P'\), and denote by \(K\subset P\) and  the fundamental (\(\mathfrak {A}_5\)-invariant) conics. We have \(\mathfrak {A}_5\)-equivariant (Klein) projections \(p:S\dasharrow P\) and \(p':S\dasharrow P'\) of the anticanonical model
the fundamental (\(\mathfrak {A}_5\)-invariant) conics. We have \(\mathfrak {A}_5\)-equivariant (Klein) projections \(p:S\dasharrow P\) and \(p':S\dasharrow P'\) of the anticanonical model  with center \(P'\), resp. P. Precomposition with an element of
with center \(P'\), resp. P. Precomposition with an element of  exchanges these projections.
exchanges these projections.
Proposition 4.2
The Klein planes are disjoint with S and the Klein projections are finite morphisms of degree 5. Together they define a finite morphism

that is birational onto its image.
The first assertion of Proposition 4.2 is [20, Theorem 5].
Proof
We focus on \(p:S\rightarrow P\). Let us first note that  is \(\mathfrak {A}_5\)-invariant and equals the base locus of the linear system of anticanonical curves parametrized by
is \(\mathfrak {A}_5\)-invariant and equals the base locus of the linear system of anticanonical curves parametrized by  . The curve part Y of
. The curve part Y of  has degree \(<5\). The class \([Y]\in H^2(S; \mathbb {Z})\) of Y is \(\mathfrak {A}_5\)-invariant. Since the span of \(K_S\) is supplemented in \(H^2(S; \mathbb {C})\) by an irreducible \(\mathfrak {A}_5\)-representation isomorphic to V, we must have
has degree \(<5\). The class \([Y]\in H^2(S; \mathbb {Z})\) of Y is \(\mathfrak {A}_5\)-invariant. Since the span of \(K_S\) is supplemented in \(H^2(S; \mathbb {C})\) by an irreducible \(\mathfrak {A}_5\)-representation isomorphic to V, we must have  for some integer \(d\geqslant 0\). But then
for some integer \(d\geqslant 0\). But then

and so \(Y=\varnothing \). It follows that the base locus is finite. Since it is a linear section of S it has at most five points. But Lemma 4.1 shows that \(P'\) has no orbit of size \(\leqslant 5\) and so the base locus is empty.
To see that \(p:S\rightarrow P\) is surjective, suppose its image is a curve, say of degree m. The preimage of a general line in P in S is an anticanonical curve and hence connected. This implies that \(m=1\). But then S lies in hyperplane and this is a contradiction.
So p is a surjection of nonsingular surfaces. If some irreducible curve is contracted by p, then this curve will have negative self-intersection. The only curves on S with that property are the lines, and then a line is being contracted. Since \(\mathfrak {A}_5\) acts transitively on the lines, all of them are then contracted. In other words, the exceptional set is the union \(C_\infty \) of the 10 lines on S. But \(C_\infty \) has self-intersection \((-2K_S)^2=20>0\) and hence cannot be contracted.
So the preimage of a point in P is finite. This is also the intersection of the quintic surface S with a codimension 2 linear subspace and so this fiber consists of five points, when counted with multiplicity.
For the last assertion, we notice that since one of the components of f has degree 5, the degree of \(S\xrightarrow {\scriptscriptstyle f}f(S)\) must divide 5. So it is either 1 or 5. If it is 5 then p and \(p'\) will have the same generic fiber so that \(p'\) factors through p via an isomorphism \(h:P\xrightarrow {\scriptscriptstyle \cong \,}P'\). But this would make the \(\mathfrak {A}_5\)-representations I and \(I'\) projectively equivalent, which is not the case. (We could alternatively observe that then the elements of  preserve the fibers of p so that we get in fact an action of \(\mathfrak {S}_5\) on P which makes p \(\mathfrak {S}_5\)-equivariant. But there is no projective representation of \(\mathfrak {S}_5\) on \(\mathbb {P}^2\).) \(\square \)
preserve the fibers of p so that we get in fact an action of \(\mathfrak {S}_5\) on P which makes p \(\mathfrak {S}_5\)-equivariant. But there is no projective representation of \(\mathfrak {S}_5\) on \(\mathbb {P}^2\).) \(\square \)
The proof of the next proposition makes use of the Thom–Boardman polynomial for the \(A_2\)-singularity locus. Let us first state the general result that we need. Let f be a morphism between two compact, nonsingular complex surfaces. Assume first that f has a smooth locus of critical points (\(=\) ramification divisor) \(\Sigma ^1(f)\). As Whitney and Thom observed, \(f|\Sigma ^1(f)\) need not be a local immersion: generically it will have a finite set \(\Sigma ^{1,1}(f)\) of (Whitney) cusp singularities; at such a point f exhibits a stable map-germ which in local-analytic coordinates can be given by  .
.
In the more general case when \(\Sigma ^1(f)\) is a reduced divisor (when defined by the Jacobian determinant), \(\Sigma ^{1,1}(f)\) is defined as a 0-cycle on the source manifold. While is not so hard to prove that the degree of \(\Sigma ^{1,1}(f)\) is a characteristic number of the virtual normal bundle  of f, it is another matter to obtain a closed formula for it. In the present case it is equal to
of f, it is another matter to obtain a closed formula for it. In the present case it is equal to  (see for instance [21, Theorem 5.1], where this is listed as the case \(A_2\)).
(see for instance [21, Theorem 5.1], where this is listed as the case \(A_2\)).
Proposition 4.3
(The ramification curve) The ramification curve R of the finite morphism \(p:S\rightarrow P\) is a singular irreducible member of the Wiman–Edge pencil, and hence obtained as an \(\mathfrak {A}_5\)-curve by means of the procedure of Lemma 3.9.
Proof
The divisor class [R] is given by the well-known formula  . Since
. Since  is \(-3\) times the class of a line, and \(p^*\) takes the class of a line to the class of hyperplane section (i.e., \(-K_S\)), we have
is \(-3\) times the class of a line, and \(p^*\) takes the class of a line to the class of hyperplane section (i.e., \(-K_S\)), we have  . It follows that \([R]=-2K_S\). Since R is \(\mathfrak {A}_5\)-invariant, it must be a member of the Wiman–Edge pencil. In particular, R is reduced.
. It follows that \([R]=-2K_S\). Since R is \(\mathfrak {A}_5\)-invariant, it must be a member of the Wiman–Edge pencil. In particular, R is reduced.
We now apply the above formula to \(p:S\rightarrow P\). The Chern classes of the virtual normal bundle of p are easily computed:  and
and  takes the value \(-2\) on the fundamental class [S] of S. We find that
takes the value \(-2\) on the fundamental class [S] of S. We find that

So \(\Sigma ^{1,1}(p)\) is a 0-cycle whose support is an \(\mathfrak {A}_5\)-invariant subset of S contained in R. In Sect. 3.6, we found that \(\mathfrak {A}_5\) has two 6-element orbits in S (each being the singular locus of an irreducible member of the Wiman–Edge pencil) and that any other \(\mathfrak {A}_5\)-orbit has at least 10 elements. Since R is a member of the Wiman–Edge pencil, we conclude that that it must be one with six nodes (and that each node has multiplicity 3 in \(\Sigma ^{1,1}(p)\)). This also proves that  is a local isomorphism at the 20-element orbit \(\Delta \). \(\square \)
is a local isomorphism at the 20-element orbit \(\Delta \). \(\square \)
Remark 4.4
The assertion of Proposition 4.3 can be confirmed by computation. If \(\pi :S\rightarrow \mathbb {P}^2\) is the blowing down morphism and \(\phi :S\rightarrow \mathbb {P}^5 = \mathbb {P}(E)\) is the \(\mathfrak {S}_5\)-equivariant anti-canonical embedding, then the composition  and the \(\mathfrak {A}_5\)-equivariant projection \(\mathbb {P}(E)\dashrightarrow \mathbb {P}(I)\) is given by
and the \(\mathfrak {A}_5\)-equivariant projection \(\mathbb {P}(E)\dashrightarrow \mathbb {P}(I)\) is given by

where

Here \(\lambda = ({1+\sqrt{5}})/{2}\) and \(\lambda ' = ({1-\sqrt{5}})/{2}\) are two roots of the quadratic equation \(t^2-t-1 = 0\). Here we use the coordinates in the plane in which the equation of the Wiman–Edge pencil is written. Computing the Jacobian \(J(f_0,f_1,f_2)\) we find the equation of a irreducible singular member of the pencil with parameters  .
.
Proposition 4.5
The preimage  of the fundamental conic in P is a nonsingular member of the Wiman–Edge pencil. The ordered 4-tuple \((C_0, C_\infty , C_K, C_{K'})\) consists of four distinct members of the Wiman–Edge pencil which lie in harmonic position: there is a unique affine coordinate for \(\mathscr {C}\) that identifies this 4-tuple with \((0, \infty , 1, -1)\).
of the fundamental conic in P is a nonsingular member of the Wiman–Edge pencil. The ordered 4-tuple \((C_0, C_\infty , C_K, C_{K'})\) consists of four distinct members of the Wiman–Edge pencil which lie in harmonic position: there is a unique affine coordinate for \(\mathscr {C}\) that identifies this 4-tuple with \((0, \infty , 1, -1)\).
Proof
It is clear that \(C_K\) is an \(\mathfrak {A}_5\)-invariant member of \(|-2K_S|\) and therefore a member of the Wiman–Edge pencil. It is defined by the quadric Q and similarly \(C_{K'}\) is defined by the quadric \(Q'\). The last clause of the proposition then follows as \(C_0\), resp. \(C_\infty \), is defined by \(Q+Q'\), resp. \(Q-Q'\).
If \(C_K\) is singular, then it must be one of \(C_\mathrm{c}, C'_\mathrm{c}, R, R'\). We shall exclude each of these possibilities.
Suppose that \(C_K=C_\mathrm{c}\) or \(C'_\mathrm{c}\). Then let Y be an irreducible component of \(C_K\). Now both Y and K are conics and since p is a linear projection, \(Y\xrightarrow {\scriptscriptstyle p\;} K\) must be of degree 1. On the other hand, R meets \(C_K\) transversally in \(\Delta \), and so Y meets R transversally in four distinct points. This implies that \(Y\xrightarrow {\scriptscriptstyle p\;} K\) must have degree 3 and we arrive at a contradiction.
We cannot have \(C_K=R\), for then p would ramify along  and so
and so  would be 2-divisible: this would make it twice an anticanonical divisor (a hyperplane section) and R is clearly not of that type. If \(C_K=R'\), then
would be 2-divisible: this would make it twice an anticanonical divisor (a hyperplane section) and R is clearly not of that type. If \(C_K=R'\), then  must ramify in the singular part
must ramify in the singular part  of \(R'\) and so R contains
of \(R'\) and so R contains  . This contradicts the fact that the two members R and \(R'\) of the Wiman–Edge pencil intersect transversally. \(\square \)
. This contradicts the fact that the two members R and \(R'\) of the Wiman–Edge pencil intersect transversally. \(\square \)
We can also improve the statement about the birationality of the map \((p,p')\).
Theorem 4.6
The map

is a local isomorphism onto its image. Further,

where \((h,h')\) is the standard basis in  , and hence the composite of f with the Segre embedding
, and hence the composite of f with the Segre embedding

has degree 20.
Proof
We have already proved that the map is of degree 1 onto its image and hence coincides with the normalization of the image.
It remains to show that \((p,p')\) is a local isomorphism. Suppose it is not. Since the projection p, resp. \(p'\), is a local isomorphism on  , resp.
, resp.  , the map could only fail to be local isomorphism at some \(x\in R\cap R'\). Let L be the kernel of the derivative at x. Then L is mapped to 0 under the composition with the both projections. This implies that L coincides with the tangent line of R and \(R'\) at x. But we know that two curves in the Wiman–Edge pencil intersect transversally at a base point. This contradiction proves the assertion.
, the map could only fail to be local isomorphism at some \(x\in R\cap R'\). Let L be the kernel of the derivative at x. Then L is mapped to 0 under the composition with the both projections. This implies that L coincides with the tangent line of R and \(R'\) at x. But we know that two curves in the Wiman–Edge pencil intersect transversally at a base point. This contradiction proves the assertion.
Next represent h, resp. \(h'\), by general lines \(\ell \subset P\), resp.  . Then \(f^*(h.h')\) is represented by
. Then \(f^*(h.h')\) is represented by  . This is evidently a plane section of S and hence is a class of degree 5. Since p and \(p'\) are also of degree 5, it follows that \(f_*(1)\) is as asserted. \(\square \)
. This is evidently a plane section of S and hence is a class of degree 5. Since p and \(p'\) are also of degree 5, it follows that \(f_*(1)\) is as asserted. \(\square \)
Remark 4.7
The map  is not injective. We will make this explicit in Remark 5.7, but we here give a general argument that implies that there must exist a whole curve of fibers consisting of more than a single point. Let us write f for \((p,p')\). The double point formula asserts that its virtual number of double points is equal to the degree of
is not injective. We will make this explicit in Remark 5.7, but we here give a general argument that implies that there must exist a whole curve of fibers consisting of more than a single point. Let us write f for \((p,p')\). The double point formula asserts that its virtual number of double points is equal to the degree of  [21]. The degree of
[21]. The degree of

is equal to  . On the other hand, if
. On the other hand, if  is the fundamental class (so that \(K_S^2=5\mu _S\)) then \(c(\theta _S)=1+K_S+ 7\mu _S\) (the coefficient 7 is the topological Euler characteristic of S) and
is the fundamental class (so that \(K_S^2=5\mu _S\)) then \(c(\theta _S)=1+K_S+ 7\mu _S\) (the coefficient 7 is the topological Euler characteristic of S) and
Thus

This tells us that the degree of \(\nu _f\) is 103. It follows that the number of virtual double points is \(-28\). This can only be interpreted as saying that the double point locus of f must contain a curve on S with negative self-intersection.
4.3 The projection of irregular orbits
Let us describe the images of the irregular \(\mathfrak {A}_5\)-orbits in S under the projection map \(p:S\rightarrow P\). Since the projection is \(\mathfrak {A}_5\)-equivariant, the image of an irregular \(\mathfrak {A}_5\)-orbit in S is an irregular orbit in the Klein plane. According to Lemma 4.1, there are \(\mathfrak {A}_5\)-orbits in P of size 6, 10, 15 (all outside the fundamental conic) and of 12 and 20 (all on the fundamental conic), of which those of size 6 and 10 come in pairs, the others being unique. The other irregular orbits in P are of size 30 and are parametrized by a rational curve. On the other hand, by Corollary 3.15, in S there are two \(\mathfrak {A}_5\)-orbits in S of size 6 and 10, one of size 15 and 20, and an irreducible curve of orbits of size 30.
This immediately implies that the orbits on S of cardinalities 6, 10, 15 are mapped one-to-one to the orbits of the same cardinality in the Klein plane. This is also true for the 20-element orbit, since it consists of the base points of the Wiman–Edge pencil \(\mathscr {C}\) and hence is mapped to the 20-element orbit on the conic. The size 12 orbit in K must be the image of an orbit in S whose size is divisible by 12 and so this can only be a regular orbit. Since the \(\mathfrak {A}_5\)-orbits of size 30 in S and in P are parametrized by an irreducible curve; p will map the generic point of the former to the generic point of the latter. This information, insofar relevant here is displayed in Table 3; it will help us to determine the p-images of the special members of the pencil.
4.4 The projection of the Wiman–Edge pencil
We will later investigate the p-images of the special members of the Wiman–Edge pencil, but at this point it is convenient to already make the following observation.
Proposition 4.8
The divisor \(p_*C_\infty \) is the sum of the 10 lines that are spanned by the antipodal pairs in the 20-element orbit \(p(\Delta )\) on K. Each singular point of \(p_*C_\infty \) lies on exactly two lines and the resulting \(\left( {\begin{array}{c}10\\ 2\end{array}}\right) =45\) double points make up two irregular \(\mathfrak {A}_5\)-orbits, one of which is the unique 15-element orbit defined by pairs of lines which meet in S (and so the other has size 30).
Proof
The image of a line on S is a line in P and so \(p_*C_\infty \) is a sum of 10 lines. The polars of these lines make up an \(\mathfrak {A}_5\)-orbit in P of size \(\leqslant 10\). There is only one such orbit and it has exactly 10 elements.
The singular locus of \(C_\infty \) is a 15-element orbit and we observed that this orbit maps bijectively onto the unique 15-element orbit in P. It follows from the discussion in Sect. 3.6, that the stabilizer of each singular point of \(C_\infty \) is the group \(\mathfrak {D}_4^{\mathrm{ev}}\). Its projection has the same stabilizer group. Thus the image of  consists of 15 points. Since there is only one orbit in P of cardinality 15, the remaining \(45-15 = 30\) points form an orbit of \(\mathfrak {A}_5\) in P. \(\square \)
consists of 15 points. Since there is only one orbit in P of cardinality 15, the remaining \(45-15 = 30\) points form an orbit of \(\mathfrak {A}_5\) in P. \(\square \)
This has implications for a generic member C of \(\mathscr {C}\), as follows. The curve \(p_*C_\infty \) being reduced and of geometric genus 6, it follows that \(p_*C\) has the same property. As p is linear, \(p_*C\) is a plane curve of the same degree as C, namely 10. So the arithmetic genus of \(p_*C\) is \((10-1)(10-2)/2=36\), and hence its genus defect is 30. Since the singular set of C specializes to a subset of the singular set of \(C_\infty \), it follows that this singular set consists of 30 nodes and makes up an \(\mathfrak {A}_5\)-orbit (but remember that such orbits move in a curve and can degenerate into an orbit of smaller size).
So \(C\in \mathscr {C}\mapsto p_*C\) defines a morphism from the base \(\mathscr {B}\) of the Wiman–Edge pencil (a copy of \(\mathbb {P}^1\)) to \(|\mathscr {O}_P(10)|\). We denote its image by \(p_*\mathscr {B}\). It is clear that every point of \(p_*\mathscr {B}\) will be an \(\mathfrak {A}_5\)-invariant curve. An \(\mathfrak {A}_5\)-invariant curve in P admits an \(\mathfrak {A}_5\)-invariant equation (because every homomorphism \(\mathfrak {A}_5\rightarrow \mathbb {C}^\times \) is trivial), and so every member of \(p_*\mathscr {C}\) lands in the projectivization of  (recall that P is the projectivization of the dual of I).
(recall that P is the projectivization of the dual of I).
Since \(\mathfrak {A}_5\) acts on I as the group of orientation-preserving elements of a Coxeter group of type \(H_3\), this space is easy to determine using the invariant theory of Coxeter groups: if \(\Phi _2\) is an equation for K and \(\Phi _6,\Phi _{10},\Phi _{15}\) an equation for the \(\mathfrak {A}_5\)-invariant union of resp. 6, 10 and 15 lines, then these generate the \(\mathfrak {A}_5\)-invariants in the symmetric algebra of I. The first three generate the invariants of the Coxeter group and are algebraically independent (\(\Phi _{15}{}^2\) is a polynomial in these). So  is of dimension 3 and has the basis
is of dimension 3 and has the basis  . Thus every \(\mathfrak {A}_5\)-invariant decimic in P can be written by the equation
. Thus every \(\mathfrak {A}_5\)-invariant decimic in P can be written by the equation

In particular, \(p_*\mathscr {B}\) is a plane curve. Since \(p_*\Delta \) is the transversal intersection of the 10 lines union and K (the common zero set of \(\Phi _2\) and \(\Phi _{10}\)), we also see from equation (3) that every \(\mathfrak {A}_5\)-invariant decimic in P passes through \(p_*\Delta \) and is there tangent to the 10 lines union unless it contains K as an irreducible component of multiplicity 2 (i.e., \(c=0\)).
The formula (3) also proves the following
Proposition 4.9
(The net of \(\mathfrak {A}_5\)-decimics) All members of the net of \(\mathfrak {A}_5\)-decimics intersect the fundamental conic transversally at 20 points and they are all tangent at these points to one of the 10 lines that joins two antipodal points.
Of course, the 20 points in the statement of Proposition 4.9 are the projection of the set \(\Delta \) of base points of the Wiman–Edge pencil.
Proposition 4.10
The members of \(p_*\mathscr {C}\) distinct from 5K are reduced and intersect K transversally in \(p_*\Delta \). The map \(\mathscr {B}\rightarrow p_*\mathscr {B}\) defined by \(C\mapsto p_*C\) is injective, and \(p_*\mathscr {B}\) is a curve of degree 5 in \(|\mathscr {O}_P(10)|\).
Proof
If \(C\in \mathscr {C}\) is not equal to \(C_K\) then

Since this is also the size of \(p(C)\cap K=p(\Delta )\), it follows that \(p_*C\) is reduced and meets K transversally in \(p(\Delta )\).
Let \(C_1, C_2\) be members of the Wiman–Edge pencil distinct from \(C_K\). Since \(p_*C_i\) is reduced, the map \(p:C_i\rightarrow p_*C_i\) is a normalization and so the equality \(p_*C_1=p_*C_2\) lifts to an \(\mathfrak {A}_5\)-equivariant isomorphism \(C_1\cong C_2\). As \(\mathscr {C}\) is the universal family, it follows that \(C_1=C_2\). So the map \(\mathscr {B}\rightarrow p_*\mathscr {B}\) is injective.
It also follows that for \(z\in P\) generic, then through each of the five points of \(p^{-1}(z)\) passes exactly one member of \(\mathscr {C}\) and these members are distinct and smooth. This means that the hyperplane in \(|\mathscr {O}_P(10)|\) of decimics passing through z meets \(p_*\mathscr {B}\) transversally in five points and so the curve in question has degree 5. \(\square \)
In particular, \(p_*\mathscr {C}\) is not a pencil. We can be a bit more precise. If \(a\Phi _2{}^5+b\Phi _6\Phi _2{}^2+c\Phi _{10}=0\) represents \(p_*C\in p_*\mathscr {C}\), with \(p_*C\not =5K\), then the fact that \(p_*C\) is transversal to K implies that \(c\not =0\). So such a curve has unique equation for which \(c=1\). In particular, \(p_*R\) has an equation of the form

(We will see later that this curve is in fact the Klein decimic.) It follows that \(\Phi _2, \Phi _6, \Phi _R, \Phi _{15}\) still generate the algebraic \(\mathfrak {A}_5\)-invariants.
Proposition 4.11
The plane curve \(p_*\mathscr {B}\) has two singular points, namely the points represented by \(p_*R\) and by 5K, where it has a singularity of type \(A_4\), resp. \(E_8\) (having local-analytic parameterizations  , resp.
, resp.  ).
).
Proof
Let \(x\in \Delta \). Since p has simple ramification at x, we can find local-analytic coordinates \((z_1,z_2)\) at x and \((w_1,w_2)\) at p(x) such that \(p^*w_1=z_1^2\) and \(p^*w_2=z_2\), and such that K is at p(x) given by \(w_2=0\). So the ramification locus R is given at x by \(z_1=0\) and \(C_K\) by \(z_2=0\).
A tangent direction at x not tangent to \(C_K\) has in the \((z_1,z_2)\)-coordinates a unique generator of the form \((\lambda , 1)\). We therefore can regard \(\lambda \) as a coordinate for the complement in  of the point defined by \(T_xC_K\) and hence as a coordinate for the complement
of the point defined by \(T_xC_K\) and hence as a coordinate for the complement  of the point representing \(C_K\). This means that the member of
of the point representing \(C_K\). This means that the member of  corresponding to \(\lambda \) has a local parametrization at x given by
corresponding to \(\lambda \) has a local parametrization at x given by  . Its image under p has then the local parametrization
. Its image under p has then the local parametrization  , which shows that \(\lambda ^2\), when regarded as a regular function on \(\mathscr {B}^+\), is in fact a regular function on its image \(p_*\mathscr {B}^+\).
, which shows that \(\lambda ^2\), when regarded as a regular function on \(\mathscr {B}^+\), is in fact a regular function on its image \(p_*\mathscr {B}^+\).
Now let us make these coordinate choices compatible with the chosen basis of invariants. For this we choose a third root \(\Phi _6^{1/3}\) of \(\Phi _6\) and take \(w_1=\Phi _R\Phi _6^{-5/3}\) (this means that \(z_1\) must be a square root of this) and \(w_2=\Phi _2\Phi _6^{-1/3}\). We write a member of \(p_*\mathscr {B}^+\) uniquely as

with a and b polynomials of degree \(\leqslant 5\) and 5 being attained. If we multiply this equation by \(\Phi _6^{-5/3}\), then it becomes

It follows from the preceding that \(b(\lambda )=\lambda ^2\). Hence a has degree 5. By Proposition 4.10, the curve \(\lambda \mapsto (a(\lambda ),\lambda ^2)\) must be injective. This means that \(a(\lambda )-a(-\lambda )\) is nonzero when \(\lambda \not =0\). This can only happen when there is at most one odd power of \(\lambda \) appearing in a. This power must then be 5, of course. It follows that \(\mathbb {P}^1\cong \mathscr {B}\rightarrow p_*\mathscr {B}\) is given by

where \(a_5, a_4, a_2\) are constants with \(a_5\not =0\). The proposition follows from this. \(\square \)
5 Images of some members of the Wiman–Edge pencil in the Klein plane
5.1 The preimage of a fundamental conic
We will characterize \(C_K\) and \(C_{K'}\) as members of \(\mathscr {C}\) by the fact that they support an exceptional even theta characteristic. Recall that a theta characteristic of a projective smooth curve C is a line bundle \(\kappa \) over \(C_K\) endowed with an isomorphism \(\phi :\kappa ^{\otimes 2}\cong \omega _{C}\). It is called even or odd according to the parity of the dimension of \(H^0(C, \kappa )\).
The strong form of Clifford’s theorem as stated in [2] implies that

provided that C is not hyperelliptic. If  is 1-dimensional and without fixed points, then the associated morphism
is 1-dimensional and without fixed points, then the associated morphism  is of degree \(\leqslant g(C)-1\) and has as fibers the moving part of
is of degree \(\leqslant g(C)-1\) and has as fibers the moving part of  . We can obtain this morphism by means of a linear projection of the canonical image: the natural map
. We can obtain this morphism by means of a linear projection of the canonical image: the natural map  is injective (with image a 3-dimensional subspace), so that dually, we have a projection onto a projective plane
is injective (with image a 3-dimensional subspace), so that dually, we have a projection onto a projective plane

The latter contains a conic that can be identified with the image of  under the Veronese map. The composition with the canonical map
under the Veronese map. The composition with the canonical map  has image in this conic and thus realizes
has image in this conic and thus realizes  . Note that this conic can be understood as a quadric in
. Note that this conic can be understood as a quadric in  of rank 3 that contains the canonical image of C.
of rank 3 that contains the canonical image of C.
Proposition 5.1
The morphism \(C_K\rightarrow K\) is obtained as the complete linear system of an even theta characteristic \(\kappa \) on \(C_K\) followed by the (Veronese) embedding \(K\subset P\). The \(\mathfrak {A}_5\)-action on \(C_K\) lifts to an action of the binary icosahedral group \(\widetilde{\mathfrak {A}}_5\) on \(\kappa \) in such a way that \(H^0(C_K, \kappa )\) is an irreducible \(\widetilde{\mathfrak {A}}_5\)-representation of degree 2. Similarly for  , albeit that \(H^0(C_{K'}, \kappa ')\) will be the other irreducible \(\widetilde{\mathfrak {A}}_5\)-representation of degree 2.
, albeit that \(H^0(C_{K'}, \kappa ')\) will be the other irreducible \(\widetilde{\mathfrak {A}}_5\)-representation of degree 2.
There are no other pairs \((C, \theta )\), where C is a member of  and \(\theta \) is an \(\mathfrak {A}_5\)-invariant theta characteristic with \(\dim |\theta |=1\).
and \(\theta \) is an \(\mathfrak {A}_5\)-invariant theta characteristic with \(\dim |\theta |=1\).
Proof
Observe that the preimage of a line in P meets \(C_K\) in a canonical divisor and that any effective degree 2 divisor on K spans a line in P. This implies that the fibers of \(C_K\rightarrow K\) belong to the divisor class of a theta characteristic  . The \(\mathfrak {A}_5\)-action on \(C_K\) need not lift to such an action on \(\kappa \), but its central extension, the binary icosahedral group \(\overline{\mathfrak {A}}_5\), will (in a way that makes \(\phi \) equivariant). Thus \(H^0(C_K, \kappa )\) becomes an \(\widetilde{\mathfrak {A}}_5\)-representation. It contains a 2-dimensional (base point free) subrepresentation which accounts for the morphism \(C_K\rightarrow K\). To see that this inclusion is an equality, we note that by Clifford’s theorem as cited above, \(\dim H^0(C_K, \kappa )\leqslant 3\). If it were equal to 3, then \(\widetilde{\mathfrak {A}}_5\) would have a trivial summand in \(H^0(C_K, \kappa )\) and hence so would \(H^0(C_K, \kappa ^{\otimes 2})= H^0(C_K, \omega _{C_K})\). This contradicts the fact that the latter is of type
. The \(\mathfrak {A}_5\)-action on \(C_K\) need not lift to such an action on \(\kappa \), but its central extension, the binary icosahedral group \(\overline{\mathfrak {A}}_5\), will (in a way that makes \(\phi \) equivariant). Thus \(H^0(C_K, \kappa )\) becomes an \(\widetilde{\mathfrak {A}}_5\)-representation. It contains a 2-dimensional (base point free) subrepresentation which accounts for the morphism \(C_K\rightarrow K\). To see that this inclusion is an equality, we note that by Clifford’s theorem as cited above, \(\dim H^0(C_K, \kappa )\leqslant 3\). If it were equal to 3, then \(\widetilde{\mathfrak {A}}_5\) would have a trivial summand in \(H^0(C_K, \kappa )\) and hence so would \(H^0(C_K, \kappa ^{\otimes 2})= H^0(C_K, \omega _{C_K})\). This contradicts the fact that the latter is of type  as an \(\mathfrak {A}_5\)-representation.
as an \(\mathfrak {A}_5\)-representation.
It is clear that we obtain \((C_{K'}, \kappa ')\) as the transform/pull-back of \((C_K, \kappa )\) under an element of  .
.
If \((C, \theta )\) is as in the proposition, then C lies on an \(\mathfrak {A}_5\)-invariant quadric of rank 3. This quadric will be defined by \(\lambda Q+\lambda ' Q'\) for some  (with Q and \(Q'\) as in Sect. 2.5), and so the rank condition implies \(\lambda =0\) or \(\lambda '=0\). In other words, \((C, \theta )\) equals \((C_K,\kappa )\) or \((C_{K'}, \kappa ')\). \(\square \)
(with Q and \(Q'\) as in Sect. 2.5), and so the rank condition implies \(\lambda =0\) or \(\lambda '=0\). In other words, \((C, \theta )\) equals \((C_K,\kappa )\) or \((C_{K'}, \kappa ')\). \(\square \)
5.2 The image of reducible singular members
Recall that \(C_\mathrm{c}\) and \(C'_\mathrm{c}\) are the \(\mathfrak {A}_5\)-orbit of a special conic. So the following proposition tells us what their p-images are like.
Proposition 5.2
The projection p maps each special conic isomorphically onto a conic in P that is tangent to four lines that are the projections of lines on S, and passes through four points of the 10-element \(\mathfrak {A}_5\)-orbit.
Proof
Let Y be a special conic. Since Y is part of \(C_\mathrm{c}\) or \(C'_\mathrm{c}\), Y meets \(\Delta \) in four distinct points and \(p_*Y\) is a degree 2 curve which meets \(p(\Delta )\) in four points. In particular p maps Y isomorphically onto its image (not on a double line). For each \(a\in Y\cap \Delta \), p(a) and its antipode span a line in P and according to Proposition 4.10, p(Y) is tangent to the line at p(a). \(\square \)
5.3 The decimics of Klein and Winger
Let us call a projective plane endowed with a group G of automorphisms isomorphic to \(\mathfrak {A}_5\) a Klein plane (but without specifying an isomorphism \(G\cong \mathfrak {A}_5\)). Such a plane is unique up to isomorphism (it is isomorphic to both P and \(P'\)). For what follows it is convenient to make the following definition.
Definition 5.3
(Special decimics) We call a reduced, G-invariant curve in a Klein plane of degree 10 a special decimic if it is singular at each fundamental point and its normalization is rational. If the singularity at a fundamental point is an ordinary node, we call it a Winger decimic; otherwise (so when it is worse than that) we call it a Klein decimic.
We will see that each of these decimics is unique up to isomorphism, and that p(R) is a Klein decimic and \(p(R')\) a Winger decimic. We will also show that the singularity of a Klein decimic at a fundamental point must be a double cusp (i.e., with local analytic equation \((x^3-y^2)(y^3-x^3)\)). As to our naming: a Klein curve appears in [18, Chapter 4, Section 3] (p. 218 in the cited edition), and a Winger curve appears in [26, Section 9].
Let us first establish the relation between special decimics and the Wiman–Edge pencil. Let K be a copy of a \(\mathbb {P}^1\) and let  be a subgroup isomorphic to \(\mathfrak {A}_5\). Recall that K has a unique G-orbit \(F^\#\) of size 12 (think of this as the vertex set of a regular icosahedron) which comes in six antipodal pairs. Let us denote by
be a subgroup isomorphic to \(\mathfrak {A}_5\). Recall that K has a unique G-orbit \(F^\#\) of size 12 (think of this as the vertex set of a regular icosahedron) which comes in six antipodal pairs. Let us denote by  the antipodal involution, and let \(\overline{K}\) be obtained from \(\widetilde{Y}\) by identifying every \(z\in F^\#\) with
the antipodal involution, and let \(\overline{K}\) be obtained from \(\widetilde{Y}\) by identifying every \(z\in F^\#\) with  as to produce an ordinary node. This is just the curve of arithmetic genus 6 that we constructed in Lemma 3.9.
as to produce an ordinary node. This is just the curve of arithmetic genus 6 that we constructed in Lemma 3.9.
Notice that the normalization of a special decimic factors through this quotient of K: it is the image of \(\overline{K}\) under a 2-dimensional linear system of degree 10 divisors on \(\overline{K}\) that comes from a 3-dimensional irreducible subrepresentation of \(H^0(\overline{K}, \mathscr {O}_{\overline{K}}(10))\). In order to identify these subrepresentations, we focus our attention on the dualizing sheaf \(\omega _{\overline{K}}\) of \(\overline{K}\). This is the subsheaf of the direct image of \(\omega _K(F^\#)\) characterized by the property that the sum of the residues in a fiber add up to zero. So \(H^0(\overline{K}, \omega _{\overline{K}})\) is the subspace of \(H^0(K,\omega _K(F^\#))\) consisting of differentials whose residues at the two points of any antipodal pair add up to zero.
Lemma 5.4
There is an exact sequence of G-representations
where the last term denotes the reduced cohomology of F. Further, \(\widetilde{H}^0(F; \mathbb {C})\) is an irreducible G-representation of dimension 5 (hence of type W).
Proof
For every \(x\in F\) there is a linear form on \(H^0(K, \omega _K(F^\#))\) that assigns to \(\alpha \in H^0(K, \omega _K(F^\#))\) the sum of the residues at the associated antipodal pair on K. By the residue formula, these six linear forms add up to zero. Apart from that, residues can be arbitrarily described and we thus obtain the exact sequence. The character of the permutation representation on F (which can be thought of as the set of six lines through opposite vertices of the icosahedron) is computed to be that of trivial representation plus that of W. This implies that \(\widetilde{H}^0(F; \mathbb {C})\cong W\) as G-representations. \(\square \)
We know by Propositions 3.10 and 4.3 that the dualizing sheaf of \(\overline{K}\) defines the canonical embedding for \(\overline{K}\) and that the 6-dimensional G-representation \(H^0(\overline{K}, \omega _{\overline{K}})\) decomposes into two irreducible subrepresentations of dimension 3 that are not of the same type. This enables us to prove that there are only two isomorphism types of special decimics.
Corollary 5.5
(Classification of special decimics) Let \(Y\subset P\) be a special decimic and let \(\overline{K}\rightarrow Y\) define a partial G-equivariant normalization (so that the six nodes of \(\overline{K}\) lie over the six fundamental points of P). Then Y can be identified in a G-equivariant manner with the image of \(\overline{K}\) under the linear system that comes from one of the two irreducible 3-dimensional G-subrepresentations of \(H^0(\overline{K}, \omega _{\overline{K}})\). In fact, \(p_*R\) and \(p'_*R\) are special decimics and every special decimic is isomorphic to one of them.
Proof
The line bundle \(\omega _K(F^\#)\) is of degree 10. The fact that \(\omega _{\overline{K}}\) is of degree  implies that
implies that  is the complete linear system of degree 10. As the G-embedding \(Y\subset P\) is of degree 10, the G-embedding \(Y\subset P\) is definable by a 3-dimensional G-invariant subspace of \(H^0(K, \omega _K(F^\#))\). It follows from Lemma 5.4 that this subrepresentation must be contained in \(H^0(\overline{K}, \omega _{\overline{K}})\), and hence is given by one of its 3-dimensional summands.
is the complete linear system of degree 10. As the G-embedding \(Y\subset P\) is of degree 10, the G-embedding \(Y\subset P\) is definable by a 3-dimensional G-invariant subspace of \(H^0(K, \omega _K(F^\#))\). It follows from Lemma 5.4 that this subrepresentation must be contained in \(H^0(\overline{K}, \omega _{\overline{K}})\), and hence is given by one of its 3-dimensional summands.
Let us write \(E_K\) for \(H^0(\overline{K}, \omega _{\overline{K}})\) and \(\mathbb {P}_K\) for  . The canonical map \(\overline{K}\rightarrow \mathbb {P}_K\) is an embedding and realizes \(\overline{K}\) as a member of the Wiman–Edge pencil: if we regard this embedding as an inclusion, then the \(\mathfrak {A}_5\)-embedding \(R\subset \mathbb {P}_S\) is obtained from the G-embedding \(\overline{K}\subset \mathbb {P}_K\) via a compatible pair of isomorphisms \((G, E_K)\cong (\mathfrak {A}_5, E_S)\). The preimage
. The canonical map \(\overline{K}\rightarrow \mathbb {P}_K\) is an embedding and realizes \(\overline{K}\) as a member of the Wiman–Edge pencil: if we regard this embedding as an inclusion, then the \(\mathfrak {A}_5\)-embedding \(R\subset \mathbb {P}_S\) is obtained from the G-embedding \(\overline{K}\subset \mathbb {P}_K\) via a compatible pair of isomorphisms \((G, E_K)\cong (\mathfrak {A}_5, E_S)\). The preimage  of \(S\subset \mathbb {P}_S\) is a G-invariant quintic del Pezzo surface which contains \(\overline{K}\). We have a decomposition
of \(S\subset \mathbb {P}_S\) is a G-invariant quintic del Pezzo surface which contains \(\overline{K}\). We have a decomposition  into two irreducible subrepresentations such that the two associated linear systems of dimension 2 reproduce the projections
into two irreducible subrepresentations such that the two associated linear systems of dimension 2 reproduce the projections  and \(p'|R\). So \(p_*R\) and \(p'_*R\) represent the two types of special decimics. \(\square \)
and \(p'|R\). So \(p_*R\) and \(p'_*R\) represent the two types of special decimics. \(\square \)
Theorem 5.6
The preimage  of the set of fundamental points is the disjoint union of
of the set of fundamental points is the disjoint union of  and
and  . Moreover, \(p_*R'\) is a Winger decimic and \(p_*R\) is a Klein decimic.
. Moreover, \(p_*R'\) is a Winger decimic and \(p_*R\) is a Klein decimic.
Proof
We know that the singular set of R makes up an \(\mathfrak {A}_5\)-orbit and that such an \(\mathfrak {A}_5\)-orbit is mapped to F. The same is true for \(R'\) and so each fundamental point is a singular point of both \(p_*R\) and \(p_*R'\). For every singular point x of R,  consists of \(k\leqslant 5-2= 3\) points. So
consists of \(k\leqslant 5-2= 3\) points. So  is an \(\mathfrak {A}_5\)-invariant set of size
is an \(\mathfrak {A}_5\)-invariant set of size  .
.
Our irregular orbit catalogue for the \(\mathfrak {A}_5\)-action on S (see Sect. 3.6) shows that only \(k = 1\) is possible, so that this must be the 6-element orbit in S different from  , i.e.,
, i.e.,  . This proves that the (disjoint) union of
. This proves that the (disjoint) union of  and
and  make up a fiber of p. In particular, \(p_*R'\) has an ordinary double point at p(x) and hence is a Winger decimic. On the other hand, \(p_*R\) has multiplicity at least 4 at p(x): this is because the restriction of p to a local branch of R has a singularity at x (because of the presence of the other branch). So \(p_*R\) must be a Klein decimic. \(\square \)
make up a fiber of p. In particular, \(p_*R'\) has an ordinary double point at p(x) and hence is a Winger decimic. On the other hand, \(p_*R\) has multiplicity at least 4 at p(x): this is because the restriction of p to a local branch of R has a singularity at x (because of the presence of the other branch). So \(p_*R\) must be a Klein decimic. \(\square \)
Remark 5.7
Theorem 5.6 shows that there is a unique \(\mathfrak {A}_5\)-equivariant bijection

that commutes with p. This gives rise to a bijection \(\sigma :F\cong F'\) between the set of fundamental points in P and those in \(P'\). Similarly, \(p'\) will determine an \(\mathfrak {A}_5\)-equivariant bijection  . The composition
. The composition  is a permutation of F that commutes with the \(\mathfrak {A}_5\)-action. Since that \(\mathfrak {A}_5\)-action contains 5-cycles (which have just one fixed point in F), it follows that this permutation must be the identity: the two bijections are each others inverse. It follows that for every
is a permutation of F that commutes with the \(\mathfrak {A}_5\)-action. Since that \(\mathfrak {A}_5\)-action contains 5-cycles (which have just one fixed point in F), it follows that this permutation must be the identity: the two bijections are each others inverse. It follows that for every  , the set \(\{x, \sigma (x)\}\) is a fiber of
, the set \(\{x, \sigma (x)\}\) is a fiber of  .
.
We can now also say a bit more about the special decimics.
Proposition 5.8
The singular set of a Winger decimic consists of 36 ordinary double points, and a local branch at each fundamental point has that node as a hyperflex. The singular points that are not fundamental make up a 30-element orbit.
Proof
For the first assertion, we essentially follow Winger’s argument. The normalization \(q:\widetilde{Y}\rightarrow Y\subset P\) is a rational curve that comes with an automorphism group \(G\cong \mathfrak {A}_5\). The points of \(\widetilde{Y}\) mapping to a flex point or worse make up a divisor D of degree  (if t is an affine coordinate of \(\widetilde{Y}\), and
(if t is an affine coordinate of \(\widetilde{Y}\), and  is a coordinate system for P such that \(q^*z_0\), resp. \(q^*z_i\), is a polynomial of degree \(10-i\), resp. \(\leqslant 10-i\), then D is the defined by the Wronskian determinant \((z_0,z_1,z_2)\) and is viewed as having degree \((10+9+8)-3=24\)). If a point of \(\widetilde{Y}\) maps to cusp or a hyperflex (or worse) then it appears with multiplicity \(\geqslant 2\). We prove that each of the two points of \(\widetilde{Y}\) lying over a fundamental point of P has multiplicity \(\geqslant 2\) in D. This implies that D is \(\geqslant \) twice the 12-element G-orbit in \(\widetilde{Y}\) and hence, in view of its degree, must be equal to this. It will then follow that Y has only nodal singularities and that these will be 36 in number by the genus formula.
is a coordinate system for P such that \(q^*z_0\), resp. \(q^*z_i\), is a polynomial of degree \(10-i\), resp. \(\leqslant 10-i\), then D is the defined by the Wronskian determinant \((z_0,z_1,z_2)\) and is viewed as having degree \((10+9+8)-3=24\)). If a point of \(\widetilde{Y}\) maps to cusp or a hyperflex (or worse) then it appears with multiplicity \(\geqslant 2\). We prove that each of the two points of \(\widetilde{Y}\) lying over a fundamental point of P has multiplicity \(\geqslant 2\) in D. This implies that D is \(\geqslant \) twice the 12-element G-orbit in \(\widetilde{Y}\) and hence, in view of its degree, must be equal to this. It will then follow that Y has only nodal singularities and that these will be 36 in number by the genus formula.
Let us first note that since G has no nontrivial 1-dimensional character, Y admits a G-invariant equation. Let \(x\in P\) be a fundamental point. Let \(U\subset P\) be the affine plane complementary to the polar of x and make it a vector space by choosing x as its origin. Then \(G_x\) acts linearly on U. The stabilizer \(G_x\) is a dihedral group of order 10, and we can choose coordinates \((w_1,w_2)\) such that \((w_1, w_2)\mapsto (w_2,w_1)\) and \((w_1, w_2)\mapsto (\zeta _5w_1,\zeta _5^{-1}w_2)\) define generators of \(G_x\). The algebra of \(G_x\)-invariant polynomials is then generated by \(w_1w_2\) and \(w_1{}^5+w_2{}^5\).
The germ of Y at x admits \(G_x\)-invariant equation and this is given by \(w_1w_2+\text {order}\geqslant 2\). So the tangent lines of the branches of Y at x are the coordinate lines. The subgroup of \(G_x\) generated by \((w_1, w_2)\mapsto (\zeta _5w_1,\zeta _5^{-1}w_2)\) fixes each branch. So the branch whose tangent line is \(w_1=0\) has a local equation of the type
This branch meets \(w_1=0\) at the origin with multiplicity \(\geqslant 4\) and hence has there a hyperflex.
So  is an \(\mathfrak {A}_5\)-invariant 30-element subset of P and it suffices to prove that this is an \(\mathfrak {A}_5\)-orbit. This set does not meet the fundamental conic K (for \(p_*R'\) is transversal to that conic). There are unique \(\mathfrak {A}_5\)-orbits in
is an \(\mathfrak {A}_5\)-invariant 30-element subset of P and it suffices to prove that this is an \(\mathfrak {A}_5\)-orbit. This set does not meet the fundamental conic K (for \(p_*R'\) is transversal to that conic). There are unique \(\mathfrak {A}_5\)-orbits in  of size 6 and 10; the others have size 30 and 60. Hence
of size 6 and 10; the others have size 30 and 60. Hence  is a 30-element orbit in
is a 30-element orbit in  . \(\square \)
. \(\square \)
5.4 Construction of the Klein decimic
We now give a construction of the Klein decimic, which will at the same time show that it will have double cusp singularities at the fundamental points.
Let P be a Klein plane. We first observe that its fundamental set F does not lie on a conic. For if it did, then this conic would be unique, hence \(\mathfrak {A}_5\)-invariant and so its intersection with K would then produce an orbit with \(\leqslant 4\) elements, which we know does not exist. This implies that for each \(x\in F\) there is a conic \(K_x\) which meets F in  .
.
Now blow up F. The result is a cubic surface X for which the strict transform \(\widetilde{K}_x\) of \(K_x\) is a line (an exceptional curve) and these lines are pairwise disjoint(Footnote 3). The set of six exceptional curves arising from the blow-up and the \(\widetilde{K}_x\) form what is called a double six in X. So they can be simultaneously blown down to form a copy \(P^\dagger \) of a projective plane. The naturality of this construction implies that the \(\mathfrak {A}_5\)-symmetry is preserved. In particular, \(P^\dagger \) comes with a nontrivial \(\mathfrak {A}_5\)-action, and so we have defined a fundamental conic  . The image of \(\bigcup _x\widetilde{K}_x\) in \(P^\dagger \) is an \(\mathfrak {A}_5\)-invariant subset of size 6 and so this must be the fundamental set
. The image of \(\bigcup _x\widetilde{K}_x\) in \(P^\dagger \) is an \(\mathfrak {A}_5\)-invariant subset of size 6 and so this must be the fundamental set  . So the diagram \(P\xleftarrow {\scriptscriptstyle \;q\,}X\xrightarrow {\scriptscriptstyle q^\dagger } P^\dagger \) is involutive. The birational map
. So the diagram \(P\xleftarrow {\scriptscriptstyle \;q\,}X\xrightarrow {\scriptscriptstyle q^\dagger } P^\dagger \) is involutive. The birational map
is defined by the linear system \(I_K\) of quintics in P which have a node (or worse) at each fundamental point, so that \(P^\dagger \) gets identified with the projective space dual to \(|I_K|\).
Lemma 5.9
If \(\ell _x\) is the polar line of x, then  and hence \(K_x\) is tangent to K at these two points.
and hence \(K_x\) is tangent to K at these two points.
Proof
The divisor  in K is \(\mathfrak {A}_5\)-invariant and of degree
in K is \(\mathfrak {A}_5\)-invariant and of degree  . Given the \(\mathfrak {A}_5\)-orbit sizes in K (12, 20, 30, 60), this implies that that this divisor is twice the 12-element orbit. Hence \(K_x\) meets K in two distinct points of this orbit and is there tangent to K. Assigning to x the polar of \(K\cap K_x\) then gives us a map from F onto a 6-element orbit of P. This orbit can only be F itself. We thus obtain a permutation of F which commutes with the \(\mathfrak {A}_5\)-action. Since every point of F is characterized by its \(\mathfrak {A}_5\)-stabilizer, this permutation must be the identity. \(\square \)
. Given the \(\mathfrak {A}_5\)-orbit sizes in K (12, 20, 30, 60), this implies that that this divisor is twice the 12-element orbit. Hence \(K_x\) meets K in two distinct points of this orbit and is there tangent to K. Assigning to x the polar of \(K\cap K_x\) then gives us a map from F onto a 6-element orbit of P. This orbit can only be F itself. We thus obtain a permutation of F which commutes with the \(\mathfrak {A}_5\)-action. Since every point of F is characterized by its \(\mathfrak {A}_5\)-stabilizer, this permutation must be the identity. \(\square \)
Corollary 5.10
The Cremona transformation \(q^\dagger q^{-1}:P\dashrightarrow P^\dagger \) takes \(K\subset P\) to a Klein decimic in \(P^\dagger \). This Klein decimic has a double cusp (with local-analytic equation \((x^2-y^3)(x^3-y^2)=0\)) at each fundamental point, and is smooth elsewhere.
Proof
Since q is an isomorphism over K, we can identify K with \(q^{-1}K\). Any singular point of \(q^\dagger q^{-1}K\) will of course be the image of some \(K_x\). Since we can regard \(K_x\) as the projectivized tangent space of the fundamental point in \(P^\dagger \) to which it maps, Lemma 5.9 shows that the image of K at this fundamental point is as asserted: we have two cusps meeting there with different tangent lines. \(\square \)
Note that by the involutive nature of this construction, \(q(q^\dagger )^{-1}\) will take \(K^\dagger \) to the Klein decimic in P.
Remark 5.11
Theorem 5.6 and the preceding corollary imply that the double cusp singularity appears as a discriminant curve of a finite morphism between surface germs of degree 4. Here is a local description for it that also takes into account the \(\mathfrak {D}_5\)-symmetry: there exist a local-analytic coordinate system \((z_1,z_2)\) for S at a singular point of R and a local-analytic coordinate system \((w_1,w_2)\) at its image in P such that
Note that it is indeed of degree 4 at the origin. The ramification locus is defined by  , hence is near the origin given by \( z_1 z_2=0\). The image of the ramification locus at the origin is the double cusp, for the \( z_1\)-axis, parametrized by
, hence is near the origin given by \( z_1 z_2=0\). The image of the ramification locus at the origin is the double cusp, for the \( z_1\)-axis, parametrized by  is the the parametrized cusp
is the the parametrized cusp  and likewise \(z_2\)-axis maps to the parametrized cusp
and likewise \(z_2\)-axis maps to the parametrized cusp  .
.
The \(\mathfrak {A}_5\)-isotropy groups of the two points is a dihedral isotropy group of order 10 and so the map-germ must have this symmetry as well. We can see this being realized here as in fact coming from two linear representations of this group. Let \(\mathfrak {D}_5\) be the dihedral group of order 10, thought of as the semi-direct product of the group \(\mu _5\) of the 5th roots of unity and an order 2 group whose nontrivial element s acts by inversion: \(s\zeta =\zeta ^{-1}s\). Then letting \(\mathfrak {D}_5\) act on the source, resp. target, by
makes the map-germ \(\mathfrak {D}_5\)-equivariant. It can also be verified that the \(\Sigma ^{1,1}\)-multiplicity of this germ is 3, as it must be, in view of the proof of Proposition 4.3.
Remark 5.12
We have seen that the curve of Wiman decimics in P contains both 5K and the \(\mathfrak {A}_5\)-invariant sum of 10 lines. It has as a remarkable counterpart: the pencil of sextics spanned by 3K and the \(\mathfrak {A}_5\)-invariant sum of six lines. This pencil was studied in detail by Winger [26] and is discussed in [8, 9.5.11]. The six lines meet K in the 12-element orbit and this intersection is evidently transversal. It follows that this orbit is the base locus of the Winger pencil (as we will call it) and that all members of the pencil except 3K have a base point as a flex point (with tangent line the fundamental line passing through it). Note that a general member W of the pencil is smooth of genus 10.
Winger shows that this pencil has, besides its two generators, which are evidently singular, two other singular members. Both are irreducible; one of them has as its singular locus a node at each fundamental point (the 6-element orbit of \(\mathfrak {A}_5\)) and the other, which we shall call the Winger sextic, has as its singular locus a node at each point of the 10-element orbit of \(\mathfrak {A}_5\), and each local branch at such a point has this point as a flex point. So their normalizations have genus 4 and 0 respectively. The former turns out be isomorphic to the Bring curve (whose automorphism group is known to be isomorphic to \(\mathfrak {S}_5\)) and the latter will be isomorphic as an \(\mathfrak {A}_5\)-curve to K.
In fact, as an abstract curve with \(\mathfrak {A}_5\)-action, the Winger sextic can be obtained in much the same way as the curve constructed in Lemma 3.9, simply by identifying the antipodal pairs of its 20-element orbit so as to produce a curve with 10 nodes. This plane sextic is also discussed in [9]. With the help of the Plücker formula (e.g., [8, formula 1.50]), it then follows that the dual curve of the Winger sextic is a Klein decimic. (A priori this curve lies in the dual of P, but in the presence of the fundamental conic \(K\subset P\) we can regard it as a curve in P: just assign to each point of the Winger curve the K-polar of its tangent line.)
Other remarkable members of this pencil include the two nonsingular Valentiner sextics with automorphism group isomorphic to \(\mathfrak {A}_6\) (Footnote 4).
6 Passage to \(\mathfrak {S}_5\)-orbit spaces
The goal of this section to characterize the Wiman curve as a curve on \(\overline{\mathscr {M}}_{0,5}\), or rather its \(\mathfrak {S}_5\)-orbit space in \(\mathfrak {S}_5\backslash \overline{\mathscr {M}}_{0,5}\). The latter is simply the moduli space of stable effective divisors of degree 5 on \(\mathbb {P}^1\).
6.1 Conical structure of \(\mathfrak {S}_5 \backslash \overline{\mathscr {M}}_{0,5}\)
We first want to understand how the \(\mathfrak {S}_5\)-stabilizer \(\mathfrak {S}_{5, z}\) of a point \(z\in \overline{\mathscr {M}}_{0,5}\) acts near z. The finite group action on the complex-analytic germ of \(\overline{\mathscr {M}}_{0,5}\) at z can be linearized in the sense that it is complex-analytically equivalent to the action on the tangent space. It then follows from a theorem of Chevalley that the local orbit space at \(\mathfrak {S}_5\backslash \overline{\mathscr {M}}_{0,5}\) is nonsingular at the image of z if and only if \(\mathfrak {S}_{5, z}\) acts on \(T_z\overline{\mathscr {M}}_{0,5}\) as a complex reflection group.
Lemma 6.1
The \(\mathfrak {S}_5\)-stabilizer of any point not in \(\Delta \) is a Coxeter group (and hence a complex reflection group) so that \(\mathfrak {S}_5\backslash \overline{\mathscr {M}}_{0,5}\) is nonsingular away from the point \(\delta \) that represents the orbit \(\Delta \).
Proof
If z is represented in the Hilbert–Mumford model by \((x_1,\dots , x_5)\in (\mathbb {P}^1)^5\), then the tangent space \(T_z\overline{\mathscr {M}}_{0,5}\) fits naturally in a short exact sequence:

where  is the space of vector fields on \(\mathbb {P}^1\) (which in terms of an affine coordinate t has basis \({\partial }/{\partial t}, t{\partial }/{\partial t}, t^2{\partial }/{\partial t}\)) and the map is given by evaluation at \(x_1, \dots , x_5\) respectively. With the help of this formula it is fairly straightforward to determine the action of \(\mathfrak {S}_{5, z}\) on \(T_z\overline{\mathscr {M}}_{0,5}\). When \(\mathfrak {S}_{5, z}\) is of order 2, we need to verify that \(\mathfrak {S}_{5, z}\) leaves a line in \(T_z\overline{\mathscr {M}}_{0,5}\) pointwise fixed. This is left to the reader. There are three other cases to consider:
is the space of vector fields on \(\mathbb {P}^1\) (which in terms of an affine coordinate t has basis \({\partial }/{\partial t}, t{\partial }/{\partial t}, t^2{\partial }/{\partial t}\)) and the map is given by evaluation at \(x_1, \dots , x_5\) respectively. With the help of this formula it is fairly straightforward to determine the action of \(\mathfrak {S}_{5, z}\) on \(T_z\overline{\mathscr {M}}_{0,5}\). When \(\mathfrak {S}_{5, z}\) is of order 2, we need to verify that \(\mathfrak {S}_{5, z}\) leaves a line in \(T_z\overline{\mathscr {M}}_{0,5}\) pointwise fixed. This is left to the reader. There are three other cases to consider:
Case 1: \(z=(1, \zeta _3, \zeta _3^2, 0, \infty )\), and \(\mathfrak {S}_{5,z}\cong \mathfrak {S}_3^{\mathrm{ev}}\) is the group generated by \(t\mapsto \zeta _3t\) and the involution \(t\mapsto t^{-1}\) (which gives the exchanges \(\zeta _3\leftrightarrow \zeta _3^2\) and \(0\leftrightarrow \infty \)). The fact that  maps onto the direct sum of tangent spaces at the third root of unity implies that
maps onto the direct sum of tangent spaces at the third root of unity implies that

is an isomorphism. Multiplication by \(\zeta _3\) acts here as \((v_0, v_\infty )\mapsto (\zeta _3v_0, \zeta _3^{-1}v_\infty )\) and inversion exchanges \(v_0\) and \(v_\infty \). We thus find that \(\mathfrak {S}_{5,z}\) acts as the Coxeter group \(A_2\) on \(T_z\overline{\mathscr {M}}_{0,5}\).
Case 2: \(z=(0,0,1,\infty , \infty )\), and \(\mathfrak {S}_{5,z}\cong \mathfrak {D}_8\) acts in the obvious manner. We again find that  is an isomorphism. The group \(\mathfrak {S}_{5,z}\) now acts as the Coxeter group \(B_2\): It consists of the signed permutations of \((v_0, v_\infty )\).
is an isomorphism. The group \(\mathfrak {S}_{5,z}\) now acts as the Coxeter group \(B_2\): It consists of the signed permutations of \((v_0, v_\infty )\).
Case 3: \(z=(1,\zeta _5, \zeta _5^2, \zeta _5^3, \zeta _5^4)\), and \(\mathfrak {S}_{5,z}\cong \mathfrak {D}_{10}\) is generated by \(t\mapsto \zeta _5t\) and the involution \(t\mapsto t^{-1}\) (which gives the exchanges \(\zeta _5^i\leftrightarrow \zeta _5^{-i}\)). For \(i\geqslant -1\) let  be the restriction of the vector field \(t^{i+1}{d}/{dt}\). Then scalar multiplication by \(\zeta _5\) multiplies \(v^{(i)}\) by \(\zeta _5^{-i}\), so that this is a basis of eigenvectors for this action. The vectors
be the restriction of the vector field \(t^{i+1}{d}/{dt}\). Then scalar multiplication by \(\zeta _5\) multiplies \(v^{(i)}\) by \(\zeta _5^{-i}\), so that this is a basis of eigenvectors for this action. The vectors  span the image of
span the image of  , and hence \(v^{(2)}\) and \(v^{(3)}\) span \(T_z\overline{\mathscr {M}}_{0,5}\). Multiplication by \(\zeta _5\) sends
, and hence \(v^{(2)}\) and \(v^{(3)}\) span \(T_z\overline{\mathscr {M}}_{0,5}\). Multiplication by \(\zeta _5\) sends  to
to  and the involution sends it to
and the involution sends it to  . Thus it acts through the Coxeter group \(I_2(5)\). \(\square \)
. Thus it acts through the Coxeter group \(I_2(5)\). \(\square \)
It is clear from Proposition 3.2 that the \(\mathfrak {A}_5\)-orbit space of every smooth member of \(\mathscr {C}\) is a smooth rational curve. This is also true for a singular member, for we have seen that \(\mathfrak {A}_5\) is transitive on its irreducible components and that an irreducible component is rational (a quotient curve of a rational curve is rational). It is clear that \(\mathfrak {S}_5\backslash \overline{\mathscr {M}}_{0,5}\) will inherit this structure. Since the base locus \(\Delta \) is a single \(\mathfrak {A}_5\)-orbit and all members of the Wiman–Edge pencil are nonsingular at \(\Delta \), it then follows that the image of the Wiman–Edge pencil gives \(\mathfrak {A}_5\backslash \overline{\mathscr {M}}_{0,5}\) the structure of a quasi-cone with vertex \(\delta \).
Proposition 6.2
Regard \(\mathbb {P}^2\) as a projective cone with vertex the origin o of the affine part \(\mathbb {C}^2\subset \mathbb {P}^2\). Let \(\mathfrak {C}_6\) be the automorphism group of this cone generated by

Then \(\mathfrak {S}_5\backslash \overline{\mathscr {M}}_{0,5}\) is as a quasi-cone isomorphic to \(\mathfrak {C}_6\backslash \mathbb {P}^2\) (which has an \(A_2\)-singularity at its vertex) and embeds in a projective space by means of the 5-dimensional linear system defined by the degree 6 subspace of  . This embedding is of degree 6 and is such that \(C_0\) maps onto a line; any other member of \(\mathscr {C}\) maps onto a conic.
. This embedding is of degree 6 and is such that \(C_0\) maps onto a line; any other member of \(\mathscr {C}\) maps onto a conic.
Proof
The type of this cone can be determined by a local study at a point of \(\Delta \) in the way we did this in the proof of Lemma 6.1. One such point is represented in the Hilbert–Mumford model by  . The \(\mathfrak {S}_5\)-stabilizer of z is cyclic of order 6 with a generator \(\sigma \) with
. The \(\mathfrak {S}_5\)-stabilizer of z is cyclic of order 6 with a generator \(\sigma \) with
and the tangent space \(T_z\overline{\mathscr {M}}_{0,5}\) is identified with  . If we identify \(T_0\mathbb {P}^1\) with \(\mathbb {C}\) by taking the coefficient of \({\partial }/{\partial t}\vert _{t=0}\), then we see that \(\sigma \) acts as
. If we identify \(T_0\mathbb {P}^1\) with \(\mathbb {C}\) by taking the coefficient of \({\partial }/{\partial t}\vert _{t=0}\), then we see that \(\sigma \) acts as  . So if we pass to
. So if we pass to  , then
, then  . An affine neighborhood of the vertex of the cone \(\mathfrak {S}_5\backslash \overline{\mathscr {M}}_{0,5}\) is the quotient of \(\mathbb {C}^2\) by the automorphism group generated by \(\sigma \).
. An affine neighborhood of the vertex of the cone \(\mathfrak {S}_5\backslash \overline{\mathscr {M}}_{0,5}\) is the quotient of \(\mathbb {C}^2\) by the automorphism group generated by \(\sigma \).
The diagonal form of \(\sigma \) shows that it leaves invariant only two lines through the origin: the \(u_2\)-axis defined by \(u_1=0\), on which it acts faithfully with order 6, and the \(u_1\)-axis defined by \(u_2=0\) on which it acts with order 3. Since \(C_0\) and \(C_\infty \) are the only members of \(\mathscr {C}\) that are \(\mathfrak {S}_5\)-invariant, these axes must define their germs at z. The \(\mathfrak {S}_5\)-stabilizer of z (which we have identified with \(\mathfrak {C}_6\)) acts on the germ of \(C_\infty \) at 0 through a subgroup of \(\mathfrak {S}_3\) (for it preserves a line on the quintic del Pezzo surface) and so \(\mathfrak {C}_6\) cannot act faithfully on it. It follows that \(C_0\) is defined by \(u_1=0\).
Since \(\sigma ^3\) sends \((u_1,u_2)\) to  , its algebra of invariants is
, its algebra of invariants is  . Now \(\sigma \) sends \((u_1, u_2^2)\) to \((\zeta _3 u_1, \zeta _3^{-1}u_2^2)\), so that its orbit space produces a Kleinian singularity of type \(A_2\). Following Klein, its algebra of invariants is generated by \(u_1^3, u_1u_2^2, u_2^6\). So the degree 6 part of
. Now \(\sigma \) sends \((u_1, u_2^2)\) to \((\zeta _3 u_1, \zeta _3^{-1}u_2^2)\), so that its orbit space produces a Kleinian singularity of type \(A_2\). Following Klein, its algebra of invariants is generated by \(u_1^3, u_1u_2^2, u_2^6\). So the degree 6 part of  has basis \(u_0^6, u_0^3u_1^3, u_0^3u_1u_2^2, u_2^6, u_1^6, u_1^2u_2^4\), \(u_1^4u_2^2\), and this \(\mathfrak {C}_6\backslash \mathbb {P}^2\) in \(\mathbb {P}^5\). Its image is clearly of degree 6. We have seen that the image of \(C_0\) is given by \(u_1=0\) and the above basis restricted to nonzero monomials are \(u_0^6\) and \(u_2^6\) and so its image is a line. If we substitute \(u_2=\lambda u_1\) (with \(\lambda \) fixed), then the monomials in question span \(u_0^6,u_0^3u_1^3, u_1^6\) and so the image of this line is indeed a conic. \(\square \)
has basis \(u_0^6, u_0^3u_1^3, u_0^3u_1u_2^2, u_2^6, u_1^6, u_1^2u_2^4\), \(u_1^4u_2^2\), and this \(\mathfrak {C}_6\backslash \mathbb {P}^2\) in \(\mathbb {P}^5\). Its image is clearly of degree 6. We have seen that the image of \(C_0\) is given by \(u_1=0\) and the above basis restricted to nonzero monomials are \(u_0^6\) and \(u_2^6\) and so its image is a line. If we substitute \(u_2=\lambda u_1\) (with \(\lambda \) fixed), then the monomials in question span \(u_0^6,u_0^3u_1^3, u_1^6\) and so the image of this line is indeed a conic. \(\square \)
Remark 6.3
The conclusion of the previous lemma and proposition agrees with the explicit isomorphism  from Remark 6.6 below. The only singular point of the quotient is the point
from Remark 6.6 below. The only singular point of the quotient is the point  , which is a rational double point of type \(A_2\). The points projecting to the singular point satisfy \(I_4=I_8 = 0\). We know that \(I_4 = 0\) defines the Wiman curve on S and \(I_8 = 0\) defines the union \(C_K+C_K'\). They intersect at 20 base points with the subgroup \(\mathfrak {S}_3^{\mathrm{odd}}\) as the stabilizer subgroup.
, which is a rational double point of type \(A_2\). The points projecting to the singular point satisfy \(I_4=I_8 = 0\). We know that \(I_4 = 0\) defines the Wiman curve on S and \(I_8 = 0\) defines the union \(C_K+C_K'\). They intersect at 20 base points with the subgroup \(\mathfrak {S}_3^{\mathrm{odd}}\) as the stabilizer subgroup.
The weighted projective space  is obtained as the quotient of \(\mathbb {P}^2\) by a cyclic group of order 6 acting on coordinates as
is obtained as the quotient of \(\mathbb {P}^2\) by a cyclic group of order 6 acting on coordinates as

The linear space of \(\mathfrak {C}_3\)-invariant homogeneous polynomials of degree 6 is spanned by six monomials \(x_0^6,x_1^6,x_0^4x_1^2,x_0^2x_1^4,x_2^6,x_0^3x_2^3\). They define a \(\mathfrak {C}_6\)-invariant map \(\mathbb {P}^2\rightarrow \mathbb {P}^5\) which factors through the quotient  . In terms of weighted homogeneous coordinates \(t_0,t_1,t_2\) in
. In terms of weighted homogeneous coordinates \(t_0,t_1,t_2\) in  it is given by monomials of the map \(t_0^6,t_1^3,t_0^4t_1,t_0^2t_1^2,t_2^2,t_0^3t_2\). The restriction of the map to the coordinate line \(t_0 = 0\) is given by the monomials \(t_1^3,t_2^2\). This shows that the image of the Wiman curve under the composition
it is given by monomials of the map \(t_0^6,t_1^3,t_0^4t_1,t_0^2t_1^2,t_2^2,t_0^3t_2\). The restriction of the map to the coordinate line \(t_0 = 0\) is given by the monomials \(t_1^3,t_2^2\). This shows that the image of the Wiman curve under the composition

is a line. One can interpret this map as the map

where V(5) is the space of binary quintic. According to [1], this map can be given explicitly by

where S, T are fundamental invariants of degrees 2 and 3 of binary forms of degree 4 satisfying \(S^3-27T^2\) equal to the discriminant. The reference gives explicit expressions for the coefficients \(B_i\) as polynomials of degree 24 in basic invariants \(I_4,I_8,I_{12}\) of binary quintic forms.
6.2 The cross ratio map
The embedding of \(\mathfrak {S}_5\backslash \overline{\mathscr {M}}_{0,5}\) in projective 5-space that we found in Proposition 6.2 has a modular interpretation, which we now give.
As was mentioned in Sect. 2.1, the conic bundles of S have such an interpretation on \(\overline{\mathscr {M}}_{0,5}\) as forgetful morphisms
(it forgets the ith point). The notation \(\overline{\mathscr {M}}_{0,4}{}^{(i)}\) used here means that we do not renumber the four points and let them be indexed by  ; this helps to make manifest the \(\mathfrak {S}_5\)-action on the product
; this helps to make manifest the \(\mathfrak {S}_5\)-action on the product  for which the morphism
for which the morphism

is \(\mathfrak {S}_5\)-equivariant. The following is well known.
Lemma 6.4
The map  is injective.
is injective.
Proof
On \(\mathscr {M}_{0,5}\) this is clear, since given an ordered 5-element subset \((x_1, \dots , x_5)\) of a smooth rational curve C, there is a unique affine coordinate z on C such that \((z(x_1), z(x_2), z(x_3))=(0, \infty , 1)\), and then \(z(x_i)=f_i(C;x_1,x_2, x_3, x_4)\) for \(i=4,5\). Since this even allows \(x_4=x_5\), we have in fact injectivity away from the zero dimensional strata. A typical zero dimensional stratum is represented in a Hilbert–Mumford stable manner by a 5-term sequence in \(\{1,2,3\}\) with at exactly two repetitions, e.g., (1, 2, 3, 1, 2) and then the value of \(f_i\) on it is computed by removing the ith term and stipulating that of the four remaining two items two that are not repeated are made equal (and are then renumbered in an order preserving manner such that all terms lie in  ). (In our example the value of \(f_1\) is (2, 1, 1, 2), the value of \(f_2,f_3, f_4\) is (1, 2, 1, 2), and the value of \(f_5\) is (1, 2, 2, 1).) Elementary combinatorics shows that f is here injective, too. \(\square \)
). (In our example the value of \(f_1\) is (2, 1, 1, 2), the value of \(f_2,f_3, f_4\) is (1, 2, 1, 2), and the value of \(f_5\) is (1, 2, 2, 1).) Elementary combinatorics shows that f is here injective, too. \(\square \)
Recall that \(\overline{\mathscr {M}}_{0,4}{}^{(i)}\) is naturally a 3-pointed smooth rational curve and that the \(\mathfrak {S}_5\)-stabilizer of the factor \(\overline{\mathscr {M}}_{0,4}{}^{(i)}\), \(\mathfrak {S}_{5,i}\) (the permutation group of  ), acts on \(\overline{\mathscr {M}}_{0,4}{}^{(i)}\) through the full permutation group of these three points. Since \(\mathfrak {S}_{5,i}\backslash \overline{\mathscr {M}}_{0,4}{}^{(i)}\) is independent of any numbering, it is canonically isomorphic to \(\mathfrak {S}_{4}\backslash \overline{\mathscr {M}}_{0,4}\), and hence with \(\mathbb {P}^1\) (such an isomorphism can be given by the j-invariant of the double cover of \(\mathbb {P}^1\) ramifying in a prescribed 4-element subset). So the \(\mathfrak {S}_5\)-orbit space of
), acts on \(\overline{\mathscr {M}}_{0,4}{}^{(i)}\) through the full permutation group of these three points. Since \(\mathfrak {S}_{5,i}\backslash \overline{\mathscr {M}}_{0,4}{}^{(i)}\) is independent of any numbering, it is canonically isomorphic to \(\mathfrak {S}_{4}\backslash \overline{\mathscr {M}}_{0,4}\), and hence with \(\mathbb {P}^1\) (such an isomorphism can be given by the j-invariant of the double cover of \(\mathbb {P}^1\) ramifying in a prescribed 4-element subset). So the \(\mathfrak {S}_5\)-orbit space of  is then identified with
is then identified with  . Since we can regard
. Since we can regard  as the linear system of degree 5 on \(\mathbb {P}^1\), it is a projective space of dimension 5. Let
as the linear system of degree 5 on \(\mathbb {P}^1\), it is a projective space of dimension 5. Let

be obtained from f by passing to the \(\mathfrak {S}_5\)-orbit spaces and denote by

its precomposite with the quotient morphism. It follows from Lemma 6.4 that \(\Phi \) is injective and Proposition 6.2 tells us that \(\mathfrak {S}_5\backslash \overline{\mathscr {M}}_{0,5}\) naturally embeds in a 5-dimensional projective space as a quasi-cone.
Theorem 6.5
The morphism \(\widetilde{\Phi }^*\) takes the hyperplane class of  to
to  , and \(\Phi \) is projectively equivalent to the projective embedding found in Proposition 6.2. In particular, \(\widetilde{\Phi }(C_\infty )\) is a line in
, and \(\Phi \) is projectively equivalent to the projective embedding found in Proposition 6.2. In particular, \(\widetilde{\Phi }(C_\infty )\) is a line in  .
.
Proof
The hyperplane class of  pulled back to \((\mathbb {P}^1)^5\) is the sum of the degree 1 classes coming from the factors. The map
pulled back to \((\mathbb {P}^1)^5\) is the sum of the degree 1 classes coming from the factors. The map
is of degree 6. The sum of the two special conics that appear as fibers of \(f_5:\overline{\mathscr {M}}_{0,5}\rightarrow \overline{\mathscr {M}}_{0,4}\) represent the pull-back of a degree 2 class on \(\overline{\mathscr {M}}_{0,4}\) and so the pull-back of the degree 1 class on \( \mathbb {P}^1\) is 3 times the sum of these two special conics. Hence the hyperplane class pulled back to \(\overline{\mathscr {M}}_{0,5}\) is equal to  . The degree of the image of \(\Phi \) is then computed as
. The degree of the image of \(\Phi \) is then computed as

This is also the degree of the image of \(\mathfrak {S}_5\backslash \overline{\mathscr {M}}_{0,5}\) in  embedded as a quasi-cone. One verifies in straightforward manner that \(\mathfrak {C}_6\backslash \mathbb {P}^2\) is simply-connected and so
embedded as a quasi-cone. One verifies in straightforward manner that \(\mathfrak {C}_6\backslash \mathbb {P}^2\) is simply-connected and so  is infinite cyclic. It follows that the two morphisms must be projectively equivalent. \(\square \)
is infinite cyclic. It follows that the two morphisms must be projectively equivalent. \(\square \)
Remark 6.6
Let V(5) be the space of binary quintic forms. It is classically known (and a fact that can be found in any text book on invariant theory) that the subalgebra of \(\text {SL}_2\)-invariants in the polynomial algebra  is generated by the Clebsch invariants \(I_4, I_8,I_{12},I_{18}\) of degrees indicated in the subscripts (the last invariant is skew, i.e., it is not a
is generated by the Clebsch invariants \(I_4, I_8,I_{12},I_{18}\) of degrees indicated in the subscripts (the last invariant is skew, i.e., it is not a  -invariant). Their explicit form can be found in Salmon’s book [22]. There is one basic relation among these invariants, which is of the form
-invariant). Their explicit form can be found in Salmon’s book [22]. There is one basic relation among these invariants, which is of the form
Since the subspace spanned by elements of degrees 4k is the subalgebra freely generated by the first three invariants, we see that the GIT-quotient  is isomorphic to the weighted projective plane
is isomorphic to the weighted projective plane  . So in view of the discussion above, we obtain
. So in view of the discussion above, we obtain

With the help of exact sequence (4) we can identify \(H^0(S,\omega _S^{-k})^{\mathfrak {S}_5}\) with  . In other words, the zero set (or, more precisely, closed subscheme) of any invariant of degree
. In other words, the zero set (or, more precisely, closed subscheme) of any invariant of degree  pulls back to a curve on S defined by an \(\mathfrak {S}_5\)-invariant section of \(\omega _S^{-k}\). It then makes sense to ask what the curves on S are corresponding to the basic invariants \(I_4,I_8,I_{12},I_{18}\), as these correspond to \(\mathfrak {S}_5\)-invariant sections of
pulls back to a curve on S defined by an \(\mathfrak {S}_5\)-invariant section of \(\omega _S^{-k}\). It then makes sense to ask what the curves on S are corresponding to the basic invariants \(I_4,I_8,I_{12},I_{18}\), as these correspond to \(\mathfrak {S}_5\)-invariant sections of  respectively. We see for example right away that \(I_4\) corresponds to our Wiman curve.
respectively. We see for example right away that \(I_4\) corresponds to our Wiman curve.
The discriminant \(\Delta \) of a binary quintic is a polynomial in coefficients of degree 8, and as such it must be a linear combination of \(I_4^2\) and \(I_8\). In fact, it is known that  . It is also a square of an element
. It is also a square of an element  and so D must correspond to the curve \(C_\infty \). It is clear that any \(\text {SL}_2\)-invariant in
and so D must correspond to the curve \(C_\infty \). It is clear that any \(\text {SL}_2\)-invariant in  is a linear combination of \(\Delta =D^2\) and \(I_4^2\), in other words, has the form \((aD+bI_4)(aD-bI_4)\) for some \((a, b)\not =(0,0)\). So this defines on S a reducible \(\mathfrak {S}_5\)-invariant divisor which is the sum of two \(\mathfrak {A}_5\)-invariant divisors. In other words, it represents the union of two \(\mathfrak {S}_5\)-conjugate members of the Wiman–Edge pencil.
is a linear combination of \(\Delta =D^2\) and \(I_4^2\), in other words, has the form \((aD+bI_4)(aD-bI_4)\) for some \((a, b)\not =(0,0)\). So this defines on S a reducible \(\mathfrak {S}_5\)-invariant divisor which is the sum of two \(\mathfrak {A}_5\)-invariant divisors. In other words, it represents the union of two \(\mathfrak {S}_5\)-conjugate members of the Wiman–Edge pencil.
The invariant \(I_{18}\), being the, up to proportionality unique, invariant of degree 18 must represent a unique curve on S defined by an \(\mathfrak {S}_5\)-invariant section of \(\omega _S^{-9}\). According to Clebsch [6, p. 298], the invariant \(I_{18}\) vanishes on a binary form when its four zeros are invariant with respect to an involution of \(\mathbb {P}^1\) and the remaining zero is a fixed point of this involution. This is precisely the locus parametrized by  and according to Remark 3.14 indeed defined by a section of \(\omega _S^{-9}\).
and according to Remark 3.14 indeed defined by a section of \(\omega _S^{-9}\).
Notes
Edge calls them Hesse duads for the following reason. It follows from observing the Petersen graph the stabilizer subgroup of each line acts on the line by permuting three intersection points with other lines. If one considers these points as the zero set of a binary form \(\phi \) of degree 3, then its Hessian binary form of degree 2 given as the determinant of the matrix of second partial derivatives of \(\phi \) has zeros at two points, the Hessian duad.
We follow the now standard ATLAS notation for finite groups.
This surface is isomorphic to the Clebsch diagonal cubic surface in \(\mathbb {P}^4\) defined by
 ,
,  ; the evident \(\mathfrak {S}_5\)-symmetry accounts for its full automorphism group and its isomorphism type is characterized by that property. The intersection of this cubic surface with the quadric defined by
; the evident \(\mathfrak {S}_5\)-symmetry accounts for its full automorphism group and its isomorphism type is characterized by that property. The intersection of this cubic surface with the quadric defined by  is the Bring curve mentioned in Remark 5.12; its automorphism group is also \(\mathfrak {S}_5\).
is the Bring curve mentioned in Remark 5.12; its automorphism group is also \(\mathfrak {S}_5\).The first author uses the opportunity to correct the statement in [8, Remark 9.5.11] where the Valentiner curve was incorrectly identified with the Wiman sextic.
References
Abdesselam, A.: A computational solution to a question by Beauville on the invariants of the binary quintic. J. Algebra 303(2), 771–788 (2006)
Arbarello, E., Cornalba, M., Griffiths, P.A., Harris, J.: Geometry of Algebraic Curves. Vol. I. Grundlehren der Mathematischen Wissenschaften, vol. 267. Springer, New York (1985)
Candelas, Ph., de la Ossa, X., van Geemen, B., van Straten, D.: Lines on the Dwork pencil of quintic threefolds. Adv. Theor. Math. Phys. 16(6), 1779–1836 (2012)
Cheltsov, I., Shramov, C.: Cremona Groups and the Icosahedron. Monographs and Research Notes in Mathematics. CRC Press, Boca Raton (2016)
Cheltsov, I., Kuznetsov, A., Shramov, C.: Coble fourfold, \(S_6\)-invariant quartic threefolds, and Wiman–Edge Sextics (2017). arXiv:1712.08906
Clebsch, A.: Ueber die Anwendung der quadratischen Substitution auf die Gleichungen fünften Grades und die geometrische Theorie des ebenen Fünfecks. Math. Ann. 4(2), 284–345 (1871)
Coble, A.B.: An application of the form-problems associated with certain Cremona groups to the solution of equations of higher degree. Trans. Amer. Math. Soc. 9(4), 396–424 (1908)
Dolgachev, I.V.: Classical Algebraic Geometry. Cambridge University Press, Cambridge (2012)
Dolgachev, I.V.: Quartic surfaces with icosahedral symmetry. Adv. Geom. 18(1), 119–132 (2018). arXiv:1604.02567
Edge, W.L.: A pencil of four-nodal plane sextics. Proc. Cambridge Philos. Soc. 89(3), 413–421 (1981)
Edge, W.L.: A pencil of specialized canonical curves. Proc. Cambridge Philos. Soc. 90(2), 239–249 (1981)
Farb, B., Looijenga, E.: Geometry of the Wiman–Edge pencil, II: hyperbolic, conformal and modular aspects (in preparation)
Fulton, W., Harris, J.: Representation Theory. Graduate Texts in Mathematics, vol. 129. Readings in Mathematics. Springer, New York (1991)
González-Aguilera, V., Rodríguez, R.E.: A pencil in \(\widetilde{\mathfrak{M}}_6\) with three points at the boundary. Geom. Dedic. 42(3), 255–265 (1992)
Griffiths, Ph., Harris, J.: Principles of Algebraic Geometry. Wiley, New York (1994)
Inoue, N., Kato, F.: On the geometry of Wiman’s sextic. J. Math. Kyoto Univ. 45(4), 743–757 (2005)
Kapranov, M.M.: Chow Quotients of Grassmannians. I. In: Gel’fand, S., Gindikin, S. (eds.) I.M. Gel’fand Seminar. Advances in Soviet Mathematics, vol. 16.2, pp. 29–110. American Mathematical Society, Providence (1993)
Klein, F.: Vorlesungen über das Ikosaeder und die Auflösung der Gleichungen vom fünften Grade. Reprint of the 1884 original. Edited, with an introduction and commentary by Peter Slodowy. Birkhäuser, Basel (1993)
Mukai, S.: Curves and Grassmannians. In: Yang, J.-H., Namikawa, Y., Uneo, K. (eds.) Algebraic Geometry and Related Topics. Conference Proceedings and Lecture Notes in Algebraic Geometry, vol. 1, pp. 19–40. International Press, Cambridge (1993)
Rauschning, J., Slodowy, P.: An aspect of icosahedral symmetry. Canadian Math. Bull. 45(4), 686–696 (2002)
Rimányi, R.: Thom polynomials, symmetries and incidences of singularities. Invent. Math. 143(3), 499–521 (2001)
Salmon, G.: Lessons Introductory to the Modern Higher Algebra. Hodges, Foster and Co., Dublin (1876) (5th edn. reprinted by Chelsea, New York (1986))
Shepherd-Barron, N.I.: Invariant theory for \(S_5\) and the rationality of \({M}_6\). Compositio Math. 70(1), 13–25 (1989)
Wiman, A.: Ueber die algebraischen Curven von den Geschlechtern \(p=4,5\) and \(6\) welche eindeutige Transformationen in sich besitzen. Bihang till Kongl. Svenska Vetenskapsakad. Handlingar 21(3), 2–41 (1895)
Wiman, A.: Zur Theorie der endlichen Gruppen von birationalen Transformationen in der Ebene. Math. Ann. 48(1–2), 195–240 (1896)
Winger, R.M.: On the invariants of the ternary icosahedral group. Math. Ann. 93(1), 210–216 (1925)
Zagier, D.: Lines on the Dwork quintic pencil and its higher degree analogues. J. Differential Geom. 97(1), 177–189 (2014)
Acknowledgements
We thank Shigeru Mukai for helpful information regarding genus 6 curves.
Author information
Authors and Affiliations
Corresponding author
Additional information
In memory of William L. Edge
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Dolgachev, I., Farb, B. & Looijenga, E. Geometry of the Wiman–Edge pencil, I: algebro-geometric aspects. European Journal of Mathematics 4, 879–930 (2018). https://doi.org/10.1007/s40879-018-0231-3
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40879-018-0231-3





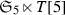 which extends the T[5]-action and is compatible with the
which extends the T[5]-action and is compatible with the 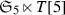 -equivariant lift of
-equivariant lift of  of lines on the Dwork pencil.
of lines on the Dwork pencil.
 :
: :
: when z is generic. An orbit of this type has size 60 and decomposes into two
when z is generic. An orbit of this type has size 60 and decomposes into two  :
: (take
(take 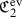 (let
(let  equal to
equal to  and
and  .
.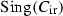 and
and  .
. ,
, 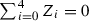 ; the evident
; the evident  is the Bring curve mentioned in Remark
is the Bring curve mentioned in Remark