Skip to main content

Advertisement

SpringerLink
Log in

Two-Step Inversion of Geoacoustic Parameters with Bottom Reverberation and Transmission Loss in the Deep Ocean

  • Published:
Acoustics Australia Aims and scope Submit manuscript

Abstract

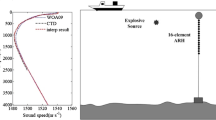
The parameters of deep ocean sediments are relevant for accurately predicting the sound field; however, it is difficult to measure the parameters in situ. Most inversion methods used in shallow water are inapplicable in the deep ocean because of the considerable differences in propagation characteristics. At present, no method for simultaneously obtaining sound speed, density, and attenuation that considers the sensitivity of sediment parameters is yet available. This study proposes a two-step inversion of geoacoustic parameters in the deep ocean. On the basis of the half-space model, the decline tendency of bottom reverberation level with travel time is used for the inversion of sound speed and density, whereas transmission loss is used for inversion of attenuation. Inversion results can be practical for acoustic applications when this method is used. Experimental data from the South China Sea in the summer of 2014 are processed during the inversion process. The sediment parameters obtained from the inversion process are close to the laboratory-measured sampling values and may be used to predict the sound field in various applications, such as in transmission loss in the deep ocean.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13

Similar content being viewed by others

References

  1. Prior, M.K., Harrison, C.H.: Estimation of seabed reflection loss properties from direct blast pulse shape. J. Acoust. Soc. Am. 116(3), 1341–1344 (2004)

    Article  Google Scholar 

  2. Yang, K., Ma, Y.: A geoacoustic inversion method based on bottom reflection signals. Acta Phys. Sin. 58(3), 1798–1805 (2009)

    Google Scholar 

  3. Guo, X., Yang, K., Ma, Y., Yang, Q.: Geoacoustic inversion based on modal dispersion curve for range-dependent environment. Chin. Phys. Lett. 32(12), 74–77 (2015)

    Article  Google Scholar 

  4. Guo, X., Yang, K., Ma, Y.: A far distance wideband geoacoustic parameter inversion method based on a modal dispersion curve. Acta Phys. Sin. 64(17), 174302-1–174302-9 (2015)

    Google Scholar 

  5. Gerstoft, P., Ellis, D.D.: Application of multifrequency inversion methods to obtain seabed properties from broadband reverberation data. J. Acoust. Soc. Am. 100(4), 2665–2665 (1996)

    Article  Google Scholar 

  6. Zhou, J., Guan, D., Shang, E., Luo, E.: Long-range reverberation and bottom scattering strength in shallow water. Chin. J. Acoust. 6(1), 151–153 (1982)

    Google Scholar 

  7. Yang, K., Ma, Y., Sun, C., Miller, J.H., Potty, G.R.: Multistep matched-field inversion for broad-band data from ASIAEX2001. IEEE J. Ocean. Eng. 29(4), 964–972 (2005)

    Article  Google Scholar 

  8. Yang, K., Chapman, N.R., Ma, Y.: Estimating parameter uncertainties in matched field inversion by a neighborhood approximation algorithm. J. Acoust. Soc. Am. 121(2), 833–843 (2007)

    Article  Google Scholar 

  9. Chapman, N.R.: Modeling ocean-bottom reflection loss measurements with the plane-wave reflection coefficient. J. Acoust. Soc. Am. 73(5), 1601–1607 (1983)

    Article  Google Scholar 

  10. Dong, H., Chapman, N.R., Hannay, D.E., Dosso, S.E.: Estimation of seismic velocities of upper oceanic crust from ocean bottom reflection loss data. J. Acoust. Soc. Am. 127(4), 2182–2192 (2010)

    Article  Google Scholar 

  11. Yang, K., Xiao, P., Duan, R., Ma, Y.: Bayesian inversion for geoacoustic parameters from ocean bottom reflection loss. J. Comput. Acoust. 25(3), 1750019-1–1750019-17 (2017)

    MathSciNet  Google Scholar 

  12. Shuanglin, W., Li, Z., Qin, J.: Geoacoustic inversion for bottom parameters in the deep-water area of the South China Sea. Chin. Phys. Lett. 32(12), 70–73 (2015)

    Google Scholar 

  13. Guo, X., Yang, K., Ma, Y.: Geoacoustic inversion for bottom parameters via Bayesian theory in deep ocean. Chin. Phys. Lett. 34(03), 68–72 (2017)

    Google Scholar 

  14. Ellis, D.D., Crowe, D.V.: Bistatic reverberation calculations using a three-dimensional scattering function. J. Acoust. Soc. Am. 89(5), 2207–2214 (1991)

    Article  Google Scholar 

  15. Jackson, D.R., Winebrenner, D.P., Ishimaru, A.: Application of the composite roughness model to high-frequency bottom backscattering. J. Acoust. Soc. Am. 79(5), 1410–1422 (1986)

    Article  Google Scholar 

  16. Jackson, D.R., Briggs, K.B.: High-frequency bottom backscattering: roughness versus sediment volume scattering. J. Acoust. Soc. Am. 92(92), 962–977 (1992)

    Article  Google Scholar 

  17. Williams, K.L., Jackson, D.R.: Bistatic bottom scattering: model, experiments, and model/data comparison. J. Acoust. Soc. Am. 103(1), 169–181 (1997)

    Article  Google Scholar 

  18. Porter, M.B.: The Bellhop Manual and User’s Guide: Preliminary Draft, pp. 17–20. Heat, Light, and Sound Research, Inc, LaJolla (2011)

    Google Scholar 

  19. Argyris, J.H., Scharpf, D.W.: Finite elements in time and space. Nucl. Eng. Des. 10(4), 456–464 (1969)

    Article  Google Scholar 

  20. Harrsion, C.H.: Fast bistatic signal-to-reverberation-ratio calculation. J. Comput. Acoust. 13(02), 317–340 (2008)

    Article  MathSciNet  Google Scholar 

  21. Locarnini, R.A., Mishonov, A.V., Antonov, J.I., Boyer, T.P., Garcia, H.E., Baranova, O.K., Zweng, M.M., Johnson, D.R.: World Ocean Altas 2009 Volume 1: Temperature. U.S. Government Printing Office, Washington DC (2009)

    Google Scholar 

  22. Antonov, J.I., Seidov, D., Boyer, T.P., Locarnini, R.A., Mishonov, A.V., Garcia, H.E.: World Ocean Altas 2009 Volume 1: Salinity. U.S. Government Printing Office, Washington DC (2009)

    Google Scholar 

  23. Zhang, X., Cheng, C., Liu, Y.: Acoustic propagation effect caused by subtropical mode water of northwestern Pacific. Acta Oceanol. Sin. 36(9), 94–102 (2014)

    Google Scholar 

  24. Hamilton, E.L., Bachman, R.T.: Sound velocity and related properties of marine sediments. J. Acoust. Soc. Am. 72(6), 1891–1904 (1982)

    Article  Google Scholar 

  25. Holland, J.H.: Adaptation in natural and artificial systems: an introductory analysis with applications to biology, control, and artificial intelligence. Q. Rev. Biol. 6(2), 126–137 (1992)

    Google Scholar 

  26. Kennedy, J., Eberhart, R.: Particle swarm optimization. IEEE Int. Conf. Neural Netw. 4(8), 1942–1948 (1995)

    Google Scholar 

  27. Langdon, W.B., Poli, R.: Evolving problems to learn about particle swarm optimizers and other search algorithms. IEEE Trans. Evol. Comput. 11(5), 561–578 (2007)

    Article  Google Scholar 

  28. Ling, S.H., Iu, H.H.C., Leung, F.H.F., Chan, K.Y.: Improved hybrid particle swarm optimized wavelet neural network for modeling the development of fluid dispensing for electronic packaging. IEEE Trans. Industr. Electron. 55(9), 3447–3460 (2008)

    Article  Google Scholar 

  29. Hamilton, E.L.: Variations of density and porosity with depth in deep-sea sediments. J. Sediment. Res. 46(2), 280–300 (1976)

    Google Scholar 

Download references

Acknowledgements

We thank all the researchers and staff for their help in the research program of the South China Sea in summer 2014. We also appreciate the reviewer for the comments and suggestions, which are highly insightful and very helpful for improving this manuscript.

Author information

Authors and Affiliations

  1. School of Marine Science and Technology, Northwestern Polytechnical University, Xi’an, 710072, Shaanxi, China

    Kunde Yang, Liya Xu & Qiulong Yang

  2. Key Laboratory of Ocean Acoustics and Sensing (Northwestern Polytechnical University), Ministry of Industry and Information Technology, Xi’an, 710072, Shaanxi, China

    Kunde Yang, Liya Xu & Qiulong Yang

  3. CAS Key Laboratory of Ocean and Marginal Sea Geology, South China Sea Institute of Oceanology, Guangzhou, 510301, Guangdong, China

    Ganxian Li

Authors
  1. Kunde Yang
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Liya Xu
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Qiulong Yang
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Ganxian Li
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Kunde Yang.

Additional information

Project supported by the National Natural Science Foundation of China (Grant No. 41476028).

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Yang, K., Xu, L., Yang, Q. et al. Two-Step Inversion of Geoacoustic Parameters with Bottom Reverberation and Transmission Loss in the Deep Ocean. Acoust Aust 46, 131–142 (2018). https://doi.org/10.1007/s40857-018-0130-2

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s40857-018-0130-2

Keywords

PACS Nos

Search

Navigation