Abstract
We prove the global non-linear stability, without symmetry assumptions, of slowly rotating charged black holes in de Sitter spacetimes in the context of the initial value problem for the Einstein–Maxwell equations: if one perturbs the initial data of a slowly rotating Kerr–Newman–de Sitter (KNdS) black hole, then in a neighborhood of the exterior region of the black hole, the metric and the electromagnetic field decay exponentially fast to their values for a possibly different member of the KNdS family. This is a continuation of recent work of the author with Vasy on the stability of the Kerr–de Sitter family for the Einstein vacuum equations. Our non-linear iteration scheme automatically finds the final black hole parameters as well as the gauge in which the global solution exists; we work in a generalized wave coordinate/Lorenz gauge, with gauge source functions lying in a suitable finite-dimensional space. We include a self-contained proof of the linear mode stability of Reissner–Nordström–de Sitter black holes, building on work by Kodama–Ishibashi. In the course of our non-linear stability argument, we also obtain the first proof of the linear (mode) stability of slowly rotating KNdS black holes using robust perturbative techniques.








We’re sorry, something doesn't seem to be working properly.
Please try refreshing the page. If that doesn't work, please contact support so we can address the problem.
Notes
This is the setting for the non-linear stability of the static model of de Sitter space, both for the Einstein vacuum equations, see [61, “Appendix C”], and for the Einstein–Maxwell system.
In any case, this is not the right equation to consider for charged black holes, as it ignores the coupling of the electromagnetic field and the metric tensor.
This can be deduced from [58, Theorem 1] applied to the equation \((\delta _g d+d\delta _g)A=0\).
In fact, for \(\gamma _3>0\) small, one can check that \(\Theta =0\). However—and this is crucial for Einstein–Maxwell—even a finite-dimensional family \(\Theta \) of gauge modifications would cause no problems.
The point is that this expression does not involve first derivatives of g, which has the advantage of making the gauge-fixed Einstein–Maxwell system principally scalar without having to assign different regularities to g and A.
Here, \(N^*(\Gamma \cap \{\sigma =1\})\) is the quotient \(\mathcal I/\mathcal I^2\), where \(\mathcal I\) is the space of \({\mathcal C}^\infty \) functions on \(\{\tau _s=0,\ \sigma =1\}\) vanishing on \(\Gamma \).
The results in [61] are stated for slowly rotating KdS spacetimes, but extend immediately to slowly rotating KNdS spacetimes as well.
See “Appendix A” for the definition of Sobolev spaces \({\bar{H}}^s\) of extendible distributions.
In the notation of [72], we discuss the case \(n=2\), \(\kappa ^2=2\) (see [72, equation (2\(\cdot \)12)]), \(q=Q\), \(\lambda =\Lambda /3\) (see [72, equation (2\(\cdot \)14)]), so \(E_0=Q/r^2\) (see [72, equation (2\(\cdot \)9)]), and there are a number of sign changes due to the different sign convention adopted here.
The O(3)-invariance, as opposed to merely SO(3)-invariance, rules out operators related to the orientation of \(\mathbb {S}^2\) such as
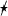 .
.These three calculations provide us with a complete orthogonal basis of \(L^2(\mathbb {S}^2;S^2T^*\mathbb {S}^2)\) and thus with the spectrum of
 acting on symmetric 2-tensors.
acting on symmetric 2-tensors.In these expressions, the operators \(\widehat{\delta }{}^*\), \(\iota _\rho \equiv \iota _{\rho ^{\widehat{\sharp }}}\) and \(\iota _\mathbf {X}\equiv \iota _{\mathbf {X}^{\widehat{\sharp }}}\), with \(\widehat{\sharp }\) indicating that one uses \({\widehat{g}}\) to compute the musical isomorphisms, the metric \({\widehat{g}}\) is fixed, i.e. these operators are not subject to the modifications by \((\updelta \dot{g},\updelta \dot{A})\); thus, for instance, \(\updelta (\widehat{\delta }{}^*\mathbf {X})=\widehat{\delta }{}^*(\updelta \mathbf {X})\).
By (5.16), this is the aspherical part of the tensor \(2 G_g\mathscr {L}_1(\dot{g},\dot{A})\), which is the sum of the linearized Einstein tensor and the contribution from the linearized stress-energy-momentum tensor.
There is a consistency condition for such a system to be well-posed. Indeed, differentiating the constraint, we find the necessary pointwise condition \((\gamma '+T^t\gamma )(v_0)-h'=0\) for all \(v_0\in \mathbb {R}^3\) with \(\gamma (v_0)=h\), which is equivalent to \(\gamma '+T^t\gamma =\alpha \gamma \) for a scalar \(\alpha \) satisfying \(\alpha h=h'\).
Another motivation for choosing the coefficients of X and Y equal is the requirement that the master variables we will describe below be regular at the event and cosmological horizons; see the discussion around equation (5.61).
The necessary symbolic calculations are quite lengthy and were performed using mathematica.
In [72, equation (C\(\cdot \)9b)], the factor r on the right hand side is extraneous.
Without further calculations, this almost follows directly from (5.57): if \((X,Y,\mathcal A)\) are arbitrary, i.e. not necessarily solutions of the linearized Einstein–Maxwell system, then the equation (5.57) is equal to some linear combination (with coefficients meromorphic in \(\sigma \)) of the components of the linearized Einstein–Maxwell system and their derivatives; thus, if the coefficients of this linear combination are regular at \(\sigma =0\), then we can indeed conclude that for a stationary perturbation \((X,Y,\mathcal A)\), the master variables \(\Psi _\pm ^0\) solve (5.69) in their domain of definition.
At frequencies \(\sigma \ne 0\), this is again automatic, as \(\Phi \) and \(\mathcal A\) are linear combinations of \(\Psi _\pm \) by the definition of the latter, and then X and Y can be recovered from \(\Phi \), \(\mathcal A\) and their derivatives by means of (5.50).
A simple calculation verifies that these quantities indeed solve (5.88).
There is an inconsequential typo in the matrix multiplying \(\gamma _2''\) in [61]; the matrix given here is the correct one.
References
Andersson, L., Blue, P.: Hidden symmetries and decay for the wave equation on the Kerr spacetime. Ann. Math. 182, 787–853 (2015)
Andersson, L., Blue, P.: Uniform energy bound and asymptotics for the Maxwell field on a slowly rotating Kerr black hole exterior. J. Hyperbolic Differ. Equ. 12(04), 689–743 (2015)
Lars A., Ma, S. Paganini, C., Whiting, B.F.: Mode stability on the real axis. Preprint arXiv:1607.02759 (2016)
Anderson, M.T.: Existence and stability of even-dimensional asymptotically de Sitter spaces. Ann. Henri Poincaré 6(5), 801–820 (2005)
Aretakis, S.: Stability and Instability of Extreme Reissner–Nordström Black Hole Spacetimes for Linear Scalar Perturbations I. Commun. Math. Phys. 307(1), 17–63 (2011)
Aretakis, S.: Stability and Instability of Extreme Reissner–Nordström black hole spacetimes for linear scalar perturbations II. Ann. Henri Poincaré 12(8), 1491–1538 (2011)
Baskin, D.: A parametrix for the fundamental solution of the Klein–Gordon equation on asymptotically de Sitter spaces. J. Funct. Anal. 259(7), 1673–1719 (2010)
Baskin, D.: Strichartz estimates on asymptotically de Sitter spaces. Ann. Henri Poincaré 14(2), 221–252 (2013)
Beig, R., Chruściel, P.T., Schoen, R.: KIDs are non-generic. In: Annales Henri Poincaré, vol. 6, pp. 155–194. Springer (2005)
Bony, J.-F., Häfner, D.: Decay and non-decay of the local energy for the wave equation on the de Sitter–Schwarzschild metric. Commun. Math. Phys. 282(3), 697–719 (2008)
Bartnik, R., Isenberg, J.: The Constraint Equations. In: The Einstein Equations and the Large Scale Behavior of Gravitational Fields: 50 Years of the Cauchy Problem in General Relativity, pp. 1–38. Birkhäuser Basel, Basel (2004)
Blue, P.: Decay of the Maxwell field on the Schwarzschild manifold. J. Hyperbolic Differ. Equ. 5(4), 807–856 (2008)
Bott, R., Tu, L.W.: Differential Forms in Algebraic Topology, vol. 82. Springer, Berlin (2013)
Baskin, D., Vasy, A., Wunsch, J.: Asymptotics of radiation fields in asymptotically Minkowski space. Am. J. Math. 137(5), 1293–1364 (2015)
Baskin, D., Vasy, A., Wunsch, J.: Asymptotics of scalar waves on long-range asymptotically Minkowski spaces. Preprint arXiv:1602.04795 (2016)
Bieri, L., Zipser, N.: Extensions of the Stability Theorem of the Minkowski Space in General Relativity, vol. 45. American Mathematical Society, Providence (2009)
Carter, B.: Hamilton–Jacobi and Schrödinger separable solutions of Einstein’s equations. Commun. Math. Phys. 10(4), 280–310 (1968)
Choquet-Bruhat, Y.: Théorème d’existence pour certains systèmes d’équations aux dérivées partielles non linéaires. Acta Mathematica 88(1), 141–225 (1952)
Choquet-Bruhat, Y.: General Relativity and the Einstein Equations. Oxford University Press, Oxford (2009)
Choquet-Bruhat, Y., Geroch, R.: Global aspects of the Cauchy problem in general relativity. Commun. Math. Phys. 14(4), 329–335 (1969)
Costa, J.L., Girão, P.M., Natário, J., Silva, J.D.: On the global uniqueness for the Einstein–Maxwell-scalar field system with a cosmological constant: I. Well posedness and breakdown criterion. Class. Quantum Gravity 32(1), 015017, 33 (2015)
Costa, J.L., Girão, P.M., Natário, J., Silva, J.D.: On the global uniqueness for the Einstein–Maxwell-scalar field system with a cosmological constant. Part 2. Structure of the solutions and stability of the Cauchy horizon. Commun. Math. Phys. 339(3), 903–947 (2015)
Costa, J.L., Girão, P.M., Natário, J., Silva, J.D.: On the global uniqueness for the Einstein–Maxwell-scalar field system with a cosmological constant: part 3. Mass inflation and extendibility of the solutions. Ann. PDE 3(1), 8 (2017)
Chandrasekhar, S.: The Mathematical Theory of Black Holes. Oxford classic texts in the physical sciences. Oxford University Press, Oxford (2002)
Civin, D.: Quantitative mode stability for the wave equation on the Kerr–Newman spacetime. Preprint arXiv:1405.3620 (2014)
Civin, D.: Stability of charged rotating black holes for linear scalar perturbations. PhD thesis, University of Cambridge (2015)
Christodoulou, D., Klainerman, S.: The Global Nonlinear Stability of the Minkowski Space. Princeton mathematical series, vol. 41. Princeton University Press, Princeton (1993)
Dafermos, M.: Stability and instability of the Cauchy horizon for the spherically symmetric Einstein–Maxwell–scalar field equations. Ann. of Math. (2) 158(3), 875–928 (2003)
DeTurck, D.M.: Existence of metrics with prescribed Ricci curvature: local theory. Invent. Math. 65(1):179–207 (1981/82)
Dias, Ó.J.C., Godazgar, M., Santos, J.E.: Linear mode stability of the Kerr–Newman black hole and its quasinormal modes. Phys. Rev. Lett. 114(15), 151101 (2015)
Dafermos, M., Holzegel, G., Rodnianski, I.: A scattering theory construction of dynamical vacuum black holes. Preprint arXiv:1306.5364 (2013)
Dafermos, M., Holzegel, G., Rodnianski, I.: The linear stability of the Schwarzschild solution to gravitational perturbations. Preprint arXiv:1601.06467 (2016)
Dafermos, M., Luk, J.: The interior of dynamical vacuum black holes I: The \({C}^0\)-stability of the Kerr Cauchy horizon. Preprint arXiv:1710.01722 (2017)
Dafermos, M., Rodnianski, I.: A proof of Price’s law for the collapse of a self-gravitating scalar field. Inventiones Mathematicae 162(2), 381–457 (2005)
Dafermos, M., Rodnianski, I.: The wave equation on Schwarzschild–de Sitter spacetimes. Preprint arXiv:0709.2766 (2007)
Dafermos, M., Rodnianski, I.: Lectures on black holes and linear waves. Evol. Equ. Clay Math. Proc. 17, 97–205 (2008)
Dafermos, M., Rodnianski, I.: The red-shift effect and radiation decay on black hole spacetimes. Commun. Pure Appl. Math. 62(7), 859–919 (2009)
Dafermos, M., Rendall, A.D.: Strong cosmic censorship for surface-symmetric cosmological spacetimes with collisionless matter. Commun. Pure Appl. Math. 69(5), 815–908 (2016)
Dafermos, M., Rodnianski, I., Shlapentokh-Rothman, Y.: Decay for solutions of the wave equation on Kerr exterior spacetimes III: The full subextremal case \(\vert a\vert <M\). Ann. of Math. (2) 183(3), 787–913 (2016)
Dyatlov, S.: Exponential energy decay for Kerr–de Sitter black holes beyond event horizons. Math. Res. Lett. 18(5), 1023–1035 (2011)
Dyatlov, S.: Quasi-normal modes and exponential energy decay for the Kerr–de Sitter black hole. Commun. Math. Phys. 306(1), 119–163 (2011)
Dyatlov, S.: Asymptotic distribution of quasi-normal modes for Kerr–de Sitter black holes. In: Annales Henri Poincaré, vol. 13, pp. 1101–1166. Springer (2012)
Dyatlov, S.: Spectral gaps for normally hyperbolic trapping. Ann. Inst. Fourier (Grenoble) 66(1), 55–82 (2016)
Finster, F., Kamran, N., Smoller, J., Yau, S.-T.: The long-time dynamics of Dirac particles in the Kerr–Newman black hole geometry. Adv. Theor. Math. Phys. 7(1), 25–52 (2003)
Finster, F., Kamran, N., Smoller, J., Yau, S.-T.: Decay of solutions of the wave equation in the Kerr geometry. Commun. Math. Phys. 264(2), 465–503 (2006)
Friedrich, H.: On the hyperbolicity of Einstein’s and other gauge field equations. Commun. Math. Phys. 100(4), 525–543 (1985)
Friedrich, H.: On the existence of \(n\)-geodesically complete or future complete solutions of Einstein’s field equations with smooth asymptotic structure. Commun. Math. Phys. 107(4), 587–609 (1986)
Friedrich, H.: On the global existence and the asymptotic behavior of solutions to the Einstein–Maxwell–Yang–Mills equations. J. Differ. Geom. 34(2), 275–345 (1991)
Finster, F., Smoller, J.: Linear stability of the non-extreme Kerr black hole. arXiv:1606.08005 (2016)
Gundlach, C., Calabrese, G., Hinder, I., Martín-García, J.M.: Constraint damping in the Z4 formulation and harmonic gauge. Class. Quantum Gravity 22(17), 3767 (2005)
Graham, C.R., Lee, J.M.: Einstein metrics with prescribed conformal infinity on the ball. Adv. Math. 87(2), 186–225 (1991)
Higuchi, A.: Symmetric tensor spherical harmonics on the N-sphere and their application to the de Sitter group SO(N,1). J. Math. Phys. 28(7), 1553–1566 (1987)
Hintz, P.: Global well-posedness of quasilinear wave equations on asymptotically de Sitter spaces. Annales de l’Institut Fourier 66(4), 1285–1408 (2016)
Hintz, P.: Resonance expansions for tensor-valued waves on asymptotically Kerr–de Sitter spaces. J. Spectr. Theory 7, 519–557 (2017)
Häfner, D., Nicolas, J.-P.: Scattering of massless Dirac fields by a Kerr black hole. Rev. Math. Phys. 16(01), 29–123 (2004)
Hirsch, M.W., Shub, M., Pugh, C.C.: Invariant Manifolds. Springer, Berlin (1977)
Hintz, P., Vasy, A.: Non-trapping estimates near normally hyperbolic trapping. Math. Res. Lett. 21(6), 1277–1304 (2014)
Hintz, P., Vasy, A.: Asymptotics for the wave equation on differential forms on Kerr–de Sitter space. Preprint arXiv:1502.03179 (2015)
Hintz, P., Vasy, A.: Semilinear wave equations on asymptotically de Sitter, Kerr–de Sitter and Minkowski spacetimes. Anal. PDE 8(8), 1807–1890 (2015)
Hintz, P., Vasy, A.: Global analysis of quasilinear wave equations on asymptotically Kerr–de Sitter spaces. Int. Math. Res. Not. 2016(17), 5355–5426 (2016)
Hintz, P., Vasy, A.: The global non-linear stability of the Kerr–de Sitter family of black holes. Preprint arXiv:1606.04014 (2016)
Hintz, P., Vasy, A.: Analysis of linear waves near the cauchy horizon of cosmological black holes. J. Math. Phys. 58(8), 081509 (2017)
Iantchenko, A.: Quasi-normal modes for de Sitter–Reissner–Nordström Black Holes. Preprint arXiv:1407.3654 (2014)
Iantchenko, A.: Quasi-normal modes for massless Dirac fields in Kerr–Newman–de Sitter black holes. Preprint arXiv:1511.09233 (2015)
Ishibashi, A., Kodama, H.: Stability of higher-dimensional Schwarzschild black holes. Prog. Theor. Phys. 110(5), 901–919 (2003)
Ionescu, A.D., Klainerman, S.: On the global stability of the wave-map equation in Kerr spaces with small angular momentum. Ann. PDE 1(1), 1–78 (2015)
Isenberg, J., Maxwell, D., Pollack, D.: A gluing construction for non-vacuum solutions of the Einstein-constraint equations. Adv. Theor. Math. Phys. 9(1), 129–172 (2005)
Isenberg, J.A., Murchadha, N.Ó., York Jr., J.W.: Initial-value problem of general relativity. III. Coupled fields and the scalar-tensor theory. Phys. Rev. D 13(6), 1532 (1976)
Isenberg, J.: Constant mean curvature solutions of the Einstein constraint equations on closed manifolds. Class. Quantum Gravity 12(9), 2249 (1995)
Kerr, R.P.: Gravitational field of a spinning mass as an example of algebraically special metrics. Phys. Rev. Lett. 11(5), 237 (1963)
Kodama, H., Ishibashi, A.: A master equation for gravitational perturbations of maximally symmetric black holes in higher dimensions. Progress Theor. Phys. 110(4), 701–722 (2003)
Kodama, H., Ishibashi, A.: Master equations for perturbations of generalised static black holes with charge in higher dimensions. Prog. Theor. Phys. 111(1), 29–73 (2004)
Kodama, H., Ishibashi, A., Seto, O.: Brane world cosmology: Gauge-invariant formalism for perturbation. Phys. Rev. D 62(6), 064022 (2000)
Klainerman, S.: Uniform decay estimates and the Lorentz invariance of the classical wave equation. Commun. Pure Appl. Math. 38(3), 321–332 (1985)
Klainerman, S.: The null condition and global existence to nonlinear wave equations. In: Nonlinear systems of partial differential equations in applied mathematics, Part 1 (Santa Fe, N.M., 1984). Lectures in Appl. Math., pp. 293–326. Amer. Math. Soc., Providence, RI (1986)
Kodama, H., Sasaki, M.: Cosmological perturbation theory. Prog. Theor. Phys. Suppl. 78, 1–166 (1984)
Kay, B.S., Wald, R.M.: Linear stability of Schwarzschild under perturbations which are non-vanishing on the bifurcation 2-sphere. Class. Quantum Gravity 4(4), 893 (1987)
Konoplya, R.A., Zhidenko, A.: Stability of multidimensional black holes: complete numerical analysis. Nucl. Phys. B 777(1), 182–202 (2007)
Konoplya, R.A., Zhidenko, A.: Instability of higher-dimensional charged black holes in the de Sitter world. Phys. Rev. Lett. 103(16), 161101 (2009)
LIGO Scientific Collaboration and Virgo Collaboration.: Observation of gravitational waves from a binary black hole merger. Phys. Rev. Lett. 116, 061102 (2016)
Lindblad, H., Rodnianski, I.: Global existence for the Einstein vacuum equations in wave coordinates. Commun. Math. Phys. 256(1), 43–110 (2005)
Lindblad, H., Rodnianski, I.: The global stability of Minkowski space-time in harmonic gauge. Ann. of Math. (2) 171(3), 1401–1477 (2010)
Luk, J.: The null condition and global existence for nonlinear wave equations on slowly rotating Kerr spacetimes. J. Eur. Math. Soc. 15(5), 1629–1700 (2013)
Melrose, R.B.: The Atiyah–Patodi-Singer index theorem. Research Notes in Mathematics, vol. 4. A K Peters Ltd, Wellesley (1993)
Marzuola, J., Metcalfe, J., Tataru, D., Tohaneanu, M.: Strichartz estimates on Schwarzschild black hole backgrounds. Commun. Math. Phys. 293(1), 37–83 (2010)
Moncrief, V.: Odd-parity stability of a Reissner-Nordström black hole. Phys. Rev. D 9(10), 2707 (1974)
Moncrief, V.: Stability of Reissner–Nordström black holes. Phys. Rev. D 10(4), 1057 (1974)
Moncrief, V.: Gauge-invariant perturbations of Reissner–Nordström black holes. Phys. Rev. D 12, 1526–1537 (1975)
Moschidis, G.: The \(r^p\)-weighted energy method of dafermos and Rodnianski in general asymptotically flat spacetimes and applications. Ann. PDE 2(1), 1–194 (2016)
Melrose, R., Barreto, A.S., Vasy, A.: Analytic continuation and semiclassical resolvent estimates on asymptotically hyperbolic spaces. Commun. Partial Differ. Equ. 39(3), 452–511 (2014)
Metcalfe, J., Tataru, D., Tohaneanu, M.: Price’s law on nonstationary space-times. Adv. Math. 230(3), 995–1028 (2012)
Newman, E.T., Couch, E., Chinnapared, K., Exton, A., Prakash, A., Torrence, R.: Metric of a rotating, charged mass. J. Math. Phys. 6(6), 918–919 (1965)
Nonnenmacher, S., Zworski, M.: Quantum decay rates in chaotic scattering. Acta Math. 203(2), 149–233 (2009)
Perlmutter, S., et al.: Measurements of \(\Omega \) and \(\Lambda \) from 42 high-redshift supernovae. Astrophys. J. 517(2), 565 (1999)
Podolskỳ, J., Griffiths, J.B.: Accelerating Kerr–Newman black holes in (anti-)de Sitter space-time. Phys. Rev. D 73(4), 044018 (2006)
Pretorius, F.: Evolution of binary black-hole spacetimes. Phys. Rev. Lett. 95, 121101 (2005)
Price, R.H.: Nonspherical perturbations of relativistic gravitational collapse. I. Scalar and gravitational perturbations. Phys. Rev. D 5(10), 2419 (1972)
Riess, A.G., et al.: Observational evidence from supernovae for an accelerating universe and a cosmological constant. Astron. J. 116(3), 1009 (1998)
Ringström, H.: Future stability of the Einstein-non-linear scalar field system. Inventiones Mathematicae 173(1), 123–208 (2008)
Regge, T., Wheeler, J.A.: Stability of a Schwarzschild singularity. Phys. Rev. 108, 1063–1069 (1957)
Sbierski, J.: On the existence of a maximal cauchy development for the Einstein equations: a dezornification. In: Annales Henri Poincaré, vol. 17, pp. 301–329. Springer (2016)
Barreto, A.S., Zworski, M.: Distribution of resonances for spherical black holes. Math. Res. Lett. 4, 103–122 (1997)
Schlue, V.: Global results for linear waves on expanding Kerr and Schwarzschild de Sitter cosmologies. Commun. Math. Phys. 334(2), 977–1023 (2015)
Schlue, V.: Decay of the Weyl curvature in expanding black hole cosmologies. Preprint arXiv:1610.04172 (2016)
Speck, J.: The global stability of the Minkowski spacetime solution to the Einstein-nonlinear system in wave coordinates. Anal. PDE 7(4), 771–901 (2014)
Saint-Raymond, X.: A simple Nash–Moser implicit function theorem. Enseign. Math. (2) 35(3–4), 217–226 (1989)
Shlapentokh-Rothman, Y.: Exponentially growing finite energy solutions for the Klein–Gordon equation on sub-extremal Kerr spacetimes. Commun. Math. Phys. 329(3), 859–891 (2014)
Shlapentokh-Rothman, Y.: Quantitative mode stability for the wave equation on the Kerr spacetime. Ann. Henri Poincaré 16(1), 289–345 (2015)
Sterbenz, J., Tataru, D.: Local energy decay for Maxwell fields part I: spherically symmetric black-hole backgrounds. Int. Math. Res. Not. 2015(11), 3298–3342 (2015)
Stogin, J.: Global stability of the nontrivial solutions to the wave map problem from Kerr \(|a|\ll {M}\) to the hyperbolic plane under axisymmetric perturbations preserving angular momentum. Preprint arXiv:1610.03910 (2016)
Schleich, K., Witt, D.M.: A simple proof of Birkhoff’s theorem for cosmological constant. J. Math. Phys. 51(11), 112502 (2010)
Tataru, D.: Local decay of waves on asymptotically flat stationary space-times. Am. J. Math. 135(2), 361–401 (2013)
Michael, E., Taylor, M.E.: Partial Differential Equations I–III. Springer, Berlin (1996)
Tataru, D., Tohaneanu, M.: A local energy estimate on Kerr black hole backgrounds. Int. Math. Res. Not. 2, 248–292 (2011)
Vasy, A.: The wave equation on asymptotically de Sitter-like spaces. Adv. Math. 223(1), 49–97 (2010)
Vasy, A.: Microlocal analysis of asymptotically hyperbolic and Kerr-de Sitter spaces (with an appendix by Semyon Dyatlov). Invent. Math. 194(2), 381–513 (2013)
Vishveshwara, C.V.: Stability of the Schwarzschild Metric. Phys. Rev. D 1, 2870–2879 (1970)
Wald, R.M.: Note on the stability of the Schwarzschild metric. J. Math. Phys. 20(6), 1056–1058 (1979)
Wald, R.M.: General Relativity. University of Chicago press, Chicago (2010)
Warnick, C.M.: On quasinormal modes of asymptotically anti-de Sitter black holes. Commun. Math. Phys. 333(2), 959–1035 (2015)
Whiting, B.F.: Mode stability of the Kerr black hole. J. Math. Phys. 30(6), 1301–1305 (1989)
Wunsch, J., Zworski, M.: Resolvent estimates for normally hyperbolic trapped sets. In: Annales Henri Poincaré, vol. 12, pp. 1349–1385. Springer (2011)
Zilhão, M., Cardoso, V., Herdeiro, C., Lehner, L., Sperhake, U.: Testing the nonlinear stability of Kerr–Newman black holes. Phys. Rev. D 90(12), 124088 (2014)
Zerilli, F.J.: Effective potential for Even–Parity Regge–Wheeler gravitational perturbation equations. Phys. Rev. Lett. 24, 737–738 (1970)
Zipser, N.: The global nonlinear stability of the trivial solution of the Einstein–Maxwell equations. PhD thesis, Harvard University (2000)
Zworski, M.: Mathematical study of scattering resonances. Preprint arXiv:1609.03550 (2016)
Zworski, M.: Resonances for asymptotically hyperbolic manifolds: Vasy’s method revisited. J. Spectr. Theory 6, 1087–1114 (2016)
Acknowledgements
I would like to thank András Vasy, Maciej Zworski, Jim Isenberg, Sergiu Klainerman, and Yakov Shlapentokh-Rothman for valuable discussions and for their interest and support. I am very grateful to Mihalis Dafermos, and to an anonymous referee, for valuable comments on both content and exposition. I would also like to thank the Miller Institute at the University of California, Berkeley, for support.
Author information
Authors and Affiliations
Corresponding author
Appendices
Appendix A: Review of b-Geometry and b-Analysis
We only give a very brief account of the aspects of b-geometry and b-analysis which are used in the present paper; for a more detailed overview, we refer the reader to [61, “Appendix A”] as well as to Melrose’s book [84] on the subject.
Fix a smooth connected \((n+1)\)-dimensional manifold M with non-empty boundary \(\partial M\). We denote by \(\mathcal V_{\mathrm {b}}(M)\subset \mathcal V(M)\) the space of b-vector fields, smooth vector fields on M which are tangent to \(\partial M\). Away from \(\partial M\), these are simply ordinary smooth vector fields. Near the boundary, with \((\tau ,x^1,\ldots ,x^n)\) denoting adapted local coordinates near a point in \(\partial M\), namely with \(\partial M\) given by the vanishing of \(\tau \), a b-vector field V takes the form
Correspondingly, b-vector fields are the space of sections of a natural vector bundle \({}^{{\mathrm {b}}}TM\rightarrow M\), called b-tangent bundle, which over the interior \(M^\circ \) is naturally isomorphic to the standard tangent bundle, and which near the boundary in the above coordinates has the basis \(\{\tau \partial _\tau ,\partial _{x^1},\ldots ,\partial _{x^n}\}\); in particular, \(\tau \partial _\tau \) is non-vanishing at \(\tau =0\) as a b-vector field. One can check that \(\tau \partial _\tau \) is in fact well-defined, i.e. independent of the choice of adapted local coordinates. The space \(\mathrm {Diff}_{\mathrm {b}}^*(M)\) of b-differential operators is the universal enveloping algebra of \(\mathcal V_{\mathrm {b}}(M)\), thus elements of \(\mathrm {Diff}_{\mathrm {b}}^m(M)\) are finite linear combinations (with \({\mathcal C}^\infty (M)\) coefficients) of products of up to m b-vector fields. If \(E,F\rightarrow M\) are two smooth vector bundles, one can more generally define m-th order b-differential operators \(\mathrm {Diff}_{\mathrm {b}}^m(M;E,F)\) mapping \({\mathcal C}^\infty (M;E)\) into \({\mathcal C}^\infty (M;F)\), e.g. using local trivializations of E and F.
The dual bundle \({}^{{\mathrm {b}}}T^*M\) of \({}^{{\mathrm {b}}}TM\), called the b-cotangent bundle, is correspondingly spanned by \(\frac{d\tau }{\tau },dx^1,\ldots ,dx^n\); here \(\frac{d\tau }{\tau }\) is smooth (and non-degenerate) as a b-1-form up to \(\tau =0\). A smooth b-metric g on M is then a smooth section of the second symmetric tensor power \(S^2\,{}^{{\mathrm {b}}}T^*M\); in local coordinates as above, this means that
If M arises as the compactification of a manifold \(M^\circ \) without boundary as in equation (3.17), then a smooth b-metric on M is asymptotically stationary on \(M^\circ \) in the following sense: letting \(t:=-\log \tau \), we have \(\frac{d\tau }{\tau }=-dt\), and a smooth function \(a\in {\mathcal C}^\infty (M)\), having a Taylor expansion in powers of \(\tau \), has a Taylor expansion on \(M^\circ \) in powers of \(e^{-t}\); thus, \(g=g_0+\widetilde{g}\) with
approaches the stationary metric \(g_0\) exponentially fast as \(t\rightarrow \infty \). Conversely, if \(M^\circ \) is equipped with a metric g approaching a stationary metric exponentially fast at some rate \(\alpha >0\), then g extends to be a smooth b-metric on M plus an error term (in general non-smooth) of size \(\tau ^\alpha \). In the case of interest in the present paper, this remainder term will be conormal, or more generally lie in a weighted b-Sobolev space which we discuss further below.
We further have the b-differential \({}^{{\mathrm {b}}}d\), acting between sections of the exterior powers \(\Lambda ^k\,{}^{{\mathrm {b}}}T^*M\); they are defined by extension of the usual exterior differential d from \(M^\circ \); thus, acting on functions, one has
and in general \({}^{{\mathrm {b}}}d\in \mathrm {Diff}_{\mathrm {b}}^1(M;\Lambda ^k\,{}^{{\mathrm {b}}}T^*M,\Lambda ^{k+1}\,{}^{{\mathrm {b}}}T^*M)\).
On M, we naturally have the b-density bundle \({}^{{\mathrm {b}}}\Omega ^1(M)\), with local trivialization induced by \(|\frac{d\tau }{\tau }dx^1\ldots dx^n|\); fixing a nowhere vanishing b-density \(\nu \) on M, this allows us to define the \(L^2\) space \(L^2_{\mathrm {b}}(M;\nu )\equiv L^2(M;\nu )\). We drop the density \(\nu \) from the notation from now on. (For compact M, different choices of \(\nu \) lead to equivalent norms.) For integer \(k\ge 0\) and real \(\alpha \in \mathbb {R}\), we then define the weighted b-Sobolev space
For compact M, \(H_{{\mathrm {b}}}^{k,\alpha }(M)\) can be endowed with a Hilbert space structure by means of a finite collection of b-vector fields which span \({}^{{\mathrm {b}}}T_p M\) over every \(p\in M\); the norms for any two such collections are equivalent. For non-integer \(s\in \mathbb {R}\), the space \(H_{{\mathrm {b}}}^{s,\alpha }(M)\) is defined using duality, that is \(H_{{\mathrm {b}}}^{s,\alpha }(M)^*=H_{{\mathrm {b}}}^{-s,-\alpha }(M)\), and interpolation. We point out that the definition of the space \(H_{{\mathrm {b}}}^{s,\alpha }(M)\) as a Hilbert space for M compact does not require the choice of a metric. Elements of the space \(H_{{\mathrm {b}}}^{\infty ,\alpha }(M)=\bigcap _{s\in \mathbb {R}}H_{{\mathrm {b}}}^{s,\alpha }(M)\) are called conormal (with respect to \(L^2_{\mathrm {b}}\)); for M compact, this space carries a natural Fréchet space structure. Near a point on \(\partial M\), using coordinates \((\tau ,x^1,\ldots ,x^n)\) as above, and letting \(t=-\log \tau \), the space \(H_{{\mathrm {b}}}^{s,\alpha }(M)\) is locally the same (as a Hilbert space, up to equivalence of norms) as the space \(e^{-\alpha t}H^s(M^\circ )\), where the Sobolev space on \(M^\circ \) is defined by testing with products of the vector fields \(\partial _t,\partial _{x^1},\ldots ,\partial _{x^n}\).
Suppose next that \(\Omega \subset M\) is a non-empty open subset of M. One can then define the space of supported distributions \({\dot{\mathscr {D}}}(\Omega )\) as the space of distributions \(u\in \mathscr {D}(M)={\dot{\mathcal C}}^\infty (M;\Omega ^1 M)^*\) with \({\text {supp}}u\subset \Omega \). (The same definition applies for M without boundary.) We then define \({\dot{H}}_{{\mathrm {b}}}^{s,\alpha }(\Omega )=H_{{\mathrm {b}}}^{s,\alpha }(M)\cap {\dot{\mathscr {D}}}(\Omega )\); this thus consists of elements of \(H_{{\mathrm {b}}}^{s,\alpha }(M)\) which are supported in \({\bar{\Omega }}\). The space of extendible distributions, \({\bar{\mathscr {D}}}(\Omega )\), is equal to the space of restrictions \(u|_\Omega \) for \(u\in \mathscr {D}(M)\); we likewise define \({\bar{H}}_{{\mathrm {b}}}^{s,\alpha }(\Omega )=H_{{\mathrm {b}}}^{s,\alpha }(M)|_{\Omega }\), with the natural (quotient) norm. Thus, elements of \({\bar{H}}_{{\mathrm {b}}}^{s,\alpha }(\Omega )\) automatically have extensions to \(H_{{\mathrm {b}}}^{s,\alpha }(M)\) (with the same norm).
If \(E\rightarrow M\) is a smooth vector bundle, weighted b-Sobolev spaces \(H_{{\mathrm {b}}}^{s,\alpha }(M;E)\) are defined using local trivializations of E; for \(\Omega \subset M\) as above, one can likewise define spaces \({\dot{H}}_{{\mathrm {b}}}^{s,\alpha }(M;E)\) and \({\bar{H}}_{{\mathrm {b}}}^{s,\alpha }(M;E)\) of supported and extendible sections of E over \(\Omega \).
Appendix B: Explicit Expressions for the Mode Stability Analysis
In this appendix, we list the explicit formulas for a number of functions arising in Sect. 5; we recall that the quantities x, y, z, m were defined in (5.47), H in (5.46), \(\tilde{c}\) in (5.55), \(a_+\) in (5.56), and \(\hat{c}\) in (5.66).
The expressions for the functions used in equation (5.49) are then:
The functions appearing in equation (5.50) are given as follows:
The functions used in equation (5.65) are:
The functions appearing in equation (5.67) take the following form:
Rights and permissions
About this article
Cite this article
Hintz, P. Non-linear Stability of the Kerr–Newman–de Sitter Family of Charged Black Holes. Ann. PDE 4, 11 (2018). https://doi.org/10.1007/s40818-018-0047-y
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s40818-018-0047-y


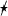 .
. acting on symmetric 2-tensors.
acting on symmetric 2-tensors.