Skip to main content
SpringerLink
Log in

Optimal control analysis of a mathematical model on smoking

  • Original Article
  • Published:
Modeling Earth Systems and Environment Aims and scope Submit manuscript

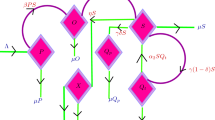
Abstract

In this paper,the dynamics of smoking behavior under the influence of educational and media programs is modeled in the presence of two control strategies. Optimal control theory is applied to a non-linear mathematical model on smoking: impact of anti-smoking campaign which helps in obtaining time dependent case detection strategy while minimizing the cost of implementation of such strategy. We prove the existence of an optimal control set and analyze the necessary and sufficient conditions, optimality and transversality conditions. The optimality of the system is deduced analytically and solved numerically.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9

Similar content being viewed by others

References

  • Ahmad A, Farman M, Ahmad MO, Raza N, Abdullah (2018) Dynamical behavior of SIR epidemic model with non-integer time fractional derivatives: a mathematical analysis. Int J Adv Appl Sci 5(1):123–129

    Google Scholar 

  • Ahmad A, Farman M, Yasin F, Ahmad MO (2020) Dynamical transmission and effect of smoking in society. Int J Adv Appl Sci 5(2):71–75

    Google Scholar 

  • Arafa AAM, Rida SZ, Khalil M (2012) Fractional modeling dynamics of HIV and 4 T-cells during primary infection. Nonlinear Biomed Phys 6:1–7

    Google Scholar 

  • Ashraf F, Ahmad A, Saleem MU, Farman M, Ahmad MO (2018) Dynamical behavior of HIV immunology model with non-integer time fractional derivatives. Int J Adv Appl Sci 5(3):39–45

    Google Scholar 

  • Biazar J (2006) Solution of the epidemic model by Adomian decomposition method. Appl Math Comput 173:1101–1106

    Google Scholar 

  • Bonyah E, Khan MA, Okosun KO, Islam S (2017) A theoretical model for Zika virus transmission. PLoS One 12(10):1–26

    Google Scholar 

  • Buonomo B, Lacitignola D (2008) On the dynamics of an SEIR epidemic model with a convex incidence rate. Ricerche Mat 57:261–281

    Google Scholar 

  • Busenberg S, Driessche P (1990) Analysis of a disease transmission model in a population with varying size. J Math Biol 28:65–82

    Google Scholar 

  • Castilho C (2006) Optimal control of an epidemic through educational campaigns. Electron J Differ Eq:1–11

    Google Scholar 

  • El-Sayed AMA, Rida SZ, Arafa AAM (2009) On the solutions of time-fractional bacterial chemotaxis in a diffusion gradient chamber. Int J Nonlinear Sci 7:485–495

    Google Scholar 

  • Fleming wendell H, Rishel Raymond W (1975) Deterministics and Stochastic Optimal Control, vol 1. Springer Verlag, New York

    Google Scholar 

  • Fister KR, Lenhart S, McNally JS (1998) Optimzing chemothearpy in an HIV model. Electron J Diff Eq:1–12

    Google Scholar 

  • Garsow C Castillo, Jordan-Salivia G, Rodriguez Herrera A (1997) Mathematical models for the dynamics of tobacco use recovery and relapse Technical Report Series BU-1505- M: Cornell University Ithaca NY USA

  • Haq F, Shah K, Rahman GU, Shahzad M (2018) Numerical solution of fractional order smoking model via laplace Adomian decomposition method. Alex Eng J 57:1061–1069

    Google Scholar 

  • https://en.wikipedia.org/wiki/Epidemiology. 17th Nov 2016

  • Kar TK, Jana S (2013) A theoretical study on mathematical modeling of an infectious disease with application of optimal control. BioSystems 111:37–50

    Google Scholar 

  • Kribs-Zaleta CM (1999) Structured models for heterosexual disease transmission. Math Biosci 160:83–108

    Google Scholar 

  • Kusum Lata, Mishra SN, Mishra AK (2020) An optimal control problem for carrier dependent disease. BioSystems 187:1–10

    Google Scholar 

  • Lenhart S, Workman J (2007) Optimal Control Applied to Biological Model. Chapman and Hall/CRC,

  • Liu X, Wang C (2010) Bifurcation of a predator-prey model with disease in the prey. Nonlinear Dyn 62:841–850

    Google Scholar 

  • Lukes DL (1982) Differential equations: classical to controlled. Acad Press NY 162:182

    Google Scholar 

  • Matintu SA (2017) Smoking as epedemic modeling and simulation study. Am J Appl Math 5:31–38

    Google Scholar 

  • Misra AK, Sharama A, Shukla JB (2011) Modeling and analysis of effect of awareness programs by media on the spread of infectious diseases. Math Comput Model 53:1221–1228

    Google Scholar 

  • Misra AK, Sharma A (2014) Modeling the impact of awareness created by media campaigns on vaccination coverage in a variable population. J Biol Sys 22:249–270

    Google Scholar 

  • Misra AK, Sharama A, Singh V (2011) Effect of awareness programs in controlling the prevalence of an epidemic with time delay. J Biol Sys 19:389–402

    Google Scholar 

  • Misra AK, Sharma A, Shukla JB (2015) Stability analysis and optimal control of an epidemic model with awareness programs by media. BioSystems 138:53–62

    Google Scholar 

  • Njankou SDD, Nyabadza F (2016) An optimal control for Ebola virus disease. J Biol Sys 24(1):1–21

    Google Scholar 

  • Algahtani Obaid J, Momani Anwar Zeb Gul Zaman Shahar, Jung IH (2015) Mathematical study of smoking model by incorporating campaign class. Department of Mathematics King Saud University, Saud Arabia

    Google Scholar 

  • Okosun KO, Makinde OD (2014) A co-infection model of malaria and cholera diseases with optimal control. Math Biosci 258:19–32

    Google Scholar 

  • Okosun KO, Khan MA, Bonyah E, Ogunlade ST (2017) On the dynamics of HIV-AIDS and cryptosporidiosis. Eur Phys J Plus 132(8):363

    Google Scholar 

  • Pontryagin LS, Boltyanskii VG, Gamkrelidze RV, Mishchenko EF (1962) The mathematical theory of optimal process. Interscience Publishers, New York

    Google Scholar 

  • Sharomi O, Gumel AB (2008) Curtailing smoking dynamics a mathematical modeling approach. Appl Math Comput 195:475–499

    Google Scholar 

  • Shukla JB, Ram Naresh, Rani Verma Sandhya, Manju Agarwal (2020) Modeling the effect of sanitation in a human habitat to control the spread of bacterial diseases. Model Earth Syst Environ 6(1):39–49

    Google Scholar 

  • Shyam Sundar, Kumar Mishra Ashish, Ram Naresh (2018) Modeling the impact of media awareness programs on mitigation of carbon dioxide emitted from automobiles. Model Earth Syst Environ 4:349–357

    Google Scholar 

  • Verma V, Bhadauria Archana S (2019) Global dynamics of a mathematical model on smoking:impact of anti-smoking campaign. J Math Model 7(1):49–62

    Google Scholar 

  • World Health Organization report on tobacco (2013) http://www.who.int/tobacco/globalreport/2013/en/index.html

  • Zaman G (2011) Qualitative behavior of giving up smoking model. Bull Malaysian Math Sci Soc. 2:403–415

    Google Scholar 

Download references

Acknowledgements

The authors thank the handling editor and anonymous referees for their valuable comments and suggestions which led to an improvement of our original manuscript.

Author information

Authors and Affiliations

  1. Faculty of Mathematical and Statistical Sciences, Institute of Natural Sciences & Humanities, Shri Ramswaroop Memorial University, Barabanki, 225003, India

    Vinay Verma

Authors
  1. Vinay Verma
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Vinay Verma.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Verma, V. Optimal control analysis of a mathematical model on smoking. Model. Earth Syst. Environ. 6, 2535–2542 (2020). https://doi.org/10.1007/s40808-020-00847-1

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s40808-020-00847-1

Keywords

Search

Navigation