Skip to main content

Advertisement

SpringerLink
Log in

Drought forecasting using data-driven methods and an evolutionary algorithm

  • Original Article
  • Published:
Modeling Earth Systems and Environment Aims and scope Submit manuscript

Abstract

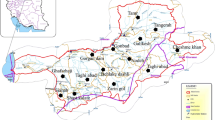
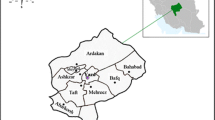
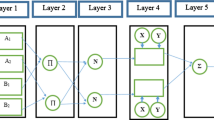
The present study focuses on quantitative (exact) and qualitative (classifying) drought forecasting in Gorganrood, Iran, based on monthly time-series of standard precipitation index (SPI) with 1–6 months lead-times. In so doing, recursive multi-layer perceptron (RMLP) and recursive support vector regression (RSVR) were optimized via an imperialist competitive algorithm (ICA). A traditional approach, autoregressive integrated moving average (ARIMA), has also been applied in this case. In quantitative forecasting, ICA-RMLP and ICA-RSVR models outperformed ARIMA ones according to three performance criteria namely, correlation coefficient (R), root mean square error (RMSE), and mean absolute error (MAE). For example, in SPI 24 and one month lead time forecasting; R, RMSE, and, MSE values for ARIMA model equaled to 0.90, 0.484, and 0.322 while, for ICA-RMLP equaled to 0.967, 0.277, and 0.188, respectively. In contrast, the criteria for ICA-RSVR were evaluated 0.969, 0.278, and 0.186, respectively. Increases in lead-times decreased the forecasting accuracy for both qualitative and quantitative forecasting. However, increases in SPI scales provided more accurate results. Whereas, in the quantitative forecasting, model could provide appropriate forecasts for all scales of SPI. According to the performance of the proposed framework, it would be practical for developing a drought warning system.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7

Similar content being viewed by others

References

  • Akaike H (1974) A new look at the statistical model identification. IEEE Trans Autom Control 19(6):716–723

    Article  Google Scholar 

  • Almedeij J (2016) Long-term periodic drought modeling. Stochastic Environ Res Risk Assess 30(3):901–910

    Article  Google Scholar 

  • Araghinejad S (2013) Data-driven modeling: using MATLAB® in water resources and environmental engineering. vol 67. Springer Science & Business Media, Berlin

    Google Scholar 

  • Atashpaz-Gargari E, Lucas C (2007) Imperialist competitive algorithm: an algorithm for optimization inspired by imperialistic competition. In 2007 IEEE Congress on Evolutionary Computation, 4661–4667

  • Azarnivand A, Banihabib ME (2016) A multi-level strategic group decision making for understanding and analysis of sustainable watershed planning in response to environmental perplexities. Group Decis Negot. doi:10.1007/s10726-016-9484-8

    Google Scholar 

  • Bacanli UG, Firat M, Dikbas F (2009) Adaptive neuro-fuzzy inference system for drought forecasting. Stoch Environ Res Risk Assess 23(8):1143–1154

    Article  Google Scholar 

  • Barua S, Ng AWM, Perera BJC (2012) Artificial neural network–based drought forecasting using a nonlinear aggregated drought index. J Hydrol Eng 17(12):1408–1413

    Article  Google Scholar 

  • Belayneh A, Adamowski J (2013) Drought forecasting using new machine learning methods/Prognozowanie suszy z wykorzystaniem automatycznych samouczących się metod. J Water Land Dev 18(9):3–12

    Article  Google Scholar 

  • Box GE, Jenkins GM, Reinsel GC, Ljung GM (2015) Time series analysis: forecasting and control. Wiley, Hoboken

    Google Scholar 

  • Bozorg-Haddad O, Azarnivand A, Hosseini-Moghari SM, Loáiciga HA (2016a) Development of a comparative multiple criteria framework for ranking Pareto optimal solutions of a multiobjective reservoir operation problem. J Irrig Drain Eng 142(7):04016019

    Article  Google Scholar 

  • Bozorg-Haddad O, Azarnivand A, Hosseini-Moghari SM, Loáiciga HA (2016b) WASPAS application and evolutionary algorithm benchmarking in optimal reservoir optimization problems. J Water Resour Plann Manage 143(1):04016070

    Article  Google Scholar 

  • Cherkassky V, Ma Y (2004) Practical selection of SVM parameters and noise estimation for SVM regression. Neural Netw 17(1):113–126

    Article  Google Scholar 

  • Cheval S, Busuioc A, Dumitrescu A, Birsan MV (2014) Spatiotemporal variability of meteorological drought in Romania using the standardized precipitation index SPI. Clim Res 60(3):235–248

    Article  Google Scholar 

  • Chisadza B, Tumbare MJ, Nyabeze WR, Nhapi I (2015) Linkages between local knowledge drought forecasting indicators and scientific drought forecasting parameters in the Limpopo River Basin in Southern Africa. Int J Disaster Risk Reduct 12:226–233

    Article  Google Scholar 

  • Chitsaz N, Hosseini-Moghari SM (2017) Introduction of new datasets of drought indices based on multivariate methods in semi-arid regions. Hydrol Res. doi:10.2166/nh.2017.254

    Google Scholar 

  • Chitsaz N, Azarnivand A, Araghinejad S (2016) Pre-processing of data-driven river flow forecasting models by singular value decomposition (SVD) technique. Hydrol Sci J 61(12):2164–2178

    Article  Google Scholar 

  • Dastorani MT, Afkhami H (2011) Application of artificial neural networks on drought prediction in Yazd (Central Iran). Desert 16(1):39–48

    Google Scholar 

  • Durdu ÖF (2010) Application of linear stochastic models for drought forecasting in the Büyük Menderes river basin, western Turkey. Stoch Environ Res Risk Assess 24(8):1145–1162

    Article  Google Scholar 

  • Edwards DC (1997) Characteristics of 20th century drought in the United States at multiple time scales (No. afit-97-051). Air force inst of tech wright-patterson afb oh

  • Eslamian S (ed) (2014) Handbook of engineering hydrology: modeling, climate change, and variability. CRC Press, Boca Raton

    Book  Google Scholar 

  • Gorgij AD, Kisi O, Moghaddam AA (2016) Groundwater budget forecasting, using hybrid wavelet-ANN-GP modelling: a case study of Azarshahr Plain, East Azerbaijan, Iran. Hydrol Res. doi:10.2166/nh.2016.202

    Google Scholar 

  • Guttman NB (1999) Accepting the Standardized Precipitation Index: a calculation algorithm. J Am Water Resour Assoc 35(2):311–322

    Article  Google Scholar 

  • Hornik K, Stinchcombe M, White H (1989) Multilayer feedforward networks are universal approximators. Neural Netw 2(5):359–366

    Article  Google Scholar 

  • Javan K, Lialestani MRFH, Nejadhossein M (2015) A comparison of ANN and HSPF models for runoff simulation in Gharehsoo River watershed, Iran. Model Earth Syst Environ 1(4):41

    Article  Google Scholar 

  • Jayanthi H, Husak GJ, Funk C, Magadzire T, Adoum A, Verdin JP (2014) A probabilistic approach to assess agricultural drought risk to maize in Southern Africa and millet in Western Sahel using satellite estimated rainfall. Int J Disaster Risk Reduct 10:490–502

    Article  Google Scholar 

  • Kan G, Yao C, Li Q, Li Z, Yu Z, Liu Z, Liang K (2015) Improving event-based rainfall-runoff simulation using an ensemble artificial neural network based hybrid data-driven model. Stoch Environ Res Risk Assess 29(5):1345–1370

    Article  Google Scholar 

  • Kisi O, Dailr AH, Cimen M, Shiri J (2012) Suspended sediment modeling using genetic programming and soft computing techniques. J Hydrol 450:48–58

    Article  Google Scholar 

  • McKee TB, Doesken NJ, Kleist J (1993) The relationship of drought frequency and duration to time scales. In: Proceedings of the 8th Conference on Applied Climatology, vol 17, no 22, American Meteorological Society, Boston, pp 179–183

  • Mishra AK, Desai VR (2005) Drought forecasting using stochastic models. Stochastic. Environ Res Risk Assess 19(5):326–339

    Article  Google Scholar 

  • Mishra AK, Desai VR (2006) Drought forecasting using feed-forward recursive neural network. Ecol Model 198(1):127–138

    Article  Google Scholar 

  • Mishra AK, Singh VP (2010) A review of drought concepts. J Hydrol 391(1):202–216

    Article  Google Scholar 

  • Mishra AK, Singh VP (2011) Drought modeling—A review. J Hydrol 403(1):157–175

    Article  Google Scholar 

  • Mishra AK, Desai VR, Singh VP (2007) Drought forecasting using a hybrid stochastic and neural network model. J Hydrol Eng 12(6):626–638

    Article  Google Scholar 

  • Modarres R (2007) Streamflow drought time series forecasting. Stoch Environ Res Risk Assess 21(3):223–233

    Article  Google Scholar 

  • Morid S, Smakhtin V, Bagherzadeh K (2007) Drought forecasting using artificial neural networks and time series of drought indices. Int J Climatol 27(15):2103–2111

    Article  Google Scholar 

  • Pandey PK, Nyori T, Pandey V (2017) Estimation of reference evapotranspiration using data driven techniques under limited data conditions. Model Earth Syst Environ 1–13

  • Pangapanga PI, Jumbe CB, Kanyanda S, Thangalimodzi L (2012) Unravelling strategic choices towards droughts and floods’ adaptation in Southern Malawi. Int J Disaster Risk Reduct 2:57–66

    Article  Google Scholar 

  • Partal T, Cigizoglu HK, Kahya E (2015) Daily precipitation predictions using three different wavelet neural network algorithms by meteorological data. Stoch Environ Res Risk Assess 29(5):1317–1329

    Article  Google Scholar 

  • Reed PM, Hadka D, Herman JD, Kasprzyk JR, Kollat JB (2013) Evolutionary multiobjective optimization in water resources: the past, present, and future. Adv Water Resour 51(1):438–456

    Article  Google Scholar 

  • Schwarz G (1978) Estimating the dimension of a model. Annal Stat 6(2):461–464

    Article  Google Scholar 

  • Shamshirband S, Amirmojahedi M, Gocić M, Akib S, Petković D, Piri J, Trajkovic S (2015) Estimation of reference evapotranspiration using neural networks and cuckoo search algorithm. J Irrig Drain Eng 142(2):04015044

    Article  Google Scholar 

  • Sharma N, Zakaullah M, Tiwari H, Kumar D (2015) Runoff and sediment yield modeling using ANN and support vector machines: a case study from Nepal watershed. Model Earth Syst Environ 1(3):23

    Article  Google Scholar 

  • Sudheer KP, Gosain AK, Ramasastri KS (2003) Estimating actual evapotranspiration from limited climatic data using neural computing technique. J Irrig Drain Eng 129(3):214–218

    Article  Google Scholar 

  • Taormina R, Chau KW (2015) Neural network river forecasting with multi-objective fully informed particle swarm optimization. J Hydroinformatics 17(1):99–113

    Article  Google Scholar 

  • Tay FE, Cao L 2001 Application of support vector machines in financial time series forecasting. Omega 29(4):309–317

    Article  Google Scholar 

  • Udmale PD, Ichikawa Y, Manandhar S, Ishidaira H, Kiem AS, Shaowei N, Panda SN (2015) How did the 2012 drought affect rural livelihoods in vulnerable areas? Empirical evidence from India. Int J Disaster Risk Reduct 13:454–469

    Article  Google Scholar 

  • Vapnik V (1995) The nature of statistical learning theory. Springer Verlag, New York

    Book  Google Scholar 

  • Wagh VM, Panaskar DB, Muley AA, Mukate SV, Lolage YP, Aamalawar ML (2016) Prediction of groundwater suitability for irrigation using artificial neural network model: a case study of Nanded tehsil, Maharashtra, India. Model Earth Syst Environ 2(4):196

    Article  Google Scholar 

  • Wilhite DA, Glantz MH (1985) Understanding: the drought phenomenon: the role of definitions. Water Int 10(3):111–120

    Article  Google Scholar 

  • Wilhite DA, Rosenberg NJ, Glantz MH (1986) Improving federal response to drought. J Climate Appl Meteorol 25(3):332–342

    Article  Google Scholar 

  • Wu CL, Chau KW, Li YS (2008) River stage prediction based on a distributed support vector regression. J Hydrol 358(1):96–111

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Irrigation & Reclamation Engineering, Faculty of Agricultural Engineering & Technology, College of Agriculture & Natural Resources, University of Tehran, Karaj, Iran

    Seyed-Mohammad Hosseini-Moghari, Shahab Araghinejad & Ali Azarnivand

Authors
  1. Seyed-Mohammad Hosseini-Moghari
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Shahab Araghinejad
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Ali Azarnivand
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Seyed-Mohammad Hosseini-Moghari.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Hosseini-Moghari, SM., Araghinejad, S. & Azarnivand, A. Drought forecasting using data-driven methods and an evolutionary algorithm. Model. Earth Syst. Environ. 3, 1675–1689 (2017). https://doi.org/10.1007/s40808-017-0385-x

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s40808-017-0385-x

Keywords

Search

Navigation