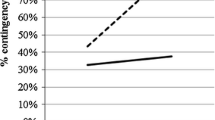
Abstract
College algebra has been noted as a critical course in post-secondary institutions because it serves as a gateway for major selection and college completion. Combinatorial topics like repeatable permutations are often overlooked in K-12 and undergraduate curricula. Likewise, students’ achievement and motivation are affected by the type of classroom climate created in the undergraduate mathematics classroom. Inquiry-based mathematical education (IBME) is a viable instructional approach because of its focus on community meaning-making of the mathematical content. However, lecture-style approaches still dominate post-secondary mathematics classrooms even though they have been criticized for their focus on procedural knowledge and disinviting environment. Therefore, the purpose of this quasi-experimental study was to test the effects of instructional approach (i.e., lecture-style vs. IBME) and social support (i.e., absence or presence) on undergraduate student motivation and achievement of combinatorial mathematics. Findings indicated that intentional social support-building – regardless of pedagogical method – had the strongest effects on students’ perceived autonomy-support, competence and achievement. Although no differing pedagogical effects were discovered (most likely due to the one-time implementation of the lesson formats), the findings provide evidence for the necessity of community-building efforts -- an aspect of education that is often overlooked in the undergraduate mathematics classroom.




Similar content being viewed by others
References
Adams, G. L., & Engelmann, S. (1996). Research on direct instruction: 25 years beyond DISTAR. Seattle: Educational Achievement Systems.
Aelterman, N., Vansteenkiste, M., Haerens, L. Boenens, B., Fontaine, J.R.J., & Reeve, J. (2018). Toward an integrative and fine-grained insight in motivation and demotivating teaching styles: The merits of a circumplex approach. Journal of Educational Psychology. Advance online publication. https://doi.org/10.1037/edu0000293.
Artigue, M., & Blomhøj, M. (2013). Conceptualizing inquiry-based education in mathematics. ZDM: The International Journal of Mathematics Education, 45, 797810. https://doi.org/10.1007/s11858-013-0506-6.
Betz, N. E., & Hackett, G. (1983). The relationship of mathematics self-efficacy expectations to the selection of science-based college majors. Journal of Vocational Behavior, 23, 329–345. https://doi.org/10.1016/0001-8791(83)90046-5.
Black, A. E., & Deci, E. L. (2000). The effects of instructors' autonomy support and students' autonomous motivation on learning organic chemistry: A self-determination theory perspective. Science Education, 84, 740–756. https://doi.org/10.1002/1098-237X(200011)84:6<740::AID-SCE4>3.0.CO;2-3.
Bressoud, D. (2015). Insights from the MAA National Study of college Calculus. Mathematics Teacher, 109, 179–185.
Bybee, R. W. (2015). The BSCS 5E instructional model: Creating teachable moments. Arlington: NSTA Press.
Bybee, R. W. (2019). Using the BSCS 5E instructional model to introduce STEM disciplines. Science & Children, 56(6), 8–12.
Bybee, R. W., Taylor, J. A., Gardner, A., Van Scotter, P., Powell, J. C., Westbrook, A., & Landes, N. (2006). The BSCS 5E instructional model: Origins and effectiveness. Colorado Springs: BSCS.
Castellanos, M. (2018). Examining Latinas’ STEM career decision-making process: A psychosociocultural approach. The Journal of Higher Education, 89, 527–552. https://doi.org/10.1080/00221546.2018.1435133.
Chen, B., Vansteenkiste, M., Beyers, W., Boone, L., Deci, E.L., Van der Kapp-Deeder, J … Verstuyf, J. (2015). Basic psychological need satisfaction, need frustration, and need strength across four cultures. Motivation and Emotion, 39, 216–236. https://doi.org/10.1007/s11031-014-9450-1.
Cheon, S. H., Reeve, J., & Moon, L. S. (2012). Experimentally-based, longitudinally designed, teacher-focused intervention to help physical education teachers be more autonomy supportive toward their students. Journal of Sport & Exercise Psychology, 34, 365–396.
Dawkins, P. C. (2017). On the importance of set-based meanings for categories and connectives in mathematical logic. International Journal of Research in Undergraduate Mathematics Education, 3, 496–522. https://doi.org/10.1007/s40753-017-0055-4.
Deci, E. L., & Ryan, R. M. (2000). The" what" and" why" of goal pursuits: Human needs and the self-determination of behavior. Psychological Inquiry, 11, 227–268. https://doi.org/10.1207/S15327965PLI1104_01.
Eagan, K. (2016). Becoming more student-centered? An examination of faculty teaching practices across STEM and non-STEM disciplines between 2004 and 2014: A report prepared for the Alfred P. Sloan Foundation.
Eizenberg, M. M., & Zaslavsky, O. (2004). Students’ verification strategies for combinatorial problems. Mathematical Thinking and Learning, 6, 12–36. https://doi.org/10.1207/s15327833mtl0601_2.
Ellis, J., Kelton, M. L., & Rasmussen, C. (2014). Student perceptions of pedagogy and associated persistence in calculus. ZDM: The International Journal on Mathematics Education, 46, 661–673. https://doi.org/10.1007/s11858-014-0577-z.
English, L. D. (2005). Combinatorics and the development of children’s combinatorial reasoning. In G. A. Jones (Ed.), Exploring probability in school: Challenges for teaching and learning (pp. 121–141). New York: Springer.
Estrada, M., Eroy-Reveles, A., & Matsui, J. (2018). The influence of affirming kindness and community on broadening participation in the STEM career pathways. Social Issues and Policy Review, 12, 258–297. https://doi.org/10.1111/sipr.12046.
European Schoolnet (2018). Science, Technology, Engineering and Mathematics Education Policies in Europe. Scientix Observatory report. October 2018, European Schoolnet, Brussels.
Ferguson, C. J. (2009). An effect size primer: A guide for clinicians and researchers. Professional Psychology: Research and Practice, 40, 532–538. https://doi.org/10.1037/a0015808.
Freeman, S., Eddy, S. L., McDonough, M., Smith, M. K., Okoroafor, N., Jordt, H., & Wenderoth, M. P. (2014). Active learning increases student performance in science, engineering, and mathematics. PNAS, 111, 8410–8415 www.pnas.org/cgi.doi/10.1073/pnas.1319030111.
Frisby, B. N., & Martin, M. M. (2010). Instructor-student and student-student rapport in the classroom. Communication Education, 59, 146–164. https://doi.org/10.1080/03634520903564362.
Gorham, J. (1988). The relationship between verbal teacher immediacy behaviors and student learning. Communication Education, 37, 40–53. https://doi.org/10.1080/03634528809378702.
Haberler, Z., Laursen, S. L., & Hayward, C. N. (2018). What’s in a name? Framing struggles of a mathematics education reform community. International Journal of Research in Undergraduate Mathematics Education, 4, 415–441. https://doi.org/10.1007/s40753-018-0079-4.
Hattie, J. (2009). Visible learning: A synthesis of over 800 meta-analyses relating to achievement. New York: Routledge.
Hattie, J., Fisher, D., & Frey, N. (2017). Visible learning for mathematics: What works best to optimize student learning. Thousand Oaks: Corwin.
Hayward, C. N., Kogan, M., & Laursen, S. L. (2016). Facilitating instructor adoption of inquiry-based learning in college mathematics. International Journal of Research in Undergraduate Mathematics, 2, 59–81. https://doi.org/10.1007/s40753-015-0021-y.
Herriott, S. R., & Dunbar, S. R. (2009). Who takes college algebra? PRIMUS, 19, 74–87. https://doi.org/10.1080/10511970701573441.
Hu, S., Kuh, G. D., & Li, S. (2008). The effects of engagement in inquiry-oriented activities on student learning and personal development. Innovative Higher Education, 33, 71–82. https://doi.org/10.1007/s10755-008-9066-z.
Johnson, E., Keller, R., & Fukawa-Connelly, T. (2018). Results from a survey of abstract algebra instructors across the United States: Understanding the choice to (not) lecture. International Journal of Research in Undergraduate Mathematics, 4, 254–285. https://doi.org/10.1007/s40753-017-0058-1.
Keller, M. M., Woolfolk Hoy, A., Goetz, T., & Frenzel, A. C. (2016). Teacher enthusiasm: Reviewing and redefining a complex construct. Educational Psychology Review, 28, 743–769. https://doi.org/10.1007/s10648-015-9354-y.
Kirschner, P. A., Sweller, J., & Clark, R. E. (2006). Why minimal guidance during instruction does not work: An analysis of the failure of constructivist, discovery, problem-based, experiential, and inquiry-based teaching. Educational Psychologist, 41, 75–86. https://doi.org/10.1080/00461520701263426.
Klahr, D., & Nigam, M. (2004). The equivalence of learning paths in early science instruction effects of direct instruction and discovery learning. Psychological Science, 15, 661–667. https://doi.org/10.1111/j.0956-7976.2004.00737.x.
Kozioff, M. A., LaNunziata, L., Cowardin, J., & Bessellieu, F. B. (2001). Direct instruction: Its contributions to high school achievement. The High School Journal, 84(2), 54–71.
Kranzler, J. H., & Pajares, F. (1997). An exploratory factor analysis of the mathematics self-efficacy scale revised (MSES-R). Measurement and Evaluation in Counseling and Development, 29, 215–228.
Lahdenperä, J., Postareff, L., & Rämö, J. (2018). Supporting quality of learning in university mathematics: A comparison of two instructional designs. International Journal of Research in Undergraduate Mathematics. https://doi.org/10.1007/s40753-018-0080-y.
Laursen, S. L., & Rasmussen, C. (2019). I on the prize: Inquiry approaches in undergraduate mathematics. International Journal of Research in Undergraduate Mathematics, 5, 129–146. https://doi.org/10.1007/s40753-019-00085-6.
Laursen, S. L., Hassi, M. L., Kogan, M., & Weston, T. J. (2014). Benefits for women and men of inquiry-based learning in college mathematics: A multi-institution study. Journal for Research in Mathematics Education, 45, 406–418. https://doi.org/10.5951/jresematheduc.45.4.0406.
Lin, Y., Durbin, J. M., & Rancer, A. S. (2017). Perceived instructor argumentativeness, verbal aggressivness, and classroom climate in relation to student state motivation and math anxiety. Communication Education, 66, 330–349. https://doi.org/10.1080/03634523.2016.1245427.
Lockwood, E. (2013). A model of students’ combinatorial thinking. Journal of Mathematical Behavior, 32, 251–265. https://doi.org/10.1016/j.jmathb.2013.02.008.
Lockwood, E., Wasserman, N. H., & McGuffey, W. (2018). Classifying combinations: Investigating undergraduate students’ responses to different categories of combination problems. International Journal of Research in Undergraduate Mathematics, 4, 305–322. https://doi.org/10.1007/s40753-018-0073-x.
Marsh, H. W., & Hattie, J. (2002). The relation between research productivity and teaching effectiveness: Complementary, antagonistic, or independent constructs? Journal of Higher Education, 73, 603–641. https://doi.org/10.1080/00221546.2002.11777170.
McAuley, E., Duncan, T., & Tammen, V. V. (1987). Psychometric properties of the intrinsic motivation inventory in a competitive sport setting: A confirmatory factor analysis. Research Quarterly for Exercise and Sport, 60, 48–58. https://doi.org/10.1080/02701367.1989.10607413.
McDuffie, A. R., & Graeber, A. O. (2003). Institutional norms and policies that influence college mathematics professors in the process of changing to reform-based practices. School Science and Mathematics, 103, 331–344. https://doi.org/10.1111/j.1949-8594.2003.tb18210.x.
Moreno, S. E., & Muller, C. (1999). Success and diversity: The transition through first-year calculus in the university. American Journal of Education, 108, 30–57.
Niemiec, C. P., & Ryan, R. M. (2009). Autonomy, competence, and relatedness in the classroom: Applying self-determination theory to educational practice. Theory and Research in Education, 7, 133–144. https://doi.org/10.1177/1477878509104318.
Niemiec, C. P., Lynch, M. F., Vansteenkiste, M., Bernstein, J., Deci, E. L., & Ryan, R. M. (2006). The antecedents and consequences of autonomous self-regulation for college: A self-determination theory perspective on socialization. Journal of Adolescence, 29, 761–775. https://doi.org/10.1016/j.adolescence.2005.11.009.
Patrick, H., Ryan, A., & Kaplan, A. (2007). Early adolescents' perceptions of the classroom social environment, motivational beliefs, and engagement. Journal of Educational Psychology, 99, 83–98. https://doi.org/10.1037/0022-0663.99.1.8.
President’s Council of Advisors on Science and Technology (PCAST) (2012). Engage to excel: Producing one million additional college graduates with degrees in science, technology, engineering, and mathematics (Executive Report). Retrieved from The White House Office of Science and Technology Policy website: http://www.whitehouse.gov/sites/default/files/microsites/ostp/pcast-executive-report-final_2-13-12.pdf
Rakes, C. R., Valentine, J. C., McGatha, M. B., & Ronau, R. N. (2010). Methods of instructional improvement in algebra: A systematic review and meta-analysis. Review of Educational Research, 80, 372–400. https://doi.org/10.3102/0034654310374880.
Rasmussen, C., & Kwon, O. N. (2007). An inquiry-oriented approach to undergraduate mathematics. Journal of Mathematical Behavior, 26, 189–194. https://doi.org/10.1016/j.jmathb.2007.10.001.
Rasmussen, C., & Marrongelle, K. (2006). Pedagogical content tools: Integrating student reasoning and mathematics into instruction. Journal for Research in Mathematics Education, 37, 388–420. https://doi.org/10.2307/30034860.
Reeve, J. (2006). Teachers as facilitators: What autonomy-supportive teachers do and why their students benefit. The Elementary School Journal, 106, 225–236. https://doi.org/10.1086/501484.
Reeve, J., & Jang, H. (2006). What teachers say and do to support students' autonomy during a learning activity. Journal of Educational Psychology, 98, 209–218. https://doi.org/10.1037/0022-0663.98.1.209.
Reeve, J., Bolt, E., & Cai, Y. (1999). Autonomy-supportive teachers: How they teach and motivate students. Journal of Educational Psychology, 91, 537–548. https://doi.org/10.1037/0022-0663.91.3.537.
Reeve, J., Ryan, R. M., Deci, E. L., & Jang, H. (2007). Understanding and promoting autonomous self-regulation: A self-determination theory perspective. In D. Schunk & B. Zimmerman (Eds.), Motivation and self-regulated learning: Theory, research, and application (pp. 223–244). Mahwah: Lawrence Erlbaum Associates Publishers.
Richmond, V. P., Gorham, J. S., & McCroskey, J. C. (1987). The relationship between selected immediacy behaviors and cognitive learning. Communication Yearbook, 10, 574–590. https://doi.org/10.1080/23808985.1987.11678663.
Rockswald, G. K. (2012). Essentials of college algebra with modeling and visualizations (4th ed.). New York: Pearson.
Rodríguez-Meirinhos, A., Antolín-Suárez, L., Brenning, K., Vansteenkiste, M., & Olivia, A. (2019). A bright and dark path to adolescents’ functioning: The role of need satisfaction and need frustration across gender, age, and socioeconomic status. Journal of Happiness Studies. Advanced online publication. https://doi.org/10.1007/s10902-018-00072-9.
Ryan, R. M. (1982). Control and information in the intrapersonal sphere: An extension of cognitive evaluation theory. Journal of Personality and Social Psychology, 43, 450–461. https://doi.org/10.1037/0022-3514.43.3.450.
Ryan, R. M., & Deci, E. L. (2017). Self-determination theory: Basic psychological needs in motivation, development, and wellness. New York: The Guilford Press.
Salazar, D.A. (2014). Salazar’s grouping method: Effects on student’s achievement in integral calculus. Journal of Education and Practice, 5, 119–126.
Salazar, D. A. (2015). Razalas’ grouping method and mathematics achievement. Journal of Education and Practice, 6(8), 118–127.
Smith, B. (2015). The evolution of my rapport: One professor's journey to building instructor/student relationships. College Teaching, 63, 35–36. https://doi.org/10.1080/87567555.2014.999023.
Spector, B., Burkett, R. S., & Leard, C. (2007). Mitigating resistance to teaching science through inquiry: Studying self. Journal of Science Teacher Education, 18, 185–208. https://doi.org/10.1007/s10972-006-9035-2.
Stains, M., Harshman, J., Barker, M. K., Chasteen, S. V., Cole, R., DeChenne-Peters, S. E., et al. (2018). Anatomy of STEM teaching in north American universities. Science Education, 359, 1468–1470. https://doi.org/10.1126/science.aap8892.
Starcher, K. (2011). Intentionally building rapport with students. College Teaching, 59, 162. https://doi.org/10.1080/87567555.2010.516782.
Stigler, J. W., Givvin, K. B., & Thompson, B. J. (2010). What community college developmental mathematics students understand about mathematics. MathAMATYC Educator, 1(3), 4–16.
Sun, S., Pan, W., & Wang, L. L. (2010). A comprehensive review of effect size reporting and interpreting practices in academic journals in education and psychology. Journal of Educational Psychology, 102, 989–1004. https://doi.org/10.1037/a0019507.
Tabachnick, B. G., & Fidell, L. S. (2013). Using multivariate statistics (6th ed.). Boston: Pearson Education.
Trusty, J., Thompson, B., & Petrocelli, J. V. (2004). Practical guide for reporting effect size in quantitative research in the “journal of counseling & development”. Journal of Counseling & Development, 82, 107–110. https://doi.org/10.1002/j.1556-6678.2004.tb00291.x.
Vansteenkiste, M., & Ryan, R. M. (2013). On psychological growth and vulnerability: Basic psychological need satisfaction and need frustration as a unifying principle. Journal of Psychotherapy Integration, 23, 263–280. https://doi.org/10.1037/a0032359.
Walker, J. T., Martin, T. M., Haynie, L., Norwood, A., White, J., & Grant, L. (2007). Preferences for teaching methods in a baccalaureate nuring program: How second-degree and traditional students differ. Nursing Education Perspectives, 28, 246–250.
Washburn, M. H. (2004). Is your classroom woman-friendly?: Ten strategies for reaching this goal. College Teaching, 52(4), 156–159. https://doi.org/10.3200/CTCH.52.4.156-159.
Westermann, K., & Rummel, N. (2012). Delaying instruction: Evidence from a study in a university relearning setting. Instructional Science, 40, 673–689. https://doi.org/10.1007/s11251-012-9207-8.
Williams, G. C., & Deci, E. L. (1996). Internalization of biopsychosocial values by medical students: A test of self-determination theory. Journal of Personality and Social Psychology, 70, 767–779. https://doi.org/10.1037/0022-3514.70.4.767.
Wright, E. L., Sunal, D. W., & Day, J. B. (2004). Reform in undergraduate science classrooms. In D. W. Sunal, E. L. Wright, & J. B. Day (Eds.), Reform in undergraduate science teaching for the 21st century (pp. 137–152). Greenwich: Information Age Publishing.
Yu, S., Levesque-Bristol, C., & Vasteenkiste, M. (2018). Chinese education examined via the lens of self-determination. Educational Psychology Review, 30, 177–214. https://doi.org/10.1007/s10648-016-9395-x.
Acknowledgements
This research was supported in part by a Faculty-Undergraduate Student Engagement (FUSE) grant from Western Kentucky University.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of Interest
On behalf of all authors, the corresponding author states that there is no conflict of interest.
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
Appendix 1
Appendix 2
Name: __________________________.
Summative Evaluation Rubric
Question | Description | Score |
|---|---|---|
Q1 | Give one point for each of the following: -Student uses logic (no formula) to try and find a solution -Student finds correct number of permutations | /2 |
Q2 | Student finds correct number of permutations using the mathematical relationship nr | /1 |
Q3a | Give one point for each of the following: -Student states problem is not a repeatable permutation -Student states that chairs are not repeatable | /2 |
Q3b | Give one point for each of the following: -Student states problem is a repeatable permutation -Student states that order of the numbers matters -Student states that numbers are repeatable -Student identifies n as 6 (or the number of different options on the die) -Student identifies r as 3 (or the number of times the die was rolled) -Student states that solution is 216, or 63 | /6 |
Q3c | Give one point for each of the following: -Student states problem is a repeatable permutation -Student states that order of the numbers matters -Student states that numbers are repeatable -Student identifies n as 10 (or the numbers to choose from) -Student identifies r as 9 (or the number of spaces in the password) -Student states that solution is 109 | /6 |
Total | /17 |
The percentage I got correct is: ____________.
Appendix 3
Rights and permissions
About this article
Cite this article
Duffin, L.C., Keith, H.B., Rudloff, M.I. et al. The Effects of Instructional Approach and Social Support on College Algebra Students’ Motivation and Achievement: Classroom Climate Matters. Int. J. Res. Undergrad. Math. Ed. 6, 90–112 (2020). https://doi.org/10.1007/s40753-019-00101-9
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40753-019-00101-9