Abstract
Transient climate sensitivity tends to increase on multiple timescales in climate models subject to an abrupt CO2 increase. The interdependence of radiative and ocean heat uptake processes governing this increase are reviewed. Heat uptake tends to be spatially localized to the subpolar oceans, and this pattern emerges rapidly from an initially uniform distribution. Global climatic impact of heat uptake is studied through the lens of the efficacy concept and a linear systems perspective in which responses to individual climate forcing agents are additive. Heat uptake can be treated as a slowly varying forcing on the atmosphere and surface, whose efficacy is strongly determined by its geographical pattern. An illustrative linear model driven by simple prescribed uptake patterns demonstrates the emergence of increasing climate sensitivity as a consequence of the slow decay of high-efficacy subpolar heat uptake. Evidence is reviewed for the key role of shortwave cloud feedbacks in setting the high efficacy of ocean heat uptake and thus in increasing climate sensitivity. A causal physical mechanism is proposed, linking subpolar heat uptake to a global-scale increase in lower-tropospheric stability. It is shown that the rate of increase in estimated inversion strength systematically slows as heat uptake decays. Variations in heat uptake should therefore manifest themselves as differences in low cloud feedbacks.
Similar content being viewed by others
Introduction
Climate change is driven first and foremost by sustained differences between incoming and outgoing radiation at the top of the atmosphere. Accordingly, scientific study of climate change is anchored in the planetary energy budget. All climate models, from the simplest toy model to the most sophisticated coupled Earth System Model, solve a thermodynamic problem of the form
where E represents the energy content of the system (atmosphere, ocean, land, and ice), R is the net downward radiative flux at the top of the atmosphere, and the overbars denote a global average.
Addition of CO2 or other radiatively active substance to the atmosphere pushes the energy budget out of balance by a certain amount \(\overline {F}\), causing energy to accumulate in the Earth system and leading to changes in (among other things) surface temperature \(\overline {T_{s}}\). Given enough time, the radiative imbalance \(\overline {R}\) will decay back toward zero as a warmer planet emits more energy to space. The equilibrium climate change \({\Delta } \overline {T_{s}}\) can then be characterized by
where λ is a constant of proportionality between radiative forcing and equilibrium temperature response.Footnote 1 This is the forcing–feedback framework that has long been used to quantify equilibrium climate sensitivity. The Charney Report [13] gave a likely range of λ = 1.7±0.8 W m −2 K −1, and that range has remained remarkably similar over time [8, 21].
Is Eq. 2 anything more than a diagnostic statement about the equilibrium change in response to a specific set of forcing agents? Does λ quantify the complex feedback processes operating in a climate model or in nature in a physically meaningful way that can then be applied to non-equilibrium, time-evolving and spatially complex climate variations? Such questions have been studied at length as the focus of the scientific community has shifted from equilibrium sensitivity [11–13, 30, 32] to transient response [2–4, 25, 26, 28, 31, 33, 35, 44, 50, 57, 63, 65].
Climate feedback analysis is based on the notion that the TOA radiative response scales first and foremost with the global mean \({\Delta } \overline {T_{s}}\). Then, the RHS of Eq. 2 is effectively a linear Taylor-series expansion of this response [38, 51]. It is then natural to separate the radiative response into additive components associated with individual physical processes affecting either the longwave (LW) or shortwave (SW) flux (e.g., changes in water vapor, lapse rate, cloudiness, and surface albedo). If each of these processes scale with \({\Delta } \overline {T_{s}}\) and are physically independent to leading order, then individual additive contributions to λ can be computed. Such calculations give insight into the processes determining climate sensitivity and its uncertainties [21, 59].
Equilibrium climate sensitivity is an important but strictly theoretical benchmark. Because of the great thermal inertia and dynamic nature of the oceans, we live now and forevermore in a transient world with a non-equilibrium energy budget. Under transient climate change, the planet gains energy at a rate \(d\overline {E}/dt = \overline {N}(t)\). Strictly speaking, \(\overline {N}(t)\) is the TOA imbalance, but this is usually assumed to be equivalent to the rate of ocean heat uptake (OHU)—an excellent assumption on timescales longer than 1 year [26, 45].
Assuming that an analogous linearization of the TOA radiative response is valid in the transient regime, the planetary energy budget is
We include an explicit time-dependence for λ because it is well-established that AOGCMs exhibit such time-dependence. More specifically, as we review below, most models exhibit increasing climate sensitivity (or decreasing feedback parameter λ) during transient adjustment to steady radiative forcing.
The main thesis of this paper is that there are systematic, physical, and causal links between OHU and TOA radiative response that give rise to time-dependent climate sensitivity. Simply put, \(\overline {N}\) and λ in Eq. 3 are not physically independent. We focus on steady radiative forcing and the abrupt CO2 quadrupling experiments in CMIP5 [61] (rather than specific future scenarios or the so-called Transient Climate Response under gradually increasing CO2 [21]) in order to understand processes and timescales internal to the climate system.
Our paper is laid out as follows. In “Ocean Heat Uptake and Time-Dependent Climate Sensitivity,” we review the spatial patterns of OHU and time-dependent climate sensitivity in the CMIP5 models. In “Linearity, Efficacy, and Feedback,” we review the concept of efficacy of a climate forcing agent, its connection to a linear systems view of climate change, and the extension of these ideas to the concept of a slowly varying OHU as a high-efficacy forcing on transient warming. In “An Illustrative Linear Model of Time-Dependent Climate Sensitivity,” we implement this concept in a strictly linear illustrative model driven by combinations of CO2 radiative forcing and simple prescribed patterns of OHU. This model demonstrates how time-dependent climate sensitivity emerges as a consequence of the slow decay of a high-efficacy subpolar mode of OHU. In “What Determines the Efficacy of Ocean Heat Uptake?”, we review classic and recent results showing the key role of SW cloud feedbacks in the increasing climate sensitivity. We propose a causal physical mechanism for this connection: subpolar OHU drives a global-scale increase in lower-tropospheric stability, and gradual waning of this effect leads to increasing rates of low cloud loss during transient warming. Some new evidence for this mechanism from CMIP5 models is presented. In “Conclusion” we offer a summary and future research priorities.
Ocean Heat Uptake and Time-Dependent Climate Sensitivity
Spatial Patterns of Ocean Heat Uptake
Ocean heat uptake occurs through sustained delivery of disequilibrium water from depth to the upper ocean, which is in turn strongly thermally coupled to the atmosphere through sea surface heat fluxes [25]. These mixing processes are spatially complex [4, 6, 16, 25, 53, 65] and largely determined by ocean dynamics [16, 25, 40]. Preferred locations for the “delayed warming” associated with OHU include the Southern Ocean and the northern North Atlantic. AOGCMs are rarely integrated out to equilibrium due to the long timescales and computational cost. One study with ECHAM5/MPIOM found equilibration timescales of about 1200 years for the surface and 5000 years for the deep ocean [39].
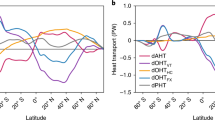
On short timescales, there can be substantial variation in the spatial structure of OHU. Figure 1 (reproducing Fig. A1 from Rose et al. [53]) shows zonally averaged OHU from CMIP5 models [61] for two time slices following abrupt quadrupling of CO2. OHU is relatively uniform across the globe for the first few years, as the entire upper ocean is out of equilibrium. By year 100, there is reasonable agreement across the models that OHU is largely localized to the subpolar oceans. The spatial structure of oceanic heat storage is not the same due to ocean circulation and heat transport [40], with substantial inter-model variability [22]. However, from a radiative perspective, the key quantity is the pattern of anomalous surface heat fluxes as plotted in Fig. 1. We take these fluxes as synonymous with OHU even though the fluxes are positive (out of the ocean) in some locations. The influence of this spatial structure on radiative processes will be discussed below.
(Reproduction of Fig. A1 of [53]) Net surface heat flux anomalies (positive up) in CMIP5 models immediately following abrupt quadrupling of CO2 (a) and after 100 years (b). Black curve shows ensemble mean of 16 different AOGCMs. Also shown: the idealized heat uptake scenarios q H (blue) and q T (red) used in aquaplanet simulations [53, 55], discussed further below. The CMIP5 models used here are ACCESS1-0, BCC-CSM1-1, CanESM2, CCSM4, CSIRO-Mk3-6-0, GFDL-CM3, GFDL-ESM2G, GFDL-ESM2M, INM-CM4, IPSL-CM5A-LR, IPSL-CM5B-LR, MIROC5, MIROC-ESM, MPI-ESM-LR, MRI-CGCM3, and NorESM1-M
Time-Dependence of the Transient Energy Budget
Systematic study of the factors governing transient climate change began in the 1990s with the widespread use of coupled AOGCMs. Time variations in the simulated λ have since been noted and discussed by many authors [2–4, 23, 24, 26, 27, 38, 44, 50, 57, 63, 65].
Gregory et al. [27] first suggested using the transient response of an AOGCM to an abrupt, steady radiative forcing to estimate equilibrium climate sensitivity. The method is illustrated here in Fig. 2 for the CMIP5 abrupt CO2 quadrupling scenarios and two different models (CCSM4 and GFDL-CM3, see Table 1). Global, annual average TOA radiation \(\overline {R}\) is plotted against the surface temperature anomaly \({\Delta } \overline {T_{s}}\) in a scatterplot spanning the 150-year simulation. Linear regression is used to calculate “effective radiative forcing” ERF (the intercept at \({\Delta } \overline {T_{s}}=0\)), “effective climate sensitivity” ΔT e f f (extrapolation to equilibrium at \({\Delta } \overline {R} = 0\)), and the feedback parameter λ (the slope in W m −2 K −1). This was the basis of the equilibrium climate sensitivity values reported in the IPCC AR5 [21].Footnote 2 Similar plots for other CMIP5 models appear in [3]. Such figures are colloquially known as “Gregory plots” in honor of their progenitor [27].
The evolving planetary energy budgets in two CMIP5 AOGCMS after abrupt quadrupling of CO2 presented as Gregory plots [27], i.e., scatterplots of \(\overline {R}\) versus \({\Delta } \overline {T_{s}}\). Each data point represents a global, annual average. A single ensemble member was used for each model. The two models are the NCAR CCSM4 and the GFDL-CM3. Red lines are regressions for different time intervals, with their slopes listed in units of W m −2 K −1 in the legend. The red arrows indicate the effective radiative forcing ERF and effective climate sensitivity ΔT e f f for 4 ×CO 2, as defined in the IPCC AR5 [21]
Figure 2 illustrates several long-running themes in the literature. The two models disagree quantitatively on forcing, feedback, and climate sensitivity; however, both exhibit increasing sensitivity with time. As indicated by the concave curvature of the scatterplots, the slope λ decreases as the models warm up. The radiative imbalance decays most rapidly per degree warming over the first few years, and more slowly thereafter. Both models in fact show that the slope continues to decrease throughout the 150-year simulation.
The roughly 1 W m −2 difference between the intercepts of the 10-year regression lines (dashed) and the 150-year regression lines (solid) can be interpreted as part of the “rapid adjustment” of the radiative forcing advocated by Williams et al. [63]. However, the physics of this adjustment is not entirely clear. Previous studies have revealed radiatively-important rapid tropospheric adjustments to CO2 forcing that occur independently of surface warming [1, 14, 29, 33, 58]. On scales of years to decades, the adjustment must include an active role for the oceans, which may not be cleanly separable from stratospheric and tropospheric adjustments [56]. We submit that the adjustment in Fig. 2 is intimately linked to the changing pattern of OHU pictured in Fig. 1, consistent with [56]. On the other hand, Fig. 2 also shows that λ continues to decrease over the second half of the simulations, during which time the dominance of subpolar OHU is well-established. We will return to these points below.
The curvature in Fig. 2 suggests that ΔT e f f (based on 150 years of integration following the methodology of the IPCC AR5 [21]) is an underestimate of the true equilibrium climate sensitivity. This curvature seems to be a robust feature of CMIP5 models [2, 26, 38]. We would like to better understand the physical mechanisms governing this increase in climate sensitivity in the AOGCMs, along with any potential implications for detectability of climate sensitivity from inherently transient observations.
Linearity, Efficacy, and Feedback
How linear is the climate system under transient warming? Some have posited that the curvature in Fig. 2 is indicative of a genuinely non-linear set of interactions governing the transient radiative feedback in AOGCMs [2, 38, 42, 48]. This calls into the question the value of linear models such as Eq. 3. On the other hand, other ways of expressing the leading-order linearity of the climate system may be more useful for understanding transient climate change [26]. It is certainly worth a careful look; linearity is too powerful an analytical tool to be abandoned lightly.
Efficacy of a Climate Forcing and Additive Responses
Radiative forcing agents are not all equal in their ability to drive climate change; that is, the proportionality λ between \(\overline {F}\) and \({\Delta } \overline {T_{s}}\) varies for different agents [17, 32, 41]. The “efficacy” factor is the amount of warming produced per W m −2 of a particular forcing agent relative to the CO2 standard [33]. For example, both ozone and volcanic forcing are found to cause substantially less warming per W m −2 than CO2 and thus have efficacies smaller than 1 – with implications for observationally based estimates of equilibrium climate sensitivity [41].
The efficacy concept is rooted in a different linearity assumption than underlies Eq. 2. Efficacy can only be measured in single-forcing model simulations. The key assumption is that the climate response to multiple forcing agents is additive. Specifically, if each agent exerts a radiative forcing \(\overline {F_{i}}\), elicits a response \({\Delta } \overline {T_{i}}\), and these are related by \(\overline {F_{i}} = \lambda _{i} {\Delta } \overline {T_{i}}\) , then the response to the combined forcing \({\sum }_{i} \overline {F_{i}}\) is
where in the last equality ε i = λ C O2/λ i are the efficacies of each agent.
Expanding out Eq. 2 for this combined forcing case and solving for λ gives
The combined feedback λ is a weighted average of feedbacks on individual forcings, where the weighting is the fraction of the total temperature response caused by that particular forcing. It is important to recognize that, in the presence of forcing agents with non-unit efficacy, the feedbacks are not additive in the same proportion as the forcing and response, even if the climate system is linear and Eq. 4 holds.
The additive assumption Eq. 4 has been tested in many types of climate models, and is generally a good approximation [7, 17, 41, 53]. There are of course some limitations to this perspective. Large climate changes involving significant changes in sea ice extent can involve demonstrably non-linear threshold and hysteresis behavior [20, 52, 54]. However, there is little evidence of such threshold behavior in future global warming scenarios [5]. The assumption in Eq. 4—which has been called “system linearity” as opposed to “linearity in time” [26]—may be the most useful starting point for theories of climate sensitivity [24, 26, 35, 65].
Efficacy of Ocean Heat Uptake
Winton et al. [65] proposed thinking about OHU as a forcing on the atmosphere and sea surface, rather than strictly a response of the coupled system. This takes advantage of the clear timescale separation between the tightly coupled atmosphere-upper ocean system and the deep ocean heat uptake processes [24, 35, 38]. One supposes that ocean dynamics impose a quasi-fixed heat sink upon the upper ocean, and the fast components of the climate system remain close to equilibrium with this heat sink and the radiative forcing. Invoking the additive assumption Eq. 4, the transient warming is interpreted as
where \({\Delta } \overline {T_{CO2}}\) is the equilibrium warming, and \({\Delta } \overline {T_{OHU}}(t) < 0\) is a cooling driven by slowly varying OHU. Several authors have invoked this concept in a linear two-box model, representing OHU as a diffusive mixing between the upper and deep ocean [24–26, 35]. The conceptual advantage of this perspective is that it permits investigation of the impact of OHU on the atmospheric radiative-dynamical processes that determine λ(t). Since \(\overline {N}\) is now just another type of forcing, we can quantify its efficacy relative to CO2 as above. The efficacy is simply the ratio ε = λ C O2/λ O H U of feedback parameters that would operate on CO2 or OHU in isolation [53].
The curvature of the Gregory plots in Fig. 2 indicates that ε in the abrupt CO2-quadrupling scenario is larger than 1. That is to say, it takes less than 1 W m −2 of OHU to fully mitigate the global warming from 1 W m −2 of CO2-induced radiative forcing. This is a relatively robust feature of the CMIP5 models. Geoffroy et al. [23] compute ε for the CMIP5 models by fitting to the two-box model with an efficacy factor for deep ocean heat uptake. Their formulation is identical to that presented above on timescales for which the upper ocean is in quasi-equilibrium. They report a multi-model mean ε = 1.28 with a standard deviation of 0.25.
From Eqs. 5 and 6, the transient feedback is
For example, at the time the coupled system has achieved half its equilibrium warming, \({\Delta } \overline {T_{CO2}} / {\Delta } \overline {T} = 2\) and \({\Delta } \overline {T_{OHU}} / {\Delta } \overline {T} = -1\). For a system with ε > 1, Eq. 7 then implies that λ(t)>λ C O2. As the system approaches equilibrium, \({\Delta } \overline {T_{OHU}} \rightarrow 0\) and λ(t) → λ C O2. Decreasing λ, or equivalently, increasing climate sensitivity, is a direct consequence of the large efficacy of OHU.
While ε is robustly greater than 1 in the CMIP5 models, it is not necessarily steady in time. Paynter and Frölicher [46] showed that ε(t) increases from about 1.4 to values greater than 2 during the first 180 years following abrupt CO2-quadrupling in the GFDL-CM3. It is important to understand the physical origins of this non-unit efficacy of OHU, as well as how it may vary in time and across models.
Rose et al. [53] used idealized slab ocean GCM simulations to quantify \({\Delta } \overline {T_{OHU}}\) and ε for two simple prescribed OHU patterns. These patterns (denoted as q H and q T for “high latitudes” and “tropics,” respectively) are sketched in Fig. 1. q H is an idealization of the subpolar OHU pattern typically found in transient AOGCMs, while q T might be considered analogous to a La-Niña-like enhancement of tropical heat uptake [55]. While in both cases the OHU is spatially localized, the response is global [53, 55]. It is also strongly dependent on the spatial structure of OHU. In a small ensemble of idealized GCMs, the efficacy of q H ranges from 1.6 to 2.2, while the efficacy of q T ranges from 0.5 to 0.6 [53]. Removing 1 W m −2 from the subpolar sea surface is a far more effective way to cool the planet than removing the same 1 W m −2 from the tropical sea surface, by a factor of 3 to 4.
While highly idealized, these results suggests that the efficacy of OHU is strongly determined by its spatial pattern. More specifically, ε > 1 in the CMIP5 models first and foremost because of the subpolar maximum in OHU (Fig. 1). This is consistent with the efficacy of radiative forcing agents and “ghost forcings” [32, 33, 36]. Surface-based, high-latitude forcings are typically the most effective at changing global surface temperatures. It is also possible (though not yet demonstrated) that inter-model spread in ε [23, 65], as well as unforced temporal variations in ε(t) [46], may be primarily due to variations in the spatial pattern of OHU (e.g., the spread in Fig. 1).
The Local Feedback Perspective
Some radiative feedback processes are highly localized. The classic example is the surface albedo feedback, which has global consequences but is driven by surface temperature change at locations near the snow and ice edge. In the context of transient climate change with time-dependent warming patterns [2], the accuracy of Eq. 3 might be improved by using a local linearization of the energy budget
where r is a geographical location, F is the anomalous atmospheric heat transport, and λ l o c is a locally defined feedback parameter [4, 15, 18, 19, 53]—the proportionality between local surface temperature and local TOA radiative response.
The local perspective Eq. 8 introduces substantial complexity, particularly involving F and its interactions with radiative processes [4, 43, 53]. Its worth as a conceptual tool depends on whether it provides new simple insights into climate sensitivity.
One possibility is that λ l o c (r) is more universal than global λ: local radiation may correlate strongly with local temperatures regardless of the global structure of the climate forcing and response. In this perspective, efficacies (whether of radiative forcings or OHU) are determined by spatial patterns of warming ΔT(r) activating local feedbacks. For example, sea ice retreat in the Southern Ocean is associated with strongly positive local feedbacks, but these are suppressed while OHU delays the local warming. Boer and Yu [7] first showed that ΔT(r) is strongly shaped by spatial patterns of λ l o c (r) in a GCM, and in fact argued that the additive principle Eq. 4 is a consequence of fixed λ l o c (r).
Armour et al. [4] invoked the assumption of fixed λ l o c (r) to explain time-dependence of λ(t) in transient climate change. The CCSM4 energy budget in Fig. 2 is well-approximated by convolving the simulated time-dependent ΔT(r,t) with a fixed local feedback λ l o c (r) [4], itself diagnosed from an equilibrium 2 ×CO 2 scenario in a slab ocean version of the same model [6].
The problem with the local perspective is twofold. First, it does not necessarily get us closer to understanding the rate and pattern of surface warming ΔT(r,t), which requires knowledge of (or closure assumptions for) N(r,t) and ∇⋅F(r,t) (the OHU and dynamic heating rate, respectively). Secondly, the assumption that λ l o c (r) is independent of N(r) has been directly tested and found to be false: CO2,q H and q T each excite a unique feedback pattern λ l o c (r) in idealized GCMs [53], dominated by differences in lapse rate and SW cloud feedbacks. There is no universal rule coupling local warming to local radiation. Instead, the response to each different forcing and OHU pattern must be understood as a global-scale, non-local dynamic adjustment of the atmosphere with unique vertical structures [55]. Rather than the additive principle following from local feedbacks [7], we posit that the response of the climate system to complex and time-evolving forcing is best understood as an additive but non-local response to individual simple forcings.
An Illustrative Linear Model of Time-Dependent Climate Sensitivity
We are advocating for a linear systems approach to understanding transient warming, driven by a time-evolving OHU. Here, we provide an illustrative model of this perspective. We suppose that Eq. 6 is exact, and that \({\Delta } \overline {T_{CO2}}\) can be measured from equilibrium single-forcing simulations in shallow slab ocean GCMs. Furthermore, a spatially complex pattern of OHU can be decomposed into sums of simpler, spatially localized patterns, and the responses will be additive.
Model Description
For the sake of a concrete but idealized illustration, we adopt the aquaplanet CAM4 results of Rose et al. [53, 55] which define three responses \({\Delta } \overline {T_{CO2}},{\Delta } \overline {T_{T}}\), and \({\Delta } \overline {T_{H}}\) associated respectively with CO2,q T , and q H . We subject this hypothetical system to an abrupt quadrupling of CO2 and allow it to adjust toward equilibrium. The OHU is a linear combination of q T and q H :
where a T ,a H are coefficients for the tropical and high-latitude OHU patterns.
We suppose that each coefficient decays in time, with the e-folding time for q T is much shorter than for q H . These are loosely associated with adjustment times of the upper and deep ocean [24, 35]. The q T mode might also be considered part of the rapid oceanic adjustment described by Rugenstein et al. [56]. We add random noise to each coefficient to represent interannual variability in surface heat fluxes and ocean dynamics:
where r T and r H are zero-mean Gaussian random processes (we choose a standard deviation of 0.2). We choose decay timescales τ T =20 years and τ H = 300 years. Amplitudes a T0,a H0 are set by two conditions at t = 0: the TOA imbalance is identical to the radiative forcing for 4 ×CO 2, and \({\Delta } \overline {T} = 0\). From Eq. 6, the response (surface temperature and TOA radiation) at any time is simply the appropriate linear combination of globally averaged responses from the GCM. We do not perform new GCM simulations here, but rather use the equilibrated, time-averaged output of the simulations described by Rose et al. [53, 55] to define the single-forcing responses for our illustrative model.
Climate Sensitivity in the Illustrative Model
The first 300 years of transient warming is plotted in Fig. 3. The timeseries of \({\Delta } \overline {T_{s}}(t)\) is shown in the grey line on the right panel. The left panel shows the Gregory plot for the illustrative model. It has the same concave curvature found in the CMIP5 models ([3], Fig. 2). In this case, the equilibrium warming \({\Delta } \overline {T_{CO2}}\) is known to be 3.4 K, and the effective extrapolated sensitivity (solid red line) underestimates this by about 0.6 K. We emphasize that this model is strictly linear by construction. The curvature in Fig. 3 is entirely due to temporal changes in the spatial pattern of OHU, along with the differing efficacies of the two OHU modes. Time-dependent climate sensitivity in the illustrative model is consistent with the gradual emergence of high-latitude heat uptake with ε > 1 in the CMIP5 models.
Transient warming in the illustrative linear model (first 300 years after quadrupling CO2). The model is a linear combination of equilibrium responses to CO2 and two idealized modes of ocean heat uptake ([53], Fig. 1) with different decay timescales plus stochastic variability. Left: Scatterplot of the evolving planetary energy budget [27] and regression lines, as in Fig. 2. The green star at 3.4 K indicates the true equilibrium warming for 4 ×CO 2. Right: Timeseries of global mean surface temperature (thick grey line) and components of the TOA feedback calculated from radiative kernels [19, 60]. These are plotted as signed feedbacks; the thick black line is −λ(t). Clear-sky longwave feedbacks are expressed with respect to fixed relative humidity [34]. Feedback are computed annually and smoothed by a 10-year running average
Despite being generated by a strictly linear model, the curvature in the left panel of Fig. 3 means that none of the regression lines capture all the important behaviors of the system (in analogy with the CMIP5 models in Fig. 2). The regression over years 0–20 (before the dominant high-latitude OHU pattern has emerged) gives an accurate assessment of the radiative forcing (7.6 W m −2) but severely underestimates equilibrium sensitivity. Regression over years 50–300 (in which OHU is dominated by q H ) provides a reasonable estimate of \({\Delta } \overline {T_{CO2}}\), but underestimates \(\overline {F}\). In this context, the “fast adjustment” to the forcing [63] is actually the emergence of the long-term OHU pattern, dominated by q H with its large efficacy. Regression over the entire 300 years underestimates both \(\overline {F}\) and \({\Delta } \overline {T_{CO2}}\) . The slope λ = 2.1 W m −2 K −1 is very close to \(\lambda _{CO_{2}}\) in this model (λ = 2.2 W m −2 K −1, [53]). However, this fit is not particularly meaningful since regressing over several hundred more years would yield a smaller λ (though also a better estimate of \({\Delta } \overline {T_{CO2}}\)).
Feedback in the Illustrative Model
Radiative kernel analysis [60] can be used to decompose λ(t) in our illustrative model into physical components. Here, we use aquaplanet-specific kernels [19]. The radiative kernel method requires a convolution of the kernels with 3D temperature and moisture anomaly fields. For our illustrative model, these anomalies are simply linear combinations of the single-forcing GCM responses from Rose et al. [53, 55], with the time evolution given by Eqs. 9 and 1. We compute the feedback components at 1-year intervals and plot the resulting timeseries (smoothed by 10-year running averages) in the right panel of Fig. 3. We express the clear-sky longwave feedback components with respect to fixed relative humidity, eliminating a large cancelation between the traditional water vapor and lapse rate feedbacks [34].
Consistent with the concave shape of the Gregory plot, −λ (thick black line) becomes less negative with time (climate sensitivity increases). However, the most obvious curvature in the Gregory plot occurs during the early part of the transient and is clearly associated with the rapid decay of q T . The timeseries reveals a much slower increase in climate sensitivity associated with decay of q H (approach to equilibrium). The kernel calculation shows that this is due primarily to two factors: less negative lapse rate and cloud feedbacks. Consistently, in single-forcing scenarios both clouds and clear-sky LW feedbacks contribute to the large efficacy of q H [53]. Note that the shorter-term fluctuations in λ(t) are due to time-dependence of ε(t) imposed through the stochastic terms in Eq. 1 —a crude representation of the variability in surface heat flux patterns that would occur in nature or in a coupled AOGCM.
Why does λ decrease as the influence of the heat uptake wanes, when λ in response to q H alone is actually smaller? We emphasize, again, that this time-dependence in λ is a consequence of the time-dependence of the OHU—both its spatial pattern and its magnitude. The feedbacks are not additive in the same proportion as the climate response. After the rapid decay of the tropical uptake term, the feedback evolves according to Eq. 7 with ε ≈ 1.6 (the calculated value for q H in CAM4 [53], though ε(t) also varies slightly due to the stochastic variation in the OHU pattern). λ must therefore slowly decrease in magnitude, as discussed in “Efficacy of Ocean Heat Uptake.”
In physical terms, for a given radiative forcing \(\overline {F}\), the rate of OHU required to mitigate half the equilibrium warming is not \(\overline {F}/2\). If the efficacy of OHU is greater than 1, less energy needs to be taken up by the oceans. The global TOA imbalance at this “halfway point” would thus be smaller than \(\overline {F}/2\). The second half of the warming, in which the oceans approach thermal equilibrium, would occur with smaller changes in the planetary energy budget.
Geoffroy et al. [23] make a similar argument with the linear two-box OHU model. They invoke a single efficacy factor, meant to relate the long-term spatial structure of OHU. The “fast” mode in their model is associated with upper ocean heat uptake and is assumed to have an efficacy of one. Our illustrative model instead supposes that the heat uptake during the early part of the transient is a linear combination of q T and q H , each of which has a unique efficacy. But the physical idea is very similar: during the early transient, heat uptake is closer to globally uniform (Fig. 1).
What Determines the Efficacy of Ocean Heat Uptake?
We have advocated thinking about the time-dependence of transient warming as a linear, non-local response to a complex and time-evolving pattern of OHU. For a deeper physical understanding of these issues, we now look at what determines the efficacy of OHU, including its relation to spatial structure.
The Interdependence of OHU, Feedback, and Clouds
There are suggestions running through the literature about the non-independence of \(\overline {N}\) and λ. Perhaps beginning with Murphy [44], a number of studies have pointed specifically to SW cloud feedbacks associated with oceanic low cloud cover as a key source of the time-dependence of λ. Senior and Mitchell [57] found that increasing climate sensitivity in a long AOGCM integration was almost all associated with increasingly positive cloud feedbacks. Williams et al. [63] noted that transient warming in AOGCMs features increased low cloud relative to equilibrium warming in slab-ocean GCMs. All these studies advanced arguments linking time-dependence in the cloud feedback to changes in lower-tropospheric stability [44, 57, 63], a theme we return to below.
In the CMIP5 ensemble, the single largest contributor to curvature in the Gregory plots is the SW cloud component, principally over ocean [2, 3]. Consistent with this, fitting the CMIP5 models to the two-box energy balance model reveals that the enhanced efficacy of OHU is mostly due to SW rather than LW effects [23]. Andrews et al. [2] look at spatial contributions to global λ(t), and find that 60 % of the change comes from the tropics, particularly the tropical Pacific. They test the hypothesis that the change in λ arises from the evolving spatial pattern of warming in the AOGCMs. A fixed final warming pattern ΔT(r) is scaled down and imposed on a transient AGCM while preserving the global mean timeseries \({\Delta } \overline {T}(t)\) from the AOGCM. The resulting simulations show much less time-dependence in λ (the Gregory plots are essentially straight lines). To summarize these studies, the CMIP5 models are in good agreement that (i) effective climate sensitivity increases (λ decreases) with time in transient warming, (ii) the increase is dependent on time-variations of OHU (with ε > 1) and associated time-dependence of spatial patterns of warming, and (iii) SW cloud effects are the key radiative player in this adjustment, and they are intrinsically linked to the spatial patterns of OHU and warming.
Idealized model studies also point in the same direction. As has been mentioned earlier, Rose et al. [53] found large and robust differences in SW cloud feedbacks in their single forcing scenarios, the feedback on q H being more positive and that on q T more negative than the feedback on CO2. The clouds thus contribute strongly to setting the efficacies of the OHU patterns.
Trossman et al. [62] compared transient responses to 2 ×CO 2 in several versions of a coupled GCM in which either or both of the ocean circulation and the cloud radiative feedback are held fixed. Consistent with previous studies [64, 67], they find that changes in ocean circulation (with emphasis on the slowdown of the inter hemispheric MOC) provide a cooling effect. This study offers a careful quantification of the coupled ocean circulation—cloud effect. The major conclusion is that the cooling effect of ocean circulation is largely carried out by clouds, and is much reduced when clouds are held fixed. In other words, the cloud feedback and the ocean circulation are not separable in their AOGCM. The mechanism is not studied in detail, but the authors suggest a coupling between meridional heat transport in the ocean, sea surface heat fluxes, and lower tropospheric stability.
Ocean Heat Uptake and Lower Tropospheric Stability
We now offer some speculative suggestions about connections between OHU and radiative feedback mediated through lower-tropospheric stability (LTS) and low cloud cover. The relationship between LTS and low clouds is well-known from observations [37, 66]. Low marine stratus and stratocumulus clouds are frequently found at the top of inversion-capped moist boundary layers. All else being equal, an increase in the strength of the inversion reduces the entrainment of dry tropospheric air and leads to increased cloud cover. Subtropical marine clouds play a key cooling role due to their high albedo, low altitude, and location over the vast, dark subtropical sea surface.
A useful metric for LTS is the so-called “estimated inversion strength” or EIS [66], which normalizes the LTS with respect to the temperature-dependent slope of the moist adiabat. A change in EIS is one of four basic cloud-controlling mechanisms recently reviewed by Bretherton [9] on the basis of observations, GCMs, and high-resolution cloud modeling. Greenhouse warming is almost universally associated with increased EIS in AOGCMs [47]. If this were the dominant cloud-controlling factor, it would suggest a strongly negative SW cloud feedback. The emerging consensus is that this is not the case, and that global net cloud feedback is positive [9, 21]. The dominant factor seems to be a “thermodynamic” decrease in low cloudiness due to increased specific humidity gradients across the inversion as the whole column warms [9]. On the other hand, EIS anomalies have been shown to be sensitive to spatial patterns of SST changes [48]. It is thus plausible that the stability mechanism is the dominant factor in the time-dependence of cloud feedback.
We propose here that the stability-induced effect on low clouds is the key determinant of the efficacy of OHU. Specifically, we submit that subpolar OHU stabilizes the lower troposphere and thereby enhances low cloud cover. We propose that this effect is non-local—the stabilizing effect and cloud response are felt in the subtropics due to the three-dimensional dynamic response of the atmosphere to localized OHU. Rose and Rencurrel [55] show that the mid-troposphere warms more rapidly relative to the surface in an idealized 2 ×CO 2 + q H scenario compared to an equilibrium 2 ×CO 2 warming. From the additive principle, a transient warming scenario might therefore show a gradual reduction in the rate of EIS increase as the OHU decays. This in turn would favor increasingly positive SW cloud feedback with time, consistent with the CMIP5 results.
We propose that the appropriate metric for these stability effects on cloud feedbacks in transient simulations is the normalized change \({\Delta } EIS / {\Delta } \overline {T_{s}}\)—i.e., the change in inversion strength per degree global warming. This adopts the same normalization used to express the cloud feedbacks themselves, and is a meaningful measure of contributions to the SW cloud feedback if cloud changes are proportional to ΔE I S.
Figure 4 shows the evolution of \({\Delta } EIS / {\Delta } \overline {T_{s}}\) for the CCSM4 and GFDL-CM3 abrupt 4 ×CO 2 experiments. EIS is calculated from air temperature data at 700 and 1000 hPa and standard thermodynamic formulas [66], and the difference is taken from the pre-industrial control for each model. The stability metric is plotted for several different time slices. It is positive everywhere but the high latitudes, indicating increased inversion strength with warming. The two models disagree on the magnitude of the change. However, as posited above, both models show that \({\Delta } EIS / {\Delta } \overline {T_{s}}\) decreases monotonically throughout the simulation as OHU diminishes. This is consistent with an increasingly positive SW cloud feedback.
Normalized changes in lower-tropospheric stability in CMIP5 abrupt 4 ×CO 2 scenarios. The quantity plotted is \({\Delta } EIS / {\Delta } \overline {T_{s}}\), where EIS is the estimated inversion strength [66], and changes are computed with respect to pre-industrial controls for several different time slices after CO2 quadrupling, as indicated in the legend. Dashed lines are GFDL-CM3 while solid lines are CCSM4. Also plotted (black solid line): the same metric for equilibrium warming of the slab ocean (SOM) version of CCSM4 [6]
It is desirable to see if this reduction in the rate of increase in inversion strength per degree global warming continues during the long approach to equilibrium. A slab ocean (SOM) version of CCSM4 has previously been used to assess equilibrium sensitivity in that model [6]. We calculated the equilibrium \({\Delta } EIS / {\Delta } \overline {T_{s}}\) as the difference between 2 ×CO 2 and 1 ×CO 2 simulations in the SOM (black curve in Fig. 4). It is also positive from mid-latitudes equatorward but weaker by half than the transient CCSM4 results. If the comparison is valid, it suggests that the approach to equilibrium involves substantial changes to the vertical structure of the warming.
Conclusion
Through a mixture of review, demonstration, and speculation, we have advocated the following: (i) increasing climate sensitivity with time is a robust feature of transient warming in AOGCMs. (ii) The early adjustment of AOGCMs to an abrupt radiative forcing involves significant reorganization of the spatial structure of OHU, from globally uniform to dominantly subpolar. (iii) Climate sensitivity continues to increase after the dominant subpolar OHU pattern is well-established. (iv) These phenomena are best understood from a linear systems perspective, treating the OHU as a slowly-evolving forcing on the fast upper ocean–atmosphere system. (v) The efficacy of OHU (treated as a forcing) is strongly determined by its spatial pattern. Efficacy can be measured through the equilibrium responses of a shallow slab ocean model to prescribed OHU patterns and CO2 increase. (vi) The efficacy of OHU in AOGCMs is robustly greater than 1 because of the dominant subpolar OHU pattern. (vii) The slow increase in climate sensitivity during transient warming is a consequence of the high-efficacy OHU pattern decaying toward equilibrium. (viii) The high efficacy of the dominant subpolar OHU pattern is primarily due to a more positive SW cloud feedback, compared to the equilibrium response to CO2. (ix) A plausible mechanism linking OHU to cloud feedback is changes in lower tropospheric stability. Spatially localized subpolar OHU projects non-locally onto the vertical structure of warming, enhancing tropospheric warming relative to the surface. (x) The rate of increase in Estimated Inversion Strength per unit global warming slows during the course of transient warming, consistent with an increasingly positive SW cloud feedback and increasing climate sensitivity.
Of the points enumerated above, (i)–(iii) are well-established across a number of studies and models. Point (iv) is our own interpretation of the minimal physics. Point (v) is based largely on idealized model studies, and while there is good evidence for its robustness, careful investigation across the model hierarchy is still needed. We have demonstrated the plausibility of points (vi)–(vii) with our idealized linear illustrative model, but these should be considered as hypotheses to guide future investigations. Point (viii) is a robust result across multiple studies and lines of evidence. Point (ix) is a new hypothesis, extrapolating from published results. Point (x) is a new result that we have demonstrated here in two different comprehensive models, and serves as partial confirmation of hypothesis (ix).
In this work, we have largely treated “ocean heat uptake” as synonymous with patterns of sea surface heat fluxes, even though the anomalous fluxes may be out of the ocean at many locations or times (Fig. 1). In the additive perspective, we need not distinguish between localized heat uptake and release. A complex and time-evolving pattern of heat fluxes may be meaningfully decomposed into sums of simple, spatially localized heat sources or sinks. The key point is that there are global impacts to these localized forcings, and their efficacy depends strongly on their location.
An important implication is that temporal variations in both magnitude and spatial pattern of OHU (and thus also in its global efficacy) may be expressed radiatively through SW cloud responses. The same may be said about inter-model differences in OHU. This is a tantalizing proposition, as cloud feedbacks continue to be the largest source of spread in estimates of climate sensitivity [10, 21, 59]. If part of that spread is driven in systematic ways by patterns of sea surface heat fluxes, it may be more reducible and falsifiable than typically acknowledged.
In light of this, we suggest as a priority for future research understanding the physics linking OHU to tropospheric stratification, and connecting this to ongoing studies of the environmental constraints on cloud feedbacks [9, 47–49, 68]. Another priority should be understanding the spatial structure of OHU, how it evolves on different timescales, and how realistically these processes are modeled in current AOGCMs. Finally, longer integrations of AOGCMs would enable a better understanding of the equilibration process, including the role of changing ocean circulation [39, 62, 64].
Notes
This defines a sign convention: λ is a positive number, corresponding to a net negative radiative feedback governing adjustment to equilibrium. Sign conventions and notation vary widely in the literature.
By convention, ERF and ΔT e f f are both halved and expressed relative to a doubling of CO2.
References
Andrews T, Forster PM. CO2 forcing induces semi-direct effects with consequences for climate feedback interpretations. Geophys Res Lett. 2008;35. doi:10.1029/2007GL032273.
Andrews T, Gregory JM, Webb MJ. The dependence of radiative forcing and feedback on evolving patterns of surface temperature change in climate models. J Clim. 2015;28:1630–48. doi:10.1175/JCLI-D-14-00545.1.
Andrews T, Gregory JM, Webb MJ, Taylor KE. Forcing, feedbacks and climate sensitivity in CMIP5 coupled atmosphere- ocean climate models. Geophys Res Lett. 2012;39. doi:10.1029/2012GL051607 10.1029/2012GL051607.
Armour KC, Bitz CM, Roe GH. Time-varying climate sensitivity from regional feedbacks. J Clim. 2013;26:4518–34.
Armour KC, Eisenman I, Blanchard-Wrigglesworth E, McCusker KE, Bitz CM. The reversibility of sea ice loss in a state-of-the-art climate model. Geophys Res Lett. 2011;38(L16705). doi:10.1029/2011GL048739.
Bitz C, Shell K, Gent P, Bailey D, Danabasoglu G, Armour K, Holland M, Kiehl J. Climate sensitivity of the Community Climate System Model, version 4. J Clim. 2012;25:3053–70.
Boer GJ, Yu B. Climate sensitivity and response. Clim Dyn 2003;20:415–29.
Bony S, Stevens B, Held I, Mitchell JF, Dufresne JL, Emanuel KA, Friedlingstein P, Griffies S, Senior C. Carbon dioxide and climate: perspectives on a scientific assessment. In: Asrar GR and Hurrell JW, editors. Climate science for serving society. Netherlands: Springer; 2013. p. 391–413.
Bretherton CS. Insights into low-latitude clouds feedbacks from high-resolution models. Phil Trans R Soc Lond A. 2015;373. doi:10.1098/rsta.2014.0415.
Caldwell PM, Zelinka MD, Taylor KE, Marvel K. Quantifying the sources of intermodel spread in equilibrium climate sensitivity. J Clim. 2016;29:513–24.
Cess RD, Potter GL. A methodology for understanding and intercomparing atmospheric climate feedback processes in general circulation models. J Geophys Res. 1988;93(D7):8305–14. doi:10.1029/JD093iD07p08305.
Cess RD, Potter GL, Blanchet JP, Boer GJ, Del Genio AD, Déqué M, Dymnikov V, Galin V, Gates WL, Ghan SJ, Kiehl JT, Lacis AA, Le Treut H, Li ZX, Liang XZ, McAvaney BJ , Meleshko VP, Mitchell JFB, Morcrette JJ, Randall DA, Rikus L, Roeckner E, Royer JF, Schlese U, Sheinin DA, Slingo A, Sokolov AP, Taylor KE, Washington WM, Wetherald RT, Yagai I, Zhang MH. Intercomparison and interpretation of climate feedback processes in 19 atmospheric general circulation models. J Geophys Res. 1990;95(D10):16,601–15. doi:10.1029/JD095iD10p16601.
Charney JG, Arakawa A, Baker DJ, Bolin B, Dickinson RE, Goody RM, Leith CE, Stommel HM, Wunsch CI. Carbon dioxide and climate: a scientific assessment. Washington, DC: Tech. Rep., National Academy of Sciences; 1979.
Colman RA, McAvaney BJ. On tropospheric adjustment to forcing and climate feedbacks. Clim Dyn. 2011;36:1649–58. doi:10.1007/s00382-011-1067-4.
Crook JA, Forster PM, Stuber N. Spatial patterns of modeled climate feedback and contributions to temperature response and polar amplification. J Clim. 2011;24:3575–92.
Exarchou E, Kuhlbrodt T, Gregory JM, Smith RS. Ocean heat uptake processes: a model intercomparison. J Clim. 2015;28:887–908. doi:10.1175/JCLI-D-14-00235.1.
de F, Forster PM, Blackburn M, Glover R, Shine KP. An examination of climate sensitivity for idealised climate change experiments in an intermediate general circulation model. Clim Dyn. 2000;16:833–49.
Feldl N, Roe GH. Four perspectives on climate feedbacks. Geophys Res Lett. 2013;40. doi:10.1002/grl.50711.
Feldl N, Roe GH. The nonlinear and nonlocal nature of climate feedbacks. J Clim. 2013;26:8289–304. doi:10.1175/JCLI-D-12-00631.1.
Ferreira D, Marshall J, Rose BEJ. Climate determinism revisited: multiple equilibria in a complex climate model. J Clim 2011;24:992–1012.
Flato G, Marotzke J, Abiodun B, Braconnot P, Chou S, Collins W, Cox P, Driouech F, Emori S, Eyring V, Forest C, Gleckler P, Guilyardi E, Jakob C, Kattsov V, Reason C, Rummukainen M. Evaluation of climate models. In: Stocker T, Qin D, Plattner GK, Tignor M, Allen SK, Boschung J, Nauels A, Xia Y, Bex V, and Midgley P, editors. Climate Change 2013: the physical science basis. Contribution of working group I to the fifth assessment report of the intergovernmental panel on climate change, chap. 9. Cambridge, UK: Cambridge University Press; 2013.
Frölicher TL, Sarmiento JL, Paynter DJ, Dunne JP, Krasting JP, Winton M. Dominance of the Southern Ocean in anthropogenic carbon and heat uptake in CMIP5 models. J Clim. 2015;28 :862–86.
Geoffroy O, Saint-Martin D, Bellon G, Volnotere A, Olivié DJL, Tytéca S. Transient climate response in a two-layer energy-balance model. part ii: representation of the efficacy of deep-ocean heat uptake and validation for CMIP5 AOGCMs. J Clim. 2013;26:1859–76.
Geoffroy O, Saint-Martin D, Olivié DJL, Volnotere A, Bellon G, Tytéca S. Transient climate response in a two-layer energy-balance model. part i: analytical solution and parameter calibration using CMIP5 AOGCM experiments. J Clim. 2013;26:1841–57.
Gregory JM. Vertical heat transports in the ocean and their effect on time-dependent climate change. Clim Dyn. 2000;16:501–15.
Gregory JM, Andrews T, Good P. The inconstancy of the transient climate response parameter under increasing CO2. 2015;373. doi:10.1098/rsta.2014.0417.
Gregory JM, Ingram WJ, Palmer MA, Jones GS, Stott PA, Thorpe RB, Lowe JA, Johns TC, Williams KD. A new method for diagnosing radiative forcing and climate sensitivity. Geophys Res Lett. 2004;31. doi:10.1029/2003GL018747.
Gregory JM, Mitchell JFB. The climate response to CO2 of the Hadley Centre coupled AOGCM with and without flux adjustments. Geophys Res Lett. 1997;24:1943–6.
Gregory JM, Webb M. Tropospheric adjustment induces a cloud component in CO2 forcing. J Clim. 2008;21:58–71. doi:10.1175/2007JCLI1834.1.
Hansen J, Lacis A, Rind D, Russell G, Stone P, Fung I, Ruedy R, Lerner J. Climate sensitivity: analysis of feedback mechanisms. In: Hansen JE and Takahashi T, editors. Climate processes and climate sensivity, no. 29 in geophysical monographs. Washington: American Geophysical Union; 1984. p. 130–63.
Hansen J, Russell G, Lacis A, Fung I, Rind D, Stone P. Climate response times: dependence on climate sensitivity and ocean mixing. Science 1985;229:857–9. doi:10.1126/science.229.4716.857.
Hansen J, Sato M, Ruedy R. Radiative forcing and climate response. J Geophys Res. 1997;102. doi:10.1029/96JD03436.
Hansen J, Sato M, Ruedy R, Nazarenko L, Lacis A, Schmidt GA, Russell G, Aleinov I, Bauer M, Bauer S, Bell N, Cairns B, Canuto V, Chandler M, Cheng Y, Genio AD, Faluvegi G, Fleming E, Friend A, Hall T, Jackman C, Kelley M, Kiang N, Koch D, Lean J, Lerner J, Lo K, Menon S, Miller R, Minnis P, Novakov T, Oinas V, Perlwitz J, Perlwitz J, Rind D, Romanou A, Shindell D, Stone P, Sun S, Tausnev N, Thresher D, Wielicki B, Wong T, Yao M, Zhang S. Efficacy of climate forcings . J Geophys Res. 2005;110(D18104). doi:10.1029/2005JD005776.
Held IM, Shell KM. Using relative humidity as a state variable in climate feedback analysis. J Clim. 2012; 25:2578–82.
Held IM, Winton M, Takahashi K, Delworth T, Zeng F, Vallis GK. Probing the fast and slow components of global warming by returning abruptly to preindustrial forcing. J Clim. 2010;23 :2418–27.
Kang SM, Xie SP. Dependence of climate response on meridional structure of external thermal forcing. J Clim. 2014;27:5593–600. doi:10.1175/JCLI-D-13-00622.1.
Klein SA, Hartmann DL. The seasonal cycle of low stratiform clouds. J Clim 1993;6:1587–606.
Knutti R, Rugenstein MAA. Feedbacks, climate sensitivity and the limits of linear models. Phil Trans R Soc Lond A. 2015;373. doi:10.1098/rsta.2015.0146.
Li C., von Storch J.S., Marotzke J. Deep-ocean heat uptake and equilibrium climate response. Clim Dyn. 2013;40:1071–86.
Marshall J, Scott JR, Armour KC, Campin JM, Kelley M, Romanou A. The ocean’s role in the transient response of climate to abrupt greenhouse gas forcing. Clim Dyn. 2015;44:2287–99.
Marvel K, Schmidt GA, Miller RL, Nazarenko LS. Implications for climate sensitivity from the response to individual forcings. Nature Clim Change 2015. doi:10.1038/NCLIMATE2888.
Meraner K, Mauritsen T, Voigt A. Robust increase in equilibrium climate sensitivity under global warming. Geophys Res Lett. 2013;40. doi:10.1002/2013GL058118.
Merlis TM. Interacting components of the top-of-atmosphere energy balance affecting changes in regional surface temperature. Geophys Res Lett. 2014;41. doi:10.1002/2014GL061700.
Murphy J.M. Transient response of the Hadley Centre coupled ocean-atmosphere model to increasing carbon dioxide. part III: analysis of global-mean response using simple models. J Clim 1995;8:496–514.
Palmer MD, McNeall DJ. Internal variability of Earth’s energy budget simulated by CMIP5 climate models. Environ Res Lett. 2014;9. doi:10.1088/1748-9326/9/3/034016.
Paynter D, Frölicher TL. Sensitivity of radiative forcing, ocean heat uptake, and climate feedback to changes in anthropogenic greenhouse gases and aerosols. J Geophys Res Atmos. 2015;120:9837–54. doi:10.1002/2015JD023364.
Qu X, Hall A, Klein SA, Caldwell PM. On the spread of changes in marine low cloud cover in climate model simulations of the 21st century. Clim Dyn. 2014;42:2603–26. doi:10.1007/s00382-013-1945-z 10.1007/s00382-013-1945-z.
Qu X, Hall A, Klein SA, Caldwell PM. The strength of the tropical inversion and its response to climate change in 18 CMIP5 models. Clim Dyn. 2015;45:375–96. doi:10.1007/s00382-014-2441-9.
Qu X, Hall A, Klein SA, DeAngelis AM. Positive tropical marine low-cloud cover feedback inferred from cloud-controlling factors. Geophys Res Lett. 2015;42. doi:10.1002/2015GL065627.
Raper SCB, Gregory JM, Stouffer RJ. The role of climate sensitivity and ocean heat uptake on AOGCM transient temperature response. J Clim. 2002;15:124–30.
Roe GH. Feedbacks, timescales, and seeing red. Ann Rev Earth Planet Sci 2009;37:93–115.
Rose BEJ. Stable Waterbelt climates controlled by tropical ocean heat transport: a nonlinear coupled climate mechanism of relevance to Snowball Earth. J Geophys Res. 2015;120:1404–23. doi:10.1002/2014JD022659.
Rose BEJ, Armour KC, Battisti DS, Feldl N, Koll DDB. The dependence of transient climate sensitivity and radiative feedbacks on the spatial pattern of ocean heat uptake. Geophys Res Lett. 2014;41. doi:10.1002/2013GL058955.
Rose BEJ, Ferreira D, Marshall J. The role of oceans and sea ice in abrupt transitions between multiple climate states. J Clim. 2013;26:2862–2879. doi:10.1175/JCLI-D-12-00175.1.
Rose BEJ, Rencurrel MC. The vertical structure of tropospheric water vapor: comparing radiative and ocean-driven climate changes. J Clim. 2016;29:4251–68. doi:10.1175/JCLI-D-15-0482.1 10.1175/JCLI-D-15-0482.1.
Rugenstein MAA, Gregory JM, Schaller N, Sedlácek J, Knutti R. Multi-annual ocean-atmosphere adjustments to radiative forcing. J Clim. 2016;29:5643–59. doi:10.1175/JCLI-D-16-0312.1.
Senior CA, Mitchell JFB. The time-dependence of climate sensitivity. Geophys Res Lett 2000;27:2685–8.
Sherwood SC, Bony S, Boucher O, Bretherton C, Forster PM, Gregory JM, Stevens B. Adjustments in the forcing-feedback framework for understanding climate change. Bull Amer Meteor Soc. 2015;96:217–28. doi:10.1175/BAMS-D-13-00167.1.
Soden BJ, Held IM. An assessment of climate feedbacks in coupled ocean-atmosphere models. J Clim 2006;19(14):3354–60.
Soden BJ, Held IM, Colman R, Shell KM, Kiehl JT, Shields CA. Quantifying climate feedbacks using radiative kernels. J Clim. 2008;21:3504–20.
Taylor KE, Stouffer RJ, Meehl GA. An overview of CMIP5 and the experiment design. Bull Amer Meteor Soc. 2012:485–98. doi:10.1175/BAMS-D-11-00094.1.
Trossman DS, Palter JB, Merlis TM, Huang Y, Xia Y. Large-scale ocean circulation-cloud interactions reduce the pace of transient climate change. Geophys Res Lett. 2016;43:3935–43. doi:10.1002/2016GL067931.
Williams KD, Ingram WJ, Gregory JM. Time variation of effective climate sensitivity in GCMs. J Clim 2008;21:5076–90.
Winton M, Griffies SM, Samuels BL, Sarmiento JL, Frölicher TL. Connecting changing ocean circulation with changing climate. J Clim 2013;26:2268–78.
Winton M, Takahashi K, Held IM. Importance of ocean heat uptake efficacy to transient climate change. J Clim 2010;23:2333–44.
Wood R, Bretherton CS. On the relationship between stratiform low cloud cover and lower-tropospheric stability. J Clim 2006;19:6425–32.
Zhang R, Kang SM, Held IM. Sensitivity of climate change induced by the weakening of the Atlantic meridional overturning circulation to cloud feedback. J Clim 2010;23:378–89. doi:10.1175/2009JCLI3118.1.
Zhou C, Zelinka MD, Dessler AE, Klein SA. The relationship between interannual and long-term cloud feedbacks. Geophys Res Lett 2015;42. doi:10.1002/2015GL066698.
Acknowledgements
We thank Jonathan Gregory, Maria Rugenstein, and the editor Mark Zelinka whose insightful comments helped improve this paper. We acknowledge the World Climate Research Programme’s Working Group on Coupled Modelling, which is responsible for CMIP, and we thank the climate modeling groups for producing and making available their model output. For CMIP, the US Department of Energy’s Program for Climate Model Diagnosis and Intercomparison provides coordinating support and led development of software infrastructure in partnership with the Global Organization for Earth System Science Portals. We also acknowledge support from the Computational and Information Systems Laboratory at the National Center for Atmospheric Research for access to the CCSM4 SOM simulations shown in Fig. 4. The aquaplanet radiative kernels used to produce Fig. 3 were kindly provided by Nicole Feldl. Kyle Armour originally produced the CMIP5 surface flux plots in Fig. 1, and also shared with BR many inspiring discussions about feedback, climate sensitivity, and the oceans. This work was supported by NSF Award AGS-1455071.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interests
On behalf of all authors, the corresponding author states that there is no conflict of interest.
Additional information
This article is part of the Topical Collection on Climate Feedbacks
Rights and permissions
About this article
Cite this article
Rose, B.E.J., Rayborn, L. The Effects of Ocean Heat Uptake on Transient Climate Sensitivity. Curr Clim Change Rep 2, 190–201 (2016). https://doi.org/10.1007/s40641-016-0048-4
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40641-016-0048-4