1 Introduction

Young students attending the evening mathematical seminar at the Moscow State School no. 57, will most probably encounter the following problem:

figure a

Is it possible to tile the \(8\times 8\) chessboard without two opposite corners with \(2\times 1\) dominoes?

A simple parity argument shows that it is, indeed, not possible. A more difficult question is in how many ways we can tile the full \(8\times 8\), and, more generally, \(2n\times 2n\) chessboard with the \(2\times 1\) dominos.

In 1961, a Dutch physicist Piet Kasteleyn found complete solutions of several ’arrangement problems’ of such nature (Kasteleyn 1963). In particular, he showed that the number of domino tilings of a chessboard of a size \(2n\times 2n\) is given by

$$\begin{aligned} \begin{aligned} Z_n&= \prod _{m=0}^{n-1} \prod _{k=0}^{n-1} \left( 4 - 2\cos \left( \frac{2m+1}{2n+1}\pi \right) - 2\cos \left( \frac{2k+1}{2n+1}\pi \right) \right) . \end{aligned} \end{aligned}$$
(1.1)

There is a one-to-one correspondence between the domino tilings and the dimer configurations, or, in other words, the perfect matchings of a corresponding graph, as Fig. 1 demonstrates. A perfect matching of a graph is a subset of its edges such that every vertex of the graph is incident to exactly one edge of the subset.

Fig. 1
figure 1

Correspondence between the domino tilings and the dimer matchings on boxes \(2n\times 2n\)

Full size image

The method developed by Kasteleyn is not only applicable to counting the number of domino tilings, or equivalently, dimer configurations, but can also be used to compute the weighted sums of the form:

$$\begin{aligned} \begin{aligned} Z_n&= \sum _{M\in {\mathcal {M}}(G_{2n\times 2n})}w(M), \end{aligned} \end{aligned}$$
(1.2)

where \({\mathcal {M}}(G_{2n\times 2n})\) is a collection of all dimer configurations of the square box of size \(2n\times 2n\). For any dimer configuration (matching) M, its weight is given by

$$\begin{aligned} w(M) =\prod _{e\in M} w(e),\quad w(e) ={\left\{ \begin{array}{ll} u,&{}\text { for horizontal edges},\\ v&{}\text { for vertical edges}, \end{array}\right. } \quad u,v>0. \end{aligned}$$

Obtaining explicit expressions for the partition functions\(Z_n\) (1.2) is important in Statistical Physics, as it allows the computation of the free energyF(u, v) given by

$$\begin{aligned} F(u,v) = -\lim _{n\rightarrow \infty } \frac{1}{n^2} \log Z_n, \end{aligned}$$
(1.3)

and, by analysing the free energy, one is able to determine some important macroscopic properties of the systems in the thermodynamic limit. In particular, the singularities of the free energy function indicate the presence of the phase transitions.

It turns out (Cohn et al. 2001; Kenyon et al. 2006), that it is easier to compute a weighted partition function of the form (1.2) if we embed the \(2n\times 2n\) square grid on a torus (see Fig. 2).

Fig. 2
figure 2

A dimer configuration (matching) on the \(4\times 4\) box on a torus

Full size image

The partition function \(Z_n^{{\mathbb {T}}}\) for weighted dimer matchings on a torus possesses an elegant explicit expression:

$$\begin{aligned} Z_n^{{\mathbb {T}}} = \frac{1}{2}\left( -f^{(n)}(1,1)+f^{(n)}(-1,1)+f^{(n)}(1,-1)+f^{(n)}(-1,-1)\right) , \end{aligned}$$
(1.4)

where f is a Laurent polynomial in two variables x, y, namely,

$$\begin{aligned} f=4(u^2+v^2) - u^2(x+x^{-1}) -v^2(y+y^{-1}). \end{aligned}$$

and for every integer \(n\ge 1\),

$$\begin{aligned} f^{(n)}(x,y)= \prod _{m=0}^{n-1} \prod _{k=0}^{n-1} f\bigl (e^{2\pi i\frac{m}{n}}x, e^{2\pi i\frac{k}{n}} y\bigr ). \end{aligned}$$
(1.5)

The limiting free energy F does not depend on whether we consider the partition function \(Z_n\) or \(Z_n^{{\mathbb {T}}}\). In both cases,

$$\begin{aligned} \lim _{n\rightarrow \infty } \frac{1}{n^2} \log Z_n = \lim _{n\rightarrow \infty } \frac{1}{n^2} \log Z_n^{{\mathbb {T}}} =\int _{0}^{1} \int _{0}^1 \log | f(e^{2\pi i \theta _1}, e^{2\pi i \theta _2})| d\theta _1 d\theta _2.\qquad \end{aligned}$$
(1.6)

More generally, expressions of a form (1.4) and (1.6) hold for all planar simple bipartite \(\mathbb Z^2\)-periodic graphs and some associated polynomials f. For example, for the honeycomb lattice, \(f=a+bx+cy\), where a, b, c are the weights of the horizontal, north-east, and south-east edges, respectively.

Okounkov, Kenyon, and Sheffield [see Kenyon et al. (2006)] obtained a beautiful limiting shape result for the coefficients of \(f^{(n)}(x,y)\) in (1.5) for the special ’dimer’ polynomials f. In the present note we discuss the generalization of the result of Okounkov, Kenyon, and Sheffield to arbitrary Laurent polynomials in d variables, where \(d\ge 2\).

2 Decimation of Polynomials

A Laurent polynomial in d commuting variables \(z_1\),...,\(z_d\), can be presented as a sum:

$$\begin{aligned} f({{\varvec{z}}}) = \sum _{{{\varvec{m}}}\in {{\mathbb {Z}}}^d} f_{{{\varvec{m}}}} {{\varvec{z}}}^{{{\varvec{m}}}}, \end{aligned}$$

where we use the multi-index notation \({{\varvec{m}}}=(m_1,\ldots ,m_d)\). The sum has a finite number of terms: there are only finitely many \({{\varvec{m}}}\)’s with \(f_{{{\varvec{m}}}}\ne 0\). The multi-indices \({{\varvec{m}}}\in {{\mathbb {Z}}}^d\) with \(f_{{\varvec{m}}}\ne 0\) are called the exponent vectors. The set of all exponent vectors is called the support of f and is denoted by \(\textsf {supp}(f)\).

Now, fix an arbitrary integer \(n\ge 1\). Then, the nth decimation of a Laurent polynomial \(f(z_1,\ldots ,z_d)\) is defined as:

$$\begin{aligned} f^{(n)}(z_1,\ldots , z_d) = \prod _{k_1=1}^{n} \ldots \prod _{k_d=1}^n f\left( e^{2\pi i k_1/n} z_1,\ldots ,e^{2\pi i k_d/n} z_d\right) . \end{aligned}$$
(2.1)

Our interest in these polynomials arose when studying decimations (renormalization transformation) of the so-called principle algebraic actions—a natural class of algebraic dynamics, see Arzhakova et al. (2018) for more details. Such polynomials have been considered earlier by Purbhoo (2008) who studied approximations of amoebas.In the present paper, we will discuss properties of the decimated polynomials.

For every n, a decimated polynomial \(f^{(n)}\) is again a Laurent polynomial

$$\begin{aligned} f^{(n)}({{\varvec{z}}}) = \sum _{{{\varvec{m}}}\in {{\mathbb {Z}}}^d} f_{{{\varvec{m}}}}^{(n)} {{\varvec{z}}}^{{{\varvec{m}}}}. \end{aligned}$$

Moreover, the resulting exponent vectors of \(f^{(n)}\) are entry-wise divisible by n. In other words, \(f^{(n)}\) is a Laurent polynomial in \(z_1^n, \ldots , z_d^n\).

Example 1

Consider a polynomial \(f(x,y) = 1-x-y\). Then, the first three decimations are (see Fig. 3):

  1. 1.

    \(f^{(1)}(x,y) = 1-x-y\);

  2. 2.

    \(f^{(2)}(x,y) = 1-2x^2 -2y^2 -2x^2y^2+y^4+x^4 \);

  3. 3.

    \(f^{(3)}(x,y)=1-3x^3-3y^3+3x^6+3y^6-3x^6y^3-3x^3y^6-21x^3y^3-y^9-x^9\).

Fig. 3
figure 3

Black circles correspond to the exponent vectors of \(f=f^{(1)}\), namely, (0, 0),(1, 0), and (0, 1); the exponent vectors of \(f^{(2)}\) and \(f^{(3)}\) are denoted by the gray and the white circles, respectively

Full size image

We remind the reader that the Newton polytope \({\mathcal {N}}(f)\) of a Laurent polynomial \(f(z_1,\ldots ,z_d)\) is a subset of \({\mathbb {R}}^d\) which is a convex hull of the exponent vectors of \(f(z_1,\ldots ,z_d)\). Note that the Newton polytopes of \(f^{(n)}\) and of f satisfy the following relation:

$$\begin{aligned} {\mathcal {N}}(f^{(n)}) =n^d {{\mathcal {N}}}(f). \end{aligned}$$

Therefore, when n increases, the Newton polytope of \(f^{(n)}\) grows, and so do the absolute values of the non-zero coefficients of \(f_{{\varvec{m}}}^{(n)}\). In fact, their growth rate is exponential in n. The natural question is whether there is a scaling limit of the coefficients of \(f^{(n)}\). Namely, whether the limits

$$\begin{aligned} \lim _{n \rightarrow \infty } \frac{1}{n^d} \log |f^{(n)}_{{{\varvec{m}}}_n}|, \end{aligned}$$
(2.2)

exist for sequences \({{\varvec{m}}}_n\in \textsf {supp}(f^{(n)})\) such that \(\frac{{{\varvec{m}}}_n}{n^d}\rightarrow {{\varvec{u}}}\in {\mathcal {N}}(f)\).

In Kenyon et al. (2006), it was shown that for special ‘dimer’ polynomials in 2 variables, the limits (2.2) do exist. However, the method of Kenyon et al. (2006) is not applicable to general Laurent polynomials as it relies on the physical and combinatorial properties of a two-dimensional model of dimer matchings. The polynomials that arise in this model form a subset in the set of two-dimensional Laurent polynomials and possess certain physical interpretation which allows to show that the associated surface tension is strictly convex (Sheffield 2005). The convexity of the surface tension implies the existence of the desired limit; however, a generic Laurent polynomial does not allow a ’dimer’ interpretation and, thus, cannot be analysed using the methods of Kenyon et al. (2006). However, the tropical geometry provides a convenient framework to address the limit questions in general case.

3 The Scaling Limit

In tropical algebra, the standard addition and multiplication of real numbers are redefined as follows:

  • tropical addition: \(a\oplus b = \max \{a,b\}\);

  • tropical multiplication: \(a\odot b = a+b\).

Hence, \(2\oplus 5=5\) and \(2\odot 5=7\). The tropical operations allow to define tropical polynomials. For example, consider \(f(x,y) = 2x^2 - 4x^2y + y\); its tropical analogue is then

$$\begin{aligned} F(x,y) = (2\odot x\odot x)\oplus (-\,4\odot x \odot x\odot y)\oplus (1\odot y). \end{aligned}$$

Using the tropical operations, defined above, one can easily evaluate F at any \((x,y)\in {\mathbb {R}}^2\)

$$\begin{aligned} F(x,y)= \max \{ 2+2x, -4 +2x+y, y\}. \end{aligned}$$

Tropical geometry incorporates many facets of algebraic geometry and convex analysis (Maclagan and Sturmfels 2015).

Let us consider a Laurent polynomial \(f({\varvec{z}}) = \sum _{{\varvec{m}}} f_{{\varvec{m}}} {\varvec{z}}^{\varvec{m}}\). The tropicalization of \(f({{\varvec{z}}})\), denoted by \(\textsf {trop}(f)({{\varvec{t}}})\), is a function on \({\mathbb {R}}^d\) defined as follows: for any \({{\varvec{t}}}=(t_1,\ldots ,t_d)\in {\mathbb {R}}^d\), take

$$\begin{aligned} \begin{aligned} \textsf {trop}(f)({{\varvec{t}}})&=\bigoplus _{{{\varvec{m}}}\in \text {supp}(f)} \log |f_{{\varvec{m}}}|\odot {{\varvec{t}}}^{{{\varvec{m}}}}\\&=\max _{{{\varvec{m}}}\in \text {supp}(f)} \left( \log |f_{{\varvec{m}}}|+m_1t_1+\ldots m_d t_d\right) \\&=\max _{{{\varvec{m}}}\in \text {supp}(f)} \left( \log |f_{{\varvec{m}}}|+\langle {{\varvec{m}}},{{\varvec{t}}}\rangle \right) , \end{aligned} \end{aligned}$$
(3.1)

where \(\langle \cdot ,\cdot \rangle \) denotes the standard scalar product on \({\mathbb {R}}^d\). Tropicalization of f is thus a tropical analogue of the Laurent polynomial \(\sum _{{{\varvec{m}}}} \log |f_{{\varvec{m}}}| {{\varvec{z}}}^{{{\varvec{m}}}}\).

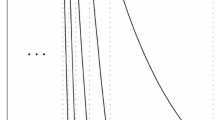
The tropical variety of \(f({{\varvec{z}}})\) is the set of all points \({{\varvec{t}}}\in {\mathbb {R}}^d\) such that the maximum in (3.1) is achieved at at least two monomials. Therefore, the tropicalization of f is a piecewise affine convex function on \({\mathbb {R}}^d\); each component of the complement of the tropical variety defines a domain where a certain monomial of f is maximal, c.f. (3.1). Figure 4 shows the tropical varieties of the first 4 decimations of a polynomial \(1+x+y\).

Fig. 4
figure 4

Tropical varieties of \(\textsf {trop}(f^{(n)})\) for \(f=1+x+y\) and \(n=1,2,3,4\)

Full size image

In a joint work with Doug Lind and Klaus Schmidt (Arzhakova et al. 2018), we established the following result on the existence of scaling limits of tropicalizations of the decimated polynomials \(f^{(n)}\).

Theorem 1

For every non-zero Laurent polynomial \(f({\varvec{z}})\) and all \({{\varvec{t}}}\in {\mathbb {R}}^d\), there exists a limit

$$\begin{aligned} \lim _{n\rightarrow \infty } \frac{1}{n^d} \textsf {trop}(f^{(n)})({{\varvec{t}}}) = R_f({{\varvec{t}}}), \end{aligned}$$
(3.2)

where \(R_f:{\mathbb {R}}^d\rightarrow {\mathbb {R}}\) is the Ronkin function of f, given by

$$\begin{aligned} \begin{aligned} R_{f}({\varvec{t}})&=\int _{0}^1\cdots \int _{0}^1 \log | f(e^{t_1 +2\pi i \theta _1},\ldots ,e^{t_d +2\pi i \theta _d} )|d\theta _1 \ldots d\theta _d \\&= \int _{{\varvec{\theta }}\in {\mathbb {T}}^d} \log \bigl | f(e^{ {\varvec{t}} +2\pi i \varvec{\theta }})\bigl |d \varvec{\theta }. \end{aligned} \end{aligned}$$
(3.3)

Sketch of the proof

(The full proof can be found in Arzhakova et al. (2018)) The first observation relates the Ronkin functions of f and \(f^{(n)}\); namely, \(R_{f^{(n)}}({{\varvec{t}}})=n^d R_{f}({{\varvec{t}}})\). Hence, it suffices to compare \(\textsf {trop}(f^{(n)})\) and \(R_{f}\).

The Ronkin function can be easily bounded from above: indeed, let us denote by \(\sharp \textsf {supp}(f^{(n)})\) the number of integer points inside the support of \(f^{(n)}\). Then,

$$\begin{aligned} R_{f^{(n)}}({{\varvec{t}}})&=\int _{{\mathbb {T}}^d}\log \Bigl | \sum _{{{\varvec{m}}}} f_{{{\varvec{m}}}}^{(n)} e^{\langle {{\varvec{t}}},{{\varvec{m}}}\rangle } e^{2\pi i \langle {{\varvec{m}}},{\varvec{\theta }}\rangle }\Bigr | d{\varvec{\theta }}\\&\le \int _{{\mathbb {T}}^d}\log \sum _{{{\varvec{m}}}\in \textsf {supp}(f^{(n)})}\Bigl | f_{{{\varvec{m}}}}^{(n)} e^{\langle {{\varvec{t}}},{{\varvec{m}}}\rangle } e^{2\pi i \langle {{\varvec{m}}},{\varvec{\theta }}\rangle }\Bigr | d{\varvec{\theta }}\\&=\int _{\mathbb T^d}\log \sum _{{{\varvec{m}}}\in \textsf {supp}(f^{(n)})}\Bigl | f_{{{\varvec{m}}}}^{(n)} e^{\langle {{\varvec{t}}},{{\varvec{m}}}\rangle } \Bigr |\\&\le \log \left( \sharp \textsf {supp}(f^{(n)}) \max _{{{\varvec{m}}}\in \textsf {supp}(f^{(n)})} \exp \left( \log |f^{(n)}_{{\varvec{m}}}|+{\langle {{\varvec{t}}},{{\varvec{m}}}\rangle }\right) \right) \\&= \log \sharp \textsf {supp}(f^{(n)}) + \max _{{{\varvec{m}}}\in \textsf {supp}(f^{(n)})}\left( \log |f^{(n)}_{{\varvec{m}}}|+{\langle {{\varvec{t}}},{{\varvec{m}}}\rangle }\right) \\&= \log \sharp \textsf {supp}(f^{(n)})+\,\textsf {trop}(f^{(n)})({{\varvec{t}}}). \end{aligned}$$

Hence, for all \(n\in {{\mathbb {Z}}}\) and \({{\varvec{t}}}\in {\mathbb {R}}^d\) one has

$$\begin{aligned} R_f({{\varvec{t}}}) =\frac{1}{n^d} R_{f^{(n)}}({{\varvec{t}}})\le \frac{1}{n^d} \log \sharp \textsf {supp}(f^{(n)}) +\frac{1}{n^{d}}\textsf {trop}(f^{(n)})({{\varvec{t}}}). \end{aligned}$$

Since the cardinality of the support of \(f^{(n)}\) grows at most as \(\text {const}\cdot n^d\), we immediately conclude that

$$\begin{aligned} R_f({{\varvec{t}}}) \le \liminf _{n\rightarrow \infty } \frac{1}{n^{d}}\textsf {trop}(f^{(n)})({{\varvec{t}}}). \end{aligned}$$
(3.4)

Let us start the discussion of the lower bound of \(R_f({{\varvec{t}}})\) with the following observation. Suppose that \({{\varvec{z}}}=(z_1,\ldots ,z_d)\in ({\mathbb {C}}^*)^d\) is a d-tuple of non-zero complex numbers; denote by \(t_j\in {\mathbb {R}}\) and \(\phi _j\in {\mathbb {T}}\sim [0,1)\) the modulus and the argument of \(z_j\) for every \(j=1,\ldots , d\), i.e., \(z_j=e^{t_j+2\pi i \phi _j}\). Note that

$$\begin{aligned}&\frac{1}{n^d} |\log f^{(n)}({{\varvec{z}}})| =\frac{1}{n^d} \sum _{k_1=0}^{n-1}\cdots \sum _{k_d=0}^{n-1} \log \nonumber \\&\qquad \times \left| f\left( e^{t_1+2\pi i \phi _1 +2\pi i {k_1}/n}, \ldots , e^{t_d+2\pi i \phi _d +2\pi i {k_d}/n}\right) \right| . \end{aligned}$$
(3.5)

The expression on the right hand side is a Riemann sum for the integral (3.3) defining the Ronkin function \(R_f({{\varvec{t}}})\). Note also, that despite the fact f may have zeros on a torus \(\{{{\varvec{z}}}: |{{\varvec{z}}}|=e^{{{\varvec{t}}}}\}\), the function \(\log |f|\) is still integrable since the singularities are only logarithmic. One naturally expects that for almost all \({{\varvec{z}}}\), the Riemann sums in (3.5) converge to \(R_f({{\varvec{t}}})\). However, establishing such convergence turns out to be a rather intricate Diophantine problem (Dimitrov 2016; Lind et al. 2013).

Fortunately, in order to establish the lower bound, one does not have to deal with a convergence problem in a complete generality. It suffices to prove that the Riemann sums are bounded from above by \(R_f({{\varvec{t}}})\).

We say that the initial value \({{\varvec{z}}}= (e^{t_1+2\pi i \phi _1} , \ldots , e^{t_d+2\pi i \phi _d})\) is good if the points of the set

$$\begin{aligned} Q_n({{\varvec{z}}})=\Bigl \{ \left( e^{t_1+2\pi i \phi _1 +2\pi i {k_1}/n}, \ldots , e^{t_d+2\pi i \phi _d +2\pi i {k_d}/n}\right) ,\quad k_1,\ldots k_d=0,\ldots n-1\Bigr \} \end{aligned}$$

do not fall or come too close (depending on n) to the variety of f: \(V_f=\{{{\varvec{z}}}\in ({\mathbb {C}}^*)^d:\ f({{\varvec{z}}})=0\}\). For good points, it is relatively easy to show that the Riemann sums are close to the value of the integral \(R_f({{\varvec{t}}})\). On the contrary, for the ’bad’ initial values \({{\varvec{z}}}\), the points in \(Q_n({{\varvec{z}}})\), which are close to \(V_f\), give a negative contribution to the sum (3.5). Hence, one is able to conclude that for all \({{\varvec{z}}}\) with \(|z_1|=e^{t_1}, \ldots , |z_d|=e^{t_d}\),

$$\begin{aligned} \limsup _{n\rightarrow \infty } \frac{1}{n^d} \log |f^{(n)}({{\varvec{z}}})| \le R_f({{\varvec{t}}}), \end{aligned}$$
(3.6)

or, equivalently,

$$\begin{aligned} |f^{(n)}({{\varvec{z}}})| \le \exp ( n^d(R_f({{\varvec{t}}})+o(1)). \end{aligned}$$
(3.7)

The final part of the argument is based on a relatively simple statement from the Fourier analysis: if the absolute value of a complex (trigonometric) polynomial is bounded from above by some constant M on a torus \({{\mathbb {T}}}_{{\varvec{t}}}=\{{{\varvec{z}}}:\ |{{\varvec{z}}}|=e^{{\varvec{t}}}\}\) then the absolute values of all of its monomials are also bounded from above by the same constant. Therefore, applying this result to \(f^{(n)}\) and the inequality (3.7), we conclude that that for all \({{\varvec{m}}}\)

$$\begin{aligned} |f_{{\varvec{m}}}^{(n)} e^{\langle {{\varvec{t}}},{{\varvec{m}}}\rangle }| \le \exp ( n^d(R_f({{\varvec{t}}})+o(1)), \end{aligned}$$

and, hence,

$$\begin{aligned} \textsf {trop}(f^{(n)})({{\varvec{t}}}) =\max _{{{\varvec{m}}}} \left( \log |f^{(n)}_{{\varvec{m}}}|+{\langle {{\varvec{t}}},{{\varvec{m}}}\rangle }\right) \le n^d(R_f({{\varvec{t}}})+o(1)). \end{aligned}$$
(3.8)

Combining the inequalities (3.4) and (3.8), we obtain the desired result. \(\square \)

Remark 1

Theorem 1 provides some insight on the geometry of tropical varieties of \(f^{(n)}\). In Fig. 4, the similarity between the shapes of tropical varieties of decimations of \(f=1+x+y\) for various n is not accidental. Let us recall the notion of an amoeba of a Laurent polynomial f of d variables that was first suggested by Gelfand, Kapranov, and Zelevinsky in Gelfand et al. (2008). An amoeba of f denoted by \(A_f\) is an image of the variety \(V_f\) under the map \(\text {Log} :V_f \mapsto {\mathbb {R}}^d\) given by the formula \(\text {Log}(z_1, \ldots , z_d) = (\log |z_1|, \ldots , \log |z_d|)\).

The amoeba \( A_f\) is a closed subset of \({\mathbb {R}}^d\) with a non-empty convex complement. The Ronkin function \(R_f\) is strictly convex over \( A_f\) and affine on each component of \({\mathbb {R}}^d \backslash A_f\) (Mikhalkin 2004) (Fig. 5).

Fig. 5
figure 5

Amoeba \( A_f\) for \(f=1+x+y\)

Full size image

It is easy to see that \( A_f\) coincides with \( A_{f^{(n)}}\) for every positive n. According to Theorem 1, \( \frac{1}{n^d} \textsf {trop}(f^{(n)})({\varvec{t}})\) is a sequence of piecewise-affine convex functions converging to the Ronkin function \(R_f\) which is affine on the complement of \( A_f\) and strictly convex inside \( A_f\). Therefore, the outer boundary of the tropical varieties \(\frac{1}{n^d} \textsf {trop}(f^{(n)})\) converge to the boundary of \( A_f\) as n approaches infinity.

3.1 Surface Tension

The Legendre transform (or a dual) of a function \(F:{\mathbb {R}}^d\rightarrow {\mathbb {R}}\) is defined as

$$\begin{aligned} F^*({{\varvec{t}}}) = \sup _{{{\varvec{u}}}\in {\mathbb {R}}^d}( \langle {{\varvec{t}}},{{\varvec{u}}}\rangle - F({{\varvec{u}}})). \end{aligned}$$

The Legendre transform \(F^*\) is always a convex function; moreover, for a convex closed function F, the Legendre transform is an involution:

$$\begin{aligned} F^{**}({{\varvec{u}}})=F({{\varvec{u}}}). \end{aligned}$$

Suppose f is a Laurent polynomial. Then, the tropicalization of f is, in fact, a Legendre transform of the function F defined as follows:

$$\begin{aligned} F({{\varvec{u}}}) ={\left\{ \begin{array}{ll} -\log | f_{{\varvec{m}}}|,&{}\text { if } {{\varvec{u}}}={{\varvec{m}}}\in \textsf {supp}(f),\\ +\infty ,&{}\text { otherwise}, \end{array}\right. }. \end{aligned}$$

Indeed, one has

$$\begin{aligned} F^*({{\varvec{t}}})=\sup _{{{\varvec{u}}}\in {\mathbb {R}}^d}( \langle {{\varvec{t}}},{{\varvec{u}}}\rangle - F({{\varvec{u}}}))= \sup _{{{\varvec{m}}}\in \textsf {supp}(f)}\left( \langle {{\varvec{t}}},{{\varvec{m}}}\rangle - (-\log |f_{{{\varvec{m}}}}|)\right) = \textsf {trop}(f)({{\varvec{t}}}). \end{aligned}$$

Applying the Legendre transform once again, we obtain \( F^{**} = \textsf {trop}(f)^*\). Since F, in general, is not convex, \(F^{**}\ne F\). However, \(F^{**}\) is easy to describe; namely, \(F^{**}=\textsf {conv}(F)\), where \(\textsf {conv}(F)\) is the so-called greatest convex minorant or a convex hull of F: the largest convex function satisfying \(\textsf {conv}(F)({{\varvec{u}}})\le F({{\varvec{u}}})\) for all \({{\varvec{u}}}\). Clearly, \(\textsf {conv}(F)({{\varvec{u}}})=+\,\infty \) for al \({{\varvec{u}}}\not \in {\mathcal {N}}(f)\) and is finite on \({\mathcal {N}}(f)\).

Using the above arguments for the polynomials \(f^{(n)}\) and the result of the Theorem 1, one immediately obtains the following result:

Corollary 1

Let \(\textsf {conv} (F^{(n)})\) be the greatest convex minorant of

$$\begin{aligned} F^{(n)}= {\left\{ \begin{array}{ll}-\log | f_{{\varvec{m}}}^{(n)} |,&{}\text { if } {{\varvec{u}}}={{\varvec{m}}}\in \textsf {supp}(f^{(n)}),\\ +\infty ,&{}\text { otherwise}. \end{array}\right. } \end{aligned}$$

Then, for all \({{\varvec{u}}}\in {\mathbb {R}}^d\),

$$\begin{aligned} \sigma _f({{\varvec{u}}}):=\lim _{n\rightarrow \infty }\frac{1}{n^d} \textsf {conv} (F^{(n)})(n^d{{\varvec{u}}}) = -\,R_f^*({{\varvec{u}}}). \end{aligned}$$

By analogy with Kenyon et al. (2006), we refer to the function \(\sigma _f\) as to the surface tension off.

Corollary 1 should be seen as a weaker, but at the same time, a more general version of the result established in Kenyon et al. (2006) for polynomials appearing in dimer problems. It turns out that these polynomials are rather special in the following sense: for such polynomials, one is able to define the surface tension using the coefficients of \(f^{(n)}\) without the need to resort to convex hulls of the coefficients. In other words, some form of convexity is already present in the coefficients of \(f^{(n)}\). It is, of course, very interesting to identify such polynomials. Kenyon and Okounkov (2006) showed that for every Harnack curve, one can construct a polynomial of 2 variables, whose algebraic variety is the given Harnack curve, and for which the surface tension is well defined. At the present moment, it is not clear which conditions could play a similar role in higher dimensions.

Finally, we would like to remark that the use of tropical geometric methods to study limits of partition functions or similar quantities is very natural, and has been proposed in Itenberg and Mikhalkin (2012).