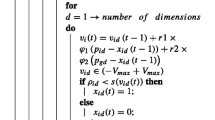Genetic algorithm as self-test path and circular self-test path design method

Abstract

The paper presents the use of Genetic Algorithm to search for non-linear Autonomous Test Structures (ATS) in Built-In Testing approach. Such structures can include essentially STP and CSTP and their modifications. Non-linear structures are more difficult to analyze than the widely used structures such as independent Test Pattern Generator and the Test Response Compactor realized by Linear Feedback Shift Registers. To reduce time-consuming test simulation of sequential circuit, it was used an approach based on the stochastic model of pseudo-random testing. The use of stochastic model significantly affects the time effectiveness of the search for evolutionary autonomous structures. In test simulation procedure, the block of sequential circuit memory is not disconnected. This approach does not require a special selection of memory registers such as BILBOs. A series of studies to test circuits set ISCAS’89 are made. The results of the study are very promising.

1 Introduction

Digital systems should provide services according to the specifications reliably. Impairments of dependability are associated with a large class of faults, errors and failures. These impairments may be caused by design, produce or rarely operational imperfections and improper use. There are lots of possible circuit failures: single stuck at 0 or 1 faults, delay and synchronization faults, bridging and open faults, in Metal Oxide Semiconductor technique (MOS) these faults consist in transistor stuck on or stuck off in a logical gates [1]. Some faults cannot be logically represented. Other class of faults can be connected with operational timing frequency and they are related to change impedance parameters, but in that case the built-in testing is one of the most resistant technique because of common silicon space. Faults that are stimulated may manifest itself as an error. For do that the fault have to be stimulated and propagated to one of internal (to memory module of sequential circuit) or external (primary) circuit output. The error, that is accessible from circuit output, is an information on detected fault and indicates that functional specification of circuit is violated. There is therefore a need for hardware testing.

For Very Large Scale Integration circuits (VLSI), the Built-In Self-Testing (BIST) concept is well used. Embedding the whole or major part of the tester into the circuit is considered as BIST. Production standard involves the use of Linear Feedback Shift Registers (LSFR) that are used as a Test Pattern Generators (TPG) and Test Response Compactors (TRC) in a signature analysis [2]. These LFSR registers can generate pseudo-random test vectors that may cover many faults. For the evaluation of the effectiveness of coating defects by sequence of test vectors, the Fault Coverage (FC) is applied. Multi-Input Signature Registers (MISR) and Single-Input Signature Registers (SISR) are mainly used as TRC registers [3]. These Compactors perform data compression generally lossy, but are known lossless Zero-Aliasing ones without faults masking phenomena.

There is also a non-linear technique with Self-Test Path (STP) or Circular STP (CSTP). Some modifications of these self-testing techniques are also known, e.g., Circular CSTP (C2STP) [4]. Contrary to linear technique, the Circuit Under Test (CUT) in non-linear technique is a feedback of STP or CSTP, thus posing a problem with parameter selection for these structures. These structures can be implemented in Field Programmable Gate Arrays (FPGA) [5], Application Specific Integrated Circuit (ASIC), System-on-Chip (SOC), which consist of many virtual Intellectual Property modules (IP Core). For SOC, the STP structures can also link IP modules [6].

Nevertheless, simulations presented in this paper show that it is possible to design such BIST, modeled as NLFSR, that achieve higher effectiveness than those of solutions reported in the literature and often are minimized. The minimization is related to the concept of external self-testing, where internal Memory Module (MM) of the circuit is disconnected during test, thus no additional conditions are imposed on its operation. It should be noted that both in linear and non-linear testing techniques, the circuit MM is typically included into self-testing structure registers as results from ability to improve testability and application of Design for Testability (DFT). An important observations was made in [7].

The properties of evolutionary algorithms make possible to solve a non-linear structures designing problem. The modeling of NLFSRs is important for the sake of correct representation of it. In this paper, many evolutionary models of non-linear register for evolutionary computer simulations are shown. In addition, many different design methods, often with the use of Genetic Algorithms (GATTO, GATTO$+$, GATTO*, SELFISH GENE GA [8,9,10]) and deterministic systems based, among other things, on Automatic Test Pattern Generation (ATPG) [11], Cellular Automata (CA) [12], Finite State Machines (FSM), and Binary Decision Diagrams (BDD) are used to built-in testing design. There are some solutions that can create a sequence of test vectors. In this paper, we are searching for not only a selection of sequences, but for structures that can generate these sequences with good FC parameter.

The paper is organized as follows. In Sect. 2, basic information on NLFSR as ATS, essentially STP and evolutionary are presented. Section 3 includes some description of the Genetic Algorithm and its using to create ATS structures. Next, in Sect. 4, some results of evolutionary searching for STP/CSTP structures are presented, and finally Sect. 5 concludes the paper.

The paper is an extended version of a previously published article titled “Genetic Algorithm for Self-Test Path and Circular Self-Test Path Design” that was presented at ACIIDS 2017 conference [7].

2 Non-linear feedback shift register as STP and CSTP model

Self-Test Path, Circular Self-Test Path and Condensed Circular Self-Test Path (C2STP) and in general NLFSRs can be seen as realization of Autonomous Test Structure (ATS).

In Fig. 1, a schema of autonomous structure STP that works accordingly to (1) is presented.

Fig. 1

Self-test path model

In Fig. 1, $V_{i}$ is an element of STP and it is mainly D-type flip-flop, t is a discrete time (clock time) and $p=n+m-1$ is a length of STP (number of flip-flops).

$$\begin{aligned} \left| {\begin{array}{c} V_{0}(t+1)\\ V_{1}(t+1)\\ \vdots \\ V_{m-1}(t+1)\\ \vdots \\ V_{p-2}(t+1)\\ V_{p-1}(t+1)\\ \end{array}}\right| =T* \left| {\begin{array}{c} V_{0}(t)\\ V_{1}(t)\\ \vdots \\ V_{m-1}(t)\\ \vdots \\ V_{p-2}(t)\\ V_{p-1}(t)\\ \end{array}}\right| \oplus \left| {\begin{array}{c} f_{0}(V_\mathrm{input}(t))\oplus S_\mathrm{in}\\ f_{1}(V_\mathrm{input}(t))\\ \vdots \\ f_{m-1}(V_\mathrm{input}(t))\\ \vdots \\ 0\\ 0\\ \end{array}}\right| \nonumber \\ , \end{aligned}$$

(1)

where $\oplus$ denotes an addition operator over GF(2) and

$$\begin{aligned} V_{\mathrm{input}}(t)=V_{m-1}(t),\ldots ,V_{p-2}(t),V_{p-1}(t) \end{aligned}$$

(2)

and

$$\begin{aligned} T=\left| {\begin{array}{ccccccc} 0 &{}\quad 0 &{}\quad \dots &{}\quad 0 &{}\quad \dots &{}\quad 0 &{}\quad 0 \\ 1 &{}\quad 0 &{}\quad \dots &{}\quad 0 &{}\quad \dots &{}\quad 0 &{}\quad 0 \\ \vdots &{}\quad \vdots &{}\quad \ddots &{}\quad \vdots &{}\quad \dots &{}\quad \vdots &{}\quad \vdots \\ 0 &{}\quad 0 &{}\quad \dots &{}\quad 1 &{}\quad \dots &{}\quad 0 &{}\quad 0 \\ \vdots &{}\quad \vdots &{}\quad \dots &{}\quad \vdots &{}\quad \ddots &{}\quad \vdots &{}\quad \vdots \\ 0 &{}\quad 0 &{}\quad \dots &{}\quad 0 &{}\quad \dots &{}\quad 1 &{}\quad 0 \\ \end{array}}\right| \end{aligned}$$

(3)

is the Connection Matrix for D-type flip-flops which are used to create STP register. If some $i\mathrm{th}$ flip-flop is a T-type one then $[T_{i,i}]=1$. The last element in the first row of the matrix $[T_{0,p-1}]=1$ for CSTP structure and in the rest of the paper ATS based on CSTP. The schema of CSTP is shown in Fig. 2.

Fig. 2

Circular self-test path model

Fig. 3

External, top-feedback ExOR register

Fig. 4

Internal, bottom-feedback ExOR register

Fig. 5

External–internal, top–bottom ExOR register

2.1 Using additional linear feedback

By taking into account the type of additional STP linear feedback, it can be distinguished different connection matrix forms: external, Top-Feedback ExOR (4) (Fig. 3), internal, Bottom-Feedback ExOR (5) (Fig. 4) and external–internal, Top–Bottom-Feedback ExOR (6) (Fig. 5).

$$\begin{aligned} T_{g}= & {} \left| {\begin{array}{ccccccc} g_{0} &{}\quad g_{1} &{}\quad \dots &{}\quad g_{m-1} &{}\quad \dots &{}\quad g_{p-2} &{}\quad g_{p-1}=1 \\ 1 &{}\quad 0 &{}\quad \dots &{}\quad 0 &{}\quad \dots &{}\quad 0 &{}\quad 0 \\ \vdots &{}\quad \vdots &{}\quad \ddots &{}\quad \vdots &{}\quad \dots &{}\quad \vdots &{}\quad \vdots \\ 0 &{}\quad 0 &{}\quad \dots &{}\quad 1 &{}\quad \dots &{}\quad 0 &{}\quad 0 \\ \vdots &{}\quad \vdots &{}\quad \dots &{}\quad \vdots &{}\quad \ddots &{}\quad \vdots &{}\quad \vdots \\ 0 &{}\quad 0 &{}\quad \dots &{}\quad 0 &{}\quad \dots &{}\quad 1 &{}\quad 0 \\ \end{array}}\right| , \end{aligned}$$

(4)

$$\begin{aligned} T_{h}= & {} \left| {\begin{array}{ccccccc} 0 &{}\quad 0 &{}\quad \dots &{}\quad 0 &{}\quad \dots &{}\quad 0 &{}\quad h_{0}=1 \\ 1 &{}\quad 0 &{}\quad \dots &{}\quad 0 &{}\quad \dots &{}\quad 0 &{}\quad h_{1} \\ \vdots &{}\quad \vdots &{}\quad \ddots &{}\quad \vdots &{}\quad \dots &{}\quad \vdots &{}\quad \vdots \\ 0 &{}\quad 0 &{}\quad \dots &{}\quad 1 &{}\quad \dots &{}\quad 0 &{}\quad h_{m-1} \\ \vdots &{}\quad \vdots &{}\quad \dots &{}\quad \vdots &{}\quad \ddots &{}\quad \vdots &{}\quad \vdots \\ 0 &{}\quad 0 &{}\quad \dots &{}\quad 0 &{}\quad \dots &{}\quad 1 &{}\quad h_{p-1} \\ \end{array}}\right| , \end{aligned}$$

(5)

$$\begin{aligned} T_{gh}= & {} \left| {\begin{array}{ccccccc} g_{0} &{}\quad g_{1} &{}\quad \dots &{}\quad g_{m-1} &{}\quad \dots &{}\quad g_{p-2} &{}\quad g_{p-1}=h_{0}\\ 1 &{}\quad a_{1,1} &{}\quad \dots &{}\quad a_{1,m-1} &{}\quad \dots &{}\quad a_{1,p-2} &{}\quad h_{1} \\ \vdots &{}\quad \vdots &{}\quad \ddots &{}\quad \vdots &{}\quad \dots &{}\quad \vdots &{}\quad \vdots \\ 0 &{}\quad 0 &{}\quad \dots &{}\quad 1 &{}\quad \dots &{}\quad a_{m-1,p-2} &{}\quad h_{m-1} \\ \vdots &{}\quad \vdots &{}\quad \dots &{}\quad \vdots &{}\quad \ddots &{}\quad \vdots &{}\quad \vdots \\ 0 &{}\quad 0 &{}\quad \dots &{}\quad 0 &{}\quad \dots &{}\quad 1 &{}\quad h_{p-1} \\ \end{array}}\right| ,\nonumber \\ \end{aligned}$$

(6)

where

$$\begin{aligned} a_{i,j}=\left\{ \begin{array}{ll} 1 &{}\quad \hbox { if }\ h_{i}=g_{j}=1 , \\ 0 &{}\quad \hbox { if } h_{i}\ne g_{j} \hbox { or } h_{i}=g_{j}=0 ,\\ \end{array} \right. \end{aligned}$$

(7)

and $g_{p-1}=h_{0}=1$, $g_{i}, h_{j}, a_{i,j}\in \mathrm{GF}(2)$.

2.2 Using connection matrices

NLFSR register can be connected to CUT in different ways. Equation (1) can be expressed simply by (8)

$$\begin{aligned} V(t+1)=T*V(t) \oplus F(V(t)). \end{aligned}$$

(8)

It is possible to change connection schema from CUT to STP/CSTP register using output matrices (OM) in a few modes ((10), (11), (12)) according to (9)

$$\begin{aligned} V(t+1)=T*V(t) \oplus \mathrm{OM}*F(V(t)). \end{aligned}$$

(9)

Output matrix can be realized by

$$\begin{aligned} \mathrm{OM}_{\mathrm{E}}= & {} \left| {\begin{array}{ccccccc} 1 &{}\quad 0 &{}\quad \dots &{}\quad {0} &{}\quad \dots &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 1 &{}\quad \dots &{}\quad 0 &{}\quad \dots &{}\quad 0 &{}\quad 0 \\ \vdots &{}\quad \vdots &{}\quad \ddots &{}\quad \vdots &{}\quad \dots &{}\quad \vdots &{}\quad \vdots \\ 0 &{}\quad 0 &{}\quad \dots &{}\quad 1 &{}\quad \dots &{}\quad 0 &{}\quad 0 \\ \vdots &{}\quad \vdots &{}\quad \dots &{}\quad \vdots &{}\quad \ddots &{}\quad \vdots &{}\quad \vdots \\ 0 &{}\quad 0 &{}\quad \dots &{}\quad 0 &{}\quad \dots &{}\quad 0 &{}\quad 0 \\ \end{array}}\right| , \end{aligned}$$

(10)

$$\begin{aligned} \mathrm{OM}_{1}= & {} \left| {\begin{array}{ccccccc} 0 &{}\quad 1 &{}\quad \dots &{}\quad 0 &{}\quad \dots &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad \dots &{}\quad 1 &{}\quad \dots &{}\quad 0 &{}\quad 0 \\ \vdots &{}\quad \vdots &{}\quad \ddots &{}\quad \vdots &{}\quad \dots &{}\quad \vdots &{}\quad \vdots \\ 1 &{}\quad 0 &{}\quad \dots &{}\quad 0 &{}\quad \dots &{}\quad 0 &{}\quad 0 \\ \vdots &{}\quad \vdots &{}\quad \dots &{}\quad \vdots &{}\quad \ddots &{}\quad \vdots &{}\quad \vdots \\ 0 &{}\quad 0 &{}\quad \dots &{}\quad 0 &{}\quad \dots &{}\quad 0 &{}\quad 0 \\ \end{array}}\right| , \end{aligned}$$

(11)

$$\begin{aligned} \mathrm{OM}_{\mathrm{Free}}= & {} \left| {\begin{array}{ccccccc} 1 &{}\quad 1 &{}\quad \dots &{}\quad 0 &{}\quad \dots &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 1 &{}\quad \dots &{}\quad 1 &{}\quad \dots &{}\quad 0 &{}\quad 0 \\ \vdots &{}\quad \vdots &{}\quad \ddots &{}\quad \vdots &{}\quad \dots &{}\quad \vdots &{}\quad \vdots \\ 1 &{}\quad 1 &{}\quad \dots &{}\quad 1 &{}\quad \dots &{}\quad 0 &{}\quad 0 \\ \vdots &{}\quad \vdots &{}\quad \dots &{}\quad \vdots &{}\quad \ddots &{}\quad \vdots &{}\quad \vdots \\ 0 &{}\quad 0 &{}\quad \dots &{}\quad 0 &{}\quad \dots &{}\quad 0 &{}\quad 0 \\ \end{array}}\right| . \end{aligned}$$

(12)

Fig. 6

Circuit outputs to register inputs connection type a output matrix E, b output matrix 1, c output matrix free

The OM$_\mathrm{E}$ matrix is identity matrix, but OM$_1$ matrix must meet the following condition (13):

$$\begin{aligned} \forall _i{} \exists _{0 \le j \le m-1}! [\mathrm{OM}_{i,j}]\!=\!1 \quad \mathrm{and}\quad \forall _j{} \exists _{0 \le i \le m-1}! [\mathrm{OM}_{i,j}]=1, \end{aligned}$$

(13)

where i and j represent the rows and columns of OM$_1$ matrix, respectively, and m is a number of circuit outputs. Matrix OM$_{\mathrm{Free}}$ must meet the following condition (14):

$$\begin{aligned} \forall _{0\le i \le m-1} \exists _{0\le j\le m-1} [\mathrm{OM}_{i,j}]=1. \end{aligned}$$

(14)

Depending on the contents of the minor, the three types of output connection matrices can be distinguished as output matrix E, output matrix 1 and output matrix free (Fig. 6). The similar notations can be applied to input connection matrices (IM) [7].

Observe that $[X_{\mathrm{input}}]_{n}=[x_{0},\ldots ,x_{n-1}]^{\mathrm{T}}$ symbolizes circuit inputs, then input matrix can be represented simple as (16) according to (15)

$$\begin{aligned}&X_{\mathrm{input}}(t+1)=\mathrm{IM}*V(t+1), \end{aligned}$$

(15)

$$\begin{aligned}&\mathrm{IM}=\left| {\begin{array}{ccccccc} 0 &{}\quad \dots &{}\quad 0 &{}\quad \dots &{}\quad 0 &{}\quad 0\\ 0 &{}\quad \dots &{}\quad 0 &{}\quad \dots &{}\quad 0 &{}\quad 0\\ \vdots &{}\quad \ddots &{}\quad \vdots &{}\quad \dots &{}\quad \vdots &{}\quad \vdots \\ i_{m-1,0} &{}\quad \dots &{}\quad i_{m-1,m-1} &{}\quad \dots &{}\quad i_{m-1,p-2} &{}\quad i_{m-1,p-1}\\ \vdots &{}\quad \ddots &{}\quad \vdots &{}\quad \ddots &{}\quad \vdots &{}\quad \vdots \\ i_{p-2,0} &{}\quad \dots &{}\quad i_{p-2,m-1} &{}\quad \dots &{}\quad i_{p-2,p-2} &{}\quad i_{p-2,p-1}\\ i_{p-1,0} &{}\quad \dots &{}\quad i_{p-1,m-1} &{}\quad \dots &{}\quad i_{p-1,p-2} &{}\quad i_{p-1,p-1}\\ \end{array}}\right| . \end{aligned}$$

(16)

There are few forms of input matrix, analogously to OMs (17), (18), (19) and specific ones (20) and (21):

$$\begin{aligned} \mathrm{IM}_{\mathrm{E}}= & {} \left| {\begin{array}{cccccc} 0 &{}\quad \dots &{}\quad 0 &{}\quad \dots &{}\quad 0 &{}\quad 0\\ 0 &{}\quad \dots &{}\quad 0 &{}\quad \dots &{}\quad 0 &{}\quad 0\\ \vdots &{}\quad \ddots &{}\quad \vdots &{}\quad \dots &{}\quad \vdots &{}\quad \vdots \\ 0 &{}\quad \dots &{}\quad 1 &{}\quad \dots &{}\quad 0 &{}\quad 0\\ \vdots &{}\quad \ddots &{}\quad \vdots &{}\quad \ddots &{}\quad \vdots &{}\quad \vdots \\ 0 &{}\quad \dots &{}\quad 0 &{}\quad \dots &{}\quad 1 &{}\quad 0\\ 0 &{}\quad \dots &{}\quad 0 &{}\quad \dots &{}\quad 0 &{}\quad 1\\ \end{array}}\right| , \end{aligned}$$

(17)

$$\begin{aligned} \mathrm{IM}_{1}= & {} \left| {\begin{array}{cccccc} 0 &{}\quad \dots &{}\quad 0 &{}\quad \dots &{}\quad 0 &{}\quad 0\\ 0 &{}\quad \dots &{}\quad 0 &{}\quad \dots &{}\quad 0 &{}\quad 0\\ \vdots &{}\quad \ddots &{}\quad \vdots &{}\quad \dots &{}\quad \vdots &{}\quad \vdots \\ 0 &{}\quad \dots &{}\quad 0 &{}\quad \dots &{}\quad 1 &{}\quad 0\\ \vdots &{}\quad \ddots &{}\quad \vdots &{}\quad \ddots &{}\quad \vdots &{}\quad \vdots \\ 0 &{}\quad \dots &{}\quad 0 &{}\quad \dots &{}\quad 0 &{}\quad 1\\ 0 &{}\quad \dots &{}\quad 1 &{}\quad \dots &{}\quad 0 &{}\quad 0\\ \end{array}}\right| , \end{aligned}$$

(18)

$$\begin{aligned} \mathrm{IM}_{\mathrm{Free}}= & {} \left| {\begin{array}{cccccc} 0 &{}\quad \dots &{}\quad 0 &{}\quad \dots &{}\quad 0 &{}\quad 0\\ 0 &{}\quad \dots &{}\quad 0 &{}\quad \dots &{}\quad 0 &{}\quad 0\\ \vdots &{}\quad \ddots &{}\quad \vdots &{}\quad \dots &{}\quad \vdots &{}\quad \vdots \\ 0 &{}\quad \dots &{}\quad 1 &{}\quad \dots &{}\quad 0 &{}\quad 1\\ \vdots &{} \quad \ddots &{}\quad \vdots &{}\quad \ddots &{}\quad \vdots &{}\quad \vdots \\ 0 &{}\quad \dots &{}\quad 0 &{}\quad \dots &{}\quad 1 &{}\quad 0\\ 0 &{}\quad \dots &{}\quad 1 &{}\quad \dots &{}\quad 1 &{}\quad 1\\ \end{array}}\right| , \end{aligned}$$

(19)

$$\begin{aligned} \mathrm{IM}_{1 \mathrm{Long}}= & {} \left| {\begin{array}{ccccccc} 0 &{}\quad \dots &{}\quad 0 &{}\quad \dots &{}\quad 0 &{}\quad 0\\ 0 &{}\quad \dots &{}\quad 0 &{}\quad \dots &{}\quad 0 &{}\quad 0\\ \vdots &{}\quad \ddots &{}\quad \vdots &{}\quad \dots &{}\quad \vdots &{}\quad \vdots \\ 1 &{}\quad \dots &{}\quad 0 &{}\quad \dots &{}\quad 0 &{}\quad 0\\ \vdots &{}\quad \ddots &{}\quad \vdots &{}\quad \ddots &{}\quad \vdots &{}\quad \vdots \\ 0 &{}\quad \dots &{}\quad 1 &{}\quad \dots &{}\quad 0 &{}\quad 0\\ 0 &{}\quad \dots &{}\quad 0 &{}\quad \dots &{}\quad 1 &{}\quad 0\\ \end{array}}\right| , \end{aligned}$$

(20)

$$\begin{aligned} \mathrm{IM}_{\mathrm{Free Long}}= & {} \left| {\begin{array}{ccccccc} 0 &{}\quad \dots &{}\quad 0 &{}\quad \dots &{}\quad 0 &{}\quad 0\\ 0 &{}\quad \dots &{}\quad 0 &{}\quad \dots &{}\quad 0 &{}\quad 0\\ \vdots &{}\quad \ddots &{}\quad \vdots &{}\quad \dots &{}\quad \vdots &{}\quad \vdots \\ 1 &{}\quad \dots &{}\quad 1 &{}\quad \dots &{}\quad 1 &{}\quad 0\\ \vdots &{}\quad \ddots &{}\quad \vdots &{}\quad \ddots &{}\quad \vdots &{}\quad \vdots \\ 0 &{}\quad \dots &{}\quad 1 &{}\quad \dots &{}\quad 1 &{}\quad 0\\ 1 &{}\quad \dots &{}\quad 0 &{}\quad \dots &{}\quad 1 &{}\quad 1\\ \end{array}}\right| . \end{aligned}$$

(21)

All of the input matrices must satisfy the following formula (22):

$$\begin{aligned} \forall _{0 \le i <m-1, 0 \le j \le p-1} [\mathrm{IM}_{i,j}]=0. \end{aligned}$$

(22)

Additionally, matrices IM$_{\mathrm{E}}$, IM$_{1}$ and IM$_{\mathrm{Free}}$ must satisfy the following formula (23):

$$\begin{aligned} \forall _{i \le p-1, 0 \le j < m-1} [\mathrm{IM}_{i,j}]=0. \end{aligned}$$

(23)

IM$_{\mathrm{E}}$ matrix is identity matrix, but IM$_{1}$ matrix must meet the following conditions (24 and 25):

$$\begin{aligned} \forall _{m-1 \le i \le p-1} \exists _{m-1 \le j \le p-1}! [\mathrm{IM}_{i,j}]=1, \end{aligned}$$

(24)

and

$$\begin{aligned} \forall _{m-1 \le j \le p-1} \exists _{m-1 \le i \le p-1}! [\mathrm{IM}_{i,j}]=1, \end{aligned}$$

(25)

where i and j represent the rows and columns of IM$_1$ matrix, respectively.

Matrix IM$_{\mathrm{Free}}$ must meet the following condition (26):

$$\begin{aligned} \forall _{m-1 \le i \le p-1} \exists _{m-1 \le j\le p-1} [\mathrm{IM}_{i,j}]=1. \end{aligned}$$

(26)

Matrices IM$_{1\mathrm{Long}}$ and IM$_{\mathrm{FreeLong}}$ satisfy similar conditions to IM$_{1}$ and IM$_{\mathrm{FreeLong}}$, respectively, without fulfilling the (23) condition.

In Fig. 7, schema of all input matrix types are presented, and in Fig. 8, the example of connection schema (XOR matrix circuit) coded by some IM$_{\mathrm{Free}}$ is shown.

Fig. 7

Register outputs to circuit inputs connection type a input matrix E, b input matrix 1, c input matrix free, d input matrix 1 long, e input matrix free long

Fig. 8

Input matrix connection schema interpretation

2.3 Configuration of ATS model

The following linear feedback types can be chosen when configuring the ATS model:

• AIJ Top–Bottom LFSR (1–1500), additional external and internal linear feedbacks are possible,

• Bottom LFSR (1500–3000), additional internal linear feedback is possible,

• Shift Register (3000–4500), no additional linear feedback,

• Top LFSR (4500–6000), additional external linear feedback is possible,

• Top–Bottom LFSR (6000–7500), additional external and internal linear feedbacks (other than AIJ Top–Bottom LFSR) are possible.

To configure the STP register connections with the tested circuit, the following connection diagram types were distinguished: for circuit inputs,

• Input Matrix 1 (1–300), complex connections available to the part of the STP register that controls inputs of the tested circuit,

• Input Matrix 1 Long (300–600), complex connection, while allowing connections with any component of the STP register,

• Input Matrix E (600–900), simple connections (as shown in Fig. 1),

• Input Matrix Free (900–1200), connections through XOR matrices, but only with those STP register components that control inputs of the tested circuit,

• Input Matrix Free Long (1200–1500), connection through XOR matrices with any STP register components.

for circuit outputs:

• Output Matrix 1 (1–100), complex connections, available for those components of STP register that are responsible circuit response.

• Output Matrix E (100–200), simple connections (as shown in Fig. 1),

• Output Matrix Free (200–300), connections through XOR matrices, but only with those STP components that are responsible for circuit response receiving.

In brackets, there are identifiers being useful in analysis of simulation graphs presented in Fig. 11 and so on. In Fig. 9, all STP configurations are presented (CSTP configurations have a similar notation that starts from 7500 to 15000).

Fig. 9

ATS-STP configuration

3 Genetic algorithm as NLFSR design method

Genetic algorithm (GA) has some useful features, such as the ability to deliver multiple point solutions, and so the lack of concentration of solutions around a certain subclass of STP/CSTP structure and configuration. The algorithm mimics natural evolutionary processes, and therefore there exists the possibility of self-control calculations in such a way that a solution better adapted to a greater extent affects the entire population of solutions (selective pressure).

The GA directs the search in the space of feasible solutions by environmental evaluation of the fitness function of each solution (individual). The course of the algorithm is presented in Fig. 10.

The process of STP/CSTP design creation is a complicated one, especially due to the difficulty of non-linear circuit feedback and BIST simulation time. Every individual has to be simulated and this process is a great time-consuming task. In [7], the stochastic model of pseudo-random testing, which significantly reduces this problem, was described. Using the stochastic model, the simulation of each solution is well reduced due to the conversion of exploration FC in search of a suitable length of sequence. Fitness function can be described as some optimization problem in which one is looking for such $x^*\in V(p)$ that maximizes the following formula (27):

$$\begin{aligned} f(x^{*})=\max _{x\in V(p)} f(x) , \end{aligned}$$

(27)

where V(p) is a multidimensional vector of parameters. The fitness function is defined as follows (28):

$$\begin{aligned} \mathrm{Fitness}(x \in V(p))= & {} w_{0}x_{0}+w_{1}(x_{1\mathrm{max}}-x_{1})\nonumber \\&+\,w_{2}(x_{2\mathrm{max}}-x_{2}) , \end{aligned}$$

(28)

where $x_{0}$ is a length of sequence, $x_{1}$ is a number of ExORs used to create additional linear feedback, $x_{2}$ is a number of T-type flip-flops used to design NLFSR and $\sum _{i=0}^{n=2}w_{i}=1$.

The linear code of solution (chromosome) is a binary array of bit values that stores

• Initial state of register;

• Initial state of circuit memory module (MM);

• Type of register flip-flops, e.g., D, T;

• Schema of additional external/internal linear feedback;

• Type and values of Input Matrix IM;

• Type and values of Output Matrix OM;

• Number of included circuit memory elements MM as part of ATS.

Fig. 10

Evolution in genetic algorithm

Table 1 ISCAS’89 subset

In the initial stage of the genetic algorithm, essentially random $P_{0}$ population base is created. The population is further assessed by the environment (fitness function). Based on the adaptation of individuals, their reproduction to temporary populations $T_{i}$ is made. Then from $T_{i}$ using genetic operators crossover and mutation with some probabilities, the descendant population (Offspring) $O_{i}$ is created. Next evaluation of the newly established offspring population $P_{i+1}$ takes place iteratively until the stopping criteria are fulfilled. This evolutionary process is common to all Genetic Algorithms. The ability to generate invalid connection matrices, i.e., not meeting the above conditions, was excluded by a particular type of chromosome encoding. With this approach, it is not necessary to use repair algorithms or penalty function for a faulty solution.

The criterion for stopping the algorithm is to reach an acceptable FC value or exceed a predetermined number of generations.

4 Results

The experiments presented here were performed for a subset of ISCAS’89 sequential circuits presented in Table 1.

Fig. 11

Simulation graph for s349 a sequence length vs. sequence id, b FC vs. sequence id and c FC vs. sequence length. STP (Id 1–7500), CSTP (Id 7501–15000)

Fig. 12

Simulation graph for s382 a sequence length vs. sequence id, b FC vs. sequence id and c FC vs. sequence length. STP (Id 1–7500), CSTP (Id 7501–1500)

Fig. 13

Simulation graph for s444 a sequence length vs. sequence id, b FC vs. sequence id and c FC vs. sequence length. STP (Id 1–7500), CSTP (Id 7501–15000), CSTP with additional DFF (Id 15001–22500)

Fig. 14

Simulation graph for s820 a sequence length vs. sequence id, b FC vs. sequence id and c FC vs. sequence length. STP (Id 1–7500), CSTP (Id 7501–15000), CSTP with additional DFF (Id 15001–22500)

Table 2 ATS statistical results for s208.1 circuit

In Fig. 11b, one can notice a specific repeatability of FC 0.6–0.8 for STP/CSTP resulting from the presence of type 1 Long connection matrix (e.g., Seq. Id. 300–600, 1800–2100 and so on). This type of matrix can actually reduce the length of the ATS structure and thereby reduce the length of the test sequence (Fig. 11a). For other connection matrices, FC reaches the value of 1. However, the described phenomenon occurs for the s349, only.

Figure 12a shows that for the s382 within certain ATS structures, the focused values of FC of small discrepancies are obtained. Figure 12b for the same circuit can be noted that only a few configurations of ATS structure can be able to obtain the FC at around 0.9 (Seq. Id 2100–2300 for STP, 9700–9800 and 12800–12900 for CSTP). In these structures, matrices such as Input Matrix Free and Output Matrix Free are used. An interesting area is that identified by Id Seq. 10500 and 11700, there is ATS structure realized by a simple Shift Register (SR) generating short sequences, which, however, allow for the acquisition of a relatively high FC value. In this area, there is an additional CSTP feedback. The charts shown in Fig. 13 for the s444 are in some ways similar to the graph in Fig. 12 for the s382. Both test circuits are traffic light controllers and have the BCD counters (timers).

In Fig. 14 for the s820, it can be seen that almost independently of the ATS structure the FC is recovered in the range of 0.3–0.45. The best achieved result was FC $=0.598$. The s820 circuit has only a few flip-flops but some portion of the state space which should be taken into account is fault dependent.

Statistical analysis of the results showed a correlation from low (below than 0.1) to strong (greater than 0.9), between the length of the sequences and FC for the specified ATS structures. For example, for s208.1, the correlation ranges between 0.19 and 0.914 (Table 2). Figure 15 shows the FC dependence on the length of test sequence for many ATS (more precisely STP) configurations. The correlation coefficient value is 0.7. Figure 16 can be seen that the vast majority of the structure ATS (sequence ID) generates test sequences of length 1000, except for a singularity identified by the 10500–11500th corresponds to the CSTP structure based on the Shift Register without the additional linear feedback. Interestingly, in

Fig. 15

Correlation between the length of sequence and FC for s208.1 circuit. ATS configuration ID from 1 to 100 (Fig. 9)

Fig. 16

Simulation graph for s1196 a sequence length vs. sequence id, b FC vs. sequence id and c FC vs. sequence length. STP (Id 1–7500), CSTP (Id 7501–15000), CSTP with additional DFF (Id 15001–22500)

Fig. 17

Simulation graph for s1238 a sequence length vs. sequence id, b FC vs. sequence id and c FC vs. sequence length. STP (Id 1–7500), CSTP (Id 7501–15000), CSTP with additional DFF (Id 15001–22500)

Fig. 18

Simulation graph for s1423 a sequence length vs. sequence id, b FC vs. sequence id and c FC vs. sequence length. STP (Id 1–7500), CSTP (Id 7501–15000), CSTP with additional DFF (Id 15001–22500)

Fig. 19

Simulation graph for s1494 a sequence length vs. sequence id, b FC vs. sequence id and c FC vs. sequence length. STP (Id 1–7500), CSTP (Id 7501–15000), CSTP with additional DFF (Id 15001–22500)

Fig. 20

s1196 density and distribution function that reached a FC $\ge 0.7$, b FC $\ge 0.8$, c FC $\ge 0.9$, d FC $\ge 0.95$

Fig. 21

STP for s298 without use of internal flip-flops

Fig. 22

STP for s298 with use of 1 internal flip-flop

Fig. 23

STP for s298 with use of 2 internal flip-flops

Fig. 24

STP for s298 with use of 3 internal flip-flops

Fig. 25

STP for s298 with use of 4 internal flip-flops

Fig. 26

STP for s298 with use of 5 internal flip-flops

Fig. 27

STP for s298 with use of 6 internal flip-flops

Fig. 28

STP for s298 with use of 7 internal flip-flops

Fig. 29

STP for s298 with use of 8 internal flip-flops

Fig. 30

STP for s298 with use of 9 internal flip-flops

Fig. 31

STP for s298 with use of 10 internal flip-flops

Fig. 32

STP for s298 with use of 11 internal flip-flops

Fig. 33

STP for s298 with use of 12 internal flip-flops

Fig. 34

STP for s298 with use of 13 internal flip-flops

Fig. 35

STP for s298 with use of 14 internal flip-flops

Fig. 16, there is a high correlation between the length of the generated sequence and the value of FC. Most ATS structures for this circuit cover from 0.7 to nearly 0.9 faults beyond the aforementioned singularity. The results of the study for s1238 in Fig. 17, with slightly less FC from 0.7 to 0.8, are quite similar. In Fig. 18, one can see that the FC depends on the structure of the ATS oscillates from about 0.35 to 0.5, with a maximum value of 0.530. There is also a singularity in the range of 10500–12000. Compared to the plots Figs. 16 and 18 there are more different sequence lengths, and the FC value is in the lower range. As with the circuit in Fig. 17 and smaller in Figs. 11, 12 and  13, there are ATS configurations that generate short cycles. In Fig. 19, almost all ATS structures have generated sequences longer than 1000 test vectors. Restricting the sequence length to 1000 vectors is too restrictive for medium-sized circuits (Table 1). Despite long sequences, FC values oscillate between 0.35 and 0.7 depending on the ATS structure. There is a very high dependency between ATS, exactly STP and FC (island areas, clusters in plots). Information about excessive limitation of 1000 sequence length vectors results from the developed stochastic faults model and the need to reduce the computer time-consuming circuit simulation, for example, for s1196 shown in Fig. 20. From Fig. 20, one needs to generate a long test sequence, for example, to get FC $=0.95$ (Fig. 20d) probability of close 1 would generate a sequence of 10,000 vectors. This is obviously a necessary condition, but not sufficient due to the variety of ATS structures researched. Figures 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34 and 35 show in detail the effect of incremental including internal memory elements of a sequential circuit into STP structure on diagnostic performance of s298 circuit testing. With the increase in the number of included memory elements, STP increases the sequence length, but also increases FC. This incorporation of memory elements into STP allows one to convert a sequential circuit into a combinational circuit whose testing process is simplified. In a combinational circuit, the output depends entirely on the input and in the sequential circuit also on the state of the internal memory. The ability to disconnect system memory (MM) results from the use of special, e.g., BILBO multifunctional registers. Disconnecting the internal memory of the sequential system during testing is a standard and widely used approach.

In Table 3, the FC values obtained for a subset of ISCAS’89 are presented. In test simulation procedure, the block of sequential circuit memory is not disconnected. In other case, the greatest value of FC $=0.997$ was calculated for the structure of the CSTP including all s298 circuit flip-flops (MM) (Fig. 35).

As mentioned earlier, to increase the circuit testability, all or some of circuit (MM) elements should be included into self-testing register (STP or CSTP) (Fig. 36). Disconnecting the (MM) elements, converts the sequential circuit (CUT) to a combinational one, that is easier to test. The effect of disconnecting memory elements from the sequential circuit s298 is shown in Figs. 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34 and 35.

5 Conclusions and future work

Genetic algorithm was able to find appropriate solutions, i.e., the structures of ATS, which were able to generate adequate quality test sequences and the high value of FC was possible to obtain. The conducted experiments show that it is possible to identify ATS structures with a high correlation coefficient between the sequence length and FC. Finding a suitable ATS structure evolutionary with those properties requires the circuit test simulation without faults, and therefore significantly affects the efficiency of the search (exploration) of the solution space. Next, the diagnostic efficacy of ATS structure has to be finally confirmed by simulation circuits with faults, which is much more time complex task. The genetic algorithm used as the method of designing ATS structures was controlled by standard values of crossover and mutation operators. Crossover and mutation processes are specific for encoding connection matrices and exclude unacceptable forms. It should be noted that memory block of circuit operates in accordance with the specification and has not been disconnected, and so the same process of testing simulation was significantly complicated. As demonstrated in the research, the use of even a small subset of the internal memory of the sequential circuit as part of the STP/CSTP register allows for significant increase of fault coverage value. The results of sequential circuits testing even without disconnecting internal memory are comparable to other methods known from the literature. Including circuit memory elements into the STP/CSTP register radically increases the sequence length and FC, but imposes specific system solutions on the sequential circuit memory block, e.g., BILBO register. Research analysis has shown that there is a correlation between FC and the length of the test sequence. The value of the correlation coefficient reaches more than 0.9 for certain ATS structures, rarely reaching small values less than 2. The high correlation within specific ATS structures makes 

it possible to use deterministic local optimization algorithms or evolutionary exploitation process to select the appropriate connection matrices, additional linear feedback and type of flip-flops used to create STP/CSTP register.

Table 3 ISCAS’89 benchmark fault coverage results

Fig. 36

Memory module under test disconnection

In the future, research will be conducted on the classical testing structures such as independent test pattern generators (LFSRs) and test response compactors (MISRs, SISRs) or cellular automata. It is also very important to enrich used faults model by other types of faults such as open line, bridging and cross-talk faults. Other research related to the selection of other evolutionary algorithms for ATS design will also be made.