Aggregative context-aware fitness functions based on feature selection for evolutionary learning of characteristic graph patterns

Abstract

We propose aggregative context-aware fitness functions based on feature selection for evolutionary learning of characteristic graph patterns. The proposed fitness functions estimate the fitness of a set of correlated individuals rather than the sum of fitness of the individuals, and specify the fitness of an individual as its contribution degree in the context of the set. We apply the proposed fitness functions to our evolutionary learning, based on Genetic Programming, for obtaining characteristic block-preserving outerplanar graph patterns and characteristic TTSP graph patterns from positive and negative graph data. We report some experimental results on our evolutionary learning of characteristic graph patterns, using the context-aware fitness functions.

1 Introduction

Genetic Algorithm (GA) and Genetic Programming (GP) [8, 16] are representative evolutionary learning methods and widely used as probabilistic methods for solving computationally hard learning problems. The evaluation value of individuals, called the fitness, plays a central role in controlling the process of evolutionary learning. In usual setting, fitness of individuals depends on the performance of individuals only.

In this paper, fitness functions aware of context are considered in the sense that the fitness of an individual depends on a set of individuals relevant to it, instead of the individual only. Three new aggregative context-aware fitness functions based on a feature selection method [19] are proposed for evolutionary learning of characteristic graph patterns. Using the proposed fitness functions, we estimate the fitness of a set of correlated individuals rather than the sum of fitness of the individuals, and define the fitness of an individual as its contribution degree in the context of the set of correlated individuals.

We address the problem of finding a general pattern that covers positive examples as much as possible and does not cover negative examples as much as possible. Therefore, it is desirable to diversify patterns to cover all the positive examples as much as possible, in the course of evolutionary computation. We introduce a consistency-based feature selection algorithm, super-CWC [19] to ensure this diversity with a small number of individuals. This algorithm constructs a minimal set of features by which positive examples are consistently discriminated from negative examples as much as possible.

Graph classification [17] is an important task of classifying graphs with class labels in a graph database into two or more classes and has received wide attention as the amount of graph-structured data has increased. Thus, we incorporate the context-aware fitness function to our Genetic Programming-based evolutionary learning method that obtains characteristic graph patterns that classify given positive and negative graph data. To model many chemical compounds, outerplanar graphs are known to be used [3]. Block-preserving outerplanar graph patterns (bpo-graph patterns) [18, 24] are graph-structured patterns with structured variables and can represent characteristic graph structures of outerplanar graphs. TTSP (Two-Terminal Series Parallel) graphs are used as data models for electric networks and scheduling. TTSP graph patterns [21] are graph-structured patterns with structured variables and can represent characteristic graph structures of TTSP graphs.

We have proposed Genetic Programming-based evolutionary learning methods that incorporate a fitness function ignoring context for acquiring characteristic bpo-graph patterns from positive and negative outerplanar graphs [14, 23] and acquiring characteristic TTSP graph patterns from positive and negative TTSP graphs [11]. Then we have proposed a context-aware fitness function using Matthews Correlation Coefficient (MCC) as a correlation measure [22], for our evolutionary learning of characteristic bpo-graph patterns.

Feature selection using evolutionary methods such as genetic algorithm has been widely studied [1, 2, 5, 15, 25]. In this paper, we consider using a feature selection method in Genetic Programming. In different setting from ours, using context awareness in Genetic Programming is considered and context-aware crossover operator is proposed [9]. As evolutionary learning methods from graph-structured data, Genetic Network Programming (GNP) [6] and Graph Structured Program Evolution (GRAPE) [20] are proposed. We proposed Genetic Programming-based learning of characteristic tree patterns from both positive and negative tree-structured data [10, 12, 13]. Mining frequent subgraphs in outerplanar graphs [3], finding minimally generalized bpo-graph patterns and enumerating frequent bpo-graph patterns from positive outerplanar graphs [18, 24], and finding minimally generalized TTSP patterns and enumerating frequent TTSP graph patterns from positive TTSP graphs [7, 21] are known. These approaches [3, 7, 18, 21, 24] are different from our evolutionary learning method in that our method learns from positive and negative graph-structured data.

This paper is an extended version of the conference paper [22]. In the previous work [22], we proposed a Genetic Programming-based evolutionary learning method that incorporates a context-aware fitness function using Matthews Correlation Coefficient (MCC) as a correlation measure for acquiring characteristic bpo-graph patterns from positive and negative outerplanar graphs and reported some experimental results. In this paper, we report three-way extended results as follows. We propose three new aggregative context-aware fitness functions using Mutual Information (MI), Symmetric Uncertainty (SU) and Inconsistency Rate (ICR) as correlation measures, based on feature selection for evolutionary learning of characteristic graph patterns. We report new experimental experiments on large data set by our evolutionary learning for obtaining characteristic block-preserving outerplanar patterns from positive and negative graph data. We report new application of the proposed fitness functions to our Genetic Programming-based evolutionary learning for obtaining characteristic TTSP graph patterns from positive and negative graph data.

This paper is organized as follows. In Sect. 2, we summarize our evolutionary learning framework for acquiring characteristic graph patterns. In Sect. 3, we propose Genetic Programming-based learning methods for acquiring characteristic bpo-graph patterns and characteristic TTSP graph patterns from positive and negative outerplanar graph data, by incorporating context-aware fitness functions based on the feature selection method [19]. In Sect. 4, we report some experimental results on our evolutionary learning of characteristic bpo-graph patterns and TTSP graph patterns. Finally, in Sect. 5, we present the conclusion and future work.

2 Preliminaries

In this paper, a graph means a connected graph with labeled or unlabeled vertices and labeled edges. A graph pattern is defined as a graph-structured pattern having structured variables (variables), which is a graph representation of characteristic common features of graph-structured data. A variable of a graph pattern is a list of one or two distinct vertices of the graph pattern. A variable has a label, called a variable label. We assume that all variables in a graph pattern have mutually distinct variable labels. In this section, we review block-preserving outerplanar graph patterns.

2.1 Acquisition of characteristic outerplanar graph patterns using genetic programming

We review a block-preserving outerplanar graph pattern as a graph pattern having outerplanar graph structure, and a block tree pattern, which is a tree representation of a block-preserving outerplanar graph pattern, according to [14, 18, 23, 24]. An outerplanar graph is a planar graph which can be drawn in the plane such that all vertices belong to the outer boundary. By an outerplanar graph, we mean a connected outerplanar graph with labeled vertices and labeled edges.

A vertex of a graph is called a cut-vertex if the removal of the vertex makes the graph disconnected. An edge of an outerplanar graph is called a bridge if the removal of the edge makes the graph disconnected. We remark that both endpoints of a bridge are cut-vertices. A graph is said to be biconnected if the graph has no cut-vertex. A block of an outerplanar graph is a maximal biconnected subgraph which has at least three vertices. We consider two types of variables, (1) a terminal variable, which is a list of just one vertex, and (2) a bridge variable, which is a list of two distinct vertices. A block-preserving outerplanar graph pattern (bpo-graph pattern) is a graph pattern which is obtained from an outerplanar graph by replacing some bridges with bridge variables and adding terminal variables to vertices.

A variable in a bpo-graph pattern can be replaced with an arbitrary outerplanar graph. Let p be a bpo-graph pattern and q an outerplanar graph. Let us consider a terminal variable $(v_1)$ of p, or a bridge variable $(v_1,v_2)$ of p. Let $(u_1)$ or $(u_1,u_2)$ be a list of distinct vertices in q such that the vertex label of $v_i$ is equal to the vertex label of $u_i$ for any $i\in \{1,2\}$. A new bpo-graph pattern is obtained by replacing the variable $(v_1)$ or $(v_1,v_2)$ with q in the following way. We attach q to p by removing the variable $(v_1)$ or $(v_1,v_2)$ and identifying the vertices $v_1$ or $v_1,v_2$ with the vertices $u_1$ or $u_1,u_2$ of q, respectively. We say that a bpo-graph pattern p matches an outerplanar graph G if G is obtained from p by replacing all the variables of p with certain outerplanar graphs. For a bpo-graph pattern p, a block tree pattern t(p) [18, 24] is a tree representation of the bpo-graph pattern p. A block tree pattern is an unrooted and unordered tree with block vertices which have block labels having coded information of blocks of the bpo-graph pattern. We use block tree patterns as individuals in Genetic Programming, which is an evolutionary learning method dealing with tree structures.

Let us consider examples in Fig. 1. Let p be a bpo-graph pattern and $g_1,g_2,g_3$ and G outerplanar graphs. t(p) is the block tree pattern of p. The bpo-graph pattern p has two bridge variables, $(v_1,v_2)$ labeled with X and $(v_5,v_7)$ labeled with Y, and one terminal variable $(v_4)$ labeled with Z. The outerplanar graph G is obtained from p by replacing the variables $(v_1,v_2)$, $(v_5,v_7)$ and $(v_4)$ with $g_1$, $g_2$ and $g_3$, respectively, as follows. First, we remove the variables $(v_1,v_2)$, $(v_5,v_7)$ and $(v_4)$. Next, we identify the vertices $v_1,v_2$ in p with the vertices $u_1,u_2$ in $g_1$ and $v_5,v_7$ in p with $u_5,u_7$ in $g_2$, respectively. We also identify the vertex $v_4$ with the vertex $u_{10}$ in $g_3$. Thus we see that the bpo-graph pattern p matches the outerplanar graph G.

Fig. 1

A bpo-graph pattern p and the block tree pattern t(p) of p. Outerplanar graphs $g_1$, $g_2$, $g_3$ and G. A box with lines to its elements represents a variable. A variable label is inside a box. A block vertex is drawn by a filled black circle. The bpo-graph pattern p matches the outerplanar graph G

We explain a Genetic Programming-based learning method [23] for acquiring characteristic bpo-graph patterns from positive and negative outerplanar graph data. In this paper we consider the following problem [14].

Problem of acquisition of characteristic block-preserving outerplanar graph patterns

Input: A finite set D of positive and negative outerplanar graph data.

Problem: Find a bpo-graph pattern having high fitness w.r.t. D.

A bpo-graph pattern as an individual is considered a binary classifier of outerplanar graph data. We define the fitness of a bpo-graph pattern p w.r.t. D, denoted by $fitness_{D}(p)$, to be a kind of accuracy of classifying positive and negative graph data w.r.t. D. We consider a bpo-graph pattern having high fitness to be a characteristic bpo-graph pattern. We present a context-aware fitness function, which is defined by an individual ranking method based on feature selection in Sect. 3, for our evolutionary learning method.

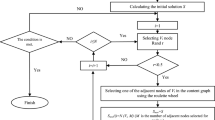
When we apply a GP operator to a block tree pattern, we fix a root in the block tree pattern to designate the affected portion of the block tree pattern by the GP operator. Figure 2 shows an example of applying crossover operator to block tree patterns. Using label information of connecting vertices and edges from positive examples of outerplanar graphs, our learning method [23] generates block tree patterns such that the corresponding bpo-graph patterns satisfy valence relations.

Fig. 2

A genetic operator crossover applied to block tree patterns $t(p_1)$ and $t(p_2)$

Fig. 3

A TTSP graph pattern p and the parse tree t(p) of p. TTSP graphs $g_1$, $g_2$ and G. A variable label is inside a box. The TTSP graph pattern p matches the TTSP graph G

2.2 Acquisition of characteristic TTSP graph patterns using genetic programming

We review TTSP graph patterns as a graph pattern having TTSP graph structure and a parse tree of a TTSP graph pattern, according to [11, 21].

A multidag is a directed connected graph which allows multiple edges and does not contain any cycle. A multidag is said to be two-terminal if it has exactly one source and one sink. A TTSP graph is a two-terminal edge-labeled multidag recursively defined as follows. (1) A multidag consisting of two vertices u and v, and a single edge from u to v is a TTSP graph. The vertices u and v are its source and its sink, respectively. (2) For $i=1,2$, let $G_i$ be a TTSP graph which has $u_i$ as its source and $v_i$ as its sink. Then the graph obtained by performing either of the following two operations is a TTSP graph. (a) Parallel operation: Identify $u_1$ with $u_2$, and identify $v_1$ with $v_2$. The resulting graph has $u_1(=u_2)$ as its source and $v_1(=v_2)$ as its sink. (b) Series operation: Identify $u_2$ with $v_1$. The source and the sink of the resulting graph are $u_1$ and $v_2$, respectively.

TTSP graph patterns are graph patterns which are obtained by replacing some edges of TTSP graphs with variables, where variables are lists of two vertices. We can replace a variable in a TTSP graph pattern with any TTSP graph, in a manner similar to a bridge variable in a bpo-graph pattern without checking vertex labels of identified vertices. All variables in a TTSP graph pattern are assumed to have unique labels. A TTSP graph pattern p is said to match a TTSP graph G if G is obtained from p by replacing all the variables with certain TTSP graphs. We use parse trees t(p) [21], which are tree representations of TTSP graph patterns p and have the structure of rooted trees with ordered or unordered children, as individuals in Genetic Programming, which is an evolutionary learning method dealing with tree structures.

Let us consider examples in Fig. 3. We give a TTSP graph pattern p and the parse tree t(p) of p, and TTSP graphs $g_1$, $g_2$ and G. The TTSP graph pattern p has two variables, $(v_1,v_2)$ labeled with X and $(v_3,v_4)$ labeled with Y. The TTSP graph G is obtained from the TTSP graph pattern p by replacing the variables $(v_1,v_2)$ and $(v_3,v_4)$ with TTSP graphs $g_1$ and $g_2$, respectively. Thus we see that the TTSP graph pattern p matches the TTSP graph G.

We explain a Genetic Programming-based learning method [11] for obtaining characteristic TTSP graph patterns from positive and negative TTSP graph data. The problem we address is the following [11].

Problem of acquisition of characteristic TTSP graph patterns

Input: A finite set D of positive and negative TTSP graph data.

Problem: Find a TTSP graph pattern having high fitness w.r.t. D.

A TTSP graph pattern as an individual is considered a binary classifier of TTSP graph data. We define the fitness of a TTSP graph pattern p w.r.t. D, denoted by $fitness_{D}(p)$, to be a kind of accuracy of classifying positive and negative graph data w.r.t. D. We consider a TTSP graph pattern having high fitness to be a characteristic TTSP graph pattern, which matches many positive and few negative data represented as TTSP graphs. We present a context-aware fitness function, which is defined by an individual ranking method based on feature selection in Sect. 3, for our evolutionary learning method. For example, applying crossover operator to parse trees is illustrated in Fig. 4.

Fig. 4

A genetic operator crossover applied to parse trees $t(p_1)$ and $t(p_2)$

3 New fitness functions based on feature selection

We propose new context-aware fitness functions and give GP-based learning methods incorporating the proposed functions for acquiring characteristic bpo-graph patterns and TTSP graph patterns. The proposed context-aware fitness functions employ super-CWC [19] (CWC, for short), which is a state-of-the-art feature selection algorithm. Context-aware fitness functions evaluate each individual based on its importance in a group, while conventional fitness functions evaluate each individual independently in population. Since the fitness of an individual is evaluated within a group (i.e. context), if the group including the individual is changed, the fitness of this individual may be also changed. This aspect is very important to find a general pattern to cover the whole set of positive examples because even if each selected pattern has relatively high coverage of positive examples, each coverage does not necessarily imply the high coverage of the whole positive examples by the selected individuals.

3.1 Consistency-based feature selection CWC

The problem of finding a small set of features for discriminating class labels is called supervised feature selection. A very fast and accurate consistency-based feature selection algorithm CWC of filter approach is proposed by Shin et al. [19]. We show the algorithm CWC in Algorithm 1. A feature set is said to be consistent, if it can completely determine all the class labels.

Table 1 Examples of a dataset for feature selection and the values of correlation measures

CWC successfully overcomes a few problems inherent in conventional algorithms: (1) the redundancy problem, (2) the feature interaction problem. To explain these problems, let us consider the feature selection of the data consisting of four instances $\{d_1,d_2,d_3,d_4\}$ shown in Table 1. Each feature is denoted by $F_i\in \{F_1,F_2,F_3,F_4\}$, and the variable of class labels is denoted by C.

We consider a correlation measure between the values of a single feature and class labels, for example, mutual information. The mutual information between $F_i$ and C is denoted by $I(F_i;C)$. If we select features according to the correlation measure by setting a cut-off point, for example, $I(F_i; C)\ge 0.3$, then $F_1$ and $F_2$ are selected. However, even if $F_2$ is selected in addition to $F_1$, it does not add any information to determine class labels since $I(F_1;C)=I(F_2;C)=I(\{F_1,F_2\};C)\approx 0.31$ (the redundancy problem). On the other hand, we have $I(F_3;C)=0.0$ and $I(F_4;C)=0.0$. Hence, $F_3$ and $F_4$ are useless to determine the class label C at all if $F_3$ or $F_4$ is used alone. However, the set of features $\{F_3,F_4\}$ can uniquely determine class labels since $I(\{F_3,F_4\};C)=1.0$ (the interaction problem).

This example suggests that not only a single feature but a group of features should be also considered to evaluate the effect of selected features relevant to class labels. In general, if the interaction among features are considered, it causes a combinatorial explosion in computation. CWC effectively computes the interaction among features while it avoids such a combinatorial problem by a greedy-style algorithm.

CWC is a consistency-based feature selection method. Consistency is the property of a feature set by which all the class labels are uniquely determined. CWC starts its procedure with a consistency data set. Therefore, if the initial data set is not consistent, minor rows are deleted (the denoising process at the first line in Algorithm 1). After that, CWC sorts features by a correlation measure between $F_i$ and C. Let H(X) denote the (empirical) entropy of the random variable X, and H(X, Y) denote the joint entropy of X and Y. Let P(X) denote the empirical probability of X, and $cov(X, Y)$ denote the covariance between X and Y. In the CWC implementation, one of the following measures is selected as an option.

• Mutual information (MI): $MI(F_i, C) = H(F_i) + H(C) - H(F_i, C)$

• Symmetric uncertainty (SU):

  $$\begin{aligned} SU (F_i, C) = 2\frac{I(F_i; C)}{H(F_i)+H(C)} \end{aligned}$$

• Inconsistency rate (ICR) [26]:

  $$\begin{aligned} ICR (F_i, C) = \sum _{C}\left( P(C = c) - \max _v P(C = c, F_i = v)\right) \end{aligned}$$

• Matthews correlation coefficient (MCC) (only for binary class):

  $$\begin{aligned} MCC (F_i, C) = \frac{cov (F_i, C)}{ \sqrt{cov (F_i, F_i)\cdot cov (C, C)}} \end{aligned}$$

CWC explores a minimal consistent subset of given features based on a backward-deletion strategy with very high accuracy.

3.2 Fitness function based on CWC-ranking

We propose fitness functions based on CWC-ranking. Let p be a graph pattern and D a finite set of positive and negative graph-structured data w.r.t. a specific phenomenon. In this paper, the setting for a graph pattern p and a finite set D of positive and negative graph-structured data is (1) p is a bpo-graph pattern and D is a finite set of positive and negative outerplanar graph data, or (2) p is a TTSP graph pattern and D is a finite set of positive and negative TTSP graph data. If a graph pattern p matches an example graph G, then we classify G as positive according to p. Otherwise we classify G as negative according to p. Let TP denote the number of true positive examples in D according to p, TN the number of true negative examples, FP the number of false positive examples and FN the number of false negative examples. The balanced accuracy of p w.r.t. D, denoted by $balanced\_accuracy(p$), is a basic measure used in our previous work [10, 23] and defined as follows. $balanced\_accuracy (p) = \frac{\text{1 }}{\text{2 }} \times (\frac{\text{ TP }}{\text{ TP }+\text{ FN }} + \frac{\text{ TN }}{\text{ TN }+\text{ FP }}).$

Using ranked patterns obtained from a CWC output, we define a context-aware fitness function. The input of CWC is a dataset described by a set of features $\{F_1,\ldots ,F_N\}$ with a variable C for class labels. The output of CWC is a minimal subset $S \subseteq \{F_1,\ldots ,F_N\}$ such that S has the binary consistency, that is, S uniquely determines class labels, where each feature $F_i \in S$ is assigned an evaluation value. We call such the set S of features the selected minimal feature set by CWC.

Table 2 An example of an input table to CWC, obtained by the matching relation between bpo-graph patterns and outerplanar graphs

We consider, in this paper, a graph pattern p to be a feature, a set of graph patterns in a generation to be a set of features, and a positive or negative of an example to be a class label $C=1$ or 0, respectively. If a pattern p matches an example, then we set the value of feature p as 1, otherwise 0. Table 2 shows an input table to CWC, obtained by the matching relation between bpo-graph patterns and outerplanar graphs. For feature $F_i$ which corresponds to a graph pattern p and a variable C for class labels which corresponds to a finite set D of positive and negative graph data, we use the correlation measures: Mutual Information $MI (F_i, C)$ (denoted by $MI (p)$), Symmetric Uncertainty $SU (F_i, C)$ (denoted by $SU (p)$), Inconsistency Rate $ICR (F_i, C)$ (denoted by $ICR (p)$), and Matthews Correlation Coefficient $MCC (F_i, C)$ (which coincides with $MCC (p)$. We define $ICR ^*(p)=1-ICR (p).$ Also we define $MCC ^*(p)=(MCC (p)+1)/2$, according to [10]. For binary classification by a graph pattern p, the values of $MI (p), SU (p), ICR ^*(p)$ and $MCC ^*(p)$ are between 0 and 1. The value $MI (p), SU (p), ICR ^*(p), MCC ^*(p)$ of 1 means that the correlation of a graph pattern p and a variable C for class labels is maximum.

As the correlation measure between two patterns p and q, we use the phi coefficient $\phi (p,q)$. We also introduce two parameters $\ell$ and u which determine the scope of graph patterns affected by the selected minimal feature set by CWC. Let $(\ell ,u)$ be $(*,*)$ or a pair of real numbers $\ell$ and u with $0 \le \ell \le u \le 1$. We define the predicate $\textsc {CWCrank}(p,(\ell ,u))$ for a graph pattern p and parameters $\ell$ and u as follows. As the correlation measure between a pattern p and C used in the line 4 of the CWC algorithm, we use $MI (p)$, $SU (p)$, $ICR ^*(p)$ and $|MCC (p)|$ for a correlation measure of CWC-fitness MI, SU, $ICR ^*,\;MCC ^*$, respectively. Let S be the selected minimal feature set by CWC. The predicate $\textsc {CWCrank}(p,(*,*))$ is true if p is in S, and false otherwise. The predicate $\textsc {CWCrank}(p,(\ell ,u))$ is true if (1) p is in S, or (2) p is not in S, and there exists a pattern q in S such that $\ell \le \phi (p,q) \le u$ holds. Otherwise, the predicate $\textsc {CWCrank}(p,(\ell ,u))$ is false.

The CWC-fitness using a correlation measure M (= MI, SU, $ICR ^*$, $MCC ^*$) of a graph pattern p and parameters $\ell$ and u w.r.t. D, denoted by $\textsc {CWCfitness}(M,p,(\ell ,u))$, is defined as follows. CWC-fitness using $MCC ^*$ is given in our previous work [22]. In this paper, we propose context-aware fitness functions CWC-fitness using $MI ,SU$ and $ICR ^*$.

$$\begin{aligned}&\textsc {CWCfitness}(MI ,p,(\ell ,u)) \\&\quad = \left\{ \begin{array}{ll} MI (p) &{} \text{ if } \textsc {CWCrank}(p,(\ell ,u)) \text{ is } \text{ true } \\ 0 &{} \text{ otherwise } \end{array} \right. \end{aligned}$$

$$\begin{aligned}&\textsc {CWCfitness}(SU ,p,(\ell ,u)) \\&\quad = \left\{ \begin{array}{ll} SU (p) &{} \text{ if } \textsc {CWCrank}(p,(\ell ,u)) \text{ is } \text{ true } \\ 0 &{} \text{ otherwise } \end{array} \right. \end{aligned}$$

$$\begin{aligned}&\textsc {CWCfitness}(ICR ^*,p,(\ell ,u)) \\&\quad = \left\{ \begin{array}{ll} ICR ^*(p) &{} \text{ if } \textsc {CWCrank}(p,(\ell ,u)) \text{ is } \text{ true } \\ 0 &{} \text{ otherwise } \end{array} \right. \end{aligned}$$

$$\begin{aligned}&\textsc {CWCfitness}(MCC ^*,p,(\ell ,u)) \\&\quad = \left\{ \begin{array}{ll} MCC ^*(p) &{} \text{ if } \textsc {CWCrank}(p,(\ell ,u)) \text{ is } \text{ true } \\ 0 &{} \text{ otherwise } \end{array} \right. \end{aligned}$$

The value of the above-defined fitness functions $balanced\_accuracy(p)$ and $\textsc {CWCfitness}(M,p,(\ell ,u))$ for all M = MI, SU, $ICR ^*$, $MCC ^*$ of a graph pattern p is between 0 and 1, and a graph pattern having high fitness is a good classifier of graph-structured data.

We explain the reason for introducing the proposed CWC-fitness functions. In computing $\textsc {CWCfitness}(M,p,(\ell ,u))$, by setting $u=1$, we can define the fitness of a graph pattern not selected by CWC to be the same fitness as a graph pattern selected by CWC, and avoid giving different values of fitness to isomorphic graph patterns. Also we can give positive fitness to a graph pattern which is not selected by CWC nor isomorphic to a graph pattern selected by CWC. Then we can keep diversity of populations of graph patterns.

Example 1    We give an example to illustrate the meaning of the proposed CWC-fitness functions. Let $D = \{ G_1, G_2, G_3, G_4\}$ be a finite set of positive and negative graph data, $\mathcal{F} = \{ p_1, p_2, p_3, p_4, p_5, p_6 \}$ a finite set of graph patterns, and C the variable for class labels in Table 2.

First, we explain the calculation of $\textsc {CWCfitness}(MI ,p,(*,*))$. The selected minimal feature set by CWC using $MI$ is $\mathcal{F'} = \{p_3, p_4\}$. We have $MI(p_3,C)=MI(p_4,C)\approx 0.311$. Then we have $\textsc {CWCfitness}(MI ,p,(*,*))=0.0$ for $p=p_1, p_2, p_5, p_6$ and $\textsc {CWCfitness}(MI ,p,(*,*))\approx 0.311$ for $p=p_3, p_4$.

Next, we explain the calculation of $\textsc {CWCfitness}(MI ,p,(0.8,1.0))$. The value of phi coefficient $\phi (p,q)$ for $p=p_1, p_2, p_5, p_6$ and $q=p_3, p_4$ is as follows. $\phi (p_1, p_3)\approx -\,0.333, \phi (p_2, p_3)\approx -\,0.577,\phi (p_5, p_3)\approx -0.577, \phi (p_6, p_3)\approx -\,0.333,\phi (p_1, p_4)\approx -\,0.333, \phi (p_2, p_4)\approx 0.577,\phi (p_5, p_4)\approx 0.577, \phi (p_6, p_4)= 1.0$. We have $\textsc {CWCrank}(p_6,(0.8,1.0)) =$ true and $\textsc {CWCrank}(p,(0.8,1.0)) =$ false for $p=p_1, p_2, p_5$. Then we have $\textsc {CWCfitness}(MI ,p,(0.8,1.0))=0.0$ for $p=p_1, p_2, p_5$ and $\textsc {CWCfitness}(MI ,p,(0.8,1.0))\approx 0.311$ for $p=p_3, p_4, p_6$.

Similarly, we calculate CWC-fitness of $p_3$ using $SU , ICR ^*, MCC ^*$ as follows. The selected minimal feature set by CWC using $SU , ICR ^*, MCC ^*$ is $\mathcal{F'} = \{p_3, p_4\}$. We have $SU(p_3,C) \approx 0.344,ICR^*(p_3,C)=0.75$, and $MCC^*(p_3,C) \approx 0.211$. Then we have, $\textsc {CWCfitness}(SU,p_3,(*,*)) =$ $\textsc {CWCfitness}(SU,p_3,(0.8,1.0))\approx 0.344$, $\textsc {CWCfitness}(ICR ^*,p_3,(*,*)) =$ $\textsc {CWCfitness}(ICR ^*,p_3,(0.8,1.0))=0.75$, and $\textsc {CWCfitness}(MCC ^*,p_3,(*,*)) =\textsc {CWCfitness}(MCC ^*,p_3,(0.8,1.0))\approx 0.211$.

Table 3 The average fitness of best individuals, the average number of vertices, the average specificness of individuals of final populations and the average run-time for the context-aware and context-ignoring methods over ten GP runs, using the first data set

We discuss the applicability of our proposed CWC-fitness functions. Our method is based on the framework of considering bpo-graph patterns or TTSP graph patterns as features and the matching relation as the binary class label. Thus we can apply the proposed CWC-fitness functions to evolutionary learning of characteristic graph or tree patterns of other types than bpo-graph patterns or TTSP graph patterns, from positive and negative graph or tree data. We can also apply the proposed CWC-fitness functions to evolutionary learning of characteristic binary classifiers from positive and negative data. But we cannot apply the idea of CWC-fitness function to symbolic regression or function learning problems.

4 Experimental results

We report experimental results on acquiring characteristic bpo-graph patterns and TTSP graph patterns by our evolutionary learning method using the context-aware fitness functions proposed in Sect. 3. We also report comparative experimental results on our evolutionary learning method using the context-ignoring fitness function.

By a context-aware method we mean our evolutionary learning method for obtaining characteristic graph patterns from positive and negative graph data, using the context-aware fitness function $\textsc {CWCfitness}(M,p,(\ell ,u))$ for M = MI, SU, $ICR ^*$, $MCC ^*$. We proposed three context-aware fitness functions $\textsc {CWCfitness}(M,p,(\ell ,u))$ for M = MI, SU, $ICR ^*$ in Sect. 3 of this paper. The context-aware fitness function $\textsc {CWCfitness}(MCC ^*,p,(\ell ,u))$ was given in our previous work [22]. By a context-ignoring method we mean our evolutionary learning method for obtaining characteristic graph patterns from positive and negative graph data, using the context-ignoring fitness function $balanced\_accuracy(p)$ representing the balanced accuracy, which is a widely used measure of accuracy for binary classification in related work including our previous work [23].

The experimental results in Table 3 on acquiring characteristic bpo-graph patterns by the context-aware method using the fitness function $\textsc {CWCfitness}(MCC ^*,p,(\ell ,u))$ and the context-ignoring method were reported in [23]. The other experimental results in this section are newly reported in this paper. The implementation of our methods is in Java and Scala on Windows 10 (64-bit).

Table 4 The average fitness of best individuals, the average number of vertices, the average specificness of individuals of final populations and the average run-time for the context-aware and context-ignoring methods over ten GP runs, using the second data set

4.1 Experimental results on acquiring bpo-graph patterns

We report experimental results on acquiring characteristic bpo-graph patterns from positive and negative outerplanar graph data, using the context-aware and context-ignoring methods. Using canonical representations as keys and fitness values as values in a HashMap table [23], our method records canonical representations of block tree patterns and their fitness. Using the matching algorithm [18, 24] for bpo-graph patterns and outerplanar graphs, we calculate the fitness of bpo-graph patterns represented by block tree patterns as individuals. GP parameters we use in the experiments are as follows: population size: 50, reproduction probability: 0.05, crossover probability: 0.50, mutation probability: 0.45, selection method: roulette wheel selection, tournament selection (size 2), elite selection (size 3), maximum number of generations: 200. The experimental data are extracted from the file “CAD2DA99.sdz" in the NCI database [4].

We consider five experimental settings which use the context-aware method using $\textsc {CWCfitness}(M,p,(\ell ,u))$ for M = MI, SU, $ICR ^*$, $MCC ^*$ or the context-ignoring method using $balanced\_accuracy(p)$. For each of the five settings, we performed ten GP runs for acquiring characteristic bpo-graph patterns from positive and negative outerplanar graph data, using the same GP parameters and experimental data mentioned above. For the context-aware method, we set two parameters $\ell$ and u as $(\ell ,u)=(*,*),(0.8,1.0)$.

The best individuals by the context-aware method mean the best individuals over all generations, and the best individuals by the context-ignoring method mean the best individuals at the final generation. We report the average values of four evaluation indexes over ten GP runs with their standard deviation.

In Table 3, we report the experimental results using the first experimental data set consisting of 88 positive data and 88 negative data. Table 3 shows the average fitness of best individuals of the context-aware and context-ignoring methods. It is meaningless to compare the values of fitness itself of the different settings of the above five experimental settings, since values of fitness are based on the values of the corresponding different correlation measures. Table 3 shows the average number of vertices and the average specificness of individuals of final populations for the both methods. The specificness of a bpo-graph pattern p is defined as $EN /( EN + VN )$, where $EN$ and $VN$ denote the number of edges and the number of variables of the corresponding block tree pattern t(p) of p. A bpo-graph pattern which has many vertices or high specificness is considered to be a specific graph pattern. Table 3 shows average run-time for the both methods. Table 4 shows the experimental results using the second experimental data set consisting of 434 positive data and 434 negative data for the context-aware method using the correlation measure $MCC ^*$ and the context-ignoring method.

The experimental results in the previous work [22] in Table 3 show that many values of the number of vertices and the specificness of bpo-graph patterns obtained by the context-aware method using the correlation measure $MCC ^*$ are higher than those of the context-ignoring method. In this paper, we show that these good properties of the context-aware method are extended and hold for the context-aware method using three new correlation measures MI, SU, $ICR ^*$ in almost all values in Table 3 and for the large data set of outerplanar graphs in Table 4. From these experimental results, we can say that the context-aware methods obtained characteristic bpo-graph patterns which are more specific than the bpo-graph patterns obtained by the context-ignoring method.

Table 5 The average fitness of best individuals, the average number of vertices, the average specificness of individuals of final populations and the average run-time for the context-aware and context-ignoring methods over ten GP runs

4.2 Experimental results on acquiring TTSP graph patterns

We report experimental results, in a manner similar to the results on bpo-graph patterns, on our evolutionary learning of characteristic TTSP graph patterns, using the context-aware fitness function proposed in Sect. 3 and a previous fitness function $balanced\_accuracy(p)$ ignoring context which is used in [23]. Using the matching algorithm [21] for TTSP graph patterns and TTSP graphs, we calculate the fitness of TTSP graph patterns represented by parse trees as individuals. We implemented our GP-based learning method for acquiring characteristic TTSP graph patterns from positive and negative TTSP graph data, using a CWC-ranking method in Sect. 3.

GP parameters we use in the experiments are as follows: population size: 50, reproduction probability: 0.05, inversion probability: 0.05, crossover probability: 0.45, mutation probability: 0.45, selection method: roulette wheel selection, tournament selection (size 4), elite selection (size 3), maximum number of generations: 200. As the experimental data we use 500 positive data and 500 negative data which have the structure of TTSP graph. The experimental data are synthetic data. Table 5 shows the average fitness of best individuals, the average number of vertices, the average specificness of individuals of final populations and the average run-time for the context-aware and context-ignoring methods over ten GP runs. Figure 5 shows the average values of the fitness of the individuals with the highest fitness in each generation for context-aware methods using the correlation measures and parameters and the context-ignoring method.

In Table 3, many values of the number of vertices and the specificness of bpo-graph patterns obtained by the context-aware method using the correlation measure $MCC ^*$ in the previous work [22] are shown to be higher than those of the context-ignoring method. In this paper, we show that these good properties of the context-aware method are extended and hold for the context-aware method using four correlation measures MI, SU, $ICR ^*$, $MCC ^*$ in almost all values and for the large data set of TTSP graphs in Table 5. From these experimental results, we can say that the context-aware methods obtained characteristic TTSP graph patterns which are more specific than the TTSP graph patterns obtained by the context-ignoring method.

Fig. 5

Fitness of best individuals as TTSP graph patterns over generations by the context-aware and context-ignoring methods

5 Conclusion

In this paper, we have proposed aggregative context-aware fitness functions based on feature selection for evolutionary learning of characteristic block-preserving outerplanar graph patterns and characteristic TTSP graph patterns from positive and negative graph data. We have reported some experimental results on our evolutionary learning of characteristic graph patterns, using the context-aware fitness functions. The proposed methods obtained characteristic block-preserving outerplanar graph patterns and characteristic TTSP graph patterns which are more specific than the graph patterns obtained by the previous method. We plan to apply our methods to a large data set of other types of graph data modeled as outerplanar graphs or TTSP graphs.