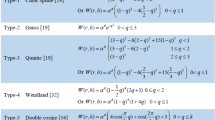1 Introduction

Since its emergence proposed by Lucy [26] and Gingold and Monaghan [17] to originally solve astrophysics problems in open space, smoothed particles hydrodynamics (SPH) has been developing by many researchers and employed in various fields such as fluid dynamics [9, 19, 29], solid mechanics [4, 12, 25] and fluid–structure interaction [2, 27, 34]. Several corrections and modifications have been proposed to increase the accuracy of SPH predictions. To name a few, Monaghan [28] proposed the artificial viscosity to properly capture shocks physics, Libersky et al. [23] and Krongauz and Belytschko [22] proposed corrected derivatives with linear completeness, Lind et al. [24] and Sun et al. [36] used a particle shifting technique based on Fick’s law of diffusion to slightly redistribute particles in each time step in a more uniform arrangement in order to have more accurate fields approximations, and Antuono et al. [3] added an artificial density diffusive term to the continuity equation to smooth out spurious noises affecting density and, consequently, pressure.

As a truly meshless method, in the sense that there is even no need for any background mesh, SPH uses mass points to approximate field functions and their derivatives in order to discretize and solve governing equations. Hence, as opposed to mesh-based methods SPH can conveniently handle problems with large displacements and moving boundaries. However, SPH is not widespread in the field of solid mechanics despite proposed stabilization methods, since in modeling of solid materials deformation instabilities, namely tensile instability and zero-energy modes, are prevailing, sever and therefore hard to stabilize. Tensile instability as Swegle et al. [37] noted occurs at the presence of tensile stress. This instability causes particles to non-physically clump together which leads to unrealistic fractures under large deformations even if no fracture criterion is defined. To reduce tensile instability, Gray et al. [18] added repulsive forces to the momentum equations between particles in tension in order to prevent particles clumping. Belytschko et al. [6] performed a stability analysis and found that the source of tensile instability is the recurring update of SPH kernels. This procedure imparts Eulerian character to the kernels, hereinafter called Eulerian kernels, as during a simulation other particles pass through a particle’s kernel support domain. Hence, on the contrary as Bonet and Kulasegaram [8] and Rabczuk et al. [32] showed defining kernels in terms of the material coordinates, hereinafter called Lagrangian kernels, prevents tensile instability leading to stable solutions in tensile regimes.

The other major instability intrinsic to SPH, spurious zero-energy modes, stems from the fact that SPH discretization of the divergence of the stress tensor is rank deficient similar to meshless methods employing nodal quadrature [5] and therefore solutions of boundary value problems are not unique and may include undesirable spurious modes. To remove the spurious modes, Dyka et al. [13] proposed the stress point method which was later used and developed by Vignjevic et al. [40] and Randles and Libersky [35]. The method tends to stabilize SPH by utilizing additional quadrature points named stress points. However, since an additional set of points must be handled the method not only is hard to be incorporated into a SPH code but also is not efficient. Another common practice is to use higher-order derivatives to stabilize numerical methods. Bonet and Kulasegaram [7] employed a least-square stabilization method based on the residual of the Poisson-like governing equations. Vidal et al. [39] proposed a stabilized updated Lagrangian SPH scheme in which instabilities activated due to updating the reference configuration are controlled by adding a Laplacian filter to the SPH gradient approximation. Although using higher-order derivatives render enhanced stability for SPH, it is expensive to correctly approximate them. Inspired by the similarity between SPH and single integration point finite element (FE) method Ganzenmüller [15] proposed identifying zero-energy modes as nonlinear parts of the velocity field and then penalizing the spurious displacements to force particles back to their theoretically ideal positions. The method, called hourglass control borrowed from FE, was applied to total Lagrangian SPH [15] and updated Lagrangian SPH [16] and proved to be able to hinder not only zero-energy modes but also tensile instability. It is worth mentioning that updated Lagrangian SPH must not be confused with Eulerian SPH. In updated Lagrangian SPH kernels are only re-calculated once the particles pairwise displacement exceeds a given threshold as opposed to Eulerian SPH where kernels are re-calculated in every time step. Note that the term Eulerian only refers to the type of kernel and not to the Eulerian perspective of a continuum. Therefore, Eulerian SPH in this context should not be interpreted as an SPH scheme where particles are fixed in space.

As mentioned above, SPH in its plain Eulerian form suffers from two major instabilities, namely tensile instability and zero-energy modes. Although a total Lagrangian scheme removes the tensile instability, it lacks applicability to deal with large deformations, the main advantage of SPH over mesh-based methods, and to naturally handle contact problems. In order to circumvent these issues, an updated Lagrangian scheme was proposed in which the reference configuration and consequently kernels must be regularly updated which again triggers tensile instabilities. Besides, regardless of which kernel type, Eulerian or Lagrangian, is employed, zero-energy spurious modes occur anyway since they are not initiated by a certain stress state. Needless to say, dealing with problems of fluid–structure interaction (FSI) requires at least Eulerian SPH to predict the fluid’s behavior; therefore, it needs extra care and effort to implement and manage two different descriptions for SPH. That being said, this paper aims to propose a stabilization scheme in the Eulerian SPH framework that removes the tensile instability and zero-energy modes under large deformations and high strain rates. To this end, the hourglass control scheme proposed by Ganzenmüller et al. [16] is borrowed and incorporated into the Eulerian framework. This is done with a little change to an Eulerian SPH code and enables accurate analyses of solid materials under large deformations as well as straightforward modeling of contact and FSI problems in a monolithic manner.

The rest of this paper is organized as follows. The next section is dedicated to explain the SPH description of the solid mechanics governing equations alongside the hourglass control scheme and its implementation in Sect. 2.4. To verify the proposed scheme several cases in different regimes under different loading conditions are simulated and results are presented in Sect. 3. Finally the benefits of using the proposed stabilization scheme are discussed.

2 SPH formulation for solids

SPH is a particle-based numerical method employed to solve systems of partial differential equations. In SPH, a material volume is discretized by particles which carry quantities such as velocity, density, volume, pressure and stress, and describe the state of material at their position. Later on, information stored for each particle is used to construct SPH approximations of field functions and their derivatives.

SPH approximations do not require any connectivity between particles as in, e.g., FE nor a background mesh used in, e.g., element-free Galerkin. Therefore, SPH is a true meshless method and, in turn, suitable for problems with large deformations. The SPH approximations at a given point are calculated using only a limited number of particles located in a support domain, the size of which is controlled by a smoothing length. A kernel function determines how strong each surrounding particle influences the SPH approximation at a given point and is typically defined as a bell-shaped function gradually decreasing with the distance between a particle and the point. There are several common kernel functions such as splines of various order or a truncated Gaussian. In our case, a cubic spline kernel is employed which is defined by:

$$\begin{aligned} \!W\,(x,h) = \frac{k}{h^d} \left\{ \begin{array}{lll} \left( 2-q\right) ^3 - 4\left( 1-q\right) ^3, &{} 0 \le q< 1, \\ \\ \left( 2-q\right) ^3, &{} 1 \le q < 2, \\ &{} \\ 0, &{} q \ge 2. \end{array} \right. \end{aligned}$$
(1)

where \( x = |{{\varvec{x}}}| \) is the Euclidean norm of the position vector \( {{\varvec{x}}} \) at current deformed configuration and \( q=x/h \) with h being the smoothing length of the kernel. d is the number of dimensions and k is the normalization factor which equals \(5/(14 \pi )\) for 2D and \(1/(4\pi )\) for 3D cases. According to Eq. 1, the radius of a support domain is twice the parameter h which is proportional to the particles spacing, \(\varDelta \)p, and in this study \( h = 1.3 \varDelta p \) is used. As the cubic spline proved to yield satisfactory results, it is used throughout this work although different kernels might improve convergence [11].

The development of the SPH approximation for any function \(A({{\varvec{x}}})\) begins with the following mathematical identity.

$$\begin{aligned} \!A({{\varvec{x}}}) = \int A({{\varvec{x}}}')\, \delta ({{\varvec{x}}} - {{\varvec{x}}}')\,d{{\varvec{x}}}', \end{aligned}$$
(2)

where \(\delta \) is the Dirac delta function. To obtain an SPH approximation, the Dirac delta function is replaced by the kernel function which can be considered as a smoothed, finite delta function. Additionally, the integral is discretized using the mid-point quadrature which results in the following SPH approximation of a field function.

$$\begin{aligned} \!\left\langle A({{\varvec{x}}})\right\rangle = \sum \limits _{j=1}^{N}A({{\varvec{x}}}_j)\,W\left( |{{\varvec{x}}} - {{\varvec{x}}}_j|,h\right) \,V_j, \end{aligned}$$
(3)

where \(V_j\) is the volume of particle j evaluated by the ratio of its mass \(m_j\) to its density \(\rho _j\) and N is the number of particles within the support domain. The \(\left<{\cdots }\right>\) symbol denotes an approximation of a function and, for the sake of simplicity, will be dropped in the rest of the paper. Besides, in SPH governing equations are collocated at each particle and, hence, the following approximations of a field function at particles position are employed.

$$\begin{aligned} \!\left\langle A_i \right\rangle = \sum \limits _{j=1}^{N}\frac{m_j}{\rho _j}\,A_j\,W_{ij}, \end{aligned}$$
(4)

with \(A_j=A({{\varvec{x}}}_j)\) and \(W_{ij}=W\,\left( |{{\varvec{x}}}_i - {{\varvec{x}}}_j|,h\right) \). In order to discretize the governing equations, derivatives of field functions at particles position need to be evaluated. It is straightforward to do that by using Eq. 4 and taking the derivative of the kernel function. Therefore, gradient of a function is given by

$$\begin{aligned} \!\nabla A_i = \sum \limits _{j=1}^{N}\frac{m_j}{\rho _j}\,A_j \,\nabla W_{ij}. \end{aligned}$$
(5)

However, the following forms of gradient are commonly employed since they possess better convergence properties.

$$\begin{aligned} \begin{aligned} \!\nabla A_i&= \sum \limits _{j=1}^{N}\frac{m_j}{\rho _j}\left( A_j - A_i\right) \nabla W_{ij}\\ \!\nabla A_i&= {\rho _i}\sum \limits _{j=1}^{N}m_j\left( \frac{A_j}{{{\rho _j}^2}}+\frac{A_i}{{{\rho _i}^2}}\right) \nabla W_{ij} \end{aligned} \end{aligned}$$
(6)

Having said that, using Taylor expansion up to second order it was shown that the SPH derivative approximations can be second-order accurate if the kernel gradients in Eq. 6 are replaced by the corrected one. To obtain the corrected kernel gradient correction matrix \({{\varvec{L}}}\) is introduced to the kernel gradient as

$$\begin{aligned} \!{\tilde{\nabla }} W_{ij}= {{\varvec{L}}}_i\,\nabla W_{ij}. \end{aligned}$$
(7)

In order for the SPH derivative approximations to be second-order accurate the following condition must be satisfied

$$\begin{aligned} \!\sum \limits _{j=1}^{N}\frac{m_j}{\rho _j}\left( {{\varvec{x}}}_j - {{\varvec{x}}}_i\right) {\tilde{\nabla }} W_{ij} = {{\varvec{I}}} \end{aligned}$$
(8)

where \({{\varvec{I}}}\) is a second-order unit tensor. Substituting Eq. 7 in Eq. 8, the correction matrix is obtained as

$$\begin{aligned} \!{{\varvec{L}}}_i = \left( \sum \limits _{j=1}^{N}\frac{m_j}{\rho _j}\left( {{\varvec{x}}}_j - {{\varvec{x}}}_i\right) \otimes \nabla W_{ij}\right) ^{-1}. \end{aligned}$$
(9)

Having said that, it has been realized that discretization of the stress divergence in momentum equations using the corrected gradient, Eq. 7, does not essentially lead to accurate approximations. We have found employing the following normalized gradient instead results in a robuster scheme.

$$\begin{aligned} \!{\hat{\nabla }} W_{ij}= \frac{\nabla W_{ij}}{\sum \nolimits _{j}\frac{m_j}{\rho _j}\,W_{ij}}. \end{aligned}$$
(10)

Hence, in the present study the corrected gradient, Eq. 7, is employed to approximate the velocity gradient and the velocity divergence, and the normalized gradient, Eq. 10, is only used to calculate stress divergence.

2.1 SPH discretization of governing equations

The conservation laws of mass, momentum and energy are employed to correctly define particles movement during simulations. Since SPH follows material points in space, material derivatives are used and the conservation laws are discretized at each particle position using SPH approximations. Here, the following discretized governing equations are employed.

$$\begin{aligned} \!\left\{ \begin{aligned} \frac{\text {d}\rho _i}{\text {d}t}&= \rho _i\sum \nolimits _{j=1}^{N}{\frac{m_j}{\rho _j}\left[ {{\varvec{v}}}_{ij}\cdot {\tilde{\nabla }} W_{ij} + \Pi _{ij}^{\text {diff}}\cdot \nabla W_{ij}\right] }\\ \,\!\frac{\text {d}{{\varvec{v}}}_i}{\text {d}t}&= \sum \nolimits _{j=1}^{N} m_j \left[ \frac{\varvec{\varSigma }_i {-} \epsilon {{\varvec{R}}}_{i} f_{ij}^n}{\rho _i^2}\cdot {\hat{\nabla }} W_{ij} {-} \frac{\varvec{\varSigma }_j {-} \epsilon {{\varvec{R}}}_{j} f_{ij}^n}{\rho _j^2}\cdot {\hat{\nabla }} W_{ji} {+} \Pi _{ij}^{\text {visc}} \cdot \nabla W_{ij}\right] \end{aligned} \right. \nonumber \\ \end{aligned}$$
(11)

where \( {{\varvec{v}}}_{ij} = {{\varvec{v}}}_i-{{\varvec{v}}}_j \) is the relative velocity of particle i with respect to particle j and \(\varvec{\varSigma }\) is the stress tensor decomposed into pressure P (positive in compression) and deviatoric stress \({{\varvec{S}}}\) as

$$\begin{aligned} \varvec{\varSigma } = -P{{\varvec{I}}}+{{\varvec{S}}} \end{aligned}$$
(12)

The pressure term is evaluated using a equation of state expressed as

$$\begin{aligned} P = K\left( \frac{\rho }{\rho _0}-1\right) \end{aligned}$$
(13)

with K being the bulk modulus and \( \rho _0 \) being the initial density. Elastic deformations follow the theory of linear elasticity and the deviatoric stress at point i is evolved using the Jaumann stress rate as

$$\begin{aligned} \!\frac{\text {d}{{\varvec{S}}}_i}{\text {d}t} = 2\mu \left( \dot{{{\varvec{E}}}}_i - \frac{1}{3} \text {tr} \left( \dot{{{\varvec{E}}}}_i \right) {{\varvec{I}}} \right) - {{\varvec{S}}}_i \, \varvec{\varOmega }_i + \varvec{\varOmega }_i \, {{\varvec{S}}}_i \end{aligned}$$
(14)

where \( \mu \) is the shear modulus. \( \dot{{{\varvec{E}}}} \) and \(\varvec{\varOmega }\) are the rate of strain tensor and the rotation tensor, respectively, which are defined as

$$\begin{aligned} \begin{aligned} \!\dot{{{\varvec{E}}}}&= \frac{1}{2}\left( \nabla {{\varvec{v}}} + \nabla {{\varvec{v}}}\,^{\text {T}} \right) \\ \!\varvec{\varOmega }&= \frac{1}{2}\left( \nabla {{\varvec{v}}} - \nabla {{\varvec{v}}}\,^{\text {T}} \right) \end{aligned} \end{aligned}$$
(15)

where the velocity gradient tensor is approximated by

$$\begin{aligned} \!\nabla {{\varvec{v}}}_i = \sum \limits _{j=1}^{N}\frac{m_j}{\rho _j}\left( {{\varvec{v}}}_j - {{\varvec{v}}}_i\right) {\tilde{\nabla }} W_{ij}. \end{aligned}$$
(16)

In Eq. 11, the term \(\Pi _{ij}^{\text {visc}}\) is the artificial viscosity added to the momentum equation in order to diminish unphysical oscillations due to shock waves. \(\Pi _{ij}^{\text {visc}}\) proposed by Monaghan [28] is applied which is given by

$$\begin{aligned} \!\Pi _{ij}^{\text {visc}} = \left\{ \begin{array}{ll} \left( \alpha c_{\text {s}} - \beta \phi _{ij}\right) \phi _{ij} \,/ \rho _{ij}, &{} {{\varvec{v}}}_{ij} \cdot {{\varvec{x}}}_{ij} < 0 \\ &{} \\ 0, &{} {{\varvec{v}}}_{ij} \cdot {{\varvec{x}}}_{ij} \ge 0 \end{array} \right. \end{aligned}$$
(17)

where \({{\varvec{x}}}_{ij} = {{\varvec{x}}}_i-{{\varvec{x}}}_j \) is the relative position vector of particle i with respect to particle j, \(c_{\text {s}}=\sqrt{K/\rho _0}\) is the speed of sound, \( \alpha \) and \( \beta \) are the model parameters, here, equal to 2.0 and 1.0, respectively, \( \rho _{ij} \) is the average density of particles i and j, and \(\phi _{ij}\) is defined by

$$\begin{aligned} \!\phi _{ij} = \frac{h \left( {{\varvec{v}}}_{ij} \cdot {{\varvec{x}}}_{ij}\right) }{x_{ij}^2}, \end{aligned}$$
(18)

where \( x_{ij} = |{{\varvec{x}}}_{ij}| \) is the Euclidean norm of the relative position vector \( {{\varvec{x}}}_{ij} \).

Additionally, the term \(\epsilon {{\varvec{R}}}_{i}f_{ij}^n\) exerts inter-particle repulsive forces to reduce the tensile instability where n is a dimensionless exponent set to 4.0, and \(f_{ij}=W(x_{ij},h)\,/\,W(\varDelta p,h)\) is a normalized repulsion function. \(\epsilon \) is a dimensionless scaling factor, here, set to 0.3 and \({{\varvec{R}}}_{\gamma =i,j}\) is the unscaled artificial tensor defined by

$$\begin{aligned} \!{{\varvec{R}}}_{\gamma }={{\varvec{Q}}}^T\hat{{{\varvec{R}}}_{\gamma }}{{\varvec{Q}}} \end{aligned}$$
(19)

where \({{\varvec{Q}}}\) is a rotation matrix consists of the stress tensor’s eigenvectors and \(\hat{{{\varvec{R}}}_{\gamma }}\) is the unscaled stress tensor defined in the principal frame as

$$\begin{aligned} \!\hat{{{\varvec{R}}}}^{ab}_{\gamma } = \left\{ \begin{array}{cl} \hat{\varvec{\varSigma }}^{ab}_\gamma , &{} a=b\,\, \text {and} \,\,\hat{\varvec{\varSigma }}^{ab}_\gamma \ge 0, \\ &{} \\ 0, &{} \text {else}, \end{array} \right. \end{aligned}$$
(20)

with a and b indicating spatial components and \(\hat{\varvec{\varSigma }}\) being the diagonalized stress tensor.

Moreover, \( \Pi _{ij}^{\text {diff}} \) is the density diffusion proposed by Antuono et al. [3] added to the continuity equation so as to better stabilize the method at the presence of high frequency numerical noises in the pressure field by smoothing the density field. \( \Pi _{ij}^{\text {diff}} \) is defined by

$$\begin{aligned} \!\Pi _{ij}^{\text {diff}} = 2\delta h c_{\text {s}} \frac{\left( \rho _j - \rho _i \right) }{\rho _i} \frac{\left( {{\varvec{x}}}_j - {{\varvec{x}}}_i\right) }{x_{ij}^2} \end{aligned}$$
(21)

with \( \delta \) being a dimensionless parameter which normally is set to 0.1 for problems of fluid dynamics [3, 36]. It is worth mentioning that the density diffusion is only applied to the case of fracture modeling with \( \delta \) being 0.01.

2.2 Plasticity model

An elastic predictor-plastic corrector algorithm is used to calculate plastic strain at each point. In order to model materials behavior beyond elastic region, a J2 plasticity model is employed introducing a yield function as

$$\begin{aligned} \!\Phi = \sigma _{\text {eq}} - \sigma _{\text {y}} \end{aligned}$$
(22)

where \(\sigma _{\text {eq}} = \sqrt{\frac{3}{2} {{\varvec{S}}}:{{\varvec{S}}}}\) is von Mises equivalent stress and \(\sigma _{\text {y}}\) is a yield stress. Assuming the loading to be elastic the yield function is evaluated according to Eq. 22 (elastic predictor). A material point experiences plastic deformation only if \(\Phi > 0\) thereby stress must be returned to the yield surface which is defined by \(\Phi = 0\) (plastic corrector). To do this, the cutting-plane return mapping algorithm explained in Neto et al. [30] is employed. Cutting-plane algorithm is an explicit method which not only is easier to be implemented comparing with implicit methods, especially for complicated yield functions, but also guarantees to meet the plastic consistency condition (\(\Phi = 0\)). The plastic consistency condition is met by accurate calculation of plastic strains which alters the deviatoric stress tensor and the yield surface so as to reasonably equate the von Mises stress and the yield stress in Eq. 22.

As to yield stress, Johnson–Cook constitutive model [21] is employed which describes strain hardening and strain rate hardening as well as materials temperature softening. Hence, yield stress is expressed as

$$\begin{aligned} \!\sigma _{\text {y}}= & {} \left[ A + B\left( \varepsilon _{\text {eff}}^{\text {p}}\right) ^n\right] \left[ 1\right. \nonumber \\&+ \left. C\text {ln}\left( \frac{{\dot{\varepsilon }}_{\text {eff}}^{\text {p}}}{\dot{\varepsilon _0}}\right) \right] \left[ 1-\left( \frac{T-T_{\text {ref}}}{T_{\text {melt}}-T_{\text {ref}}}\right) ^m\right] \end{aligned}$$
(23)

where \(\varepsilon _{\text {eff}}^{\text {p}}\) is equivalent plastic strain, \({\dot{\varepsilon }}_{\text {eff}}^{\text {p}}\) is equivalent plastic strain rate, \(\dot{\varepsilon _0}\) is a reference plastic strain rate, T is current temperature, \(T_{\text {ref}}\) is a reference temperature and \(T_{\text {melt}}\) is melting temperature. Additionally, A, B, C, n and m are material-dependent constants. In Eq. 23, the three parentheses describe strain hardening, strain rate hardening and softening due to temperature change during plastic deformation, respectively.

For an adiabatic behavior assumption, there will be no heat flux and only plastic work is considered as the volumetric heat source. Then, the temperature change is obtained using the following rate equation.

$$\begin{aligned} \!{\dot{T}} = \eta \,\frac{\varvec{\varSigma }:\dot{{{\varvec{E}}}}^{\text {p}}}{\rho \,C_{\text {P}}} \end{aligned}$$
(24)

with \(\dot{{{\varvec{E}}}}^{\text {p}}\) being the plastic strain rate, \(\eta \) being the Quinney-Taylor coefficient, typically around 0.9, and \(C_{\text {P}}\) being the heat capacity.

2.3 Damage model

In dealing with materials failure, a criterion is needed to determine when a particle can no longer carry a load. Here, the Johnson–Cook dynamic failure criterion proposed by Johnson and Cook [21] is employed in which fracture is described by a damage parameter, D. The evolution of the damage parameter is defined as

$$\begin{aligned} \!{\dot{D}} = \frac{{\dot{\varepsilon }}_{\text {eff}}^{\text {p}}}{\varepsilon _{\text {f}}^{\text {p}}} \end{aligned}$$
(25)

with \(\varepsilon _{\text {f}}^{\text {p}}\) being the equivalent plastic strain at fracture determined by

$$\begin{aligned} \!\varepsilon _{\text {f}}^{\text {p}}= & {} \left[ D_1 + D_2 \text {exp}\left( D_3\sigma ^\star \right) \right] \left[ 1 + D_4 \text {ln}\left( \frac{{\dot{\varepsilon }}_{\text {eff}}^{\text {p}}}{\dot{\varepsilon _0}}\right) \right] \left[ 1\right. \nonumber \\&\left. +D_5 \left( \frac{T-T_{\text {ref}}}{T_{\text {melt}}-T_{\text {ref}}}\right) \right] \end{aligned}$$
(26)

where \(\sigma ^\star = -\frac{P}{\sigma _{\text {eq}}}\) is the stress triaxiality ratio and \(D_1\) to \(D_5\) are the material-dependent constants. The damage parameter is zero until the yield stress is reached and then starts growing with plastic strain up to failure where \(D = 1\). At failure the deviatoric stress of the failed particle is set to zero and kept zero for the rest of the simulation.

2.4 Hourglass control scheme

Here the scheme proposed by Ganzenmüller et al. [16] in order to prevent spurious zero-energy modes is employed. Due to the fact that the stabilization method is based on the similarity between zero-energy modes in SPH and hourglass modes in finite element simulations, the scheme is called hourglass control. Since SPH approximation results in mean fields within each particle’s neighborhood similar to FE using single-point reduced integration elements, Ganzenmüller [15] concluded that according to Flanagan and Belytschko [14] only a fully linear velocity field can be represented. Therefore, displacements or velocities not compatible with the linear field are identified as zero-energy modes which must be corrected.

The linear displacement field within a particle’s support domain must be defined by the deformation gradient as it is a linear operator itself. Therefore, zero-energy modes are those parts of the displacement field which cannot be expressed by the deformation gradient. The relative position vector of particle i with respect to particle j is defined by deformation gradient, \({{\varvec{F}}}\), as

$$\begin{aligned} \!\left\langle {{\varvec{x}}}_{ij}\right\rangle ^i = {{\varvec{F}}}_i{{\varvec{X}}}_{ij} \end{aligned}$$
(27)

where \({{\varvec{x}}}_{ij}\) and \({{\varvec{X}}}_{ij}\) are relative position vectors in the current deformed and initial undeformed configurations, respectively. \(\left\langle \,\,\,\right\rangle ^i\) denotes that \({{\varvec{x}}}_{ij}\) is a theoretically exact relative position vector calculated by the deformation gradient of the particle i, \(F_i\), with respect to initial configuration which is evaluated in every time step by

$$\begin{aligned} \!{{\varvec{F}}}_i = {{\varvec{I}}} + \sum \limits _{j=1}^{N}\frac{m_j}{{\rho _0}_j}\left( {{\varvec{u}}}_j - {{\varvec{u}}}_i\right) \otimes {\tilde{\nabla }} W(X_{ij}) \end{aligned}$$
(28)

with \(\rho _0\) and \({\tilde{\nabla }} W(X_{ij})\) being the density and corrected kernel gradient, respectively, in the initial configuration. In Eq. 28, \({{\varvec{u}}}_i\) is the displacement of particle i defined by

$$\begin{aligned} \!{{\varvec{u}}}_i = {{\varvec{x}}}_i - {{\varvec{X}}}_i \end{aligned}$$
(29)

where \({{\varvec{x}}}_i\) and \({{\varvec{X}}}_i\) are the position vectors of particle i in current and initial configurations, respectively. \(\nabla W(X_{ij})\) is calculated once at the beginning of simulations and kept unchanged as long as particles neighbor list does not change. However, the neighbor list must be frequently updated, e.g., for simulations involving large particle displacements as suggested by Vidal et al. [39], for contact problems and for the sake of computational efficiency, which makes it impossible to use Eq. 28 throughout the whole course of the simulation. To address this problem, an intermediate reference configuration is considered which coincides with the initial configuration at the beginning of the simulation and later on is replaced with the current configuration each time the neighbor list is updated. Then the deformation gradient at point i is calculated using

$$\begin{aligned} \!{{\varvec{F}}}_i = {{\varvec{F}}}_i^{\text {ref}}{{\varvec{F}}}_i^{\text {init}} \end{aligned}$$
(30)

where \({{\varvec{F}}}_i^{\text {ref}}\) is the deformation gradient with respect to the reference configuration evaluated by Eq. 28 using quantities described in the reference configuration and \({{\varvec{F}}}_i^{\text {init}}\) is the deformation gradient of particle i in the reference configuration with respect to the initial configuration. \({{\varvec{F}}}_i^{\text {init}}\) initially is a second-order unit tensor and is replaced with \({{\varvec{F}}}_i\) each time the neighbor list is updated.

Having calculated the deformation gradient, using Eq. 30 the exact relative position vector, \(\left\langle {{\varvec{x}}}_{ij}\right\rangle \), is evaluated and compared with the estimated one, \({{\varvec{x}}}_{ij}\), providing an error vector showing how much a particle has deviated form its true position due to a zero-energy mode. The error vector \(\varvec{\varepsilon }_{ij}\) is expressed as the difference between the average exact relative position vector and the estimated relative position vector defined by

$$\begin{aligned} \!\varvec{\varepsilon }_{ij} = \frac{1}{2}\left( \left\langle {{\varvec{x}}}_{ij}\right\rangle ^i + \left\langle {{\varvec{x}}}_{ij}\right\rangle ^j\right) - {{\varvec{x}}}_{ij} = \frac{1}{2}\left( {{\varvec{F}}}_i + {{\varvec{F}}}_j\right) {{\varvec{X}}}_{ij} - {{\varvec{x}}}_{ij}.\nonumber \\ \end{aligned}$$
(31)

The following subsections explain two hourglass control methods as introduced by Ganzenmüller et al. [16], stiffness-based and viscosity-based, in which this error vector employed to control the amount of the stabilization.

2.4.1 Stiffness-based hourglass control

In order to minimize the error and, in turn, prevent zero-energy modes, a penalty force proportional to the error vector magnitude is exerted on particles to counterbalance spurious displacements. For the sake of conservation of angular momentum, the penalty force acts along the particles relative position vector in the current configuration by projecting the error vector on that direction. Besides, \(\varvec{\varepsilon }\) is weighted by the kernel function and the particle volume so that the force is formulated in the spirit of SPH which finally results in the following equation.

$$\begin{aligned} \!{{\varvec{f}}}_i^{\text {stiff}} = -\xi \sum \limits _{j=1}^{N}\frac{m_i}{\rho _i}\frac{m_j}{\rho _j}W_{ij}\frac{E}{X_{ij}^2}\frac{\varvec{\varepsilon }_{ij}\cdot {{\varvec{x}}}_{ij}}{x_{ij}}\frac{{{\varvec{x}}}_{ij}}{x_{ij}} \end{aligned}$$
(32)

where \(E=9K\mu /(3K+\mu )\) is the elastic modulus, \(\xi \) is a scaling factor and \( X_{ij} = |{{\varvec{X}}}_{ij}| \) is the Euclidean norm of the relative position vector \( {{\varvec{X}}}_{ij} \). The elastic modulus is divided by \(X_{ij}^2\) in order for the stiffness-based hourglass control force to be compatible with the elastic energy.

2.4.2 Viscosity-based hourglass control

It is known from FE that stiffness-based hourglass control works well for problems with linear deformations, e.g., linear elasticity. However, being nonlinear, plastic deformations are hindered by stiffness-based hourglass control as if the material appears stiffer than it should be. Hence, another hourglass control based on viscous forces was proposed to circumvent the problem which instead of being dependent on particles position as in Eq. 32 is based on particles velocity. The viscosity-based hourglass control is motivated by the bulk (linear) part of the artificial viscosity, Eq. 17, which is scaled by the norm of the error vector, \(\varepsilon _{ij} = |\varvec{\varepsilon }_{ij}|\), normalized by the norm of the relative position vector in the initial configuration, \( X_{ij} \), to damp parts of particles velocity caused by zero-energy modes and, then, defined by

$$\begin{aligned} \!{{\varvec{f}}}_i^{\text {visc}} = \left\{ \begin{array}{ll} -\zeta \sum \limits _{j=1}^{N}\frac{m_im_j}{\rho _{ij}}\frac{\varepsilon _{ij}}{X_{ij}} \frac{c_{\text {s}} h \left( {{\varvec{v}}}_{ij} \cdot {{\varvec{x}}}_{ij}\right) }{{x}_{ij}^2}\nabla W_{ij}, &{} \left( {{\varvec{v}}}_{ij} \cdot {{\varvec{x}}}_{ij}\right) \left( \varvec{\varepsilon }_{ij} \cdot {{\varvec{x}}}_{ij}\right) < 0 \\ &{} \\ 0, &{} \left( {{\varvec{v}}}_{ij} \cdot {{\varvec{x}}}_{ij}\right) \left( \varvec{\varepsilon }_{ij} \cdot {{\varvec{x}}}_{ij}\right) \ge 0 \end{array} \right. \nonumber \\ \end{aligned}$$
(33)

where \(\zeta \) is a scaling factor and the uncorrected kernel derivative is employed. Besides the condition is also modified to ensure that hourglass control forces are only applied if the relative velocity increases the error vector magnitude. In practical tests, it has been realized that a combined hourglass control defined by the following form works best for problems with plastic deformations.

$$\begin{aligned} \!{{\varvec{f}}}_i^{\text {comb}} = \chi {{\varvec{f}}}_i^{\text {visc}} + \left( 1 - \chi \right) {{\varvec{f}}}_i^{\text {stiff}} \end{aligned}$$
(34)

where \( \chi \) is a combination weight factor to scale the stiffness- and viscosity-based hourglass control’s contributions. In summary, the hourglass control scheme originally developed for total Lagrangian SPH is applied in an Eulerian SPH framework by calculating the deformation gradient which would otherwise not be required in the Eulerian scheme.

3 Results and discussion

Several cases are studied using the proposed hourglass control scheme, and the results are compared with FE simulations and SPH simulations stabilized only by artificial viscosity and artificial stress. No other stabilization methods such as artificial viscosity and artificial stress are applied when SPH simulations are stabilized by the hourglass control scheme except for the case of metal cutting for which additionally the density diffusion is used. In addition, two cases are also simulated by the stabilized total Lagrangian SPH formulation explained in Ganzenmüller [15] in order to provide a comparison between the present stabilized Eulerian SPH and the stabilized total Lagrangian SPH. FE results are obtained using the commercial software Abaqus/Explicit (version 2017) employing reduced integration linear elements with default hourglass control. Material properties shown in Table 1 are used in all simulations with the exception of the case of an oscillating plate. Rigid boundaries in the cases of upsetting and Taylor impact as well as the cutting tool in the case of metal cutting are represented as rigid triangulated surfaces. Interactions between an SPH particle and a surface are defined as a repulsive Hertzian normal force and a Coulomb friction tangential force between a sphere with a diameter equal to the particle spacing and the spatially closest triangle of the surface.

Table 1 Summary of material properties for aluminum Al6061-T6 [38] and polymethyl methacrylate (PMMA)
Full size table

3.1 Elastic tension

This case is carried out so as to demonstrate the capability of the scheme to prevent the instabilities observed as a material undergoes linear elastic deformations. Tensile behavior of a 2D rectangular model of elastic aluminum clamped at both ends is modeled using stiffness-based hourglass control. SPH prediction for nominal tensile strain of 0.45 is shown in Fig. 1 alongside FE result. Although a discrepancy between results is observed around the corners owing to the smoothing nature of SPH, there is a very good agreement between SPH and FE results showing that the hourglass control can effectively prevent both tensile instabilities and spurious zero-energy modes which would not be possible in the absence of the hourglass control. As Fig. 2 shows, although artificial viscosity and artificial stress are employed, instabilities occur for very small strains and propagate throughout the geometry which finally leads to an unphysical fracture.

Fig. 1
figure 1

Elastic tension results for the von Mises stress contour. Initial SPH undeformed body (left), SPH result stabilized by stiffness-based hourglass control scheme with \(\xi =10\) (middle) and FE result (right)

Full size image
Fig. 2
figure 2

Elastic tension SPH results obtained using artificial viscosity and artificial stress: instabilities occur at very small strain levels propagating over the whole body

Full size image

3.2 Oscillating plate

To further check the accuracy of the proposed scheme in dealing with large elastic deformations oscillation of thin elastic plates is simulated and compared with analytical solution [18, 33]. Figure 3 shows the initial 2D geometry of a thin plate clamped on the left side. Herein, oscillation of two plates, both of free length of 0.2m, but, one 0.02m wide and the other 0.01m wide, are studied. According to the analytical solution, the following distribution for initial velocity along y axis, \(v_y\), is applied to a plate’s free length.

Fig. 3
figure 3

Geometry of an oscillating plate

Full size image
$$\begin{aligned} \!v_y(x) = v_l\frac{f(x)}{f(l)} \end{aligned}$$
(35)

where \(v_l\) is the initial velocity of the free end of the plate, herein is equal to \(5\%\) of the speed of sound, and f(x) is defined as

$$\begin{aligned} \begin{aligned} \!f(x) =&\left( \text {cos}\,kl+\text {cosh}\,kl\right) \left( \text {cosh}\,kx-\text {cos}\,kx\right) \\&+\left( \text {sin}\,kl-\text {sinh}\,kl\right) \left( \text {sinh}\,kx-\text {sin}\,kx\right) \end{aligned} \end{aligned}$$
(36)

being k as the wave number which is calculated using \(kl=1.875\) for the fundamental mode of oscillation. Unlike other cases, in this section results are presented using a soft elastic material with the following properties; \(\rho _0 ={1000}{\hbox { kg/m}^{3}}\), \(K={3.25}\hbox { MPa}\) and \(\mu ={0.715}\hbox { MPa}\). Moreover, the geometries are discretized in a way that there are 20 particles across the plates’ width.

Solutions are stabilized by stiffness-based hourglass control scheme with \(\xi = 0.5\) and \(\xi = 1.0\) for plates with \(h_e={0.02}{\mathrm{m}}\) and \(h_e={0.01}{\mathrm{m}}\), respectively. Figure 4 shows the von Mises stress field for the given plates after several cycles when the free end of a plate is at its highest position proving the good stabilization properties of the scheme which is further supported by a very good agreement between the obtained oscillations period with the analytical ones reported in Table 2. As it was expected, since we are using thin plate theory the discrepancy between the calculated period and analytical one decreases as the aspect ratio of the plate increases. Additionally, Table 2 shows a very good agreement between the present scheme and the stabilized total Lagrangian SPH. That being said, computation times presented in Table 3 show that the total Lagrangian scheme is around \(25\%\) faster that the present stabilized Eulerian scheme. This speedup is obtained by skipping kernel updates at every time step and by avoiding any neighbor list updates. Nevertheless, the material models employed in this paper use the rate of deformation tensor to calculate the Cauchy stress tensor which, consequently, requires a transformation of Cauchy stress to first Piola-Kirchhoff stress which then is used in the momentum equation. Hence, the total Lagrangian scheme involves more matrix operations than the Eulerian scheme in order to calculate forces exerted on a particle from its surrounding particles. These extra operations which include the inversion of the deformation gradient for all particles at every time step diminish the efficiency of the total Lagrangian scheme. Besides, in order to better illustrate the favorable effect of the proposed hourglass control scheme results for the wider plate obtained using only artificial viscosity and artificial stress at three moments during its oscillation are presented in Fig. 5. Though it seems employing artificial viscosity and artificial stress can prevent instabilities at early stages, as the simulation proceeds spurious modes gradually propagate throughout the whole domain which causes the oscillation amplitude to drop as shown in Fig. 6.

Fig. 4
figure 4

Oscillating plate von Mises stress for \({0.02}{\mathrm{m}}\) width at \({2.465}{\mathrm{s}}\) (left) and \({0.01}{\mathrm{m}}\) width at \({2.17}{\mathrm{s}}\) (right)

Full size image
Table 2 Comparison of the obtained period of the plates oscillations with analytical values
Full size table
Table 3 Computation times for 2.5 s of oscillation of the thin plates
Full size table
Fig. 5
figure 5

Oscillating plate von Mises stress calculated using only artificial viscosity and artificial stress at \({0.075}{\mathrm{s}}\) (left), \({0.63}{\mathrm{s}}\) (middle) and \({1.75}{\mathrm{s}}\) (right)

Full size image
Fig. 6
figure 6

Temporal evolution of the deflection of the oscillating plate’s free end with and without hourglass (HG) control

Full size image
Fig. 7
figure 7

Initial geometries for the upsetting test: SPH (left) and FE (right)

Full size image
Fig. 8
figure 8

Results for von Mises stress field (left column) and equivalent plastic strain (right column) obtained by the present scheme (top row), stabilized total Lagrangian SPH (middle row) and finite element method (bottom row)

Full size image

3.3 Upsetting test

Having shown the effectiveness of the stiffness-based hourglass control in modeling elastic deformations, this case aims at verifying that the hourglass control can stabilize SPH simulations dealing with fairly large plastic deformations. An aluminum cylinder of 5 mm radius and 5 mm height, Fig. 7, is placed between the rigid plates and then compressed to half of its height as the top plate moves down while the bottom one is fixed. It has been realized, although, stiffness-based hourglass control hinders plastic deformations a reasonably small amount of it can help obtaining better results. Hence, the combined hourglass control for which \(\chi =0.5\), \(\xi = 0.2\) and \(\zeta = 10\) is employed. As can be seen in Fig. 8, there is a good agreement among the present scheme, stabilized total Lagrangian SPH and FE as a result of accurately predicted deformations which manifests itself as the correspondence between SPH particles and FE nodes positions. In addition, computation times of the upsetting test for the proposed scheme and the stabilized total Lagrangian SPH are reported in Table 4 showing that in this case the total Lagrangian scheme is faster than the proposed Eulerian scheme by about \(12\%\). Ba and Gakwaya [4] reported a much higher efficiency obtained by using a total Lagrangian scheme implemented as a user element subroutine in ABAQUS instead of using the Eulerian SPH solver of ABAQUS. Since the speedup is partly gained by skipping neighbor list updates, the amount of gained efficiency depends on the neighbor search algorithm employed in the Eulerian scheme. In that work an all-pair neighbor search algorithm which needs \(N^2\) operations for N particles is reported to be used by ABAQUS for Eulerian SPH. This results in a significantly higher speedup for the total Lagrangian scheme compared to the present work where a linked-list neighbor search algorithm is used for the Eulerian scheme.

Table 4 Computation times for \(5\,{\upmu {\mathrm{s}}}\) of compaction of the aluminum specimen
Full size table
Fig. 9
figure 9

Initial geometries for the Taylor bar impact test: SPH (left) and FE (right)

Full size image

3.4 Taylor bar impact

In order to test the hourglass control under a high strain rate loading impact of a long aluminum bar to a rigid surface, Fig. 9, with the impact velocity of 295 m/s is modeled. Diameter and height of the bar are 7.595 mm and 37.975 mm, respectively. The combined hourglass control is used with \(\chi =0.5\), \(\xi = 0.2\) and \(\zeta = 10\). Once again there is a good agreement between SPH and FE as it can be seen in Fig. 10. Besides, convergence of the calculated mushroom diameter and bar’s height using the proposed scheme and FE was studied and is presented in Fig. 11 showing both methods are convergent. Although FE has a bit higher rate of convergence, as expected, both methods converge to values which are quiet close to each other. Additionally, experimental values for the mushroom diameter and the bar’s height reported by House et al. [20] are indicated in Fig. 11 showing that both methods predict the mushroom diameter very well. However, there is an error of around \(10\%\) in the prediction of the bar’s height indicating that the material model could be improved. Moreover, von Mises stress field obtained using SPH without hourglass control is also shown in Fig. 12. Instabilities are observed shortly after impact at the impact site, propagate upwards inside the bar and decrease the accuracy of the solution. Comparing Figs. 10 and 12, the proposed hourglass control scheme can effectively prevent spurious zero-energy modes that might happen during high strain rate deformations.

Fig. 10
figure 10

Comparison of Taylor bar impact results obtained using stabilized Eulerian SPH (top) and FE (bottom). a, d von Mises stress at \(20~{\upmu {\mathrm{s}}}\), b, e von Mises stress at \(45~{\upmu {\mathrm{s}}}\), c, f equivalent plastic strain at the end of the simulations

Full size image
Fig. 11
figure 11

Convergence study and comparison of the mushroom diameter (left) and the bar height (right) during Taylor bar impact calculated by the proposed hourglass controlled SPH and FE

Full size image
Fig. 12
figure 12

Propagation of instabilities and their adverse effect on the simulation accuracy in the Taylor bar impact test using unstabilized Eulerian SPH

Full size image

3.5 Metal cutting

Since fracture criteria and damage models are strongly dependent on stress and strain fields, it is imperative to control instabilities of SPH simulations so as to properly model the failure of materials. SPH is employed to model the process of metal cutting in which the cutting tool moves across the aluminum workpiece at a constant velocity of 10 m/s and, in turn, removes a chip of material from the surface. Considering that the fracture criterion is dependent on pressure, in order to have the pressure field correctly calculated the density diffusion method is applied to filter out density noises and consequently pressure noises. The focus, here, is on the chip formation modeled by SPH with and without hourglass control. Figure 13 shows a serrated chip formation modeled using hourglass control. As the cutting tool moves, shear bands are formed across the chip which eventually leads to cracks formation, propagation and breakage of the chip. Results obtained using SPH without hourglass control are presented in Fig. 14 which again show a serrated chip formation, however there is no clear crack initiation and propagation since the fields are not correctly calculated due to the instabilities. Comparing results presented in Figs. 13 and 14 emphasizes the importance of preventing the instabilities, specially, in dealing with materials failure and also proves the ability of the proposed hourglass control scheme in doing so.

Fig. 13
figure 13

Chip formation in cutting modeling using hourglass control; von Mises stress (left) and damage parameter (right); the rows represent different times

Full size image
Fig. 14
figure 14

Same as middle row of Fig. 13 but without hourglass control

Full size image

3.6 Fluid–structure interaction

Although the stabilized total Lagrangian SPH is somewhat faster than the proposed Eulerian scheme in dealing with merely solid mechanics problems, it does not considerably outperform its Eulerian counterpart when it comes to solving FSI problems. In SPH simulations of FSI problems, the number of solid particles is usually not comparable to the number of fluid particles. In this case, the computational speedup achieved by employing the total Lagrangian scheme will be marginal since for fluid particles kernel calculations must be done every time step and neighbor lists are frequently updated. Besides, having both Eulerian and Lagrangian SPH running together adds complications to the implementation, e.g., due to additional data bookkeeping, and it is not straightforward to make both schemes work together efficiently.

Here, the process of abrasive flow machining is simulated. It is employed to polish internal surfaces as abrasive grains suspended in a carrier fluid hit the surface and gradually smoothen it. The process is monolithically simulated at a microscopic scale by employing Eulerian SPH to discretize all of the involved phases. Figure 15 shows a simplified two-dimensional setup used to simulate polishing of a PMMA micro-channel through removing the rectangular roughness in the middle of the channel. The carrier fluid is a Newtonian fluid of 2 mPas viscosity carrying abrasive circular iron grains. The hydrodynamics of the problem is solved by the \(\delta ^{+}\)-SPH scheme introduced by Sun et al. [36]. The abrasive grains are modeled as rigid clusters of particles whose movements are calculated by a rigid body motion solver explained in Polfer et al. [31]. The solid phase is modeled by the proposed stabilized Eulerian scheme. The interactions between the fluid particles and solid or cluster particles are resolved by the model proposed by Adami et al. [1]. The contact between rigid clusters and the surface is modeled by inter-particle repulsive forces calculated according to Cleary et al. [10]. A periodic boundary condition is imposed on the right and left side of the simulation domain meaning that particles leaving the domain on the right side re-enter the domain on the left side. Besides, surface particles are removed from the simulation domain once their damage parameter becomes larger than 1 due to impacts of the grains on to the surface. The abraded surface after \({3.5}\, {\upmu }{\mathrm{s}}\) of machining obtained by Eulerian SPH stabilized by hourglass control and without hourglass control is shown in Fig. 16. The results prove that the present scheme is capable of preventing instabilities in this complex material removal situation. In the absence of an effective stabilization scheme to prevent zero-energy modes, instabilities initiate close to the top left corner of the rectangular roughness, where most grains hit the surface, then slowly propagate across the solid phase even in regions far from the impact site. Eventually, the particle distribution becomes very disordered due to successive spurious movements which leads to inaccurate calculations of kernel derivatives and consequently velocity gradients, and penetration of fluid particles in the solid phase as well.

Fig. 15
figure 15

Two-dimensional setup used to simulate the process of abrasive flow machining with the solid material in gray, the abrasive grains in light blue and the carrier fluid in dark blue. A periodic boundary condition is imposed on the left and right side of the simulation domain

Full size image
Fig. 16
figure 16

Results for 3.5 ms of abrasive flow machining obtained by (top) the present scheme and (bottom) Eulerian SPH without hourglass control

Full size image

4 Conclusion

This paper presents a stabilization scheme to prevent the notorious tensile instability and zero-energy modes. The scheme is based on the stabilization algorithm named hourglass control proposed by Ganzenmüller [15] in the Lagrangian SPH framework to prevent spurious zero-energy modes. That being said, since many SPH codes are implemented in the Eulerian framework it might not be straightforward to turn them into Lagrangian codes considering the existing code structure. Furthermore, it might be even necessary to have Lagrangian and Eulerian codes work together as, e.g., for FSI problems. To address this issue, the hourglass control algorithm is incorporated into the Eulerian SPH formulation which can be done easily by a few changes to an existing code. Thus, the present paper presents a scheme to model solid material deformations using stabilized Eulerian SPH that does not suffer from the tensile stability nor zero-energy modes. Furthermore, the results reveal that the hourglass control scheme is not only applicable to total or updated Lagrangian SPH but also to Eulerian SPH.

In order to verify the stabilization scheme, several cases were modeled and the results were compared with finite element simulations and stabilized total Lagrangian SPH simulations. It was shown that the hourglass control algorithm, although originally developed to prevent zero-energy modes, can also hinder the tensile instability. Two cases were used to examine the stiffness-based hourglass control. The obtained results assured accurate SPH elastic responses in the presence of large tensile strains which are highly susceptible to tensile instability as well as long elastodynamic responses by preventing zero-energy mode initiation and propagation. Two further cases were carried out to investigate the capability of the proposed scheme to stabilize nonlinear solutions. Since employing stiffness-based hourglass control tends to overestimate a given material’s stiffness, viscosity-based hourglass control was utilized to predict elastoplastic behavior. However, we found out that still a small amount of stiffness-based control can lead to more accurate results. Therefore, the combined hourglass control was employed and the obtained results revealed high accuracy in comparison with finite element simulations as well as convergence of the proposed scheme. Another case was devoted to emphasize the importance of stabilization when dealing with fracture modeling. It demonstrated that the hourglass control scheme leads to a better estimation of stress and strain fields on which most fracture criteria depend. Thus, fracture processes which consist of crack initiation, crack propagation and final rupture can be modeled adequately. A final case simulating material removal by an abrasive suspension illustrates the versatility of Eulerian SPH in a three-phase scenario where the solid structure is again stabilized using the proposed scheme.