Abstract
The effects of boundary (liquid/solid) slip on hydrodynamics are well recognized. However, it is extremely difficult to quantify in-situ boundary slip in a lubrication contact. Therefore, an effective interfacial parameter that is well correlated with the lubrication effect is of practical significance. This paper presents an examination of common interfacial parameters, including surface tension, contact angle, contact angle hysteresis, and a recently proposed spreading parameter. Specimen surfaces of different hydro/oleophobicity were prepared and characterized using the aforementioned interfacial parameters. These samples were further used as bearing surfaces in hydrodynamic lubrication tests. The correlations of these parameters with the measured lubricating film thickness were examined and compared. The key parameter closely related to the hydrodynamic effect was identified.
Article PDF
Similar content being viewed by others
References
Spikes H A. The half-wetted bearing: Part 1–Extended Reynolds equation. J Eng Tribol 217: 1–14 (2003)
Choo J H, Glovnea R P, Forrest A K, Spikes H A. A low friction bearing based on liquid slip at the wall. J Tribol 129: 611–620 (2007)
Guo F, Wong P L. Full and partial boundary slippage effect on squeeze film bearings. Tribol Int 43: 997–1004 (2010)
Tauviqirrahman M, Ismail R, Jamari J, Schipper D J. Combined effect of texturing and boundary slippage in lubricated sliding contacts. Tribo Int 66: 274–281 (2013)
Craig V S J, Neo C, Williams D R M. Shear-dependent boundary slip in an aqueous Newtonian liquid. Phys Rev Lett 87(5): 054504 (2001)
Zhu Y X, Granick S. Rate-dependent slip of Newtonian liquid at smooth surfaces. Phys Rev Lett 87(9): 096105 (2001)
Spikes H A, Granick S. Equation for slip of simple liquids at smooth solid surfaces. Langmuir 19: 5065–5071 (2003)
Hild W, Opitz A, Schaefer J, Scherge M. The effect of wetting on the microhydrodynamics of surfaces lubricated with water and oil. Wear 254: 871–875 (2003)
Baudry J, Charlaix E, Tonck A, Mazuyer D. Experimental evidence for a large slip effect at a nonwetting fluid-solid interface. Langmuir 17: 5232–5236 (2001)
Tretheway D C, Meinhart C D. Apparent fluid slip at hydrophobic microchannel walls. Phys Fluids 14: L9–L12 (2002)
Guo F, Yang S, Ma C, Wong P. Experimental study on lubrication film thickness under different interface wettabilities. Tribol Lett 54: 81–88 (2014)
Bongaerts J, Fourtouni K, Stokes J. Soft-tribology: lubrication in a compliant PDMS–PDMS contact. Tribol Int 40: 1531–1542 (2007)
Joseph P, Tabeling P. Direct measurement of the apparent slip length. Phys Rev E 71: 035303 (2005)
Kikuchi K, Mochizuki O. Micro PIV measurement of slip flow on a hydrogel surface. Meas Sci Technol 25: 065702 (2014)
Ponjavic A, Chennaoui M, Wong J S S. Through-thickness velocity profile measurements in an elastohydrodynamic contact. Tribo Lett 50(2): 261–277 (2013)
Kalin M, Polajnar M. The correlation between the surface energy, the contact angle and the spreading parameter, and their relevance for the wetting behavior of DLC with lubricating oils. Tribol Int 66: 225–233 (2013).
Kalin M, Polajnar M. The wetting of steel, DLC coatings, ceramics and polymers with oils and water: The importance and correlations of surface energy, surface tension, contact angle and spreading. App Surf Sci 293: 97–108 (2014)
Fowkes F M. Attractive forces at interfaces. J Ind & Eng Chem 56: 40–52 (1964)
Wang D, Wang X, Liu X, Zhou F. Engineering a titanium surface with controllable oleophobicity and switchable oil adhesion. J Phys Chem C 114: 9938–9944 (2010).
Bhushan B, Her E K. Fabrication of superhydrophobic surfaces with high and low adhesion inspired from rose petal. Langmuir. 26: 8207–8217 (2010)
Owens D K, Wendt R. Estimation of the surface free energy of polymers. J App Poly Sci 13: 1741–1747 (1969)
Yaminsky V. Molecular mechanisms of hydrophobic transitions. J Adhes Sci Technol 14: 187–233 (2000)
Extrand C. Contact angles and their hysteresis as a measure of liquid-solid adhesion. Langmuir 20: 4017–4021 (2004)
Whyman G, Bormashenko E, Stein T. The rigorous derivation of Young, Cassie–Baxter and Wenzel equations and the analysis of the contact angle hysteresis phenomenon. Chem Phys Lett 450: 355–359 (2008)
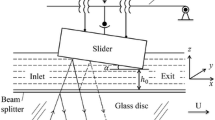
Guo F, Wong P L, Fu Z, Ma C. Interferometry measurement of lubricating films in slider-on-disc contacts. Tribol Lett 39: 71–79 (2010)
Guo L, Wong P L, Guo F, Liu H C. Determination of thin hydrodynamic lubricating film thickness using dichromatic interferometry. Appl Optics 53: 6066–6072 (2014)
Guo F, Wong P L. A multi-beam intensity-based approach for lubricant film measurements in non-conformal contacts. J Eng Tribol 216(5): 281–291 (2002)
Ma G J, Wu C W, Zhou P. Multi-linearity algorithm for wall slip in two-dimensional gap flow. Int J Numer Meth Eng 69: 2469–2484 (2007)
Guo L, Wong PL, Guo F. Boundary yield stress and interfacial potential energy barrier in thin film hydrodynamic lubrication. Tribol Lett 62: 7 (2016)
MacDougall G, Ockrent C. Surface energy relations in liquid/solid systems. I. The adhesion of liquids to solids and a new method of determining the surface tension of liquids. Proc Royal Soc Lond A Math Phys & Engg Sci 981: 151–173 (1942)
Barrat J L, Bocquet L. Large slip effect at a nonwetting fluid-solid interface. Phys Rev Lett 82: 4671 (1999)
Huang D M, Sendner C, Horinek D, Netz R R, Bocquet L. Water slippage versus contact angle: A quasiuniversal relationship. Phys Rev Lett 101: 22610 (2008)
Acknowledgments
The work described in this paper was fully supported by the Research Grants Council of Hong Kong (Project No. CityU123411) and Natural Science Foundation of China (Project No. 51275252). The authors would also like to express sincere thanks to Dr. X. Zhou of SKF for providing the EGC coating in this work.
Author information
Authors and Affiliations
Corresponding author
Additional information
This article is published with open access at Springerlink.com
Liang GUO. He received his Ph.D. degree from the Department of Mechanical and Biomedical Engineering, City University of Hong Kong in 2016. He is currently a postdoctoral fellow in the same department. His research interests include interfacial effect in hydrodynamic lubrication and contact mechanics.
Patrick WONG. He obtained his PhD degree from the University of Hong Kong in 1990, and his BSc degree from City University, London in 1983. Dr. Wong started his academic career in the City University of Hong Kong since 1990. He is currently an associate professor in the Department of Mechanical and Biomedical Engineering in the City University of Hong Kong. His research interests include rolling element bearings, interfacial phenomena, and lubrication.
Feng GUO. He got his Ph.D. degree in mechanical engineering from the City University of Hong Kong in 2003. He is now employed as a full-time professor in Qingdao University of Technology. His main work is concentrated on fundamental research and university education in tribology. His research interests include numerical computation of liquid film lubrication, optical interferometry for lubricating film measurement, interfaces in tribology and new lubrication techniques.
Rights and permissions
Open Access: The articles published in this journal are distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Guo, L., Wong, P. & Guo, F. Identifying the optimal interfacial parameter correlated with hydrodynamic lubrication. Friction 4, 347–358 (2016). https://doi.org/10.1007/s40544-016-0131-9
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40544-016-0131-9