Skip to main content
SpringerLink
Log in

A new type of bilateral vibro-impact model: random vibration analysis

  • Published:
International Journal of Dynamics and Control Aims and scope Submit manuscript

Abstract

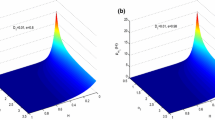
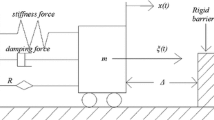
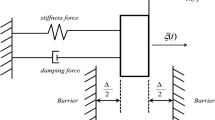
In this work, a novel class of bilateral vibro-impact model is proposed. Unlike the traditional impact model, the energy dissipation of the novel bilateral system is measured by the model of the restitution coefficient dependent with velocity. Then the random vibration of the system is investigated in the presence of Gaussian white noise excitations. The motions of the unperturbed impact system are firstly considered and grouped into two categories. Then, the mean drift and diffusion coefficients of the two kinds of motion are calculated with the stochastic averaging methodology for energy envelope under the assumed condition that the impact vibration system is quasi-conservative. Subsequently, the probability density functions of stationary responses are computed with solving the averaged Fokker-Plank-Kolmogorov equation. Finally, two illustrations are chosen to demonstrate the reliability of the presented technique. And, the validation of analytical results is verified by the simulation data generated by Monte Carlo.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16

Similar content being viewed by others

Code availability

The code that support the findings of this study are available from the corresponding author upon reasonable request.

References

  1. Dimentberg MF, Iourtchenko DV (1999) Towards incorporating impact losses into random vibration analyses: a model problem. Probabilistic Eng Mech 14:323–328

    Article  Google Scholar 

  2. Ibrahim RA (2009) Vibro-impact dynamics: modeling, mapping and applications. Springer, Berlin

    Book  Google Scholar 

  3. Kecik K, Brzeski P, Perlikowski P (2016) Non-linear dynamics and optimization of a harvester-absorber system. Int J Struct Stab Dyn 17:1740001

    Article  Google Scholar 

  4. Liu WB, Dai HL et al (2017) Suppressing wind-induced oscillations of prismatic structures by dynamic vibration absorbers. Int J Struct Stab Dyn 17:1750056

    Article  MathSciNet  Google Scholar 

  5. Pratiknyo YB, Setiawan R, Suweca IW (2019) Experimental and theoretical investigation of combined expansion tube-axial splitting as impact energy absorbers. Int J Struct Stab Dyn 20:2050021

    Article  Google Scholar 

  6. Zhuravlev VF (1976) A method for analyzing vibration-impact systems by means of special functions. Mech Solids 11:23–27

    MathSciNet  Google Scholar 

  7. Dimentberg M, Menyailov A (1979) Response of a single-mass vibroimpact system to white-noise random excitation. ZAMM - J Appl Math Mech 59:709–716

    Article  MathSciNet  Google Scholar 

  8. Ivanov AP (1994) Impact oscillations: linear theory of stability and bifurcations. J Sound Vib 178:361–378

    Article  MathSciNet  Google Scholar 

  9. Xu W, Li C, Yue X, Rong H (2016) Stochastic responses of a vibro-impact system with additive and multiplicative colored noise excitations. Int J Dyn Control 4:393–399

    Article  MathSciNet  Google Scholar 

  10. Dimentberg MF, Iourtchenko DV (2004) Random vibrations with impacts: a review. Nonlinear Dyn 36:229–254

    Article  MathSciNet  Google Scholar 

  11. Er G-K (1998) An improved closure method for analysis of nonlinear stochastic systems. Nonlinear Dyn 17:285–297

    Article  MathSciNet  Google Scholar 

  12. Zhu HT (2015) Stochastic response of a vibro-impact Duffing system under external Poisson impulses. Nonlinear Dyn 82:1001–1013

    Article  MathSciNet  Google Scholar 

  13. Zhu HT (2015) Stochastic response of a parametrically excited vibro-impact system with a nonzero offset constraint. Int J Dyn Control 4:180–194

    Article  MathSciNet  Google Scholar 

  14. Chen L, Qian J, Zhu H, Sun J (2019) The closed-form stationary probability distribution of the stochastically excited vibro-impact oscillators. J Sound Vib 439:260–270

    Article  Google Scholar 

  15. Yurchenko D, Song L (2006) Numerical investigation of a response probability density function of stochastic vibroimpact systems with inelastic impacts. Int J Non Linear Mech 41:447–455

    Article  Google Scholar 

  16. Wang L, Ma S, Sun C et al (2018) The stochastic response of a class of impact systems calculated by a new strategy based on generalized cell mapping method. J Appl Mech 85:54502

    Article  Google Scholar 

  17. Kecskemethy A, Lüder J (1996) Rigid and elastic approaches for the modeling of collisions with friction in multibody systems. Zeitschrift für Angew Math und Mech 76:243–244

    MATH  Google Scholar 

  18. Wang Y, Mason MT (1992) Two-Dimensional Rigid-Body Collisions With Friction. J Appl Mech 59:635

    Article  Google Scholar 

  19. Johnson KL (1985) Contact Mechanics. In: Cambridge, UK: Cambridge University Press

  20. Stronge WJ (1995) Theoretical coefficient of restitution for planar impact of rough elasto-plastic bodies. Am Soc Mech Eng Appl Mech Div AMD 205:351–362

    Google Scholar 

  21. Thornton C (1997) Coefficient of restitution for collinear collisions of elastic-perfectly plastic spheres. J Appl Mech Asme 64:383–386

    Article  Google Scholar 

  22. Mesarovic SD, Fleck NA (1999) Spherical indentation of elastic-plastic solids. Proc Math Phys Eng ences 455:2707–2728

    Article  Google Scholar 

  23. Vu-Quoc L, Zhang X (2000) A normal force-displacement model for contacting spheres accounting for plastic deformation: force-driven formulation. J Appl Mech 67:363–371

    Article  Google Scholar 

  24. Kogut L, Etsion I (2002) Elastic-plastic contact analysis of a sphere and a rigid flat. J Appl Mech 69:657–662

    Article  Google Scholar 

  25. Zhang X, Vu-Quoc L (2002) Modeling the dependence of the coefficient of restitution on the impact velocity in elasto-plastic collisions. Int J Impact Eng 27:317–341

    Article  Google Scholar 

  26. Weir G, Mcgavin P (2008) The coefficient of restitution for the idealized impact of a spherical, nano-scale particle on a rigid plane. Proc R Soc A Math 464:1364–5021

    Google Scholar 

  27. Etsion I, Kligerman Y, Kadin Y (2005) Unloading of an elastic–plastic loaded spherical contact. Int J Solids Struct 42:3716–3729

    Article  Google Scholar 

  28. Kharaz AH, Gorham DA (2000) A study of the restitution coefficient in elastic-plastic impact. Philos Mag Lett 80:549–559

    Article  Google Scholar 

  29. Minamoto H, Kawamura S (2011) Moderately high speed impact of two identical spheres. Int J Impact Eng 38:123–129

    Article  Google Scholar 

  30. Ma D, Liu C (2015) Contact law and coefficient of restitution in elastoplastic spheres. J Appl Mech 82:121006–121015

    Article  Google Scholar 

  31. Liu D, Li J, Meng Y (2019) Probabilistic response analysis for a class of nonlinear vibro-impact oscillator with bilateral constraints under colored noise excitation. Chaos Solitons Fractals 122:179–188

    Article  MathSciNet  Google Scholar 

  32. Kumar P, Narayanan S, Gupta S (2016) Bifurcation analysis of a stochastically excited vibro-impact Duffing-Van der Pol oscillator with bilateral rigid barriers. Int J Mech ences 127:103–117

    Article  Google Scholar 

  33. Yang G, Xu W, Gu X, Huang D (2016) Response analysis for a vibroimpact Duffing system with bilateral barriers under external and parametric Gaussian white noises. Chaos Solitons Fractals 87:125–135

    Article  MathSciNet  Google Scholar 

  34. Chen L, Zhu H, Sun JQ (2019) Novel method for random vibration analysis of single-degree-of-freedom vibroimpact systems with bilateral barriers. Appl Math Mech 40:1759–1776

    Article  Google Scholar 

  35. Su M, Xu W, Zhang Y, Yang G (2021) Response of a vibro-impact energy harvesting system with bilateral rigid stoppers under Gaussian white noise. Appl Math Model 89:991–1003

    Article  MathSciNet  Google Scholar 

  36. Qian J, Chen L (2021) Random vibration of SDOF vibro-impact oscillators with restitution factor related to velocity under wide-band noise excitations. Mech Syst Signal Process 147:107082

    Article  Google Scholar 

  37. Zhu W, Lin YK (1905) stochastic averaging of energy envelope. J Eng Mech 117:1890–1905

    Article  Google Scholar 

Download references

Funding

The National Natural Science Foundation of China (No. 11672111, No. 12072118), the Program for New Century Excellent Talents in Fujian Province University, the Natural Science Foundation of Fujian Province of China (No. 2019J01049).

Author information

Authors and Affiliations

  1. College of Civil Engineering, Huaqiao University, Xiamen, 361021, China

    Jiamin Qian, Lincong Chen & Shichuan Liu

  2. Key Laboratory for Intelligent Infrastructure and Monitoring of Fujian Province, Huaqiao University, Xiamen, 361021, China

    Jiamin Qian & Lincong Chen

Authors
  1. Jiamin Qian
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Lincong Chen
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Shichuan Liu
    View author publications

    You can also search for this author in PubMed Google Scholar

Contributions

JQ: Investigation, Data curation, Writing—original draft. LC: Conceptualization, Methodology, Supervision, Project administration. SL: Data Collation, textual corrigendum.

Corresponding author

Correspondence to Lincong Chen.

Ethics declarations

Conflicts of interest

The authors declare that they have no conflict of interest.

Availability of data and material

The data and material that support the findings of this study are available from the corresponding author upon reasonable request.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Qian, J., Chen, L. & Liu, S. A new type of bilateral vibro-impact model: random vibration analysis. Int. J. Dynam. Control 9, 829–839 (2021). https://doi.org/10.1007/s40435-021-00759-7

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s40435-021-00759-7

Keywords

Search

Navigation