1 Introduction

The construction and transportation industries heavily rely on cranes in their day-to-day activities. Cranes carry massive payloads, therefore any flaw in their operation can cause long delays in production, property damage, injuries, and even fatalities in some cases. As a result of automation technologies, which supply the cranes with discrete-time control capabilities, faster, taller and even larger cranes have been produced [1]. Accordingly, the need for efficient controllers that guarantee fast turn-over times and smooth operations, while all the safety requirements are met, has been growing [2]. There have been many experimental and theoretical research attempts for mathematical modelling and control of cranes over the past years. Despite the increased research in the field of crane dynamics and control, some of the major concerns associated with the crane operations are yet to be addressed.

Since overhead crane systems operate on pre-defined sets of tracks within a limited space, payload oscillation in point-to-point maneuvers is a challenging problem in crane operations. Simulated results of a scaled overhead crane showed a sway angle up to 4° during maneuvering [3]. A generic crane positioning operation includes three stages: loading the ladle, moving it to the new location, and lastly unloading the ladle. If one of these stages conflict with one another, the operation would either fail or be delayed. Thus, precise position control and rapid rest to rest motion is critical [4].

Although different control strategies have been developed so far to reduce the residual oscillations in overhead crane systems, the problem persists [5]. In particular, a number of input shaping techniques have been derived and implemented over the past four decades to suppress the payload swing in real time [3, 6, 7]. The early shaping techniques were focused on eliminating the residual oscillations of the payloads, the damping ratio and the natural frequency of the crane. Although according to Vaughan et al. [5], the robustness of these shapers [known as zero vibration (ZV)] were enhanced later, increasing robustness resulted in slower system responses. Using the straight transfer transformation method, Terashima et al. [4] developed a three-dimensional loop control strategy for a rotary crane in point to point maneuvers. Their findings indicated that their control method was successful in eliminating the centrifugal force effects and residual oscillations. In another effort to reduce payload oscillations, Starr [8] implemented a double step acceleration profile to suspend an object. By employing a linear approximation to determine the oscillation period, they derived an analytical expression for the acceleration profile. In 2012, Maleki et al. [9] proved that the shape of the input is equivalent to a notch filter that applies to a general input signal. They also suggested that input is centered on the natural frequency of the payload oscillation. Numerical verifications and experiments they conducted for crane maneuvers with different cable lengths demonstrated the ability of their approach in suppressing the residual payload oscillations. Maleki et al.’s work was further advanced compared to Parker et al. [10, 11], whom based on their simulation observations concluded that the verification presented in [9] was only applicable to low acceleration and slow speed commands. Alhazza and Masoud [12, 13] introduced a new strategy with a single variable acceleration that was able to eliminate residual and travel payload oscillations of an overhead crane. Compared to the initial double step acceleration profile, the profile they proposed was able to provide a smoother acceleration profile. The proposed strategy further accounted for the effects of damping. Through the application of numerical simulations and experiments, they were able to prove that residual oscillations for different damping ratios could be eliminated.

Pendulum models, which are commonly adopted in oscillation modelling of cranes, do not include hoisting for simplification purposes. However, hoisting is a critical step in a point-to-point crane maneuver as it relates to the variations in cable length and adds a new level of non-linearity to the equations of motion. To account for this shortcoming and to ensure that the hoisting complexities are addressed, Maleki et al. [9] introduced different sets of input shaping controllers. After comparing different input shaping techniques, they showed that residual vibrations could be reduced to an acceptable level by input shapers. To further evaluate the effects of hoisting, a new line of research has been focused on double pendulum models for cranes. The need for these models is more evident for heavy lifts, which their hooks and payloads are comparable in term of weight and their hoisting mechanisms behave similar to a double pendulum. The design of control systems for this type of overhead crane systems should compensate for the double oscillations that are expected to occur in an uncontrolled motion. Command shapers that are designed for the first mode oscillations are particularly applicable to multi-degree of freedom systems because they prevent the higher modes of oscillations to appear once odd integer multiples are used as frequencies. Masoud et al. [14] used this concept to develop feedback-based shapers for an overhead system in a double pendulum platform. Point-to-point crane maneuvers are repetitive series of rest to rest motions with identical conditions. Therefore, by adopting iterative learning controls (ILC), they proposed a repetitive cyclic process in which the input could be controlled and modified for every cycle. This flexibility makes the approach suitable for application in crane industry [15].

This article is aimed to discuss how to control an overhead crane in rest to rest maneuvers using input shaping method and a genetic algorithm (GA) as the optimization technique to tune the jib input acceleration. To achieve this outcome, a polynomial function is implemented as the input for the jib acceleration to move the payload on a specific trajectory that satisfies the system constraints and secures the target conditions. The parameters of this polynomial are optimized using the proposed GA strategy. GA is suitable for non-convex problems such as crane maneuvers. A fitness function is applied to establish an optimal set of polynomial coefficients. The proposed algorithm provides an interaction with the problem to be solved through an objective function, which measures the quality of the solution. Compared with the existing control methods for the overhead crane system, the proposed control technique shows superior anti-swing control performance. The controller is able to precisely limit the payload swing angle to safely carry sensitive loads, liquid, and chemicals. Moreover, unlike the existing methods which are driven by single and/or double steps, the introduced approach uses a continuous input function which results in quicker time responses. Also, allowing the GA to tune the controller input parameters reduces the overhead system sensitivity to any inaccuracy in the hoisting cable length.

2 Mathematical model

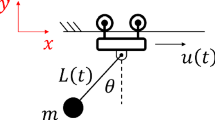
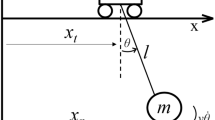
The proposed model for the overhead crane consists of a moving massless platform (jib) confined to move in the horizontal direction (x) with an acceleration function of \( {\ddot{{\rm u}}} \), as shown in Fig. 1. A variable length cable connects a lumped mass m to the platform. The attached mass represents the payload and it is free to swing in the x–y plane with the rotation angle \( \uptheta \). The model captures all three stages of a rest-to-rest maneuver, including hoisting (raising), cruising, and lowering.

Fig. 1
figure 1

The overhead crane model consists of a rotating lumped mass attached to a sliding massless platform

Full size image

Jib acceleration and deceleration periods occur during hoisting and lowering operations, respectively. Initial and desired final conditions are defined as:

$$ \begin{aligned} &\uptheta_{{\rm i}} = 0 ,\quad {\dot{\theta }}_{{\rm i}} = 0 \\ &\uptheta\left( {{{\rm t}}_{{\rm h}} } \right) = 0 ,\quad {\dot{\theta }}\left( {{{\rm t}}_{{\rm h}} } \right) = 0 \\ \end{aligned} $$
(1)

where \( \uptheta_{{\rm i}} \) and \( {\dot{\theta }}_{{\rm i}} \) represent the mass angular position and angular velocity at the onset of hoisting, and th, \( \uptheta\left( {{{\rm t}}_{{\rm h}} } \right) \) and \( {\dot{\theta }}\left( {{{\rm t}}_{{\rm h}} } \right) \) are the hoisting time, rotation, and angular velocity at the end of hoisting, respectively.

The jib final velocity at the end of hoisting is given by:

$$ \mathop \smallint \limits_{0}^{{{{\rm t}}_{{\rm h}} }} {\ddot{{\rm u}}}\left( {{\rm t}} \right) {{\rm dt}} = {{\rm v}}_{{\rm f}} $$
(2)

where vf is the desired jib velocity at the end of hoisting. A polynomial function \( \left( {{\ddot{{\rm u}}}\left( {{\rm t}} \right)} \right) \) is adopted to provide an adequate level of smoothness and continuity as:

$$ {\ddot{{\rm u}}}\left( {{\rm t}} \right) = \mathop \sum \limits_{{{\rm n} = 0}}^{{\rm N}} {{\rm a}}_{\rm n} {{\rm t}}^{{\rm n}} $$
(3)

where an are the polynomial coefficients and t is the operation time. The constant coefficients are determined by a GA to satisfy the boundary conditions [Eq. (1)] and system constraints. The system constrains, given by Eq. (2), are applied in terms of maximum input acceleration and maximum swing angle as:

$$ \left| {{\ddot{{\rm u}}}\left( {{\rm t}} \right)} \right| \le {{\rm a}}_{ \hbox{max} } ,\quad \left| {\uptheta\left( {{\rm t}} \right)} \right| \le\uptheta_{ \hbox{max} } $$
(4)

where \( \uptheta_{ \hbox{max} } \) and \( {{\rm a}}_{ \hbox{max} } \) are the maximum swing angle and maximum jib acceleration, respectively. The equation of motion of the overhead crane system is derived using Lagrange’s equation as:

$$ {{\rm l}}\left( {{\rm t}} \right){\ddot{\theta }} + 2{{\rm r}}{\dot{\theta }} + {{\rm g}}\sin\uptheta = {\ddot{{\rm u}}}\left( {{\rm t}} \right) \cos\uptheta $$
(5)

where \( {{\rm l}}\left( {{\rm t}} \right) \) is the cable length, \( {{\rm r}} \) is the constant hoisting speed, and \( {{\rm g}} \) is the gravitational acceleration. Equation (5) is the general form of the system equation of motion. Assuming the oscillations to be small, the equation of motion can be linearized as:

$$ \left( {{{\rm l}}_{{\rm i}} + {{\rm rt}}} \right){\ddot{\theta }} + 2{{\rm r}}{\dot{\theta }} + {{\rm g}}\uptheta = {\ddot{{\rm u}}}\left( {{\rm t}} \right) $$
(6)

where li is the initial length of the hoisting cable. Equation (6) describes the lowering stage of the maneuver once a negative \( {{\rm r}} \) is fed into the equation. The equation of motion is solved in two different forms depending on the variability of the cable length. These two scenarios are elaborated in the following.

2.1 Case 1: constant cable length

The first scenario considers a constant cable length throughout the entire maneuver of transferring the payload. Therefore, \( {{\rm r }} = 0 \) and the hoisting and lowering intervals, become acceleration and deceleration periods without any change in cable length. Substituting the acceleration term in Eq. (6) with Eq. (3), the equation of motion is reduced to:

$$ {{\rm l}}{\ddot{\theta }} + {{\rm g}}\uptheta = \mathop \sum \limits_{{{{\rm n}} = 0}}^{{\rm N}} {{\rm a}}_{{\rm n}} {{\rm t}}^{{\rm n}} $$
(7)

A GA optimization technique is implemented to acquire the unknown coefficients that satisfy the system conditions given by Eqs. (1) and (2). The three conditions represented by these equations require three coefficients of the input function to be found. The remaining \( \left( {{{\rm N}} - 3} \right) \) coefficients are independent of the system conditions, but optimal values are assigned to these coefficients in order to satisfy the system constraints [Eq. (4)] and minimize the maneuver time. Different number of polynomial coefficients (four, five, and six) are implemented and discussed in Sect. 4. Equation (7) is solved in an exact form given by:

$$ \begin{aligned}&\uptheta\left( {{\rm t}} \right) = {{\rm A sin}}\left( {\upomega_{{\rm n}} {{\rm t}}} \right) + {{\rm B cos}}\left( {\upomega_{{\rm n}} {{\rm t}}} \right) + \mathop \sum \limits_{{{{\rm n}} = 0}}^{{\rm N}} {{\rm b}}_{{\rm n}} {{\rm t}}^{{\rm n}} \\& {{\rm A}} = - \frac{{{{\rm b}}_{1} }}{{\upomega_{{\rm n}} }} , \quad {{\rm B}} = - {{\rm b}}_{0} \\& {{\rm b}}_{{\rm N}} = \frac{{{{\rm a}}_{{\rm N}} }}{{\upomega_{{\rm n}}^{2} }},\quad {{\rm b}}_{{{{\rm N}} - 1}} = \frac{{{{\rm a}}_{{{{\rm N}} - 1}} }}{{\upomega_{{\rm n}}^{2} }},\quad {{\rm b}}_{{\rm i}} = \frac{{{{\rm a}}_{{\rm i}} - \left( {{{\rm i}} + 1} \right)\left( {{{\rm i}} + 2} \right){{\rm b}}_{{{{\rm i}} + 2}} }}{{\upomega_{{\rm n}}^{2} }},\quad {{\rm i}} = 0, 1, \ldots , {{\rm N}} - 2 \\ \end{aligned} $$
(8)

where \( \upomega_{{\rm n}} \) is the system natural frequency. The coefficients given by Eq. (8) can be presented in a matrix form,

$$ \begin{aligned} {\mathbf{B}} = &\varvec{\varGamma}\left[ {\begin{array}{*{20}c} {a_{0} } \\ \vdots \\ {a_{N} } \\ \end{array} } \right] \\ {\varvec{\Gamma}} = & \left[ {\begin{array}{*{20}l} {\upgamma_{1,1} } \hfill & {} \hfill & \ldots \hfill & {} \hfill & {\upgamma_{{1,{{\rm N}}}} } \hfill \\ \vdots \hfill & {} \hfill & {} \hfill & {} \hfill & \vdots \hfill \\ {\upgamma_{{{{\rm N}} - 2,1}} } \hfill & {} \hfill & \ldots \hfill & {} \hfill & {\upgamma_{{{{\rm N}} - 2,{{\rm N}}}} } \hfill \\ 0 \hfill & \ldots \hfill & 0 \hfill & {1/\upomega_{{\rm n}}^{2} } \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & \ldots \hfill & 0 \hfill & {1/\upomega_{{\rm n}}^{2} } \hfill \\ \end{array} } \right] \\\upgamma_{{{{\rm p}},{{\rm q}}}} = & \left\{ {\begin{array}{*{20}l} { - \frac{{\left( {{{\rm p}} + 1} \right)\left( {{{\rm p}} + 2} \right)\upgamma_{{{{\rm p}} + 2,{{\rm q}}}} }}{{\upomega_{{\rm n}}^{2} }},} \hfill & {{{\rm p}} > q} \hfill \\ {1/\upomega_{{\rm n}}^{2} ,} \hfill & {{{\rm p}} = {{\rm q}}} \hfill \\ {0,} \hfill & {{{\rm p}} < q} \hfill \\ \end{array} } \right. \\ \end{aligned} $$
(9)

Applying system conditions [Eqs. (1) and (2)] to [Eq. (8)] yields the following system of equations:

$$ \begin{aligned} &\uptheta\left( {{{\rm t}}_{{\rm h}} } \right) = {{\rm A sin}}\left( {\upomega_{{\rm n}} {{\rm t}}_{{\rm h}} } \right) + {{\rm B cos}}\left( {\upomega_{{\rm n}} {{\rm t}}_{{\rm h}} } \right) + \mathop \sum \limits_{{{{\rm n}} = 0}}^{{\rm N}} {{\rm b}}_{{\rm n}} {{\rm t}}_{{\rm h}}^{{\rm n}} \\ & {\dot{\theta }}\left( {{{\rm t}}_{{\rm h}} } \right) = {{\rm A}}\upomega_{{\rm n}} {{\rm cos}}\left( {\upomega_{{\rm n}} {{\rm t}}_{{\rm h}} } \right) - {{\rm B}}\upomega_{{\rm n}} {{\rm sin}}\left( {\upomega_{{\rm n}} {{\rm t}}_{{\rm h}} } \right) + \mathop \sum \limits_{{{{\rm n}} = 1}}^{{\rm N}} {{\rm nb}}_{{\rm n}} {{\rm t}}_{{\rm h}}^{{{{\rm n}} - 1}} \\ & \mathop \sum \limits_{{{{\rm n}} = 0}}^{{\rm N}} \frac{{{{\rm a}}_{{\rm n}} }}{{{{\rm n}} + 1}} {{\rm t}}_{{\rm h}}^{{{{\rm n}} + 1}} = {{\rm v}}_{{\rm f}} \\ \end{aligned} $$
(10)

Equation (10) can be re-written in a matrix form as follows:

$$ \begin{aligned} & {\varvec{\Omega}}\left[ {\begin{array}{*{20}c} {{{\rm a}}_{1} } & \ldots & {{{\rm a}}_{{\rm N}} } \\ \end{array} } \right]^{{\rm T}} = {\mathbf{M}}_{3} \\ & {\varvec{\Omega}} = \left[ {\begin{array}{*{20}c} {\varOmega_{1} } \\ {\varOmega_{2} } \\ \end{array} } \right] \\ & {\varvec{\Omega}}_{1} = \left[ {\begin{array}{*{20}l} {1 - \cos \left( {\upomega_{{\rm n}} {{\rm t}}_{{\rm h}} } \right)} \hfill & {{{\rm t}}_{{\rm h}} - \frac{1}{{\upomega_{{\rm n}} }}\sin \left( {\upomega_{{\rm n}} {{\rm t}}_{{\rm h}} } \right)} \hfill & {{{\rm t}}_{{\rm h}}^{2} } \hfill & \ldots \hfill & {{{\rm t}}_{{\rm h}}^{{\rm N}} } \hfill \\ {\upomega_{{\rm n}} {{\rm sin}}\left( {\upomega_{{\rm n}} {{\rm t}}_{{\rm h}} } \right)} \hfill & {1 - {{\rm cos}}\left( {\upomega_{{\rm n}} {{\rm t}}_{{\rm h}} } \right)} \hfill & {2{{\rm t}}_{{\rm h}} } \hfill & \ldots \hfill & {{{\rm Nt}}_{{\rm h}}^{{{{\rm N}} - 1}} } \hfill \\ \end{array} } \right]\Gamma \\ & {\varvec{\Omega}}_{2} = \left[ {\begin{array}{*{20}c} {{{\rm t}}_{{\rm h}} } & {\frac{1}{2}{{\rm t}}_{{\rm h}}^{2} } & {\frac{1}{3}{{\rm t}}_{{\rm h}}^{3} } & \ldots & {\frac{1}{{{{\rm N}} + 1}}{{\rm t}}_{{\rm h}}^{{{{\rm N}} + 1}} } \\ \end{array} } \right] \\ & {\mathbf{M}}_{3} = \left[ {\begin{array}{*{20}c} 0 & 0 & {{{\rm v}}_{{\rm f}} } \\ \end{array} } \right]^{{\rm T}} \\ \end{aligned} $$
(11)

Equations (11) will be rewritten as:

$$ \begin{aligned} & {\mathbf{M}}_{1} {\hat{\mathbf{a}}} + {\mathbf{M}}_{2} {\bar{\mathbf{a}}} = {\mathbf{M}}_{3} \\ & {\mathbf{M}}_{1} = {\varvec{\Omega}}_{{{\mathbf{p}},{\mathbf{q}}}} ,\quad {{\rm p}} = 1,2,3,\quad {{\rm q}} = 1,2,3 \\ & {\mathbf{M}}_{2} = {\varvec{\Omega}}_{{{\mathbf{p}},{\mathbf{q}}}} ,\quad {{\rm p}} = 1,2,3,\quad {{\rm q}} = 4,5, \ldots , {{\rm N}} + 1 \\ & {\hat{\mathbf{a}}} = \left[ {\begin{array}{*{20}c} {{{\rm a}}_{0} } & {{{\rm a}}_{1} } & {{{\rm a}}_{2} } \\ \end{array} } \right]^{{\rm T}} \\ & {\bar{\mathbf{a}}} = \left[ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {{{\rm a}}_{3} } & {{{\rm a}}_{4} } \\ \end{array} } & {\begin{array}{*{20}c} \ldots & {{{\rm a}}_{{\rm N}} } \\ \end{array} } \\ \end{array} } \right]^{{\rm T}} \\ \end{aligned} $$
(12)

where \( {\hat{\mathbf{a}}} \) is the dependent coefficients vector, and \( {\bar{\mathbf{a}}} \) is the independent coefficients vector. Therefore, the dependent coefficients are found as:

$$ {\hat{\mathbf{a}}} = {\mathbf{M}}_{1}^{ - 1} \left( {{\mathbf{M}}_{3} - {\mathbf{M}}_{2} {\bar{\mathbf{a}}}} \right) $$
(13)

The independent coefficients vector \( \left( {{\bar{\mathbf{a}}}} \right) \) is determined by applying a GA such that the system constraints are attained.

2.2 Case 2: variable cable length

This case considers variability in the cable length during payload hoisting and lowering. Changing the cable length adds and removes damping from the system in lowering and raising movements, respectively. An exact solution cannot be found for this case due to the nonlinearity in the equation of motion [Eq. (6)]. Since the system final conditions given by Eq. (1) cannot by explicitly achieved, a tolerance must be implemented in the solver. These conditions will be imposed in the GA process along with other constraints from Eq. (4). However, the system condition given by Eq. (2) can be used to introduce one dependent coefficient as follows:

$$ {{\rm a}}_{0} = \frac{1}{{{{\rm t}}_{{\rm h}} }}\left( {{{\rm v}}_{{\rm f}} - \mathop \sum \limits_{{{{\rm n}} = 1}}^{{\rm N}} \frac{{{{\rm a}}_{{\rm n}} }}{{{{\rm n}} + 1}} {{\rm t}}_{{\rm h}}^{{{{\rm n}} + 1}} } \right) $$
(14)

Thus, the GA technique will consider \( N - 1 \) independent coefficients to satisfy system conditions and constraints.

3 Optimization method: genetic algorithm

A genetic algorithm is employed to find an optimal set of input polynomial coefficients. The GA process includes initialization, selection, crossover, mutation, elitism, and fitness evaluation. A population of 100 chromosomes is selected. The number of alleles assigned to each chromosome depends on the number of independent coefficients in the corresponding case. Although, a maximum of 10,000 generations is allowed, the fitness function usually takes fewer generations to reach the targeted plateau.

Ranking method is implemented in the GA selection stage. Two different crossover operators are used with this method: one-point crossover and blending. In one-point crossover approach, one random position is selected to cut the chromosomes. The first part of the first parent is then hooked up to the second part of the second parent to generate the first offspring. The same procedure is done in reverse order to create the second offspring. In blending method, a random percentage is to produce the first and second generations as follows:

$$ \begin{aligned} {{\rm OS}}_{1} = {{\rm B}} \times {{\rm P}}_{1} + \left( {1 - {{\rm B}}} \right) \times {{\rm P}}_{2} \hfill \\ {{\rm OS}}_{2} = \left( {1 - {{\rm B}}} \right) \times {{\rm P}}_{1} + {{\rm B}} \times {{\rm P}}_{2} \hfill \\ \end{aligned} $$
(15)

where \( {{\rm OS}}_{{\rm i}} \), \( {{\rm P}}_{{\rm i}} ,\;{{\rm and}}\;{{\rm B }} \) represent the ith offspring, the ith parent, and the blending percentage, respectively.

Mutation is performed by replacing an allele with a random number in the range of the expected solution. Mutation percentage does not exceed 1%, while the crossover percentage is 90% due to the nature of the GA procedure.

Elitism is exercised in the GA process to assure that the best chromosome (i.e. lowest fitness value) is transferred to the next generation without any modification. The elite chromosome does not bypass any crossover or mutation, but a copy of the elite is reserved for the next generation.

The defined fitness function (\( {{\rm F}} \)) consists of three parts: the maximum jib acceleration (\( {{\rm f}}_{1} \)), the maximum payload swing angle (\( {{\rm f}}_{2} \)), and the final vibration amplitude (\( {{\rm f}}_{3} \)). Each component is given a different weight \( \left( {{\rm w}} \right) \) as:

$$ {{\rm F}} = \sum {{\rm w}}_{{\rm i}} {{\rm f}}_{{\rm i}} $$
(16)

where:

$$ {{\rm f}}_{1} = \left| {{\ddot{{\rm u}}}_{ \hbox{max} } } \right|,\quad {{\rm f}}_{2} = \left| {\uptheta_{ \hbox{max} } } \right|,\quad {{\rm and}}\quad {{\rm f}}_{3} = \sqrt {\uptheta_{{\rm f}}^{2} + \frac{{{\dot{\theta }}_{{\rm f}}^{2} }}{{{{\rm w}}_{{\rm n}}^{2} }}} . $$
(17)

4 Numerical results and discussions

To evaluate the functionality of proposed optimization strategy, two test cases are studied and presented in the following. The first case is the crane model with a constant cable length with different input functions. The other case is the model with a variable hoisting cable length, which is also used for sensitivity and convergence analysis. The crane has a maximum jib speed (\( {{\rm v}}_{{\rm f}} \)) of 0.3 m/s and a maximum acceleration (\( {{\rm a}}_{ \hbox{max} } \)) of 0.9 m/s2. The payload angle should not exceed \( 3 \)° during the maneuvers (\( \uptheta_{ \hbox{max} } = 3 \)°). For the variable cable length case, since the system final conditions given by Eq. (1) cannot by explicitly achieved, a solution tolerance of 0.1° is accepted for the final vibration magnitude. The polynomial coefficients of the proposed input functions for the constant, variable-hoisting and variable-lowering cases are listed in Tables 1, 2, and 3, respectively. Each table includes the four, five and six coefficient cases, with the corresponding final time (\( {{\rm t}}_{{\rm f}} \)).

Table 1 Input polynomial coefficients for the constant cable length case
Full size table
Table 2 Input polynomial coefficients for the variable cable length (hoisting motion)
Full size table
Table 3 Input polynomial coefficients for variable cable length (lowering motion)
Full size table

4.1 Case 1: constant hoisting cable length

Polynomial functions with four, five, and six constants are studied for a constant cable length case to reach an optimal number of coefficients. The payload angle and jib acceleration trajectories are shown in Fig. 2 for these three scenarios. The plots indicate noticeable differences between the outputs of the functions with four and five polynomial coefficients. However, the differences are minimal between the five and six coefficients cases, suggesting that a polynomial function with five constants is sufficient.

Fig. 2
figure 2

Payload angle and jib acceleration for a constant cable length case with four, five, and six coefficients

Full size image

The jib velocity reaches the desired velocity in all three cases, as shown in Fig. 3. Implementing the polynomial functions with five and six coefficients, however, results in faster responses.

Fig. 3
figure 3

Jib velocity for a constant cable length case with four, five, and six coefficients

Full size image

The payload angular motion and jib acceleration prediction of the input shaping controller is compared with the uncontrolled motion in Figs. 4 and 5. Time-optimal rigid body (TORB) illustrates the uncontrolled motion, while the other three trajectories represent different number of polynomial coefficients used in the controller. Payload reaches the final position in 2 s using TORB command, compared to 2.6 s using the proposed input shaping technique. However, the vibration amplitude of the motion induced by TORB is considerably larger, which makes the controlled motion more feasible and preferable.

Fig. 4
figure 4

A comparison between controlled constant-cable-length payload motion (1. four, 2. five, and 3. six coefficients) and TORB

Full size image
Fig. 5
figure 5

A comparison between controlled constant-cable-length jib acceleration (1. four, 2. five, and 3. six coefficients) and TORB acceleration output

Full size image

Figure 6 shows the effect of changing the maximum allowable payload swing angle on the maximum jib acceleration and maneuver time for the constant cable length case. Increasing the allowable payload angle is equivalent to decreasing the system constraints, which leads to a shorter maneuver time. On the other hand, allowing the system to have a larger payload angle leads to higher acceleration values.

Fig. 6
figure 6

The effect of changing the maximum allowable payload swing angle on the maximum jib acceleration and maneuver time for the constant-cable length model

Full size image

4.2 Case 1: variable hoisting cable length

Figure 7 shows the jib acceleration and payload angle trajectories of a variable cable length model for three different cases according to the number of polynomial coefficients (four, five, and six). As discussed earlier, the cable length varies throughout the maneuver to reach specific end conditions. Raising and lowering the payload tune the jib acceleration profile so that all conditions and constraints are met.

Fig. 7
figure 7

Payload angle and jib acceleration trajectories are compared for a variable-cable-length case with four, five, and six coefficients

Full size image

As depicted in Fig. 8, although jib velocity changes throughout the maneuver, it always reaches 0.3 m/s in cruising section. The more number of coefficients used in the polynomial acceleration function, the faster the jib reaches its required cruise velocity.

Fig. 8
figure 8

Jib velocity for a variable-cable-length case with four, five, and six coefficients

Full size image

Figures 9 and 10 show how the controller and TORB commands affect the payload angle and jib acceleration, respectively. Similar to the constant cable length case, the time it takes for the jib to reach the final position (0.5 m) using TORB is shorter compared to the controlled input. However, the vibration amplitude of the controlled payload motion is considerably smaller regardless of the number of polynomial coefficients. The controlled inputs satisfy all system constraints and produce feasible solutions.

Fig. 9
figure 9

A comparison between controlled variable-cable-length payload motion (1. four, 2. five, and 3. six independent coefficients) and TORB

Full size image
Fig. 10
figure 10

A comparison between controlled variable cable length jib acceleration (1. four, 2. five, and 3. six independent coefficients) and TORB

Full size image

4.3 System sensitivity and convergence analysis

Figures 11 and 12 show how sensitive the final vibration amplitude is to the initial cable length for both the constant and variable cable length, respectively. The plots suggest that sensitivity is not significantly affected by changing the number of coefficients of the input function. As expected, the minimum vibration amplitudes are observed near the original length, which is represented by the length ratio of 1.

Fig. 11
figure 11

Sensitivity study of changing cable length on the final vibration amplitude for the constant cable length case

Full size image
Fig. 12
figure 12

Sensitivity study of changing cable length on the final vibration amplitude for the variable cable length case

Full size image

For a constant cable length, GA is applied to optimize input parameters and reduce the sensitivity of the output to the cable length, as shown in Fig. 13. The fitness function is modified to include the vibration amplitude for a range of cable lengths. In this case, it is set to be 0.8 to 1.2 of the initial cable length. The added part to the fitness function is as follows:

$$ {{\rm f}} = \sum {{\rm A}}_{{\rm f}} \left( {{\rm L}} \right) $$
(18)

where \( {{\rm A}}_{{\rm f}} \left( {{\rm L}} \right) \) is the vibration amplitude for different cable length in the specified range. As evident from Fig. 13, the proposed optimization strategy is capable of optimizing the input parameters in order to reduce the system sensitivity to small changes in cable length. The limitation factor, however, is the final time, which increases as the system sensitivity drops.

Fig. 13
figure 13

The effect of optimizing input parameters to reduce sensitivity of the vibration amplitude to the cable length for different maneuver times

Full size image

Elite fitness is plotted in Fig. 14 as a function of generations to show the convergence progress in reaching the optimal solution. The convergence starts at a fast rate due to the large range of initial set, then it slows down as it gets closer to the optimal solution.

Fig. 14
figure 14

The convergence progress of the elite fitness as it reaches the optimal solution

Full size image

5 Conclusions

A robust input shaping control method was introduced to dissipate the payload oscillations in point-to-point overhead crane maneuvers. The implemented genetic algorithms procedure was demonstrated to be capable of optimizing and tuning the jib input acceleration in order to satisfy the system conditions and constraints. The controlled payload motion was compared against the uncontrolled motion for a number of different cases and conditions. The introduced input shaper limits the payload sway motion within a specific range, which is critical in handling sensitive loads. In compared with previous techniques, the new input control method provides a faster system response as it is driven by a continuous input function. Also, employing a GA optimization strategy reduced the system sensitivity to the variations in cable length and improved the handling maneuvers with significant robustness.