Skip to main content

Advertisement

SpringerLink
Log in

Adaptive fuzzy exponential terminal sliding mode controller design for nonlinear trajectory tracking control of autonomous underwater vehicle

  • Published:
International Journal of Dynamics and Control Aims and scope Submit manuscript

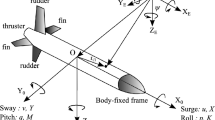
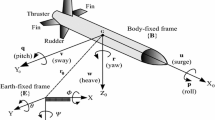
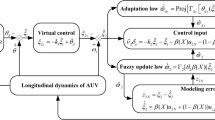
Abstract

This paper addresses an adaptive fuzzy exponential terminal sliding mode trajectory tracking control design for autonomous underwater vehicle (AUV) using time delay estimation. The proposed control scheme assures quick convergence due to a nonlinear expression in to an integral augmented sliding surface results in nonlinear sliding mode termed as integral-fast terminal sliding mode control (IFTSMC). Furthermore, control law requires no prior knowledge about highly nonlinear underwater vehicle model due to the time delay estimation method. Meanwhile, fuzzy logic system incorporated as adaptation mechanism afford for varying switching function and adaptive exponential reaching law utilized for faster reaching time in path tracking control performance. Finally, the effectiveness and robustness of the proposed control strategy are demonstrated through numerical simulations with Cyclops AUV in presence of parameter perturbations and unidentified disturbances like ocean current, wave and measurement noise.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10

Similar content being viewed by others

References

  1. Arimoto S, Miyazaki F (1984) Stability and robustness of PID feedback control for robot manipulators of sensor capability. In: Brady M, Paul R (eds) Robot research. MIT Press, Cambridge, pp 783–799

    Google Scholar 

  2. Yoerger D, Slotine J (1985) Robust trajectory control of underwater vehicles. IEEE J Oceanic Eng 10(4):462–470

    Article  Google Scholar 

  3. Goheen KR, Jefferys ER (1990) Multivariable self-turning autopilots for autonomous underwater vehicles. IEEE J Oceanic Eng 15(3):144–151

    Article  Google Scholar 

  4. Triantafyllou MS, Grosenbaugh MA (1991) Robust control for underwater vehicle systems with time delays. IEEE J Oceanic Eng 16(1):146–151

    Article  Google Scholar 

  5. Nakamura Y, Savant S (1992) Nonlinear tracking control of autonomous underwater vehicles. In: Proceedings of IEEE international conference on robotics and automation, vol 3, pp 44–49

  6. Antonelli G, Chiaverini S, Sarkar N, West M (2001) Adaptive control of an autonomous underwater vehicle: experimental results on ODIN. IEEE Trans Control Syst Technol 9(5):756–765

    Article  Google Scholar 

  7. Silvestre C, Pascoal A, Kaminer I (2002) On the design of gain scheduled trajectory tracking controllers. Int J Robust Nonlinear Control 12:797–839

    Article  MathSciNet  Google Scholar 

  8. Pisano A, Usai E (2004) Output-feedback control of an underwater vehicle prototype by higher-order sliding modes. Automatica 40:1525–1531

    Article  MathSciNet  Google Scholar 

  9. Feng Z, Allen R (2004) Reduced order \(H^{\infty }\) control of an autonomous underwater vehicle. Control Eng Pract 13:1511–1520

    Article  Google Scholar 

  10. Yuh J (1990) A neural net controller for underwater robotic vehicles. IEEE J Oceanic Eng 15(3):161–166

    Article  Google Scholar 

  11. DeBitetto PA (1995) Fuzzy logic for depth control of unmanned undersea vehicles. IEEE J Oceanic Eng 20(3):242–248

    Article  Google Scholar 

  12. Londhe PS, Santhakumar M, Patre BM, Waghmare LM (2017) Task space control of an autonomous underwater vehicle manipulator system by robust single-input fuzzy logic control scheme. IEEE J Oceanic Eng 42(1):13–28

    Google Scholar 

  13. Moura A, Rijo R, Silva P, Crespo S (2010) A multi-objective genetic algorithm applied to autonomous underwater underwater vehicles for sewage outfall plume dispersion observations. Appl Soft Comput 10(4):1119–1126

    Article  Google Scholar 

  14. Wang JS, Lee CSG (2003) Self-adaptive recurrent neuro-fuzzy control of an autonomous underwater vehicle. IEEE Trans Robot Autom 19(2):283–295

    Article  Google Scholar 

  15. Cristi R, Papoulias FA, Healey AJ (1990) Adaptive sliding mode control of autonomous underwater vehicles in the dive plane. IEEE J Oceanic Eng 15(3):152–160

    Article  Google Scholar 

  16. Fossen TI, Sagatun S (1991) Adaptive control of nonlinear systems: a case study of underwater robotic systems. J Robotic Syst 8(3):393–412

    Article  Google Scholar 

  17. Healey AJ, Lienard D (1993) Multivariable sliding mode control for autonomous diving and steering of unmanned underwater vehicles. IEEE J Oceanic Eng 18(3):327–339

    Article  Google Scholar 

  18. Soylu S, Buckham BJ, Podhorodeski RP (2008) A chattering-free sliding-mode controller for underwater vehicles with fault tolerant infinity-norm thrust allocation. Ocean Eng 35:1647–1659

    Article  Google Scholar 

  19. Zhou HY, Liu KZ, Feng XS (2011) State feedback sliding mode control without chattering by constructing Hurwitz matrix for AUV movement. Int J Autom Comput 8(2):262–268

    Article  Google Scholar 

  20. Kim M, Joe H, Kim J, Yu SC (2015) Integral sliding mode controller for precise manoeuvring of autonomous underwater vehicle in the presence of unknown environmental disturbances. Int J Control 26(2):1–11

    MathSciNet  MATH  Google Scholar 

  21. Wang Y, Gu L, Gao M, Zhu K (2015) Multivariable output feedback adaptive terminal sliding mode control for underwater vehicles. Asian J Control 17(6):1–19

    MathSciNet  MATH  Google Scholar 

  22. Xu J, Wang M, Qiao L (2015) Dynamical sliding mode control for the trajectory tracking of underactuated unmanned underwater vehicles. Ocean Eng 105:54–63

    Article  Google Scholar 

  23. Santhakumar M, Asokan T (2010) Investigations on the hybrid tracking control of an underactuated autonomous underwater robot. Adv Robot 24:1529–1556

    Article  Google Scholar 

  24. Zhu D, Sun B (2013) The bio-inspired model based hybrid sliding-mode tracking control for unmanned underwater vehicles. Eng Appl Artif Intell 26:2260–2269

    Article  Google Scholar 

  25. Bartolini G, Pisano A (2010) Black-box position and attitude tracking for underwater vehicles by second-order sliding-mode technique. Int J Robust Nonlinear Control 20(2):1594–1609

    Article  MathSciNet  Google Scholar 

  26. Ismail ZH, Putranti VWE (2015) Second order sliding mode control scheme for an autonomous underwater vehicle with dynamic region concept. Math Probl Eng 20:1–13

    Article  MathSciNet  Google Scholar 

  27. Lee PM, Hong SW, Lim YK, Lee CM, Jeon BH, Park JW (1999) Discrete-time quasi-sliding mode control of an autonomous underwater vehicle. IEEE J Oceanic Eng 24(3):388–395

    Article  Google Scholar 

  28. Prasanth Kumar R, Dasgupta A, Kumar CS (2007) Robust trajectory control of underwater vehicles using time delay control law. Ocean Eng 34:842–849

    Article  Google Scholar 

  29. Kim J, Joe H, Yu SC, Lee JS, Kim M (2015) Time delay controller design for position control of autonomous underwater vehicle under disturbances. IEEE Trans Industr Electron 63(2):1052–1061

    Article  Google Scholar 

  30. Fossen TI (1994) Guidance and control of ocean vehicles. Wiley, New York, pp 448–451

    Google Scholar 

  31. Feng Y, Yu X, Man Z (2002) Non-singular terminal sliding mode control of rigid manipulators. Automatica 38(12):21592167

    Article  MathSciNet  Google Scholar 

  32. Chen W, Wei Y, Zeng J, Han H, Jia X (2015) Adaptive terminal sliding mode NDO-based control of underactuated AUV in vertical plane. Discret Dyn Nat Soc 21:1–9

    Google Scholar 

  33. Elmokadem T, Zribi M, Toumi KY (2015) Trajectory tracking sliding mode control of underactuated AUVs. Nonlinear Dyn 24:22–35

    MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Instrumentation Engineering, Government College of Engineering, Jalgaon, 425001, India

    G. V. Lakhekar

  2. Department of Instrumentation Engineering, Shri Guru Gobind Singhji Institute of Engineering and Technology, Nanded, 431606, India

    L. M. Waghmare

Authors
  1. G. V. Lakhekar
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. L. M. Waghmare
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to G. V. Lakhekar.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Lakhekar, G.V., Waghmare, L.M. Adaptive fuzzy exponential terminal sliding mode controller design for nonlinear trajectory tracking control of autonomous underwater vehicle. Int. J. Dynam. Control 6, 1690–1705 (2018). https://doi.org/10.1007/s40435-017-0387-6

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s40435-017-0387-6

Keywords

Search

Navigation