Skip to main content
SpringerLink
Log in

Free and forced vibration analysis of 3D graphene foam truncated conical microshells

  • Technical Paper
  • Published:
Journal of the Brazilian Society of Mechanical Sciences and Engineering Aims and scope Submit manuscript

Abstract

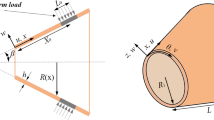
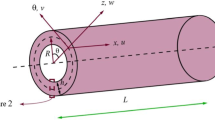
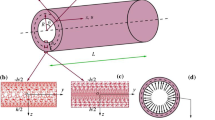
This paper analyzes the free and forced vibrations of three-dimensional graphene foam (3D-GrF) truncated conical microshells. Different distributions of the 3D-GrF are considered. In accordance with Love’s thin shell theory and the modified couple stress theory, governing equations which consider the size effect are established by the Hamilton’s principle. Then, vibration characteristics of 3D-GrF truncated conical microshells are studied through the Galerkin’s method. A series of results show that the apex angle, the 3D-GrF distribution, the foam coefficient, the circumferential wave number and the material length scale parameter play important roles on vibration characteristics of the conical microshells.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8

Similar content being viewed by others

References

  1. Wu Y, Yi N, Huang L, Zhang T, Fang S, Chang H, Li N, Oh J, Lee JA, Kozlov M (2015) Three-dimensionally bonded spongy graphene material with super compressive elasticity and near-zero Poisson’s ratio. Nat Commun 6:6141

    Article  Google Scholar 

  2. Qin Z, Jung GS, Kang MJ, Buehler MJ (2017) The mechanics and design of a lightweight three-dimensional graphene assembly. Sci Adv 3(1):e1601536

    Article  Google Scholar 

  3. Yavari F, Chen Z, Thomas AV, Ren W, Cheng H-M, Koratkar N (2011) High sensitivity gas detection using a macroscopic three-dimensional graphene foam network. Sci Rep 1:166

    Article  Google Scholar 

  4. Xu X, Zhang Q, Yu Y, Chen W, Hu H, Li H (2016) Naturally dried graphene aerogels with superelasticity and tunable Poisson’s ratio. Adv Mater 28(41):9223–9230

    Article  Google Scholar 

  5. Qiu L, Huang B, He Z, Wang Y, Tian Z, Liu JZ, Wang K, Song J, Gengenbach TR, Li D (2017) Extremely low density and super-compressible graphene cellular materials. Adv Mater 29(36):1701553

    Article  Google Scholar 

  6. Sha J, Li Y, Villegas Salvatierra R, Wang T, Dong P, Ji Y, Lee S-K, Zhang C, Zhang J, Smith RH (2017) Three-dimensional printed graphene foams. ACS Nano 11(7):6860–6867

    Article  Google Scholar 

  7. Lv L, Zhang P, Cheng H, Zhao Y, Zhang Z, Shi G, Qu L (2016) Solution-processed ultraelastic and strong air-bubbled graphene foams. Small 12(24):3229–3234

    Article  Google Scholar 

  8. Strek W, Tomala R, Lukaszewicz M, Cichy B, Gerasymchuk Y, Gluchowski P, Marciniak L, Bednarkiewicz A, Hreniak D (2017) Laser induced white lighting of graphene foam. Sci Rep 7:41281

    Article  Google Scholar 

  9. Ghazi A, Berke P, Kamel KEM, Sonon B, Tiago C, Massart T (2019) Multiscale computational modelling of closed cell metallic foams with detailed microstructural morphological control. Int J Eng Sci 143:92–114

    Article  Google Scholar 

  10. Ghazi A, Tiago C, Sonon B, Berke P, Massart T (2020) Efficient computational modelling of closed cell metallic foams using a morphologically controlled shell geometry. Int J Mech Sci 168:105298

    Article  Google Scholar 

  11. Redenbach C, Shklyar I, Andrä H (2012) Laguerre tessellations for elastic stiffness simulations of closed foams with strongly varying cell sizes. Int J Eng Sci 50(1):70–78

    Article  Google Scholar 

  12. Shi X, Liu S, Nie H, Lu G, Li Y (2018) Study of cell irregularity effects on the compression of closed-cell foams. Int J Mech Sci 135:215–225

    Article  Google Scholar 

  13. Wang C, Zhang C, Chen S (2016) The microscopic deformation mechanism of 3D graphene foam materials under uniaxial compression. Carbon 109:666–672

    Article  Google Scholar 

  14. Wang YQ, Zhang ZY (2019) Bending and buckling of three-dimensional graphene foam plates. Results Phys 13:102136

    Article  Google Scholar 

  15. Stölken JS, Evans A (1998) A microbend test method for measuring the plasticity length scale. Acta Mater 46(14):5109–5115

    Article  Google Scholar 

  16. Liu D, He Y, Dunstan D, Zhang B, Gan Z, Hu P, Ding H (2013) Anomalous plasticity in the cyclic torsion of micron scale metallic wires. Phys Rev Lett 110(24):244301

    Article  Google Scholar 

  17. Liu D, He Y, Tang X, Ding H, Hu P, Cao P (2012) Size effects in the torsion of microscale copper wires: experiment and analysis. Scr Mater 66(6):406–409

    Article  Google Scholar 

  18. Şimşek M, Reddy J (2013) Bending and vibration of functionally graded microbeams using a new higher order beam theory and the modified couple stress theory. Int J Eng Sci 64:37–53

    Article  MathSciNet  Google Scholar 

  19. Yang F, Chong A, Lam DCC, Tong P (2002) Couple stress based strain gradient theory for elasticity. Int J Solids Struct 39(10):2731–2743

    Article  Google Scholar 

  20. Lou J, He L, Wu H, Du J (2016) Pre-buckling and buckling analyses of functionally graded microshells under axial and radial loads based on the modified couple stress theory. Compos Struct 142:226–237

    Article  Google Scholar 

  21. Ke L-L, Wang Y-S, Yang J, Kitipornchai S (2012) Free vibration of size-dependent Mindlin microplates based on the modified couple stress theory. J Sound Vib 331(1):94–106

    Article  Google Scholar 

  22. Wang YQ, Liu YF, Zu JW (2019) On scale-dependent vibration of circular cylindrical nanoporous metal foam shells. Microsyst Technol 25(7):2661–2674

    Article  Google Scholar 

  23. Sexton LT, Horne LP, Martin CR (2007) Developing synthetic conical nanopores for biosensing applications. Mol BioSyst 3(10):667–685

    Article  Google Scholar 

  24. Lan W-J, Holden DA, Liu J, White HS (2011) Pressure-driven nanoparticle transport across glass membranes containing a conical-shaped nanopore. J Phys Chem C 115(38):18445–18452

    Article  Google Scholar 

  25. Yan J, Zhang L, Liew K, He L (2014) A higher-order gradient theory for modeling of the vibration behavior of single-wall carbon nanocones. Appl Math Model 38(11–12):2946–2960

    Article  MathSciNet  Google Scholar 

  26. Ansari R, Rouhi H, Rad AN (2014) Vibrational analysis of carbon nanocones under different boundary conditions: an analytical approach. Mech Res Commun 56:130–135

    Article  Google Scholar 

  27. Dehkordi SF, Beni YT (2017) Electro-mechanical free vibration of single-walled piezoelectric/flexoelectric nano cones using consistent couple stress theory. Int J Mech Sci 128:125–139

    Article  Google Scholar 

  28. Mohammadi K, Mahinzare M, Rajabpour A, Ghadiri M (2017) Comparison of modeling a conical nanotube resting on the Winkler elastic foundation based on the modified couple stress theory and molecular dynamics simulation. Eur Phys J Plus 132(3):115

    Article  Google Scholar 

  29. Zienkiewicz OC, Taylor RL, Zhu JZ (2005) The finite element method: its basis and fundamentals. Elsevier, Amsterdam

    MATH  Google Scholar 

  30. Park S, Gao X-L (2008) Variational formulation of a modified couple stress theory and its application to a simple shear problem. Zeitschrift für angewandte Mathematik und Physik 59(5):904–917

    Article  MathSciNet  Google Scholar 

  31. Magnucki K, Stasiewicz P (2004) Elastic buckling of a porous beam. J Theor Appl Mech 42(4):859–868

    MATH  Google Scholar 

  32. Magnucka-Blandzi E (2008) Axi-symmetrical deflection and buckling of circular porous-cellular plate. Thin Walled Struct 46(3):333–337

    Article  Google Scholar 

  33. Jabbari M, Mojahedin A, Khorshidvand A, Eslami M (2014) Buckling analysis of a functionally graded thin circular plate made of saturated porous materials. J Eng Mech 140(2):287–295

    Article  Google Scholar 

  34. Nieto A, Boesl B, Agarwal A (2015) Multi-scale intrinsic deformation mechanisms of 3D graphene foam. Carbon 85:299–308

    Article  Google Scholar 

  35. Leissa AW (1973) Vibration of shells. Technical report NASA SP-288, National Aeronautics and Space Administration

  36. Song Z, Zhang L, Liew K (2016) Dynamic responses of CNT reinforced composite plates subjected to impact loading. Compos B Eng 99:154–161

    Article  Google Scholar 

  37. Wang YQ, Zu JW (2017) Vibration behaviors of functionally graded rectangular plates with porosities and moving in thermal environment. Aerosp Sci Technol 69:550–562

    Article  Google Scholar 

  38. Irie T, Yamada G, Tanaka K (1984) Natural frequencies of truncated conical shells. J Sound Vib 92(3):447–453

    Article  Google Scholar 

  39. Lam K, Hua L (1999) Influence of boundary conditions on the frequency characteristics of a rotating truncated circular conical shell. J Sound Vib 223(2):171–195

    Article  Google Scholar 

  40. Tadi Beni Y, Mehralian F (2016) The effect of small scale on the free vibration of functionally graded truncated conical shells. J Mech Mater Struct 11(2):91–112

    Article  MathSciNet  Google Scholar 

Download references

Acknowledgements

This research was supported by the National Natural Science Foundation of China (Grant nos. 11922205 and 11672071), LiaoNing Revitalization Talents Program (Grant no. XLYC1807026), and the Fundamental Research Funds for the Central Universities (Grant no. N2005019).

Author information

Authors and Affiliations

  1. Department of Mechanics, Northeastern University, Shenyang, 110819, China

    Yun Fei Liu, Xue Ling & Yan Qing Wang

  2. Key Laboratory of Ministry of Education on Safe Mining of Deep Metal Mines, Northeastern University, Shenyang, 110819, China

    Yan Qing Wang

Authors
  1. Yun Fei Liu
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Xue Ling
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Yan Qing Wang
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Yan Qing Wang.

Additional information

Technical Editor: José Roberto de França Arruda.

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Liu, Y.F., Ling, X. & Wang, Y.Q. Free and forced vibration analysis of 3D graphene foam truncated conical microshells. J Braz. Soc. Mech. Sci. Eng. 43, 133 (2021). https://doi.org/10.1007/s40430-021-02841-9

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s40430-021-02841-9

Keywords

Search

Navigation