Skip to main content
SpringerLink
Log in

Shear-induced particle migration in the flow of particle suspensions through a sudden plane expansion

  • Technical Paper
  • Published:
Journal of the Brazilian Society of Mechanical Sciences and Engineering Aims and scope Submit manuscript

Abstract

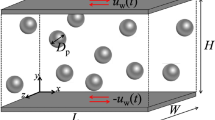
This work investigates the creeping flow of particle suspensions through an abrupt 1:4 plane expansion. The suspension is composed by non-Brownian, rigid spherical particles suspended in a viscous Newtonian liquid. The flow is described by mass and momentum conservation equations together with a convection–diffusion transport equation that accounts for shear-induced particle migration according to the diffusive flux model. The resulting set of fully coupled, nonlinear differential equations is solved with a stabilized finite element method. A detailed parametric study is presented in terms of suspension bulk concentration, particle Péclet number and ratio of diffusivity coefficients, and the numerical results show significant effects of these parameters on the particle concentration field in the flow.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8

Similar content being viewed by others

References

  1. Tadros TF (2011) Rheology of dispersions: principles and applications. John Wiley & Sons, New Jersey

    Google Scholar 

  2. Tadros TF (2012) Dispersion of powders in liquids and stabilization of suspensions. John Wiley & Sons, New Jersey

    Book  Google Scholar 

  3. Barnes HA (1980) A survey of industrial problems and academic progress. Dispersion Rheology. R.I.C. Industrial Division Report, 1981

  4. Bird RB, Armstrong RC, Hassager O (1987) Dynamics of polymeric liquids. Fluid mechanics, vol 1. John Wiley & Sons, New Jersey

    Google Scholar 

  5. Macosko CW (1994) Rheology: principles, measurements and applications. Wiley, New Jersey

    Google Scholar 

  6. Stickel JJ, Powell RL (2005) Fluid mechanics and rheology of dense suspensions. Ann Rev Fluid Mech 37:129–149

    Article  MathSciNet  MATH  Google Scholar 

  7. Bahiraei M (2016) Particle migration in nanofluids: a critical review. Int J Therm Sci 109:90–113

    Article  Google Scholar 

  8. Leighton D, Acrivos A (1987) The shear-induced migration of particles in concentrated suspensions. J Fluid Mech 181:415–439

    Article  Google Scholar 

  9. Abbott JR, Tetlow N, Graham AL, Altobelli SA, Fukushima E, Mondy LA, Stephens TS (1991) Experimental observations of particle migration in concentrated suspensions: Couette flow. J Rheol 35:773–797

    Article  Google Scholar 

  10. Altobelli SA, Givler RC (1991) Velocity and concentration measurements of suspensions by nuclear magnetic resonance imaging. J Rheol 35:721–734

    Article  Google Scholar 

  11. Graham AL, Altobelli SA (1991) NMR imaging of shear-induced diffusion and structure in concentrated suspensions. J Rheol 35:191–201

    Article  Google Scholar 

  12. Sinton SA, Chow A (1991) NMR flow imaging of fluids and solid suspensions in poiseuille flow. J Rheol 35:735–772

    Article  Google Scholar 

  13. Phillips RJ, Armstrong RC, Brown RC, Graham AL, Abbott JR (1992) A constitutive equation for concentrated suspensions that accounts for shear-induced particle migrations. Phys Fluids 4:30–40

    Article  MATH  Google Scholar 

  14. Koh CJ, Hookham P, Leal LG (1994) An experimental investigation of concentrated suspension flows in a rectangular channel. J Fluid Mech 266:1–32

    Article  Google Scholar 

  15. Phan-Thien N, Graham AL, Altobelli SA, Abbott JR, Mondy LA (1995) Hydrodynamic particle migration in a concentrated suspension undergoing flow between rotating eccentric cylinders. Ind Eng Chem Res 34:3187–3194

    Article  Google Scholar 

  16. Hampton RE, Mammoli AA, Graham AL, Tetlow N, Altobelli SA (1997) Migration of particles undergoing pressure-driven flow in a circular conduit. J Rheol 41:621–640

    Article  Google Scholar 

  17. Subia SR, Ingber MS, Mondy LA, Altobelli SA, Graham AL (1998) Modelling of concentrated suspensions using a continuum constitutive equation. J Fluid Mech 373:193–219

    Article  MATH  Google Scholar 

  18. Butler JE, Bonnecaze RT (1999) Imaging of particle shear migration with electrical impedance tomography. Phys Fluids 11:1982–1994

    Article  MATH  Google Scholar 

  19. Han M, Kim C, Kim M, Lee S (1999) Particle migration in tube flow of suspensions. J Rheol 43:1157–1174

    Article  Google Scholar 

  20. Norman JT, Nayak HV, Bonnecaze RT (2005) Migration of buoyant particles in low-Reynolds-number pressure-driven flows. J Fluid Mech 523:1–35

    Article  MATH  Google Scholar 

  21. Timberlake DM, Morris JF (2005) Particle migration and free-surface topography in inclined plane flow of a suspension. J Fluid Mech 538:309–341

    Article  MATH  Google Scholar 

  22. van Dinther AMC, Schroen CGPH, Vergeldt FJ, van der Sman RGM (2012) Suspension flow in microfluidic devices a review of experimental techniques focusing on concentration and velocity gradients. Adv Colloid Interface Sci 173:23–34

    Article  Google Scholar 

  23. Graham AL, Mammoli AA, Busch MB (1998) Effects of demixing on suspension rheometry. Rheol Acta 37:139–150

    Article  Google Scholar 

  24. Tetlow N, Graham AL, Ingber MS, Rubia SR, Mondy LA, Altobelli SA (1998) Particle migration in a Couette apparatus: experiment and modeling. J Rheol 42:307–327

    Article  Google Scholar 

  25. Chapman B (1990) Shear-induced migration phenomena in concentrated suspensions. PhD thesis, University of Notre-Dame, Notre Dame

  26. Chow AW, Sinton SW, Iwamiya JH, Stephens TS (1994) Shear-induced migration in Couette and parallel-plate viscometers: NMR imaging and stress measurements. Phys Fluids 6:2561–2576

    Article  Google Scholar 

  27. Krishnan GP, Beimfohr S, Leighton D (1996) Shear-induced radial segregation in bidisperse suspensions. J Fluid Mech 321:371–393

    Article  Google Scholar 

  28. Kim JM, Lee SG, Kim C (2008) Numerical simulations of particle migration in suspension flows: frame-invariant formulation of curvature-induced migration. J Nonnewton Fluid Mech 150:162–176

    Article  MATH  Google Scholar 

  29. Miller RM, Morris JF (2006) Normal stress-driven migration and axial development in pressure-driven flow of concentrated suspensions. J Nonnewton Fluid Mech 135:149–165

    Article  MATH  Google Scholar 

  30. Rebouças RB, Siqueira IR, de Souza Mendes PR, Carvalho MS (2016) On the pressure-driven flow of suspensions: particle migration in shear sensitive liquids. J Nonnewton Fluid Mech 234:178–187

    Article  MathSciNet  Google Scholar 

  31. Ahmed GMY, Singh A (2011) Numerical simulation of particle migration in asymmetric bifurcation channel. J Nonnewton Fluid Mech 166:42–51

    Article  MATH  Google Scholar 

  32. Yadav S, Reddy MM, Singh A (2015) Shear-induced particle migration in three-dimensional bifurcation channel. Int J Multiph Flow 76:1–12

    Article  Google Scholar 

  33. Campana DM, Silva LDV, Carvalho MS (2017) Slot coating flows of non-colloidal particle suspensions. AIChE J 63:1122–1131

    Article  Google Scholar 

  34. Siqueira IR, Carvalho MS (2017) Particle migration in planar die-swell flows. J Fluid Mech 825:49–68

    Article  MathSciNet  Google Scholar 

  35. Siqueira IR, Rebouças RB, Carvalho MS (2017) Particle migration and alignment in slot coating flows of elongated particle suspensions. AIChE J 63:3187–3198

    Article  Google Scholar 

  36. Siqueira IR, Rebouças RB, Carvalho MS (2017) Migration and alignment in the flow of elongated particle suspensions through a converging–diverging channel. J Nonnewton Fluid Mech 243:56–63

    Article  MathSciNet  Google Scholar 

  37. Rao RR, Mondy LA, Baer TA, Altobelli SA, Stephens TS (2002) NMR measurements and simulations of particle migration in non-Newtonian fluids. Chem Eng Commun 189(1):1–22

    Article  Google Scholar 

  38. Lavrenteva OM, Nir A (2016) Shear-induced particles migration in a Bingham fluid. J Nonnewton Fluid Mech 238:80–91

    Article  MathSciNet  Google Scholar 

  39. Manica R, de Bortoli AL (2004) Simulation of sudden expansion flows for power-law fluids. J Nonnewton Fluid Mech 121:35–40

    Article  MATH  Google Scholar 

  40. Ternik P, Marn J, Zunič Z (2006) Non-Newtonian fluid flow through a planar symmetric expansion: shear-thickening fluids. J Nonnewton Fluid Mech 135:136–148

    Article  MATH  Google Scholar 

  41. Ternik P (2009) Planar sudden symmetric expansion flows and bifurcation phenomena of purely viscous shear-thinning fluids. J Nonnewton Fluid Mech 157:15–25

    Article  MATH  Google Scholar 

  42. Dhinakaran S, Oliveira MSN, Pinho FT, Alves MA (2013) Steady flow of power-law fluids in a 1:3 planar sudden expansion. J Nonnewton Fluid Mech 198:48–58

    Article  Google Scholar 

  43. Missirlis K, Assimacopoulos D, Mitsoulis E (1998) A finite volume approach in the simulation of viscoelastic expansion flows. J Nonnewton Fluid Mech 78:91–118

    Article  MATH  Google Scholar 

  44. Oliveira PJ (2003) Asymmetric flows of viscoelastic fluids in symmetric planar expansion geometries. J Nonnewton Fluid Mech 114:33–63

    Article  MATH  Google Scholar 

  45. Rocha GN, Poole RJ, Oliveira PJ (2007) Bifurcation phenomena in viscoelastic flows through a symmetric 1:4 expansion. J Nonnewton Fluid Mech 141:1–17

    Article  MATH  Google Scholar 

  46. Poole RJ, Alves MA, Oliveira PJ, Pinho FT (2007) Plane sudden expansion flows of viscoelastic liquids. J Nonnewton Fluid Mech 145:79–91

    Article  MATH  Google Scholar 

  47. Poole RJ, Pinho FT, Alves MA, Oliveira PJ (2009) The effect of expansion ratio for creeping expansion flows of UCM fluids. J Nonnewton Fluid Mech 163:35–44

    Article  MATH  Google Scholar 

  48. Sousa PC, Coelho PM, Oliveira MSN, Alves MA (2011) Laminar flow in three-dimensional squaren-square expansions. J Nonnewton Fluid Mech 166:1033–1048

    Article  MATH  Google Scholar 

  49. Vradis GC, Ötügen MV (1997) The axisymmetric sudden expansion flow of a non-Newtonian viscoplastic fluid. J Fluids Eng 110:193–200

    Article  Google Scholar 

  50. Jay P, Magnin A, Piau JM (2002) Viscoplastic fluid flow through a sudden axisymmetric expansion. AIChE J 47(10):2155–2166

    Article  Google Scholar 

  51. Alexandrou AN, McGilvreay TM, Burgos G (2001) Steady Herschel-Bulkley fluid flow in three-dimensional expansions. J Nonnewton Fluid Mech 100:77–96

    Article  MATH  Google Scholar 

  52. Nassar B, de Souza Mendes PR, Naccache MF (2011) Flow of elasto-viscoplastic liquids through an axisymmetric expansion–contraction. J Nonnewton Fluid Mech 166:386–394

    Article  MATH  Google Scholar 

  53. Hermany L, dos Santos DD, Frey S, Naccache MF, de Souza Mendes PR (2013) Flow of yield-stress liquids through an axisymmetric abrupt expansion–contraction. J Nonnewton Fluid Mech 201:1–9

    Article  Google Scholar 

  54. Link FB, Frey S, Thompson RL, Naccache MF, de Souza Mendes PR (2015) Plane flow of thixotropic elasto-viscoplastic materials through a 1:4 sudden expansion. J Nonnewton Fluid Mech 220:162–174

    Article  MathSciNet  Google Scholar 

  55. Leonard EF, West AC, Shapley NC, Larsen MU (2004) Dialysis without membrances: How and why? Blood Purif 22:92–100

    Article  Google Scholar 

  56. Faivre M, Abkarian M, Bickraj K, Stone HA (2006) Geometrical focusing of cells in a microfluidic device: an approach to separate blood plasma. Birheology 43:147–159

    Google Scholar 

  57. Jaggi RD, Sandoz R, Effenhauser CS (2007) Microfluidic depletion of red blood cells from whole blood in high-aspect-ratio microchannels. Microfluid Nanofluid 3:47–53

    Article  Google Scholar 

  58. Arola DF, Powell RL, McCarthy MJ, Li T-Q, Ödberg L (1998) NMR imaging of pulp suspension flowing through an abrupt pipe expansion. AIChE J 44:2597–2606

    Article  Google Scholar 

  59. Jossic L, Magnin A (2005) Structuring of gelled suspensions flowing through a sudden three-dimensional expansion. J Nonnewton Fluid Mech 127:201–212

    Article  Google Scholar 

  60. Moraczewski T, Tanga H, Shapley NC (2005) Flow of a concentrated suspension through an abrupt axisymmetric expansion measured by nuclear magnetic resonance imaging. J Rheol 49:1409–1428

    Article  Google Scholar 

  61. Moraczewski T, Shapley NC (2006) The effect of inlet conditions on concentrated suspension flows in abrupt expansions. Phys Fluids 18:123303

    Article  MATH  Google Scholar 

  62. Moraczewski T, Shapley NC (2007) Pressure drop enhancement in a concentrated suspension flowing through an abrupt axisymmetric contraction–expansion. Phys Fluids 19:103304

    Article  MATH  Google Scholar 

  63. Xi C, Shapley NC (2008) Flows of concentrated suspensions through an asymmetric bifurcation. J Rheol 52:625–647

    Article  Google Scholar 

  64. Nott PR, Brady JF (1994) Pressure-driven flow of suspensions: simulation and theory. J Fluid Mech 275:157–199

    Article  MATH  Google Scholar 

  65. Mendoza CI, Santamaría-Holek I (2009) The rheology of hard sphere suspensions at arbitrary volume fractions: an improved differential viscosity model. J Chem Phys 130:044904

    Article  Google Scholar 

  66. Einstein A (1911) Berichtigung zu meiner arbeit: Eine nene bestimmung der molekuldimension. Annalen der Physik 34:591–592

    Article  MATH  Google Scholar 

  67. Krieger IM (1972) Rheology of monodisperse latices. Adv Colloid Interface Sci 3:111–136

    Article  Google Scholar 

  68. Szady MJ, Salamon TR, Liu AW, Armstrong RC, Brown RA (1995) A new mixed finite element method for viscoelastic flows governed by differential constitutive equations. J Nonnewton Fluid Mech 59:215–243

    Article  Google Scholar 

  69. Guénette R, Fortin M (1995) A new mixed finite element method for computing viscoelastic flows. J Nonnewton Fluid Mech 60:27–52

    Article  Google Scholar 

  70. Pasquali M, Scriven LE (2002) Free surface flows of polymer solutions with models based on the conformation tensor. J Nonnewton Fluid Mech 108:363–409

    Article  MATH  Google Scholar 

  71. Duff IS, Erisman AM, Reid JK (1989) Direct method for sparse matrices. OUP Oxford, Oxford

    MATH  Google Scholar 

  72. Bolstad JH, Keller HB (1986) A multigrid continuation method for elliptic problems. J Sci Stat Comput 7:1081–1104

    Article  MathSciNet  MATH  Google Scholar 

Download references

Acknowledgements

The authors would like to acknowledge the financial support from the Brazilian Research Council (CNPq) and the Industrial Partnership for Research in Interfacial Materials & Engineering (IPRIME) of the University of Minnesota.

Author information

Authors and Affiliations

  1. Department of Chemical and Biomolecular Engineering, Rice University, Houston, TX, 77005, USA

    Ivan Rosa de Siqueira

  2. Department of Mechanical Engineering, Pontifícia Universidade Católica do Rio de Janeiro, Rio de Janeiro, RJ, 22451-900, Brazil

    Márcio Silveira da Carvalho

Authors
  1. Ivan Rosa de Siqueira
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Márcio Silveira da Carvalho
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Ivan Rosa de Siqueira.

Additional information

Technical Editor: Francisco Ricardo Cunha.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

de Siqueira, I.R., da Carvalho, M.S. Shear-induced particle migration in the flow of particle suspensions through a sudden plane expansion. J Braz. Soc. Mech. Sci. Eng. 40, 228 (2018). https://doi.org/10.1007/s40430-018-1155-z

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s40430-018-1155-z

Keywords

Search

Navigation