Skip to main content

Advertisement

SpringerLink
Log in

Reliability-based optimization design of the latch needle mechanism in double-needle warp knitting machine

  • Technical Paper
  • Published:
Journal of the Brazilian Society of Mechanical Sciences and Engineering Aims and scope Submit manuscript

Abstract

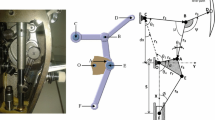
Based on the matrix method and clearance vector model, a simple, accurate, efficient and general mechanical reliability analysis method is presented to analyze the reliability of a complex linkage mechanism with structural errors and clearances. The output error variances of the latch needle mechanism in double-needle warp knitting machine are obtained based on this matrix method and verified by Monte-Carlo method. Then, an optimization design method for the latch needle mechanism is presented with the use of genetic algorithm, considering the motion requirement and output errors. The optimized latch needle mechanism can meet the double-dwell motion requirement, and has higher displacement accuracy and reliability under the same structural errors and clearance conditions. This method has practical engineering value in solving the contradiction between high precision loop-forming motion and multi-link accumulative errors, reducing cost, and providing a reference for the optimization design for loop forming mechanism in a warp knitting machine.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8

Similar content being viewed by others

References

  1. Ray SC (2012) Fundamentals and advances in knitting technology. Woodhead Publishing Ltd, Sawston

    Book  Google Scholar 

  2. Liu X, Hu XD, Chen HL (2012) An analysis on the kinematics of looping mechanism of warp knitting machine. Knitt Ind 2:3–5

    Google Scholar 

  3. Shen HP, Li M, Wang MQ et al (2015) Knitting motion analysis and mechanism design for multi-bar warp knitting machine. China Mech Eng 26:1457–1470

    Google Scholar 

  4. Huang XZ, Zhang YM (2010) Robust tolerance design for function generation mechanisms with joint clearances. Mech Mach Theory 45(9):1286–1297

    Article  MATH  Google Scholar 

  5. Wittwer JW, Chase KW, Howell LL (2004) The direct linearization method applied to position error in kinematic linkages. Mech Mach Theory 39:681–693

    Article  MathSciNet  MATH  Google Scholar 

  6. Zhang GJ, Cheng Q, Shao XY et al (2008) Accuracy analysis for planar linkage with multiple clearances at turning pairs. Chin J Mech Eng 21:36–40

    Article  Google Scholar 

  7. Kim J, Song WJ, Kang BS (2010) Stochastic approach to kinematic reliability of open-loop mechanism with dimensional tolerance. Appl Math Model 34:1225–1237

    Article  MathSciNet  MATH  Google Scholar 

  8. Huang XZ, Zhang YM (2012) Probabilistic approach to system reliability of mechanism with correlated failure models. Math Probl Eng 2012:243–253

    Google Scholar 

  9. Zhang JF, Du XP (2015) Time-dependent reliability analysis for function generation mechanisms with random joint clearances. Mech Mach Theory 92:184–199

    Article  Google Scholar 

  10. Wu JN, Yan SZ, Zuo MJ (2016) Evaluating the reliability of multi-body mechanisms: a method considering the uncertainties of dynamic performance. Reliab Eng Syst Saf 149:96–106

    Article  Google Scholar 

  11. Shi Z (1997) Synthesis of mechanical error in spatial linkages based on reliability concept. Chin J Mech Eng 32(2):255–259

    Google Scholar 

  12. Erkaya S, Uzmay İ (2009) Determining link parameters using genetic algorithm in mechanisms with joint clearance. Mech Mach Theory 44:222–234

    Article  MATH  Google Scholar 

  13. Li T, Jia QX, Chen G, Sun HX (2016) Optimization control for space manipulator motion reliability considering multi-index and multi-factor. Int J Hybrid Inf Technol 9(6):273–282

    Article  Google Scholar 

  14. Farajtabar M, Daniali HM, Varedi SM (2016) Error compensation for continuous path operation of 3-RRR planar parallel manipulator with clearance in the joints. J Sci Eng 7:20–33

    Google Scholar 

  15. Gholaminezhad I, Jamali A, Assimi H (2016) Multi-objective reliability-based robust design optimization of robot gripper mechanism with probabilistically uncertain parameters. Nat Comput Appl Forum 2016:1–12

    Google Scholar 

  16. Choi JH, Lee SJ, Choi DH (1998) Stochastic linkage modeling for mechanical error analysis of planar mechanisms. Mech Based Des Struct Mach 26:257–276

    Article  Google Scholar 

  17. Lee SJ, Gilmore BJ (1991) The determination of the probabilistic properties of velocities and accelerations in kinematic chains with uncertainty. J Mech Des 113(1):9–13

    Article  Google Scholar 

  18. Lin PD, Chen JF (1992) Accuracy analysis of planar linkages by the matrix method. Mech Mach Theory 27:507–516

    Article  Google Scholar 

  19. Huang JH, Cao QL (2015) Sinker design of the double needle bar warp knitting machine. Knitt Ind 2:18–21

    Google Scholar 

Download references

Acknowledgements

This project is supported by National Natural Science Foundation of China (51375084), Research Fund for the Doctoral Program of Higher Education of China (20130075110002) and the Fundamental Research Funds for the Central Universities (CUSF-DH-D-2017061).

Author information

Authors and Affiliations

  1. College of Mechanical Engineering, Donghua University, Shanghai, 201620, China

    Liuyuan Su, Zhuo Meng & Yize Sun

  2. Yili Technology Co. Ltd, Huafeng Group, Putian, 351146, Fujian, China

    Xiaoyi Ge

Authors
  1. Liuyuan Su
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Zhuo Meng
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Yize Sun
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Xiaoyi Ge
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Zhuo Meng.

Additional information

Technical Editor: Marcelo A. Trindade.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Su, L., Meng, Z., Sun, Y. et al. Reliability-based optimization design of the latch needle mechanism in double-needle warp knitting machine. J Braz. Soc. Mech. Sci. Eng. 40, 205 (2018). https://doi.org/10.1007/s40430-018-1134-4

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s40430-018-1134-4

Keywords

Search

Navigation