Skip to main content
SpringerLink
Log in

Flow and convective heat transfer of Casson fluid between squeezing porous disks in the presence of thermal radiation, viscous dissipation, and variable heat source/sink

  • Technical Paper
  • Published:
Journal of the Brazilian Society of Mechanical Sciences and Engineering Aims and scope Submit manuscript

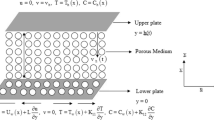
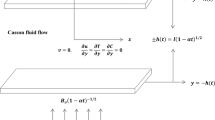
Abstract

In the present study, the combined effect of non-uniform heat source/sink, suction/injection , thermal radiation, and viscous dissipation is investigated on the unsteady squeezing flow and heat transfer of non-Newtonian Casson fluids. By means of a suitable similarity transformation, the governing equations are converted to a set of non-linear ordinary differential equations which are solved analytically applying Homotopy perturbation method. In addition, convergence of the derived solution is examined by comparing the analytical solution with a corresponding numerical solution obtained by the fourth-order Runge–Kutta method. An excellent agreement is observed between the analytical and numerical results. The influences of relevant parameters on the velocity and temperature fields, skin friction coefficient, and local Nusselt number are demonstrated in details. The results reveal that temperature is an increasing function of the heat generation parameter. Furthermore, the velocity and temperature profiles grow with increase the suction parameter.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14

Similar content being viewed by others

References

  1. Stokes JR, Telford JH (2004) Measuring the yield behaviour of structured fluids. J Nonnewton Fluid Mech 124(1–3):137–146

    Article  MATH  Google Scholar 

  2. Renardy M (2010) The mathematics of myth: yield stress behavior as a limit of non-monotone constitutive theories. J Nonnewton Fluid Mech 165(9–10):519–526

    Article  MATH  Google Scholar 

  3. Balmforth NJ, Frigaard IA, Ovarlez G (2014) Yielding to stress: recent developments in viscoplastic fluid mechanics. Annu Rev Fluid Mech 46(1):121–146

    Article  MathSciNet  MATH  Google Scholar 

  4. Coussot P, Tocquer L, Lanos C, Ovarlez G (2009) Macroscopic vs. local rheology of yield stress fluids. J Nonnewton Fluid Mech 158(1–3):85–90

    Article  Google Scholar 

  5. Paszynski M, Schaefer R (2005) The modified Fluid Particle Model for non-linear Casson fluid and its parallel distributed implementation. Comput Methods Appl Mech Eng 194:4386–4410

    Article  MATH  Google Scholar 

  6. Metivier C, Nouar C (2011) Stability of a Rayleigh–Bénard Poiseuille flow for yield stress fluids—Comparison between Bingham and regularized models. Int J Non-Linear Mech 46:1205–1212

    Article  Google Scholar 

  7. Bleyer J, Maillard M, Buhan PD, Coussot P (2015) Efficient numerical computations of yield stress fluid flows using second-order cone programming. Comput Methods Appl Mech Eng 283:599–614

    Article  MathSciNet  Google Scholar 

  8. Casson N (1959) A flow equation for pigment-oil suspensions of the printing ink type. Reprinted from Rheology of disperse systems

  9. Mukhopadhyay S, De PR, Bhattacharyya K, Layek GC (2016) Casson fluid flow over an unsteady stretching surface. Ain Shams Eng J 4(4):933–938

    Article  Google Scholar 

  10. Chhabra RP, Richardson JF (2008) Chapter 1—non-Newtonian fluid behaviour. Non-Newtonian flow and applied rheology (Second Edition). Butterworth-Heinemann, Oxford, pp 1–55

    Google Scholar 

  11. Das B, Batra RL (1993) Secondary flow of a Casson fluid in a slightly curved tube. Int J Non-Linear Mech 28:567–577

    Article  MATH  Google Scholar 

  12. Sankar DS, Lee U (2008) Two-fluid non-linear model for flow in catheterized blood vessels. Int J Non-Linear Mech 43:622–631

    Article  MATH  Google Scholar 

  13. Sankar DS (2009) A two-fluid model for pulsatile flow in catheterized blood vessels. Int J Non-Linear Mech 44:337–351

    Article  MATH  Google Scholar 

  14. Mukhopadhyay S, Mondal IC, Chamkha AJ (2013) Casson fluid flow and heat transfer past a symmetric wedge. Heat Transf Asian Res 42(8):665–675

    Article  Google Scholar 

  15. Malik MY, Naseer M, Nadeem S, Rehman A (2014) The boundary layer flow of Casson nanofluid over a vertical exponentially stretching cylinder. Appl Nanosci 4(7):869–873

    Article  Google Scholar 

  16. Abolbashari MH, Freidoonimehr N, Nazari F, Rashidi MM (2015) Analytical modeling of entropy generation for Casson nano-fluid flow induced by a stretching surface. Adv Powder Technol 26(2):542–552

    Article  Google Scholar 

  17. Sher Akbar N (2015) Influence of magnetic field on peristaltic flow of a Casson fluid in an asymmetric channel: application in crude oil refinement. J Magn Magn Mater 378:463–468

    Article  Google Scholar 

  18. Ramana Reddy JV, Sugunamma V, Sandeep N (2017) Enhanced heat transfer in the flow of dissipative non-Newtonian Casson fluid flow over a convectively heated upper surface of a paraboloid of revolution. J Mol Liq 229:380–388

    Article  Google Scholar 

  19. Ibrahim SM, Lorenzini G, Vijaya Kumar P, Raju CSK (2017) Influence of chemical reaction and heat source on dissipative MHD mixed convection flow of a Casson nanofluid over a nonlinear permeable stretching sheet. Int J Heat Mass Transf 111:346–355

    Article  Google Scholar 

  20. Pal D, Roy N, Vajravelu K (2016) Effects of thermal radiation and Ohmic dissipation on MHD Casson nanofluid flow over a vertical non-linear stretching surface using scaling group transformation. Int J Mech Sci 14:257–267

    Article  Google Scholar 

  21. Chaudhary MA, Merkin JH (1993) The effects of blowing and suction on free convection boundary layers on vertical surfaces with prescribed heat flux. J Eng Math 27(3):265–292

    Article  MathSciNet  MATH  Google Scholar 

  22. Pal D, Mandal G (2017) Thermal radiation and MHD effects on boundary layer flow of micropolar nanofluid past a stretching sheet with non-uniform heat source/sink. Int J Mech Sci 126:308–318

    Article  Google Scholar 

  23. Pal D, Mandal Gopinath (2017) Effects of Hall current on magnetohydrodynamic heat transfer of nanofluids over a non-linear stretching/shrinking sheet. Int J Appl Comput Math 3(2):1103–1120

    Article  MathSciNet  Google Scholar 

  24. Pal D, Mandal G (2016) Influence of Lorentz force and thermal radiation on heat transfer of nanofluids over a stretching sheet with velocity–thermal slip. Int J Appl Comput Math. https://doi.org/10.1007/s40819-016-0257-5

    Google Scholar 

  25. Maity S, Singh SK, Kumar AV (2016) Unsteady three dimensional flow of Casson liquid film over a porous stretching sheet in the presence of uniform transverse magnetic field and suction/injection. J Magn Magn Mater 419:292–300

    Article  Google Scholar 

  26. Shaw S, Mahanta G, Sibanda P (2016) Non-linear thermal convection in a Casson fluid flow over a horizontal plate with convective boundary condition. Alex Eng J 55(2):1295–1304

    Article  Google Scholar 

  27. Mahmood M, Asghar S, Hossain MA (2009) Transient mixed convection flow arising due to thermal diffusion over a poroussensor surface inside a squeezing horizontal channel. Int J Therm Sci 48:1619–1626

    Article  Google Scholar 

  28. Ahmed N, Khan U, Khan SI, Xiao-Jun Y, Zaidi ZA, Mohyud-Din ST (2013) Magneto hydrodynamic (MHD) squeezing flow of a Casson fluid between parallel disks. Int J Phys Sci 8:1788–1799

    Article  Google Scholar 

  29. Mittal RC, Pandit S (2017) Numerical simulation of unsteady squeezing nanofluid and heat flowbetween two parallel plates using wavelets. Int J Therm Sci 118:410–422

    Article  Google Scholar 

  30. Engmann J, Servais C, Burbidge AS (2005) Squeeze flow theory and applications to rheometry: a review. J Nonnewton Fluid Mech 132(13):1–27

    Article  MATH  Google Scholar 

  31. Siddiqa S, Begum N, Hossain MA (2016) Radiation effects from an isothermal vertical wavy cone with variable fluid properties. Appl Math Comput 289:149–158

    MathSciNet  Google Scholar 

  32. Saddiqa S, Begum N, Hossain AMA, Al-Rashed A (2017) Numerical estimation of thermal radiation effects on marangoni convection of dusty fluid. J Therm Sci Eng Appl 10:1–7

    Article  Google Scholar 

  33. He JH (2000) A coupling method of a homotopy technique and a perturbation technique for non-linear problems. Int J Non-Linear Mech 35(1):37–43

    Article  MathSciNet  MATH  Google Scholar 

  34. Ateş I, Zegeling PA (2017) A homotopy perturbation method for fractional-order advection-diffusion-reaction boundary-value problems. Appl Math Model 47:425–441

    Article  MathSciNet  Google Scholar 

  35. Hatami M, Khazayinejad M, Jing D (2016) Forced convection of Al2O3–water nanofluid flow over a porous plate under the variable magnetic field effect. Int J Heat Mass Transf 102:622–630

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Mechanical Engineering, Amirkabir University of Technology, Hafez Ave, Tehran, P.O. Box 15878-4413, Iran

    A. Ahmadpour, M. Nasiri, M. Khazayinejad & N. Asgharian

  2. Young Researchers Club, Sari Branch, Islamic Azad University, Sari, Iran

    M. Khazayinejad

Authors
  1. A. Ahmadpour
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. M. Nasiri
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. M. Khazayinejad
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. N. Asgharian
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to A. Ahmadpour.

Additional information

Technical Editor: Cezar Negrao.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Ahmadpour, A., Nasiri, M., Khazayinejad, M. et al. Flow and convective heat transfer of Casson fluid between squeezing porous disks in the presence of thermal radiation, viscous dissipation, and variable heat source/sink. J Braz. Soc. Mech. Sci. Eng. 40, 135 (2018). https://doi.org/10.1007/s40430-018-1058-z

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s40430-018-1058-z

Keywords

Search

Navigation