Abstract
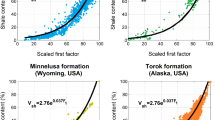
Factor analysis of well logging data can be effectively applied to calculate shale volume in hydrocarbon formations. A global optimization approach is developed to improve the result of traditional factor analysis by reducing the misfit between the observed well logs and theoretical data calculated by the factor model. Formation shaliness is directly calculated from the factor scores by a nonlinear regression relation, which is consistent in the studied area in Alaska, USA. The added advantage of the implementation of the Simulated Annealing method is the estimation of the theoretical values of nuclear, sonic, electrical as well as caliper well-logging data. The results of globally optimized factor analysis are compared and verified by independent estimates of self-potential log-based deterministic modeling. The suggested method is tested in two different shaly-sand formations in the North Aleutian Basin of Alaska and the comparative study shows that the assumed nonlinear connection between the factor scores and shale volume is applicable with the same regression constants in different burial depths. The study shows that factor analysis solved by the random search technique provides an independent in situ estimate to shale content along arbitrary depth intervals of a borehole, which may improve the geological model of the hydrocarbon structure in the investigated area.







Similar content being viewed by others
References
Asfahani J (2014) Statistical factor analysis technique for characterizing basalt through interpreting nuclear and electrical well logging data (case study from Southern Syria). Appl Radiat Isot 84:33–39
Bartlett MS (1937) The statistical conception of mental factors. Br J Psychol 28:97–104
Beauducel A, Harms C, Hilger N (2016) Reliability estimates for three factor score estimators. Int J Stat Probab 5(6):94
Bücker C, Shimeld J, Hunze S, Brückmann W (2000) Data report: logging while drilling data analysis of Leg 171A, a multivariate statistical approach. Proc Ocean Drill Program Sci Results Sci Results 171A:1
Coimbra R, Horikx M, Huck S, Heimhofer U, Immenhauser A, Rocha F, Dinis J, Duarte LV (2017) Statistical evaluation of elemental concentrations in shallow-marine deposits (Cretaceous, Lusitanian Basin). Mar Pet Geol 86:1029–1046
Dobróka M, Szabó NP, Tóth J, Vass P (2016) Interval inversion approach for an improved interpretation of well logs. Geophysics 81(2):D155–D167
Geman S, Geman D (1984) Stochastic relaxation, Gibbs distributions, and Bayesian restoration of images. IEEE Trans Pattern Anal Mach Intell PAMI-6:721–741
Jöreskog KG (2007) Factor analysis and its extensions. In: Cudeck R, MacCallum RC (eds) Factor analysis at 100: historical developments and future directions. Erlbaum, Mahwah, pp 47–77
Kaiser HF (1958) The varimax criterion for analytical rotation in factor analysis. Psychometrika 23:187–200
Marquardt DW (1963) An algorithm for least-squares estimation of nonlinear parameters. J Soc Ind Appl Math 11(2):431–441
Metropolis N, Rosenbluth MN, Teller AH, Teller E (1953) Equation of State calculations by fast computing machines. J Chem Phys 21:1087–1092
Odokuma-Alonge O, Adekoya J (2013) factor analysis of stream sediment geochemical data from Onyami drainage system, Southwestern Nigeria. Int J Geosci 4(3):656–661
Sen MK, Stoffa PL (1995) Global optimization methods in geophysical inversion, vol 4, 1st edn. Elsevier, Amsterdam
Shaw R, Srivastava S (2007) Particle swarm optimization: a new tool to invert geophysical data. Geophysics 72(2):F75–F83
Soupiosa P, Akcab I, Mpogiatzisc P, Basokurb AT, Papazacho C (2011) Applications of hybrid genetic algorithms in seismic tomography. J Appl Geophys 75(3):479–489
Szabó NP (2011) Shale volume estimation based on the factor analysis of well-logging data. Acta Geophys 59:935–953
Szabó NP, Dobróka M (2013) Extending the application of a shale volume estimation formula derived from factor analysis of wireline logging data. Math Geosci 45:837–850
Szabó NP, Dobróka M (2017) Robust estimation of reservoir shaliness by iteratively reweighted factor analysis. Geophysics 82(2):D69–D83
Szabó NP, Dobróka M, Turai E, Szűcs P (2014) Factor analysis of borehole logs for evaluating formation shaliness: a hydrogeophysical application for groundwater studies. Hydrogeol J 22:511–526
Szűcs P, Civan F, Virág M (2006) Applicability of the most frequent value method in groundwater modeling. Hydrogeol J 14:31–43
van Laarhoven PJ, Aarts EH (1987) Simulated annealing: theory and applications, volume 37 of the series mathematics applied, pp 7–15
Yin C, Hodges G (2007) Simulated annealing for airborne EM inversion. Geophysics 72(4):F189–F195
Acknowledgements
The research was supported by the National Research, Development and Innovation Office—NKFIH, Project No. K109441. The authors would like to thank The Alaska Oil and Gas Conservation Commission (AOGCC) for the permission to use their digital well log data that was obtained from their website, via the link: http://doa.alaska.gov/ogc/DigLog/diglogindex.html.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Abordán, A., Szabó, N.P. Metropolis algorithm driven factor analysis for lithological characterization of shallow marine sediments. Acta Geod Geophys 53, 189–199 (2018). https://doi.org/10.1007/s40328-017-0210-z
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40328-017-0210-z