Interplanetary patched-conic approximation with an intermediary swing-by maneuver with the moon

Abstract

The present work quantifies the fuel consumption of a space vehicle in bi-impulsive interplanetary trajectories with an intermediary swing-by maneuver with the Moon. In this way, an interplanetary patched-conic approximation with a lunar swing-by maneuver is formulated with an important characteristic: the swing-by maneuver is designed before the determination of the trajectory by specifying its geometry. The transfer problem is then solved by a multi-point boundary value problem (MPBVP) with two constraints. The intermediary constraint is related to the geometry of the swing-by maneuver with the Moon, and the terminal constraint is related to the altitude of the arrival at the low orbit around the target planet. The proposed algorithm is built in such way that the MPBVP is split into two-point boundary value problems (TPBVPs): the first one is solved to ensure the satisfying of the intermediary constraint, and the second TPBVP is solved next to satisfy the final constraint. Both TPBVPs are solved by means of Newton–Raphson algorithm. The proposed algorithm is then utilized to determine the Earth–Mars and Earth–Venus trajectories with several geometric configurations. The geometric configuration with the smallest fuel consumption is obtained for both missions and compared to an interplanetary patched-conic approximation without swing-by maneuver with Moon. The results show advantages in performing swing-by maneuver with the Moon for interplanetary missions by saving fuel consumption without much increase of the time of flight.

Appendix

This Appendix details the mathematical formulation of the interplanetary patched-conic approximation with an intermediary lunar swing-by maneuver. The complete trajectory is composed of five phases: a first geocentric phase, a selenocentric phase, a second geocentric phase, a heliocentric phase, and a planetocentric phase.

1.1 First geocentric phase

The mathematical formulation of the geocentric phase is based on the one described by Arthur Gagg Filho and Da Silva Fernandes (2016). For a given a value of the variables $r_0$, $v_0$ and $\phi _0$ at the initial time $t=t_0$ , after the application of the first impulse, the energy $\varepsilon _{g,1}$, the angular momentum $h_{g,1}$, the semi-major axis $a_{g,1}$, the eccentricity $e_{g,1}$, and the semilatus rectum $p_{g,1}$ can be determined as follows:

$$\begin{aligned} \varepsilon _{g,1}= & {} \frac{1}{2}v_0^2 -\frac{{\mu _\mathrm{E}} }{r_0 } ,\end{aligned}$$

(A.1)

$$\begin{aligned} h_{g,1}= & {} r_0 v_0 \hbox {cos}\left( {\phi _0 } \right) ,\end{aligned}$$

(A.2)

$$\begin{aligned} a_{g,1}= & {} \frac{r_0 }{2-Q_{g,1} } ,\end{aligned}$$

(A.3)

$$\begin{aligned} e_{g,1}= & {} \sqrt{1+Q_{g,1} \left( {Q_{g,1} -2} \right) \hbox {cos}^{2}\phi _0 } \end{aligned}$$

(A.4)

$$\begin{aligned} p_{g,1}= & {} a_{g,1} (1-e_{g,1}^2 ), \end{aligned}$$

(A.5)

where

$$\begin{aligned} Q_{g,1} =\frac{r_0 v_0^2 }{{\mu _\mathrm{E}} }. \end{aligned}$$

(A.6)

The subscript g, 1 indicates the first geocentric phase and ${\mu _\mathrm{E}}$ is the gravitational parameter of the Earth. Note that the flight path angle $\phi _0 =0^{\circ }$ at the departure from LEO, as mentioned before.

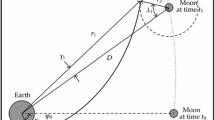
From geometry of Fig. 1, the distance $r_{g,1} (t_1 )$ of the space vehicle to Earth at the moment $t=t_1$, when the geocentric trajectory intercepts the Moon’s sphere of influence (point 1), is given by

$$\begin{aligned} r_{g,1} (t_1 )=\sqrt{D^{2}+r_s (t_1 )^{2}-2Dr_s (t_1 )\hbox {cos}\left( {\lambda _1 } \right) }, \end{aligned}$$

(A.7)

where D is the Earth–Moon mean distance, and the distance $r_s (t_1 )$ is equal to radius $R_{SM}$ of the Moon’s sphere of influence. The subscript s indicates the selenocentric phase. The phase angle $\gamma _1$ (Fig. 1) can also be determined:

$$\begin{aligned} \hbox {sin}\left( {\gamma _1 } \right) =r_s (t_1 )\frac{\hbox {sin}\left( {\lambda _1 } \right) }{r_{g,1} (t_1 )}. \end{aligned}$$

(A.8)

The magnitude $v_{g,1} (t_1 )$ of velocity vector and the flight path angle $\phi _{g,1} (t_1 )$ are obtained as

$$\begin{aligned} v_{g,1} (t_1 )= & {} \sqrt{2\left( {\varepsilon _{g,1} +\frac{{\mu _\mathrm{E}} }{r_{g,1} (t_1 )}} \right) }, \end{aligned}$$

(A.9)

$$\begin{aligned} \hbox {cos}\left( {\phi _{g,1} (t_1 )} \right)= & {} \frac{h_{g,1} }{r_{g,1} (t_1 )v_{g,1} (t_1 )}. \end{aligned}$$

(A.10)

The time of flight $\Delta t_{g,1}$ of the first geocentric trajectory is given by:

$$\begin{aligned} \Delta t_{g,1} =\sqrt{\frac{-a_{g,1}^3 }{{\mu _\mathrm{E}} }}\left( {e_{g,1} \hbox {sinh}\left( {H_{g,1} (t_1 )} \right) -H_{g,1} (t_1 )} \right) \end{aligned}$$

(A.11)

with the hyperbolic eccentric anomaly $H_{g,1} (t_1 )$ obtained from the equation:

$$\begin{aligned} \hbox {cosh}\left( {H_{g,1} (t_1 )} \right) =\frac{1}{e_{g,1} }\left( {1-\frac{r_{g,1} (t_1 )}{a_{g,1} }} \right) . \end{aligned}$$

(A.12)

The initial phase angle $\theta _{EP} (0)$ between the space vehicle and the Moon (Fig. 1) at the initial time is given by:

$$\begin{aligned} \theta _{EP} (0)=f_{g,1} (t_1 )-f_0 -\gamma _1 -\omega _M \Delta t_{g,1}, \end{aligned}$$

(A.13)

where $\omega _M$ is the angular velocity of the Moon around the Earth; $f_0$ is the true anomaly at $t=t_0$, and its value is equal to 0$^{\circ }$ (the insertion point is the perigee of the geocentric trajectory); and $f_{g,1} (t_1 )$ is the true anomaly of the space vehicle at $t=t_1$,

$$\begin{aligned} \hbox {cos}\left( {f_{g,1} (t_1 )} \right) =\frac{\hbox {cosh}\left( {H_{g,1} (t_1 )} \right) -e_{g,1} }{1-e_{g,1} \hbox {cos}\left( {H_{g,1} (t_1 )} \right) }. \end{aligned}$$

(A.14)

1.2 Selenocentric phase

The selenocentric phase, characterized by a hyperbolic trajectory, defines the motion of the space vehicle during the swing-by maneuver. At point 1,

$$\begin{aligned} \mathbf{v}_s (t_1 )=\mathbf{v}_{g,1} (t_1 )-\mathbf{v}_M (t_1 ), \end{aligned}$$

(A.15)

where $\mathbf{v}_M (t_1 )$ is the velocity vector of the Moon relative to the Earth. From Eq. (A.15), one finds the magnitude $v_s (t_1 )$ of the velocity vector and the flight path angle $\phi _{g,1} (t_1 )$ as follows:

$$\begin{aligned} v_s (t_1 )= & {} \sqrt{v_{g,1} (t_1 )^{2}+v_M ^{2}-2v_{g,1} (t_1 )v_M \hbox {cos}\left( {\phi _{g,1} (t_1 )-\gamma _1 } \right) }, \end{aligned}$$

(A.16)

$$\begin{aligned} \hbox {tg}\left( {\lambda _1 \pm \phi _s (t_1 )} \right)= & {} -\frac{v_{g,1} (t_1 )\hbox {sin}\left( {\phi _{g,1} (t_1 )-\gamma _1 } \right) }{v_M (t_1 )-v_{g,1} (t_1 )\hbox {cos}\left( {\phi _{g,1} (t_1 )-\gamma _1 } \right) }, \end{aligned}$$

(A.17)

where $v_M =\omega _M D$ is the velocity of the Moon around the Earth. The upper and the lower signal in Eq. (A.17) correspond, respectively, to a trajectory in the clockwise sense and in the counterclockwise sense. The angle $\phi _s (t_1 )$ in the above equation is taken positive, since it is based on the geometry. On the other hand, at point 1, the space vehicle is encountering the pericenter of the selenocentric trajectory; thus, $\phi _s (t_1 )$ must be taken negative following the sign convention adopted in the two-body dynamics.

The pericenter distance $r_{sP}$ and the magnitude $v_{sP}$ of the velocity vector at the periselenium at $t=t_2$ (point 2) can be determined as:

$$\begin{aligned} r_{sP}= & {} a_s \left( {1-e_s } \right) ,\end{aligned}$$

(A.18)

$$\begin{aligned} v_{sP}= & {} \sqrt{\frac{\mu _\mathrm{M} \left( {1+e_s } \right) }{a_s \left( {1-e_s } \right) }}, \end{aligned}$$

(A.19)

where $\mu _\mathrm{M}$ is the gravitational parameter of the Moon. The semi-major axis $a_s$ and eccentricity $e_s$ of the selenocentric trajectory are given by:

$$\begin{aligned} a_s= & {} \frac{r_s (t_1 )}{2-Q_s } ,\end{aligned}$$

(A.20)

$$\begin{aligned} e_s= & {} \sqrt{1+Q_s \left( {Q_s -2} \right) \hbox {cos}^{2}\left( {\phi _s (t_1 )} \right) } \end{aligned}$$

(A.21)

and

$$\begin{aligned} Q_s =\frac{r_s (t_1 )v_s (t_1 )^{2}}{\mu _\mathrm{M} }. \end{aligned}$$

(A.22)

The time of flight $\Delta t_{sp}$ to reach the periselenium is given by:

$$\begin{aligned} \Delta t_{sp} =\sqrt{\frac{\left( {-a_s } \right) ^{3}}{\mu _\mathrm{M} }}\left( {e_s \hbox {sinh}\left( {H_s (t_1 )} \right) -H_s (t_1 )} \right) , \end{aligned}$$

(A.23)

with the hyperbolic eccentric anomaly $H_s (t_1 )$ obtained from the equation:

$$\begin{aligned} \hbox {cosh}\left( {H_s (t_1 )} \right) =\frac{1}{e_s }\left( {1-\frac{r_s (t_1 )}{a_s }} \right) . \end{aligned}$$

(A.24)

Figure 1 also highlights the symmetry between point 1 and point 3 with the line of apsis as the symmetry axis. In this way, the time of flight $\Delta t_s$ of the selenocentric trajectory is given by:

$$\begin{aligned} \Delta t_s =2\Delta t_{sp}. \end{aligned}$$

(A.25)

The main parameters—radial distance $r_s (t_3 )$, magnitude $v_s (t_3 )$ of the velocity vector and flight path angle $\phi _s (t_3 )$—at $t=t_3$, when the space vehicle leaves the Moon’s sphere of influence, are calculated as described in what follows. Firstly, the true anomaly $f_s (t_1 )$ can be calculated from the equation:

$$\begin{aligned} \hbox {tg}\left( {\frac{f_s (t_1 )}{2}} \right) =\sqrt{\frac{e_s +1}{e_s -1}}\hbox {tgh}\left( {\frac{H_s (t_1 )}{2}} \right) . \end{aligned}$$

(A.26)

Due to the symmetry, the true anomaly $f_s (t_3 )$ at $t=t_3$ has the same magnitude of $f_s (t_1 )$, but occurs before the pericenter; therefore:

$$\begin{aligned} f_s (t_3 )=-f_s (t_1 ). \end{aligned}$$

(A.27)

The angle $\Delta$, depicted by Fig. 1, is given by:

$$\begin{aligned} \Delta =2\pi -\left( {f_s (t_3 )-f_s (t_1 )} \right) , \end{aligned}$$

(A.28)

with the angle $\lambda _3$ defined as:

$$\begin{aligned} \lambda _3 =\lambda _1 +\Delta +\omega _M \Delta t_s. \end{aligned}$$

(A.29)

Note that

$$\begin{aligned} \left| {\mathbf{r}_s (t_3 )} \right| =r_s (t_3 )=R_{SM}. \end{aligned}$$

(A.30)

By symmetry,

$$\begin{aligned} v_s (t_3 )= & {} v_s (t_1 ) \end{aligned}$$

(A.31)

$$\begin{aligned} \left| {\phi _s (t_3 )} \right|= & {} \left| {\phi _s (t_1 )} \right| . \end{aligned}$$

(A.32)

At point 3, the space vehicle is moving away from the pericenter, and thus $\phi _s (t_3 )$ is positive.

1.3 Second geocentric phase

When the space vehicle leaves the Moon’s sphere of influence at $t=t_3$, it starts a second geocentric phase defined by a hyperbolic trajectory. From the law of cosines, the magnitude $r_{g,2} (t_3 )$ of the position vector of the space vehicle relative to the Earth at $t=t_3$ is given by

$$\begin{aligned} \left| {\mathbf{r}_{g,2} (t_3 )} \right| =r_{g,2} (t_3 )=\sqrt{D^{2}+r_s (t_3 )^{2}-2Dr_s (t_3 )\cos \left( {\lambda _3 } \right) }. \end{aligned}$$

(A.33)

The subscript g, 2 indicates the second geocentric trajectory. The phase angle $\gamma _3$ of the space vehicle with the Moon (Fig. 1) can also be determined as:

$$\begin{aligned} \hbox {sen}\left( {\gamma _3 } \right) =r_s (t_3 )\frac{\hbox {sen}\left( {\lambda _3 } \right) }{r_g (t_3 )}. \end{aligned}$$

(A.34)

At point 3,

$$\begin{aligned} \mathbf{v}_{g,2} (t_3 )=\mathbf{v}_s (t_3 )+\mathbf{v}_\mathbf{M} (t_3 ), \end{aligned}$$

(A.35)

where $\mathbf{v}_s (t_3 )$ is the velocity vector of the Moon relative to the Earth, and $\mathbf{v}_{g,2} (t_3 )$ is the velocity vector of the space vehicle relative to the Earth. The magnitude $v_{g,2} (t_3 )$ and the flight path angle $\phi _{g,2} (t_3 )$ are then given by:

$$\begin{aligned} v_{g,2} (t_3 )= & {} \sqrt{v_s (t_3 )^{2}+v_M ^{2}-2v_s (t_3 )v_M \cos \left( {\lambda _3 +\phi _s (t_3 )} \right) } ,\end{aligned}$$

(A.36)

$$\begin{aligned} \hbox {tg}\left( {\phi _{g,2} (t_3 )-\gamma _3 } \right)= & {} \frac{-v_s (t_3 )\hbox {sin}\left( {\lambda _3 +\phi _s (t_3 )} \right) }{v_M -v_s (t_3 )\cos \left( {\lambda _3 +\phi _s (t_3 )} \right) }. \end{aligned}$$

(A.37)

Due to the geometry, $\phi _{g,2} (t_3 )$ is taken positive. Once the variables $r_{g,2} (t_3 )$, $v_{g,2} (t_3 )$ and $\phi _{g,2} (t_3 )$ are known, the parameters $\varepsilon _{g,2}$, $h_{g,2}$, $Q_{g,2}$, $a_{g,2}$, $e_{g,2}$, and $p_{g,2}$ of the second geocentric phase can be calculated from equations quite similar to Eqs. (A.1)–(A.6).

The anomalies $H_{g,2} (t_3 )$, $f_{g,2} (t_3 )$ and $M_{g,2} (t_3 )$ on leaving the Moon’s sphere of influence (point 3) are calculated as follows:

$$\begin{aligned} \hbox {cosh}(H_{g,2} (t_3 ))= & {} \frac{1}{e_{g,2} }\left( {1-\frac{r_{g,2} (t_3 )}{a_{g,2} }} \right) ,\end{aligned}$$

(A.38)

$$\begin{aligned} \hbox {tg}\left( {\frac{f_{g,2} (t_3 )}{2}} \right)= & {} \sqrt{\frac{1+e_{g,2} }{e_{g,2} -1}}\hbox {tg}\left( {\frac{H_{g,2} (t_3 )}{2}} \right) ,\end{aligned}$$

(A.39)

$$\begin{aligned} M_{g,2} (t_3 )= & {} e_{g,2} \hbox {sinh}\left( {H_{g,2} (t_3 )} \right) -H_{g,2} (t_3 ). \end{aligned}$$

(A.40)

From the geometry, the pericenter argument $\omega _{g,2}$ of the second geocentric phase is given by:

$$\begin{aligned} \omega _{g,2} =\gamma _3 +\omega _M (\Delta t_g +\Delta t_s )-f_{g,2} (t_3 ). \end{aligned}$$

(A.41)

At $t=t_4$, the geocentric trajectory touches the boundary of the Earth’s sphere of influence (point 4 in Fig. 1). Thus,

$$\begin{aligned} r_{g,2} (t_4 )= & {} R_{SE}, \end{aligned}$$

(A.42)

$$\begin{aligned} v_{g,2} (t_4 )= & {} \sqrt{\frac{{\mu _\mathrm{E}} }{p_{g,2} }}\sqrt{1+2e_{g,2} \hbox {cos}\left( {f_{g,2} (t_4 )} \right) +e_{g,2} ^{2}}, \end{aligned}$$

(A.43)

$$\begin{aligned} \hbox {cos}(\phi _{g,2} (t_4 ))= & {} \frac{h_{g,2} }{R_{SE} v_{g,2} (t_4 )}, \end{aligned}$$

(A.44)

where $R_{SE}$ is the radius of the Earth’s sphere of influence, and the anomaly $f_{g,2} (t_4 )$ is determined as:

$$\begin{aligned} \hbox {cos}(f_{g,2} (t_4 ))=\frac{1}{e_{g,2} }\left( {\frac{p_{g,2} }{R_{ST} }-1} \right) . \end{aligned}$$

(A.45)

The time of flight $\Delta t_{g,2}$ of the second geocentric phase is given by:

$$\begin{aligned} \Delta t_{g,2} =\left( {M_{g,2} (t_4 )-M_{g,2} (t_3 )} \right) \sqrt{\frac{-a_{g,2}^3 }{{\mu _\mathrm{E}} }}, \end{aligned}$$

(A.46)

with the anomalies $M_{g,2} (t_4 )$ and $H_{g,2} (t_4 )$ determined from equations similar to Eqs. (A.40) and (A.39), respectively.

1.4 Heliocentric phase

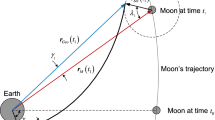
The heliocentric phase describes the motion of the space vehicle from its departure from the Earth’s sphere of influence until it reaches the Mars’s sphere of influence. This phase is characterized by an elliptic trajectory. Note that the position vector $\mathbf{r}_\mathrm{he} (t_4 )$ and the velocity vector $\mathbf{v}_\mathrm{he} (t_4 )$ of the space vehicle in the heliocentric phase at $t=t_4$ still cannot be determined, because the position of the Earth on its orbit around the Sun is unknown. To link the position of Earth, the angle $\lambda _S$ (Fig. 2) must be specified. This angle characterizes the geometry of departure of the space vehicle from the Earth’s sphere of influence and cannot be chosen arbitrarily, since it is part of the solution of the problem. For a given $\lambda _S$, the variables $r_\mathrm{he} (t_4 )$ and $v_\mathrm{he} (t_4 )$ at the beginning of the heliocentric phase are calculated as:

$$\begin{aligned} r_\mathrm{he} (t_4 )= & {} \sqrt{D_E^2 +R_{SE}^2 -2D_E R_{SE} \hbox {cos}(\lambda _S )}, \end{aligned}$$

(A.47)

$$\begin{aligned} v_\mathrm{he} (t_4 )= & {} \sqrt{v_{g,2} (t_4 )^{2}+v_E^2 -2v_{g,2} (t_4 )v_E \hbox {cos}\left( {\lambda _S +\phi _{g,2} (t_4 )} \right) }. \end{aligned}$$

(A.48)

$D_E$ is the Sun–Earth distance, and $v_E =\omega _E D_E$ is the velocity of the Earth around the Sun. The flight path angle $\phi _\mathrm{he} (t_4 )$ is given by:

$$\begin{aligned} \hbox {tg}(\phi _\mathrm{he} (t_4 )-\gamma _5 )=\frac{-v_{g,2} (t_4 )\hbox {sin}(\lambda _S +\phi _{g,2} (t_4 ))}{v_E -v_{g,2} (t_4 )\hbox {cos}(\lambda _S +\phi _{g,2} (t_4 ))}, \end{aligned}$$

(A.49)

where $\gamma _5$ is the phase angle between the space vehicle and the Earth as shown in Fig. 2 and is given by:

$$\begin{aligned} \hbox {sin}(\gamma _5 )=r_{g,2} (t_4 )\frac{\hbox {sin}(\lambda _S )}{r_\mathrm{he} (t_4 )}. \end{aligned}$$

(A.50)

From the geometry, the pericenter argument of the heliocentric trajectory is determined as:

$$\begin{aligned} \omega _\mathrm{he} =-f_\mathrm{he} (t_4 )+\omega _E (\Delta t_g +\Delta t_s +\Delta t_{g,2} )+\gamma _5 +\theta _{S0} -\pi , \end{aligned}$$

(A.51)

where $\theta _{S0}$ is the initial phase angle of the Sun as seen from the Earth at the initial time and calculated as follows:

$$\begin{aligned} \theta _{S0} =f_{g,2} (t_4 )+\omega _{g,2} -\omega _E (\Delta t_g +\Delta t_s +\Delta t_{g,2} )+\lambda _S \end{aligned}$$

(A.52)

and, with the anomalies $f_\mathrm{he} (t_4 )$, $E_\mathrm{he} (t_4 )$ and $M_\mathrm{he} (t_4 )$ determined as:

$$\begin{aligned} \hbox {cos}\left( {f_\mathrm{he} (t_4 )} \right)= & {} \frac{1}{e_\mathrm{he} }\left( {\frac{p_\mathrm{he} }{r_\mathrm{he} (t_4 )}-1} \right) , \end{aligned}$$

(A.53)

$$\begin{aligned} \hbox {tg}\left( {\frac{E_\mathrm{he} (t_4 )}{2}} \right)= & {} \sqrt{\frac{1-e_\mathrm{he} }{1+e_\mathrm{he} }}\hbox {tg}\left( {\frac{f_\mathrm{he} (t_4 )}{2}} \right) , \end{aligned}$$

(A.54)

$$\begin{aligned} M_\mathrm{he} (t_4 )= & {} E_\mathrm{he} (t_4 )-e_\mathrm{he} \hbox {sin}\left( {E_\mathrm{he} (t_4 )} \right) . \end{aligned}$$

(A.55)

The eccentricity $e_\mathrm{he}$ and the semilatus rectum $p_\mathrm{he}$ are obtained from equations quite similar to Eqs. (A.1)–(A.6).

At the time $t=t_5$, the heliocentric trajectory intercepts the Mars’s sphere of influence (point 5) with the angle $\lambda _{\mathrm{M}_t }$ as depicted in Fig. 2. At this moment, the distance of the space vehicle to the Sun $r_\mathrm{he} (t_5 )$ is determined as:

$$\begin{aligned} r_\mathrm{he} (t_5 )=\sqrt{D_{\mathrm{M}_t }^2 +R_{\mathrm{SM}_t }^2 -2D_{\mathrm{M}_t } R_{\mathrm{SM}_t } \hbox {cos}(\lambda _{\mathrm{M}_t } )}, \end{aligned}$$

(A.56)

where $D_{\mathrm{M}_t }$ is the Sun–Mars distance, and $R_{\mathrm{SM}_t }$ is the radius of Mars’s sphere of influence. Note that the distance $r_\mathrm{pla} (t_5 )=R_{\mathrm{SM}_t }$. The phase angle $\gamma _6$ of the space vehicle at the point 5 (Fig. 5) is given by

$$\begin{aligned} \hbox {sin}(\gamma _6 )=r_\mathrm{pla} (t_5 )\frac{\sin (\lambda _{\mathrm{M}_t } )}{r_\mathrm{he} (t_5 )}. \end{aligned}$$

(A.57)

The magnitude $v_\mathrm{he} (t_5 )$ of the velocity vector and the flight path angle $\phi _\mathrm{he} (t_5 )$ are given by expressions similar to Eqs. (A.9) and (A.10), but utilizing the gravitational parameter of the Sun $\mu _S$. From equations similar to Eqs. (A.53)–(A.55), the anomalies $f_\mathrm{he} (t_5 )$, $E_\mathrm{he} (t_5 )$ and $M_\mathrm{he} (t_5 )$ are calculated.

The time of flight $\Delta t_\mathrm{he}$ is given by the expression below:

$$\begin{aligned} \Delta t_\mathrm{he} =\left( {M_\mathrm{he} (t_5 )-M_\mathrm{he} (t_4 )} \right) \sqrt{\frac{a_\mathrm{he}^3 }{\mu _S }}. \end{aligned}$$

(A.58)

From the geometry, the pericenter argument of the heliocentric trajectory is obtained as:

$$\begin{aligned} \omega _\mathrm{he} =-f_\mathrm{he} (t_4 )+\omega _E (\Delta t_g +\Delta t_s +\Delta t_{g,2} )+\gamma _5 +\theta _{S0} -\pi . \end{aligned}$$

(A.59)

1.5 Planetocentric phase

The planetocentric phase is characterized by a hyperbolic trajectory relative to the target planet (Mars), and at point 5,

$$\begin{aligned} \mathbf{v}_\mathrm{pla} (t_5 )=\mathbf{v}_\mathrm{he} (t_5 )-\mathbf{v}_{\mathrm{M}_t } (t_5 ), \end{aligned}$$

(A.60)

where $\mathbf{v}_\mathrm{pla} (t_5 )$ is the velocity vector of the space vehicle relative to Mars, and $\mathbf{v}_{\mathrm{M}_t } (t_5 )$ is the velocity vector of Mars at $t=t_5$. The mathematical formulation of this phase is analogous to the selenocentric phase, but with the parameters of the target planet replacing the Moon’s parameters. The velocity of Mars around the Sun $v_{\mathrm{M}_t } =\omega _{\mathrm{M}_t } D_{M_t }$ and the gravitational parameter $\mu _{\mathrm{M}_t }$ of Mars are used. The angles $\lambda _1$ and $\gamma _1$ are replaced by $\lambda _{M_t }$ and $\gamma _6$, respectively (see Fig. 2). The time $t_5$ and $t_f$ correspond to the time $t_2$ and $t_3$ of the selenocentric phase, respectively. The space vehicle reaches the pericenter of the planetocentric phase at $t=t_f$.