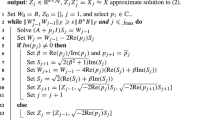Abstract
Continuous algebraic Riccati equations (CARE) appear in several important applications. A suitable approach for solving CARE, in the large-scale case, is to apply Kleinman–Newton’s method which involves the solution of a Lyapunov equation at every inner iteration. Lyapunov equations are linear, nevertheless, solving them requires specialized techniques. Different numerical methods have been designed to solve them, including ADI and Krylov-type iterative projection methods. For these iterative schemes, preconditioning is always a difficult task that can significantly accelerate the convergence. We present and analyze a strategy for solving CARE based on the use of inexact Kleinman–Newton iterations with an implicit preconditioning strategy for solving the Lyapunov equations at each inner step. One advantage is that the Newton direction is approximated implicitly, avoiding the explicit knowledge of the given matrices. Only the effect of the matrix–matrix products with the given matrices is required. We present illustrative numerical experiments on some test problems.
Similar content being viewed by others
1 Introduction
We are interested in solving continuous algebraic Riccati equations (CARE) of the form
where \(A, B, C \in \mathbb R^{n\times n}\), B and C are symmetric and positive semidefinite, and the solution of interest \(X\in \mathbb R^{n\times n}\) is symmetric, positive semidefinite, and also stabilizing, which means that the matrix \(A - BX\) is stable, i.e., its eigenvalues lie in the open left half-plane, see, e.g., (Datta 2003; Lancaster and Rodman 1995) for details. Equation (1) appears in feedback control theory problems (Benner et al. 2008a, b; Datta 2003; Mehrmann 1991) and dynamical systems (Antoulas 2005), among others. In general, for these standard applications, the matrices C and B are given in a low-rank factored form: \(C = \tilde{C}^T \tilde{C}\) and \(B= \tilde{B} \tilde{B}^T\), where \(\tilde{C}\in \mathbb R^{s\times n}\) and \(\tilde{B}\in \mathbb R^{n\times p}\), with \(p,s \ll n\).
There exist several papers concerning numerical methods for the solution of CARE; e.g., (Bini et al. 2012; Datta 2003; Lancaster and Rodman 1995; Mehrmann 1991) and references given therein. In the large and sparse case, it is a common approach to use Newton’s method to find a solution of (1), e.g., (Benner et al. 2008a; Guo and Lancaster 1998; Jbilou 2003, 2006; Kleinman 1968; Sandell 1974; Simoncini et al. 2014). For solving CARE, at every Newton step, a Lyapunov equation must be solved, which in the large-scale case should be solved using iterative methods. Two suitable ingredients when using iterative method at each inner step are: the use of an inexact iterative scheme to reduce the accumulated number of iterations and hence the total amount of work; and the addition of a preconditioner to accelerate the convergence.
In this work, we present and analyze a strategy for solving CARE based on the use of inexact Newton iterations with an implicit preconditioning scheme for solving the Lyapunov equations at each inner step. An advantage of this strategy is that the Newton direction is approximated implicitly, using an ordinary differential equation (ODE) dynamical model, to produce an iterative scheme that remains in the \(n \times n\) space of the variable matrix X. It is inspired and motivated by the algorithm developed in (Chehab and Raydan 2005) for general nonlinear vector problems. For robustness, we also propose a globalization strategy in the space of matrices that is adapted from the recent global algorithm developed and analyzed for fluid flow problems and generalized Sylvester equations in (Chehab and Raydan 2009, 2011). In Sect. 2, we describe the inexact Newton technique for solving CARE, and discuss its convergence properties. In Sect. 3, we describe and analyze our implicit preconditioned scheme for solving the Lyapunov equations that appear at each inner inexact Newton step. In Sect. 4, we present the full strategy proposed for solving CARE. In Sect. 5, we present illustrative numerical experiments for a set of different problems coming from several applications. Finally, in Sect. 6, we present some concluding remarks.
2 Inexact Newton’s method for solving CARE
In general, Newton’s method for solving a differentiable nonlinear problem \(\widehat{F}(X)=0\) is given by
where \(\widehat{F}'({X_k})\) is the Fréchet derivative of the map \(\widehat{F}\) evaluated at \(X_k\). For solving (1), the nonlinear map and its Fréchet derivative are given by
and the Newton iteration consists in solving the following linear problem for \(H_k\)
and then setting \(X_{k+1} = X_k + H_k\). Notice that the linear problem to be solved is a Lyapunov equation; and also that if the initial guess \(X_0\) is symmetric then Newton’s method generates a sequence \(\{X_k\}\) of symmetric matrices.
The Newton step can also be written as \(\mathcal {R}'(X_k)X_{k+1}= \mathcal {R}'(X_k)X_{k} - \mathcal {R}(X_k)\), which produces an equivalent formulation of Newton’s method, described in the following algorithm:

Algorithm 1 was introduced by Kleinman (1968), and it is known in the literature as the Kleinman–Newton iteration for CARE. Notice that, as in the original Newton formulation, a Lyapunov equation (step 4) must be solved at every iteration.
Before presenting the well-known theorem that summarizes the properties of the Kleinman–Newton’s method (see, e.g., Bini et al. 2012; Kleinman 1968; Lancaster and Rodman 1995), we need to introduce a definition and some standard notation. A pair (A, B) is called stabilizable if there is a feedback matrix \(K\in \mathbb R^{n\times n}\) such that \(A - BK\) is stable. The order relation on the set of symmetric matrices is the usual one: \(M\ge N\) if \(M-N\) is positive semidefinite. A symmetric solution \(X_+\) of (1) is called maximal if \(X_+\ge X\) for every symmetric solution X.
Theorem 2.1
Let \(B\in \mathbb R^{n\times n}\), \(C\in \mathbb R^{n\times n}\), and \(X_0\in \mathbb R^{n\times n}\) be all symmetric and positive semidefinite and such that \(A-BX_0\) is stable. If the pairs (A, B) and \((A^T,C)\) are stabilizable, then the Kleinman–Newton’s method for solving (1) generates a sequence \(\{X_k\}_{k\ge 0}\) such that \(\lim _{k\rightarrow \infty }X_k=X_+\), \((A-BX_k)\) is stable for all k, and \(X_1 \ge X_2 \ge \cdots \ge X_+\). Moreover, for any matrix norm, \(\{X_k\}\) converges q-quadratically to \(X_+\) from any stabilizing initial guess, i.e., there is a constant \(c>0\) such that \(\Vert X_{k+1}-X_+\Vert \le c \Vert X_k-X_+\Vert ^2\) for all \(k\ge 0\).
We note that if A is stable then \(X_0=0\) is a stabilizing initial guess, and also that in general \(X_0\ge X_1\) is not true. Stability of A can be assumed for a large class of practical applications.
Recently, for large-scale problems, the Kleinman–Newton iteration has been combined with alternating direction implicit (ADI) iterations for solving the Lyapunov equations and also with Krylov-type iterative projection methods; see, e.g., Bao et al. (2006), Benner et al. (2008a), Bini et al. (2012), Bouhamidi and Jbilou (2008), Damm (2008), El Guennouni et al. (2002), Feitzinger et al. (2009), Hackbruck and Starke (1995), Jaimoukha and Kasenally (1994), Jbilou and Riquet (2006), Jbilou (2010). For these iterative schemes applied to Lyapunov equations, preconditioning is a feature that can significantly accelerate the convergence; see Chehab and Raydan (2011), Damm (2008), Hackbruck and Starke (1995).
When using iterative methods for solving the Lyapunov equations, it is crucial to control the accuracy of the iterative scheme used at each Kleinman–Newton inner step to avoid unnecessary iterations and reduce the computational work. However, it is also important to maintain the convergence properties established in Theorem 2.1. This goal can be accomplished in the framework of inexact Newton’s methods (Dembo et al. 1982; Eisenstat and Walker 1996). In general, for solving nonlinear problems, the inexact Newton approach consists of approximating the solution of the inner linear problem in the kth Newton step up to a certain tolerance \(\eta _k>0\), which decreases when k increases. In the special case of solving Lyapunov matrix equations iteratively, at each inner step of the Kleinman–Newton’s method, the inexact Newton approach has been already analyzed by Feitzinger et al. (2009), and combined with different iterative solvers; see, e.g., Feitzinger et al. (2009), Heyouni and Jbilou (2009), Simoncini et al. (2014).
In [Feitzinger et al. (2009), Theorem 3.2], it is shown that if the Lyapunov equation (Step 4 in Algorithm 1) is approximately solved such that
for any given matrix norm \(\Vert \,\cdot \,\Vert \), then the convergence of the inexact Kleinman–Newton iterations is q-superlinear if \(\eta _k\) goes to zero, and q-quadratic if \(\eta _k \le \kappa _{\eta } \Vert \mathcal {R}(X_k)\Vert \) for some \(\kappa _{\eta }>0\). By choosing properly the sequence \(\{\eta _k\}\), such that (2) holds, the iterations used at the inner steps can be stopped prematurely, and as a consequence a significant amount of computational work can be saved; see, e.g., Feitzinger et al. (2009); Simoncini et al. 2014). In [Feitzinger et al. (2009), Theorem 4.4], it is also established that, by choosing properly the sequence \(\{\eta _k\}\), the monotonic property of the Kleinman–Newton’s method (\(X_k \ge X_{k+1}\) for \(k\ge 1\)) is maintained in the inexact case.
We present the inexact Kleinman–Newton’s method for Riccati equations in the following algorithm:

As mentioned before for the exact Kleinman–Newton’s method, \(X_0\ge X_1\) is not true for the inexact version either. In fact, usually the first (inexact) Newton step is too large and as a consequence either many iterations are needed to find the region of fast convergence or, even worse, if the Lyapunov equation is ill-conditioned then the (exact-arithmetic) convergence theory breaks down; see, e.g., Benner and Byers (1998), Guo and Lancaster (1998), Simoncini et al. (2014). To avoid this disastrously large first step, we always perform the following tolerant, inexact, and relatively inexpensive line search to move from \(X_0\) to \(X_1\):

Notice that the line search in Algorithm 3 is well defined, in the sense that it terminates in a finite number of trials; and also that it allows the first inexact Newton step to increase up to 3 times the residual norm at \(X_0\). The factor 3 is problem dependant, nevertheless it has worked effectively in practice for a wide variety of applications.
3 Implicit preconditioned iterative scheme for the inner steps
We now concentrate our attention in solving the Lyapunov equation at the kth iteration of Algorithm 2. For that we consider the following map (linear in this case), \(F_k:\mathbb R^{n \times n} \rightarrow \mathbb R^{n \times n}\), for which we need to find X such that \(F_k(X)=0\):
where \(\mathcal {A}_{k}=A- BX_{k}\) and \(\mathcal {C}_{k} = -C - X_{k}BX_{k}\). The matrix X such that \(F_k(X)=0\) will be \(X_{k+1}\), the \((k+1)\)th iterate of Algorithm 2.
We will develop an implicit inverse preconditioner iterative scheme that will approximate the Newton direction using an ODE dynamical model, specially designed for solving \(F_k(X)=0\). Our approach is inspired and motivated by the algorithm developed in (Chehab and Raydan 2005) for general nonlinear vector problems, and also on the recent global algorithms developed and analyzed for fluid flow problems and generalized Sylvester matrix equations in (Chehab and Raydan 2009, 2011). The basic underlying idea is to use in a systematic way the residual vectors as search directions, i.e., the basic iterations from \(Y_0 = X_k\) are defined as
where \(\lambda _j>0\) is the step length and the search direction is either \(+F_k(Y_j)\) or \(-F_k(Y_j)\) depending on which one is a descent direction for the following standard merit function
where we use the Frobenius inner product and the induced Frobenius norm. At the end of this section, we will show that, for the special Lyapunov equations that appear in CARE, the choice \(+F_k(Y_j)\) is always a descent direction for the merit function \(f_k(Y_j)\) at any \(Y_j\), and hence it must be used as the search direction in (4).
The convergence of (4) is attained when it is associated with a suitable derivative-free non-monotone line search globalization strategy, fully described in (La Cruz et al. 2006), and that will be discussed and adapted later in this section. For the choice of the step length \(\lambda _j>0\), there are many options for which convergence is guaranteed. A well-known and competitive choice is given by (see Chehab and Raydan 2005, 2009, 2011 for details)
where \(S_{j-1}=Y_{j}-Y_{j-1}\), and \(W_{j-1}=F_k(Y_j)-F_k(Y_{j-1})\). Obtaining the so-called spectral step length using (6) requires a reduced amount of computational work, accelerates the convergence of the process, and involves the last two iterations in such a way that incorporates first-order information into the search direction; see Birgin et al. (2014) for a review on this topic.
For adding an implicit preconditioning strategy to the basic iteration (4), let us enrich the iterates as follows:
where \(Z_j= \pm C_j\,F_k(Y_j)\), and \(C_{j}\) is an invertible approximation to \(F_k'(Y_j)^{-1}\). Notice that, in (7), if \(C_j=I\) (the identity matrix) for all j, then \(Z_j=\pm F(Y_j)\), and since \(S_{j-1} = \lambda _{j-1} Z_{j-1}\) then \(\lambda _j\) coincides with (6). Therefore, if \(C_k=I\), the method reduces to (4). On the other hand, if the sequence of iterates converges to the solution matrix \(X_{k+1}\) of \(F_k(X)=0\), and we improve the quality of the preconditioner such that \(C_j\) tends to \(F_k'(Y_{j})^{-1}\) then, as established in (Chehab and Raydan 2005), \(\lambda _{j}\) tends to 1 and we asymptotically recover Newton’s method, which possesses fast local convergence under standard assumptions. In that sense, the iterative scheme (7) is flexible and allows intermediate options, by choosing suitable approximations \(C_j\), between the identity matrix and the inverse of the Fréchet derivative operator. For building suitable approximations to \(F_k'(Y_j)^{-1} F_k(Y_j)\), we now describe an implicit preconditioning scheme, based on (7), that do not require the explicit computation of \(C_j\).
To build the implicit preconditioned direction we start from the numerical integration of the Newton flow for computing the stable steady state of
The exact solution of the equation, \(F'_k(Y)Z-F_k(Y)=0,\) defines Z as the Newton direction; while an approximative or inexact solution defines a preconditioned direction. Now, in our case, we can obtain \(Z_j\) in (7) as the steady state of
where \(Z_0=Z_{j-1}\). Notice that, indeed, the exact steady state is attained for \(Z_j = F_k'(Y_j)^{-1} F_k(Y_j)\). For solving (8), we can apply an explicit time marching scheme since the steady state is asymptotically stable; see Chehab and Raydan (2009) for details. Let \(t_m\) denote discrete times, and let us denote by \(\widehat{Z}_m\simeq Z(t_m)\). The application of the simple forward Euler method to (8) is given by
As discussed before, we want to avoid the computation of \(F_k'(Y_j)\), so \(F_k'(Y_j) \widehat{Z}_m\) is approximated by a finite difference scheme
for a small given positive real number \(\tau \). However, taking advantage of the linearity of the map \(F_k(X)\) in (3), this approximation can be simplified combining (9) and (10), and the second part of the differential system in (8) can be solved computing \(Z_j\) as the approximation of the steady state of
In other words, \(Z_j\) can be obtained by the following recursion
from \(\widehat{Z}_0=Z_{j-1}\), where
Notice also that using this simplification, the marching scheme becomes independent of \(\tau \) which is clearly a convenient feature. The iteration given by (12), in the index m, is stopped as soon as the following inequality holds:
where \(0<\theta _j<1\) is a small number, which decreases when j increases, and \(\epsilon _2>0\) is a small safeguard real number. Once (13) is satisfied for a positive integer m, we set \(Z_j= \widehat{Z}_m\). Notice that if the sequence \(\{\theta _j\}\) is chosen properly the method tends to recover asymptotically the Newton direction in (7).
Up to this point, our implicit preconditioned method for solving the Lyapunov equation (3) (IPLyap) includes two steps to move from \(Y_j\) to \(Y_{j+1}\):

The preconditioning lies on the accuracy for solving step 1 in Algorithm 4, i.e., it lies on the way the sequence \(\{\theta _j\}\) is chosen. As a suitable marching scheme for building \(Z_j\) we are using the simple forward Euler method (also called Cauchy method). More advanced time marching schemes could also be used; see Chehab and Raydan (2009) for details. To be precise, using Cauchy method, the time steps in (12) are given by
To guarantee convergence of the implicit preconditioned Algorithm 4 (IPLyap), from any initial guess, we need to add a globalization strategy. To avoid the derivatives of the merit function, we will adapt the derivative-free globalization strategy of La Cruz et al. (2006) to our preconditioned version. Assume that \(\{\psi _j\}\) is a sequence such that \(\psi _j > 0\) for all \(j \in \mathbb N\) and
Let us assume that \(0<\gamma <1\), a small positive \(\sigma _{\min }\), a large positive \(\sigma _{\max }\), such that \(0 < \sigma _{\min }< \sigma _{\max }< \infty \), and a positive integer M are given. Let \(\tau _{\min }, \tau _{\max }\) be such that \(0 < \tau _{\min }< \tau _{\max }< 1\). Given \(Y_0 \in \mathbb R^{n \times n}\), the globalized version of Algorithm 4 that allows us to obtain \(Y_{j+1}\) starting from \(Y_j\) is given below. Notice that, as mentioned before, the search direction \(Z_j= + C_j\,F_k(Y_j)\) is used at every iteration.

We now discuss some of the theoretical properties of the sequence \(\{Y_j\}\) obtained using iteratively Algorithm 5 from \(Y_0 = X_k\). As discussed in (La Cruz et al. 2006), since \(\psi _j >0\) for all j, the algorithm is well defined, i.e., the backtracking process (choosing \(\alpha _{new}\)) is guaranteed to terminate successfully in a finite number of trials. A practical backtracking scheme based on quadratic interpolation is described in (La Cruz et al. 2006).
Concerning convergence, it is established in (La Cruz et al. 2006), for general nonlinear maps, that there exists an infinite sequence of indices \(J \subset \mathbb N\) such that at every limit point of the subsequence \(\{Y_j\}_{j \in J}\), the gradient of \(f_k\) is orthogonal to the residual map \(F_k\). Therefore, if \(\Vert F_k(X)\Vert _F\) has bounded level sets, there exists a limit point \(Y_*\) of \(\{Y_j\}_{j \in \mathbb N}\) such that
where \(\nabla f_k(Y_*)\) denotes the gradient of \(f_k\) evaluated at \(Y_*\). Moreover, it is also proved in (La Cruz et al. 2006) that if a limit point is a solution then all limit points satisfy \(F_k(Y_*)=0\). In our case, the map is linear and the involved matrices A, B, and C are given, hence \(\Vert F_k(X)\Vert _F\) has bounded level sets. For the sake of completeness we will present below the theorem established in (La Cruz et al. 2006), adapted to our problem (4). First we need to obtain the gradient of \(f_k(X)=\Vert F_k(X)\Vert _F^2\).
Using properties of the trace operator, we have that for any matrix W, Y, and Z, \(\langle W,YZ\rangle = \langle Y^TW,Z\rangle = \langle WZ^T,Y\rangle \). The function \(f_k:\mathbb R^{n\times n} \rightarrow \mathbb R\) defined in (5) is differentiable and its gradient can be obtained as follows. Consider the auxiliary function \(g:\mathbb R\rightarrow \mathbb R\), given by
for any arbitrary matrix P. From basic calculus, we know that \(g'(0) = \langle \nabla f_k(X), P\rangle \). After simple algebraic manipulations, it follows that
and so the gradient of f is given by
Combining (16) and (17), we are now ready to adapt Theorems 1 and 3 in (La Cruz et al. 2006) to Algorithm 5 for solving \(F_k(X)=0\), where \(F_k(X)\) is given by (3).
Theorem 3.1
If \(\{Y_j\}\) is generated by iterating with Algorithm 5, then every limit point \(Y_*\) of \(\{Y_j\}\) satisfies
Moreover, if the limit point \(Y_*\) is the unique solution of (3), then the whole sequence \(\{Y_j\}\) converges to \(Y_*\).
One special case is the Lyapunov equation (3). If the matrix \(\mathcal {A}_k\) has negative symmetric part, then we obtain convergence as a corollary of the previous results.
Corollary 3.2
Assume that \(\{Y_j\}\) is generated using Algorithm 5 iteratively for solving (3). Assume that the symmetric part of \(\mathcal {A}_k\) is negative definite, and that \(Y_*\) is a limit point of \(\{Y_j\}\). Then \(F(Y_*)=0\).
Proof
In this case Theorem 3.1 implies
Since the symmetric part of \(\mathcal {A}_k\) is negative definite, the first term on the right-hand side satisfies
For the second term on the right-hand side, we obtain
and since \( \langle F(Y_*)^T, \mathcal {A}_k F(Y_*)^T \rangle = \frac{1}{2} \langle F(Y_*)^T, (\mathcal {A}_k +\mathcal {A}_k^T) F(Y_*)^T \rangle < 0\), then both terms must be negative when the symmetric part of A is negative definite. However, the summation of both terms is zero whenever \(F(Y_*)\ne 0\). Hence, it follows that \(F(Y_*)=0\). \(\square \)
Notice that assuming that the symmetric part of \(\mathcal {A}_k\) is negative definite is a sufficient condition for (3) to have a unique solution, and according to Corollary 3.2 to guarantee convergence of the GIPLyap Algorithm to that unique solution. This result has a clear implication for finding the solution of (1) when using (inexact) Kleinman–Newton’s method. Let us denote the symmetric part of \(\mathcal {A}_k\) as
and \(\lambda _{\min }(\mathcal {A}_k^{S})\) and \(\lambda _{\min }(\mathcal {A}_k^{S})\) as the smallest and largest eigenvalues of \(\mathcal {A}_k^{S}\), respectively. Since for all i (see, e.g., Horn and Johnson 1991)
where \( \hbox {Real}(\lambda _i(\mathcal {A}_k))\) denotes the real part of the ith eigenvalue of \(\mathcal {A}_k\), then assuming that the symmetric part of \(\mathcal {A}_k\) is negative definite, i.e. that \(\lambda _{\max }(\mathcal {A}_k^{S})<0\), implies that all the eigenvalues of \(\mathcal {A}_k\) lie in the open left half-plane, which is exactly the condition that holds for all iterates of (inexact) Kleinman–Newton’s method when solving (1).
4 Inexact implicit preconditioning strategy for solving CARE
We now present the full proposed algorithm for solving CARE in the framework of the inexact Kleinman–Newton scheme, introducing some safeguard stopping criteria. Roughly speaking, it involves three nested loops: the external one, with index k, to compute the sequence \(\{X_k\}\) of the inexact Kleinman–Newton iteration; the intermediate one, with index j, to produce the sequence \(\{Y_j\}\) and obtain an approximation to \(\{X_{k+1}\}\), which solves the Lyapunov equation given by (3), for a fixed k; and finally the inner loop, with index m, to build the preconditioned direction \(Z_j\), when moving from \(Y_j\) to \(Y_{j+1}\) at the intermediate loop.
Notice that the main computational work of Algorithm 6 is the sparse matrix–matrix products that need to be performed to obtain \(Z_j\) in Algorithm 5, during the marching scheme given by (12) and (14).

5 Numerical experiments
To give further insight into the new inexact and implicit preconditioning strategy, for solving CARE, we present the results of some numerical experiments. We implemented Algorithm 6 in MATLAB 7.3, which has unit roundoff \(\mu \approx 1.1\times 10^{-16}\).
An extension of our internal implicit preconditioning machinery, i.e., an extension of Algorithm 5, has been already compared favorably with state-of-the-art Krylov-type methods for the special case of solving generalized Sylvester equations; see Chehab and Raydan (2011) for details. Here, we are mainly interested on how to combine the sequences \(\eta _k\) and \(\theta _j\), together with the safeguard parameters \(\epsilon _1>0\), and \(\epsilon _2>0\) to observe an effective convergence of the inexact and implicit preconditioning scheme, i.e., Algorithm 6, with a controlled total number of inner iterations. It is worth mentioning that our inexact and implicit preconditioning strategy could be adapted to accelerate some other iterative inexact schemes for solving CARE.
For all experiments, we fix \(\sigma _{\min }=10^{-10}\), \(\sigma _{\max }=10^{10}\), \(\tau _{\min }=0.1\), \(\tau _{\max }=0.9\), \(\gamma =0.9\), \(M=2\), and \(\psi _0=10\), and set \(\psi _k= \psi _0/k^{1.2}\) for all \(k\ge 1\). Notice that this special choice of \(\psi _k\) guarantees that (15) holds. We choose the trial step length as \(\lambda _0=1\). We also set \(\eta _k= k^{m_\mathrm{klein}}\) in (2), for several values of \(m_{\mathrm{klein}}\); and \(\theta _j= j^{m_\mathrm{prec}}\) in (13), for several values of \(m_\mathrm{prec}\). If the preconditioner is not activated, i.e., if \(Z_j=I\) for all j, then we report the symbol \(**\) for the corresponding parameters that are not required: \(m_\mathrm{prec}\) and \(\epsilon _2\). Moreover, if the method fails to converge (i.e., more than 500 outer iterations), we use the symbol \(**\) to report the number of required iterations. In all cases, we will consider CARE for which the symmetric part of \(\mathcal {A}_k\) is negative definite for all k.
For our first experiment, we choose A as the matrix whose tridiagonal part is \(\hbox {tridiag}(-1,-4,-1)\), and such that in addition the entries \(A_{1,n}=A_{n,1}=1\), which is a special case of a test matrix described in Jbilou (2003). For the matrices B and C, we use the following three options: (i) the matrix B is fixed to be the identity matrix, and we choose C as a low-rank random matrix given by \(C = \tilde{C}^T \tilde{C}\) where \(\tilde{C}\) is an \(n\times s\) random matrix whose entries are chosen in [0,1] with a uniform distribution. For the second one (ii), the matrix B is fixed to be the identity matrix, and C is built from a truncated singular value decomposition (SVD) of the \(n\times n\) matrix \(\hbox {tridiag}(-1,2,-1)\), where the s active singular vectors are chosen randomly. For the third one (iii), we set \(B=\tilde{B}^T\tilde{B}/\Vert \tilde{B}\Vert _F\) with \(\tilde{B}=\hbox {rand}(n,p)\) and \(C=\tilde{C}^T\tilde{C}/\Vert \tilde{C}\Vert ^2_F\) where \(\tilde{C}=\hbox {rand}(n,s)\). In Tables 1, 2, and 3 we report the number of external iterations (Outer), the accumulated number of intermediate iterations (Intermediate), and also the accumulated number of inner iterations (Inner) of Algorithm 6 for different choices of the involved parameters. In Fig. 1, we show the (semilog) history of the convergence of \(\Vert R(X_k)\Vert _F\) for two different combinations: \(n=100,\;(m_\mathrm{prec},m_\mathrm{klein})=(3,2))\) and \(\epsilon _1= \epsilon _2 =10^{-2}\); and \(n=1000,\;(m_\mathrm{prec},m_\mathrm{klein})=(3,2))\) and \(\epsilon _1= \epsilon _2 =10^{-1}\), when \(C=\tilde{C}^T\tilde{C}\) and \(\tilde{C}=\hbox {rand}(n,s)\).
For our second experiment, we choose A as the two-dimensional (2D) discrete Laplacian matrix, given by \(A=\hbox {gallery}('\hbox {poisson}',n0)\) of size \(n_0^2 \times n_0^2\). The matrix B is a low-rank random matrix built as the truncated SVD of \(\hbox {pentadiag}(1,1,4,1,1)\) with p active singular vectors chosen randomly, and \(C=I\). In Table 4, we report the number of external iterations (outer), the accumulated number of intermediate iterations (intermediate), and also the total number of inner iterations (inner) of Algorithm 6 for different choices of the involved parameters.
For our third experiment, we choose A as the three-dimensional (3D) discrete Laplacian matrix of size \(n_0^3 \times n_0^3\). The matrix B is a low-rank random matrix built as the truncated SVD of \(\hbox {pentadiag}(1,1,6,1,1)\) with p active singular values chosen randomly, and \(C=I\). In Table 5, we report the number of external iterations (outer), the accumulated number of intermediate iterations (intermediate), and also the total number of inner iterations (inner) of Algorithm 6 for different choices of the involved parameters.
We can observe, from Tables 1, 2, 3, 4 and 5, and Fig. 1, that in general Algorithm 6 requires very few outer iterations, which indicates that our combined inexact scheme is asymptotically approximating the exact Newton iterations for solving CARE. The clear advantage, as can also be observed in all tables, is that for some choices of the involved parameters, the number of intermediate iterations, as well as the inner iterations, is controlled to avoid unnecessary internal iterations, and still achieve the required convergence. As expected, some combinations of the parameters \(\epsilon _1>0\), \(\epsilon _2>0\), \(m_\mathrm{klein}\), and \(m_\mathrm{prec}\) can obtain more effective results in number of inner iterations than others. In general, based on three different type of problems, the best combination of the involved parameters seems to be problem dependant, nevertheless, the choices \(m_\mathrm{prec}=3\), and \(m_\mathrm{klein}=1\) or \(m_\mathrm{klein}=2\), seem to perform effectively in all cases. Finally, we can also observe that if the implicit preconditioning strategy is not activated, i.e., if \(Z_j=I\) for all j, then the inexact scheme for solving CARE, tends to require a larger amount of intermediate iterations for small problems, and to fail to converge for larger problems.
6 Final remarks
We have introduced and analyzed a combined scheme for solving CARE based on the use of inexact Kleinman–Newton iterations with an implicit preconditioning strategy for solving the Lyapunov equations at each inexact Newton step. The internal iterative process builds the search directions implicitly, using an ODE dynamical model, to produce a preconditioned technique that accelerates the convergence for solving each internal Lyapunov equation. For robustness, the intermediate iterative process is combined with a non-monotone globalization strategy. An advantage of this combined outer–inner strategy is that the required accuracy can be controlled at each Kleinman–Newton inner step, and also at each iterative process for solving the Lyapunov equations, and as a consequence unnecessary internal iterations are avoided, reducing the total required computational work. At the same time, a suitable stopping criterion has been designed for each iterative process to maintain the convergence properties.
In the last few years, for large-scale problems, the inexact Kleinman–Newton scheme has also been combined with ADI iterations, and also with Krylov-type iterative projection methods, for solving the internal Lyapunov equations. Our inexact and implicit preconditioning strategy could be adapted and extended to accelerate the convergence of these other iterative inexact schemes for solving CARE. Nevertheless, these extensions clearly require further theoretical and numerical investigation.
References
Antoulas AC (2005) Approximation of large-scale dynamical systems. SIAM, Philadelphia
Bao L, Wei Y, Lin Y (2006) Krylov subspace methods for the generalized Sylvester equation. Appl Math Comput 175:557–573
Benner P, Byers R (1998) An exact line search method for solving generalized continuous-time algebraic Riccati equations. IEEE Trans Automat Control 43:101–107
Benner P, Li J-L, Penzl T (2008a) Numerical solution of large-scale Lyapunov equations, Riccati equations, and linear-quadratic optimal control problems. Numer Linear Algebra Appl 15:755–777
Benner P, Mena H, Saak J (2008b) On the parameter selection problem in the Newton-ADI iteration for large-scale Riccati equations. Electron Trans Numer Anal 29:136–149
Bini DA, Iannazzo B, Meini B (2012) Numerical solution of algebraic Riccati equations. SIAM, Philadelphia
Birgin EG, Martínez JM, Raydan M (2014) Spectral projected gradient methods: review and perspectives. J Stat Softw 60(3)
Bouhamidi A, Jbilou K (2008) A note on the numerical approximate solutions for generalized Sylvester matrix equations with applications. Appl Math Comput 256:687–694
Chehab J-P, Raydan M (2005) Inverse and adaptive preconditioned gradient methods for nonlinear problems. Appl Numer Math 55:32–47
Chehab J-P, Raydan M (2009) Implicitly preconditioned and globalized residual method for solving steady fluid flows. ETNA 34:136–151
Chehab J-P, Raydan M (2011) An implicit preconditioning strategy for large-scale generalized Sylvester equations. Appl Math Comput 217:8793–8803
Damm T (2008) Direct methods and ADI-preconditioned Krylov subspace methods for generalized Lyapunov equations. Numer Linear Algebra Appl 15:853–871
Datta BN (2003) Numerical methods for linear control systems design and analysis. Elsevier Press, Amsterdam
Dembo RS, Eisenstat SC, Steihaug T (1982) Inexact Newton methods. SIAM J Numer Anal 19:400–408
Eisenstat SC, Walker HF (1996) Choosing the forcing terms in inexact Newton method. SIAM J Sci Comput 17:16–32
El Guennouni A, Jbilou K, Riquet AJ (2002) Block Krylov subspace methods for solving large Sylvester equations. Numer Algorithms 29:75–96
Feitzinger F, Hylla T, Sachs EW (2009) Inexact Kleinman–Newton method for Riccati equations. SIAM J Matrix Anal Appl 31:272–288
Guo C-H, Lancaster P (1998) Analysis and modification of Newton’s method for algebraic Riccati equations. Math Comput 67:1089–1105
Hackbruck M, Starke G (1995) Preconditioned Krylov subspace methods for Lyapunov matrix equations. SIAM J Matrix Anal Appl 16:156–171
Heyouni M, Jbilou K (2009) An extended block Arnoldi algorithm for large-scale solutions of the continuous-time algebraic Riccati equation. Electron Trans Numer Anal 33:53–62
Horn RA, Johnson CR (1991) Topics in matrix analysis. Cambridge University Press, Cambridge
Jaimoukha IM, Kasenally EM (1994) Krylov subspace methods for solving large Lyapunov equations. SIAM J Matrix Anal Appl 31:227–251
Jbilou K (2003) Block Krylov subspace methods for large algebraic Riccati equations. Numer Algorithms 34:339–373
Jbilou K (2006) An Arnoldi based algorithm for large algebraic Riccati equations. Appl Math Lett 19:437–474
Jbilou K (2010) ADI preconditioned Krylov methods for large Lyapunov matrix equations. Linear Algebra Appl 432:2473–2485
Jbilou K, Riquet A (2006) Projection methods for large Lyapunov matrix equations. Linear Algebra Appl 415:344–358
Kleinman D (1968) On an iterative technique for Riccati equation computations. IEEE Trans Automat Control 13:114–115
La Cruz W, Martínez JM, Raydan M (2006) Spectral residual method without gradient information for solving large-scale nonlinear systems. Math Comput 75:1449–1466
Lancaster P, Rodman L (1995) The algebraic Riccati equation. Oxford University Press, Oxford
Mehrmann V (1991) The autonomous linear quadratic control problem, theory and numerical solution, Lecture Notes in Control and Information Sciences, 163. Springer, Berlin
Sandell NR (1974) On Newton’s method for Riccati equation solution. IEEE Trans Automat Control 19:254–255
Simoncini V, Szyld DB, Monsalve M (2014) On two numerical methods for the solution of large-scale algebraic Riccati equations. IMA J Numer Anal 34:904–920
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by Jinyun Yuan.
Marcos Raydan: Partially supported by CCCT Center at UCV.
Rights and permissions
About this article
Cite this article
Chehab, JP., Raydan, M. Inexact Newton’s method with inner implicit preconditioning for algebraic Riccati equations. Comp. Appl. Math. 36, 955–969 (2017). https://doi.org/10.1007/s40314-015-0274-8
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40314-015-0274-8