Skip to main content
SpringerLink
Log in

Picard Iteration, Chebyshev Polynomials and Chebyshev-Picard Methods: Application in Astrodynamics

  • Published:
The Journal of the Astronautical Sciences Aims and scope Submit manuscript

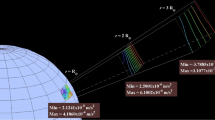
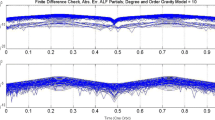
Abstract

This paper extends previous work on parallel-structured Modified Chebyshev Picard Iteration (MCPI) Methods. The MCPI approach iteratively refines path approximation of the state trajectory for smooth nonlinear dynamical systems and this paper shows that the approach is especially suitable for initial value problems of astrodynamics. Using Chebyshev polynomials, as the orthogonal approximation basis, it is straightforward to distribute the computation of force functions needed in MCPI to generate the polynomial coefficients (approximating the path iterations) to different processors. Combining Chebyshev polynomials with Picard iteration, MCPI methods iteratively refines path estimates over large time intervals chosen to be within the domain of convergence of Picard iteration. The developed vector-matrix form makes MCPI methods computationally efficient and a more systematic approach is given, leading to a modest correction to results in the published dissertation by Bai. The power of MCPI methods for solving IVPs is clearly illustrated using a simple nonlinear differential equation with a known analytical solution. Compared with the most common integration scheme, the standard Runge-Kutta 4-5 method as implemented in MATLAB, MCPI methods generate solutions with better accuracy as well as orders of magnitude speedups, on a serial machine. MCPI performance is also compared to state of the art integrators such as the Runge-Kutta Nystrom 12(10) methods applied to the relevant orbit mechanics problems. The MCPI method is shown to be well-suited to solving these problems in serial processors with over an order of magnitude speedup relative to known methods. Furthermore, the approach is parallel-structured so that it is suited for parallel implementation and further speedups. When used in conjunction with the recently developed local gravity approximations in conjunction with parallel computation, we anticipate MCPI will enable revolutionary speedups while ensuring accuracy.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16

Similar content being viewed by others

References

  1. Gravity recovery and climate experiment (grace). http://www.csr.utexas.edu/grace/gravity/

  2. Agarwal, R.P.: Nonlinear two–point boundary value problems. Indian J. Pure Appl. Math. 4, 757–769 (1973)

    MathSciNet  Google Scholar 

  3. Bai, X.: Modified Chebyshev-Picard Iteration Methods for Solution of Initial Value and Boundary Value Problems. Ph.D. dissertation, Texas A&M Univ, College Station, TX (2010)

  4. Bai, X., Junkins, J.L.: Modified chebyshev-picard iteration methods for solution of initial value problems. Monterey, CA, Kyle T. Alfriend Astrodynamics Symposium (2010)

  5. Bai, X., Junkins, J.L.: Solving initial value problems by the picard-chebyshev method with nvidia gpus. San Diego, CA, 20th Spaceflight Mechanics Meeting (2010)

  6. Bailey, P., Shampine, L.F., Waltman, P.: Existence and uniqueness of solutions of the second order boundary value problem. Bull. Am. Math. Soc. 72(1), 96–98 (1966)

    Article  MATH  MathSciNet  Google Scholar 

  7. Bailey, P.B.: On the interval of convergence of Picard’s iteration. ZAMM - J. Appl. Math. Mech. 48(2), 127–128 (1968)

    Article  MATH  Google Scholar 

  8. Clenshaw, C.W., Norton, H.J.: The solution of nonlinear ordinary differential equations in Chebyshev series. Comput. J. 6(1), 88–92 (1963)

    Article  MATH  MathSciNet  Google Scholar 

  9. Coddington, E. A., Levinson, N.: Theory of ordinary differential equations. McGraw-Hill, New York (1955)

    MATH  Google Scholar 

  10. Coles, W.J., Sherman, T.L.: Convergence of successive approximations for nonlinear two-point boundary value problems. SIAM J. Appl. Math. 15(2), 426–433 (Mar. 1967)

    Article  MATH  MathSciNet  Google Scholar 

  11. Feagin, T.: The Numerical Solution of Two Point Boundary Value Problems Using Chebyshev Series. Ph.D. dissertation, The Universtiy of Texas at Austin, Austin, TX (1973)

  12. Feagin, T., Nacozy, P.: Matrix formulation of the Picard method for parallel computation. Celest. Mech. Dyn. Astron. 29(2), 107–115 (1983)

    Article  MATH  MathSciNet  Google Scholar 

  13. Fox, L., Parker, I.B: Chebyshev polynomials in numerical analysis. UK: Oxford University Press, London (1972)

    Google Scholar 

  14. Fukushima, T.: Picard iteration method, chebyshev polynomial approximation, and global numerical integration of dynamical motions. Astron. J. 113(5), 1909–1914 (May. 1997)

    Article  MathSciNet  Google Scholar 

  15. Fukushima, T.: Vector integration of dynamical motions by the Picard-Chebyshev method. Astron. J. 113(6), 2325–2328 (1997)

    Article  Google Scholar 

  16. Junkins, J.L.: Investigation of finite-element representations of the geopotential. AIAA J. 14(6), 803–808 (1976)

    Article  MATH  MathSciNet  Google Scholar 

  17. Lindelöf, E.: Sur l application de la methode des approximations successives aux equations dif-ferentielles ordinaires du premier ordre. Comptes rendus hebdomadaires des seances de l Academie des sci. 114, 454–457 (1894)

    Google Scholar 

  18. Norton, H.J.: The iterative solution of non-linear ordinary differential equations in Chebyshev series. Comput. J. 7(2), 76–85 (1964)

    Article  MATH  MathSciNet  Google Scholar 

  19. Parker, G.E., Sochacki, J.S.: Implementing the Picard iteration. Neural, Parallel & Sci. Comput. 4(1), 97–112 (1996)

    MATH  MathSciNet  Google Scholar 

  20. Pines, S.: Uniform representation of the gravitational potential and its derivatives. AIAA J. 11, 1508–1511 (1973)

    Article  MATH  Google Scholar 

  21. Shaver, J.S.: Formulation and evaluation of parallel algorithms for the orbit determination problem. Massachusetts Institute of Technology, Department of Aeronautics and Astronautics (1980). http://books.google.com/books?id=09JvtwAACAAJ

  22. Schaub, H., Junkins, J.L.: Analytical mechanics of space systems, 2nd ed. AIAA Education series, Reston, VA (2011)

  23. Scraton, R.E.: The solution of linear differential equations in Chebyshev series. Comput. J. 8(1), 57–61 (1965)

    Article  MATH  MathSciNet  Google Scholar 

  24. Snay, R.A.: Applicability of array algebra. Rev. Geophys. 16(3), 459–464 (1978)

    Article  Google Scholar 

  25. Van, J.: de Craats. On the region of convergence of picard’s iteration. ZAMM-J. Appl. Math. Mech. 52, 487–491 (1971)

    Google Scholar 

  26. Van, J.: de Craats. On the region of convergence of picard’s iteration. ZAMM - J Appl. Math. Mech / Z. Angew. Math. Mech. 62, 487–491 (1972)

    Google Scholar 

  27. Vlassenbroeck, J., Dooren, R.V.: A Chebyshev technique for solving nonlinear optimal controlproblems. IEEE Tans. Autom. Control 33(4), 333–340 (1988)

    Article  MATH  Google Scholar 

  28. Wright, K.: Chebyshev collocation methods for ordinary differential equations. Comput. J. 6(4), 358–365 (1964)

    Article  MATH  MathSciNet  Google Scholar 

Download references

Acknowledgments

This work was conducted under the Air Force Office of Scientific Research Contract FA9550-11-1-0279; the support of our program managers Kent Miller and Julie Moses are gratefully acknowledged.

Author information

Authors and Affiliations

  1. Aerospace Engineering Department, Texas A & M University, 722 H.R. Bright Building, 3141 TAMU, College Station, TX, 77843-3141, USA

    John L. Junkins

  2. Aerospace Engineering Department, Khalifa University, Abu Dhabi, United Arab Emirates

    Ahmad Bani Younes

  3. Aerospace Engineering Department, Texas A & M University, 701 H.R. Bright Building, 3141 TAMU, College Station, TX, 77843-3141, USA

    Robyn M. Woollands

  4. Mechanical and Aerospace Engineering, Rutgers, The State University of New Jersey, 98 Brett Rd., EN B-222, Piscataway, NJ, 08854, USA

    Xiaoli Bai

Authors
  1. John L. Junkins
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Ahmad Bani Younes
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Robyn M. Woollands
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Xiaoli Bai
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to John L. Junkins.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Junkins, J.L., Bani Younes, A., Woollands, R.M. et al. Picard Iteration, Chebyshev Polynomials and Chebyshev-Picard Methods: Application in Astrodynamics. J of Astronaut Sci 60, 623–653 (2013). https://doi.org/10.1007/s40295-015-0061-1

Download citation

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s40295-015-0061-1

Keywords

Search

Navigation