Introduction

Recently, the thermodynamic properties of DNA circular molecules have been investigated by a new path integral computational method and the entropic reductions associated to the formation of the ordered helicoidal structure have been estimated [1, 2]. Now, the question arises that is there any relation between thermodynamics of DNA and its radiated waves. Previously, it has been shown that phonon are main causes of the emergence of temperature and thermodynamical evolutions [3]. In that research, it has been shown that these fields have direct effects on electrons and leads to their motions [4]. By moving electrons, some photons are produced and electromagnetic fields are emerged. Consequently, thermodynamics and entropy of each thermal system like DNA has a direct relation with its radiated waves. In the present paper, we will propose a model which lets us to obtain the relation between entropy of DNA and frequency waves. Then, we test the model in a system of ex ovo–in ovo systems. In fact, we use this model for spectroscopy of DNAs in ovo. To this aim, we mixed previous results in [1, 3, 4] with the electronic model for DNA which was discussed in [5]. In this paper, the structure of DNA was compared with an structure of electronic receiver or sender. It was argued that DNA acts like the receiver and sender of radio waves and transmits its information by exchanging waves with other DNAs. Using above results, we propose a new technique for imaging of entropy of DNAs in a chick embryo in ovo. In this mechanism, we put cells of ex ovo near cells in ovo and connect them by a magnetic field. This magnetic field is produced by an inductor in which one end of it is connected to a generator and another end is connected to an scope. In this circuit, generator produces initial current and scope take output currents. We consider differences between output and input currents and use them for considering evolutions of entropy of DNAs in a chick embryo in ovo.

The outline of the paper is as follows. In “A mathematical model for calculating the relation between entropy and frequency of waves” section, we propose a mathematical model for calculating entropy of DNAs in terms of frequency of waves. In “A review on similarity between DNA and electronic devices” section, we review similarity between DNA and electronic devices. In “Materials and methods for providing cells ex and in ovo” section, we consider material and method for providing DNAs of chick embryos in and ex ovo. In “A circuit for detecting waves of DNAs in ovo” section, we will construct the needed circuit for detecting waves of DNAs in ovo and considering evolutions of their entropy. In “Results” section, we show results and analyzed figures. The last section is devoted to conclusions.

A mathematical model for calculating the relation between entropy and frequency of waves

Each DNA has been constructed from four types of bases that couple to each other and form A–T and C–G base pairs. On the other hand, bases in a DNA construct hexagonal and pentagonal molecules which exchange information with each other (See Fig. 1). DNA has a long around 7 m; however, it is compacted in an small place around nanometer. Thus, we can expect that a curved space-time is emerged around it. To consider thermodynamics of this system, we use equivalence between thermal system and accelerating system. In fact, a rotating DNA experiences a type of acceleration and should be considered in an accelerating frame. Previously, the metric of accelerating frame has been obtained [5, 6];

$$\begin{aligned}&{{\mathrm{d}}}s^{2}=-{\mathrm{d}}t^{2} + {\mathrm{d}}r^{2} + r^{2}\left( {\mathrm{d}}\theta ^{2} + \sin ^{2}\theta {\mathrm{d}}\phi ^{2}\right) + \sum _{i=1}^{6}{\mathrm{d}}x_{i}^{2} \end{aligned}$$
(1)
Fig. 1
figure 1

The hexagonal and pentagonal molecules that form a DNA

Full size image

We assume that molecules are rotated with the acceleration. In this case, the relation between the world volume coordinates of the rotating DNA (\(\tau , \sigma\)) and the coordinates of Minkowski space-time (t, r) are [5, 6];

$$\begin{aligned}&at= e^{a\sigma } \sinh (a\tau ) \quad ar=e^{a\sigma } \cosh (a\tau ) \end{aligned}$$
(2)

where a is the acceleration of rotating molecules. We can suppose that the coordinate along the separation distance between molecules (\(x^{4} = z\)) depends on the \(r =\pm \frac{1}{a} e^{\pm a\sigma } \cosh (a\tau )\) and by using Eq. (2), rewrite Eq. (1) as:

$$\begin{aligned}&{\mathrm{d}}s^{2}_{I}=-{\mathrm{d}}t^{2} + \left( 1 + \left( \frac{{\mathrm{d}}z}{{\mathrm{d}}r}\right) ^{2} \right) {\mathrm{d}}r^{2} + r^{2}\left( {\mathrm{d}}\theta ^{2} + \sin ^{2}\theta {\mathrm{d}}\phi ^{2}\right) + \sum _{i=1}^{5}{\mathrm{d}}x_{i}^{2} \nonumber \\&\quad = \left( e^{2a\sigma } + \frac{1}{\sinh ^{2}(a\tau )}\left( \frac{{\mathrm{d}}z}{{\mathrm{d}}\tau }\right) ^{2} \right) {\mathrm{d}}\tau ^{2} - \left( e^{2a\sigma }+ \frac{1}{\cosh ^{2}(a\tau )}\left( \frac{{\mathrm{d}}z}{{\mathrm{d}}\sigma }\right) ^{2} \right) {\mathrm{d}}\sigma ^{2} \nonumber \\&\qquad + \frac{1}{\sinh (a\tau )\cosh (a\tau )}\left( \frac{{\mathrm{d}}z}{{\mathrm{d}}\tau }\frac{{\mathrm{d}}z}{{\mathrm{d}}\sigma }\right) {\mathrm{d}}\tau {\mathrm{d}}\sigma \nonumber \\&\qquad + \left( \frac{1}{a}e^{a\sigma } \cosh (a\tau )\right) ^{2}\left( {\mathrm{d}}\theta ^{2} + \sin ^{2}\theta {\mathrm{d}}\phi ^{2}\right) + \sum _{i=1}^{5}{\mathrm{d}}x_{i}^{2} \end{aligned}$$
(3)

Now, we can replace acceleration with its equivalent temperature. On the other hand, we want to obtain a relation between temperature and frequency of radiating waves by DNAs. Previously, it has been shown that temperature has the below relation with acceleration [5]:

$$\begin{aligned}&a \sim 2\pi T= \frac{2\pi T_{0}}{\sqrt{1-\frac{l_{0}^{2}\omega ^{2}}{c^{2}}}} \end{aligned}$$
(4)

where \(T_{0}\) is temperature of non-rotating DNA and \(\omega\) is the frequency of radiating waves by DNAs. Substituting Eq. (4) in Eq. (3), we obtain the below metric in terms of frequency of radiating waves:

$$\begin{aligned}&{\mathrm{d}}s^{2}= \left( e^{2\frac{2\pi T_{0}}{\sqrt{1-\frac{l_{0}^{2}\omega ^{2}}{c^{2}}}}\sigma } + \frac{1}{\sinh ^{2}\left( \frac{2\pi T_{0}}{\sqrt{1-\frac{l_{0}^{2}\omega ^{2}}{c^{2}}}}\tau \right) }\left( \frac{{\mathrm{d}}z}{{\mathrm{d}}\tau }\right) ^{2} \right) {\mathrm{d}}\tau ^{2}\nonumber \\&\qquad - \left( e^{2\frac{2\pi T_{0}}{\sqrt{1-\frac{l_{0}^{2}\omega ^{2}}{c^{2}}}}\sigma }+ \frac{1}{\cosh ^{2}\left( \frac{2\pi T_{0}}{\sqrt{1-\frac{l_{0}^{2}\omega ^{2}}{c^{2}}}}\tau \right) } \left( \frac{{\mathrm{d}}z}{{\mathrm{d}}\sigma }\right) ^{2} \right) {\mathrm{d}}\sigma ^{2} \nonumber \\&\qquad + \frac{1}{\sinh \left( \frac{2\pi T_{0}}{\sqrt{1-\frac{l_{0}^{2}\omega ^{2}}{c^{2}}}}\tau \right) \cosh \left( \frac{2\pi T_{0}}{\sqrt{1-\frac{l_{0}^{2}\omega ^{2}}{c^{2}}}}\tau \right) } \left( \frac{{\mathrm{d}}z}{{\mathrm{d}}\tau }\frac{{\mathrm{d}}z}{{\mathrm{d}}\sigma }\right) {\mathrm{d}}\tau {\mathrm{d}}\sigma \nonumber \\&\qquad + \left( \frac{1}{\frac{2\pi T_{0}}{\sqrt{1-\frac{l_{0}^{2}\omega ^{2}}{c^{2}}}}}e^{\frac{2\pi T_{0}}{\sqrt{1-\frac{l_{0}^{2}\omega ^{2}}{c^{2}}}}\sigma } \cosh \left( \frac{2\pi T_{0}}{\sqrt{1-\frac{l_{0}^{2}\omega ^{2}}{c^{2}}}}\tau \right) \right) ^{2}\left( {\mathrm{d}}\theta ^{2} + \sin ^{2}\theta {\mathrm{d}}\phi ^{2}\right) \nonumber \\&\qquad + \sum _{i=1}^{5}{\mathrm{d}}x_{i}^{2} \end{aligned}$$
(5)

Above metric is corresponded to thermal radiating DNAs. This metric depends on the temperature and radiating waves by DNAs.

To obtain the spectrum of rotating DNA with hexagonal manifolds, we should obtain the action of hexagonal and pentagonal manifolds. To this aim, we will use concept of electronic model for DNA in [5]. Instead of hexagonal and pentagonal manifolds, we use polygonal manifolds with N vertexes. For flat space-time, the action of polygonal manifold is:

$$\begin{aligned}&S_{N}=-T_{tri} \int d^{3}\sigma \sqrt{\eta ^{ab} g_{MN}\partial _{a}X^{M}\partial _{b}X^{N}+2\pi l_{s}^{2}G(F))}\nonumber \\&\quad G=\left( \sum _{n=1}^{3}\frac{1}{n!} \left( -\frac{F_{1}..F_{n}}{\beta ^{2}}\right) \right) \nonumber \\&\quad F=F_{\mu \nu }F^{\mu \nu }\quad F_{\mu \nu }=\partial _{\mu }A_{\nu }- \partial _{\nu }A_{\mu } \end{aligned}$$
(6)

where \(g_{MN}\) is the background metric, \(X^{M}(\sigma ^{a})\)’s are scalar fields which are constructed by pairing electrons, \(\sigma ^{a}\)’s are the DNA coordinates, \(a, b = 0, 1, ..., 3\) are world volume indices of rotating DNA and \(M,N=0, 1, ..., 10\) are eleven-dimensional spacetime indices. Also, G is the nonlinear field [5] and A is the photon which exchanges between molecules. In a curved space-time, with the metrics in Eq. (3), we obtain:

$$\begin{aligned}&S_{N} = - \int {\mathrm{d}}t \int _{\sigma _{0}}^{\infty }{\mathrm{d}}\sigma \left( \frac{1}{}e^{\frac{2\pi T_{0}}{\sqrt{1-\frac{l_{0}^{2}\omega ^{2}}{c^{2}}}} \sigma } \cosh \left( \frac{2\pi T_{0}}{\sqrt{1-\frac{l_{0}^{2}\omega ^{2}}{c^{2}}}} \tau \right) \right) ^{2}\nonumber \\&\qquad \left( \sinh ^{2}\left( \frac{2\pi T_{0}}{\sqrt{1-\frac{l_{0}^{2}\omega ^{2}}{c^{2}}}} \tau \right) +\cosh ^{2}\left( \frac{2\pi T_{0}}{\sqrt{1-\frac{l_{0}^{2}\omega ^{2}}{c^{2}}}} \tau \right) \right) \nonumber \\&\qquad \times \left( 1 + \frac{e^{-2\frac{2\pi T_{0}}{\sqrt{1-\frac{l_{0}^{2}\omega ^{2}}{c^{2}}}} \sigma }}{\sinh ^{2}\left( \frac{2\pi T_{0}}{\sqrt{1-\frac{l_{0}^{2}\omega ^{2}}{c^{2}}}} \tau \right) }\left( \frac{{\mathrm{d}}z}{{\mathrm{d}}\tau }\right) ^{2} + \frac{e^{-2\frac{2\pi T_{0}}{\sqrt{1-\frac{l_{0}^{2}\omega ^{2}}{c^{2}}}} \sigma }}{\cosh ^{2}\left( \frac{2\pi T_{0}}{\sqrt{1-\frac{l_{0}^{2}\omega ^{2}}{c^{2}}}} \tau \right) }\left( \frac{{\mathrm{d}}z}{{\mathrm{d}}\sigma }\right) ^{2} \right. \nonumber \\&\qquad \left. + \frac{e^{-2\frac{2\pi T_{0}}{\sqrt{1-\frac{l_{0}^{2}\omega ^{2}}{c^{2}}}} \sigma }}{\sinh \left( \frac{2\pi T_{0}}{\sqrt{1-\frac{l_{0}^{2}\omega ^{2}}{c^{2}}}} \tau \right) \cosh \left( \frac{2\pi T_{0}}{\sqrt{1-\frac{l_{0}^{2}\omega ^{2}}{c^{2}}}} \tau \right) }\left( \left( \frac{{\mathrm{d}}z}{{\mathrm{d}}\tau }\frac{{\mathrm{d}}z}{{\mathrm{d}}\sigma }\right) \right) \right. \nonumber \\&\qquad \left. -(2\pi l_{s}^{2}G(F)) \right) ^{\frac{1}{2}} \end{aligned}$$
(7)

Using the method in ref [5], we can obtain the energy for polygonal ( hexagonal and pentagonal) molecules:

$$\begin{aligned}&E_{N}= \int {\mathrm{d}}^{3}\sigma \left( 1 + \frac{e^{-2\frac{2\pi T_{0}}{\sqrt{1-\frac{l_{0}^{2}\omega ^{2}}{c^{2}}}} \sigma }}{\sinh ^{2}\left( \frac{2\pi T_{0}}{\sqrt{1-\frac{l_{0}^{2}\omega ^{2}}{c^{2}}}} \tau \right) }\left( \frac{{\mathrm{d}}z}{{\mathrm{d}}\tau }\right) ^{2} + \frac{e^{-2\frac{2\pi T_{0}}{\sqrt{1-\frac{l_{0}^{2}\omega ^{2}}{c^{2}}}} \sigma }}{\cosh ^{2}\left( \frac{2\pi T_{0}}{\sqrt{1-\frac{l_{0}^{2}\omega ^{2}}{c^{2}}}} \tau \right) }\left( \frac{{\mathrm{d}}z}{{\mathrm{d}}\sigma }\right) ^{2} \right. \nonumber \\&\qquad \left. + \frac{e^{-2\frac{2\pi T_{0}}{\sqrt{1-\frac{l_{0}^{2}\omega ^{2}}{c^{2}}}} \sigma }}{\sinh \left( \frac{2\pi T_{0}}{\sqrt{1-\frac{l_{0}^{2}\omega ^{2}}{c^{2}}}} \tau \right) \cosh \left( \frac{2\pi T_{0}}{\sqrt{1-\frac{l_{0}^{2}\omega ^{2}}{c^{2}}}} \tau \right) }\left( \left( \frac{{\mathrm{d}}z}{{\mathrm{d}}\tau }\frac{{\mathrm{d}}z}{{\mathrm{d}}\sigma }\right) \right) \right) O_{N,tot} \nonumber \\&O_{N,tot} =\sqrt{1+\frac{k^{2}_{3}}{O_{N-1,tot} \left( \frac{1}{\frac{2\pi T_{0}}{\sqrt{1-\frac{l_{0}^{2}\omega ^{2}}{c^{2}}}} }e^{\frac{2\pi T_{0}}{\sqrt{1-\frac{l_{0}^{2}\omega ^{2}}{c^{2}}}} \sigma } \cosh \left( \frac{2\pi T_{0}}{\sqrt{1-\frac{l_{0}^{2}\omega ^{2}}{c^{2}}}} \tau \right) \right) ^{4}}} \nonumber \\&\qquad \times .....\sqrt{1+\frac{k^{2}_{2}}{O_{1,tot} \left( \frac{1}{\frac{2\pi T_{0}}{\sqrt{1-\frac{l_{0}^{2}\omega ^{2}}{c^{2}}}} }e^{\frac{2\pi T_{0}}{\sqrt{1-\frac{l_{0}^{2}\omega ^{2}}{c^{2}}}} \sigma } \cosh \left( \frac{2\pi T_{0}}{\sqrt{1-\frac{l_{0}^{2}\omega ^{2}}{c^{2}}}} \tau \right) \right) ^{4}}}O_{1,I,half} \nonumber \\&O_{1,tot}=\left( \frac{1}{\frac{2\pi T_{0}}{\sqrt{1-\frac{l_{0}^{2}\omega ^{2}}{c^{2}}}} }e^{\frac{2\pi T_{0}}{\sqrt{1-\frac{l_{0}^{2}\omega ^{2}}{c^{2}}}} \sigma } \cosh \left( \frac{2\pi T_{0}}{\sqrt{1-\frac{l_{0}^{2}\omega ^{2}}{c^{2}}}} \tau \right) \right) ^{2}\nonumber \\&\qquad \sqrt{1 + \frac{K^{2}}{\left( \frac{1}{\frac{2\pi T_{0}}{\sqrt{1-\frac{l_{0}^{2}\omega ^{2}}{c^{2}}}} }e^{\frac{2\pi T_{0}}{\sqrt{1-\frac{l_{0}^{2}\omega ^{2}}{c^{2}}}} \sigma } \cosh \left( \frac{2\pi T_{0}}{\sqrt{1-\frac{l_{0}^{2}\omega ^{2}}{c^{2}}}} \tau \right) \right) ^{4}}} \nonumber \\&\qquad \times \left( \sinh ^{2}\left( \frac{2\pi T_{0}}{\sqrt{1-\frac{l_{0}^{2}\omega ^{2}}{c^{2}}}} \tau \right) +\cosh ^{2}\left( \frac{2\pi T_{0}}{\sqrt{1-\frac{l_{0}^{2}\omega ^{2}}{c^{2}}}} \tau \right) \right) \end{aligned}$$
(8)

where N is the number of vertexes. For constructing a hexagonal molecule or pentagonal one, it is sufficient to put \(N=6\) or \(N=5\). Now, we can obtain the entropy of hexagonal and pentagonal molecules. Using energies in Eq. (8) and assuming (\(z =\sigma\), \(\bar{z} =\bar{\sigma }\)), we obtain:

$$\begin{aligned}&\bar{S}_{6}^{tot}=\int \frac{{\mathrm{d}} E_{6}^{tot}}{T}\nonumber \\&=2\left[ \left( \frac{1}{\frac{2\pi T_{0}}{\sqrt{1-\frac{l_{0}^{2}\omega ^{2}}{c^{2}}}} }e^{\frac{2\pi T_{0}}{\sqrt{1-\frac{l_{0}^{2}\omega ^{2}}{c^{2}}}} \sigma } \cosh \left( \frac{2\pi T_{0}}{\sqrt{1-\frac{l_{0}^{2}\omega ^{2}}{c^{2}}}} \tau \right) \right) ^{2}\right. \nonumber \\&\qquad \left. \sqrt{1 + \frac{K^{2}}{\left( \frac{1}{\frac{2\pi T_{0}}{\sqrt{1-\frac{l_{0}^{2}\omega ^{2}}{c^{2}}}} }e^{\frac{2\pi T_{0}}{\sqrt{1-\frac{l_{0}^{2}\omega ^{2}}{c^{2}}}} \sigma } \cosh \left( \frac{2\pi T_{0}}{\sqrt{1-\frac{l_{0}^{2}\omega ^{2}}{c^{2}}}} \tau \right) \right) ^{4}}} \right. \nonumber \\&\left. \times \left( \sinh ^{2}\left( \frac{2\pi T_{0}}{\sqrt{1-\frac{l_{0}^{2}\omega ^{2}}{c^{2}}}} \tau \right) +\cosh ^{2}\left( \frac{2\pi T_{0}}{\sqrt{1-\frac{l_{0}^{2}\omega ^{2}}{c^{2}}}} \tau \right) \right) \right] ^{-6} \end{aligned}$$
(9)
$$\begin{aligned}&\bar{S}_{5}^{tot}=\int \frac{d E_{5}^{tot}}{T}\nonumber \\&\qquad 2\left[ \left( \frac{1}{\frac{2\pi T_{0}}{\sqrt{1-\frac{l_{0}^{2}\omega ^{2}}{c^{2}}}} }e^{\frac{2\pi T_{0}}{\sqrt{1-\frac{l_{0}^{2}\omega ^{2}}{c^{2}}}} \sigma } \cosh \left( \frac{2\pi T_{0}}{\sqrt{1-\frac{l_{0}^{2}\omega ^{2}}{c^{2}}}} \tau \right) \right) ^{2}\right. \nonumber \\&\qquad \left. \sqrt{1 + \frac{K^{2}}{\left( \frac{1}{\frac{2\pi T_{0}}{\sqrt{1-\frac{l_{0}^{2}\omega ^{2}}{c^{2}}}} }e^{\frac{2\pi T_{0}}{\sqrt{1-\frac{l_{0}^{2}\omega ^{2}}{c^{2}}}} \sigma } \cosh \left( \frac{2\pi T_{0}}{\sqrt{1-\frac{l_{0}^{2}\omega ^{2}}{c^{2}}}} \tau \right) \right) ^{4}}}\right. \nonumber \\&\qquad \left. \times \left( \sinh ^{2}\left( \frac{2\pi T_{0}}{\sqrt{1-\frac{l_{0}^{2}\omega ^{2}}{c^{2}}}} \tau \right) +\cosh ^{2}\left( \frac{2\pi T_{0}}{\sqrt{1-\frac{l_{0}^{2}\omega ^{2}}{c^{2}}}} \tau \right) \right) \right] ^{-5} \end{aligned}$$
(10)

Above entropies depend on total energy of rotating hexagonal and pentagonal molecules. On the other hand in Eq. (8), energies depend on the frequency of radiated waves of DNA. Thus, entropies of rotating hexagonal molecules depend on frequency of radiated waves of DNA.

A review on similarity between DNA and electronic devices

In this paper, we use the communications between DNAs for imaging of entropy. This idea has been taken from our previous work in [5]. In that paper, we have shown that structure of DNA is very similar to the structure of a receiver or sender radio waves. Before introducing mechanism, we make a review on the similarity between DNA and electronic devices.

Fig. 2
figure 2

DNA could be an inductor which produces magnetic field [5]

Full size image
Fig. 3
figure 3

By coiling DNA around various axises, some new types of inductors are produced. Each of these inductors emits a new magnetic field [5]

Full size image

Each DNA molecule contains two biopolymer strands, which are coiled around each other to build a double helix. The nitrogenous bases of the two separate strands are bounded together, according to base pairing rules (A with T, and C with G), with hydrogen bounds to make a double-stranded DNA molecule. Each base pair contains two or three electric dipoles, which produce an strong electric field along the coil. The electric fields of all bases are summed with each other and create a pure electric field along the coil. This electric field induces a force on electrons and creates a current along the coil of DNA. This leads to the emergence of an inductor in a DNA molecule (see Fig. 2).

The length of a DNA is much greater than the size of the nucleus and for this reason, the DNA has to be packed tightly in a chromosome. The degree to which DNA is compressed is called its packing ratio [5]. In a chromosome, this packing occurs during several stages. In the first stage of packing, DNA winds around a protein core to produce a “bead-like” structure termed a nucleosome. This results in a packing ratio of about 6. The second stage of packing is the coiling of beads in a helical structure called the 30 nm fiber that is found in all types of chromosomes. This structure increases the packing ratio to about 40. The final packaging happens when the fiber is organized in loops, scaffolds and domains that give a final packing ratio of about 1000–10,000 in different types of chromosomes. During these stages, four types of inductor or coil appear. One coil emerges because the electric dipoles in the structure of a DNA. A second type is produced by coiling DNA bases around the histone in a nucleosome (see Fig. 3-left hand up). A third type is created by the formation of loops in a chromatin fiber (see Fig. 3-left and, down), and finally, a fourth type of inductor emerges along the supercoil within a chromosome (see Fig. 3-right hand top). Each of these inductor types produces one type of magnetic field and plays a main role in a resonant circuit.

Materials and methods for providing cells ex and in ovo

Chicken Eggs

All of the fertilized eggs used in this consideration were Dekalb Brown eggs, which were obtained from a village in Neyshabour of Iran.

Culture Vessels

We have two types of culture vessel. In one type, we use in ovo system (Shell culture system). In another type, we use ex ovo system (Shell-less culture system).

Our culture vessels for ex ovo method are the same used in [7]; however, type of incubating, temperature and rotation were different. Similar to [7], a 450-ml polystylene plastic cup was applied as the pod for the culture vessel. A 1–1.5-cm-diameter hole was made in the side of the cup approximately 2 cm from the bottom, and the hole was plugged with a cotton pledget as a filter. A 2-mm-diameter plastic tube was inserted through the space between the pledget and the hole to provide an oxygen supply. An aqueous solution (40 ml) of benzalkonium chloride was then added to the cup. A polymethylpentene film was formed into a concave shape, carefully avoiding wrinkles and installed as an artificial culture vessel in the pod. A polystylene plastic cover was placed on top of the culture vessel.

Embryo Culture, Incubating, temperature and rotation

For in ovo method (Shell culture method ), fertilized chicken eggs were incubated at \(38^{\circ }C\) and rotated with 120 clockwise twice a day. After 48 h, in most of eggs, chick embryos begin to grow.

For ex ovo mechanism (Shell-less culture method), fertilized chicken eggs were not incubated before transferring to the culture vessels. Their eggshell was wiped and cracked and the whole egg contents were transferred to the culture vessel without pre-incubating period. The culture vessels were maintained at \(38^{\circ }C\) and rotated with 120 clockwise twice a day. After 54 h, in most of vessels, chick embryo is emerged (See Fig. 4).

Fig. 4
figure 4

Formation of chick embryo in shell-less culture vessel (in ovo) less than 48 h after incubating at \(38^{\circ }C\)

Full size image
Fig. 5
figure 5

A new circuit for imaging. This circuit is constructed from a generator, an inductor, an scope, cells in ovo and cells ex ovo. Magnetic waves pass cells of ex ovo and in ovo and carry exchanged information between them. By considering changes in these waves after going out of ovo, we can obtain exact information of chick embryo inside it

Full size image

A circuit for detecting waves of DNAs in ovo

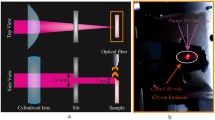
Now, we can use electronic properties of DNA for imaging of evolutions of entropy in ovo. To this aim, we consider communications between DNAs interior of ovo and exterior of ovo. We put two types of chick embryos near each other, which one is emerged interior of ovo and another is produced outside ovo. We radiate a magnetic field around 7 tesla to both of cells in and ex ovo. To do this radiation, we put both embryonic cells in and ex ovo interior an inductor. We connect an end of this inductor to one generator and send an input current to this inductor. We also connect another end of inductor to an scope like Radio-SkyPipe and measure output current. DNAs of cells in ovo and ex ovo interact with this magnetic field and change this wave and current in the inductor. If we take these currents by an cope like the Radio-SkyPipe, we can consider differences between emitted currents and receiving currents. These differences help us to determine evolutions of cells interior of in ovo like the gender or other properties of chick embryo (see Fig. 5).

For testing model, we should have a relation between current density and frequency of waves. Because entropies have been obtained in terms of frequency and circuit works only by current. Current density is corresponded to wave intensity. To include effect of wave intensity and its relation with currents, we should obtain the relation between rotating velocity or frequency and wave’s intensity. To this aim, we use below relation between total rotating velocity (\(\omega\)), rotating velocity of system (\(\omega _{0}\)) and frequency of wave (\(\omega _\mathrm{wave}\)).

$$\begin{aligned}&\omega = \omega _{0} + \omega _\mathrm{wave} \end{aligned}$$
(11)

On the other hand, the intensity of wave has below relations with rotating velocity or frequency of wave:

$$\begin{aligned}&I_\mathrm{wave} = N \frac{h}{2\pi } \omega _\mathrm{wave} \end{aligned}$$
(12)

where N is the quantum number of wave and h is the plank constant. Thus, we can rewrite Eq. (11) as follows:

$$\begin{aligned}&\omega = \left[ \omega _{0} + \frac{2 \pi I_\mathrm{wave}}{N h}\right] \end{aligned}$$
(13)

Substituting above relation in equations of entropy in “A mathematical model for calculating the relation between entropy and frequency of waves” section, we can obtain the relation with current. Now, we can test the model with observations and compare entropy which is obtained from theory with entropy which is seen in above circuit.

Results

In this research, we tried to only consider evolutions of entropy of DNAs in ovo. Also, by considering properties of this entropy, we can consider properties of chick embryo in ovo like its gender. We choose around 100 eggs for in ovo and 100 eggs for ex ovo experiments. We make a circuit of cells ex ovo, cells in ovo, scope and one voltmeter. We measure both intensity and current in this research. In “A mathematical model for calculating the relation between entropy and frequency of waves” section, we have shown that number of current have a direct relation with the number of waves. Also, number of waves have a direct relation with the entropy. Thus, number of current have a direct relation with the entropy.

Fig. 6
figure 6

Signals of chick embryo with the gender of male in ovo. These signals are taken from a circuit of cell ex ovo, in ovo and scope

Full size image
Fig. 7
figure 7

Signals of chick embryo with the gender of female in ovo. These signals are taken from a circuit of cell ex ovo, in ovo and scope

Full size image
Fig. 8
figure 8

Number of each value of current which is taken by Radio-SkyPipe for chick embryo with gender of male

Full size image
Fig. 9
figure 9

Number of each value of current which is taken by Radio-SkyPipe for chick embryo with gender of female

Full size image

In Fig. 6, we show signals of chick embryo with the gender of male. These signals were taken from a circuit of cell ex ovo, in ovo and scope. For cope, we have used of Radio-SkyPipe. In our experiments, mostly, signals of males were in moderate range of values. For example, intensity of some waves go up to 850. In Fig. 7, we show signals of chick embryo with the gender of female. These signals were in low range or high range of values. For example, intensity of some waves go up to 180. Comparing to signals of males, they were shorter or longer. To observe differences, we measure currents with a voltmeter. We show number of each value of current for chick embryo with gender of male in Fig. 8. In fact, this number has a direct relation with the entropy of DNAs in ovo. Currents begin from 0 to 100 mA. It is clear that number of currents (entropy) with moderate values (between 45 and 65) is more for males. Also, we show number of each value of current for chick embryo with gender of female in Fig. 9. Currents begin from 0 to 100 mA. Obviously, number of currents (entropy) with small (less than 40 mA) and large values (more than 65 mA) are more for females. Furthermore, there is a minimum for male around 52–55 and a minimum for female around 62–65. These numbers may change for each chick embryo.

Summary and discussion

Newly, some scientists have investigated thermodynamics of DNA and calculated its entropy [1, 2]. In another paper, they have argued that phonons which are causes of temperature and entropy have direct relations with electrons[3, 4]. Summing results of these papers, we have obtained the relation between entropy and number of radiated waves of DNA. We have tested the model by considering the relation between entropy and the exchanged waves between DNAs of chick embryo in ovo and ex ovo models. In this mechanism, we have detected waves of DNAs interior of ovo by constructing a circuit of embryonic cells in ovo and ex ovo. In this circuit, we have put cells in ovo and ex ovo inside an inductor and connect an end of this inductor to one generator and another end to an scope. Magnetic field which is produced in this inductor interacts with two types of cells interior and exterior of ovo and helps them to communicate with each other. We have considered differences between input and out put currents and obtained the evolutions of entropy of DNAs in ovo. Using changes in this entropy, we have determined the gender of embryos in ovo.