Introduction

Compared to the conventional radio frequency cavities, in plasma wakefield, the energy will be transferred from the driver bunch to the witness bunch, a way to achieve very high acceleration gradients [1–6]. The field in the plasma can be excited either by an ultra-intense, short laser pulse (or several pulses) [3, 7], or by a charged particle beam (an electron or proton beam) [8, 9]. Proton driven plasma wakefield acceleration has been recently proposed to attain electron energies of about TeV range [9–18]. Plasma wakefield generation in radially nonuniform plasma using charged particle beams [19] or in parabolic plasma channels using lasers [20–24] as drivers have been extensively studied. For the laser drivers, most of the studies are focused at parabolic channels with on-axis density minimum because of channeling properties of these channels, so that in a preformed plasma channel the laser pulse can propagate up to several Rayleigh lengths without substantial spreading. One of approaches in preventing of diffraction broadening of laser pulse and increasing of laser-plasma interaction distance is the guiding of the pulse in preformed plasma density channel [19, 25]. Therefore, generation of wakefields in a preformed channel becomes a subject of great interest.

In our recent work [26], we presented for the first time a thorough analytical model and solved the governing equations for the wakefield acceleration by proton beam in a parabolic density profile plasma, where the maximum plasma density is on the beam propagation axis along the z-direction. It has a potential application for compensating the undesirable wave front curvature in the case of a nonlinear wakefield. But in this work, a plasma channel with parabolic density distribution was considered in which the minimum density of plasma is on the beam propagation axis and the behavior of wakefields is investigated in comparison of [26]. For laser drivers, a similar problem was addressed in [22], where a perturbative method was employed to obtain the components of wakefields. The governing equations and the solution for the longitudinal wakefield E z is obtained analytically and the effects of the plasma channel radius, proton bunch parameters and wave number of plasma on the longitudinal electric field are investigated. In addition to analytical approach, the simulations of longitudinal and total radial wakefields in longitudinal and radial directions are presented using two-dimensional code LCODE [27].

The organization of the paper is as follows: "Introduction” is given in the next section followed by “Model description”. “Results and discussions” are given before the last section. Finally, “Conclusion” is presented.

Model description

The accelerating model which we have used for proton driven plasma wakefield acceleration is the plasma channel model. The plasma has a variable density as:

$$n = n_{0} \left( {1 + \frac{{r^{2} }}{{r_{\text{pl}}^{2} }}} \right),$$
(1)

where \(r_{\text{pl}}\) is the plasma channel radius, and r is the radial coordinate. The minimum density of plasma \((n_{0} )\) is on the beam propagation axis along the z-direction and \(\frac{{n_{0} r^{2} }}{{r_{\text{pl}}^{2} }}\) represent radial variation in channel density. The density profile of proton beam is described as follows:

$$n_{\text{b}} = n_{{{\text{b}}0}} e^{{\frac{{ - r^{2} }}{{2\sigma_{r}^{2} }}}} e^{{\frac{{ - \xi^{2} }}{{2\sigma_{z}^{2} }}}} ,$$
(2)

where \(\xi = z - ct\), with c speed of light, \(n_{{{\text{b}}0}} = N/\left( {(2\pi )^{3/2} \sigma_{r}^{2} \sigma_{z} } \right)\) N is the total number of protons in the bunch, and \(\sigma_{r}\) and \(\sigma_{z}\) are the beam radial and longitudinal characteristic lengths, respectively. Although the interaction of a dense (n b > n 0), short proton beam (the wavelength of the plasma wave is of the order of the bunch length, σ z  ~ λ p) with a plasma is inherently nonlinear, we can use the linear theory which predicts the plasma response to either a short electron or proton beam [9, 28]. In principle, the linear regime is valid when the plasma density perturbation is small compared to the plasma density n 0. Since the density perturbation is typically of the order of the beam peak density n b0, this criterion is equivalent to n b0/n 0 ≪ 1. The simulations have shown that the predictions of the linear theory are good up to n b0/n 0 ~ 1 [29].

We note that charge density in the system can be expressed as \(\rho = en_{\text{b}} + en_{\text{i}} - en_{\text{e}} = en_{\text{b}} + en_{0} - e(n_{0} + n_{1} ).\) Indexes b, i and e denote the beam, ions and the electrons, respectively.

Using Maxwell’s equations, the Newton’s second law of motion for the plasma electrons, the equation of continuity for the plasma, and writing quantities in terms of an equilibrium and an oscillating term \(E = E_{0} + E_{1}\), \(B = B_{0} + B_{1}\), \(v = v_{0} + v_{1}\) and assuming that \(E_{0}\), \(B_{0}\) and \(v_{0}\) are all equal to zero, we have:

$$\begin{aligned} & \nabla \cdot E_{1} = \frac{1}{{\varepsilon_{0} }}(en_{\text{b}} - en_{1} ) \hfill \\ & \frac{{\partial v_{1} }}{\partial t} = - \frac{e}{m}E_{1} \hfill \\ & \frac{{\partial n_{1} }}{\partial t} + n\nabla \cdot v_{1} = 0, \hfill \\ \end{aligned}$$
(3)

where quantities indexed with 1 denote the perturbed parameters.

Using Eq. 3, one can arrive at,

$$\frac{{\partial^{2} n_{1} }}{{\partial t^{2} }} + \omega_{{{\text{p}}0}}^{2} \left( {1 + \frac{{r^{2} }}{{r_{\text{pl}}^{2} }}} \right)n_{1} = \omega_{{{\text{p}}0}}^{2} n_{\text{b}} \left( {1 + \frac{{r^{2} }}{{r_{\text{pl}}^{2} }}} \right),$$
(4)

where \(\omega_{{{\text{p}}0}} = \left( {\frac{{n_{0} e^{2} }}{{m\varepsilon_{0} }}} \right)^{0.5}\) is the plasma frequency.

In Eq. 4, we use the change of variable \(\xi = z - ct,\) with c the speed of light. Time derivative ∂/∂t can be replaced by −c∂/∂ξ,

$$\frac{{\partial^{2} n_{1} }}{{\partial \xi^{2} }} + k_{{{\text{p}}0}}^{2} \left( {1 + \frac{{r^{2} }}{{r_{\text{pl}}^{2} }}} \right)n_{1} = k_{{{\text{p}}0}}^{2} n_{\text{b}} \left( {1 + \frac{{r^{2} }}{{r_{\text{pl}}^{2} }}} \right),$$
(5)

where k p0 is the plasma wave number. By substituting \(n_{\text{b}}\) in Eq. 5, we have:

$$\frac{{\partial^{2} n_{1} }}{{\partial \xi^{2} }} + k_{{{\text{p}}0}}^{2} \left( {1 + \frac{{r^{2} }}{{r_{\text{pl}}^{2} }}} \right)n_{1} = k_{{{\text{p}}0}}^{2} n_{{{\text{b}}0}} e^{{\frac{{ - r^{2} }}{{2\sigma_{r}^{2} }}}} e^{{\frac{{ - \xi^{2} }}{{2\sigma_{z}^{2} }}}} \left( {1 + \frac{{r^{2} }}{{r_{\text{pl}}^{2} }}} \right).$$
(6)

We can solve this differential equation using the Laplace transform of a system which is initially at rest,

$$n_{1} = \sqrt {2\pi } \sigma_{z} k_{{{\text{p}}0}} n_{{{\text{b}}0}} \left( {1 + \frac{{r^{2} }}{{r_{\text{pl}}^{2} }}} \right)^{0.5} e^{{\frac{{ - r^{2} }}{{2\sigma_{r}^{2} }}}} e^{{\frac{{ - k_{{{\text{p}}0}}^{2} \left( {1 + \frac{{r^{2} }}{{r_{\text{pl}}^{2} }}} \right)\sigma_{z}^{2} }}{2}}} \times \sin \left( {k_{{{\text{p}}0}} \left( {1 + \frac{{r^{2} }}{{r_{\text{pl}}^{2} }}} \right)^{0.5} \xi } \right).$$
(7)

For an infinite plasma \((r_{\text{pl}} \to \infty )\), this reduces to the expression derived for the perturbed density as in [30].

Also, we can solve the equations for the electric field as a function of the perturbed density. We note that the current density can be written as \(J = J_{\text{b}} + J_{\text{e}} = J_{\text{b}} + (J_{0} + J_{1} ) = J_{\text{b}} + J_{1}\) in which \(J_{\text{b}}\) and \(J_{\text{e}}\) are beam and electron current density, respectively. \(J_{0}\) and \(J_{1}\) denote the unperturbed and the perturbed electron current density, respectively.

Using the Maxwell equations, we have:

$$\begin{aligned} & \nabla^{2} E_{1} - \nabla (\nabla \cdot E_{1} ) = \frac{\partial }{\partial t}(\nabla \times B_{1} ) \\ & \nabla \times B_{1} = \mu_{0} J_{1} + \mu_{0} J_{\text{b}} \hat{z} + \frac{1}{{c^{2} }}\frac{{\partial E_{1} }}{\partial t} \\ & \nabla^{2} E_{1} - \frac{{\partial^{2} E_{1} }}{{\partial \xi^{2} }} = en_{0} \mu_{0} c\left( {1 + \frac{{r^{2} }}{{r_{\text{pl}}^{2} }}} \right)\frac{{\partial v_{1} }}{\partial \xi } - \mu_{0} ec^{2} \frac{{\partial n_{b} }}{\partial \xi }\hat{z} + \frac{e}{{\varepsilon_{0} }}\nabla n_{\text{b}} - \frac{e}{{\varepsilon_{0} }}\nabla n_{1} , \\ \end{aligned}$$
(8)

where \(\frac{{\partial v_{1} }}{\partial \xi } = \frac{e}{\text{mc}}E_{1} .\)

By substituting ∂n b/∂ξ, ∇n b, \(\nabla n_{1}\) in Eq. 8 and separating the components we will have the longitudinal and radial wakefields as:

$$ \left[ {\nabla_{\text{r}}^{2} - {\text{k}}_{{{\text{p}}0}}^{2} \left( {1 + \frac{{{\text{r}}^{2} }}{{{\text{r}}_{\text{pl}}^{2} }}} \right)} \right]{\text{E}}_{{1{\text{z}}}} \left( {{\text{r}},\xi } \right) = \frac{{ - {\text{e}}}}{{\varepsilon_{0} }}\sqrt {2\pi } \sigma_{\text{z}} {\text{n}}_{{{\text{b}}0}} {\text{k}}_{{{\text{p}}0}}^{2} \left( {1 + \frac{{{\text{r}}^{2} }}{{{\text{r}}_{\text{pl}}^{2} }}} \right) {\text{e}}^{{\frac{{ - {\text{r}}^{2} }}{{2\sigma_{\text{r}}^{2} }}}} {\text{e}}^{{\frac{{ - {\text{k}}_{{{\text{p}}0}}^{2} \left( {1 + \frac{{{\text{r}}^{2} }}{{{\text{r}}_{\text{pl}}^{2} }}} \right)\sigma_{\text{z}}^{2} }}{2}}} { \cos }\left( {{\text{k}}_{{{\text{p}}0}} \left( {1 + \frac{{{\text{r}}^{2} }}{{{\text{r}}_{\text{pl}}^{2} }}} \right)^{0.5} \zeta } \right) $$
(9)

and,

$$ \begin{aligned} \left[ {\nabla_{\text{r}}^{2} - {\text{k}}_{{{\text{p}}0}}^{2} \left( {1 + \frac{{{\text{r}}^{2} }}{{{\text{r}}_{\text{pl}}^{2} }}} \right)} \right]{\text{E}}_{{1{\text{r}}}} \left( {{\text{r}},\xi } \right) = \frac{{ - {\text{e}}}}{{\varepsilon_{0} }}\frac{\text{r}}{{\sigma_{\text{r}}^{2} }}{\text{n}}_{{{\text{b}}0}} {\text{e}}^{{\frac{{ - {\text{r}}^{2} }}{{2\sigma_{\text{r}}^{2} }}}} {\text{e}}^{{\frac{{ - \xi^{2} }}{{2\sigma_{\text{z}}^{2} }}}} - \frac{\text{e}}{{\varepsilon_{0} }}\sqrt {2\pi } \sigma_{\text{z}} {\text{n}}_{{{\text{b}}0}} {\text{k}}_{{{\text{p}}0}} {\text{e}}^{{\frac{{ - {\text{r}}^{2} }}{{2\sigma_{\text{r}}^{2} }}}} {\text{e}}^{{\frac{{ - {\text{k}}_{{{\text{p}}0}}^{2} \left( {1 + \frac{{{\text{r}}^{2} }}{{{\text{r}}_{\text{pl}}^{2} }}} \right)\sigma_{\text{z}}^{2} }}{2}}} \hfill \\ \times { \sin }\left( {{\text{k}}_{{{\text{p}}0}} \left( {1 + \frac{{{\text{r}}^{2} }}{{{\text{r}}_{\text{pl}}^{2} }}} \right)^{0.5} \xi } \right)\left[ {\frac{\text{r}}{{{\text{r}}_{\text{pl}}^{2} }}\left( {1 + \frac{{{\text{r}}^{2} }}{{{\text{r}}_{\text{pl}}^{2} }}} \right)^{ - 0.5} - \left( {\frac{\text{r}}{{\sigma_{\text{r}}^{2} }} + \frac{{{\text{k}}_{{{\text{p}}0}}^{2} \sigma_{\text{z}}^{2} {\text{r}}}}{{{\text{r}}_{\text{pl}}^{2} }}} \right)\left( {1 + \frac{{{\text{r}}^{2} }}{{{\text{r}}_{\text{pl}}^{2} }}} \right)^{0.5} + \frac{{{\text{k}}_{{{\text{p}}0}} \xi {\text{r}}}}{{{\text{r}}_{\text{pl}}^{2} }}{ \cot }\left( {{\text{k}}_{{{\text{p}}0}} \left( {1 + \frac{{{\text{r}}^{2} }}{{{\text{r}}_{\text{pl}}^{2} }}} \right)^{0.5} \xi } \right)} \right] \hfill \\ \end{aligned} $$
(10)

These equations could be compared with equations for a Gaussian beam in infinite plasma medium where (\(r_{\text{pl}} \to \infty\)). The equations reduce to their counterpart results expressed in [29, 31]. The solution for the homogeneous part of Eq. 9 with respect to the variable r for a finite parabolic plasma channel can be expressed by the Whittaker function:

$$ {\text{E}}_{{0{\text{z}}}} \left( {\text{r}} \right) = \frac{{{\text{C}}_{1} }}{\text{r}}{\text{whittakerM}}\left( {\frac{{{\text{ik}}_{{{\text{p}}0}}^{2} }}{{4\left( { - \frac{{{\text{k}}_{{{\text{p}}0}}^{2} }}{{{\text{r}}_{\text{pl}}^{2} }}} \right)^{0.5} }},0,{\text{ir}}^{2} \left( { - \frac{{{\text{k}}_{{{\text{p}}0}}^{2} }}{{{\text{r}}_{\text{pl}}^{2} }}} \right)^{0.5} } \right) + \frac{{{\text{C}}_{2} }}{\text{r}} {\text{whittakerW}}\left( {\frac{{{\text{ik}}_{{{\text{p}}0}}^{2} }}{{4\left( { - \frac{{{\text{k}}_{{{\text{p}}0}}^{2} }}{{{\text{r}}_{\text{pl}}^{2} }}} \right)^{0.5} }},0,{\text{ir}}^{2} \left( { - \frac{{{\text{k}}_{{{\text{p}}0}}^{2} }}{{{\text{r}}_{\text{pl}}^{2} }}} \right)^{0.5} } \right) $$
(11)

where \(C_{1}\) and \(C_{2}\) are constant and Whittaker M function is defined by

$${\text{WhittakerM}}\;(k, m, z) = e^{ - z/2} z^{m + 1/2} _{1} F_{1} \left( {\frac{1}{2} + m - k, 1 + 2m; z} \right),$$

where,

$$_{1} F_{1} (a;b;z) = 1 + \frac{a}{b}z + \frac{a(a + 1)}{b(b + 1)}\frac{{z^{2} }}{2!} + \ldots = \mathop \sum \limits_{k = 0}^{\infty } \frac{{(a)_{k} }}{{(b)_{k} }}\frac{{z^{k} }}{k!}.$$

Whittaker W function is expressed as:

$${\text{WhittakerW}}\;(k, m, z) = e^{ - z/2} z^{m + 1/2} U\left( {\frac{1}{2} + m - k, 1 + 2m; z} \right),$$

where,

$$U(a, b, z) = z^{ - a} _{2} F_{0} (a,1 + a - b;; - z),$$

and \(F_{0} (a, b;; z)\) is defined as a generalized hypergeometric function:

$$_{2} F_{0} (a, b;; z) = \mathop \sum \limits_{k = 0}^{\infty } (a)_{k} (b)_{k} \frac{{z^{k} }}{k!}.$$

The detailed properties of the Whittaker M and Whittaker W functions can be found in [32]. Note that for infinite plasma (\(r_{\text{pl}} \to \infty\)), the solution takes the form of the well-known modified Bessel functions as given in [33]. Solution of the inhomogeneous equation can be expressed as the sum of the homogenous solution introduced above plus solution coming from the right hand side as:

$$ \begin{aligned} {\text{E}}_{{{\text{Inhom}} - 1{\text{z}}}} \left( {{\text{r}},\xi } \right) = \frac{{{\text{C}}_{1} }}{\text{r}}{\text{whittakerM}}\left( {\frac{{{\text{ik}}_{{{\text{p}}0}}^{2} }}{{4\left( { - \frac{{{\text{k}}_{{{\text{p}}0}}^{2} }}{{{\text{r}}_{\text{pl}}^{2} }}} \right)^{0.5} }},0,{\text{ir}}^{2} \left( { - \frac{{{\text{k}}_{{{\text{p}}0}}^{2} }}{{{\text{r}}_{\text{pl}}^{2} }}} \right)^{0.5} } \right) + \frac{{{\text{C}}_{2} }}{\text{r}}{\text{whittakerW}}\left( {\frac{{{\text{ik}}_{{{\text{p}}0}}^{2} }}{{4\left( { - \frac{{{\text{k}}_{{{\text{p}}0}}^{2} }}{{{\text{r}}_{\text{pl}}^{2} }}} \right)^{0.5} }},0,{\text{ir}}^{2} \left( { - \frac{{{\text{k}}_{{{\text{p}}0}}^{2} }}{{{\text{r}}_{\text{pl}}^{2} }}} \right)^{0.5} } \right) \hfill \\ + \frac{1}{\text{r}}{\text{whittakerW}}\left( {\frac{{{\text{ik}}_{{{\text{p}}0}}^{2} }}{{4\left( { - \frac{{{\text{k}}_{{{\text{p}}0}}^{2} }}{{{\text{r}}_{\text{pl}}^{2} }}} \right)^{0.5} }},0,{\text{ir}}^{2} \left( { - \frac{{{\text{k}}_{{{\text{p}}0}}^{2} }}{{{\text{r}}_{\text{pl}}^{2} }}} \right)^{0.5} } \right) \times \mathop \smallint \nolimits \left[ {\frac{{ - 2{\text{r}}^{2} }}{\text{D}}{\text{e}}^{{ - \frac{{{\text{r}}_{\text{pl}}^{2} {\text{r}}^{2} + {\text{k}}_{{{\text{p}}0}}^{2} \sigma_{\text{r}}^{2} \sigma_{\text{z}}^{2} ({\text{r}}_{\text{pl}}^{2} + {\text{r}}^{2} )}}{{2{\text{r}}_{\text{pl}}^{2} \sigma_{\text{r}}^{2} }}}} {\text{Q cosk}}_{{{\text{p}}0}} \left( {\xi \left( {1 + \frac{{{\text{r}}^{2} }}{{{\text{r}}_{\text{pl}}^{2} }}} \right)^{0.5} } \right)({\text{r}}^{2} + {\text{r}}_{\text{pl}}^{2} )} \right] \times \hfill \\ \left[ {\left( { - \frac{{{\text{k}}_{{{\text{p}}0}}^{2} }}{{{\text{r}}_{\text{pl}}^{2} }}} \right)^{0.5} {\text{whittakerM}}\left( {\frac{{{\text{ik}}_{{{\text{p}}0}}^{2} }}{{4\left( { - \frac{{{\text{k}}_{{{\text{p}}0}}^{2} }}{{{\text{r}}_{\text{pl}}^{2} }}} \right)^{0.5} }},0,{\text{ir}}^{2} \left( { - \frac{{{\text{k}}_{{{\text{p}}0}}^{2} }}{{{\text{r}}_{\text{pl}}^{2} }}} \right)^{0.5} } \right)} \right]{\text{dr}} + \frac{1}{\text{r}}{\text{whittakerM}}\left( {\frac{{{\text{ik}}_{{{\text{p}}0}}^{2} }}{{4\left( { - \frac{{{\text{k}}_{{{\text{p}}0}}^{2} }}{{{\text{r}}_{\text{pl}}^{2} }}} \right)^{0.5} }},0,{\text{ir}}^{2} \left( { - \frac{{{\text{k}}_{{{\text{p}}0}}^{2} }}{{{\text{r}}_{\text{pl}}^{2} }}} \right)^{0.5} } \right) \times \mathop \smallint \nolimits \left[ {\frac{{2{\text{r}}^{2} }}{\text{D}}\left( { - \frac{{{\text{k}}_{{{\text{p}}0}}^{2} }}{{{\text{r}}_{\text{pl}}^{2} }}} \right)^{0.5} } \right] \hfill \\ \times \left[ {{\text{e}}^{{ - \frac{{{\text{r}}_{\text{pl}}^{2} {\text{r}}^{2} + {\text{k}}_{{{\text{p}}0}}^{2} \sigma_{\text{r}}^{2} \sigma_{\text{z}}^{2} ({\text{r}}_{\text{pl}}^{2} + {\text{r}}^{2} )}}{{2{\text{r}}_{\text{pl}}^{2} \sigma_{\text{r}}^{2} }}}} {\text{Q cosk}}_{{{\text{p}}0}} \left( {\xi \left( {1 + \frac{{{\text{r}}^{2} }}{{{\text{r}}_{\text{pl}}^{2} }}} \right)^{0.5} } \right)({\text{r}}^{2} + {\text{r}}_{\text{pl}}^{2} ){\text{whittakerW}}\left( {\frac{{{\text{ik}}_{{{\text{p}}0}}^{2} }}{{4\left( { - \frac{{{\text{k}}_{{{\text{p}}0}}^{2} }}{{{\text{r}}_{\text{pl}}^{2} }}} \right)^{0.5} }},0,{\text{ir}}^{2} \left( { - \frac{{{\text{k}}_{{{\text{p}}0}}^{2} }}{{{\text{r}}_{\text{pl}}^{2} }}} \right)^{0.5} } \right)} \right]{\text{dr}} \hfill \\ \end{aligned} $$
(12)

where \(Q = \frac{ - e}{{\varepsilon_{0} }}\sqrt {2\pi } \sigma_{z} n_{\text{b0}} k_{{{\text{p}}0}}^{2}\) and D is defined as:

$$\begin{aligned} D =\; & ir_{\text{pl}}^{2} k_{\text{p0}}^{2} {\text{whittakerW}}\left( {\frac{ik_{\text{p0}}^{2} }{4\left( { - \frac{k_{\text{p0}}^{2} }{r_{\text{pl}}^{2} }} \right)^{0.5} }},0,ir^{2} \left( { - \frac{{k_{\text{p0}}^{2} }}{{r_{\text{pl}}^{2} }}} \right)^{0.5} \right){\text{whittakerM}}\left( {\frac{{4\left( { - \frac{{k_{\text{p0}}^{2} }}{{r_{\text{pl}}^{2} }}} \right)^{0.5} + ik_{\text{p0}}^{2} }}{{4\left( { - \frac{{k_{\text{p0}}^{2} }}{{r_{\text{pl}}^{2} }}} \right)^{0.5} }},0,ir^{2} \left( { - \frac{{k_{\text{p0}}^{2} }}{{r_{\text{pl}}^{2} }}} \right)^{0.5} } \right) \\ & + 4r_{\text{pl}}^{2} \left( { - \frac{{k_{\text{p0}}^{2} }}{{r_{\text{pl}}^{2} }}} \right)^{0.5} {\text{whittakerM}}\left( {\frac{{ik_{\text{p0}}^{2} }}{{4\left( { - \frac{{k_{\text{p0}}^{2} }}{{r_{\text{pl}}^{2} }}} \right)^{0.5} }},0,ir^{2} \left( { - \frac{{k_{\text{p0}}^{2} }}{{r_{\text{pl}}^{2} }}} \right)^{0.5} } \right){\text{whittakerW}}\left( {\frac{{4\left( { - \frac{{k_{\text{p0}}^{2} }}{{r_{\text{pl}}^{2} }}} \right)^{0.5} + ik_{\text{p0}}^{2} }}{{4\left( { - \frac{{k_{\text{p0}}^{2} }}{{r_{\text{pl}}^{2} }}} \right)^{0.5} }},0,ir^{2} \left( { - \frac{{k_{\text{p0}}^{2} }}{{r_{\text{pl}}^{2} }}} \right)^{0.5} } \right) \\ & + 2r_{\text{pl}}^{2} \left( { - \frac{{k_{\text{p0}}^{2} }}{{r_{\text{pl}}^{2} }}} \right)^{0.5} {\text{whittakerW}}\left( {\frac{{ik_{\text{p0}}^{2} }}{{4\left( { - \frac{{k_{\text{p0}}^{2} }}{{r_{\text{pl}}^{2} }}} \right)^{0.5} }},0,ir^{2} \left( { - \frac{{k_{\text{p0}}^{2} }}{{r_{\text{pl}}^{2} }}} \right)^{0.5} } \right){\text{whittakerM}}\left( {\frac{{4\left( { - \frac{{k_{\text{p0}}^{2} }}{{r_{\text{pl}}^{2} }}} \right)^{0.5} + ik_{\text{p0}}^{2} }}{{4\left( { - \frac{{k_{\text{p0}}^{2} }}{{r_{\text{pl}}^{2} }}} \right)^{0.5} }},0,ir^{2} \left( { - \frac{{k_{\text{p0}}^{2} }}{{r_{\text{pl}}^{2} }}} \right)^{0.5} } \right). \\ \end{aligned}$$

The two integrals in Eq. 12 over the plasma radius were solved by numerical integrations and \(E_{{{\text{Inhom}} - 1z}}\) was obtained as a function of \(\xi\) and r.

It is to be noted here, however, that the limit of \(\frac{\text{WhittakerW}}{r}\) at r = 0 approaches infinity. So the C 2 coefficient must be zero. The boundary conditions are those of a perfectly conducting tube of the radius \(r_{\text{max }}\).Thus, boundary conditions for the longitudinal electric field can be considered as \(E_{z} (r = r_{\text{pl}} ) = 0\) [34].

Results and discussion

Analytical results

To illustrate the behavior of wakefield in plasma channel, the parameters of beam and plasma are taken to be, \(N = 1 \times 10^{11}\), \(r_{\text{pl}} = 0.7 \times 10^{ - 3} {\text{m}} = 3.25 \frac{c}{{\omega_{{{\text{p}}0}} }}\), \(\sigma_{\text{r}} = 0.43 \times 10^{ - 3} {\text{m}} = 2\frac{c}{{\omega_{{{\text{p}}0}} }}\), \(\sigma_{z} = 1 \times 10^{ - 4} {\text{m}} = 0.46\frac{c}{{\omega_{{{\text{p}}0}} }}\), \(n_{0} = 6 \times 10^{14} {\text{cm}}^{ - 3}\), \(\frac{c}{{\omega_{{{\text{p}}0}} }} = 0.215 \times 10^{ - 3} {\text{m}}\).

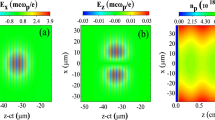
The variation of the longitudinal electric field in the longitudinal direction is presented in Fig. 1. The noticeable point in longitudinal wakefield (E z ) along the propagation axis is oscillatory behavior of wakefield and the acceleration gradient decreases with distance behind the bunch. Whereas in uniform plasma profile E z in longitudinal direction changes uniformly.

Fig. 1
figure 1

The variation of longitudinal electric field in longitudinal direction for r ≈ 0

Full size image

Figure 2 shows the variations of longitudinal electric field in longitudinal direction at different plasma channel radii. To illustrate the exact modifications of longitudinal wakefield with channel radius, the small changes of channel radius are considered. The longitudinal wakefield are so sensitive to it.

Fig. 2
figure 2

The variations of longitudinal electric field in longitudinal direction at different plasma channel radii

Full size image

As shown in this figure, by the modest increment in plasma channel radius, the acceleration gradient increases as the modest reduction in the size of proton bunch [35]. With further increases the plasma channel radius, the acceleration gradient tendency to constant level.

In Fig. 3, the variation of longitudinal electric field at different longitudinal size of the proton bunch is shown. The wakefield response is very sensitive to the bunch length. Also, longitudinal compression of the driver results in a shift of the optimum plasma density to higher value and to approximately proportional increase field amplitude [35]. Thus, the peak of accelerating field is controlled mainly by the driver length.

Fig. 3
figure 3

The variation of the longitudinal electric field at different longitudinal characteristics of bunch

Full size image

Also Fig. 4 shows the sensitivity of the longitudinal electric field to the radial characteristic of bunch. Similar to Fig. 3 by increasing the radial size of proton bunches, the generated wakefield becomes weaker. This is due to the aggregation of proton bunch [9, 28].

Fig. 4
figure 4

The variations of the longitudinal electric field at different radial characteristics of the bunch

Full size image

According to Figs. 3 and 4, it is expected that the dependence of wakefield on the number of beam particles scales nearly linearly.

Figure 5 shows the variations of longitudinal electric field at different wave numbers of the plasma. By increasing the wave number of the plasma, the oscillation of plasma electrons increases so the period of oscillations decreases. Also, by increasing the wave number of plasma, the longitudinal electric field will be amplified.

Fig. 5
figure 5

The variation of longitudinal electric field at different wave numbers of plasma

Full size image

To create the wakefield efficiently, the driver must be focused to the transverse size \(\sigma_{r} = k_{\text{p}}^{ - 1}\) and longitudinal size of bunch should be satisfy \(\sigma_{z} \approx \sqrt {2k_{\text{p}}^{ - 1} }\). So, according to Figs. 3, 4, and 5, maximum acceleration gradient can be obtained by decreasing the size of bunch that is proportional to increment of wave number of plasma.

In Figs. 2, 3, 4, and 5, the parameters variations happen in nearby distances behind the bunch and it decreases far from the beam driver as the acceleration gradient is weaken.

Simulation results

It is instructive to compare the behavior of wakefields in simulation approach with the analytical results. For this purpose, two-dimensional fully electromagnetic relativistic code, LCODE [27] is used. The cylindrical coordinates and the comoving simulation window are utilized. In our simulations, kinetic model and plasma macroparticles is used. The complete description of LCODE is described in detail in Ref. [27].

The code allows an arbitrary initial transverse profile of the plasma density over the simulation window. So according to analytical approach, we used the distribution of parabolic plasma density. For this purpose, the new plasma.bin file generated according to our plasma profile and it imported as a parabolic plasma file.

The simulation window, in units of c/ω p is 25 (in ξ) × 3 (in r). Both r and ξ steps are 0.01 c/ω p where according to the analytical parameters \(k_{\text{p}} = \frac{{\omega_{\text{p}} }}{c} = 4.65 \times 10^{3} {\text{m}}\). The beam is modeled by 4 × 107 macroparticles, and 15,000 plasma macroparticles are used. Also, initial distribution of beam particles in the transverse phase space is Gaussian and the beam current is calculated according to the parameters of the proton beam, \(I_{\text{b}} (\xi ) = \frac{{\rho_{\text{b}} (0)\sigma_{r}^{2} }}{2}\). The dependence of the beam current on the longitudinal coordinate is considered as cosine shape. The energy of proton bunch is about 1 TeV and the hydrogen plasma is used for the simulations in zero plasma temperature. The parameters of plasma and beam in simulation approach are similar to parameters in analytical approach as mentioned in previous section.

Figure 6 is presented the variations of on axis longitudinal electric field in the longitudinal and radial directions using LCODE. The behavior of longitudinal electric field in the longitudinal direction at r = 0 (Fig. 6a) is decreases with distance behind the bunch which has a good agreement with analytical results.

Fig. 6
figure 6

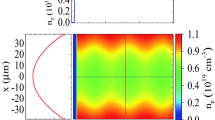
a The variations of on axis longitudinal electric field in longitudinal direction and b in radial direction for ξ = 0.43 mm for the case in Fig. 6a

Full size image

According to the Fig. 6b, the variations of longitudinal electric field in radial direction has little growth with radius and later scale down as r increases, and then go to zero. According to boundary condition of longitudinal wakefield in channel wall, \(E_{z} (r = r_{\text{pl}} ) = 0\), the decreasing treatment is expected.

The variations of total radial electric field E r  − B Ф in longitudinal and radial directions are presented in Fig. 7. In Fig. 7a, the total radial electric field generated by the proton bunch increases with the distance behind the bunch. It is one of the significant points presented in this model. In Fig. 7b we have shown the variations of the total radial wakefield E r  − B Ф in the radial direction. The radial electric field vanishes as r = 0 and it expected according to boundary condition in the origin, \(E_{r} (r = 0) = 0\). Also, linear focusing caused by the plasma channel near the origin is obviously seen. Of course, the slope would change for different values of ξ [28]. The treatment of total radial wakefield in radial direction is good agreement with the response of wakefield to positron driver in [28] (or in the other word for positive drivers). It is seen for the case shown in the figure that the overall behavior of radial forces is focusing.

Fig. 7
figure 7

a The variations of total radial electric field in longitudinal direction at r = 0.2 mm and b in radial direction at ξ = 0.64 mm

Full size image

According to Figs. 6, and 7 and as an outstanding point, we can say that the wakefield energy that was initially stored in longitudinal oscillations near the axis is gradually transferred to the radial oscillations in the near-wall of channel.

Conclusion

A plasma channel with a parabolic density profile was considered as the proposed model for investigation of proton driven plasma wakefield acceleration. Plasma channel has the minimum density on the beam propagation axis. The governing equation in longitudinal direction was presented and the solution was expressed as Whittaker functions. The effects of plasma channel radius, proton bunch parameters and plasma parameter in proton driven plasma wakefield acceleration were studied. Effect of plasma channel on the acceleration of particles and laser beam has been investigated in several reports [15, 20–24]. According to analytical results, the strong dependence on bunch length suggests that far higher accelerating fields could be generated in the PWFA scheme with modest reductions in the bunch size. Also, the modest increment in plasma channel radius is needed to obtain maximum accelerating gradient. In addition, the simulations of wakefield generation by proton bunch in plasma channel are presented using LCODE. The behaviors of longitudinal and total radial wakefields in longitudinal and radial directions are investigated.

The longitudinal electric field in the longitudinal direction decreases with distance behind the bunch while the total radial electric field increases with the distance behind the bunch. These results are the significant points which are achieved in this suggested model. The longitudinal electric field scale down as r increases (in the wall), then go to zero. The investigation of total radial electric field in radial direction showed that it vanishes as r = 0 and a linear focusing caused by the plasma channel near the origin is observed.

As another specific consequence, the wakefield energy that was initially stored in longitudinal oscillations near the axis is gradually transferred to the radial oscillations in the near-wall of channel.